94.04.25

Grzegorz Szalacha

ćwiczenie nr 51

Wyznaczanie

promienia krzywizny soczewki

metodą pierścieni Newtona

Laboratorium z fizyki

Powstawanie prążków interferencyjnych w klinie optycznym

Gdy wiązka światła pada na powierzchnię rozgraniczającą dwa różne ośrodki (różniące się współczynnikami załamania), wówczas część światła odbija się, pozostała zaś część przejdzie do drugiego ośrodka. Stosunki energetyczne między obu wiązkami fal określają wzory podane przez Fresnela. Jeżeli takie dwie powierzchnie tworzą klin, to wiązki odbite od tych powierzchni, jako pochodzące od tego samego źródła (spójne) wzajemnie ze sobą interferują. Przykładem takiego klina jest powietrzny klin interferencyjny utworzony między dwoma wewnętrznymi powierzchniami P1 i P2 płasko - równoległych płytek szklanych (rys. 1).

Rysunek 1.

We wszystkich punktach powierzchni P1 dochodzi do nałożenia się obu fal odbitych (na rysunku pokazano jeden taki punkt A). Amplituda zinterferowanej fali w A' zależy od różnicy faz obu promieni, a więc od różnicy ich dróg optycznych D.

Zakładając, iż kąt klina jest bardzo mały, a równoległa wiązka światła monochromatycznego pada na powierzchnię klina prostopadle, możemy obliczyć różnicę dróg optycznych między interferującymi promieniami. Oznaczając mianowicie grubość klina w danym miejscu przez h otrzymamy :

do geometrycznej bowiem różnicy dróg optycznych dodaje się dodatkowa różnica spowodowana skokiem fazy o p , przy odbiciu fali świetlnej na granicy powietrze szkło tj. od granicy ośrodka optycznie gęstszego. W tych miejscach klina, w których :

,k = 0,1,2,...

nastąpi na skutek interferencji wygaszanie światła. Tam natomiast, gdzie :

,k = 0,1,2,...

nastąpi interferencyjne wzmocnienie światła. W klinie, którego obie powierzchnie są płaskie zaobserwujemy więc kolejno na przemian, jasne i ciemne prążki. Każdy prążek jest miejscem geometrycznym równo odległych punktów obu powierzchni klina i stąd nazwa - prążki równej grubości.

Na rysunku 2 pokazane są miejsca, w których powstają ciemne prążki interferencyjne.

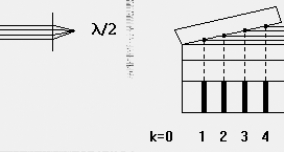
Rysunek 2.

Tak zwany zerowy prążek (k = 0) powstaje w miejscu styku obu powierzchni, czyli na krawędzi klina, pierwszy(k = 1) na wysokości
itd.

Jak nietrudno zauważyć, w takim klinie odległość wzajemna prążków jest jednakowa i jej wielkość zależy od wielkości kąta klina, co może być wykorzystane do pomiaru kąta tego klina. Deformacja prostoliniowego przebiegu prążków świadczy o odstępstwie od płaskości powierzchni i jeżeli jedna z nich, np. P1 jest wzorcową (idealnie płaską), to z obrazu obserwowanych prążków można wnioskować o wielkości odchyłki od płaskości powierzchni płytki P2, a także o miejscu jej lokalizacji. Przy tego rodzaju pomiarach należy tylko pamiętać, iż obraz interferencyjny przedstawia klin w postaci warstwowej (rysunek 2).

Prążki interferencyjne równej grubości najłatwiej

zaobserwować umieszczając na płaskiej płytce szklanej wypukło - sferyczną soczewkę. Tworzy się wówczas pomiędzy powierzchnią płytki a powierzchnią soczewki klin powietrzny o zmiennym kącie. Prążki interferencyjne powstają w takim klinie - tzw. prążki Newtona będą miały kształt kolisty. W miarę wzrostu odległości od środkowego (zerowego) prążka, utworzonego w miejscu styku obu powierzchni, kolejne prążki coraz bardziej się zagęszczają aż przestaną być w ogóle zauważalne.

Prążki Newtona można wykorzystać do wyznaczania promienia krzywizny R soczewki. Należy w tym celu zmierzyć promień rk dowolnego k-tego ciemnego prążka oraz znać długość fali użytego światła. Promień krzywizny R obliczamy ze znanego wzoru na promień R czaszy kulistej o promieniu podstawy rk i wysokości czaszy hk.

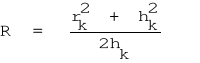
/4/

Dla dużych wartości R, ponieważ r >> h, wzór /4/ można wyrazić prościej:

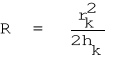
/4a/

Wysokość czaszy hk, odpowiadającą k-temu ciemnemu prążkowi można wyrazić:

/5/

Wstawiając to wyrażenie do /4a/ otrzymuje się:

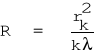
/6/

Układ pomiarowy, zasada jego działania

Jest to mikroskop, na którego stoliku umieszcza się płaską płytkę P i mierzoną soczewkę Lo. Są one oświetlone poprzez obiektyw mikroskopu równoległą wiązką światła monochromatycznego za pomocą soczewki i półprzepuszczalnego zwierciadła Z umieszczonego nad obiektywem mikroskopu. Okular ma podziałkę, za pomocą której ustawia się wybrany obraz prążka. Ustawienie i pomiar rk umożliwia przesuwny stolik mikroskopu, którego przesuw jest mierzony za pomocą czujnika zegarowego. Mała wskazówka tego czujnika wskazuje milimetry, a duża setne części milimetra. Zakres pomiaru przesuwu wynosi 10 mm.

Pomiar promienia krzywizny R soczewki

1. Powierzchnię soczewki i płytki płaskiej przemyć spirytusem i przetrzeć do sucha czystą flanelką.

2. Położyć badaną soczewkę płasko - wypukłą stroną wypukłą na płytkę płaską i umieścić na stoliku mikroskopu. Stolik powinien być ustawiony w położeniu środkowym tj. czujnik powinien wskazywać około 5 mm. Należy ustawić soczewkę tak, aby środkowy (zerowy) prążek wypadał na działkę oznaczoną cyfrą 5 podziałki okularu mikroskopu.

3. Dokonać pomiarów średnicy wybranych ciemnych prążków (przynajmniej pięciu) o możliwie dużych średnicach. Pomiary wykonywać następująco:

- podkręcając śrubą stolika liczyć liczbę ciemnych prążków przesuwających się w lewo na tle działki oznaczonej cyfrą 5

- ustawić działkę oznaczoną cyfrą 5 na środek wybranego k-tego prążka i odczytać wskazanie czujnika

- podobnie przesuwając stolik w przeciwnym kierunku od położenia zerowego ustawić działkę oznaczoną cyfrą 5 na ten sam prążek i odczytać wskazania czujnika
.

Różnica obu wskazań daje średnicę mierzonego prążka.

Promień rk będzie więc równy:

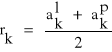
/7/

Podstawiając /7/ do /6/ obliczamy promień krzywizny R soczewki.

Opracowanie wyników pomiarów

Tabela pomiarowa.

Lp.	K					Rśr
-	-	mm	mm	mm	mm	mm
1	3	0.15	0.16
2	3	0.148	0.16	0.148	0.16	13.399
3	3	0.147	0.161
1	4	0.188	0.193
2	4	0.19	0.196	0.188	0.195	15.539
3	4	0.187	0.195
1	5	0.219	0.22
2	5	0.22	0.221	0.208	0.22	15.524
3	5	0.185	0.218

R=(14.830.1)*10-3 m

Przykład obliczeń.

- wyliczenie Rśr,

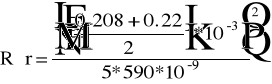
- wynik końcowy wyliczyliśmy jako średnią wyników dla poszczególnych prążków.

- błąd jest wyliczony jako odchylenie standartowe wyników dla poszczególnych prążków ( obliczeń dokonaliśmy przy pomocy kalkulatora wg poniższego wzoru )

..........................................

Wnioski:

Duże znaczenie w odczytywaniu wyników miała subiektywna ocena środka prążka - ze względu na jego szerokość. Przy pomiarze prążków nr. 4 i 5 ( dalej położonych od środka soczewki ) błąd ten miał nmiejszy wpływ na dokładność pomiaru.

---