LISTA 13

Zadanie 1
Weryfikację hipotezy o wadliwości p pewnej partii towaru przeprowadzono w oparciu o wynik pięcioelementowej
(n=5) próby prostej za pomocą następującego testu: jeżeli w próbie zaobserwujemy więcej niż jedną sztukę wadliwą
to hipotezę H0 odrzucamy w przeciwnym przypadku nie ma podstaw do jej odrzucenia. Znaleźć poziom istotności
testu oraz prawdopodobieństwo błędu drugiego rodzaju, jeśli :
H

0

: p = 0.2

H

1

: p = 0.3

53

,

0

7

,

0

3

,

0

1

5

7

,

0

3

,

0

0

5

)

/

1

(

)

/

0

(

)

/

1

(

26

,

0

9

,

0

1

,

0

1

1

8

,

0

2

,

0

0

5

1

)

/

1

(

)

/

0

(

1

)

/

1

(

H

y

przyjmujem

1

H

y

przyjmujem

1

k

wadliwe

sztuki

3

,

0

2

,

0

:

5

4

1

5

0

1

1

1

4

1

5

0

0

0

0

1

0

:

1

0



































































H

k

P

H

k

P

H

k

P

H

k

P

H

k

P

H

k

P

k

k

p

H

p

H

n





Zadanie 2
Do weryfikacji hipotezy H

0

X ~ N(4,3) przy alternatywie H

1

:N(2,2) zastosowano test x

n

<c(n), gdzie x

n

jest średnią z

próby (H

0

odrzucamy, gdy x

n

<c(n)). Wyznaczyć taką liczbę c(n) aby poziom istotności alfa=0.05. Jaka powinna być

liczba pomiarów n, aby moc testu była nie mniejsza niż 0.99.

23

66

,

4

)

2

)

(

(

33

,

2

2

2

)

(

99

,

0

)

/

)

(

(

)

/

(

1

99

,

0

1

4

3

64

,

1

)

(

64

,

1

3

4

)

(

05

,

0

3

4

)

(

3

4

(

)

/

)

(

(

05

,

0

H

y

przyjmujem

)

(

H

odrzucamy

)

(

)

2

,

2

(

~

/

)

3

,

4

(

~

/

)

2

,

2

(

~

:

)

3

,

4

(

~

:

1

1

0

1

0

1

0

1

0



























































n

n

n

c

n

n

c

H

n

c

x

P

H

k

x

P

n

n

c

n

c

n

n

n

c

n

x

x

P

H

n

c

x

P

x

n

c

x

n

c

n

N

H

x

n

N

H

x

N

X

H

N

X

H









Zadanie 3
Zmienna X ma rozkład Poissona o parametrze



.

Chcemy zweryfikować na poziomie istotności



0.05

hipotezę

H

0

:



=

0.02 przeciwko alternatywie H

1

: 1.0. Dysponujemy próbą 5-elementową. Jaka może być maksymalna moc tego

testu?

Zadanie 4
W celu weryfikacji hipotezy H

0

: X – N(1,2), H

1

: X ~ N(-2,3) na poziomie istotności 0.05 pobrano próbkę 10-

elementową. Jaka jest moc testu o obszarze krytycznym K=[-2.0; 0]. Jaki jest obszar krytyczny i moc testu
najmocniejszego?

H

0

: X ~ N(1,2)  |H

0

: N(1;

)

H

1

: X ~ N(-2,3)  |H

1

: N(-2;

)

= 0,05
n = 10
K = [-2,0 ; 0]

1) 1 – = ?

K: <-2;0>

1 – = P( K|H

1

) = P(-2 0|H

1

) = P(

u

)

P(0 u 2,11) = F(2,11) – F(0) = 0,98 – 0,5 = 0,48

2) < A
Lewostronny, na korzyść H

1

.

= 0,05
P( < A|H

0

) = 0,05

P(u <

) = -1,64 => A = -0,04

K(- ; -0,04>

1- = P( < A|H

1

) = P(u <

) = P(u < 2,07) = 0,98

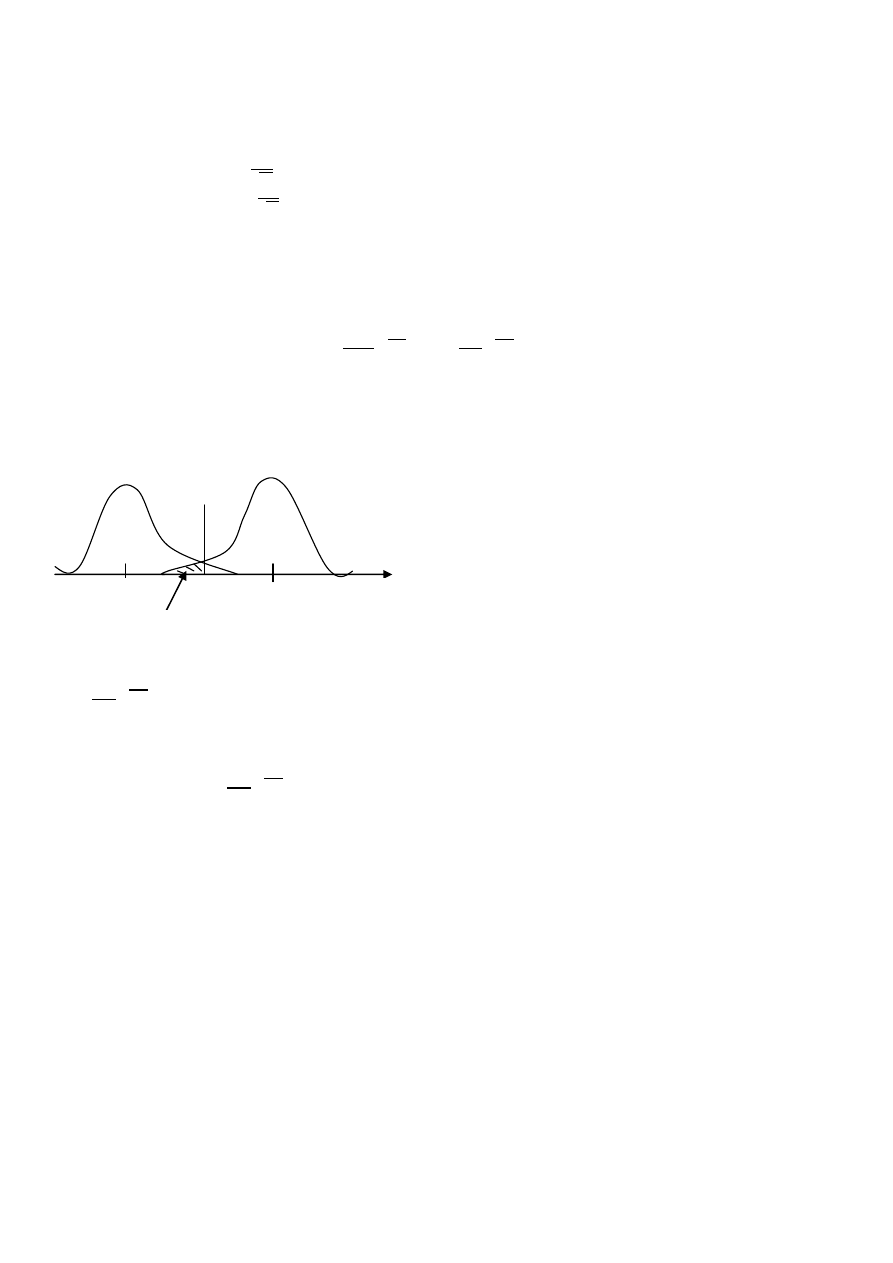
g

1

g

0

-2

1

A