MATEMATYKA - WYKŁAD Z 11.10.2010r., CZ 1. – ZBIORY
K@di Company®
All Rights Reserved
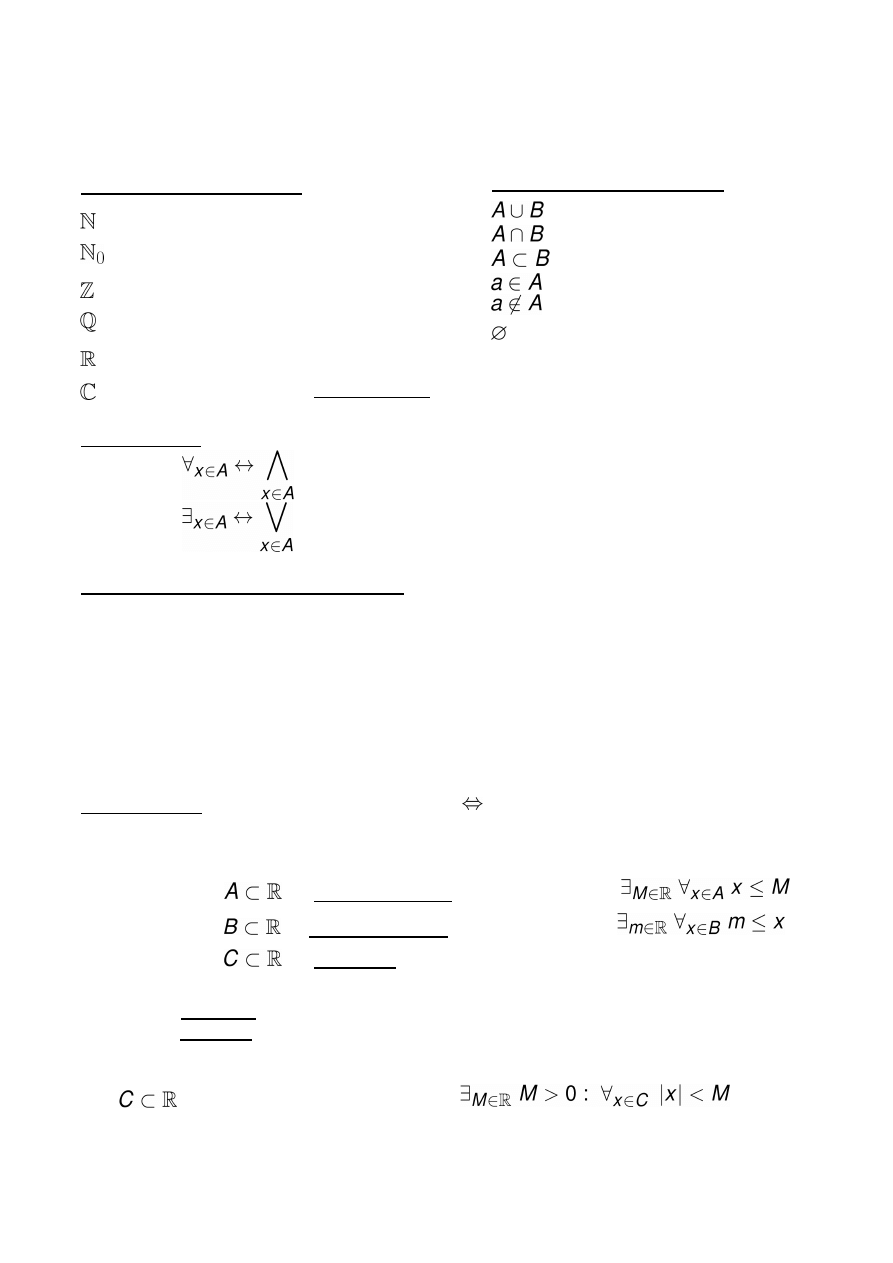
Podstawowe zbiory liczbowe:
= {1, 2, 3, …}
= {0, 1, 2, …}
- liczby całkowite
- liczby wymierne
- liczby rzeczywiste
- symbol zarezerwowany dla liczb zespolonych
Kwantyfikatory:
ogólny
czyta się jako: dla każdego x należącego do zbioru A (…)
szczegółowy
czyta się jako: istnieje takie x należące do zbioru A, że (…)
Podstawowe pojęcia logiki matematycznej:
definicja wypowiedź służąca do wyjaśnienia nowego pojęcia.
twierdzenie zdanie orzekające, najczęściej mające postać implikacji, posiadające dwa człony: założenie i
tezę. Rozumowanie wykazujące prawdziwość twierdzenia, nazywamy dowodem.
Twierdzenie, które powstało z danego przez zamianę założenia z tezą, nazywamy odwrotnym
względem danego. Nie każde twierdzenie odwrotne jest prawdziwe.
aksjomat pewnik; zdanie systemu dedukcyjnego, przyjęte bez dowodu jako wyjściowe twierdzenie tego
systemu. Z aksjomatów wyprowadza się dalsze twierdzenia, stosując określone w systemie
reguły.
(nie są to dosłowne definicje tych pojęć podane na wykładzie)
Równoważność:
symbol:
czyta się jako: (…) wtedy i tylko wtedy, gdy (…) skrót: wkw (warunek konieczny i wystarczający)
Definicje:
•
Mówimy, że zbiór
jest ograniczony od góry wtedy i tylko wtedy, gdy
.
•
Mówimy, że zbiór
jest ograniczony od dołu wtedy i tylko wtedy, gdy
.
•
Mówimy, że zbiór
jest ograniczony wtedy i tylko wtedy, gdy jest ograniczony od góry i od dołu.
Dla powyższych definicji:
•
M jest majorantą zbioru A,
•
m jest minorantą zbioru B.
Twierdzenie:
Zbiór
jest ograniczony wtedy i tylko wtedy, gdy
.
Symbole związane ze zbiorami:
suma zbiorów A i B
iloczyn zbiorów A i B (część wspólna)
zbiór A zawarty w zbiorze B
element a należy do zbioru A
element a nie należy do zbioru A
zbiór pusty

Funkcja signum:
zwraca znak argumentu, jest zdefiniowana
następująco:
Wartość bezwzględna (moduł):
funkcja zdefiniowana następująco:
Po rozpisaniu:
Z powyższych definicji wynika zatem wzór:
.
Interpretacja geometryczna wartości bezwzględnej:
wartość bezwzględna liczby jest równa jej odległości od
zera na osi liczbowej.
Twierdzenie:
Niech
i
. Wtedy:
1)
,
2)
.
Własności wartości bezwzględnej:
Definicje:
Kresem górnym (łac. supremum) zbioru
nazywamy najmniejszą majorantę zbioru A.
Kresem dolnym (łac. infimum) zbioru
nazywamy największą minorantę zbioru B.
Symbole:
kres górny zbioru A:
kres dolny zbioru B:
Przykłady:
•
zbiór liczb naturalnych nie posiada majoranty, a
zatem nie posiada kresu górnego i nie jest
ograniczony od góry;
•
zbiór
posiada majoranty: 2, 3, 1, 5, itd.,
ale kresem górnym jest 1, co zapisujemy:
,
•
zbiór
posiada minoranty: -5, -1, 0, itp.,
ale kresem dolnym jest 0, co zapisujemy:
.
Aksjomat ciągłości zbioru liczb rzeczywistych:
Każdy zbiór ograniczony od góry posiada kres górny.
Jeżeli powyższe zdanie przyjmiemy za aksjomat, to twierdzeniem na nim opartym będzie zdanie:
Każdy zbiór ograniczony od dołu posiada kres dolny.
Otoczenie punktu:
otoczenie punktu
:
często oznacza się, jako:
otoczenie
:
zbiór
otoczenie
:
zbiór
Sąsiedztwo punktu:
, gdzie V oznacza otoczenie punktu x
0
.
Wyszukiwarka
Podobne podstrony:
2010 10 11(2),12,22 zbiory, ciągi
2010 10 11(2),12,22 zbiory, ciągi
Azotany Choroba niedokrwienna serca 2010 10 11
1 2010 10 11
Ana cwicz 2010 10 11
2010 10 11 Matką byłam srednią
10.11.2010, prawo administracyjne ćwiczenia(2)
2010 10 22(2), 29, 11 05 szeregi
24 05 2010 B&K, Bazy Danych 10 11 12
loveparade 2010 anlage 11 interner entwurf sicherheitskonzept 20 05 10
WstĂŞp do Filozofii wykÂł.V - 10.11.2010, Wstęp do filozofii
24.05.2010 B&K Bazy Danych 10 11 12
Szczęśliwa Dziesiątka Disco Polo (10 11 2010)
06 - 10. 11. 2010, Filozofia, Notatki FO, III Semestr, Filozofia kultury
10 11 2010 Równowagi kwasowo zasadowe
Wykład 5 10.11.2009, Recepty, Wyklady TLP, Wykłady 2009-2010
5 Wykład (10 11 2010)
więcej podobnych podstron