68 Â

WIAT

N

AUKI

Grudzieƒ 2000

Jak podejmowaç trafne

DECYZJE

John A. Swets, Robyn M. Dawes i John Monahan

Matematycznie wspomagane rozwiàzywanie problemów
medycznych czy przemys∏owych mo˝e u∏atwiç
podejmowanie decyzji – niekiedy ratujàcych
nasze zdrowie, a nawet ˝ycie

W

patrujàc si´ w zdj´cie rentge-
nowskie piersi, lekarz zadr´-
cza si´ pytaniem, czy ledwo

widoczna plamka to tkanka nowotwo-
rowa. Trybuna∏ apelacyjny rozwa˝a u∏a-
skawienie potencjalnie groênego prze-
st´pcy. Technik na lotnisku zamartwia
si´ zestawem ultradêwi´kowych odczy-
tów: czy˝by wskazywa∏y na katastro-
falne p´kni´cie skrzyd∏a samolotu?

Wszyscy ci ludzie zmagajà si´ z de-

cyzjami diagnostycznymi. Pomimo nie-
pe∏nych lub niejednoznacznych danych
muszà rozstrzygnàç, czy dany stan ist-
nieje lub zaistnieje, czy te˝ nie. Tego
rodzaju problemy sà bardzo cz´ste w
wielu dziedzinach, jak opieka spo∏ecz-
na, bezpieczeƒstwo publiczne, biznes,
ochrona Êrodowiska, sprawiedliwoÊç,

oÊwiata, produkcja, przetwarzanie in-
formacji, wojskowoÊç czy sprawowanie
w∏adzy. A stawki mogà byç nader wy-
sokie. Niejednokrotnie b∏´dna decyzja
oznacza wyrok Êmierci.

Zapewne zabrzmi to dziwnie, ale pro-

ces podejmowania decyzji diagnostycz-
nych w rozmaitych dziedzinach jest
w swej istocie jednakowy. Tote˝ meto-
dy, które wspomagajà proces podejmo-
wania trafniejszych decyzji w jednej ga-
∏´zi przemys∏u, mo˝na zazwyczaj
stosowaç w innych. Istniejà co najmniej
dwie takie metody. Niestety, sà one nie-
znane lub ignorowane w wielu Êrodo-
wiskach. Jedna z tych metod zapewnia
lepszà dok∏adnoÊç, zwi´kszajàc szanse
podj´cia w∏aÊciwej decyzji. Druga przy-
czynia si´ do poprawy „u˝ytecznoÊci”

podejÊcia decyzyjnego, gwarantujàc, ˝e
liczba diagnoz prawid∏owych nie po-
wstaje kosztem nieracjonalnej liczby
wskazaƒ b∏´dnych (fa∏szywych alar-
mów). Sà to metody statystyczne, ale ci,
którzy cierpià na fobi´ matematycznà,
nie muszà si´ obawiaç; podstawy na-
szego wywodu sà ∏atwe do ogarni´cia.

Nikt nie twierdzi, ˝e diagnosta musi

byç zawsze niewolnikiem wzorów mate-
matycznych. W niektórych dziedzinach
(jak medycyna kliniczna czy prognozo-
wanie pogody) obiektywne narz´dzia
mogà dzia∏aç najskuteczniej jako uzupe∏-
niajàce opinie, które wzbogacajà zespó∏
przes∏anek, niekiedy je korygujà, ale nie
stanowià ostatecznego werdyktu. Jed-
nak w innych dziedzinach analizy staty-
styczne okazywa∏y si´ cz´sto trafniejsze

DECYZJE DIAGNOSTYCZNE wymagajàce wyboru
spoÊród dwóch mo˝liwoÊci: tak lub nie, podejmujà
nie tylko lekarze. Tymczasem sprawdzone ju˝ tech-
niki, które zwi´kszajà szans´ udzielenia poprawnej
odpowiedzi, bywajà lekkomyÊlnie ignorowane.

SLIM FILMS

ni˝ sàdy su-

biektywne, na-

wet te wyra˝ane

przez specjalistów

i to bardzo do-

Êwiadczonych.

W tym artykule skupi-

my si´ na prostym proble-

mie – decyzjach diagnostycz-

nych, które wymagajà wyboru

z dwóch mo˝liwoÊci: tak albo nie

(Jest nowotwór czy go nie ma? Skrzy-

d∏o samolotu jest uszkodzone, czy te˝

nie?). OczywiÊcie, Êwiat jest pe∏en pro-
blemów zawierajàcych wi´cej opcji, ale
przewa˝ajà alternatywy tak–nie.

Tajniki warsztatu

Gdyby badania diagnostyczne dostar-

cza∏y zawsze jasnych, niedwuznacznych
odpowiedzi, nie by∏yby nikomu po-
trzebne statystyczne metody podejmo-
wania decyzji. W istocie jednak surowe
wyniki badaƒ diagnostycznych wyma-
gajà interpretacji. Prosty przyk∏ad: ci-
Ênienie Êródoczne mierzy si´, by wy-
kryç, czy badana osoba ma jaskr´, która
upoÊledza wzrok i grozi Êlepotà w wy-
niku uszkodzenia nerwu wzrokowego
i innych cz´Êci oka. Bardzo niski poziom
ciÊnienia oznacza, ˝e oko pod tym
wzgl´dem jest zdrowe, podczas gdy
wysoki Êwiadczy o jaskrze. Jednak wy-
niki poÊrednie sà niejednoznaczne
i trudno na ich podstawie stwierdziç,
który pacjent ma jaskr´, a który nie.

Dane statystyczne mogà nieco rozja-

Êniç t´ diagnostycznà i decyzyjnà mg∏´.
Dla uproszczenia przyjmijmy, ˝e ciÊnie-
nie Êródoczne jest jedynym pomiarem
diagnostycznym pozwalajàcym rozpo-
znaç jaskr´. Za∏ó˝my równie˝, ˝e warto-
Êci ciÊnieƒ poni˝ej 10 na standardowej
skali pomiaru zawsze wykluczajà jaskr´,
a powy˝ej 40 zawsze Êwiadczà o choro-
bie, podczas gdy odczyty pomi´dzy 10
i 40 dotyczà zarówno uszkodzonych,
jak i zdrowych oczu.

Aby skutecznie poradziç sobie z nie-

jednoznacznoÊcià, analitycy muszà
przede wszystkim wybraç licznà popu-
lacj´ pacjentów, których wyniki badaƒ
ciÊnienia Êródocznego sà znane. Nast´p-
nie powinni okreÊliç, którzy z badanych
skar˝yli si´ na objawy charakterystycz-
ne dla jaskry, a którzy ich nie zg∏aszali.
Kolejny krok to obliczenie prawdopo-
dobieƒstwa powstania jaskry u poszcze-
gólnych pacjentów majàcych okreÊlony
wynik badania. Wreszcie, bioràc pod
uwag´ te prawdopodobieƒstwa (oraz
inne uwarunkowania, które omówimy
póêniej), muszà ustaliç rozsàdny punkt
graniczny, czyli wartoÊç progu rozstrzy-
gajàcego diagnostycznie: wyniki rów-

ne tej wartoÊci lub wy˝sze od niej pro-
wadzà do decyzji na tak (pacjent ma ja-
skr´), zaÊ poni˝ej tego progu sà podsta-
wà do odpowiedzi negatywnej (pacjent
jaskry nie ma).

Rzecz jasna, pojedyncze badania dia-

gnostyczne mogà nie mieç tak znaczà-
cego ∏adunku informacyjnego, jak ich
kombinacja. Aby zwi´kszyç dok∏adnoÊç
rozpoznania, analitycy potrafià zesta-
wiaç wyniki ró˝nych testów, z których
ka˝dy dostarcza specyficznej infor-
macji, co pozwala im wyró˝niç pomia-
ry o najwi´kszej trafnoÊci prognoz.
Algorytmy matematyczne, dzi´ki któ-
rym mo˝na wskazaç najlepsze testy do
w∏àczenia w diagnostyczny proces de-
cyzyjny i obliczyç prawdopodobieƒ-
stwo obecnoÊci patologii na podsta-
wie kojarzonych wyników badaƒ, na-
zywane sà probabilistycznymi regu∏ami
decyzyjnymi.

Ca∏kowicie obiektywne dane, jak od-

czyty pomiarów ciÊnienia, nie sà jedy-
nymi cechami, których uwzgl´dnienie
zwi´ksza dok∏adnoÊç probabilistycz-
nych regu∏ decyzyjnych; pomiarom pod-
legajà równie˝ subiektywne wra˝enia,
tote˝ i one powinny byç brane pod uwa-
g´ w procesie decyzyjnym. Mo˝na je bo-
wiem obiektywizowaç, na przyk∏ad na
podstawie listy postrzegalnych i mie-
rzalnych kryteriów (takich jak wielkoÊç
i nieregularnoÊç potencjalnie z∏oÊliwych
znamion) uszeregowanych wed∏ug ska-
li, na przyk∏ad od jednego do pi´ciu.

Je˝eli do dyspozycji mamy wi´cej ni˝

jednà probabilistycznà regu∏´ decyzyjnà,
to podejmujàc decyzj´, musimy okre-
Êliç, która z nich jest najprecyzyjniejsza.
I da si´ to zrobiç, pozostajàc obiektyw-
nym. Dok∏adnoÊç kilku probabilistycz-
nych regu∏ decyzyjnych traktujàc je ∏àcz-
nie, mo˝na oszacowaç za pomocà cha-
rakterystyk odbiornika (receiver opera-
ting characteristic curves), tzw. krzy-
wych ROC. Krzywe te zastosowano po
raz pierwszy w celu okreÊlenia, jak do-
brze sprz´t radarowy w czasie II wojny
Êwiatowej odró˝nia∏ zak∏ócenia przy-
padkowe od sygna∏ów prawid∏owo
wskazujàcych samoloty nieprzyjaciela.

Programy, które wyznaczajà takie

krzywe, analizujà, co si´ zdarzy, jeÊli
wynik testu diagnostycznego lub zesta-
wu testów zostanie wykorzystany jako
próg decyzyjny do podj´cia decyzji ty-
pu tak–nie. Jaki odsetek pacjentów, któ-
rzy rzeczywiÊcie sà w stanie odpowia-
dajàcym postawionemu pytaniu, b´dzie
rozpoznany trafnie (w wyniku prawi-
d∏owego wskazania lub na chybi∏ tra-
fi∏)? Ile osób nie wykazujàcych stanu
chorobowego zostanie omy∏kowo uzna-
ne za chore (wskazanie b∏´dne lub fa∏-
szywy alarm)?

A zatem dla ka˝dego progu wartoÊci

programy pozwalajà sporzàdziç wykres
procentowy trafnych wskazaƒ choroby
w stosunku do fa∏szywych. W jego re-
zultacie powstaje wygi´ta krzywa,
wznoszàca si´ od lewego dolnego rogu,
gdzie oba odsetki sà równe zeru, do pra-
wego górnego, gdzie oba wynoszà l00.
Im gwa∏towniej krzywa si´ zagina, tym
wi´ksza jest dok∏adnoÊç tej zale˝noÊci,
poniewa˝ liczba trafieƒ jest wi´ksza od
liczby fa∏szywych alarmów.

OczywiÊcie, trafne i b∏´dne wskaza-

nia choroby nie sà jedynymi mo˝liwymi
rezultatami. Diagnoza typu tak–nie
oparta na wartoÊci progowej b´dzie
równie˝ – prawid∏owo lub b∏´dnie –
wskazywaç przypadki zdrowia (osoby
s∏usznie lub nies∏usznie uznane za zdro-
we). Jednak te rezultaty sà dok∏adnie
dope∏nieniami poprzednich, tote˝ mo˝-
na je zaniedbaç podczas konstruowania
wspomnianych krzywych. 80% prawi-
d∏owych wskazaƒ oznacza tym samym,
˝e odsetek chybieƒ wynosi 20%.

Zak∏adajàc, ˝e tylko nieliczne diagno-

styczne metody sà doskona∏e w rozró˝-
nianiu stanu zdrowia i choroby, insty-
tucje powinny zadecydowaç, jak bardzo
istotne jest wykrycie wszystkich lub nie-
mal wszystkich prawid∏owych wskazaƒ
na chorob´ – poniewa˝ zwi´kszenie licz-
by trafnych wskazaƒ na stan chorobo-
wy zwiàzane jest równie˝ ze zwi´ksze-
niem liczby fa∏szywych alarmów. Istnieje
zatem potrzeba ustalenia sensownego
progu w konkretnych sytuacjach.

Wracajàc do przyk∏adu z jaskrà, za-

uwa˝my, ˝e klinicyÊci, którzy zadowala-
jà si´ pomiarami ciÊnienia Êródocznego,
mogà praktycznie wykryç ka˝dy przy-
padek tej choroby, jeÊli wybiorà „naj∏a-
godniejszy” próg diagnostyczny, po-
wiedzmy 10. W koƒcu próba testowa
wykazuje, ˝e ka˝dy chory na jaskr´ ma
poziom ciÊnienia wewnàtrzga∏kowego
wy˝szy od tego w∏aÊnie. Takie podejÊcie
sprawi jednak, ˝e wielu zdrowych ludzi
zostanie uznanych za chorych, niepo-
trzebnie b´dà leczeni, niepotrzebnie te˝
b´dà si´ zamartwiaç. Aby znaczàco
zmniejszyç tego rodzaju b∏´dy, klinicy-
Êci powinni ustaliç bardziej adekwatnie
diagnostyczne progi – na przyk∏ad ciÊnie-
nia Êródocznego na poziomie 35, jako ˝e
bardzo niewielu zdrowych ludzi ma tak
wysokie ciÊnienie. Z kolei tak wysoki
próg mo˝e sprawiç, ˝e nie rozpozna si´
wi´cej ni˝ po∏owy przypadków jaskry
i tym samym pozbawi si´ tych chorych
szans, które stwarza leczenie.

Ustalajàc w∏aÊciwy próg, podejmujàcy

decyzj´ biorà pod uwag´ takie elementy,
jak skutki chybieƒ oraz fa∏szywych alar-
mów, a tak˝e stopieƒ rozpowszechnie-
nia danego schorzenia w badanej popu-

Â

WIAT

N

AUKI

Grudzieƒ 2000 69

lacji. Na szcz´Êcie opracowano ju˝ zasa-
dy oparte na doÊwiadczeniu oraz meto-
dy matematyczne pomocne w wyzna-
czaniu progu diagnostycznego. Na
przyk∏ad wyraêne wyst´powanie w po-
pulacji konkretnego schorzenia lub
znaczne korzyÊci wynikajàce z popraw-
nych decyzji diagnostycznych przema-
wiajà za stosowaniem niskich progów.
I na odwrót: rzadkie wyst´powanie ja-
kiejÊ patologii lub wysoka cena za fa∏-
szywe alarmy sk∏aniajà do ustanawiania
wysokich progów diagnostycznych.

Czas na regu∏y decyzyjne

Choç regu∏y probabilistyczne i krzy-

we charakterystyczne sà cz´sto ignoro-
wane przez podejmujàcych decyzje dia-
gnostyczne, ˝ycie daje liczne przyk∏ady
ich wartoÊci. Jedna z najdramatyczniej-
szych ilustracji dotyczy psychiatrii.

Coraz cz´Êciej psychiatrzy i psycholo-

dzy kliniczni proszeni sà o okreÊlenie,
czy uwi´zione lub niezrównowa˝one
osoby mogà przejawiaç gwa∏towne re-

akcje. Ludzi, którzy wydajà si´ zagra-
˝aç innym, powinno si´ umieç zidenty-
fikowaç i leczyç dla ich dobra oraz
w imi´ bezpieczeƒstwa innych. Z kolei
ingerowanie w ˝ycie tych, którzy nie
stanowià zagro˝enia dla innych, jest
oczywiÊcie nie do przyj´cia.

˚enujàce w tym wzgl´dzie by∏o

stwierdzenie zaskakujàcego braku pre-
cyzji w przeprowadzonym w 1993 roku
nader wyrafinowanym badaniu opinii
klinicystów nie korzystajàcych ze wspo-
mnianych regu∏. Okaza∏o si´, ˝e specja-
liÊci, którzy diagnozowali kolejnych pa-
cjentów zg∏aszajàcych si´ do izby przyj´ç
miejskiego szpitala psychiatrycznego,
nie potrafili trafniej, ni˝ by to wynika∏o
z szacunków probabilistycznych, prze-
widzieç, czy pacjentki dopuszczà si´ w
swojej spo∏ecznoÊci w ciàgu najbli˝sze-
go pó∏ roku jakiegoÊ czynu noszàcego
cechy gwa∏townej przemocy. Skutecz-
noÊç tych przewidywaƒ w przypadku
m´˝czyzn by∏a tylko nieznacznie lepsza.

Ujawnienie tych wyników spowodo-

wa∏o, ˝e sformu∏owano wiele nowych

probabilistycznych regu∏ decyzyjnych
pomocnych w ocenie prawdopodobieƒ-
stwa uciekania si´ do przemocy. Jednà
z najpopularniejszych jest „Przewodnik
oceny ryzyka przemocy” (VRAG – Vio-
lence Risk Appraisal Guide), zawiera-
jàcy zestaw 12 mierzalnych zmiennych,
w tym punkty z listy kontrolnej cech
wskazujàcych na psychopati´ oraz oce-
niajàcych stopieƒ nieprzystosowania
w szkole podstawowej.

Na podstawie testu skutecznoÊci regu∏

w przewidywaniu, czy przest´pcy wy-
pisywani ze szpitala o maksymalnym
stopniu zabezpieczenia dopuszczà si´
przemocy w ciàgu kilku najbli˝szych lat,
VRAG podzieli∏ pacjentów na dwie ka-
tegorie wed∏ug stopnia tego ryzyka: „wy-
soki” i „niski”. Okaza∏o si´, ˝e czynów
gwa∏townych dopuÊci∏o si´ 55% osób
z grupy wysokiego ryzyka i jedynie 19%
z grupy ni˝szego ryzyka – uzyskano za-
tem stopieƒ Êcis∏oÊci znacznie powy˝ej
poziomu losowego. Kolejne probabili-
styczne regu∏y decyzyjne okaza∏y si´ jesz-
cze skuteczniejsze w przewidywaniu czy-

70 Â

WIAT

N

AUKI

Grudzieƒ 2000

S

kàd decydenci majà pewnoÊç, ˝e testy diagnostyczne sà
najdok∏adniejsze z mo˝liwych i za ich pomocà najlepiej

oceniç, kto spe∏nia okreÊlone warunki, a kto nie? Najbardziej
znanym sposobem rozwiàzania tego problemu jest wykreÊlenie
tzw. krzywych ROC. PodejÊcie to najlepiej zilustrowaç na przy-
k∏adzie. Poni˝ej spróbujemy opisaç kroki, jakie musi podjàç le-
karz analityk, aby oceniç poprawnoÊç diagnozy jaskry na pod-
stawie pomiaru ciÊnienia Êródocznego pacjenta.

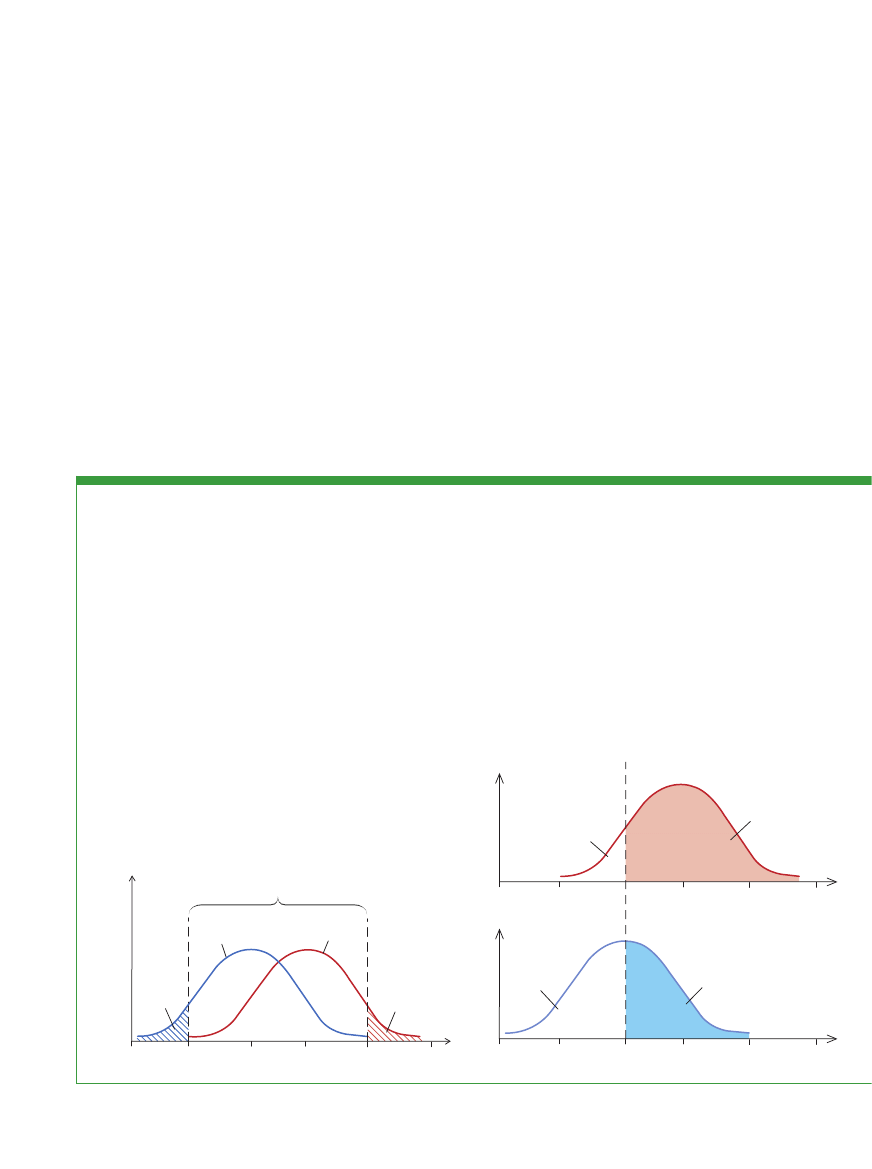
KROK 1

Znajdê licznà prób´ osób, dla których znaç b´dziesz

dwa parametry: ciÊnienie Êródoczne oraz obecnoÊç jaskry. Nast´p-
nie podziel t´ grup´ na dwie: osób zdrowych oraz cierpiàcych na ja-
skr´, i sporzàdê wykres liczby osób w zale˝noÊci od poziomu ciÊnie-
nia p∏ynu w ga∏ce ocznej. Wykres dla hipotetycznej grupy pokazuje,
˝e jeÊli odczyty ciÊnienia p∏ynu wewnàtrzga∏kowego mieszczà si´
w zakresie od 10 do 40, to trudno jednoznacznie odró˝niç osoby
zdrowe od cierpiàcych na jaskr´.

KROK 2

Wyznacz prawdopodobieƒstwo zdarzenia, ˝e diagno-

za typu tak, gdy poziom ciÊnienia p∏ynu w ga∏ce ocznej jest równy
lub wi´kszy od ustalonej wartoÊci progowej, by∏aby poprawna
w przypadku nowego pacjenta. Prawdopodobieƒstwa te znajdziesz
w wyniku okreÊlenia odsetka pacjentów, odpowiadajàcego prawi-
d∏owej diagnozie postawionej przy uwzgl´dnieniu tego progu. Na po-
ni˝szych wykresach powierzchnia pod krzywymi reprezentuje 100%
ka˝dej z badanych podgrup. GdybyÊmy za∏o˝yli, ˝e przyj´ta wartoÊç
progu okreÊlajàcego granicznà wielkoÊç ciÊnienia Êródocznego pa-
cjenta wynosi 20, wówczas 90% osób, u których wykryto jaskr´,
zosta∏oby zdiagnozowanych prawid∏owo (wskazanie trafne), ale
jednoczeÊnie w przypadku 50% osób zdrowych postawiono by nie-
prawid∏owà diagnoz´ (fa∏szywy alarm).

Trafniejsze decyzje, krok po kroku

Liczba osób o danym poziomie

ciÊnienia Êródocznego

10

0

20

30

40

50

ZDROWI

CHORZY

W tej grupie znajdujà si´ zarówno

zdrowi, jak i chorzy na jaskr´

WSZYSCY

MAJÑ JASKR¢

WSZYSCY

SÑ ZDROWI

CiÊnienie Êródoczne

Liczba osób o danym poziomie ciÊnienia Êródocznego

10

0

20

30

40

50

WARTOÂå PROGU = 20

Podgrupa zdrowych

Podgrupa chorych

10%

90%

POPRAWNE STWIERDZENIA

CHOROBY

(TRAFNE WSKAZANIA)

MYLNE WYKLUCZENIA

CHOROBY

(B¸¢DNE WSKAZANIA)

MYLNE STWIERDZENIA

CHOROBY

(FA¸SZYWE ALARMY)

POPRAWNE

WYKLUCZENIA

CHOROBY

50%

50%

CiÊnienie Êródoczne

JENNIFER JOHANSEN

nów gwa∏townych w populacji osób, któ-
re majà byç zwolnione z zak∏adów psy-
chiatrycznych, a nie b´dàcych przest´p-
cami. Niemniej znawcy problemu ciàgle
ró˝nià si´ w opiniach, czy klinicyÊci po-
winni traktowaç takie regu∏y jako pomoc-
nicze, czy te˝ podejmowaç decyzje opar-
te wy∏àcznie na statystyce.

Lepsze rozpoznanie raka

Probabilistyczne regu∏y decyzyjne

sprawdzajà si´ równie˝ w badaniach ma-
jàcych na celu wspomo˝enie radiologów
w diagnostyce raka piersi. W jednym z ta-
kich badaƒ radiolodzy w szpitalach ko-
munalnych oceniali mammogramy zgod-
nie ze zwyczajowà subiektywnà proce-
durà. Kilka miesi´cy póêniej analizowali
te same klisze wed∏ug opracowanej przez
radiologów specjalizujàcych si´ w inter-
pretacji mammogramów listy kontrolnej
postrzeganych cech, takich jak m.in. roz-
mycie granic zmian patologicznych. Na-
st´pnie za pomocà probabilistycznych re-
gu∏ decyzyjnych przekszta∏cono te wyniki

w oceny prawdopodobieƒstwa wystàpie-
nia raka piersi u ka˝dej pacjentki, u któ-
rej go stwierdzono. Radiolodzy zapozna-
li si´ z tymi ocenami prawdopodo-
bieƒstwa, niemniej ostatecznie formu∏o-
wali swe sàdy niezale˝nie od tej wiedzy.
Okaza∏o si´, ˝e dodatkowe dane by∏y
w znacznym stopniu pomocne. Radiolo-
dzy nie specjalizujàcy si´ w mammogra-
fii brali pod uwag´ statystyczne dane,
uzyskujàc lepsze wyniki i dorównujàc
w precyzji diagnozy specjalistom, którzy
korzystali ze wspomnianej listy cech.

Probabilistyczne regu∏y decyzyjne sto-

sujà ju˝ na szerokà skal´ lekarze w przy-
padku raka prostaty. Zw∏aszcza jednà
z nich. Gdy wyniki badaƒ klinicznych
uzasadniajà podejrzenie raka prostaty
(stwierdza si´ to na podstawie wywiadu,
zwyk∏ej ig∏owej biopsji oraz nieinwazyj-
nych badaƒ), powstaje problem wyboru
najlepszej metody leczenia [patrz: Marc
B. Garnick i William R. Fair „Rak prosta-
ty – walka nadal trwa”; Âwiat Nauki, luty
1999]. Otó˝ ani interwencja chirurgiczna
polegajàca na usuni´ciu guza, ani celo-

wana radioterapia zogniskowana dok∏ad-
nie na patologicznej tkance (po to by ogra-
niczyç skutki uboczne) nie usunie ca∏ko-
wicie tkanki nowotworowej, jeÊli guz
wykroczy∏ poza gruczo∏ lub rozprzestrze-
ni∏ si´ do innych cz´Êci cia∏a. Dlatego te˝
lekarze usi∏ujà w wielu przypadkach
okreÊliç stan guza, zanim zdecydujà si´
na jakàÊ metod´ leczenia. Niestety, wie-
le nowotworów, które poczàtkowo wyda-
jà si´ ograniczone tylko do torebki gru-
czo∏u krokowego, póêniej okazuje si´
bardziej rozleg∏e.

Przez lata ca∏e lekarze dysponowali

zaledwie kilkoma dobrymi sposobami
rozpoznawania, którzy pacjenci majà guz
ograniczony, a którym gro˝à przerzuty.
Ostatnio jednak lekarze i pacjenci uzy-
skali szans´ precyzyjniejszego rozpozna-
nia dzi´ki opublikowanym w Journal of
the American Medical Association z 14 ma-
ja 1997 roku tabelom zawierajàcym oce-
ny prawdopodobieƒstwa.

Autorzy tych tabel wiedzieli, ˝e ist-

niejà trzy ustalenia, z których ka˝de ma
niezale˝ny walor prognostyczny: „kli-

Â

WIAT

N

AUKI

Grudzieƒ 2000 71

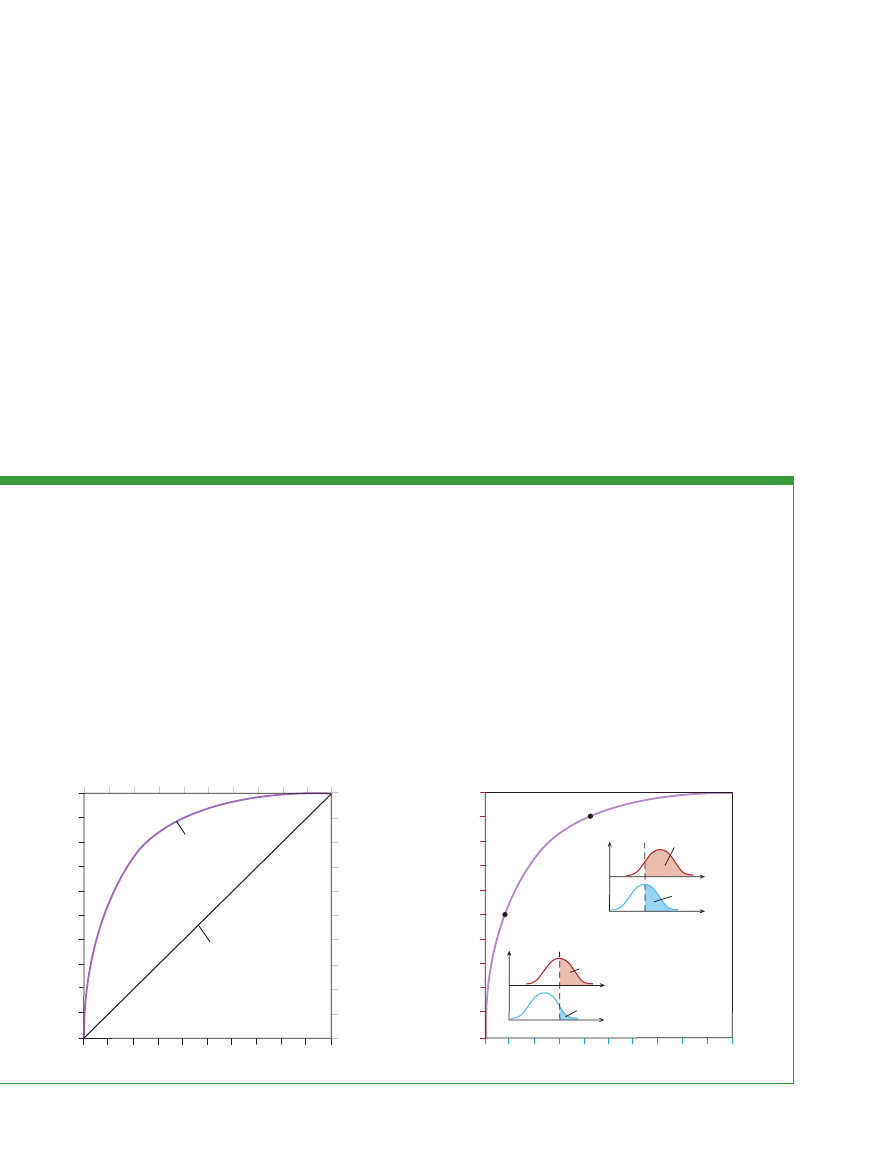
KROK 3

WykreÊl krzywà ROC dla ka˝dej mo˝liwej wartoÊci pro-

gu, odznaczajàc na pionowej osi wspó∏rz´dnych odsetek osób cho-
rych, u których prawid∏owo rozpoznano jaskr´ (wskazanie trafne), a na
poziomej – odsetek osób zdrowych, u których b∏´dnie stwierdzono
wyst´powanie jaskry (fa∏szywy alarm). Linia prosta na tym wykresie
oznacza∏aby, ˝e do wyniku poprawnego test prowadzi pó∏ na pó∏
(a zatem nie lepiej ni˝ rzut monetà). Gdy krzywe wybrzuszajà si´
w lewà stron´, znaczy to, ˝e dok∏adnoÊç testu jest wi´ksza (wy˝-
sza wartoÊç stosunku liczby wskazaƒ trafnych do liczby fa∏szywych
alarmów). Dok∏adnoÊç testu (D) du˝o precyzyjniej mo˝na jednak
zmierzyç, obliczajàc pole pod wykresem krzywej charakterystycz-
nej, które roÊnie wraz z jej wygi´ciem. Rozwa˝any przez nas proto-
kó∏ odczytów testu diagnostycznego jest umiarkowanie dok∏adny.

KROK 4

JeÊli dok∏adnoÊç testu jest zadowalajàca, wyznacz war-

toÊç progu dla diagnoz typu tak/nie. W tym celu wybierz takà wartoÊç
progu, która zapewnia wysoki odsetek wskazaƒ trafnych, utrzymujàc
jednoczeÊnie odsetek fa∏szywych alarmów na odpowiednio niskim po-
ziomie. Ka˝dy z punktów krzywej charakterystycznej reprezentuje kon-
kretnà wartoÊç progu, poczynajàc od najwy˝szej w lewym dolnym ro-
gu wykresu, a koƒczàc na najni˝szej w prawym górnym rogu. Przyj´cie
wysokiej wartoÊci progu (dolna wstawka) powoduje ograniczenie licz-
by fa∏szywych alarmów kosztem zwi´kszenia liczby nierozpoznanych
przypadków jaskry. Natomiast przyj´cie niskiej wartoÊci progu (wstaw-
ka w prawym górnym rogu)

zwi´ksza odsetek zidentyfikowanych przy-

padków choroby, ale jednoczeÊnie tak˝e liczb´ b∏´dnych wskazaƒ.
To, jaka wartoÊç progu jest optymalna dla danej populacji, zale˝y od
takich czynników, jak znaczenie diagnozowanego stanu, stopieƒ jego
wyst´powania, mo˝liwoÊci podj´cia dzia∏aƒ zaradczych u osób bada-
nych oraz finansowe, emocjonalne i inne koszty fa∏szywych alarmów.

Prawdopodobieƒstwo mylnego stwierdzenia choroby

Prawdopodobieƒstwo poprawnego stwierdzenia choroby

Prawdopodobieƒstwo poprawnego wykluczenia choroby

Prawdopodobieƒstwo mylnego wykluczenia choroby

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

KRZYWA ROC

DLA TESTU

WYKRYWAJÑCEGO

JASKR¢

(D = 0.85)

0

0

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

LINIA S¸U˚ÑCA

DO OCENY

DOK¸ADNOÂCI TESTU

(D = 0.50)

WYSOKA

WARTOÂå PROGU

(ciÊnienie = 30)

NISKA WARTOÂå PROGU

(ciÊnienie = 20)

POPRAWNE
STWIERDZENIE

MYLNE
STWIERDZENIE

POPRAWNE
STWIERDZENIE

MYLNE
STWIERDZENIE

Prawdopodobieƒstwo poprawnego stwierdzenia choroby

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

Prawdopodobieƒstwo mylnego stwierdzenia choroby

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0

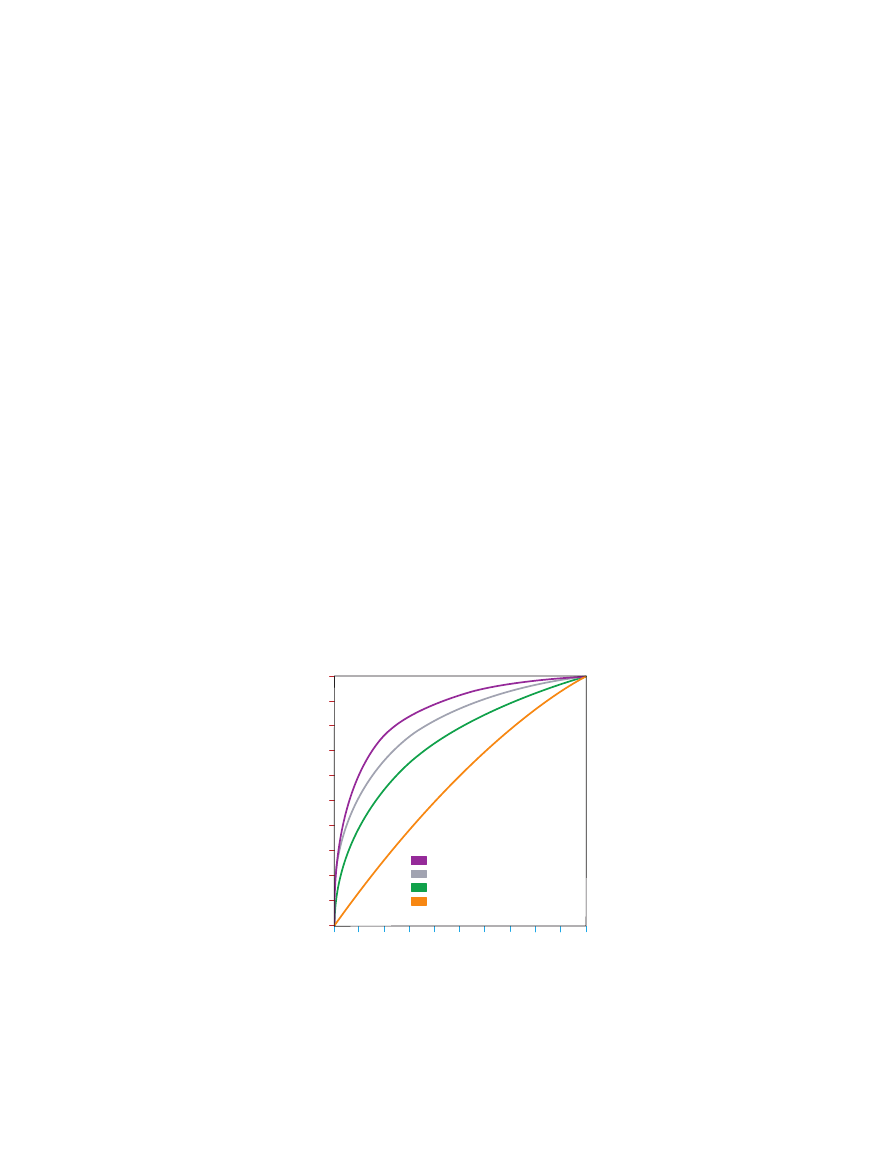
niczne stadium” guza (ustalenie oparte
na nieinwazyjnych badaniach okreÊla-
jàcych wielkoÊç i stopieƒ rozprzestrze-
niania si´ raka), poziom we krwi swo-
istego dla raka prostaty antygenu
sterczowego (PSA – prostate-specific an-
tigen) oraz punktacja w skali Gleasona
(b´dàca wskaênikiem agresywnoÊci no-
wotworu, otrzymanym na podstawie
mikroskopowej analizy materia∏u uzy-
skanego w wyniku biopsji). Dlatego te˝
opracowali probabilistycznà regu∏´ de-
cyzyjnà, w której bierze si´ pod uwag´
praktycznie ka˝dà kombinacj´ wyników
dla wymienionych trzech czynników
i okreÊla prawdopodobieƒstwo, z jakim
poczàtkowa diagnoza: „nie ma przerzu-
tów”, powinna byç trafna. Nast´pnie za-
prezentowali te oceny prawdopodo-
bieƒstw w formie przyst´pnych tabel.

Szansa na deszcz?

By∏oby b∏´dem sàdziç, ˝e tylko lekarze

stosujà w swojej praktyce probabilistycz-
ne regu∏y decyzyjne. Meteorolodzy ju˝
ponad çwierç wieku temu zaadaptowa-
li je do prognozowania pogody.

National Weather Service rutynowo

karmi danymi zwiàzanymi z pogodà pro-
gramy statystyczne wykorzystywane do
szacowania prawdopodobieƒstw wystà-
pienia tornad, huraganów, oberwania
chmury czy innych zagro˝eƒ, które mo-
gà losowo wystàpiç w ró˝nych rejonach
kraju. S∏u˝by meteorologiczne przekazu-
jà te prognozy lokalnym stacjom, gdzie
sà one modyfikowane zgodnie z na-
p∏ywajàcymi informacjami i z
uwzgl´dnieniem czynników, któ-
rych ich zdaniem programy kom-
puterowe mog∏y nie uchwyciç.

Równie˝ inne grupy specjali-

stów opanowa∏y te techniki – m.in.
komisje uniwersyteckie ustana-
wiajàce zasady przyj´ç na studia
magisterskie. W typowym przy-
padku komisja opracowuje zasa-
dy przyj´ç na podstawie dwóch
zmiennych: ocen uzyskanych pod-
czas studiów licencjackich oraz
wyników testów oceniajàcych
zdolnoÊci. Zak∏ada si´ przy tym,
˝e wyniki przekraczajàce pewien
uprzednio ustalony wysoki próg
powinny zadecydowaç o przyj´-
ciu kandydata, zaÊ wyniki poni˝ej
progu dolnego wskazaç na odrzu-
cenie. Nast´pnie komisja poddaje
bardziej subiektywnej analizie do-
kumenty kandydatów, którzy nie
zostali ani zaakceptowani, ani od-
rzuceni przez uczelnianà probabi-
listycznà regu∏´ decyzyjnà.

Jedna z uczelni prawniczych

analizuje w sposób obiektywny

poziom ukoƒczonej przez kandydata
szko∏y licencjackiej i skal´ inflacji ocen
w niej, a wi´c zmienne, które oceniano
wczeÊniej subiektywnie. Wraz ze Êred-
nià ocenà uzyskanà przez kandydata
podczas egzaminów wst´pnych i wy-
nikami testu zdolnoÊci uczelnia ta
uwzgl´dnia Êredni wynik z wczeÊniej-
szych studiów wszystkich kandydatów,
którzy starajà si´ o przyj´cie. Zmodyfi-
kowana regu∏a o wiele lepiej przewidu-
je wyniki studentów pierwszego roku
studiów prawniczych, ani˝eli pozwala∏
na to schemat z dwiema zmiennymi.

Zwodniczy próg

Dotàd uprawialiÊmy propagand´

sukcesu. Ale istot´ analiz statystycznych
najlepiej da si´ zilustrowaç na przyk∏a-
dach niepowodzeƒ w ich zastosowa-
niach przy wytyczaniu racjonalnych
progów diagnostycznych – na przyk∏ad
w testach wykrywajàcych HIV, czyli wi-
rusa powodujàcego AIDS.

Badanie na wyst´powanie HIV rozpo-

czyna si´ od stosunkowo prostego testu,
który stwierdza obecnoÊç przeciwcia∏ wy-
tworzonych przez uk∏ad odpornoÊciowy
w reakcji na pojawienie si´ tego wirusa.
Niekiedy jednak przeciwcia∏a te tworzà
si´ z zupe∏nie innych powodów. Zatem
jeÊli wynik testu (opartego na porówna-
niu z pewnà progowà obecnoÊcià prze-
ciwcia∏) jest pozytywny, laboratorium po-
winno przeprowadziç inny, bardziej
subtelny test. Ten wymóg dwóch testów
ma pomóc w ograniczeniu b∏´dnych

wskazaƒ HIV-pozytywnych. Badania na
obecnoÊç przeciwcia∏ sà szczególnie pro-
blematyczne z tego powodu, ˝e wbrew
logice liczne sprawdzone testy ró˝nià si´,
pod wzgl´dem dok∏adnoÊci i wysokoÊci
progów diagnostycznych. Ró˝ne progi
diagnostyczne mia∏yby bowiem sens,
gdyby ka˝dy test przeprowadzano na
odr´bnej populacji, tak jednak w rozwa-
˝anym przypadku nie jest.

Sà te˝ i inne k∏opoty zwiàzane z oma-

wianymi tu progami diagnostycznymi.
Ustanowiono je pierwotnie po to, by
odró˝niaç czystà krew dawców od za-
ka˝onej. Póêniej, gdy zastosowano je
do wykrywania obecnoÊci wirusa, ju˝ ich
nie modyfikowano. Zmarnowanie pó∏
kwarty niezaka˝onej krwi z powo-
du b∏´dnego pozytywnego wskazania te-
stu niewiele kosztuje; wys∏anie przestra-
szonej a niezaka˝onej osoby na dalsze
testy HIV to ju˝ powa˝niejsza sprawa
pod ka˝dym wzgl´dem. Co gorsza, pier-
wotne progi stosowano bez zastanowie-
nia u krwiodawców zarówno o niskim,
jak i wysokim stopniu ryzyka zara˝enia
wirusem, poborowych i pacjentów nar-
komanów, a wi´c grup, dla których
wspó∏czynniki wskazujàce na infekcj´ sà
w ogromnej mierze zró˝nicowane. Dla
grup wysokiego ryzyka, aby zwi´kszyç
wykrywalnoÊç, progi diagnostyczne trze-
ba okreÊlaç mniej ostro ni˝ w przypad-
ku populacji z ma∏ym ryzykiem, nawet
jeÊli cenà za to b´dzie wi´ksza liczba fa∏-
szywych wskazaƒ HIV-pozytywnych.

W ostatnich latach obserwuje si´ wpro-

wadzanie precyzyjniejszych testów wy-

krywania HIV i metod leczenia
AIDS, które chronià zdrowie i prze-
d∏u˝ajà ˝ycie. W efekcie fa∏szywe
wskazania pozytywne sà dzisiaj
rzadkie, a zara˝eni HIV wynoszà
znacznie wi´ksze korzyÊci z pod-
dania si´ badaniom diagnostycz-
nym ni˝ w przesz∏oÊci. Post´p ten
oznacza, ˝e problemem diagno-
stycznym nie jest ju˝ dziÊ wàtpli-
woÊç, kogo nazwaç zara˝onym, lecz
pytanie o to, kogo nale˝y badaç.

Przysz∏a pora, by lekarze obni-

˝yli diagnostyczne progi wskazujà-
ce, ˝e nale˝y poddaç si´ testowi –
nie powinni ju˝ czekaç, a˝ pacjent
przyjdzie z widocznymi objawami
zaka˝enia. JesteÊmy sk∏onni twier-
dziç, ˝e niemal ka˝da doros∏a oso-
ba powinna przejÊç takie badania,
a agencje rzàdowe powinny przo-
dowaç w zach´caniu do tego.

Obiektywne metody okreÊlania

progów diagnostycznych sà rów-
nie˝ niebezpiecznie rzadko stoso-
wane w niektórych ga∏´ziach prze-
mys∏u lotniczego. W przemyÊle tym
trzeba nieustannie rozpoznawaç sy-

72 Â

WIAT

N

AUKI

Grudzieƒ 2000

WIEK + PSA + WSK. GLEASONA + MRI
WIEK + PSA + WSK. GLEASONA
WIEK + PSA
WIEK

Prawdopodobieƒstwo mylnego stwierdzenia choroby

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0

Prawdopodobieƒstwo poprawnego stwierdzenia choroby

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

KRZYWE ROC porównujà mo˝liwà do osiàgni´cia do-
k∏adnoÊç diagnozy zaawansowanego stadium raka prosta-
ty za pomocà jednej lub wi´kszej liczby spoÊród nast´pu-
jàcych zmiennych: wieku pacjenta, poziomu swoistego
antygenu sterczowego PSA, z∏oÊliwoÊci nowotworu (mie-
rzonej w skali Gleasona) i wyst´powania obrazu guza na
podstawie wyników badania magnetycznym rezonansem
jàdrowym (MRI). Krzywa uwzgl´dniajàca wszystkie czte-
ry zmienne

(górna) okaza∏a si´ najlepsza.

JENNIFER JOHANSEN

tuacje, które sà trudne bàdê stosunkowo
rzadko wyst´pujà – m.in. p´kni´cia skrzy-
d∏a samolotu lub wypadki losowe zagra-
˝ajàce ˝yciu w czasie lotu. Koszty prze-
oczenia p´kni´cia skrzyd∏a sà ogromne
– jeÊli samolot rozbije si´, wielu pasa˝e-
rów mo˝e zginàç. Z drugiej strony fa∏-
szywy alarm niepotrzebnie wy∏àcza sa-
molot z lotów, co wià˝e si´ z k∏opotami
i oznacza utrat´ potencjalnego dochodu.
W pierwszym odruchu analiza korzyÊ-
ci i strat uzasadnia niski próg diagno-
styczny – przedk∏adamy wszak ˝ycie nad
pieniàdze. Przecie˝ katastrofy zdarzajà
si´ rzadko, zatem niski próg diagnostycz-
ny daje niemo˝liwà do sprawdzenia
w praktyce liczb´ fa∏szywych alarmów.
Niestety, nikt jeszcze nie zajà∏ si´ tym za-
gadnieniem, korzystajàc z dost´pnych
metod statystycznych.

Tak˝e nabywcom detektorów zderzeƒ

(jak choçby liniom lotniczym i wojsku)
nie uda∏o si´ opanowaç metod najlep-
szego ustalania progów decyzyjnych.
W wielu sytuacjach alarmy w∏àczajà si´
w trakcie lotu – gdy czujniki wskazujà, ˝e
inny samolot znajduje si´ zbyt blisko al-
bo samolot zbytnio obni˝a lot, gdy za-
mierajà silniki, czy te˝ lotnisku zagra˝a
front atmosferyczny. Tràbià jednak na
trwog´ zbyt cz´sto, g∏ównie z powodu
nieperfekcyjnie dostrojonych czujników
i poniewa˝ okreÊlono w nich raczej ni-
skie progi reakcji. Piloci z ociàganiem re-
agujà na te zwodnicze ostrze˝enia, po-
niewa˝ takie reakcje mogà te˝ skoƒczyç
si´ êle. Sytuacja ta budzi wi´c obawy: du-
˝a liczba fa∏szywych alarmów sprawi, i˝
piloci b´dà ignorowaç rzeczywiste za-
gro˝enie, a ich reakcje ulegnà os∏abieniu.
Na razie nikt nie zmusi∏ producentów
do uwzgl´dnienia wspó∏czynnika fa∏szy-
wych alarmów przy okreÊlaniu progów
reakcji urzàdzeƒ alarmowych.

Do ∏awy przysi´g∏ych

Niewàtpliwie probabilistyczne regu∏y

decyzyjne mogà podnieÊç dok∏adnoÊç po-
wtarzalnych decyzji diagnostycznych, a
ustalenie progów diagnostycznych zwi´k-
szyç ich przydatnoÊç. Metody te przyno-

szà równie˝ i inne korzyÊci. Dzi´ki stan-
daryzacji cech zwiàzanych z diagnozà re-
gu∏y prognostyczne mogà przyÊpieszyç
proces tworzenia listy cech kluczowych
w przebiegu tego procesu. Pozwalajà one
równie˝ osobom podejmujàcym decyzje
rozmawiaç o cechach ocenianych subiek-
tywnie w sposób precyzyjniejszy i prost-
szy. Pomagajà te˝ w przyuczaniu nowi-
cjuszy w tej dziedzinie.

Ciàgle jednak stosowanie regu∏ diagno-

stycznych spotyka si´ z oporem, zw∏asz-
cza gdy postrzegane sà jako narz´dzie s∏u-
˝àce do zastàpienia lub degradowania
klinicystów. Ponadto specjaliÊci chcà mieç

poczucie, ˝e rozumiejà swoje diagnozy
i zalecenia oraz ˝e mogà je wesprzeç,
przedstawiajàc tok rozumowania. Trudno
bowiem uwzgl´dniaç takie wnioski, jeÊli
ich uzasadnienie nie jest samo przez si´
zrozumia∏e.

Zdajemy sobie spraw´ ze wszystkich

tych zastrze˝eƒ. Niemniej korzyÊci ze
stosowania statystyki z pewnoÊcià
usprawiedliwiajà potrzeb´ uwzgl´d-
nienia jej przez ludzi podejmujàcych de-
cyzje. W ich r´kach znajduje si´ ˝ycie
i los innych.

T∏umaczyli

Jerzy Szapiro i Tomasz Szapiro

Â

WIAT

N

AUKI

Grudzieƒ 2000 73

Informacje o autorach

JOHN A. SWETS, ROBYN M. DAWES i JOHN MONAHAN ostatnio pracowali nad
bardziej specjalistycznym artyku∏em na ten temat, zamieszczonym w inauguracyj-
nym wydaniu magazynu American Psychological Society (Amerykaƒskiego To-
warzystwa Psychologicznego), które zosta∏o poÊwi´cone przeglàdowi wyników
badaƒ psychologicznych nad problemami pilnymi i istotnymi spo∏ecznie [patrz:
Literatura uzupe∏niajàca]. Swets jest honorowym naukowcem BBN Technologies
w Cambridge w stanie Massachussets, radiologiem w Brigham and Woman’s Ho-
spital w Bostonie i wyk∏adowcà z dziedziny polityki ochrony zdrowia w Harvard
Medical School. Dawes – szefem Katedry Charlesa Queenana, Jr., na Wydziale Na-
uk Spo∏ecznych i Decyzyjnych w Carnegie Mellon University oraz autorem ksià˝-
ki Rational Choice in an Uncertain World (Racjonalny wybór w niepewnym Êwiecie).
Monahan, psycholog, kieruje Katedrà Prawa im. Doherty’ego w University of Vir-
ginia i jest dyrektorem OÊrodka Badaƒ nad Prawem i Zdrowiem Psychicznym Fun-
dacji MacArthurów.

Literatura uzupe∏niajàca

COMBINATION OF PROSTATE-SPECIFIC ANTIGEN, CLINICAL

STAGE AND GLEASON SCORE TO PREDICT PATHOLOGICAL
STAGE OF LOCALIZED PROSTATE CANCER

. A. W. Partin i in.;

Journal of the American Medical Association, tom 277,
nr 18, s. 1445-1451, 14 V 1997.

THINK HIV: WHY PHYSICIANS SHOULD LOWER THEIR

THRESHOLD FOR HIV TESTING.

Kenneth A. Freedberg i Jef-

frey H. Samet; Archives of Internal Medicine, tom 159,
nr 17, s. 1994-2003, 27 IX 1999.

PSYCHOLOGICAL SCIENCE CAN IMPROVE DIAGNOSTIC DE-

CISIONS

, John A. Swets, Robyn M. Dawes i John Mo-

nahan; Psychological Science in the Public Interest
(dodatek do Psychological Science), tom 1, nr 1, s. 1-26,
V/ 2000.

Kwestia smaku

A

rchitekci i koneserzy win wymyÊlili dwa niekonwencjonalne zastosowania probabi-
listycznych regu∏ decyzyjnych. Zasada architektoniczna odnosi si´ do gmachów oper;

zosta∏a stworzona na podstawie dokonanej przez dyrygentów oceny jakoÊci dêwi´ku
w 23 obiektach. Dyrygenci chwalili budynki w Buenos Aires, Dreênie, Mediolanie i To-
kio. Nast´pnie w ka˝dym z 23 budynków in˝ynierowie akustycy przeprowadzili pomia-
ry wielu specyficznych w∏asnoÊci aku-
stycznych – takich jak odst´py czasowe
pomi´dzy dêwi´kiem docierajàcym bez-
poÊrednio i po odbiciu oraz rozprosze-
nie fal dêwi´kowych spowodowane nie-
równoÊcià Êcian i sklepieƒ. Analizy
statystyczne ujawni∏y nast´pnie, po∏à-
czenie których czynników prowadzi∏o
w chwalonych budynkach do niepo-
wtarzalnego dêwi´ku i które w∏asno-
Êci akustyczne okaza∏y si´ najwa˝-
niejsze. Otrzymana regu∏a mo˝e byç nie-
zwykle pomocna przy budowie nowych
gmachów operowych.

Regu∏a dla win pozwala przewidzieç

ostatecznà jakoÊç czerwonego wina bor-
deaux (mierzonà cenami aukcyjnymi)
w chwili, gdy jest jeszcze m∏ode i nie-
zdatne do picia. Tradycyjnie eksperci próbowali przewidzieç jakoÊç nowych win meto-
dà „klinicznà” – pos∏ugujàc si´ zmys∏em smaku i powonienia. Ale oko∏o 10 lat temu ba-
dacze zauwa˝yli, ˝e lata, w których sierpieƒ i wrzesieƒ by∏ suchy, a czas winobrania ciep∏y
(jeÊli tylko te okresy nast´powa∏y po wilgotnej zimie), obfitowa∏y w doskona∏e wina.
Sformu∏owali na tej podstawie „równanie bordeaux” – probabilistycznà regu∏´ decyzyj-
nà, która ∏àczy∏a warunki pogodowe i czas dojrzewania, pozwalajàc oszacowaç praw-
dopodobieƒstwo, ˝e znakomita jakoÊç wina utrzyma si´ przez ca∏e lata. Równanie to
sprawdza si´ doskonale, t∏umaczàc 83% zmian w cenach aukcyjnych dojrza∏ych win bor-
deaux. Nie zyska∏o ono jednak powszechnego uznania. „GdzieÊ mi´dzy gwa∏towne
i histeryczne” – tak opisano w gazetach reakcje kiperów na ujawnienie tego równania.

GMACH OPERY w Nowym Tokijskim Te-
atrze Narodowym dzi´ki zastosowaniu pro-
babilistycznych regu∏ decyzyjnych ma nie-
zrównanà akustyk´.

ZA ZGODÑ TAK ARCHITECTS, YANAGISAWA, TOKIO