Combustion, Explosion, and Shock Waves, Vol. 37, No. 6, pp. 717–722, 2001

Shock-Wave Deformation and Fracture of Zirconium Dioxide Ceramics

of Various Fractional Composition and Porosity

UDC 534.2+539.812

V. A. Ogorodnikov,

1

A. G. Ivanov,

1

S. V. Erunov,

1

V. I. Luchinin,

1

V. N. Mineev

2

, F. A. Akopov

2

, and G. P. Chernyshov

2

Translated from Fizika Goreniya i Vzryva, Vol. 37, No. 6, pp. 113–118, November–December, 2001.
Original article submitted November 14, 2000.

The paper reports results from measurements of free-surface velocity profiles of shock-
loaded zirconium dioxide ceramics with a porosity of 16–22% produced from compo-
sitions with a size of the coarse fraction of 0.5–2.0 mm. Shock-wave loading of ZrO

2

samples 5–20 mm thick was performed by aluminum impactors 3–12 mm thick with
a velocity of 10–100 m/sec. The measured free-surface velocity profiles were used to
assess the dynamic compressive and tensile strengths of the ceramics and the damping
properties of the ceramics.

An important problem of safe operation of nuclear

reactors at nuclear power plants (NPP) is reliable lo-
calization of the core melt in the case of an emergency.
An analysis of the possible accident scenarios in nuclear
reactors shows that in existing NPP, the core melt can
be localized using cavity catchers [1], and in projected
NPP, this can be implemented by removing the melt
in a special compartment, in which it is spread and
cooled [2]. In both cases, the materials used to clad
these structures should exhibit improved thermal and
deformation properties because they can be subjected
(along with others) to mechanical and thermal impacts.
Zirconium dioxide ceramics is currently regarded as a
promising material for these purpose [3–5]. Literature
data on shock-wave deformation and fracture of ceramic
materials, especially those of high porosity (k > 10%),
are discrepant and extremely insufficient [6, 7].

The

lack of detailed data on the kinetics of these processes
hinders the construction of computational and theoret-
ical models [8] required to describe the reaction of the
catcher material to one or another action. The present
paper, which is a continuation of [4, 5], reports results
of systematic studies of the behavior of shock-loaded
zirconium dioxide ceramics of four types with an initial

1

Russian Federal Nuclear Center, Institute
of Experimental Physics, Sarov 607190.

2

Institute of Thermal Physics of Extreme States
of the Joint Institute of High Temperatures,
Russian Academy of Sciences, Moscow 127412.

porosity of 16 to 22% produced from compositions with
a size of the coarse fraction of 0.5–2.0 mm.

The manufacture of the tested ceramics is described

in detail in [3]. The main component of zirconium diox-
ide ceramics of types I and II is Y

2

O

3

-doped ZrO

2

(mole

concentration 9.8%). Zirconium dioxide was used in the
form of grains with sizes of 0.001–1 mm, which were
produced from electrically melted ZrO

2

.

In the sin-

tered form, the size of the fine fraction reached 0.02 mm
and acted as a binder. In the manufacture zirconium
dioxide ceramics of types III and IV, the basis was
a complex disperse composition of zirconium dioxide,
which included 50% cubic and 50% tetragonal solid
solutions stabilized by Y

2

O

3

. The samples contained

30% stabilized zirconium dioxide with grain sizes less
than 0.2 mm, 15% disperse component, and 55% sta-
bilized zirconium dioxide with grain sizes of 0.5–1 mm
or 1–2 mm. Some characteristics of the examined sam-
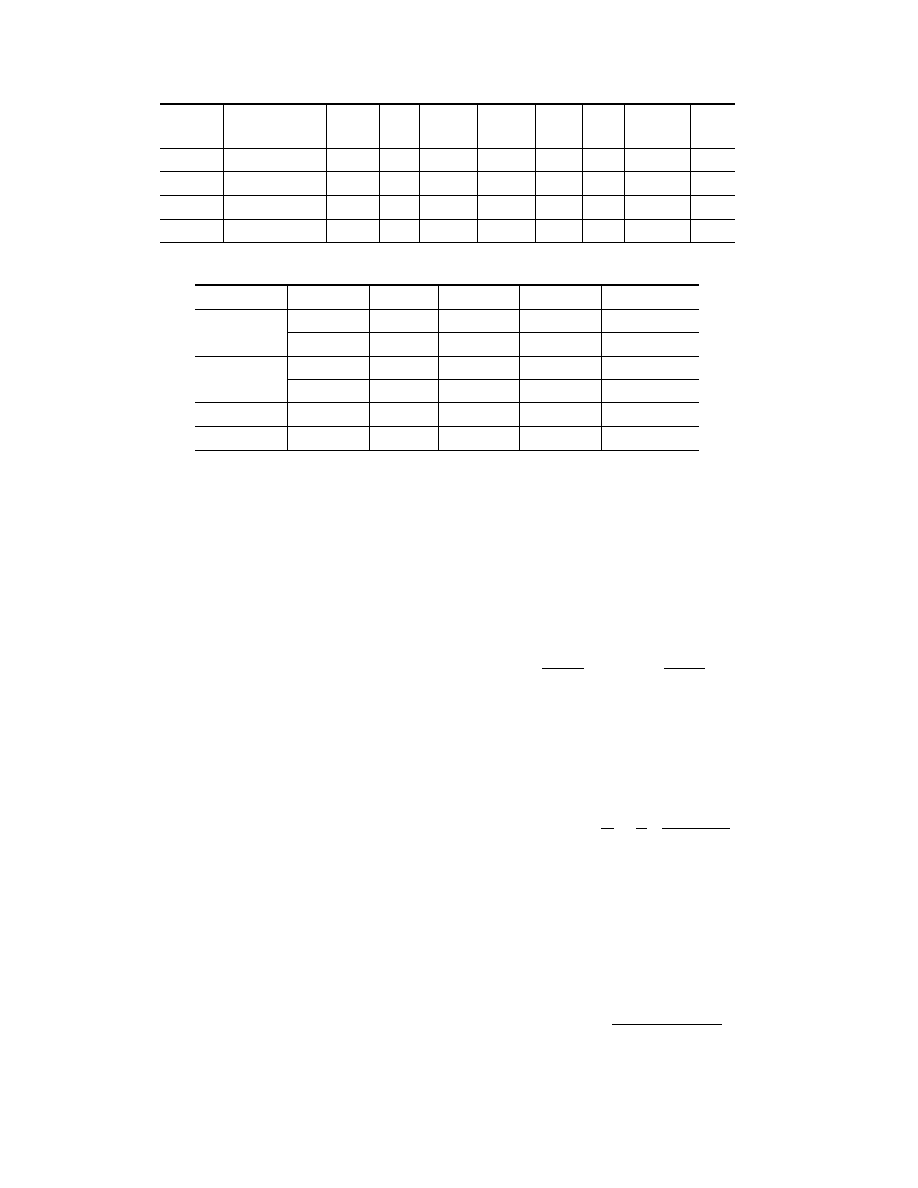
ples of zirconium dioxide ceramics are given in Table 1,
where ρ

0

is the density of the ceramics, k is open poros-

ity, c

l

and c

n

are the longitudinal and transverse velocity

of sound, respectively, ν is Poisson’s factor, E is Young’s
modulus, and σ

comp

and σ

ten

are the static compressive

and tensile strengths of ceramics, respectively.

The dynamic compressive and tensile strengths of

zirconium dioxide ceramics were tested on a BUT-76
test complex [9]. The samples were shaped like disks of
≈50 mm diameter and thickness ∆ = 5, 10 and 20 mm.
Before the experiment, special attention was given to

0010-5082/01/3706-0717 $25.00 c

2001

Plenum Publishing Corporation

717

718

Ogorodnikov, Ivanov, Erunov, et al.

TABLE 1

Ceramic

Coarse fraction

ρ

0

,

k,

c

l

,

c

n

,

ν

E,

σ

comp

,

σ

ten

,

type

size, mm

g/cm

3

%

km/sec

km/sec

GPa

MPa

MPa

I

0.5–1

4.80

22.0

3.3

2.0

0.235

54.8

90–140

9–13

II

0.5–1

4.80

17.0

3.3

2.0

0.220

54.8

—

—

III

0.5–1

4.87

16.0

3.6

1.7

0.291

62.8

115

± 15

—

IV

1–2

4.80

16.7

3.3

1.7

0.253

53.2

67

± 12

—

TABLE 2

Ceramic type

∆, mm

σ

0

, MPa

σ

0

ten

, MPa

˙

ε, 10

−3

sec

−1

λ, mJ

· cm

−2

I

5

45–60

5–30

0.3–2.3

6–12

10

26–80

7–18

0.1–0.8

3–32

II

5

55–70

4–27

0.5–1.5

8–16

10

45–118

9–16

0.1–0.5

10–41

III

5

41–116

20–70

0.1–2.3

5–44

IV

10

65–88

6–20

0.4–0.7

18–34

the quality of preparation of the face (loaded and free)
surfaces, whose nonplanarity and nonparallelelism did
not exceed 50 µm. A copper layer

≈20 µm thick was

deposited on the lateral and free surfaces of the samples
(to produce conducting surfaces) and the samples were
then pressed in aluminum casings 90 mm in diameter.
These targets were loaded by aluminum impactors 3, 6
or 12 mm thick and 75 mm in diameter, depending on
target thickness. The dimensions of “impactor–target”
pairs were chosen so as to ensure one-dimensional defor-
mation. The impactor velocities W

0

were varied in the

range of 10–100 m/sec, which yielded the following load-
ing conditions of the samples in the targets: absence of
fracture nuclei, observed for longitudinal microsections
of the samples with a 200-

× magnification, occurrence

of separate fracture nuclei in the form of micropores
or microcracks, coalescence of fracture nuclei in a main
crack, and breakup of the sample in fragments. After
loading, a targets with a sample was decelerated in a
low-density medium (polyethylene chips) and then cut
and subjected to metallographic analysis. In each ex-
periment, the free-surface velocity W (t) was continu-
ously recorded by a capacitive transducer of 20 mm di-
ameter with a guard ring. In addition, in experiments
using electric contacts, we measured the impactor ve-
locity W

0

and determined the moment of collision of

the impactor with the target, which was related to the
W (t) profile recorded by the capacitive transducer in
one measuring channel.

Figure 1a and b gives typical free-surface velocity

profiles W (t) for ceramic samples of thickness ∆ = 5,

10, and 20 mm and an initial porosity of 22% (type I)
and 17% (type II); Fig. 1c shows typical free-surface ve-
locity profiles W (t) for ceramics of types III and IV of
thickness ∆ = 5 and 10 mm, respectively, which had
close initial porosities (

≈17%) but different fractional

compositions (grain sizes 0.5–1 and 1–2 mm, respec-
tively).

From the W (t) profile, we estimated the dynamic

yield strength

σ

q

=

1

− 2ν

1

− ν

σ

HEL

= 0.5

1

− 2ν

1

− ν

ρ

0

DW

elast

and the spall strength σ

ten

= 0.5ρ

0

c

0

(∆W +δW ), where

c

0

is the volumetric velocity of sound, D is the elastic

wave velocity, W

elast

is the free-surface velocity at the

moment of emergence of the elastic wave, ∆W = W

1

−

W

2

is the difference between the velocities at the first

maximum and first minimum on the curve of W (t),

δW =

δ

c

0

+

δ

c

l

| ˙

W

1

˙

W

2

|

| ˙

W

1

+ ˙

W

2

|

is the correction for the effect of the elastoplastic be-
havior of the material on the variation in free-surface
velocity with time [10], δ is the thickness of the spalled
layer, ˙

W

1

and ˙

W

2

are the free-surface velocity gradients

in the incident rarefaction wave and at the front of the
spall pulse. As the upper bound of the spall strength,
we used values of the maximum tensile strains calcu-
lated from the expression

σ

0

= ρ

s

c

s

W

0

1 + (ρ

s

c

s

)/ρ

Al

c

Al

,

Shock-Wave Deformation and Fracture of Zirconium Dioxide Ceramics

719

Fig. 1. Free-surface velocity profiles of ZrO

2

ceramics:

(a) type I for ∆ = 5 mm and W

0

= 25.6 m/sec (curve

1), ∆ = 10 mm and W

0

= 30.4 m/sec (curve 2), and

∆ = 20 mm and W

0

= 51.8 m/sec (curve 3); points

A and B are the amplitudes of the first and second
compression waves, respectively; (b) type II for ∆ =
5 mm and W

0

= 27.8 m/sec (curve 1), ∆ = 10 mm

and W

0

= 25.1 m/sec (curve 2), and ∆ = 20 mm and

W

0

= 26.6 m/sec (curve 3); (c) curve 1 refers to type III

for ∆ = 10 mm and W

0

= 25.7 m/sec, curve 2 refers

to type IV for ∆ = 10 mm and W

0

= 33.0 m/sec,

curve 3 refers to type III for ∆ = 5 mm and W

0

=

21.2 m/sec, curve 4 refers to type III for ∆ = 5 mm
and W

0

= 19.8 m/sec, and curve 5 refers to type III

for ∆ = 5 mm and W

0

= 18.0 m/sec.

where ρ

s

and ρ

Al

are the densities of the sample and

impactor, respectively, and c

s

and c

Al

are the veloci-

ties of sound in the sample and impactor. The strain
rate of the sample material was estimated using the re-
lations ˙

ε

1

= W

0

/2∆

Al

or ˙

ε

2

= ˙

W

1

/2c

1

, where ∆

Al

is

the thickness of the aluminum impactor. From these
quantities and the spall thickness δ measured after the
experiment, we estimated the specific (per unit area)
spallation work or the fracture energy: λ = 2σ

2

0

δ/BE,

where B = 2(1

− ν)/(1 + ν)(1 − ν) and E is Young’s

modulus. Table 2 lists estimates of these characteristics
of the tested ceramics.

Photographs of longitudinal microsections of ce-

ramic samples of various types, are presented in Fig. 2,
which illustrates the occurrence of a main crack.

An analysis of W (t) profiles and data on the struc-

ture of longitudinal sections of the samples shows a
number of general regularities and some special fea-
tures of behavior of the samples under dynamic load-
ing. Thus, for example, the spall pulse that arises dur-
ing fracture and it reverberation over the thickness of
the spalled plate are recorded most reliably when at
minimum thickness of the tested samples [∆

≈ 5 mm

(see Fig. 1)] with minimum size of the coarse fraction
(

≈1 mm). This is due to manifestation of a scale ef-

fect of energetic nature during fracture, in particular,
localization of the spall fracture region in a narrower
zone for samples of smaller scale [11]. For ceramic sam-
ples of the same types but of greater thickness (10 and
20 mm) or of the same thickness but with larger size of
the coarse fraction (

≈2 mm), the spall fracture zone is

more developed and rough and the W (t) profiles have
more gently sloping edges (see Fig. 1). This “evens out”
the information on reverberation of the spall pulse over
the spall plate thickness, which hinders assessment of
the magnitude of tensile stresses during spallation σ

ten

.

Some peculiarities were also observed for ceramic

samples 5 mm thick. They were most pronounced for
the spall fracture of type III ceramics (see Fig. 1c).
Thus, with close impactor velocities (W

0

≈ const) in

repeated experiments, the W (t) profiles were different:
in some cases, a spall pulse was absent from them. Re-
sults of metallographic analysis of longitudinal sections
of the samples after loading indicate unequivocally that
in these cases, the spread of irregularities of the spall
surfaces is rather wide (see Fig. 2d). The spall pulse
and its reverberation are clearly observed in regions
where the roughness of the spall surfaces is minimal
(profile 5 in Fig. 1c and top snapshot in Fig. 2d) and
vice versa (profile 3 in Fig. 1c and bottom snapshot
in Fig. 2d). The observed differences in the behavior
of samples at close impactor velocities in repeated ex-
periments suggest that the ceramic samples have indi-
vidual properties, which are apparently related to their
actual fractional composition and porosity. The indi-
vidual properties of some samples are responsible for
the appreciable spread of spall strengths of the ceram-
ics. For ceramics of types I, II and IV, these are close
values σ

ten

≈ 5–30 MPa and σ

0

≈ 30–80 MPa. For finer

ceramics of type III, these values are somewhat higher:
σ

ten

≈ 20–70 MPa and σ

0

≈ 40–120 MPa, which does

not contradict the current concepts [12].

The shapes of the free-surface velocity profiles W (t)

for 20-mm-thick samples of ceramics of types I and II
(see Fig. 1a and b) with different initial porosities sug-
gest a fundamental difference in their behavior under
dynamic loading of identical intensity. Thus, the W (t)
profiles of 20-mm-thick samples of type II ceramics with

720

Ogorodnikov, Ivanov, Erunov, et al.

a

b

mm

5

10 mm

20 mm

c

d

10mm

d

5 mm

5 mm

5 mm

10 mm

5 mm

20 mm

Fig. 2. Photographs of longitudinal microsections of several samples: (a) ceramics of type I for ∆ = 5 mm and
W

0

= 14.0 m/sec, ∆ = 10 mm and W

0

= 10.0 m/sec, and ∆ = 20 mm and W

0

= 10.0 m/sec; (b) ceramics of type

II for ∆ = 5 mm and W

0

= 10.6 m/sec, ∆ = 10 mm and W

0

= 15.0 m/sec, and ∆ = 20 mm and W

0

= 25.7 m/sec;

(c) ceramics of types III for ∆ = 5 mm and W

0

= 17.5 m/sec and IV for ∆ = 10 mm and W

0

= 24.6 m/sec;

(d) ceramics of type III for ∆ = 5 mm and W

0

= 18.0 (top snapshot) and 21.2 m/sec (lower snapshot); δ is the

thickness of the spall layer.

TABLE 3

W

0

, m/sec

D

A

, km/sec

u

A

, m/sec

p

A

, MPa

σ

A

q

, MPa

D

B

, km/sec

u

B

, m/sec

p

B

, MPa

σ

B

q

, MPa

8.2

3.3

0.6

9.7

6.7

1.8

2.5

21.6

15.0

10.4

3.3

0.6

9.7

6.7

1.8

1.8

15.6

10.8

24.8

3.3

2.6

42.1

29.2

1.8

4.1

35.4

24.5

51.8

3.3

4.5

72.8

50.5

1.8

8.6

74.3

51.5

a porosity of 17% do not differ qualitatively from the
profiles of samples of the same ceramics 5 and 10 mm
thick. An analysis of the longitudinal section of 20-mm-
thick samples of type II ceramics after loading indicates
that they undergo spall fracture as well as samples 5
and 10 mm thick (see Fig. 2b). Similar behavior under
shock-wave deformation and fracture was observed for
samples of zirconium dioxide concrete with thicknesses
of 5, 10, and 20 mm and a porosity of

≈17% [5]. For

20-mm-thick samples of type I with increased porosity
(22%), the W (t) profiles clearly show a three-wave con-

figuration of the compression wave, which is steadily
reproduced at impactor velocities W

0

= 10–50 m/sec.

A shock wave (SW) of a similar complex structure with
two elastic waves and a plastic compression wave was
observed in expanded polystyrene [13] and sintered cop-
per [14] at rather low impactor velocities and great
thicknesses of the tested samples.

The mass veloci-

ties u

A,B

= W

A,B

/2 and pressures p

A

= ρ

0

D

A

u

A

and

p

B

= p

A

+ ρ

0

(D

B

− u

A

)(u

B

− u

A

) corresponding to the

parameters of the first (subscript A) and second (sub-
script B) compression waves at various impactor veloc-

Shock-Wave Deformation and Fracture of Zirconium Dioxide Ceramics

721

ities W

0

are listed in Table 3. The table gives wave

velocities (D

A

and D

B

) calculated from the time in-

tervals between the moment of collision of the impactor
with the sample (electrocontact gauge) and the moment
when the first or second SW emerges on the free sur-
face of the sample (capacitive transducer) recorded in
one measuring channel. In addition, the table gives cal-
culated values of the dynamic yield strengths for the
first (σ

A

q

) and second (σ

B

q

) elastic waves.

A comparison of the data obtained with the data

of Table 1 shows that the velocity of the first SW tends
to the velocity of propagation of longitudinal ultrasonic
vibrations in ceramics c

l

= 3.3 km/sec. However, at an

impactor velocity W

0

≈ 10 m/sec, the first SW pressure

is much lower than the static yield strength under com-
pression σ

comp

= 90–140 MPa. The second SW velocity

tends to the velocity of transverse ultrasonic vibrations
c

n

= 2.0 km/sec. The second SW pressure is also lower

than the static yield strength. As the impactor velocity
increases from 10 to 52 m/sec, the amplitudes of the
first and second SW increase appreciably but the value
of σ

q

is still not higher than the static strength. An

increase in σ

q

can be due to an increase in the strain

rate of the material from 5

· 10

2

to 2

· 10

3

sec

−1

. Ac-

cording to [13], the presence of two elastic compression
waves implies the simultaneous existence of two yield
strengths related to different compression conditions —
a complex strain state (pore closure and compression of
the skeleton) and one-dimensional deformation.

As can be seen from Fig. 2a and b, in the fracture

of 20-mm-thick samples of types I and II there are fun-
damental differences. The fracture of type II ceramics is
close in nature to spallation, i.e., a main crack is formed
by growth and coalescence of microcracks. Samples of
type I ceramics with higher porosity are penetrated by
a series of cracks parallel to the surfaces of the sample,
and are appreciably split. This is apparently related
to the occurrence of a splitting or fracture wave in the
samples [7, 15]. Indeed, because the fracture work is
performed at the expense of the elastic tensile energy
content, it is assumed that the reflection of the com-
pression pulse propagating from the interfaces (grain
boundaries of zirconium dioxide) deep into the sample
of a porous heterogeneous material can give rise to local
rarefaction waves moving from the boundaries of these
inhomogeneities and interference of these waves can lead
to the formation of tensile stresses and occurrence of
cracks or splitting in porous ceramics.

Results on shock-wave deformation and fracture of

zirconium dioxide ceramics of various porosity and frac-
tional composition at normal temperature showed that:

• There is a certain critical porosity (≈20% for the

ceramics considered) below which the ceramics behaves

as a viscoplastic body and above which it behaves as an
elastoviscoplastic body. A compression wave of three-
wave configuration is observed in samples with an initial
porosity

≥20% and a thickness ≥20 mm. This suggests

manifestation of the damping properties of high-porous
ceramics;

• The spall pulse and its reverberation over thick-

ness of the spall layer are recorded most reliably on
thin samples of ceramics (∆ = 5 mm) with a size of
the coarse fraction of

≤1 mm, which is attributed to

manifestation of a scale effect of energetic nature and
localization of fracture in a narrow zone;

• The difference in individual properties of the

tested samples is responsible for the spread of their
strength characteristics.

In particular,

the spall

strengths of ceramics of types I, II, and IV are close
and is 10–30 MPa, and the spall strength of ceramics of
type III is somewhat higher: 20–70 MPa, which is due
to its small grain size.

REFERENCES

1. V. N. Mineev, L. B. Borovkova, F. A. Akopov, et al.,

“External catcher made of ceramics and zirconium diox-

ide based concrete,” Atom. ´

Energ., 85, No. 2, 119–125

(1998).

2. D. Bittermann, “Principles of application of mechanical

design measures to control severe accident phenomena,

applied to the melt retention concept of the EPR,” in:

OECD Workshop on Ex-Vessel Debris Coolability Karl-

sruhe Nucleusany, November 15–18, 1999.

3. F. A. Akopov, A. A. Akopyan, B. M. Barykin, et al.,

“Behavior of zirconium dioxide ceramics under condi-

tions of operation of an external catcher,” Atom. ´

Energ.,

87, No. 1, 48–53 (1999).

4. A. M. Bragov, A. K. Lomunov, V. N. Mineev, et al.,

“Investigation of the dynamic properties of zirconium

dioxide ceramics by a modified Kolsky’s technique,” in:

Applied Problems of Strength and Plasticity (collected

scientific papers) [in Russian], No. 52 (1997), pp. 1–9.

5. V. A. Ogorodnikov, A. G. Ivanov, V. I. Luchinin, et

al., “Shock-wave deformation and fracture of zirconium

dioxide ceramics and concrete,” Atom. ´

Energ.,

88,

No. 2, 113–119 (2000).

6. D. E. Grady, “Shock wave compression of brittle solids,”

Mech. Mater., 29, 181–203 (1998).

7. G. I. Kanel’, S. V. Razorenov, A. V. Utkin, and

V. E. Fortov, “Mechanical properties of materials under

shock-wave loading,” Mekh. Tverd. Tela, No. 5, 173–188

(1999).

8. L. A. Merzhievskii, “Modeling the dynamic compression

of porous Al

2

O

3

,” Fiz. Goreniya Vzryva,

35, No. 6,

105–111 (1999).

722

Ogorodnikov, Ivanov, Erunov, et al.

9. V. N. Mineev, V. P. Pogorelov, A. G. Ivanov, et

al., “Setup for studying the behavior of materials and

constructions under dynamic loading,” Fiz. Goreniya

Vzryva, 14, No. 3, 129–133 (1978).

10. G. V. Stepanov, “Spall fracture of metals by plane

elastoplastic waves,” Probl. Prochn., No. 8, 66–69

(1976).

11. V. A. Ogorodnikov, A. G. Ivanov, V. I. Luchinin, et al.,

“Scale effects under dynamic fracture of brittle and vis-

cous materials,” Fiz. Goreniya Vzryva, 35, No. 1, 108–

114 (1999).

12. O. A. Kleshchevnikov, V. N. Sofrononv, G. G. Ivanova,

et al., “Experimental test of fracture criteria in experi-

ments with copper samples,” Zh. Teor. Fiz., 47, No. 8,

1791–1794 (1977).

13. S. I. Bodrenko, Yu. A. Krysanov, and S. A. Novikov,

“Shock wave propagation in expanded polystyrene,”

Prikl. Mekh. Tekh. Fiz., 6, 140–144 (1979).

14. R. R. Boade, “Compression of porous copper by shock

waves,” J. Appl. Phys., 39, No. 12 (1968).

15. V. I. Kulikov, “Velocity of the fracture front and dy-

namic stresses in it during explosion in hard media,”

Dokl. Akad. Nauk SSSR, 268, No. 2, 332–336 (1983).