
L
L
E
E
C
C
T
T
U
U
R
R
E
E
1
1
5
5
N
N
O
O
R
R
M
M
A
A
L
L
S
S
H
H
O
O
C
C
K
K
W
W
A
A
V
V
E
E
I
I
N
N
T
T
H
H
E
E
C
C
L
L
A
A
P
P
E
E
Y
Y
R
R
O
O
N
N
G
G
A
A
S
S
N
N
O
O
R
R
M
M
A
A
L
L
S
S
H
H
O
O
C
C
K
K
W
W
A
A
V
V
E
E
.
.
H
H
U
U
G
G
O
O
N
N
I
I
O
O
T
T
A
A
D
D
I
I
A
A
B
B
A
A
T
T
.
.
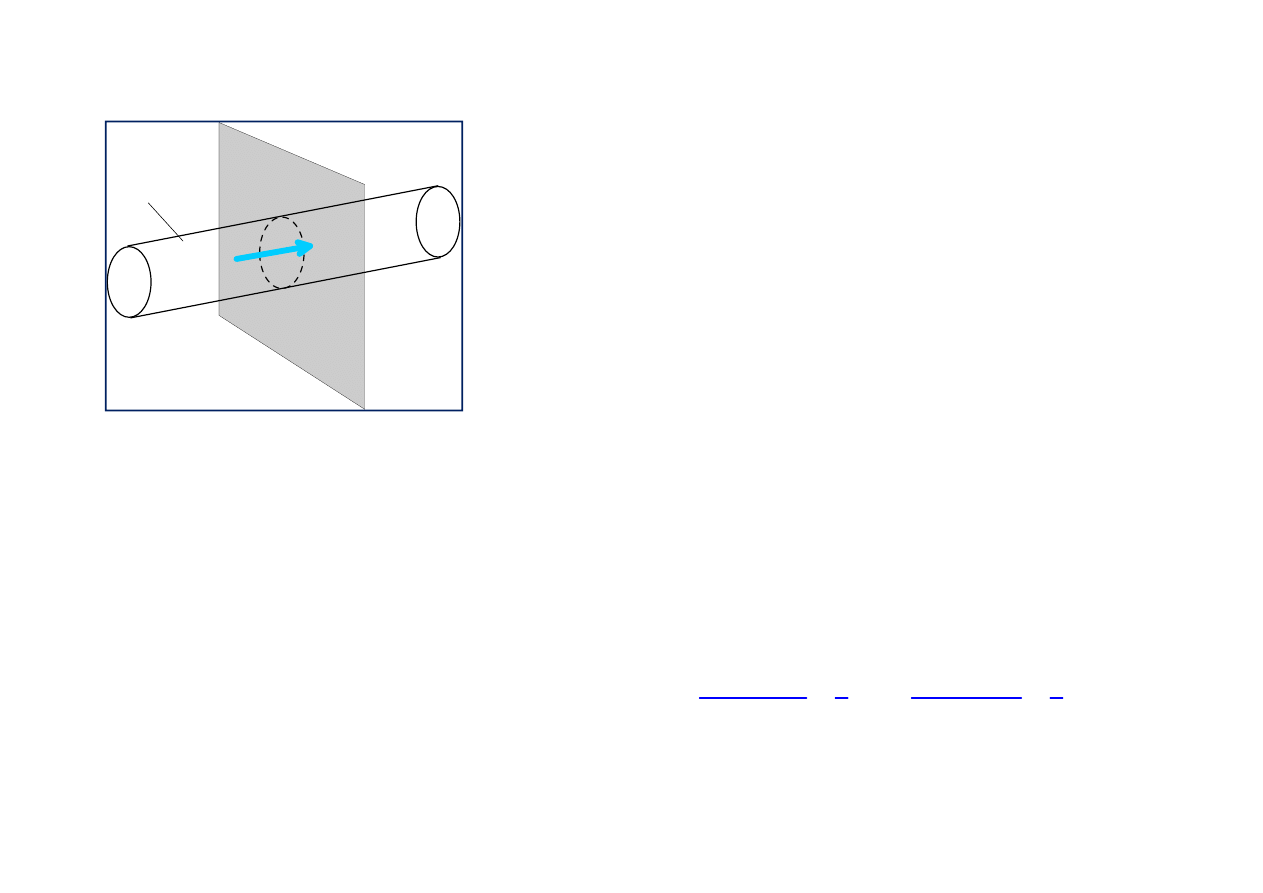
Gas dynamics admitts existence of strongly discontinuous
flow. The normal shock wave is the simplest example of
such flow
0
1
2
S
S
S
Conservation laws for the NSW
(1) Mass
v
0
n
ds
1D case
1 1
2
2
u
u
(2) Linear momentum
( v
)
n
p
ds
v
n
0
1D case
2
2
1 1
1
2 2
2
u
p
u
p
(3) Energy
2
2
1
2
1
1
1
2
2
2
1
2
(
1)
(
1)
p
p
u
u
Devide (2) by (1) …
norm
al sh
ock
w
ave
S
1
S
2
S
0

1
2
2
1
1
2
1
2
1 1
2
2
2
2
1 1
p
p
p
p
u
u
u
u
u
u
u
u
(4)
New form of (3) is
2
1
1
2
1
2
2
1
2
(
)(
)
1
p
p
u
u
u
u
(5)
Using (4) the Eq. (5) can be rewritten as
2
1
2
1
1
2
2
2
1 1
2
1
2
(
)
1
p
p
p
p
u
u
u
u
(6)
The LHS of (6) can be transformed using the mass conservation equation (1) …
1
1
2
(6)
2
2
u
p
LHS
u
1
u
2
2
2
p
u
2
u
1
1
1
p
u
1
u
2
2
1
1 1
u
p
u
2
u
2
2
1
1
1
2
1
2
p
p
p
p
Thus, we get from (6)
2
2
1
1
2
1
1
2
1
2
2
1
2
1
p
p
p
p
p
p
(7)
We multiply (7) by
1
1
p
and get the formula which involves only the ratios
1
2
and
2
1
p
p
….
1
2
2
1
1
2
2
1
1
1
1
1
2
1
1
1
1
1
1
1
p
p
(8)
We have obtained the formula describing the thermodynamic process which affects the
gas passing through the NSW. Note that it is different that the isentropic process! We
call the above formula the Hugoniot Adiabat (HA).
Let us analyse some properties of the HA. Note that for
2
1
1
1
1
we have the vertical
asymptot. If
1.4
then corrsponding ratio
2
1
6
. Thus, at the shock wave the density of
gas always increases but never more than
1
1
times.
For brevity we introduce
2
1
y
p
p
,
2
1
x
and
1
1
. The formula (8) can be now
written as
1
( )
x
y x
x
Then, we have
2
(
1)(
1)
1
( )
(1)
(
)
1
y x
y
x
Note that in case of the isentropic process, we have
( )
y x
x
, so
1
( )
y x
x
and
(1)
y
. Moreover
3
2
2(
1)(
1)
( )
(1)
(
1)
(
)
( )
(
1)
(1)
(
1)
Hugoniot
Hugoniot
isentropic
isentropic
y
x
y
x
y
x
x
y
We see that the isentropic and normal shock wave adiabats fit very well to each other in
the vicinity
1
x (they have the same values of
(1)
y
,
(1)
y
and
(1)
y
). We say that these
lines are strictly tangent at
1
x .
Physically it means that weak shock waves
are nearly isentropic and
3
2
2
2
1
1
1
1
. .
Hugoniot
isentropic
p
p
C
h o t
p
p
.
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
0
5
10
15
20
25
30
p
2
/p
1
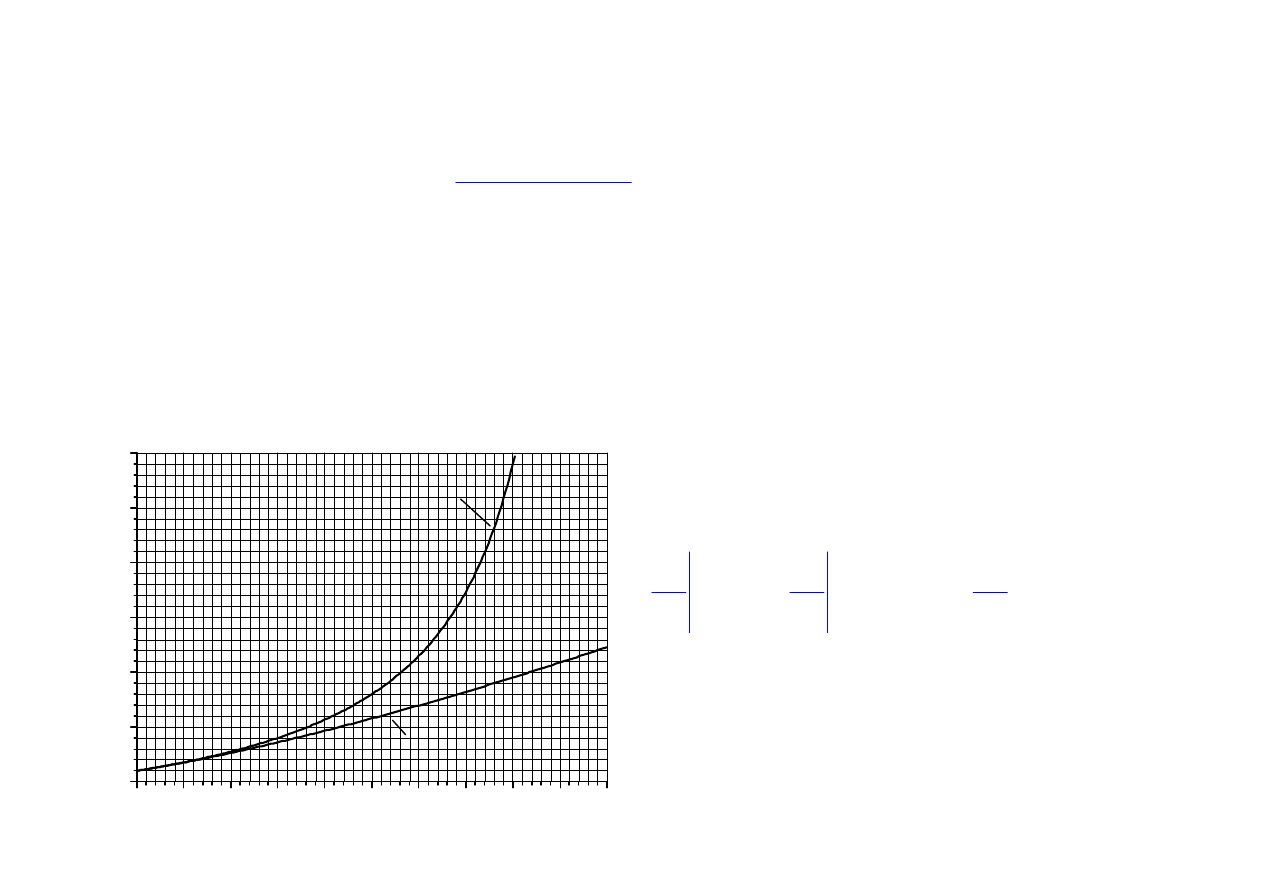
Normal shock wave (Rankin-Hugoniot)
Isentropic flow (Poisson)
Rankin-Hugoniot and Poisson adiabats ( = 1.4)

E
E
N
N
T
T
R
R
O
O
P
P
Y
Y
A
A
N
N
D
D
G
G
A
A
S
S
O
O
D
D
Y
Y
N
N
A
A
M
M
I
I
C
C
R
R
E
E
L
L
A
A
T
T
I
I
O
O
N
N
O
O
N
N
T
T
H
H
E
E
N
N
O
O
R
R
M
M
A
A
L
L
S
S
H
H
O
O
C
C
K
K
.
.
From the 1
st
Principle of Thermodynamics we have
1
(
)
p
p
dq
dp
dT
dp
dT
dp
ds
di
c
c
R
T
T
T
T
T
p
From the Clapeyron equation ….
ln
ln
ln
p
RT
p
T
const
Thus
dp
d
dT
dT
dp
d
p
T
T
p
and the differential of (mass specific) entropy can be written as
p
v
p
dp
d
dp
dp
d
ds
c
R
c
c
p
p
p
After integration we get
ln
ln
ln(
)
v
v
p
v
c
s
c
p
c
const
c
p
const

Thus, the change of entropy between two thermodynamic states can be expressed as
follows
2
1
2
1
2
2
2
1
1
1
ln
ln
ln
ln
v
v
s
s
s
p
p
p
c
c
p
Note that for the Hugoniot adiabat we have
2
2
2
1
1
1
1
0
Hugoniot
p
s
p
i.e., the shock wave cannot expand the gas (it would lead to entropy decrease which
contradics the 2
nd
Principle of Thermodynamics). Thus the ( nonrivial) shock wave
must be a compression wave! Indeed, in such case
2
2
1
1
0
p
s
p
We further observe that
1
2
2
1 1
2
2
2
1
1
1
1
1
shock
wave
and
u
u
u
u
u

Using the energy equation (integral) we also conclude that
2
2
2
1
1
2
2
1
(
) / 2
0
p
T
T
u
u
c
T
T
i.e., after crossing the shock wave the gas warms up.
We would like to know what kind of flow exists at different sides of the NSW.
Writing the energy equation in the following form
2
2
2
1
1
2
2
1
1
(
1)
(
1)
2(
1)
M
p
p
u
u
a
we obtain the following
2
1
1
1
2
1
1
1
2
2
1
2
2
2
2
2
1
(
1)
2(
1)
1
(
1)
2(
1)
p
a
u
u
u
p
a
u
u
u
Subtracting the above equations we get
2
1
2
2
1
2
1
2
1 1
2
2
1
2
(
.4)
2
1
1
1
Eq
u u
p
p
a
a
u
u
u
u
u
u

After some algebra we derive the Prandtl’s Relation
2
2
1
2
1
2
1
2
1
2
2
1
u
u
u
u
a
and u
u
u
u
u
u
a
The immediate conclusion from PR is that
1
2
u
a
and u
a
What about the Mach number?
The energy equation
2
2
2
1
2
1
1
2(
1)
a
u
a
can be divided by the square of velocity to obtain
2
2
2
2
1
1
1
1
1
a
M
u
After simple manipulations we have
2
2
1
2
1
u
a
M
From the above the following we infer that
1
1
1
u
a
M
and
2
2
1
u
a
M
Thus, the flow in front of the NSW is always supersonic, while the flow behind it –
always subsonic.
The quantity
u
a
is called the velocity coefficient. In contrast to the Mach number, the
velocity coefficient assumes values in the bounded interval, namely
1
1
1
2
,
1
1
lim
lim
1
1
M
M
The Mach number of the flow behind the wave M
2
can be expressed as the function of the
Mach number in front of the wave M
1
. To obtain this formula we use the Prandtl’s
Relation …
1
2
2
2
1
2
1
1
1
1
2
2
1
1
u u
a a
M
M
After some algebra we get
2
1
2
2
1
2 (
1)
1
2
1
M
M
M
Similarly, we can expressed the ratios of density, pressure and temperature values.
The density ratio can be evaluated as follows
1
2
1
1
1
1
1
1
1
1
2
1
1
2
2
1
2
2
1
0
0
(
)
(
)
(
)
(
)
[
(
)] 1
(
)
(
)
is
is
u
M
a
M
a
a
M
M
M
M
M M
u
M M
a
M M
a
a
To evaluate the pressure ratio (as the function of M
1
) we rewrite the momentum equation
in the following way
2
2
2
2
2
1
1
(1
)
u
u
p
u
p
p
p
M
const
p
a
Since the above expression has the same value at both sides of the shock wave, we get
2
2
1
1
2
1
2
1
1
(
)
1
1
(
)
p
M
M
p
M
M
The flow through the shock is adiabatic (total energy is conserved) and the total (or
stagnation) temperature T
0
remains the same.

Thus, we can write
0
2
2
1
1
0
2
1
(
)
(
)
1
[
(
)]
T T
M
T
M
T
T T
M
M
where the ratio
T/T
0
can be calculated from the formula derived in the Lecture 14
1
2
0
1
(
)
1
2
T
M
M
T
1
2
3
4
5
6
7
8
M
1
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
M
2
NORMAL SHOCK WAVE (
1
1.5
2
2.5
3
3.5
M
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
p
2
/
p
1
NORMAL SHOCK WAVE (
1
1.5
2
2.5
3
3.5
M
1
1
1.5
2
2.5
3
3.5
4
4.5
/
T
2
/T
1
NORMAL SHOCK WAVE (
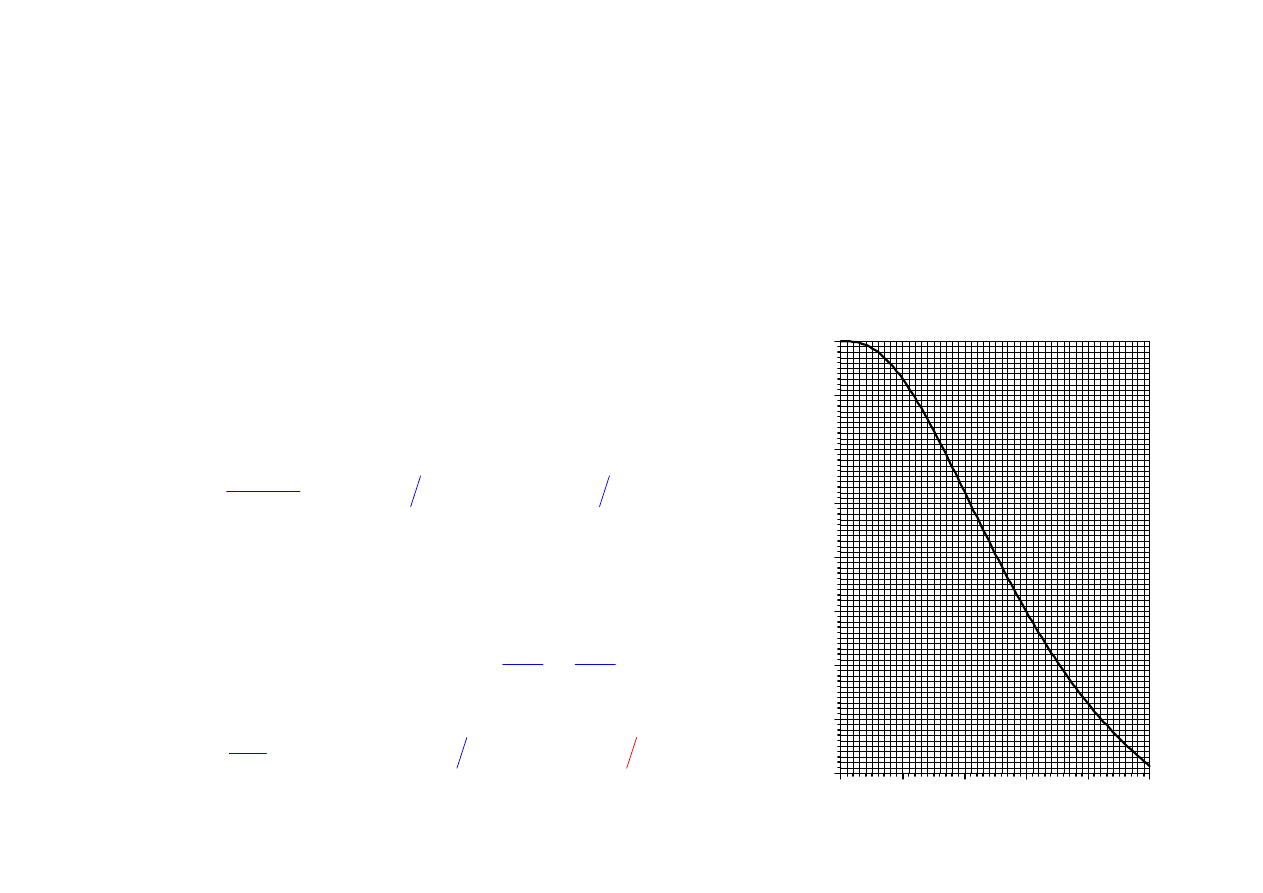
In the end, we will analyse what happens to the stagnation pressure. Conceptually, we
consider the process described as follows
01
1
2
(
)
02
01
(
)
acceleration
shock
deceleration
isentropic
wave
isentropic
p
p
p
p
p
We claim that the total (stagnation) pressure diminishes on the shock wave.
The justification of this fact goes as follows.
We know that the entropy of the gas increases on the
shock wave. The formula derived earlier can be written
for stagnation parameters, namely
2
1
02
01
02
01
0
ln
ln
v
s
s
p
p
c
Since the total temperature at both sides is the same
then
02
02
01
02
0
01
01
Clapeyron
Equation
p
T
T
T
p
Thus
2
0
1
0
0
1
02
0
(1
) ln
1
v
s
p
p
c
p
p
.
1
1.5
2
2.5
3
3.5
M
1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
p
0
2
/p
0
1
NORMAL SHOCK WAVE (
Wyszukiwarka
Podobne podstrony:
or The Use of Extracorporeal Shock Wave Therapy to Improve Fracture Healing
Shock Wave Deformation and Fracture of Zirconium Dioxide Ceramics of Various Fractional Composition
2003 Shock wave cosmology inside a black hole Smoller
Possibility of acceleration of the threshold processes for multi component gas in the front of a sho
02b Rozkład normalnyid 4039 ppt
bd normalizacja
2a Normalizacja
ODCHYŁKI NORMALNE Tablice
2006 SOM 208 Microbiology Syllabus Septic Shock
CERA NORMALNA
Normalizacja
Ceowniki Normalne
nowotwory złośliwe, Download, - ▧ Normalne, higiena
sciaga format normalny
Normalizacja kolos 1
A Toffler Future Shock
więcej podobnych podstron