[DM 2005/07]

Uwaga słowo graf oznacza graf prosty (chyba, że wyraźnie zaznaczono w treści zadania, że chodzi o multigraf).

[1/07] Udowodnij, że każdy graf można umieścić w przestrzeni R³ tak, aby krawędzie były odcinkami prostymi i aby się nie przecinały.

[2/07] Udowodnij, że dla każdego grafu G istnieje graf H taki, że G i H są homeomorficzne.

[3/07] Dla jakich parametrów n, k, r, t ∈ N grafy K_n, K_r,s, K_r,s,t, Q_k są planarne?

[4/07] Czy następujące grafy są planarne?

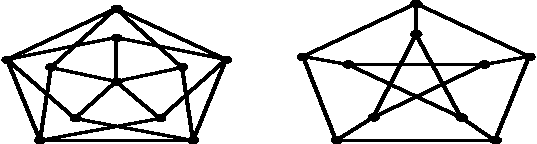
Jeśli tak - przedstaw ich płaską reprezentacje, a jeśli nie wskaż podgraf homeomorficzny z K₅ lub K_3,3 oraz wyznacz minimalną liczbę przecięć i stopień nieplanarności.

[5/07] Dla jakich r istnieją planarne grafy regularne stopnia r? Przedstaw przykłady takich grafów o najmniejszej możliwej liczbie krawędzi.

[6/07] Znajdź graf o jak największej liczbie krawędzi, którego dopełnienie jest także grafem planarnym. Czy potrafisz udowodnić, że twój przykład jest optymalny?

[7/07] Podaj przykład spójnego grafu nieplanarnego, który nie jest homeomorficzny ani z K₅ ani z K_3,3.

[8/07] Podaj przykład spójnego grafu nieplanarnego, który nie jest ściągalny ani do K₅ ani do K_3,3.

[9/07] Czy każdy graf planarny można narysować bez przecięć krawędzi tak, aby wszystkie wierzchołki leżały na prostej? Narysuj w ten sposób K₅ - e oraz K_3,3 - e.

[10/07] Czy dla każdej liczby naturalnej r istnieje graf planarny, posiadający płaską reprezentację, w której każda ściana jest incydentna z dokładnie r krawędziami i liczba ścian jest nie mniejsza niż 3?

[11/07] Udowodnij, że każdy spójny graf o n ≥ 3 wierzchołkach i 3n - 6 krawędziach zawiera co najmniej 2n - 4 trójkąty.

[12/07] Wyznacz indeks i liczbę chromatyczną grafów grafy K_n, K_r,s, K_r,s,t, Q_k dla n, k, r, t ∈ N.

[13/07] Wyznacz indeks i liczbę chromatyczną grafów z zadania [4/07].

[14/07] Czy istnieje graf kubiczny, którego indeks chromatyczny wynosi 4?

[15/07] Czy grafy K_n, K_r,s, K_r,s,t, Q_k, dla n, k, r, t ∈ N są trudne (bądź dość trudne) dla algorytmów LF, SL, SLF?

[16/07] Poniższa tabela przedstawia wymagania dotyczące harmonogramu zajęć w pewnym dniu tygodnia. W kolejnych wierszach występują kolejne klasy, a w kolumnach nauczyciele. Każdej lekcji (oznaczonej jako X) należy przydzielić odpowiednią godzinę lekcyjną. Harmonogram powinien być tak ułożony, aby budynek szkolny był wykorzystywany jak najkrócej.

Sprowadź problem do kolorowania wierzchołków lub krawędzi grafu. Narysuj odpowiedni graf i pokoloruj go jedna ze poznanych metod. Czy uzyskane rozwiązanie jest optymalne?

	Q	W	E	R	T	Y
IA	X	X		X	X
IB		X	X		X	X
IC	X		X	X		X
IIA	X	X	X		X
IIB		X		X	X	X
IIC	X		X			X

[17/07] Udowodnij, że indeks chromatyczny kubicznego grafu hamiltonowskiego wynosi 3.

[18/07] Udowodnij, że graf regularny stopnia Δ o 2005 wierzchołkach posiada indeks chromatyczny równy Δ + 1.

[19/07] Udowodnij, że dla każdego grafu G zachodzi:

[20/07] Udowodnij, że jeżeli graf G ma m krawędzi, to

[21/07] Niech k będzie długością najdłuższej ścieżki w grafie G. Udowodnij, że χ(G) ≤ k + 1.

[22/07] Udowodnij, że każdy graf G posiada co najmniej χ(G) wierzchołków o stopniu większym niż χ(G) - 2.

[23/07] Niech G będzie grafem regularnym stp. r. Wykaż, że jeżeli G posiada przegub, to χ'(G) = r + 1.

---