Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Rekurencja

1.1

Wie˙ze Hanoi

Rekurencja jest to zdolno´s´c podprogramu (procedury lub funkcji) do wywoływania sa-
mego siebie. Zacznijmy od przykładu wie˙z Hanoi. Przypu´s´cmy, ˙ze mamy trzy wie˙ze lub
trzy paliki:

,

i

. Na pierwszym paliku,

, znajduj¸a si¸e trzy kr¸a˙zki ró˙znej wielko´sci,

nanizane w porz¸adku od najwi¸ekszego na dole do najmniejszego na górze. Paliki

i

s¸a na pocz¸atku puste. Nale˙zy przenie´s´c wszystkie kr¸a˙zki z palika

na

, posługuj¸ac si¸e

w razie potrzeby palikiem

, według nast¸epuj¸acych reguł:

mo˙zna przenosi´c po jednym kr¸a˙zku z jednego palika na inny,

nie mo˙zna umieszcza´c wi¸ekszego kr¸a˙zka na mniejszym.

Rozwi¸azaniem tej łamigłówki dla trzech kr¸a˙zków jest nast¸epuj¸acy ci¸ag siedmiu przeło-

˙ze´n:

gdzie zapis

oznacza przeniesienie szczytowego kr¸a˙zka z palika

na palik

.

Chodzi nam teraz o algorytm, który dla dowolnej liczby

kr¸a˙zków wypisze ci¸ag

operacji potrzebnych do przeło˙zenia

kr¸a˙zków z palika

na palik

.

Algorytm przekładania kr¸a˙zków

je˙zeli

, to przekładamy ten jeden kr¸a˙zek

,

je˙zeli

, to:

przekładamy

kr¸a˙zków z

na pomocniczy palik

(posługuj¸ac si¸e w

razie potrzeby palikiem

),

przekładamy

-ty kr¸a˙zek z

na

,

przekładamy

kr¸a˙zków z

na

(za pomoc¸a palika

).

3

4

Rozdział 1. Rekurencja

Nietrudno zauwa˙zy´c, ˙ze je˙zeli proces przekładania

kr¸a˙zków jest prawidłowy, to

cały proces te˙z jest prawidłowy, poniewa˙z obecno´s´c najwi¸ekszego kr¸a˙zka na dole palika
nie przeszkadza w przekładaniu

mniejszych kr¸a˙zków.

Powy˙zszy algorytm opiszmy teraz za pomoc¸a rekurencyjnej procedury przenie´s, któ-

ra odwołuje si¸e sama do siebie i wypisuje ci¸ag instrukcji przeniesienia

kr¸a˙zków z palika

na palik

.

procedura przenie´s(

kr¸a˙zków z

na

, za pomoc¸a

):

je˙zeli

, to wypisz

,

je˙zeli

, to

przenie´s(

kr¸a˙zków z

na

, za pomoc¸a

),

wypisz

,

przenie´s(

kr¸a˙zków z

na

, za pomoc¸a

).

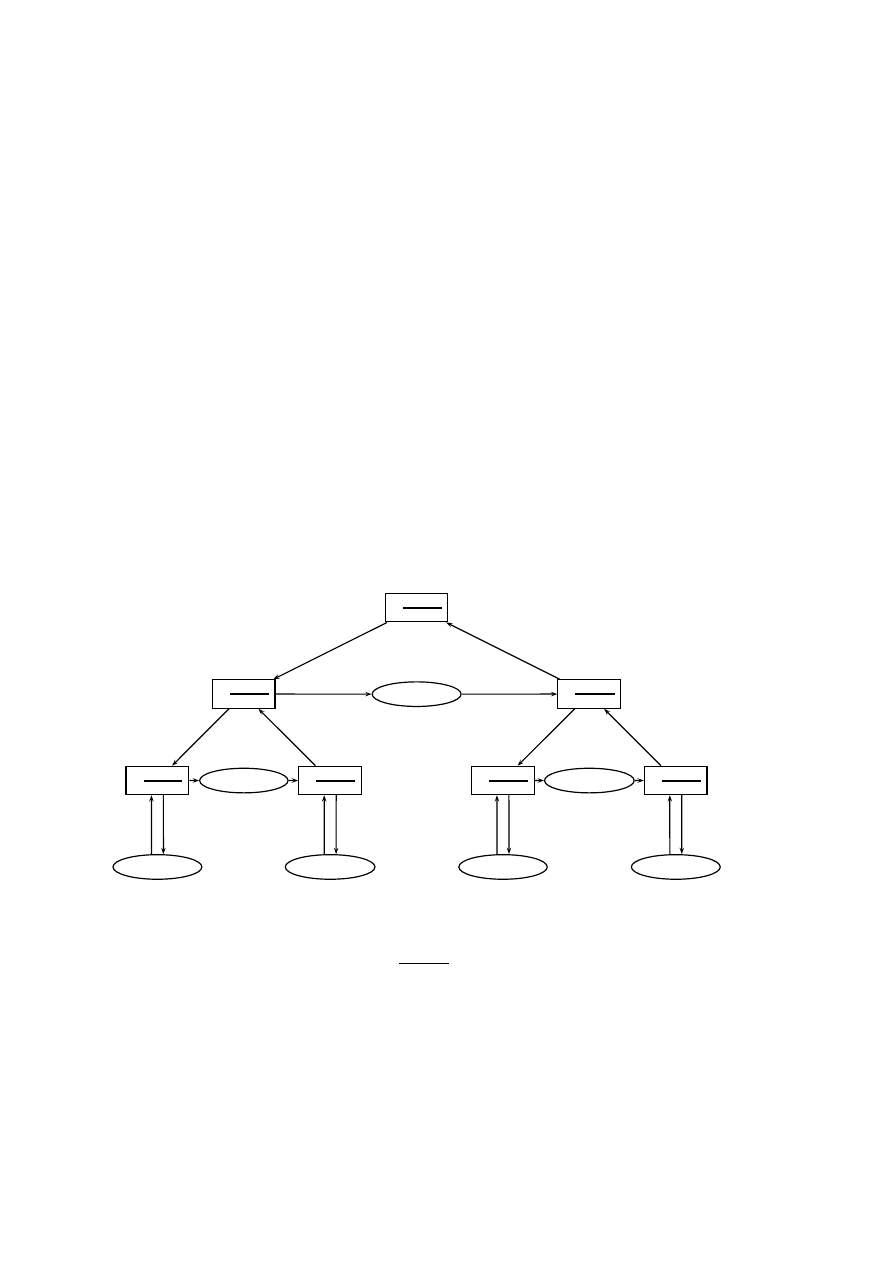
Rysunek 1.1: Schemat działania procedury przenie´s dla wie˙z Hanoi z trzema kr¸a˙zkami

Na rysunku 8.1 zilustrowano działanie procedury przenie´s dla

. Skrót

oznacza wywołanie procedury przenie´s(

kr¸a˙zków z

na

, za pomoc¸a

). Strzałki

w dół oznaczaj¸a wywołanie procedury, strzałki w gór¸e powroty po wykonaniu procedu-
ry, a strzałki poziome odpowiadaj¸a nast¸epstwu instrukcji w ramach jednego wykonania
procedury.

1.2. Algorytm Euklidesa, wersja rekurencyjna

5

1.2

Algorytm Euklidesa, wersja rekurencyjna

Innym przykładem algorytmu rekurencyjnego mo˙ze by ´c rekurencyjna wersja algorytmu
Euklidesa, który oblicza najwi¸ekszy wspólny dzielnik dwóch dodatnich liczb naturalnych

i

:

fun¯kcja NWD(a,b):

je˙zeli

, to

,

je˙zeli

, to

,

je˙zeli

, to

.

W j¸ezyku Pascal powy˙zsz¸a procedur¸e mo˙zemy zapisa´c w nast¸epuj¸acy sposób:

function NWD(a,b:integer):integer;

begin

if a=b then NWD:=a

else if

then NWD:=NWD(a-b,b)

else NWD:=NWD(a,b-a)

end;

Rysunek 1.2: Schemat działania rekurencyjnej wersji algorytmu Euklidesa

NWD(5,3):=1

NWD(2,3):=1

NWD(2,1):=1

NWD(1,1):=1

Na rysunku 8.2 przedstawiono proces obliczania funkcji NWD(7,3).

1.3

Funkcje rekurencyjne

Czasami wygodnie jest zdefiniowa´c funkcje za pomoc¸a wzoru rekurencyjnego. Na przy-
kład funkcj¸e silnia definiuje si¸e zwykle za pomoc¸a nast¸epuj¸acych dwóch równa ´n:

"!

6

Rozdział 1. Rekurencja

Podobnie mo˙zna definiowa´c inne funkcje ze zbioru liczb naturalnych w zbiór liczb natu-
ralnych. Definicja taka zawiera przepis, jak policzy´c warto´s´c funkcji dla warto´sci pocz¸atkowych,
oraz drugi przepis, jak wyliczy´c warto´s´c dla argumentu

za pomoc¸a warto´sci funkcji dla

mniejszych argumentów.

1.4

Funkcja (ci¸ag) Fibonacciego

Nast¸epnym przykładem rekurencyjnego definiowania funkcji jest funkcja Fibonacciego,
okre´slona równaniami:

!

Kolejne warto´sci funkcji Fibonacciego to:

!!!

Udowodnimy teraz przez indukcj¸e, ˙ze

(1.1)

gdzie

"

oraz

"

Równo´s´c (1.1) zachodzi dla

i

. Załó˙zmy teraz, ˙ze zachodzi dla wszystkich

argumentów mniejszych od

. Zauwa˙zmy, ˙ze

oraz

s¸a rozwi¸azaniami równania

, mamy wi¸ec

oraz

a tak˙ze

oraz

. Łatwo teraz mo˙zna pokaza´c, ˙ze

.

Poniewa˙z

, mamy

, wi¸ec warto´s´c

jest równa

!

po zaokr¸agleniu do najbli˙zszej liczby naturalnej i funkcja Fibonacciego ro´snie

wykładniczo.

1.5

Funkcja Ackermanna

Funkcja Ackermanna okre´slona jest, dla liczb naturalnych

#"

, nast¸epuj¸acymi rów-

naniami:

$"

&%

"

#"

$"

$"

"!

Funkcja Ackermanna jest przykładem funkcji maj¸acej do´s´c prost¸a definicj¸e, ale jest prak-
tycznie nieobliczalna z tego powodu, ˙ze jej warto´sci szybko rosn¸a. Na przykład:

('

)

+*

,

1.6. Algorytm sortowania przez scalanie

7

)

)

'

)

)

)

i ogólnie

)

!

1.6

Algorytm sortowania przez scalanie

Zajmijmy si¸e teraz pewnym prostym rekurencyjnym algorytem sortowania ci¸agu. Dla
prostoty załó˙zmy, ˙ze długo´s´c ci¸agu jest pot¸eg¸a dwójki.

Algorytm sortowania

je˙zeli ci¸ag ma długo´s´c jeden, to jest ju˙z posortowany,

je˙zeli ci¸ag jest dłu˙zszy, to:

dzielimy go na połowy,

sortujemy te połowy,

ł¸aczymy posortowane połowy w jeden posortowany ci¸ag.

Istota pomysłu polega na tym, ˙ze mo˙zna szybko poł¸aczy ´c dwa posortowane ci¸agi w jeden
posortowany ci¸ag. Algorytm ł¸aczenia wyja´snijmy na przykładzie. Przypu´s´cmy, ˙ze mamy
dwa ci¸agi:

'

i ˙ze chcemy je poł¸aczy´c w posortowany ci¸ag

. Na pocz¸atku ci¸ag

jest pusty. Usta-

wiamy dwa wska´zniki po jednym na pocz¸atku ka˙zdego ci¸agu (wskazane elementy b¸ed¸a
oznaczone daszkiem):

'

!

Porównujemy wskazane elementy. Mniejszy z porównanych elementów przepisujemy na
ci¸ag

i przesuwamy wska´znik w tym ci¸agu, z którego był wzi¸ety element do ci¸agu

.

W wyniku otrzymamy:

'

!

Powtarzamy ten proces tak długo, a˙z w jednym z ci¸agów ostatni element zostanie zabrany
do ci¸agu

.

'

'

'

'

'

'

'

'

!

8

Rozdział 1. Rekurencja

W takiej sytuacje pozostałe elementy tego drugiego ci¸agu przenosimy do ci¸agu

:

'

'

!

Liczba porówna ´n potrzebna do scalenia ci¸agów nie jest wi¸eksza od sumy długo´sci tych
ci¸agów.

Algorytm merge-sort (inaczej — sortowanie przez scalanie), który sortuje ci¸ag

,

mo˙zna rekurencyjnie opisa´c tak (rysunek 8.3):

merge-sort(S):

je˙zeli

ma tylko jeden element, to koniec,

je˙zeli

ma wi¸ecej elementów, to:

dzielimy ci¸ag

na połowy

i

,

merge-sort(

),

merge-sort(

),

ł¸aczymy

i

.

Rysunek 1.3: Schemat działania algorytmu merge-sort dla ci¸agu 3, 7, 5, 2, 6, 1, 8, 4

3752|6186

37|52

61|84

3|7

5|2

6|1

8|4

3

7

5

2

6

1

8

4

37

25

16

48

2357

1468

12345678

Algorytm merge-sort jest przykładem algorytmu typu „dziel i zwyci¸e˙zaj”, którego

ogólny schemat wygl¸ada tak:

je˙zeli problem jest małego rozmiaru, to rozwi¸azujemy go bezpo´srednio,

1.7. Rozwi¸azywanie równa ´n i nierówno´sci rekurencyjnych

9

je˙zeli problem jest du˙zy, to:

dzielimy problem na podproblemy,

rozwi¸azujemy podproblemy,

ł¸aczymy rozwi¸azania podproblemów w rozwi¸azanie całego problemu.

1.7

Rozwi¸azywanie równa ´

n i nierówno´

sci rekurencyjnych

Oszacujmy teraz czas działania algorytmu sortowania przez scalanie. Niech

oznacza

liczb¸e operacji porównania potrzebn¸a do posortowania ci¸agu długo´sci

. Mamy nast¸epuj¸ace

oszacowania:

(1.2)

!

(1.3)

Druga zale˙zno´s´c wynika st¸ad, ˙ze aby posortowa´c ci¸ag długo´sci

, sortujemy dwa ci¸agi

długo´sci

, a nast¸epnie potrzebujemy

porówna ´n, aby scali´c te dwie połówki. Dla pro-

stoty rozwa˙za ´n zakładamy tutaj, ˙ze

jest pot¸eg¸a dwójki,

dka jakiego´s naturalnego

.

Istnieje wiele sposobów wyliczania lub szacowania funkcji okre´slonej rekurencyjnie.

Przedstawimy teraz dwa najprostsze z nich: metod¸e podstawiania i metod¸e iteracji.

1.8

Metoda podstawiania

W metodzie podstawiania odgadujemy rozwi¸azanie albo jego oszacowanie, a nst¸epnie
pokazujemy, ˙ze jest ono poprawne. Poka˙zemy działanie tej metody szacuj¸ac zło˙zono´s´c
czasow¸a merge-sortu okre´slon¸a rekurencj¸a (1.2)-(1.3). Zgadujemy, ˙ze

dla jakiej´s stałej

i udowodnimy przez indukcj¸e, ˙ze powy˙zsza nierówno´s´c zacho-

dzi dla ka˙zdego pot¸egi dwójki

. Zachodzi ona dla

. Zakładamy teraz, ˙ze

i podstawiamy do nierówno´sci (1.3)

Ostatnia nierówno´s´c jest spełniona, je˙zeli

.

Metoda podstawiania została zastosowana w podrozdziale o funkcji Fibonacciego do

pokazania, ˙ze

(1.4)

10

Rozdział 1. Rekurencja

ale tam odgadni¸eto dokładne rozwi¸azanie. Teraz poka˙zemy jak doj´s´c do rozwi¸aznia zaczynaj¸ac
od ogólniejszej postaci. Zacznijmy od równania

!

(1.5)

Sprawd´zmy, jakie funkcje postaci

,

spełniaj¸a to równanie. Po podstawieniu do

równania (1.5) mamy

Po podzieleniu stromnami przez

, otrzymamy

"!

Jest to równanie kwadratowe z dwoma rozwi¸azaniami

oraz

, czyli dwie funkcje

oraz

spełniaj¸a równanie (1.5).

Zauwa˙zmy, ˙ze tak˙ze ka˙zda funkcja postaci

gdzie

i

to stałe, spełnia równanie (1.5). Sprawd´zmy teraz, dla jakich stałych

i

funkcja

spełnia zale˙zno´sci

i

. Otrzymujemu układ równo´sci

Powy˙zszy układ jest spełniony dla

Tak wi¸ec otrzymujemy wzór na funkcj¸e Fibonacciego

(1.6)

1.9

Metoda iteracyjna

Moteda iteracyjna polega na rozwijaniu rekursji. Jako pierwszy przykład rozwa˙zmy za-
le˙zno´s´c.

'

Dla uproszczenia zakładamy, ˙ze

jest pot¸eg¸a

'

, dla jakiego´s

naturalnego. Funkcj¸e

rozwijamy w nast¸epuj¸acy sposób:

'

1.10. Metoda rekurencji uniwersalnej

11

'

,

'

,

'

'

,

'

!!!

'

,

!!!

'

Iteracj¸e powtarzamy, a˙z ostatni składnik b¸edzie zawierał

, czyli gdy

*

.

Otrzymamy wtedy

'

,

!!!

'

'

Skorzystali´smy tu z równo´sci

oraz z faktu, ˙ze

*

i

.

Jako drugi przykład rozwa˙zmy rekursj¸e

Jak b¸edziemy j¸a rozwija´c, to otrzymamy

'

'

!!!

!!!

Dla

. Otrzymamy wtedy

)

)

(1.7)

1.10

Metoda rekurencji uniwersalnej

Przypu´s´cmy, ˙ze mamy równanie rekurencyjne

(1.8)

12

Rozdział 1. Rekurencja

gdzie

i

. Równanie takie otrzymamy szacuj¸ac czas działania algorytmu

rekurencyjnego, który metod¸a "dziel i rz¸ad´z" dzieli problem na

podproblemów rozmiaru

. Funkcja

opisuje czas potrzebny na podzielenie problemu na podproblemy i na

poł¸aczenie rozwi¸aza ´n podproblemów w rozwi¸azanie całego problemu.

Na koniec podamy bez dowodu twierdzenie mówi¸ace jak mo˙zna szacowa ´c funkcj¸e

okre´slon¸a równaniem (1.8).

Twierdzenie 1.1 (o rekurencji uniwersalnej) Niech

b¸edzie okre´slone dla nieujem-

nych liczb całkowitych równaniem rekurencyjnym

"

gdzie

,

i

"

oznacza

"

lub

. Wtedy

Je˙zeli

dla pewnej stałej

, to

.

Je˙zeli

, to

.

Je˙zeli

dla pewnej stałej

oraz

dla

pewnej stałej

, to

.

1.11

Zadania

1. Napisz program, który rekurencyjnie oblicza: a) funkcj¸e silnia, b) funkcj¸e Fibonac-

ciego, c) funkcj¸e wykładnicz¸a

.

2. Napisz program, który oblicza symbol Newtona:

a) według wzoru rekurencyjnego

b) według wzoru

!

Porównaj te programy.

3. Napisz program, który rekurencyjnie oblicza funkcj¸e:

!

4. Oblicz

'

według rekurencyjnego algorytmu Euklidesa.

5. Według algorytmu ł¸aczenia poł¸acz ci¸agi

i

'

.

1.11. Zadania

13

6. Stosuj¸ac algorytm merge-sort posortuj ci¸ag słów: słowik, wróbel, kos, jaskółka,

kogut, dzi¸ecioł, gil, kukułka, szczygieł, sowa, kruk, czubatka.

[Fragment wiersza Ptasie radio Juliana Tuwima]

7. Dana jest funkcja

:

"!

Oblicz

. Co oblicza funkcja

?

8. Dana jest funkcja

:

!

Oblicz

'

. Co oblicza funkcja

?

9. Wypisz ci¸ag przeło˙ze ´n potrzebnych do przeniesienia czterech kr¸a˙zków na wie˙zach

Hanoi.

10. Udowodnij, ˙ze algorytm opisany w podrozdziale 8.1 wymaga

przeło˙ze´n do

przeniesienia

kr¸a˙zków.