Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Kombinatoryka

1.1

Ci¸agi

Zastanówmy si¸e, ile ci¸agów długo´sci

mo˙zna utworzy´c z elementów zbioru zawieraj¸acego

symboli. Je˙zeli zbiór symboli zawiera dwa elementy:

to mo˙zna utworzy´c dwa ci¸agi długo´sci jeden:

cztery ci¸agi długo´sci dwa:

Aby uzyska´c ci¸agi długo´sci trzy, post¸epujemy w nast¸epuj¸acy sposób: bierzemy cztery
ci¸agi długo´sci dwa i najpierw do ka˙zdego z nich dopisujemy na pocz¸atku

. Otrzymujemy

w ten sposób komplet:

Zauwa˙zmy, ˙ze s¸a to wszystkie ci¸agi długo´sci trzy z pierwsz¸a liter¸a

. Potem do tych

samych czterech ci¸agów długo´sci dwa dopisujemy na pocz¸atku symbol

i otrzymujemy

komplet:

Komplety te s¸a rozł¸aczne i oba zawieraj¸a ró˙zne ci¸agi. Razem tworz¸a zbiór wszystkich
ci¸agów długo´sci trzy:

Post¸epuj¸ac podobnie, mo˙zemy otrzyma´c szesna´scie ci¸agów długo´sci cztery.

3

4

Rozdział 1. Kombinatoryka

Twierdzenie 1.1 Liczba ci¸agów długo´sci

o elementach ze zbioru

wynosi

.

Dowód przez indukcj¸e. Jak ju˙z pokazano, s¸a dwa ci¸agi długo´sci jeden.

Załó˙zmy teraz, ˙ze liczba ci¸agów długo´sci

wynosi

i zauwa˙zmy, ˙ze wszystkich

ci¸agów długo´sci

jest dwa razy wi¸ecej. Jest

ci¸agów z pierwszym elementem

i

ci¸agów z pierwszym elementem

. Razem mamy

ci¸agów długo´sci

.

Je˙zeli zbiór symboli zawiera

elementów, to powtarzaj¸ac powy˙zsze rozumowanie,

mo˙zemy si¸e przekona´c, ˙ze istnieje

ci¸agów długo´sci jeden,

ci¸agów długo´sci dwa i

ogólnie ci¸agów długo´sci

jest

razy wi¸ecej ni˙z ci¸agów długo´sci . Zachodzi zatem

twierdzenie.

Twierdzenie 1.2 Liczba ci¸agów długo´sci

o elementach ze zbioru

-elementowego wy-

nosi

.

1.2

Funkcje

Policzmy teraz, ile jest funkcji ze zbioru

w zbiór

. Przypu´s´cmy, ˙ze zbiór

zawiera

elementów:

Ka˙zd¸a funkcj¸e

z

w

mo˙zna przedstawi´c jako ci¸ag

Ci¸ag ten jest długo´sci , a jego elementy s¸a wzi¸ete ze zbioru

. Zauwa˙zmy, ˙ze ka˙zdej

funkcji odpowiada jeden ci¸ag, i na odwrót, ka˙zdy ci¸ag

opisuje jedn¸a funkcj¸e. Mianowicie funkcj¸e, która dla ka˙zdego

!

przypisuje warto´s´c

!

"

.

Przykład 1.3 Je˙zeli

składa si¸e z czterech elementów:

#

%$

'&(

a

składa si¸e z trzech elementów:

)#

'$(

to ci¸ag

opisuje funkcj¸e stał¸a (która w całej swojej dziedzinie przyjmuje warto´s´c

), a ci¸ag

%$

%$

opisuje funkcj¸e

, która przyjmuje nast¸epuj¸ace warto´sci:

*

$

$

&

$

1.3. Ci¸agi bez powtórze ´n

5

Z powy˙zszego wynika, ˙ze funkcji ze zbioru

w zbiór

jest tyle samo co ci¸agów długo´sci

z elementami ze zbioru

. Udowodnili´smy wi¸ec poni˙zsze twierdzenie.

Twierdzenie 1.4 Je˙zeli zbiór

zawiera

elementów, a zbiór

zawiera

elementów, to

liczba funkcji ze zbioru

w zbiór

wynosi

.

1.3

Ci¸agi bez powtórze ´n

Policzmy teraz, ile jest ci¸agów bez powtórze ´n, czyli ci¸agów ró˙znowarto´sciowych. Je˙zeli
elementy bierzemy ze zbioru trzyelementowego

%$

to mo˙zemy utworzy´c trzy ci¸agi jednoelementowe:

$

sze´s´c ró˙znowarto´sciowych ci¸agów dwuelementowych:

%$

'$

$

$

oraz sze´s´c ci¸agów trójelementowych:

'$

'$

'$

'$

$

$

Nie ma, oczywi´scie, dłu˙zszych ci¸agów ró˙znowarto´sciowych utworzonych z elementów
zbioru

'$(

.

Twierdzenie 1.5 Je˙zeli elementy wybieramy ze zbioru

-elementowego

, to liczba ci¸agów

-elementowych bez powtórze´n, które mo˙zna wybra´c z tego zbioru, wynosi:

*

W tym wyra˙zeniu mamy iloczyn

kolejnych liczb, poczynaj¸ac od

, a ko´ncz¸ac

na

.

Dowód. Je˙zeli budujemy ci¸ag bez powtórze ´n, to na pierwszy element ci¸agu mo˙zemy wy-
bra´c ka˙zdy z

elementów zbioru

, na drug¸a pozycj¸e w ci¸agu mo˙zemy wybra ´c ju˙z tylko

jeden z

elementów (wszystkie poza tym, który został wybrany na pierwszy element

ci¸agu) i tak dalej, na ka˙zd¸a kolejn¸a pozycj¸e mamy o jeden element do wyboru mniej.

Zauwa˙zmy, ˙ze je˙zeli

, to:

, co jest zgodne z tym, ˙ze

w takim przypadku nie mo˙zna utworzy´c ˙zadnego -elementowego ci¸agu bez powtórze ´n
z elementami ze zbioru

.

6

Rozdział 1. Kombinatoryka

1.4

Permutacje

Permutacje to ci¸agi bez powtórze ´n długo´sci

, wybierane ze zbioru

-elementowego. Na

przykład, mamy dwie permutacje dwuelementowe:

oraz sze´s´c permutacji trzyelementowych:

'$

'$

%$

%$

$

$

Zgodnie z twierdzeniem ?? liczba permutacji w zbiorze

-elementowym wynosi:

czyli jest równa

.

Funkcja silnia

okre´slona jest dla

w nast¸epuj¸acy sposób:

"

!

Dodatkowo przyjmujemy

. Mamy wi˛ec

$

$

&

$

&

*

&

Warto´sci funkcji silnia szybko rosn¸a, na przykład:

$

&$$

Dla przybli˙zonego obliczania silni korzysta si¸e ze wzoru Stirlinga:

(1.1)

Dla ka˙zdego

zachodz¸a równie˙z nast¸epuj¸ace oszacowania:

!#"

(1.2)

Dowody wzoru Stirlinga oraz powy˙zszych oszacowa ´n wychodz¸a poza zakres tego podr¸ecznika.

Czasami u˙zywa si¸e innej definicji permutacji. Mianowicie permutacja

-elementowa

to dowolna funkcja ró˙znowarto´sciowa ze zbioru

na ten sam zbiór. Na ozna-

czenie permutacji

u˙zywa si¸e zapisu:

$

&%

Przykład 1.6 Permutacja:

$

$

&

&

$'%

jest funkcj¸a, która przyjmuje nast¸epuj¸ace warto´sci:

$

&

&

$

1.5. Podzbiory

7

Dwie permutacje

-elementowe mo˙zna składa´c tak, jak składa si¸e funkcje. Zło˙zenie

permutacji

i

okre´slone jest wzorem:

Na przykład:

$

$

&

&

$

%

$

$

&

$

&'%

$

$

&

&

$

%

Zbiór wszystkich permutacji na zbiorze

z działaniem zło˙zenia ma nast¸epuj¸ace własno´sci:

Zło˙zenie permutacji jest ł¸aczne. To znaczy, dla ka˙zdych trzech permutacji

,

,

:

W´sród permutacji istnieje identyczno´s´c

!

, czyli permutacja, która ka˙zdemu

z

dziedziny przypisuje warto´s´c

!

. Identyczno´s´c jest elementem neutralnym

składania permutacji, poniewa˙z dla ka˙zdej permutacji

:

!

!

Dla ka˙zdej permutacji

istnieje permutacja odwrotna (funkcja odwrotna)

,

spełniaj¸aca warunek:

!

Powy˙zsze zale˙zno´sci oznaczaj¸a, ˙ze zbiór wszystkich permutacji na zbiorze

z

działaniem składania permutacji stanowi grup¸e.

1.5

Podzbiory

Policzmy teraz, ile podzbiorów ma sko ´nczony zbiór

-elementowy. Je˙zeli zbiór składa

si¸e z trzech elementów:

to mo˙zemy łatwo wypisa´c wszystkie jego podzbiory:

Tych podzbiorów jest osiem. Ka˙zdy zbiór trzyelementowy posiada osiem podzbiorów,
poniewa˙z nie ma znaczenia, jak nazywaj¸a si¸e elementy zbioru. Zbiór pusty ma tylko jeden
podzbiór: zbiór pusty. Je˙zeli zbiór zawiera jeden element

, to ma dwa podzbiory:

8

Rozdział 1. Kombinatoryka

a je˙zeli zbiór zawiera dwa elementy

, to ma cztery podzbiory:

Rozwa˙zmy teraz ogólnie podzbiory zbioru

'$

Z ka˙zdym podzbiorem

%$

jest zwi¸azana jego funkcja charakterystyczna, okre´slona nast¸epuj¸acym wzorem:

!

!

!

Dziedzin¸a funkcji

jest zbiór

, a przeciwdziedzin¸a zbiór

. Zauwa˙zmy,

˙ze ka˙zdemu podzbiorowi odpowiada jedna funkcja charakterystyczna, i na odwrót, je˙zeli

we´zmiemy dowoln¸a funkcj¸e:

to wyznacza ona zbiór:

!

!

Przykład 1.7 Dla

funkcja charakterystyczna

zbioru

'$

jest opisana

przez ci¸ag

, a ci¸ag

opisuje funkcj¸e charakterystyczn¸a zbioru:

%$

'&(

.

Z powy˙zszych rozwa˙za ´n wynika, ˙ze liczba podzbiorów zbioru

-elementowego jest rów-

na liczbie funkcji ze zbioru

w zbiór

. Czyli na podstawie twierdzenia ??

mamy twierdzenie poni˙zsze.

Twierdzenie 1.8 Ka˙zdy zbiór

-elementowy ma

podzbiorów.

1.6

Podzbiory

-elementowe

Zastanówmy si¸e teraz nad podzbiorami okre´slonej mocy. Mówimy, ˙ze zbiór jest mocy

,

je˙zeli zawiera

elementów. Dla zbioru czteroelementowego

%$

&

mamy jeden podzbiór pusty (zeroelementowy), cztery podzbiory jednoelementowe:

$

&(

sze´s´c podzbiorów dwuelementowych:

%$

&

%$

&

$

'&(

1.6. Podzbiory -elementowe

9

cztery podzbiory trzyelementowe:

'$(

'&(

'$

&(

'$

&

i jeden podzbiór czteroelementowy:

'$

'&(

Liczb¸e podzbiorów -elementowych zbioru

-elementowego oznacza si¸e przez

$

%

Jest to tak zwany symbol Newtona. Inaczej,

jest równe liczbie sposobów na jakie

mo˙zna wybra´c

elementów ze zbioru

elementowego. Wła´snie pokazali´smy, ˙ze:

$

&

%

$

&

%

&

$

&

%

$

&

$

%

&

$

&

&

%

Z definicji wynika, ˙ze je˙zeli

, to

. Zachodz¸a dwa wzory:

$

%

$

%

(1.3)

$

%

$

%

$

%

(1.4)

Wzór (??) bierze si¸e z prostej obserwacji, ˙ze wybranie

elementów, które nale˙z¸a do

podzbioru

, jest równowa˙zne wybraniu

elementów, które do

nie nale˙z¸a.

Aby uzasadni´c równo´s´c (??), rozwa˙zmy -elementowe podzbiory zbioru

Policzmy osobno te podzbiory, które zawieraj¸a element

, i osobno te, które go nie

zawieraj¸a. Podzbiorów nie zawieraj¸acych

jest

, bo wszystkie

elementów trze-

ba wybra´c ze zbioru

. Podzbiorów zawieraj¸acych

jest

, bo

elementów trzeba wybra´c ze zbioru

. Razem wszystkich -elementowych pod-

zbiorów zbioru

jest

.

Korzystaj¸ac z równo´sci (??), mo˙zemy oblicza´c symbole Newtona rekurencyjnie. Naj-

pierw mamy

, poniewa˙z jest jeden zeroelementowy (pusty) podzbiór zbioru zero-

elementowego (pustego). Je˙zeli mamy ju˙z policzone symbole Newtona dla

, to mo˙zemy

liczy´c, ile jest podzbiorów zbioru

-elementowego. Zaczynamy od

oraz

, a nast¸epnie korzystamy z równania (??). Metod¸e t¸e ilustruje tak zwany trójk¸at

Pascala:

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

1

5

10

10

5

1

1

6

15

20

15

6

1

10

Rozdział 1. Kombinatoryka

W

-tym wierszu (wiersze numerowane s¸a od

) znajduj¸a si¸e symbole Newtona:

$

%

$

%

$

%

$

%

Na skraju znajduj¸a si¸e jedynki, poniewa˙z

. -ty element w

-tym wierszu

dla

jest sum¸a dwóch elementów stoj¸acych bezpo´srednio nad nim:

$

%

$

%

$

%

Je˙zeli

, to symbol Newtona mo˙zna te˙z obliczy´c ze wzoru:

$

%

*

(1.5)

lub

$

%

(1.6)

Oto uzasadnienie wzoru (??): Aby wybra´c podzbiór -elementowy ze zbioru

,

wybieramy -elementowy ci¸ag bez powtórze ´n i bierzemy do podzbioru elementy tego
ci¸agu ignoruj¸ac ich kolejno´s´c. Poniewa˙z ka˙zdemu -elementowemu podzbiorowi odpo-
wiada

ci¸agów o tych samych elementach, wi¸ec podzbiorów jest

razy mniej ni˙z

-elementowych ci¸agów bez powtórze ´n. Wzór (??) wynika teraz z twierdzenia ??, a

wzór (??) bezpo´srednio ze wzoru (??).

Wzór (??) pozwala wyprowadzi´c oszacowania na warto´s´c symbolu Newtona, dla

:

$

%

*

$

%

$

*

%

Poniewa˙z, jak łatwo sprawdzi´c

"

"

dla ka˙zdego

!

. Korzystaj¸ac

z nierówno´sci

wyprowadzonej ze wzoru Stirlinga (??), otrzymujemy górne

ograniczenie:

$

%

1.7

Dwumian Newtona

Symbole Newtona wyst¸epuj¸a w znanym twierdzeniu Newtona.

Twierdzenie 1.9 (dwumian Newtona) Dla ka˙zdej liczby rzeczywistej

oraz liczby cał-

kowitej

zachodzi:

$

%

1.7. Dwumian Newtona

11

Pierwszy dowód.

jest wielomianem stopnia

. Policzmy współczynnik tego

wielomianu stoj¸acy przy

'

. Rozwa˙zmy iloczyn:

razy

Przy rozwijaniu tego wyra˙zenia wybieramy z ka˙zdego czynnika

lub

, potem wymna-

˙zamy wybrane elementy i sumujemy tak utworzone iloczyny. W iloczynie otrzymamy

wtedy, gdy

wybierzemy

razy oraz

wybierzemy

razy. Mo˙zna to zrobi ´c na

sposobów, tak wi¸ec współczynnik przy

wynosi

.

Drugi dowód przez indukcj¸e. Wzór jest oczywisty dla

. Załó˙zmy teraz, ˙ze jest

prawdziwy dla

. Mamy:

$

%

Współczynnik przy

'

po prawej stronie wynosi:

$

%

$

%

Pierwszy składnik pochodzi od iloczynu:

, a drugi od iloczynu:

. Ze

wzoru (??) wynika, ˙ze współczynnik przy

wynosi

.

Je˙zeli do wzoru Newtona podstawimy

, a potem pomno˙zymy obie strony przez

,

to otrzymamy inn¸a znan¸a wersj¸e wzoru Newtona.

Wniosek 1.10 Dla dowolnych liczb rzeczywistych

i

i dowolnej liczby całkowitej

:

$

%

Je˙zeli podstawimy

do wzoru z twierdzenia ??, to otrzymamy:

$

%

co potwierdza jeszcze raz, ˙ze wszystkich podzbiorów zbioru

-elementowego jest

.

Zobaczymy teraz, ˙ze w´sród wszystkich podzbiorów zbioru

jest tyle samo

podzbiorów mocy parzystej (o parzystej liczbie elementów) i podzbiorów mocy niepa-
rzystej (o nieparzystej liczbie elementów).

Twierdzenie 1.11 Dla ka˙zdego zbioru zawieraj¸acego

elementów, liczba podzbiorów

parzystej mocy jest równa liczbie podzbiorów nieparzystej mocy.

12

Rozdział 1. Kombinatoryka

Pierwszy dowód. Je˙zeli podstawimy

do wzoru Newtona, to otrzymamy:

$

%

Zauwa˙zmy, ˙ze w sumie po prawej stronie z plusem wyst¸epuj¸a symbole Newtona

dla parzystych , a z minusem — dla nieparzystych . Tak wi¸ec z plusem mamy liczb¸e
podzbiorów parzystej mocy, a z minusem liczb¸e podzbiorów nieparzystej mocy. Z powy˙z-
szego wzoru wynika, ˙ze podzbiorów parzystej mocy jest tyle samo co podzbiorów mocy
nieparzystej.
Drugi dowód. Rozwa˙zmy funkcj¸e

, która ka˙zdemu podzbiorowi

przyporz¸adkuje podzbiór

czyli ró˙znic¸e symetryczn¸a zbioru

i zbioru jednoelementowego

. Zauwa˙zmy, ˙ze

funkcja

ł¸aczy podzbiory w pary, poniewa˙z je˙zeli

, to

. Rzeczywi-

´scie, je˙zeli

zawiera

, to

)

i

*

. Je˙zeli natomiast

nie zawiera

, to

)

i równie˙z

*

.

Pozostaje zauwa˙zy´c, ˙ze z pary zbiorów

i

jeden jest mocy parzystej i jeden

nieparzystej.

1.8

Zasada szufladkowa Dirichleta

Zasada szyfladkowa Dirichleta w najprostszej postaci mówi, ˙ze je˙zeli mamy

kul i chce-

my je rozmie´sci´c w

szufladach, to w przynajmniej jednej szufladzie musi znale´z ´c

si˛e wi˛ecej ni˙z jedna kula.

Zasada ta jest intuicyjnie bardzo prosta, ale jest cz˛esto u˙zywana. W nieco ogólniejszej

postaci brzmi ona nast˛epuj ˛

aco:

Twierdzenie 1.12 (Zasada szufladkowa Dirichleta) Je˙zeli zbiór

podzielimy na

pod-

zbiorów, to przynajmniej jeden z tych podzbiorów ma

lub wi˛ecej elementów.

Dowód Nie wprost. Przypu´s´cmy, ˙ze ka˙zdy z

podzbiorów ma mniej ni˙z

elemen-

tów. Wtedy cały zbiór

ma mniej ni˙z

elementów; sprzeczno´s´c.

1.9

Zasada sumy

W najprostszej postaci zasada sumy, mówi ˙ze moc sumy dwóch zbiorów

i

jest równa

1.10. Zasada wł¸aczania i wył¸aczania

13

Wyobra´zmy sobie, ˙ze obliczaj¸ac praw¸a stron¸e tej równo´sci liczymy po kolei elementy
zbioru

i dla ka˙zdego elementu dodajemy

do ogólnej sumy, nast¸epnie liczymy ele-

menty zbiorów

i dla ka˙zdego dodajemy

, a na ko ´ncu liczymy elementy przekroju

i dla ka˙zdego dodajemy

. Zastanówmy si¸e teraz jaki jest udział poszczególnych

elementów w tak powstałej sumie. Je˙zeli jaki´s element wyst¸epuje tylko w

lub tylko w

, to jego udział wynosi 1. Ale tak˙ze, je˙zeli nale˙zy do obu zbiorów

i

to jego udział

wynosi

. Dlatego na ko ´ncu wynik b¸edzie równy liczbie elementów, które

nale˙z¸a do jednego lub drugiego zbioru.

Przykład 1.13 Policzmy ile spo´sród liczb od 1 do 30 jest podzielnych przez 2 lub 3. Niech

oznacza zbiór liczb z tego przedziału podzielnych przez 2, a

zbiór liczb podzielnych

przez 3. Liczby podzielne przez 2 lub 3 tworz¸a zbiór

. Mamy

oraz

zawiera liczby podzielne przez 2 i 3, czyli podzielne przez 6. Ze wzoru na sum¸e

otrzymujemy:

Podobnie mo˙zemy uzasadni´c wzór na sum¸e trzech zbiorów:

Je˙zeli zastosujemy podobne liczenie, to udział elementów, które nale˙z¸a tylko do jednego
zbioru, wynosi 1, tych, które nale˙z¸a do dwóch (ale nie do trzech naraz), wynosi

, a tych, które nale˙z¸a do wszystkich trzech zbiorów,

*

*

.

Przykład 1.14 Policzmy ile spo´sród liczb od 1 do 30 jest podzielnych przez 2, 3, lub 5.
Niech

oznacza zbiór liczb podzielnych przez 2,

zbiór liczb podzielnych przez 3,

a

podzielnych przez 5. Mamy

,

,

,

,

$

,

,

. Ze wzoru na sum¸e otrzymujemy:

$

*

Jak wida´c, tylko osiem liczb mniejszych od 30 nie jest podzielnych przez 2, 3 lub 5; s¸a to:
1, 7, 11, 13, 17, 19, 23, 29.

W nast¸epnym podrozdziale poka˙zemy jak mo˙zna obliczy ´c sumy dowolnej sko ´nczonej

klasy zbiorów.

1.10

Zasada wł¸aczania i wył¸aczania

Zacznijmy od przykładu. W grupie 100 studentów 45 uprawia koszykówk¸e, 53 pływanie,
a 28 jedno i drugie. Pytanie: ilu studentów nie uprawia ani koszykówki, ani pływania?

Zadanie to mo˙zna rozwi¸aza´c „na palcach”.

&

studentów uprawia tylko

koszykówk¸e, a

$

studentów uprawia tylko pływanie. Zatem

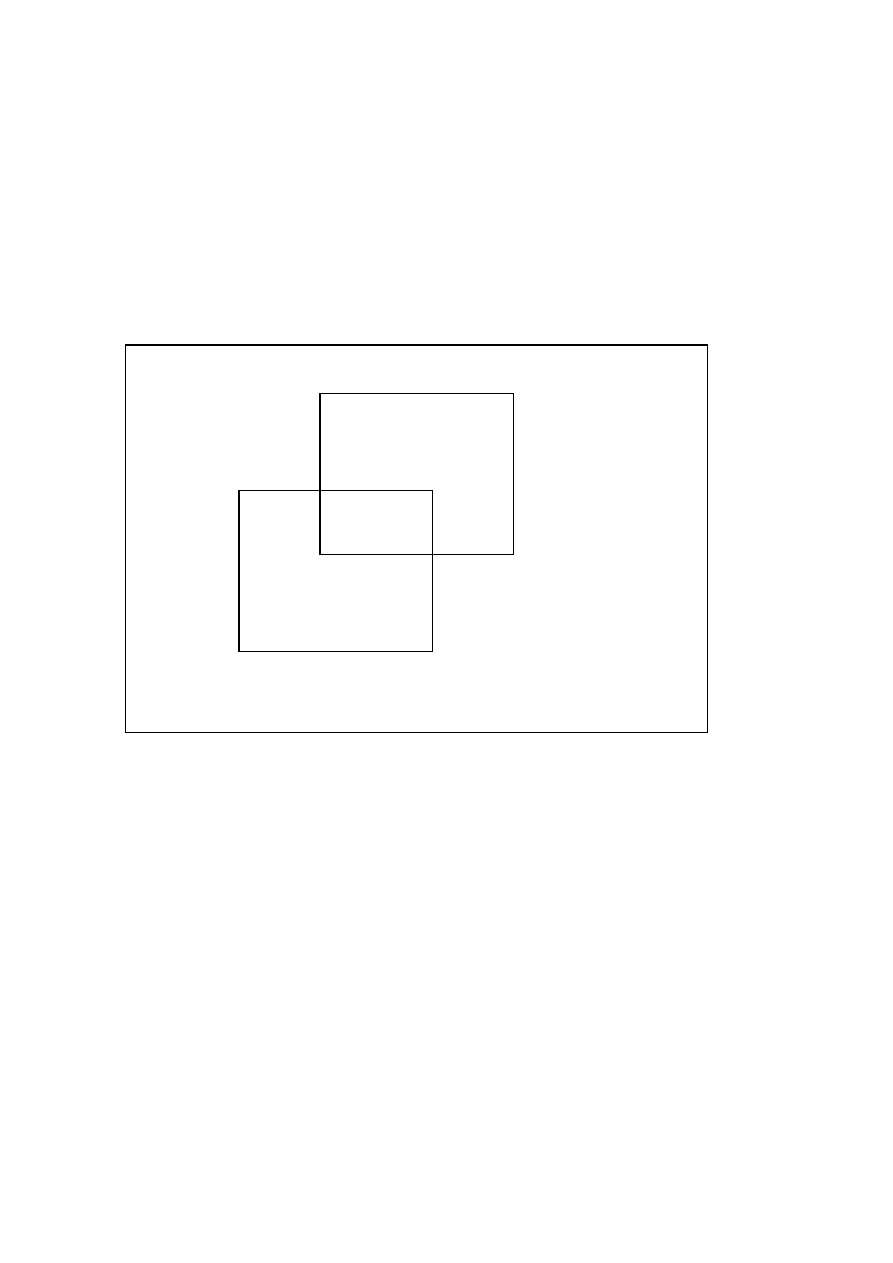
14

Rozdział 1. Kombinatoryka

Rysunek 1.1: Diagram Venna

pływanie

25

28

28

30

koszykówka

17

studentów uprawia jeden z dwóch sportów, a

$

nie uprawia ani koszykówki,

ani pływania. Na rysunku 1.1 zilustrowano ten przykład. Jest to tak zwany diagram Venna
.

Przypu´s´cmy teraz, ˙ze s¸a tak˙ze studenci graj¸acy w szachy. Graj¸acych w szachy jest

55. Takich, którzy graj¸a w koszykówk¸e i szachy, jest 32, takich, którzy graj¸a w szachy
i pływaj¸a, jest 35, a takich, którzy uprawiaj¸a wszystkie trzy sporty, jest 20. To zadanie
te˙z mo˙zna rozwi¸aza´c za pomoc¸a diagramu Venna (rysunek 1.2). Na przykład, 8 studen-
tów uprawia koszykówk¸e i pływanie, ale nie gra w szachy, a 22 studentów nie uprawia

˙zadnego sportu.

Zasada wł¸aczania i wył¸aczania pozwala rozwi¸azywa´c tego typu zadania bez diagra-

mów Venna.

Niech

b¸edzie naszym uniwersum,

jego podzbiorami. Dla ka˙zdego

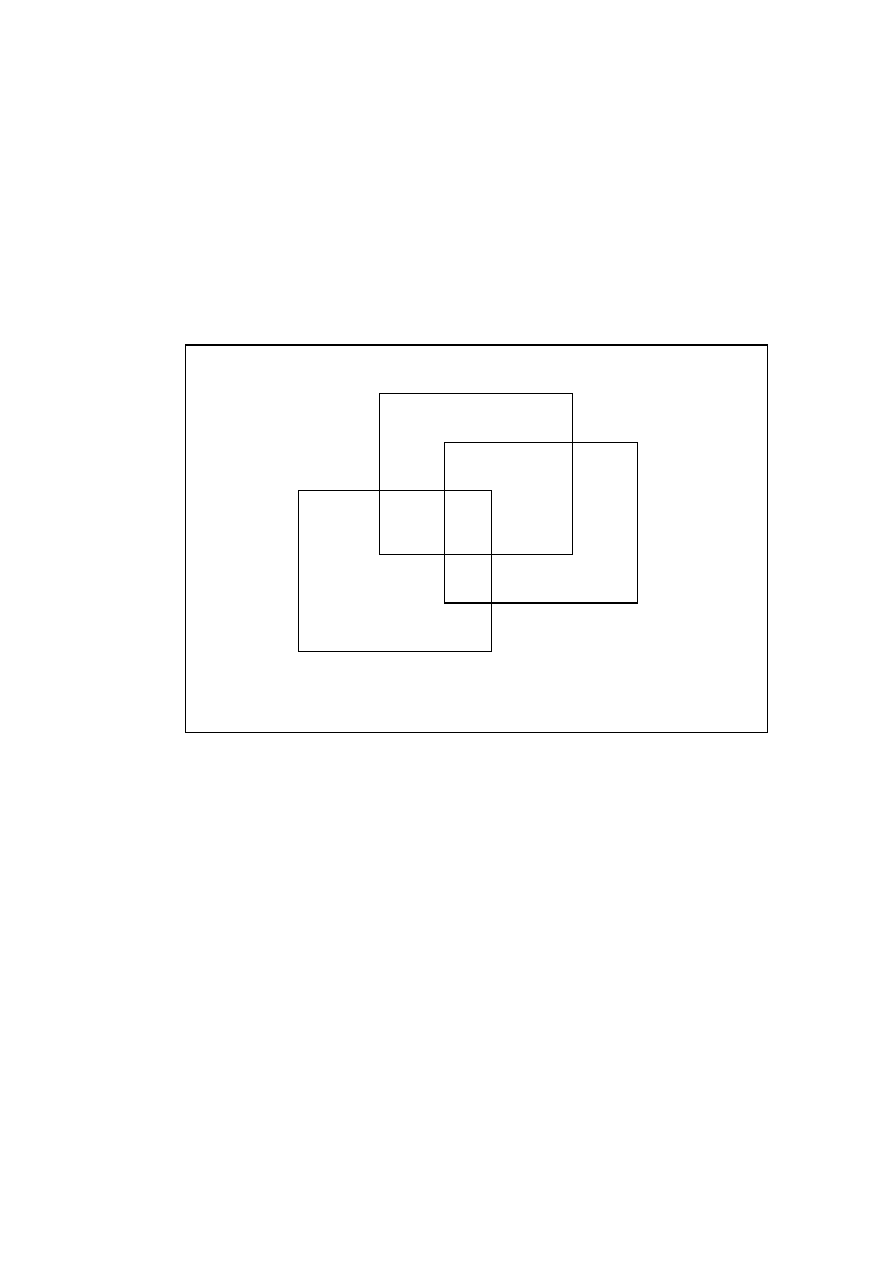
1.10. Zasada wł¸aczania i wył¸aczania

15

Rysunek 1.2: Diagram Venna

pływanie

10

15

8

20

12

5

8

22

koszykówka

szachy

podzbioru

zbioru indeksów

definiujemy zbiór:

"

"

przyjmujemy przy tym

W naszym przykładzie

to zbiór wszystkich studentów,

to uprawiaj¸acy koszykówk¸e,

— pływanie, a

— szachy:

to uprawiaj¸acy koszykówk¸e i pływanie,

to uprawiaj¸acy koszykówk¸e i szachy,

to uprawiaj¸acy pływanie i szachy,

to uprawiaj¸acy wszystkie trzy sporty.

16

Rozdział 1. Kombinatoryka

Twierdzenie 1.15 (zasada wł¸aczania i wył¸aczania) Liczba elementów uniwersum

, któ-

re nie nale˙z¸a do ˙zadnego podzbioru

"

, wynosi:

(1.7)

Sumujemy tutaj po wszystkich podzbiorach

zbioru

.

Dowód. Podobnie jak w poprzednim podrozdziale, ˙zeby obliczy ´c sum¸e (??), liczymy ele-
menty poszczególnych zbiorów

, i dla ka˙zdego elementu dodajemy

do sumy

(

, gdy

jest parzyste, lub

, gdy

jest nieparzyste). Udział pojedynczego elemen-

tu

w tak utwirzonej sumie wynosi

czyli jest równy sumie współczynników

dla tych podzbiorów

, dla

których

.

Je˙zeli

nie nale˙zy do ˙zadnego z podzbiorów

"

, to

jest liczony tylko raz, w zbio-

rze

, i jego udział w sumie (??) wynosi 1. Przypu´s´cmy teraz, ˙ze

nale˙zy do jaki´s

podzbiorów i niech

!

"

czyli

to indeksy tych podzbiorów, które zawieraj¸a

. Zauwa˙zmy teraz, ˙ze

wtedy

i tylko wtedy, gdy

. Rzeczywi´scie

"

"

wtedy i tylko wtedy, gdy

"

, dla ka˙zdego

!

, czyli gdy

. Tak wi¸ec udział elementu

w sumie (??)

wynosi:

Jest to suma po wszystkich podzbiorach

zbioru

. Uporz¸adkujmy teraz składniki tej

sumy według mocy podzbiorów

i niech

. Mamy

"

podzbiorów mocy

!

, wi¸ec:

"

$

!

%

"

Przedostatnia równo´s´c wynika ze wzoru Newtona.

Tak wi¸ec wkłady elementów, które nie nale˙z¸a do ˙zadnego

"

, wynosz¸a po 1, a wkłady

tych elementów, które nale˙z¸a do jakiego´s

"

, wynosz¸a po 0. A zatem suma (??) zlicza

elementy nie nale˙z¸ace do ˙zadnego

"

.

Stosuj¸ac zasad¸e wł¸aczania i wył¸aczania do przykładu ze studentami mo˙zemy teraz

policzy´c studentów, którzy nie uprawiaj¸a ˙zadnego sportu:

&

$

$

$

1.11. Przestawienia

17

Aby policzy´c moc sumy zbiorów

"

"

mo˙zemy wykorzysta´c wzór (??), przy zało˙zeniu, ˙ze

"

"

. Mamy wtedy

Twierdzenie 1.16

"

"

!

1.11

Przestawienia

Przestawieniem b¸edziemy nazywa´c permutacj¸e bez punktu stałego, czyli tak¸a permutacj¸e,
w której ˙zaden element nie stoi na swoim miejscu. Wykorzystamy teraz zasad¸e wł¸aczania
i wył¸aczania, do policzenia liczby przestawie ´n w zbiorze

-elementowym.

Twierdzenie 1.17 Liczba przestawie´n (permutacji bez punktów stałych) w zbiorze

-

elementowym wynosi:

"

"

!

Dowód. Niech

b¸edzie zbiorem wszystkich permutacji na zbiorze

, a

"

zbiorem permutacji, w których

!

jest punktem stałym, to znaczy

!

*!

. Moc zbioru

"

wynosi:

"

poniewa˙z w zbiorze

"

s¸a te permutacje, które permutuj¸a wszystkie

elementów

oprócz

!

-tego. Podobnie moc zbioru

wynosi:

"

"

bo teraz w

permutujemy

!

elementów, wszystkie oprócz tych, które nale˙z¸a do .

Permutacje bez punktów stałych to te permutacje, które nie nale˙z¸a do ˙zadnego ze zbiorów

"

. Z zasady wł¸aczania i wył¸aczania ich liczba wynosi:

Pogrupujmy teraz składniki według mocy zbiorów . Mamy

"

podzbiorów mocy

!

. Dla

ka˙zdego z nich składnik sumy wynosi

"

!

, tak wi¸ec liczba przestawie ´n wynosi:

"

"

$

!

%

!

18

Rozdział 1. Kombinatoryka

Twierdzenie wynika teraz z równo´sci:

$

!

%

!

!

1.12

Generowanie obiektów kombinatorycznych

W tym rozdziale zajmiemy si¸e algorytmami generuj ˛

acymi (wypisuj¸acymi) obiekty kom-

binatoryczne. Przedstawione algorytmy b¸ed¸a działaly według nast¸epuj¸acego schematu:

Wypisujemy pierwszy obiekt.

Powtarzamy, a˙z do napotkania ostatniego obiektu:

Przetwarzamy bie˙z¸acy obiekt tak, aby otrzyma´c nast¸epny obiekt.

Takie algorytmy maj¸a t¸a zalet¸e, ˙ze nie wymagaj¸a du˙zo pami¸eci. Nale˙zy tylko pami¸eta ´c

jeden obiekt.

Algorytmy generuj¸ace obiekty s¸a u˙zywane w przypadku, gdy chcemy sprawdzi ´c wszyst-

kie obiekty danej klasy lub wtedy, gdy chcemy wylosowa ´c obiekt danej klasy. Przypu´s´c-
my, na przykład, ˙ze chcemy wylosowa´c jaki´s 3 elementowy podzbiór zbioru

.

W tym celu losujemy liczb¸e naturaln¸a

od 1 do

$

, a nast¸epnie generujujemy

podzbiory, a˙z do elementu .

1.12.1

Generowanie podzbiorów

Zaczniemy od najprostszego przypadku wypisania wszystkich podzbiorów zbioru

Algorytm wypisuj¸acy wszystkie podzbiory zbioru

:

Pierwszy podzbiór:

.

by uzyska´c nast¸epny po

podzbiór:

Wskazujemy na najwi¸ekszy element nie nale˙z¸acy do

, czyli

!

Je˙zeli takiego

nie ma, to koniec algorytmu, zbiór

jest ostatnim podzbio-

rem.

W przeciwnym przypadku dodajemy

do

i usuwamy z

wszystkie ele-

menty wi¸eksze od

.

Przykład 1.18 Dla

$

powy˙zszy algorytm wypisze po kolei nast¸epuj¸ace zbiory:

,

$

,

,

'$

,

,

%$

,

,

'$(

.

1.12. Generowanie obiektów kombinatorycznych

19

Zauwa˙zmy, ˙ze funkcje charakterystyczne wypisywanych podzbiorów, traktowane ja-

ko binarny zapis liczb, tworz¸a ci¸ag kolejnych liczb od 0 do

. Szukaj¸ac nast¸epnego

z kolei elemenetu algorytm post¸epuje podobnie jak algorytm zwi¸ekszania o jeden liczby
w systemie dwójkowym.

1.12.2

Generowanie -elementowych podzbiorów

Algorytm generuj¸acy

elementowe podzbiory zbioru

:

Pierwszy -podzbiór to

.

Przypu´s´cmy, ˙ze ostatnio wygenerowany podzbiór, to

, gdzie

. Aby wygenerowa´c nast¸epny podzbiór:

znajdujemy najmniejsze takie

!

, ˙ze

"

;

je˙zeli

"

, to znaczy, ˙ze

)

i jest to ostatni wyge-

nerowany podzbiór.

je˙zeli

"

, to zwi¸ekszamy

"

o jeden, a elementy mniejsze od

"

zamie-

niamy na

!

najmniejszych liczb, to znaczy

dla

!

.

Dla

i

&

algorytm wypisze po kolei nast¸epuj¸ace podzbiory (podajemy je bez

nawiasów i przecinków)

$

&

$

&

$&

$

&

$

&

$

&

$&

$

$

&

&

'$&

Zauwa˙zmy,˙ze najpierw wypisywane s¸a 4-podzbiory niezawieraj¸ace 6:

$&

$

&

$

&

$

&

a pó´zniej 4-podzbiory zawieraj¸ace 6

$

&

$&

$

&

$

$

&

&

'$&

które otrzymywane s¸a w ten sposób, ˙ze do kolejnych 3-podzbiorów zbioru

dopisywana jest 6.

Jest to ogólna zasada działania tego algorytmu: aby wypisa´c

-podzbiory zbioru

!

algorytm najpierw wypisuje

podzbiory zbioru

!

, a nast¸epnie podzbiory

zawieraj¸ace element

!

(s¸a one otrzymywane przez dodawanie

!

do

podzbiorów zbio-

ru

!

).

W powy˙zszym przykładzie w´srod podzbiorów zawieraj¸acych 6 najpierw mamy te,

które s¸a utworzone z 3-podzbiorów

'$

&

z dopisan¸a 6:

$

&

$

&

$

&

a po nich nast¸epuj¸a te, które s¸a utworzone z 2-podzbiorów

'$

&(

, z dopisan¸a 5 i 6:

$

$

&

&

'$

&

20

Rozdział 1. Kombinatoryka

Dlatego, kiedy w bierz¸acym zbiorze

algorytm znalazł takie

!

, ˙ze

"

, to znaczy, ˙ze algorytm jest w trakcie wypisywania tych podzbiorów, któ-

re zawieraj¸a

"

(wszystkie wi¸eksze od

"

), plus jaki´s

!

-podzbiór zbioru

"

. Zbiór

jest ostatnim podzbiorem, w którym wyst¸epuj¸a

"

,

oraz jaki´s

!

-podzbiór zbioru

"

, a nie wyst¸epuje

"

. Według opisanej wy˙zej

zasady teraz powinny nast¸api´c podzbiory, które zawieraj¸a

"

plus jaki´s

!

-podzbiór

zbioru

"

, plus elementy

"

. Pierwszy z nich to podzbiór

!

"

"

I taki element jest wypisywany po zbiorze

.

1.12.3

Generowanie permutacji

Algorytm generowania permutacji zbioru

:

Pierwsza permutacja to

"

*!

, dla

!

.

Aby wypisa´c nast¸epn¸a po

permutacj¸e:

Znajdujemy najwi¸eksze

spełniaj¸ace warunek

je˙zeli takiego

nie ma, to bierz¸aca permutacja jest ostatnia,

je˙zeli takie

istnieje, to zamieniamy

z najmniejszym

takim, ˙ze

oraz

, a nast¸epnie odwracamy porz¸adek elementów

.

Alorytm wypisuje permutacje w porz¸adku rosn¸acym, je˙zeli potraktujemy permutacje

jako liczby zapisane z baz¸a

, a liczby

jako cyfry w tym systemie.

Na przykład przypu´s´cmy, ˙ze bierz¸ac¸a permutacj¸a jest

&$

. Algorytm znajduje

i

$

. Wtedy ta permutacja jest ostatni¸a (najwi¸eksz¸a) permutacj¸a spo´sród per-

mutacji zaczynaj¸acych si¸e od

&$

, bo od pozycji trzeciej mamy ci¸ag malej¸acy

i

jest to najwi¸ekszy ci¸ag jaki mo˙zna utworzy´c z elementów 1,2,5,6. Teraz powinny nast¸api´c
permutacje zaczynaj¸ace si¸e od

&

(czwórki na pierwszym miejscu nie zmieniamy, a

trójka na drugim miejscu powinna by´c zamieniona przez nast¸epn¸a spo´srod liczb stoj¸acych
za ni¸a, czyli przez 5). Pierwsz¸a tak¸a permutacj¸a jest ta, w której pozostałe elementy rosn¸a,
czyli

&

$

.

Przykład 1.19 Oto 10 pierwszych permutacji czteroelementowych

$

&

&$

$

&

$

&

&

$

&$

$

&

&$

$

&

$

&

&

$

&$

1.13

Zadania

1. Ile numerów rejestracyjnych samochodów mo˙zna utworzy ´c, je˙zeli ka˙zdy numer

składa si¸e z trzech liter i czterech cyfr?

Ile numerów rejestracyjnych mo˙zna utworzy´c, je˙zeli b¸edziemy dodatkowo wyma-
ga´c, aby ka˙zdy numer zaczynał si¸e od spółgłoski?

1.13. Zadania

21

2. Ile liczb trzycyfrowych zawiera cyfr˛e

&

lub

?

3. W grupie jest pi¸e´c dziewcz¸at i pi¸eciu chłopców. Na ile sposobów mo˙zna wybra ´c

podgrup¸e składaj¸ac¸a si¸e z dwóch dziewcz¸at i dwóch chłopców?

Na ile sposobów mo˙zna utworzy´c w tej grupie pi¸e´c par, z jednym chłopcem i jedn¸a
dziewczyn¸a w ka˙zdej parze?

4. Znana jest zabawka dla dzieci składaj¸aca si¸e z dwunastu sze´sciennych klocków z

naklejonymi na ´sciankach fragmentami obrazków. Na ile sposobów mo˙zna uło˙zy ´c
te klocki w prostok¸at (trzy rz¸edy po cztery klocki w rz¸edzie)?

5. Ile słów mo˙zna utworzy´c z liter słowa ULICA (litery nie mog¸a si¸e powtarza´c)?

6. Udowodnij wzór:

$

%

$

%

Wskazówka. Policz na dwa ró˙zne sposoby, ile -elementowych dru˙zyn z kapitanem
mo˙zna utworzy´c ze zbioru

sportowców.

7. Udowodnij wzór:

$

%

$

%

Wskazówka. Policz na dwa ró˙zne sposoby, ile

-elementowych grup mo˙zna utwo-

rzy´c w klasie zło˙zonej z

chłopców i

dziewcz¸at.

8. Udowodnij, ˙ze

jest najwi¸eksze dla

i

.

9. Udowodnij, ˙ze:

$

%

10. Rozwi´n wielomian

.

11. Udowodnij, ˙ze

"

$

!

%

"

$

12. Przedstaw wzór na sum¸e czterech zbiorów

,

,

i

.

13. Ile elementów zawiera ró˙znica symetryczna

?

14. Wyznacz liczb¸e elementów

oraz

, wiedz¸ac, ˙ze

,

,

$

,

,

oraz

.

15. Oblicz ile liczb mniejszych od 100 jest podzielnych przez 2, 3 lub 5.

22

Rozdział 1. Kombinatoryka

16. Oblicz ile liczb mniejszych od 100 nie jest podzielnych przez 2, 3, 5 lub 7. Udo-

wodnij, ˙ze wszystkie te liczby oprócz 1 s¸a pierwsze. Ile jest liczb pierwszych mniej-
szych od 100?

17. Wypisz wszystkie podzbiory zbioru

'$

&

.

18. Wypisz wszystkie 2 elementowe podzbiory zbioru

'$

'&

.

19. Wypisz 14 kolejnych permutacji zbioru

%$

'&

poczynaj¸ac od permutacji

456321.

20. Napisz programy realizuj¸ace opisane w tym rozdziale algorytmy generowania obiek-

tów kombinatorycznych.

1.14

Problemy

1.14.1

Rozmieszczanie przedmiotów w pudełkach.

Przypu´s´cmy, ˙ze mamy

nierozró˙znialnych kul. Udowodnij, ˙ze istnieje

$

%

sposobów ro˙zło˙zenia tych kul do

rozró˙znialnych pudełek.

Wskazówka. Ka˙zde rozmieszczenia

kul w

pudełkach mo˙ze by ´c przedstawione jako

ci ˛

ag zer i jedynek długosci

, w którym wyst˛epuje dokładnie

jedynek. Zera

symbolizuj ˛

a kule a jedynki przegrody pomi˛edzy pudełkami. Na przykład ci ˛

ag

przedstawia rozło˙zenie pi˛eciu kul do czterech pudełek, w których pierwsze pudełko za-
wiera dwie kule, drugie jest puste, trzecie zawiera jedn ˛

a kule, a czwarte dwie kule.

1.14.2

Wybór

przedmiotów

rozró˙znialnych typów

Wyobra´zmy sobie, ˙ze mamy przedmioty w

ró˙znych typach, ˙ze liczba przedmiotów ka˙z-

dego typu jest nieograniczona i ˙ze przedmioty jednego typu s ˛

a nierozró˙znialne. Zasta-

nówmy si˛e na ile sposobów mo˙zna wybra´c

przedmiotów spo´sród tych

typów, przy

zało˙zeniu, ˙ze dopuszczalne s ˛

a powtórzenia typów. Poka˙z, ˙ze mo˙zna to zrobi ´c na

$

%

sposobów.

Na ile sposobów mo˙zna wybra´c 5 monet je˙zeli mamy nieograniczone zapsy złotówek,

dwuzłotówek i pi˛eciozłotówek?

Wskazówka. Wybory przedmiotów

typów s ˛

a równowa˙zne rozkładaniu nierozró˙znial-

nych kul do

szuflad. Wło˙zenie kuli do

!

-tej szuflady oznacza, ˙ze jest ona

!

tego typu.

1.14. Problemy

23

1.14.3

Kombinacje z powtórzeniami

-elementowe kombinacje z powtórzeniami ze zbioru

-elementowego s¸a to -elementowe

wybory elementów zbioru

-elementowego, w których elementy mog¸a si¸e powtarza ´c i

w których nie jest istotna kolejno´s´c wybieranych elementów. Na przykład, mamy czte-
ry trzyelementowe kombinacje z powtórzeniami ze zbioru dwuelementowego

; oto

one:

,

,

,

.

Udowodnij, ˙ze liczba

-elementowych kombinacji z powtórzeniami ze zbioru

-

elementowego wynosi

$

%

1.14.4

Permutacje z powtórzeniami

Przypu´s´cmy, ˙ze mamy

przedmiotów

ró˙znych typów oraz, ˙ze przedmiotów typu

!

jest

"

. Rozwa˙zmy ustawienia wszystkich tych przedmiotów w ci ˛

ag. Przy tym dwa ustawienia

s ˛

a rozró˙znialne tylko, je˙zeli na jakiej´s pozycji maj ˛

a przedmioty ró˙znych typów. Poka˙z, ˙ze

takich rozró˙znialnych ustawie ´n jest

Ile słów mo˙zna utworzy´c z liter słowa MATMA (litery M i A mog¸a wyst¸api´c po dwa
razy)?

1.14.5

Podziały uporz ˛

adkowane

Mamy

elementówy zbiór

i liczby

takie, ˙ze

. Poka˙z, ˙ze

elementy zbioru

mo˙zna na

sposoby podzieli´c na

podzbiorów

, takich, ˙ze

"

"

. Zakładamy przy

tym, ˙ze kolejno´s´c podzbiorów jest istotna.

Na ile sposobów mo˙zna rozda´c 52 kartry na cztery osoby?

1.14.6

Permutacje bez punktów stałych

Udowodnij, ˙ze liczba przestawie ´n (permutacji bez punktów stałych) w zbiorze

-elementowym

jest równa zaokr¸agleniu liczby

do najbli˙zszej liczby naturalnej;

jest podstaw¸a loga-

rytmu naturalnego.

Wskazówka. Skorzystaj z twierdzenia ??, z rozwini¸ecia:

"

"

!

24

Rozdział 1. Kombinatoryka

oraz z oszacowania:

"

"

!

*

1.14.7

Liczba surjekcji

Udowodnij, ˙ze liczba surjekcji (funkcji na cał¸a przeciwdziedzin¸e) ze zbioru

-elementowego

na zbiór -elementowy wynosi:

"

"

$

!

%

!

Wskazówka. Skorzystaj z zasady wł¸aczania i wył¸aczania dla zbioru wszystkich funkcji ze
zbioru

w zbiór

. Zbiór

"

to funkcje, które nie maj¸a elementu

!

w

obrazie.