Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Rachunek prawdopodobie ´nstwa

1.1

Zdarzenia

Podstawowym poj¸eciem rachunku prawdopodobie ´nstwa jest przestrze´n zdarze´n elemen-
tarnych, któr¸a najcz¸e´sciej b¸edziemy oznacza´c przez

. W tej ksi¸a˙zce ograniczymy si¸e do

przypadków, gdy

jest zbiorem sko ´nczonym. Dzi¸eki temu b¸edziemy mogli ograniczy´c

si¸e to prostych rozwa˙za ´n.

Elementy przestrzeni

nazywamy zdarzeniami elementarnymi.

Przestrze´n zdarze´n cz¸esto zwi¸azana jest z jakim´s eksperymentem losowym (probabi-

listycznym).

Przykład 1.1

a) Przypu´s´cmy, ˙ze rzucamy monet¸a. Przestrze´n zdarze´n elementarnych

mo˙ze by´c wtedy okre´slona jako

, gdzie

oznacza wypadni¸ecie orła, a

reszki.

b) W przypadku rzutu dwoma (rozró˙znialnymi) monetami przestrze´n zdarze´n elemen-

tarnych mo˙ze by´c okre´slona jako

, gdzie

oznacza, ˙ze

wypadły dwa orły;

, ˙ze na pierwszej monecie wypadł orzeł, a na drugiej reszka;

, ˙ze na pierwszej reszka, a na drugiej orzeł; a

, ˙ze na obu monetach wypadły

reszki.

c) Przypu´s´cmy, ˙ze mamy urn¸e z sze´scioma ponumerowanymi kulami, i ˙ze kule o nu-

merach 1 i 2 s¸a białe, a kule o numerach 3,4,5 i 6 s¸a czarne. Przestrze´n zdarze´n
elementarnych mo˙ze by´c zdefiniowana jako

!

.

d) Przy rzucie kostk¸a

"#$%#!#

.

e) Przy rzucie dwiema (rozró˙znialnymi) kostkami

&('*)",+(-/.021)"3+41!5

. Zda-

rzenie

'*)",+(-

odpowiada wynikowi, gdzie na pierwszej kostce wypadło

)

oczek, a na

drugiej

+

.

f) Przy rzucie monet¸a i kostk¸a

#"5"6$5!$ 556$5!#

;

na przykład

!

opisuje wynik, gdzie na monecie wypadł orzeł, a na kostce 6 oczek.

3

4

Rozdział 1. Rachunek prawdopodobie ´nstwa

g) W przypadku rzutu

(rozró˙znialnymi) monetami przestrze´n zdarze´n elementarnych

mo˙ze by´c okre´slona jako zbiór wszystkich

elementowych ci¸agów z warto´sciami

lub

.

h) Przypu´s´cmy, ˙ze mamy urn¸e z dwoma kulami białymi i trzema czarnymi, i ˙ze losu-

jemy dwie kule z tej urny. Oznaczmy te kule przez

,

,

,

i

. Przestrzeni¸a

zdarze´n elementarnych mo˙ze tu by´c albo zbiór dwuelementowych podzbiorów zbio-
ru kul, lub zbiór dwuelementowych ci¸agów bez powtórze´n. Zale˙zy to od tego, czy
b¸edziemy rozpatrywa´c zdarzenia, w których rozró˙zniamy wylosowane kule, czy nie
rozró˙zniamy.

Mo˙zna te˙z rozpatrywa´c przestrzenie zdarze ´n nie zwi¸azane z eksperymentem:

Przykład 1.2 Przestrzeni¸a zdarze´n elementarnych mo˙ze by´c:

a) Zbiór liter lub słów wyst¸epuj¸acych w jakim´s tek´scie, ksi¸a˙zce lub li´scie.

b) Zbiór mo˙zliwych haseł potrzebnych do uzyskania dost¸epu do danych lub systemu.

Je˙zeli zbiór mo˙zliwych haseł jest zbyt mały, to łatwo mo˙zna złama´c zabezpieczenia.

c) Zbiór mo˙zliwych wylicze´n algorytmu probabilistycznego (algorytmu, który korzysta

z funkcji losuj¸acej).

Dowolny podzbior

nazywamy zdarzeniem. Pami˛etajmy, ˙ze rozwa˙zamy tyl-

ko sko´nczone przestrzenie zdarze ´n elementranych. W przypadku, gdy

nie jest zbiorem

sko´nczonym, konieczna jest inna definicja zdarzenia. Cały zbiór

nazywamy zdarzeniem

pewnym, a zbiór pusty

zdarzeniem niemo˙zliwym. Zdarzenia rozł¸aczne,

, na-

zywamy wykluczaj¸acymi si¸e. Zdarzenie

nazywamy zdarzeniem przeciwnym

do zdarzenia

.

Przykład 1.3

a) W przykładzie 1.1b, z rzutem dwoma monetami,

"

,

mamy

!4

zdarze´n. Zbiór

jest zdarzeniem polegaj¸acym na

tym, ˙ze na pierwszej monecie wypadł orzeł.

b) W przykładzie 1.1e, z rzutem dwoma kostkami, mamy

zdarze´n. Zbiór

' -

'

5-

'

5-

'*$

-

jest zdarzeniem, ˙ze suma oczek na obu kostkach wynosi 5.

c) W przykładzie 1.1c, z kulami,

"

oznacza zdarzenie, ˙ze wylosowano kul¸e

biał¸a.

d) Rzut czteroma monetami, przykład 1.1g z

, zdarzenie, ˙ze na pierwszej i trzeciej

monecie wypadły orły to

""

, a zdarzenie, ˙ze na

pierwszej i trzeciej monecie wypadło to samo to

"6

.

1.2. Prawdopodobie ´nstwo

5

1.2

Prawdopodobie ´nstwo

Definicja 1.4 Prawdopodobie´nstwo, lub rozkład prawdopodobie´nstwa, jest funkcj¸a okre´slon¸a
na zbiorze zdarze´n (w naszym przypadku na zbiorze wszystkich podzbiorów

). Ka˙zde-

mu zdarzeniu

przypisujemy liczb¸e rzeczywist¸a

'

-

, jego prawdopodobie´nstwo.

Funkcja ta musi spełnia´c warunki:

Aksjomaty prawdopodobie ´nstwa

A1)

'

-5

dla ka˙zdego

,

A2)

',

-

,

A3) Je˙zeli zdarzenia

i

s¸a rozł¸aczne, to

'

-

'

-

'

-

.

Zbiór zdarze ´n elementarnych

wraz z okre´slonym na nim prawdopodobie ´nstwem b¸edziemy

nazywa´c przestrzeni¸a probabilistyczn¸a. W przypadku, gdy przestrze ´n zdarze´n elemen-
tarnych jest zbiorem sko ´nczonym, wystarczy okre´sli´c prawdopodobie ´nstwa dla zdarze ´n
elementarnych. Musz¸a by´c tylko spełnione dwa warunki:

A4)

'

-$

dla ka˙zdego

,

A5)

'

-

,

Prawdopodobie ´nstwo dowolnego zdarzenia jest wtedy równe

'

-

'

-

Łatwo mo˙zna sprawdzi´c, ˙ze tak zdefiniowane prawdopodobie ´nstwo spełnia aksjomaty
definicji 1.4.

W przypadku, gdy przestrze ´n zdarze´n elementarnych jest zbiorem wszystkich mo˙z-

liwych wyników jakiego´s eksperymentu, najcz¸e´sciej przyjmuje si¸e, ˙ze funkcja prawdo-
podobie´nstwa przypisuje, ka˙zdemu zdarzeniu elementarnemu tak¸a sam¸a warto´s´c. Mamy
wtedy do czynienia z klasyczn¸a definicj¸a prawdopodobie ´nstwa. W tej ksi¸a˙zce b¸edziemy
najcz¸e´sciej u˙zywa´c klasycznej definicji, a w razie odst¸epstwa od tej umowy, b¸edziemy to
specjalnie zaznacza´c.

Definicja 1.5 Rozkład prawdopodobie´nstwa, w którym ka˙zde zdarzenie elementarne

ma takie samo prawdopodobie´nstwo

'

-

.

.

nazywamy rozkładem jednostajnym.

Przykład 1.6

a) Dla rzutu dwoma monetami (przykład 1.1b mo˙zemy okre´sli´c praw-

dopodobie´nstwo według klasycznej definicji: mamy wtedy

',-

#

'

-

5

'

-

#

'

-

6

Rozdział 1. Rachunek prawdopodobie ´nstwa

Ale oczywi´scie funkcja prawdopodobie´nstwa mo˙ze by´c dowoln¸a funkcj¸a spełniaj¸ac¸a
warunki A4 i A5. Na przykład

'

-

#

'

-

$

'

-

5" #

'

-

5

lub

'

-

5

',-

$

'

-

5

'

-

.

b) W przykładzie 1.2a, ze zbiorem wszystkich liter w tek´scie, prawdopodobie´nstwo

mo˙ze by´c zdefiniowane jako cz¸esto´sci wyst¸epowania poszczególnych liter w tym
tek´scie. Na podstawie cz¸esto´sci wyst¸epowania liter mo˙zna zgadywa´c w jakim j¸ezyku
napisany jest tekst. Podobnie mo˙zna rozpatrywa´c cz¸esto´s´c wyst¸epowania słów w
tek´scie i na tej podstawie zgadywa´c autorstwo tekstu.

W nast¸epuj¸acym twierdzeniu zebrano kilka prostych wniosków wynikaj¸acych z ak-

sjomatów prawdopodobie ´nstwa.

Twierdzenie 1.7

a)

'

-

b) Je˙zeli

, to

'

-

1

'

-

oraz

'

-

'

-

'

-

c)

'

-

'

-

'

-

'

-

d)

'

-

1

'

-

'

-

Dowód:

a)

Z aksjomatu A3 mamy

'

-

'

-

'

-

'

-

, a 0 jest jedyn¸a liczb¸a

spełniaj¸ac¸a równo´s´c

.

b)

Je˙zeli

, to

'

-

oraz

'

-

, a wi¸ec z aksjomatu A3

'

-

'

-

'

-

'

-

c)

Mamy

'

'

--

oraz

'

'

--

a wi¸ec z aksjomatu

A3

'

-/

'

-

'

'

--

, a poniewa˙z

, z wniosku 1.7b

mamy

'

'

--

'

-

'

-

d)

wynika bezpo´srednio z

c)

.

Przykład 1.8 (kontynuacja przykładu 1.3d) z czteroma monetami). Je˙zeli zało˙zymy roz-
kład jednostajny, to prawdopodobie´nstwo ˙ze na pierwszej i trzeciej monecie wypadł orzeł
wynosi

, a prawdopodobie´nstwo, ˙ze na pierwszej i trzeciej monecie wypadnie to samo

wynosi

.

Podobnie w przypadku, gdy rzucamy

monetami (przykład 1.1g). Przestrze´n

zdarz¸e elementarnych zawiera

ci¸agów, z czego

sprzyja zdarzeniu, ˙ze na pierw-

szej i trzeciej monecie wypadnie orzeł, a

sprzyja zdarzeniu, ˙ze na pierwszej i trzeciej

monecie jest to samo. Tak wi¸ec otrzymamy takie same prawdopodobie´nstwa jak w przy-
padku rzutu czteroma monetami.

1.3. Prawdopodobie ´nstwo warunkowe i zdarzenia niezale˙zne

7

Twierdzenie 1.9 Niech

b¸edzie rodzin¸a parami rozł¸acznych zdarze´n (

dla ka˙zdej pary indeksów

)

+

). Wtedy

'

3-

Dowód przez indukcj¸e:

Dla

twierdzenie zachodzi w sposób trywialny.

Załó˙zmy, ˙ze twierdzenie jest prawdziwe dla dowolnej rodziny

zbiorów. Rozpatrzmy

Poniewa˙z

z aksjomatu A3 i z zało˙zenia indukcyjnego wynika

6

'

-

'

3-

'

-

'

,-

Twierdzenie 1.10 Dla dowolnej rodziny zbiorów

(niekoniecznie parami rozł¸acznych)

mamy

1

'

-

Dowód przez indukcj¸e: Dla

twierdzenie zachodzi w sposób trywialny. Załó˙zmy,

˙ze twierdzenie jest prawdziwe dla dowolnej rodziny

zbiorów. Z twierdzenia 1.7c i z

zało˙zenia indukcyjnego mamy

1

'

-

1

'

-

1.3

Prawdopodobie ´nstwo warunkowe i zdarzenia nieza-
le˙zne

Definicja 1.11 Prawdopodobie´nstwo warunkowe zaj´scia zdarzenia

pod warunkiem, ˙ze

zaszło zdarzenie

oznaczane przez

'

.

-

okre´slamy jako

'

.

-

'

-

'

-

Ma to sens tylko wtedy gdy

'

-

.

8

Rozdział 1. Rachunek prawdopodobie ´nstwa

Mo˙zemy powiedzie´c, ˙ze jest to prawdopodobie ´nstwo zaj´scia zdarzenia

w sytuacji, gdy

mamy pewno´s´c, ˙ze zaszło zdarzenie

. Przy klasycznej definicji, gdy prawdopodobie ´n-

stwo oznacza cz¸esto´s´c wyst¸apienia, to prawdopodobie ´nstwo

'

.

-

oznacza jaka cz¸e´s´c

elementów zbioru

nale˙zy do zbioru

.

Wniosek 1.12

'

-

'

.

-

'

-

.

Je˙zeli

'

.

-

'

-

, to mówimy, ˙ze zdarzenie

jest niezale˙zne od zdarzenia

. W takim przypadku zaj´scie zdarzenia

nie zale˙zy od tego, czy zaszło zdarzenie

.

Je˙zeli

i

s¸a zdarzeniami o niezerowych prawdopodobie ´nstwach i

jest niezale˙zne

od

, to

jest niezale˙zne od

. Rzeczywi´scie

'

.

-

'

-

poci¸aga

'

-

'

-

'

-

, a to poci¸aga

'

-

'

-

'

-

'

.

-

Dlatego mo˙zna mówi´c, ˙ze w takim przypadku zdarzenia

i

s¸a niezale˙zne.

Definicja 1.13 Mówimy, ˙ze zdarzenia

i

s¸a niezale˙zne, je˙zeli

'

-

'

-

'

-

Przykład 1.14 (Kontynuacja przykładu 1.1c, z sze´scioma kulami). Zdarzenie

wylosowania kuli białej i zdarzenie

!

wylosowania kuli z parzystym nu-

merem s¸a niezale˙zne, poniewa˙z

'

-

oraz

'

.

-

. Po prostu cz¸esto´s´c

wyst¸epowania kuli białej w´sród kul o parzystych numerach (1 na 3) jest taka sama jak
cz¸esto´s´c wyst¸epowania kuli białej w´sród wszytkich kul (2 na 6).

Je˙zeli mamy wi¸ecej zdarze ´n

, to mówimy, ˙ze s¸a one parami niezale˙zne,

je˙zeli ka˙zde dwa zdarzenia s¸a niezale˙zne, to znaczy gdy

'

-

'

,-

'

-

dla ka˙zdej pary

)

+

.

Definicja 1.15 Zdarzenia

, s¸a niezale˙zne je˙zeli dla ka˙zdego podzbioru

mamy

'

-

Przykład 1.16 (Kontynuacja przykładu 1.1b, z rzutem dwoma monetami). Niech

b¸edzie

zdarzeniem, ˙ze na pierwszej monecie wypadł orzeł,

, ˙ze na drugiej monecie wypadł

orzeł, a

, ˙ze na obu monetach wypadło to samo. Mamy

'

-

'

-

'

-

'

-

'

-

'

-

'

-

Jak wida´c zdarzenia te s¸a parami niezale˙zne, poniewa˙z dla ka˙zdej pary indeksów

1

)

+1

mamy

'

-

'

-

'

-

. Ale zdarzenia te nie s¸a niezale˙zne,

poniewa˙z

'

-

'

-

'

-

'

-

1.4. Prawdopodobie ´nstwo całkowite

9

Przykład 1.17 W przypadku rzutu

monetami, niech

oznacza, ˙ze na

)

-tej monecie

wypadł orzeł. Wtedy zdarzenia

s¸a niezale˙zne. Łatwo sprawdzi´c, ˙ze

dla ka˙zdego

)

,

'

-

,

dla ka˙zdej pary

)

+

,

'

-

dla ka˙zdej trójki

)

+

,

'

-

, itd.

prawdopodobie´nstwo, ˙ze wypadn¸a same orły, wynosi

1.4

Prawdopodobie ´nstwo całkowite

Twierdzenie 1.18 (wzór na prawdopodobie ´nstwo całkowite.) Niech

,

b¸ed¸a zdarzeniami takimi, ˙ze:

'

3-

, dla ka˙zdego

61)

1

,

, dla

1)

+

1

(zdarzenia s¸a parami rozł¸aczne),

0

(zdarzenia daj¸a w sumie cał¸a przestrze´n).

Wtedy prawdopodobie´nsto dowolnego zdarzenia

wynosi

'

-

'

.

-

'

-

Dowód Mamy

'

-

Ponadto

'

3-

'

-

dla

)

+

wi¸ec na mocy twierdzenia 1.9 mamy

'

-

'

-

Z wniosku 1.12 mamy

'

-

'

.

-

'

-

; co daje tez¸e twierdzenia.

W przypadku dwóch zdarze ´n uzupełniaj¸acych si¸e

i

wzór z twierdzenia 1.18

wygl¸ada nast¸epuj¸aco:

'

-

'

.

-

'

-

'

.

-

'

-

(1.1)

10

Rozdział 1. Rachunek prawdopodobie ´nstwa

Przykład 1.19 Wyobra´zmy sobie urn¸e z trzema kulami: 1 biał¸a i 2 czarnymi. Przypu´s´cmy,
˙ze pierwsza osoba wylosowała jedn¸a kul¸e i schowała j¸a. Jakie jest prawdopodobie´nstwo,
˙ze druga osoba wylosuje kul¸e biał¸a? Niech

oznacza, ˙ze pierwsza osoba wylosowała

biał¸a kul¸e, wtedy

oznacza, ˙ze wylosowała czarn¸a kul¸e. Niech

oznacza, ˙ze druga

osoba wylosowała biał¸a kul¸e.

Mamy

'

-

,

'

-

,

'

.

-

oraz

'

.

-

. Razem

daje to

'

-

A jakie jest prawdopodobie´nstwo, ˙ze po drugim losowaniu w urnie zostanie biała kula?
Zajdzie to wtedy, gdy obie osoby wylosuj¸a kul¸e czarn¸a. Z wniosku 1.12 mamy

'

-

'

.

-

'

-

Jak wida´c prawdopodobie´nstwo wylosowania białej kuli jest takie samo dla pierwszego,
drugiego i trzeciego losuj¸acego.

Poniewa˙z przestrze´n zdarze´n jest tutaj mała, wi¸ec mo˙zna nasz wynik sprawdzi´c bezpo-

´srednio. Oznaczmy kule przez

,

i

. Niech przestrze´n zdarze´n elementarnych b¸edzie

('

-

'

-

',

-

'

-

'

-

'

-

Zakładamy, ˙ze ka˙zdy z tych wyników jest równie prawdopodobny. Wida´c teraz, ˙ze zdarze-
nia:

'

-

'

-"

,

('

-

'

-

oraz

'

-

('

-

'

"

-

s¸a równo prawdopodobne.

Rozwa˙zmy teraz przypadek, gdy w urnie jest

kul z czego

białych. Znowu zakłada-

my, ˙ze ka˙zdy wynik dwóch losowa´n jest równie prawdopodobny. Mamy

'

-

,

'

-

'

5-

,

'

.

-

'

-

#'

-

oraz

'

.

-

5'

-

. Razem

daje to

'

-

Czyli w tym przypadku, równie˙z druga osoba ma tak¸a sam¸a szans¸e wylosowania kuli
białej co pierwsza.

Przykład 1.20 Wyobra´zmy sobie dwie urny z kulami. W pierwszej urnie jest jedna kula
biała i jedna czarna, a w drugiej urnie dwie białe i jedna czarna. Rzucamy monet¸a. Je˙zeli
wypadnie orzeł, to losujemy kul¸e z pierwszej urny, je˙zeli reszka, to losujemy z drugiej
urny.

Jakie jest prawdopodobie´nstwo, ˙ze wylosujemy kul¸e biał¸a? Niech

oznacza wyloso-

wanie kuli białej, a

wypadni¸ecie orła na monecie, wtedy

oznacza, ˙ze na monecie

wypadła reszka. Mamy

'

-

'

-

oraz

'

.

-

-jest to prawdopodobie´nstwo wylosowania kuli białej pod warunkiem,

˙ze wypadł orzeł i losowali´smy z pierwszej urny.

'

.

-2

-jest to prawdopodobie´nstwo wylosowania kuli białej pod warun-

kiem, ˙ze wypadła reszka i losowali´smy z drugiej urny.

Korzystaj¸ac teraz ze wzoru (1.1) mamy

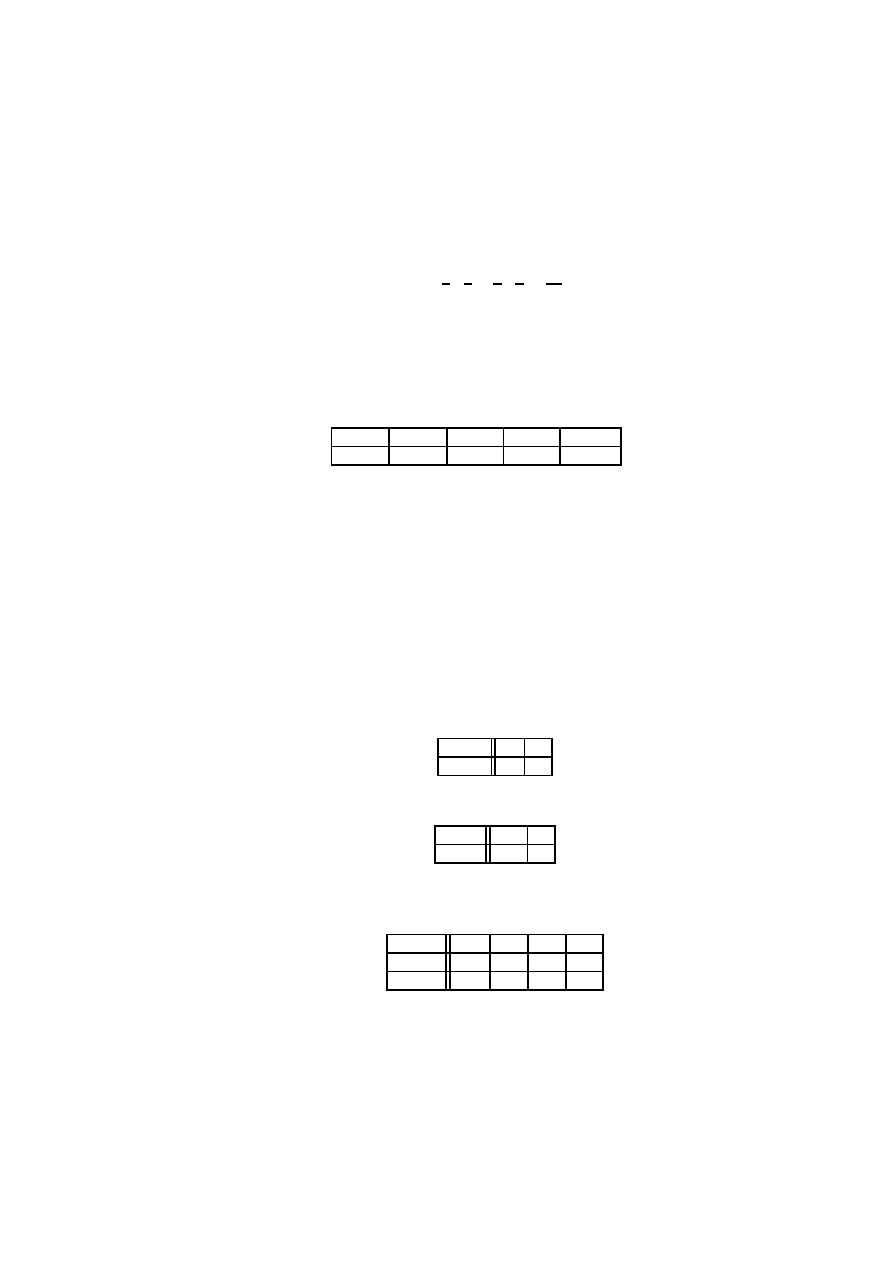
1.5. Zmienna losowa

11

'

-

Zastanówmy si¸e teraz jak powinna wygl¸ada´c przestrze´n probabilistyczna w tym przykła-
dzie. Niech

zawiera wszystkie mo˙zliwe wyniki eksperymentu.

('

-

'

"

-

'

-

'

"

-

'

-

Aby by´c w zgodzie z intuicj¸a i naszymi poprzednimi wyliczeniami rozkład prawdopodo-
bie´nstwa powinien by´c nast¸epuj¸acy:

(O,1b)

(O,2b)

(R,1b)

(R,2b)

(R,3c)}

!

!

!

Rozkład jednostajny nie jest w tym przykładzie dobry, bo mieliby´smy prawdopodobie´n-
stwo, wypadni¸ecia orła równe

.

1.5

Zmienna losowa

Definicja 1.21 Zmienna losowa

jest to dowolna funkcja z przestrzeni zdarze´n elemen-

tarnych

w zbiór liczb rzeczywistych

.

Trzeba tutaj przypomnie´c, ˙ze w tej ksi ˛

a˙zce rozwa˙zamy tylko sko ´nczone przestrzenie zda-

rze´n elementarnych. W przypadku, gdy

jest zbiorem niesko ´nczonym definicja zmiennej

losowej jest inna.

Przykład 1.22

a) Rozwa˙zmy rzut monet¸a,

(przykład 1.1a). Zmienna lo-

sowa

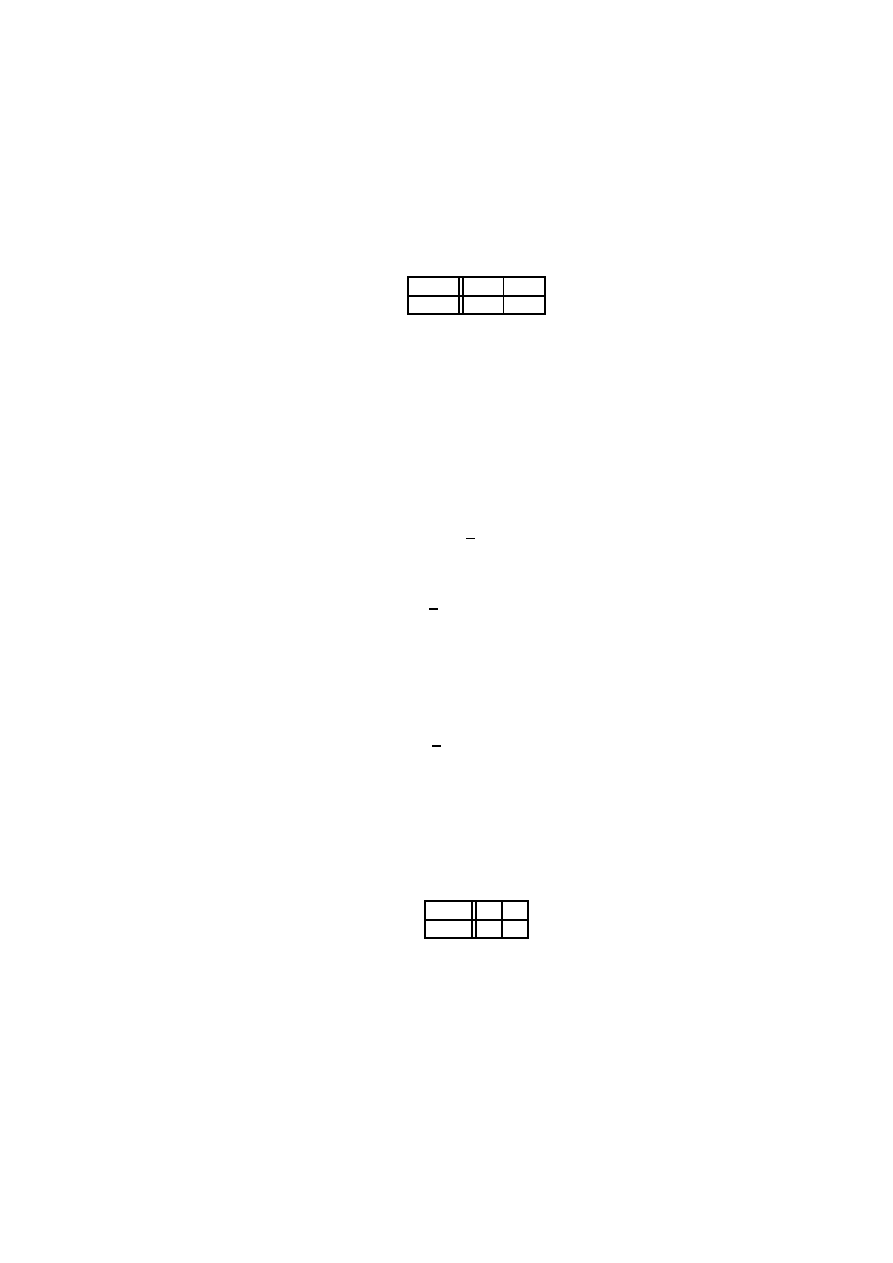
jest okre´slona tabel¸a

O

R

'

-

Inny przykład to zmienna

okre´slona tabel¸a

O

R

'

-

b) Rozwa˙zmy rzut dwoma monetami, (przykład 1.1b)

"

. Niech

i

b¸ed¸a dwoma zmiennymi losowymi okre´slonymi w tabeli

OO

OR

RO

RR

'

-

'

-

Zmienna

okre´sla wynik rzutu na pierwszszej monecie,

'

-

, je˙zeli wypadł

orzeł, i

'

-

, je˙zeli wypadła reszka. W podobny sposób zmienna losowa

okre´sla wynik rzutu na drugiej monecie.

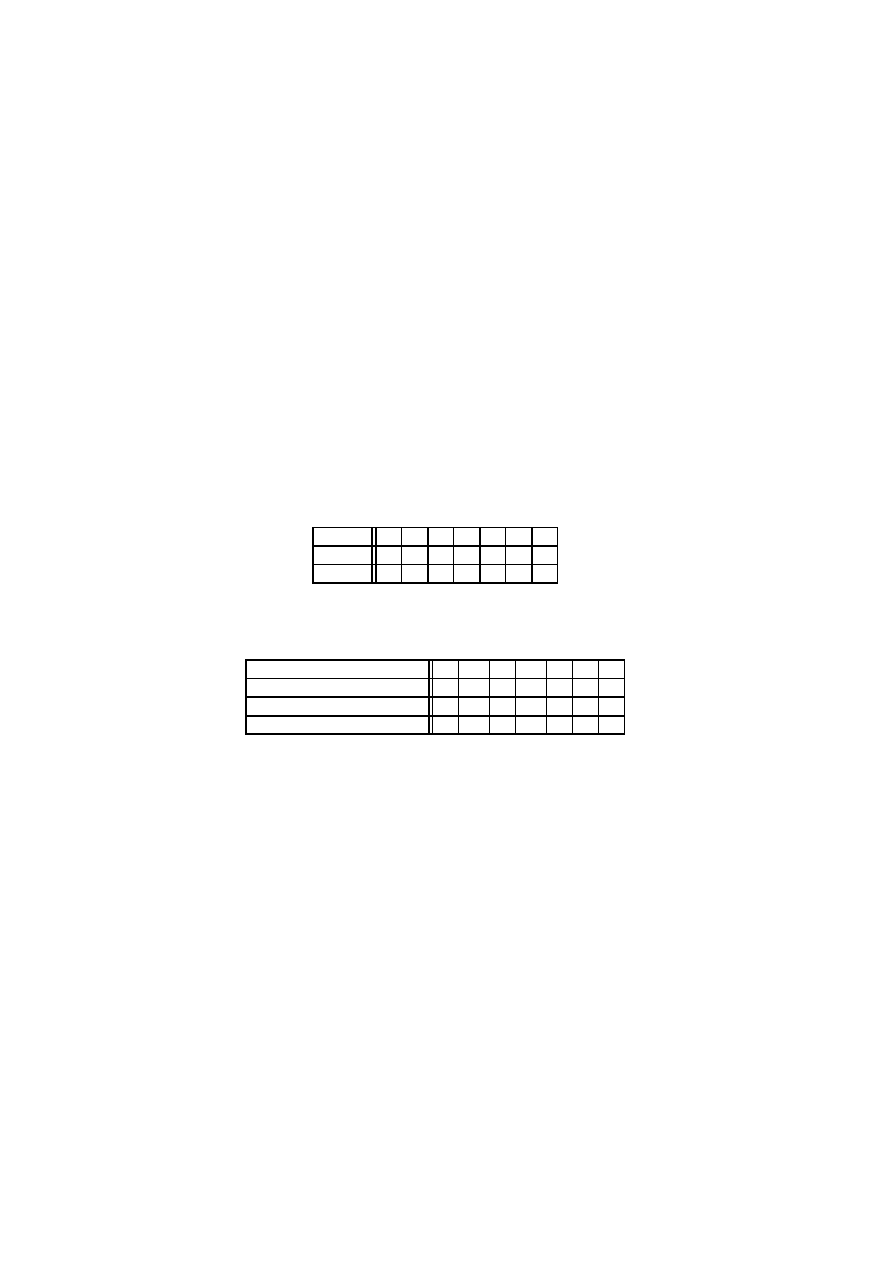
12

Rozdział 1. Rachunek prawdopodobie ´nstwa

c) Rozwa˙zmy rzut

monetami, (przykład 1.1g). Dla ka˙zdego

)

,

1

)

1

okre´slamy

zmienn¸a

;

'

-

, je˙zeli na

)

-tej monecie wypadł orzeł, oraz

'

-

,

je˙zeli wypadła reszka.

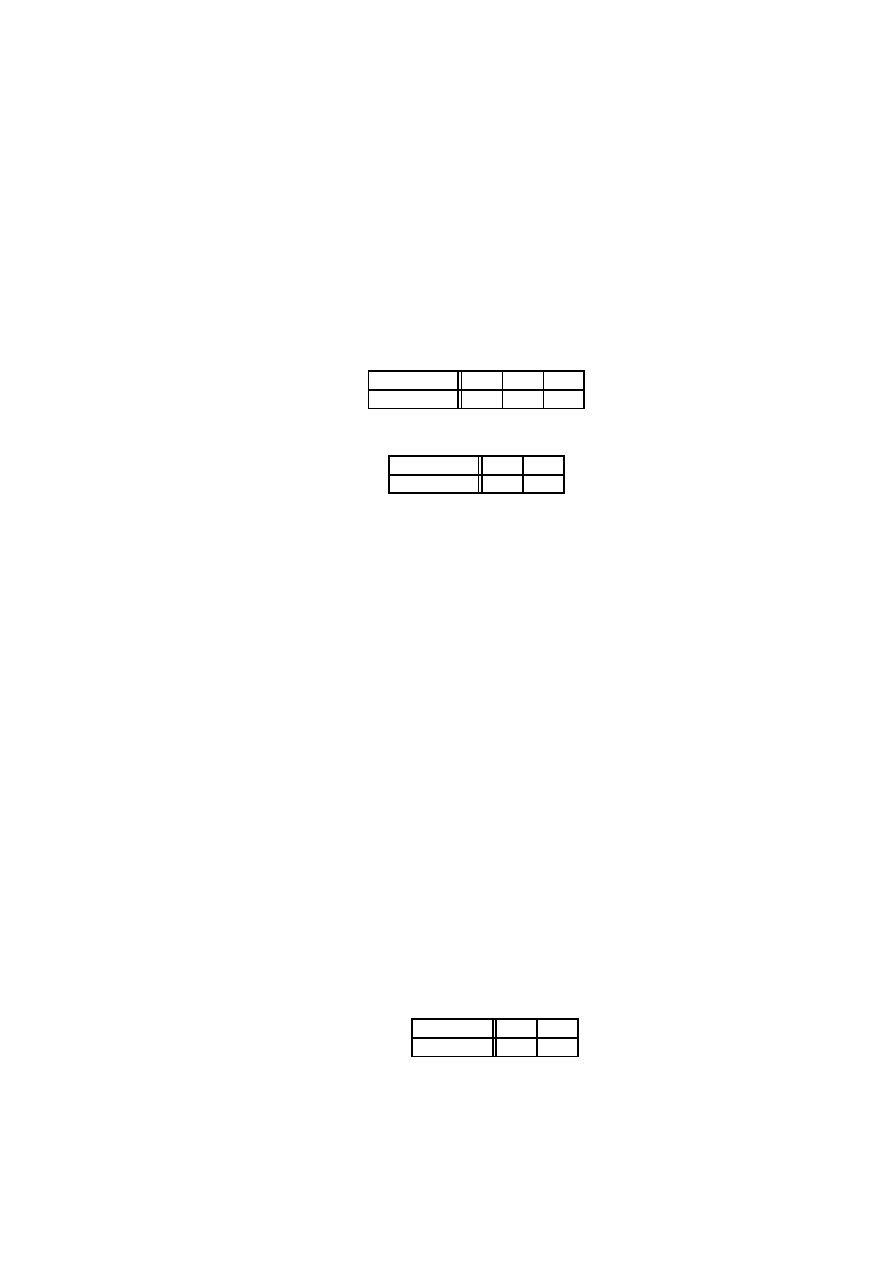
d) Rozwa˙zmy losowanie jednej kuli z urny zawieraj¸acej siedem ponumerowanych kul.

5$$"#!5

(

. Niech zmienna losowa

bedzie zdefiniowana jako

'

-

#

a zmienna losowa

jako

'

-

(

'

-

jest reszt¸a z dzielenia numeru kuli przez 2, a

'

-

reszt¸a z dzielenia przez

3). Warto´sci tych dwóch zmiennych zebrane s¸a w tabeli.

1

2

3

4

5

6

7

'

-

1

0

1

0

1

0

1

'

-

1

2

0

1

2

0

1

Mo˙zemy teraz okre´sli´c inne zmienne losowe, na przykład

,

,

. Ich warto´sci zebrano w tabeli

1

2

3

4

5

6

7

'

-

'

-

'

-

2

2

1

1

3

0

2

'

-

'

-

'

-

1

0

0

0

2

0

1

'

-

'

-

'

-

1

-2

2

-1

0

0

1

e) Rozwa˙zmy rzut dwoma kostkami (przykład 1.1e)

('*)",+(-

.(1)3+

1!#

. Niech

oznacza wynik rzutu na pierwszej kostce,

wynik rzutu na drugiej kostce.

Wtedy zmienna

okre´sla sum¸e oczek na obu kostkach.

Maj¸ac zmienn¸a losow¸a

i liczb¸e rzeczywist¸a

definiujemy zdarzenie

jako

'

-

.

'

-

Zauwa˙zmy, ˙ze je˙zeli liczba

nie nale˙zy do zbioru warto´sci

'

-

zmiennej

, to zda-

rzenie

jest zdarzeniem niemo˙zliwym. Prawdopodobie ´nstwo zdarzenia

wynosi

'

-

'

-

Definicja 1.23 Funkcj¸e

'

-

'

-

nazywamy funkcj¸a g¸esto´sci (rozkładu) prawdopodobie´nstwa zmiennej losowej

.

1.5. Zmienna losowa

13

Przykład 1.24 (Kontynuacja przykładu 1.22d) Dla zmiennej

mamy trzy niepuste zda-

rzenia

'

-

5!#

'

-

$

(

'

-

5#

Zmienna losowa

posiada wi¸ec rozkład

0

1

2

'

-

Podobnie zmienna

ma rozkład

0

1

'

-

Poniewa˙z, jak zało˙zyli´smy

jest zbiorem sko ´nczonym, to zbiór warto´sci

',

-

zmien-

nej

te˙z jest sko ´nczony. Dla

'

-

mamy

'

-

'

-

. Tak wi¸ec funkcja

g¸esto´sci przyjmuje warto´sci niezerowe tylko dla sko ´nczenie wielu argumentów. Zauwa˙z-
my, ˙ze je˙zeli

, to zdarzenia

i

wykluczaj¸a si¸e. Mamy przy

tym

Lemat 1.25 Je˙zeli

jest funkcj¸a g¸esto´sci zmiennej losowej

, to

'

-

dla ka˙zdego

.

'

-

.

Dowód. Sum¸e

'

-

rozumiemy jako sko ´nczon¸a sum¸e po zbiorze warto´sci

zmiennej

.

'

-

'

-

'

-

'

-

Zauwa˙zmy, ˙ze ostatnia podwójna suma jest sum¸a po wszystkich elementach

po-

grupowanych według warto´sci zmiennej

. Mamy wi¸ec

'

-

'

-

W dalszej cz¸e´sci przedstawiaj¸ac funkcj¸e g¸esto´sci zmiennej losowej

b¸edziemy roz-

wa˙za´c tylko te

, dla których

'

-

.

Przykład 1.26

a) Zmienna losowa

z przykładu 1.22a posiada rozkład

-1

1

'

-

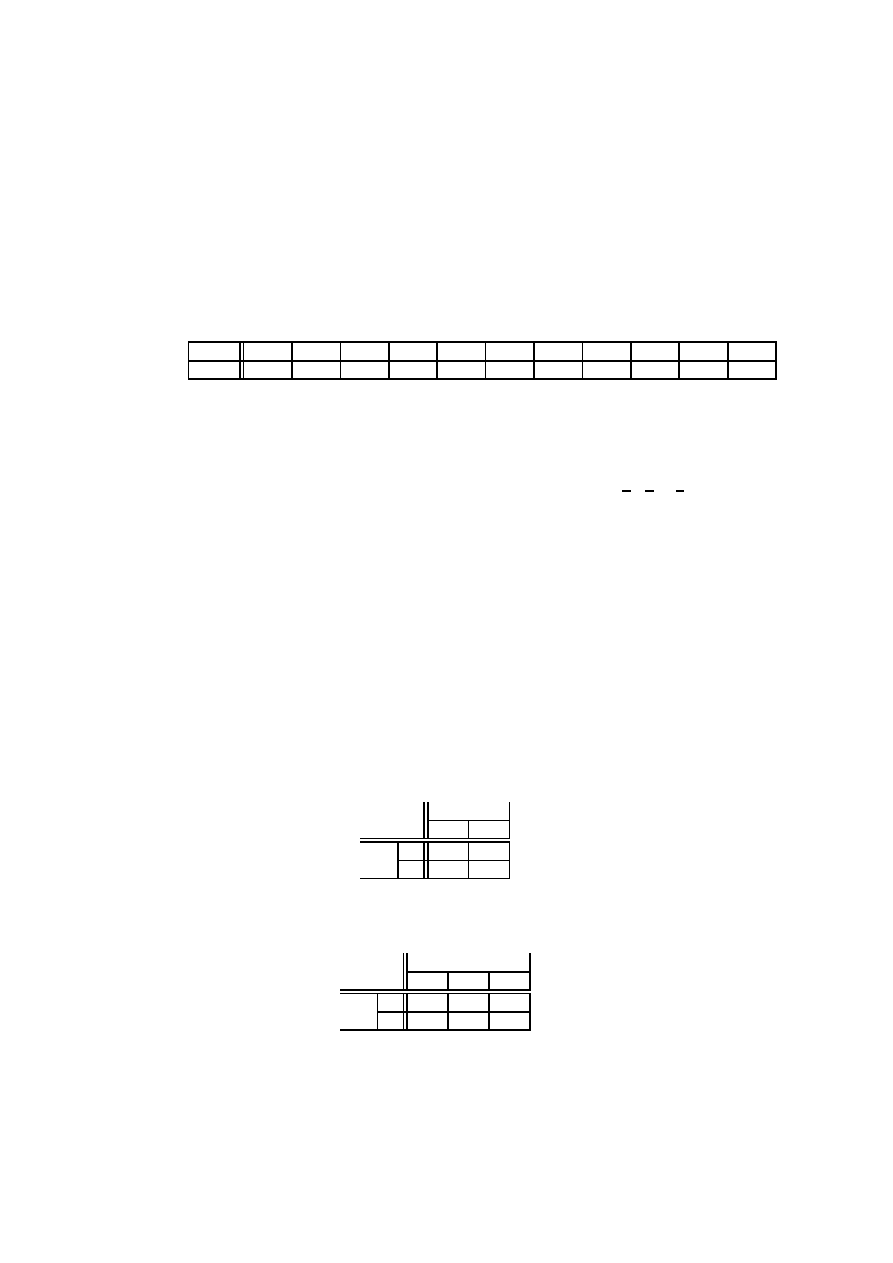
14

Rozdział 1. Rachunek prawdopodobie ´nstwa

b) Niech

oznacza sum¸e warto´sci oczek w rzucie dwoma kostkami, przykład 1.22e.

G¸esto´s´c rozkładu prawdopodobie´nstwa zmiennej losowej

przedstawia nast¸epuj¸aca

tabela:

2

3

4

5

6

7

8

9

10

11

12

'

-

!

!

!

!

!

!

!

!

!

!

!

!

Maj¸ac funkcj¸e g¸esto´sci rozkładu zmiennej

mo˙zemy okre´sla´c prawdopodobie ´nstwa

zdarze´n opisywanych za pomoc¸a zmiennej

.

Przykład 1.27

a) Dla zmiennej losowej

z przykładu 1.24. mamy

'

-

'

lub

-

'

-

'

-

pami¸etajmy, ˙ze zdarzenia

oraz

s¸a rozł¸aczne.

b) Dla zmiennej

z przykładu 1.26b mamy

'

-

!

!

!

W przypadku dwóch zmiennych losowych

i

okre´slonych na tej samej przestrzeni

zdarze´n elementarnych

mamy tak zwany ł¸aczny rozkład prawdopodobie ´nstwa, którego

g¸esto´s´c jest okre´slona jako

'

-

'

i

-

'

i

-

jest innym zapisem zdarzenia

'

-

'

-

.

Przykład 1.28

a) Ł¸aczny rozkład zmiennych losowych

i

, z przykładu 1.22b

jest przedstawiony w tabeli

0

1

0

1

b) Dla zmiennych

i

z przykładu 1.22d ł¸aczny rozkład prawdopodobie´nstwa

przedstawiony jest w tabeli:

0

1

2

0

1

Lemat 1.29 Niech

, b¸edzie g¸esto´sci¸a ł ˛

acznego rozkładu zmiennych

i

. Wtedy

1.5. Zmienna losowa

15

a)

'

-

'

-

b)

'

-

'

-

Dowód Zauwa˙zmy, ˙ze

'

-

'

-

'

-

'

-

'

-

poniewa˙z

'

-

Z drugiej strony

'

-

'

-

'

-

'

-

'

-

Podobnie mo˙zna pokaza´c, ˙ze

'

-

'

i

-

'

-

Przykład 1.30 Sumuj¸ac wiersze tabeli z przykładu 1.28b mo˙zna otrzyma´c g¸esto´s´c roz-
kładu zmiennej

, a sumuj¸ac kolumny g¸esto´s´c rozkładu

.

0

1

2

0

1

Podobnie jak dla jednej zmiennej, maj¸ac g¸esto´s´c ł¸acznego rozkładu prawdopodobie ´n-

stwa dwóch zmiennych

i

mo˙zna oblicza´c prawdopodobie ´nstwa zdarze ´n opisywa-

nych przez te zmienne.

Przykład 1.31 We´zmy zmienne

i

z przykładu 1.30. Wtedy

'

-

'

i

lub

i

-

'

i

-

'

i

-

6

oraz

'

-

'

i

lub

i

lub

i

-

16

Rozdział 1. Rachunek prawdopodobie ´nstwa

1.6

Niezale˙zno´s´c zmiennych losowych

Definicja 1.32 Zmienny losowe

i

s¸a niezale˙zne je˙zeli dla ka˙zdej pary liczb

,

mamy

'

i

-

'

-

'

-

lub inaczej, gdy

'

-

'

-

'

-

gdzie

oznacza g¸esto´s´c rozkładu ł¸acznego,

g¸esto´s´c zmiennej

, a

g¸esto´s´c

zmiennej

.

Przykład 1.33 Zmienne losowe

i

z przykładu 1.28a s¸a niezale˙zne, natomiast

zmienne

i

z przykładu 1.28b nie s¸a niezale˙zne.

Oczywi´scie mo˙ze by´c wi¸ecej zmiennych losowych okre´slonych na jednej przestrzeni

Dla trzech zmiennych losowych

,

,

ł¸aczny rozkład prawdopodobie ´nstwa, zdefinio-

wany jest jako

'

-

'

i

i

-

Mamy przy tym

'

-

'

-

'

-

'

-

'

-

'

-

oraz na przykład

'

i

-

'

-

W ogólnym przypadku

zmiennych losowych

ich ł¸aczny rozkład prawdo-

podobie´nstwa okre´slony jest jako

'

-

'

-

Podobnie jak poprzednio łatwo mo˙zna pokaza´c, ˙ze

'

i

-

'

-

Definicja 1.34 Zmienne losowe

,

,

s¸a niezale˙zne je˙zeli dla ka˙zdej trójki liczb

,

i

mamy

'

-

'

-

'

-

'

-

Podobnie mamy w przypadku

zmiennych losowych

1.6. Niezale˙zno´s´c zmiennych losowych

17

Definicja 1.35 Zmienne losowe

s¸a niezale˙zne je˙zeli dla ka˙zdej

-tki liczb

zachodzi

'

-

'

-

Przykład 1.36 Wró´cmy do przykładu z rzutem

monetami, przykład 1.22c. Dla ka˙zdego

)

zmienna losowa

jest równa

je˙zeli na

)

-tej monecie wypadł orzeł, i 1 je˙zeli na

)

-tej

monecie wypadła reszka. Zmienne

s¸a niezale˙zne.

Poka˙zemy teraz, ˙ze je˙zeli zmienne losowe

i

s¸a niezale˙zne, to niezale˙zne s¸a te˙z

zdarzenia opisywane przez te zmienne. Dokładniej

Twierdzenie 1.37 Niech

i

b¸ed¸a niezale˙znymi zmiennymi losowymi, a

i

dowol-

nymi podzbiorami zbioru liczb rzeczywistych. Wtedy zdarzenia

.

'

-

oraz

.

'

-

s¸a niezale˙zne.

Dowód Poniewa˙z zbiór warto´sci zmiennej

jest sko ´nczony, mo˙zemy wypisa´c wszystkie

elementy zbioru

'

-

. Niech

6

'

-

Podobnie niech

6

',

-

Mamy zatem

.

'

-

dla jakiego´s

)

.

'

-

dla jakiego´s

+$

oraz

.

istniej¸a

)",+

takie, ˙ze

'

-

oraz

'

-

-

czyli

'

i

-

Poniewa˙z sumowane zdarzenia wykluczaj¸a si¸e wzajemnie mamy

'

-

'

i

-

18

Rozdział 1. Rachunek prawdopodobie ´nstwa

a poniewa˙z

i

s¸a niezale˙zne

'

-

'

-

'

-

ale

'

,-

'

-

oraz

'

-

'

-

Teza twierdzenia wynika z prostego faktu, ˙ze

'

-

'

-

'

-

'

-

1.7

Warto´s´c oczekiwana, ´srednia

Definicja 1.38 Warto´s´c oczekiwana (´srednia) zniennej losowej

to liczba

'

-

'

-

'

-

Przykład 1.39 Dla zmiennej losowej

z przykładu 1.24 warto´s´c oczekiwana wynosi

'

-

Je˙zeli zmienna posiada jednostajny rozkład prawdopodobie ´nstwa, to jej warto´s´c ocze-

kiwana jest zwykł¸a ´sredni¸a arytmetyczn¸a jej warto´sci.

'

-

'

-

.

.

.

.

'

-

W ogólnym przypadku warto´s´c oczekiwana jest nazywana ´sredni¸a wa˙zon¸a.

Lemat 1.40

'

-

'

-

Dowód Je˙zeli pogrupujemy wyrazy sumy

'

-

'

-

według warto´sci zmiennej

, to otrzymamy

'

-

'

-

'

-

'

-

'

-

1.7. Warto´s´c oczekiwana, ´srednia

19

Przykład 1.41 Przypu´s´cmy, ˙ze mamy informacj¸e, ˙ze w jakiej´s grupie studenckiej połowa
studentów otrzymała ocen¸e 5 z matematyki dyskretnej, jedna trzecia otrzymała ocen¸e 4,
a jedna szósta ocen¸e 3. Jaka jest ´srednia ocena w tej grupie? Przyjmujemy, ˙ze grupa jest
przestrzeni¸a losow¸a, a zmienna losowa

jest ocen¸a studenta. Wtedy warto´s´c oczekiwana

zmiennej

'

-

!

!

!

jest ´sredni¸a ocen¸a w tej grupie.

Wniosek 1.42 Dla ka˙zdej zmiennej losowej

istnieje zdarzenie elementarne

takie, ˙ze

'

-

oraz

'

-

'

-

.

Podobnie istnieje zdarzenie

takie, ˙ze

'

-

oraz

'

-

1

'

-

.

Dowód: Udowodnimy tylko pierwsz¸a cz¸e´s´c twierdzenia, drug¸a mo˙zna udowodni´c w po-
dobny sposób.

Przypu´s´cmy, ˙ze dla ka˙zdego

z dodatnim prawdopodobie ´nstwem mamy

'

-

'

-

. Ale to prowadzi do sprzeczno´sci

'

-

'

-

'

-

'

-

'

-

'

-

'

-

'

-

W przypadku klasycznej definicji wniosek 1.42 opisuje prosty fakt, ˙ze zawsze istnieje

przynajmniej jedna warto´s´c mniejsza od lub równa warto´sci ´sredniej oraz warto´s´c wi¸eksza
od lub równa ´sredniej.

W poni˙zszym twierdzeniu zebrano podstawowe własno´sci warto´sci oczekiwanej.

Twierdzenie 1.43

a)

'

-

'

-

'

-

.

b) Je˙zeli

jest liczb¸a rzeczywist¸a, to

'

-

'

-

.

c) Je˙zeli zmienne

i

s¸a niezale˙zne, to

'

-

'

-

'

-

.

d) Je˙zeli

, to

'

-

.

Dowód:

a)

'

-

'

-

'

-

'

'

-

'

--

'

-

'

-

'

-

'

-

b)

'

-

'

-

'

-

'

-

'

-

'

-

c)

'

-

'

-

'

-

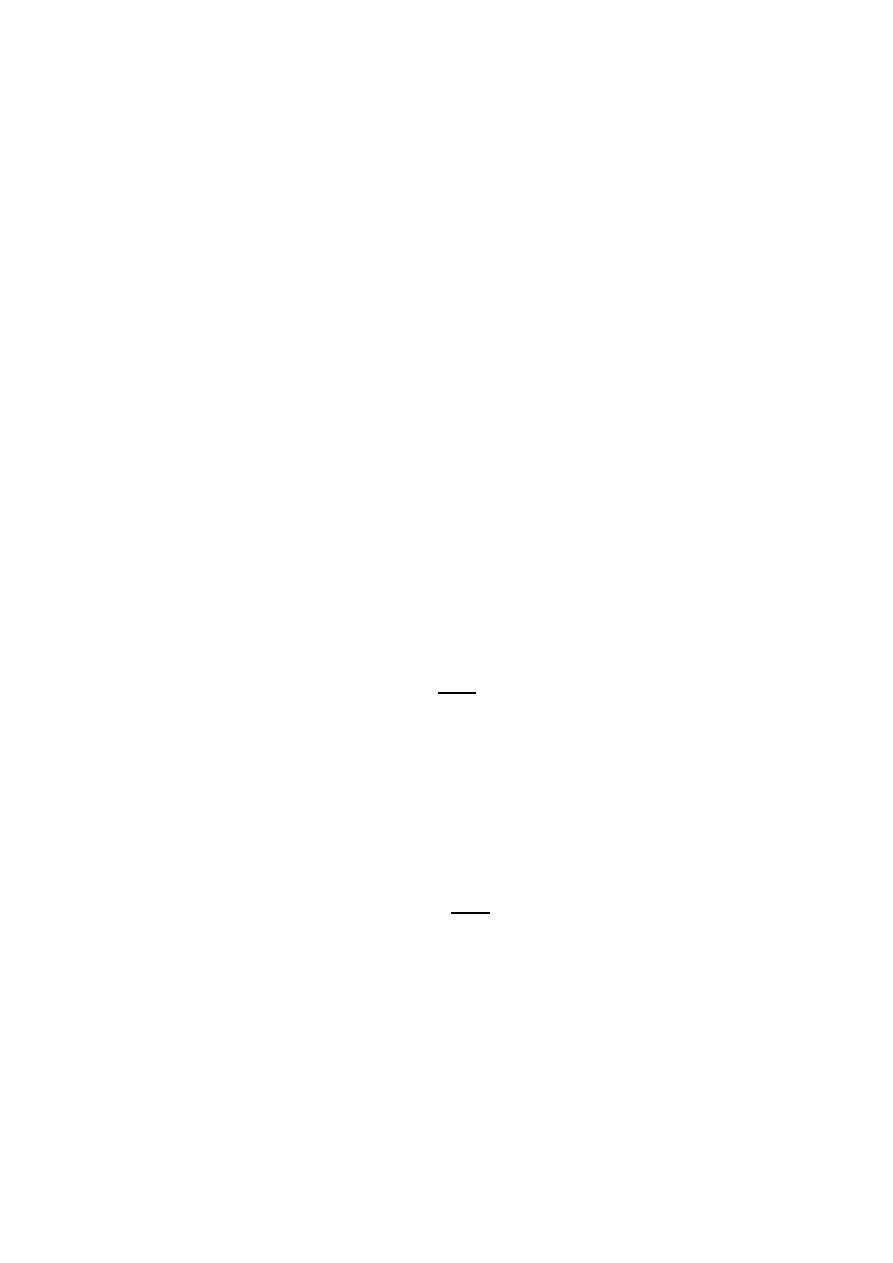
20

Rozdział 1. Rachunek prawdopodobie ´nstwa

Pogrupujmy składniki sumy według warto´sci zmiennych

i

.

'

-

'

-

'

i

-

'

-

'

-

'

-

'

-

'

-

'

-

d)

Je˙zeli dla ka˙zdego

,

'

-

, to

'

-

'

-

.

Twierdzenie 1.44 Warto´s´c oczekiwana sumy

zmiennych

jest równa

'

-

'

,-

Twierdzenie 1.45 Je˙zeli zmienne

s¸a niezale˙zne, to warto´s´c oczekiwana ich

iloczynu równa si¸e

'

-

Twierdzenie 1.46 (Nierówno´s´c Markowa) Je˙zeli zmienna losowa

przyjmuje waret´sci

nieujemne, to dla dowolnej liczby rzeczywistej

'

-

1

'

-

Dowód:

'

-

'

-

'

-

'

-

'

-

'

-

'

-

'

-

Zauwa˙zmy, ˙ze nierówno´s´c Markowa jest u˙zyteczna tylko kiedy

'

-

. Je˙zeli

bowiem

1

'

-

, to mamy trywialne oszacowanie

'

-

1

1

'

-

Przykład 1.47 Nierówno´s´c Markowa wyra˙za do´s´c prosty fakt. Przypu´s´cmy, ˙ze

okre´sla

liczb¸e pieni¸edzy posiadan¸a przez studenta. Je˙zeli warto´s´c ´srednia zmiennej

wynosi 100

złotych, to tylko połowa studentów mo˙ze mie´c 200 lub wi¸ecej złotych. Przypu´s´cmy bowiem
˙ze

cz¸e´s´c studentów posiada 200 (lub wi¸ecej) złotych. Wtedy udział tej bogatej

cz¸e´sci studentów w ´sredniej wynosi co najmniej

'

-

, i

warto´s´c ´srednia nie mo˙ze wynosi´c 100 złotych, je˙zeli zmienna

nie przyjmuje warto´sci

ujemnych.

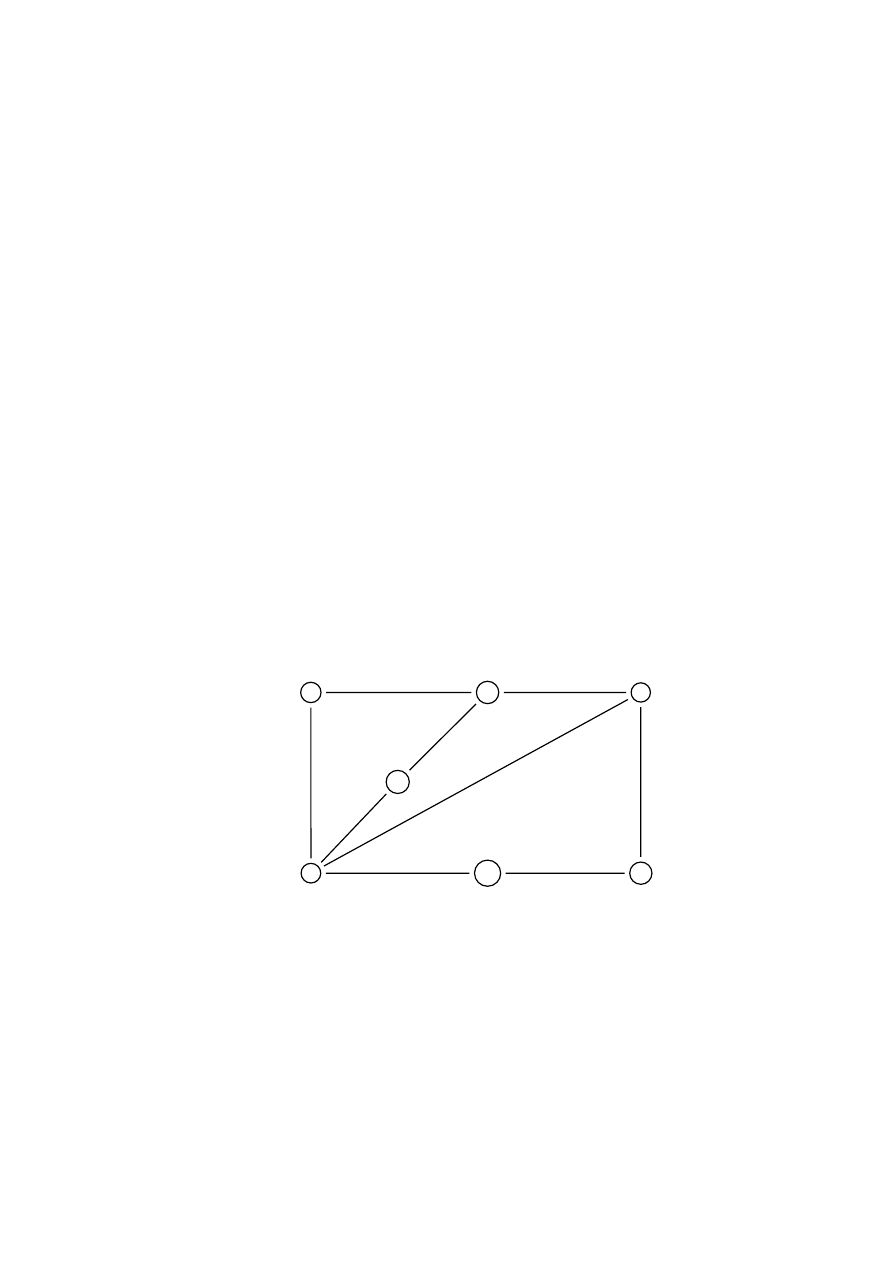
1.7. Warto´s´c oczekiwana, ´srednia

21

Poka˙zemy teraz jak mo˙zna wykorzysta´c prawdopodobie ´nstwo do rozwa˙za ´n kombina-

torycznych. Udowodnimy nast¸epuj¸ace:

Twierdzenie 1.48 Wierzchołki dowolnego grafu mo˙zna pokolorowa´c dwoma kolarami
(białym i czarnym) w taki sposób, ˙ze przynajmniej połowa kraw¸edzi ma swoje ko´nce w
ró˙znych kolorach.

Zanim przejdziemy do dowodu wyja´snjmy kilka rzeczy:

Definicja 1.49 Graf

jest to dowolny sko´nczony zbiór wierzchołków

wraz ze zbiorem

kraw¸edzi

, gdzie kraw¸edzie to pary wierzchołków.

%.0

%

Dla kraw¸edzi

0$

mówimy, ˙ze wierzchołki

i

s¸a ko ´ncami kraw¸edzi

lub, ˙ze

kraw¸ed˙z

ł¸aczy

i

.

Graf cz¸esto przedstwiamy na rysunku jako zbiór punktów poł¸aczonych łukami. Na

przykład rysunek 1.1 przedstawia graf ze zbiorem wierzchołków

i zbiorem kraw¸edzi

%

%

Rysunek 1.1: Przykład grafu

Łatwo jest pokolorowa´c ka˙zdy graf tak, aby ka˙zda kraw¸ed´z miała oba ko ´nce w jed-

nym kolorze. Wystarczy wszystkie wierzchołki pokolorowa ´c tym samym kolorem. Graf
z rysunku 1.1 mo˙zna pokolorowa´c tak, aby ka˙zda kraw¸ed´z była dwukolorowa. Trzeba
pokolorowa´c na biało wierzchołki ,

,

i

i na czarno wierzchołki

,

i

. Ale nie dla

ka˙zdego grafu jest mo˙zliwe takie pokolorowanie, w którym ka˙zda kraw¸ed˙z ma ko ´nce w
ró˙znych kolorach. Na przykład dla trójk¸ata, czyli grafu z wierzchołkami

"##

i

kraw¸edziami

#

#

5#

(patrz rysunek 1.2) nie istnieje takie pokolo-

rowanie.

22

Rozdział 1. Rachunek prawdopodobie ´nstwa

Rysunek 1.2: Trójk¸at

Dowód twierdzenia 1.48: Przypu´s´cmy, ˙ze graf ma

.

.

wierzchołków i

.

.

kraw¸edzi. Rozwa˙zmy przestrze ´n zdarze´n elementarnych

zło˙zon¸a ze wszystkich mo˙z-

liwych pokolorowa ´n wierzchołków grafu

. Jest ich

.

.

. Dla ka˙zdej kraw¸edzi

0$

okre´slmy zmienn¸a losow¸a

w nast¸epuj¸acy sposób:

'

-

, je˙zeli

w kolorowaniu

oba ko ´nce kraw¸edzi

maj¸a ró˙zne kolory i

'

-

w przeciwnym

przypadku.

'

-

, poniewa˙z w połowie kolorowa ´n ko´nce

maj¸a ró˙zne kolory.

W jednej czwartej kolorowa ´n oba ko´nce s¸a białe (kolorowa ´n, w któtych

i

maj¸a kolor

biały, jest

, bo na tyle sposobów mo˙zna pokolorowa´c pozostałe

wierzchołków)

oraz w jednej czwartej kolorowa ´n oba s¸a czarne.

Mamy wi¸ec

'

-

. Rozwa˙zmy teraz sum¸e zmiennych losowych

Warto´s´c zmiennej

'

-

to liczba ró˙znokolorowych kraw¸edzi w kolorowaniu

. Ale

'

-

'

-

Dlatego, zgodnie z wnioskiem 1.42 musi istnie´c kolorowanie

, dla którego

'

-

.

´Srednia liczba ró˙znokolorowych kraw¸edzi w kolorowaniu mo˙ze by´c obliczona bez

u˙zywania terminologii rachunku prawdopodobie ´nstwa. Policzmy ile we wszystkich kolo-
rowaniach jest ró˙znokolorowych kraw¸edzi. Z jednej strony jest to

'

liczba ró˙znokolorowych kraw¸edzi w kolorowaniu

-

Z drugiej strony

'

liczba kolorowa ´n, w których kraw¸ed´z

jest ró˙znokolorowa

-

Przedostatnia równo´s´c wynika z tego, ˙ze liczba kolorowa ´n, w których

jest ró˙znoko-

lorowa wynosi

(połowa wszystkich). ´Srednia liczba ró˙znokolorowych kraw¸edzi w

kolorowaniu wynosi wi¸ec

1.8. Wariancja

23

1.8

Wariancja

Definicja 1.50 Wariancj¸a zmiennej losowej

o warto´sci oczekiwanej

'

-

nazywamy liczb¸e

'

-

''

-

-

Wariancja

'

-

jest miar¸a tego jak bardzo warto´sci zmiennej

s¸a oddalone od ´sred-

niej. Im wi¸eksze rozrzucenie warto´sci tym wi¸eksza wariancja. W poni˙zszym twierdzeniu
zebrano podstawowe własno´sci wariancji

Twierdzenie 1.51

a)

'

-

b)

'

-

'

-

c)

'

-

'

-

d) Je˙zeli zmienne

i

s¸a niezale˙zne, to

'

-

'

-

'

-

.

e) Je˙zeli zmienne

s¸a parami niezale˙zne, to

'

-

Dowód

a)

wynika z faktu, ˙ze zmienna

'

-

przyjmuje tylko nieujemne warto´sci,

b)

'

-

''

-

-

'

-

'

-

'

-

'

-

'

-

d)

''

-

-

'

-

'

-

'

-

poniewa˙z zmienne s¸a niezale˙zne, to z twierdzenia 1.43c

''

-

-

'

-

'

-

'

-

'

-

Z drugiej strony

'

'

-

'

--

'

'

--

'

-

'

-

'

'

--

po odj¸eciu stronami dwóch ostatnich równo´sci

'

-

''

-

-

'

'

--

'

-

'

'

--

'

-

'

'

--

'

-

'

-

Twierdzenie 1.52 (Nierówno´s´c Czebyszewa) Dla zmiennej losowej

z warto´sci¸a oczekiwan¸a

'

-

oraz liczby rzeczywistej

mamy

'.

.

-

1

'

-

24

Rozdział 1. Rachunek prawdopodobie ´nstwa

Dowód: Rozwa˙zmy zmienn¸a losow¸a

. Poniewa˙z

.

'

-

.

'

-

to

'.

.

-

'

-

Stosuj¸ac nierówno´s´c Markowa dla zmiennej

mamy

'.

.

-

'

-

1

'

-

ale

'

-

''

-

-

'

-

1.9

Rozkład jednopunktowy

Z rozkładem jednopunktowym mamy do czynienia, wtedy gdy całe prawdopodobie ´nstwo
jest skupione w jednym punkcie

Definicja 1.53 Zmienna losowa

ma rozkład jednopunktowy, je˙zeli dla jekiego´s

'

-

Poniewa˙z

'

-

, to

'

-

dla ka˙zdego

.

Warto´s´c oczekiwana zmiennej

wynosi

'

-

Lemat 1.54 Je˙zeli jaka´s zmienna

przyjmuje warto´sci nieujemne i

'

-

, to zmien-

na losowa

ma rozkład jednopunktowy, to znaczy

'

-

czyli dla ka˙zdego

, je˙zeli

'

-

, to

'

-

.

Dowód: Poka˙zemy, ˙ze dla ka˙zdego

, je˙zeli

'

-

, to

'

-

. Przypu´s´cmy

bowiem, ˙ze istnieje

, takie, ˙ze

'

-

. Wtedy z nierówno´sci Markowa,

twierdzenie 1.46, mamy

'

-

1

'

-

1

'

-

Zało˙zenie, ˙ze zmienna

przyjmuje tylko warto´sci nieujemne jest istotne we wnio-

sku 1.54. Pokazuje to nast¸epuj¸acy przykład.

1.10. Rozkład zero-jedynkowy

25

Przykład 1.55 Zmienna losowa

z przykładu 1.26a z funkcj¸a g¸esto´sci:

-1

1

'

-

ma warto´s´c oczekiwan¸a

'

-

.

Wariancja zmiennej losowej

z rozkładem jednopunktowym wynosi

'

-

'

-

'

'

--

Ale i na odwrót

Lemat 1.56 Je˙zeli

'

-

, to zmienna losowa

posiada rozkład jednopunktowy.

Dowód Poniewa˙z

'

-

''

-

-

, to z lematu 1.54 wynika, ˙ze

'

-

'

-

.

Wniosek 1.57 Niech

b˛ed ˛

a dowolnymi liczbami rzeczywistymi i niech

Wtedy

przy czym równo´s´c zachodzi wtedy i tylko wtedy, gdy

dla ka˙zdego

)

.

Dowód: Niech

b˛edzie przestrzeni ˛

a z jednostajnym rozkładem prawdo-

podobie´nstwa i niech

b˛edzie zmienn ˛

a losow ˛

a okre´slon ˛

a wzorem

'*)

-

. Wtedy

jest warto´sci ˛

a oczekiwan ˛

a zmiennej

, a

jej wariancj ˛

a, która jest nieujemna i równa zeru tylko dla rozkładu jednopunktowego.

1.10

Rozkład zero-jedynkowy

Zmienna losowa

ma rozkład zero-jedynkowy, je˙zeli prawdopodobie ´nstwo jest skupio-

ne tylko w dwóch punktach 0 i 1. G¸esto´s´c rozkładu prawdopodobie ´nstwa ma wtedy posta´c

0

1

'

-

dla pewnych dodatnich

0

spełniaj¸acych warunek

/

.

Warto´s´c oczekiwana zmiennej

wynosi

'

-

a wariancja

'

-

'

-

'

'

--

'

-

26

Rozdział 1. Rachunek prawdopodobie ´nstwa

1.11

Rozkład dwumianowy — Bernoulliego

Przypu´s´cmy, ˙ze mamy seri¸e

niezale˙znych do´swiadcze´n i w ka˙zdym do´swiadczeniu dwa

mo˙zliwe wyniki: sukces z prawdopodobie ´nstwem

i pora˙zka z prawdopodobie ´nstwem

. Niech

b¸edzie zmienn¸a losow¸a równ¸a liczbie sukcesów w tej serii. Zmienna

losowa

posiada rozkład dwumianowy (Bernouliego) z parametrami

i

.

Dla uproszczenia rozwa˙za ´n załó˙zmy, ˙ze

&

. Prawdopodobie ´nstwo zdarzenia, ˙ze

wyst¸api sukces, pora˙zka, sukces i pora˙zka wynosi

, poniewa˙z wyniki do´swiad-

cze´n s¸a niezale˙zne. Dokładnie dwa sukcesy w serii czterech do´swiadcze´n b¸edziemy mieli,
je˙zeli wyst¸api jeden z ci¸agów, w których na dwóch pozycjach wyst¸epuj¸a sukcesy:

(sukces, sukces, pora˙zka, pora˙zka),
(sukces, pora˙zka, sukces, pora˙zka),
(sukces, pora˙zka, pora˙zka, sukces),
(pora˙zka, sukces, sukces, pora˙zka),
(pora˙zka, sukces, pora˙zka, sukces),
(pora˙zka, pora˙zka, sukces, sukces).

Takich ci¸agów jest

!

, bo na tyle sposobów mo˙zna wybra´c dwie pozycje, na których

b¸ed¸a sukcesy. Ka˙zdy z tych ci¸agów ma takie samo prawdopodobie ´nstwo równe

. I

poniewa˙z te ci¸agi s¸a zdarzeniami wykluczaj¸acymi si¸e, prawdopodobie ´nstwo, ˙ze wyst¸api
który´s z nich wynosi

Podobnie dla dowolnego

1

1

, prawdopodobie ´nstwo, ˙ze w serii czterech do´swiad-

cze´n wypadnie

sukcesów wynosi

W podobny sposób mo˙zna uzasadni´c, ˙ze dla dowolnego

rozkład dwumianowy z para-

metrami

i

ma posta´c

'

5-

Twierdzenie 1.58 Warto´s´c oczekiwana

'

-

zmiennej losowej

maj¸acej rozkład dwu-

mianowy o parametrach

i

wynosi

.

Dowód: Rozwa˙zmy funkcj¸e:

'

-

'

-

ze wzoru Newtona mamy

'

-

'

-

Zró˙zniczkujmy t¸a funkcj¸e

'

-

1.12. Kra ´nce rozkładu dwumianowego

27

Je˙zeli teraz podstawimy

to otrzymamy

'

-

Rozwa˙zmy ci¸ag niezale˙znych zmiennych losowych

, ka˙zda o rozkładzie

zero jedynkowym

'

-

oraz

'

-

Suma tych zmiennych

ma rozkład dwumianowy o parametrach

i

. Warto´s´c oczekiwana, ka˙zdej ze zmiennych

wynosi

'

-

, wi¸ec warto´s´c oczekiwana zmiennej

wynosi

.

Wariancja zmiennej

wynosi

'

-

. Poniewa˙z zmienne

s¸a

niezale˙zne to wariancja ich sumy wynosi

, mamy wi¸ec.

Twierdzenie 1.59 Wariancja zmiennej losowej

z rozkładem dwumianowym o parame-

trach

i

wynosi

'

-

1.12

Kra ´nce rozkładu dwumianowego

Twierdzenie 1.60 (Nierówno´sci Chernoff’a) Niech zmienna losowa

posiada rozkład

dwumianowy o parametrach

i

. Oznaczmy warto´s´c oczekiwan¸a tego rozkładu przez

. Wtedy dla dowolnej liczby rzeczywistej

,

1

1

, mamy

'

'

-

-

1

oraz

'

1'

-

-

1

1.13

Problem dnia urodzin

Zastanówmy si¸e ile osób musi znajdowa´c si¸e w pokoju, aby była du˙za szansa, ˙ze dwie
osoby maj¸a urodziny tego samego dnia.

Dla prostoty przyjmujemy, ˙ze problem dnia urodzin jest równowa˙znu problemowi

wylosowania ci¸agu

liczb

, ka˙zda spo´sród

!

mo˙zliwo´sci, tak aby

wyst¸apiło w nim jakie´s powtórzenie.

Oznaczmy przez

zdarzenie przeciwne, ˙ze wszystkie wylosowane liczby s¸a ró˙zne.

Je˙zeli zało˙zymy, ˙ze wszystkie ci¸agi s¸a równo prawdopodobne, to prawdopodobie ´nstwo,

˙ze otrzymamy ci¸ag ró˙znowarto´sciowy wynosi

'

-

'

-

'

-

'

- '

-

'

-

28

Rozdział 1. Rachunek prawdopodobie ´nstwa

'

-'

-

'

-

Skorzystamy teraz z nierówno´sci

1

'

-

1

1

Prawdopodobie ´nstwo to jest mniejsze od

wtedy gdy

'

-

, a to zachodzi

wtedy gdy

. Dla

!

, zachodzi to dla

.

Tak wi¸ec je´sli w pokoju znajduj¸a si¸e co najmniej 24 osoby, to z prawdopodobie ´nstwem

wi¸ekszym od

dwie spo´sród nich maj¸a urodziny w tym samym dniu.

1.14

Zadania

1. Zaproponuj przestrze ´n zdarze´n elementarnych dla losowania dwóch kul z urny

zawieraj¸acej 3 kule białe i 4 czarne. Przedstaw zdarzenie, ˙ze wylosowano:

a) dwie kule białe, b) kule w ró˙znych kolorach.

2. Zaproponuj przestrze ´n zdarze´n elementarnych dla ustawienia czterech liter ,

,

i

w ci¸ag.

Przedstaw zdarzenie, ˙ze

a)

i

stoj¸a obok siebie;

b)

i

s¸a rozdzielone jedn¸a liter¸a.

3. Zaproponuj przestrze ´n zdarze´n elementarnych dla nast¸epuj¸acych do´swiadcze´n:

a) Losowanie karty z talii 52 kart.

b) Losowanie 13 kart z talii 52 kart.

c) Wypełnienie kuponu totolotka.

d) Wypełnienie kuponu totalizatora piłkarskiego.

4.

,

i

s¸a zdarzeniami. Zapisa´c za pomoc¸a działa ´n na zbiorach zdarzenia:

a) zachodz¸a wszystkie trzy zdarzenia;

b) zachodzi dokładnie jedno ze zdarze ´n

,

lub

;

c) zachodz¸a dokładnie dwa ze zdarze ´n

,

,

;

d) zachodz¸a co najmniej dwa spo´sród zdarze ´n

,

,

.

5. Cyfry

5

ustawiono losowo. Jakie jest prawdopodobie ´nstwo,

a) ˙ze

i

stoj¸a obok siebie;

b) ˙ze pomi¸edzy

i

stoj¸a dwie cyfry;

c) ˙ze

,

i

stoj¸a obok siebie.

1.14. Zadania

29

6. Pokaza´c, ˙ze

'

-

'

-

'

-

7. Dane s¸a

'

-

,

'

-

i

'

-&

. Obliczy´c

'

-

,

'

-

i

'

-

.

8. Dane s¸a

'

-2

i

'

-2

, wiadomo te˙z, ˙ze

'

-2

'

-

. Obliczy´c

'

-

oraz

'

-

.

9. W urnie s¸a 4 kule białe i 3 czarne. Losujemy dwie. Jakie jest prawdopodobie ´nstwo,

˙ze wylosowane kule b¸ed¸a w ró˙znych kolorach?

10. Jakie jest prawdopodobie ´nstwo, ˙ze na przyj¸eciu, na którym jest

osób, znajdzie

si¸e osoba, która ma urodziny tego samego dnia co ja?

11. Jakie jest prawdopodobie ´nstwo, ˙ze przy okr¸agłym stole wybrane na pocz¸atku dwie

osoby usi¸ad¸a obok siebie?

12. Niech przestrze ´n zdarze´n elementarnych b¸edzie zbiorem 3 elementowych ci¸agów

zero-jedynkowych. Wypisz zdarzenia:

a) na pierwszej współrz¸ednej jest zero;

b) na pierwszej i trzeciej współrz¸ednej s¸a zera;

c) na pierwszej i trzeciej współrz˛ednej mamy ró˙zne warto´sci;

d) na wszystkich współrz¸ednych jest to samo.

Oblicz prawdopodobie ´nstwa tych zdarze ´n (rozkład jednostajny).

Czy zdarzenia te s¸a niezale˙zne?

Niech przestrze ´n zdarze´n elementarnych b¸edzie zbiorem

elementowych ci¸agów

zero-jedynkowych (rozkład jednostajny). Oblicz prawdopodobie ´nstwa tych samych
zdarze´n.

13. Rzucamy trzema kostkami. Jakie jest prawdopodobie ´nstwo, ˙ze na ˙zadnej kostce nie

wypada szóstka, je˙zeli na ka˙zdej kostce wypada inna liczba oczek.

14. Mamy dwie urny z kulami. W pierwszej urnie s¸a dwie kule białe i cztery czarne, a

w drugiej urnie trzy białe i trzy czarne. Rzucamy kostk¸a do gry. Je˙zeli wypadnie 1
lub 2, to losujemy kul¸e z pierwszej urny, je˙zeli 3,4,5 lub 6, to losujemy z drugiej
urny.

Jakie jest prawdopodobie ´nstwo, ˙ze wylosujemy kul¸e biał¸a?

Zaproponuj przestrze ´n zdarze´n elementarnych i rozkład prawdopodobie ´nstwa.

15. W urnie jest

kul w tym

białych.

osób po kolei losuje jedn¸a kul¸e bez zwracania.

a) Ile wynosi prawdopodobie ´nstwo wylosowania kuli białej dla trzeciej osoby?

b) Ile wynosi prawdopodobie ´nstwo wylosowania kuli białej dla ka˙zdej z losuj¸acych
osób?

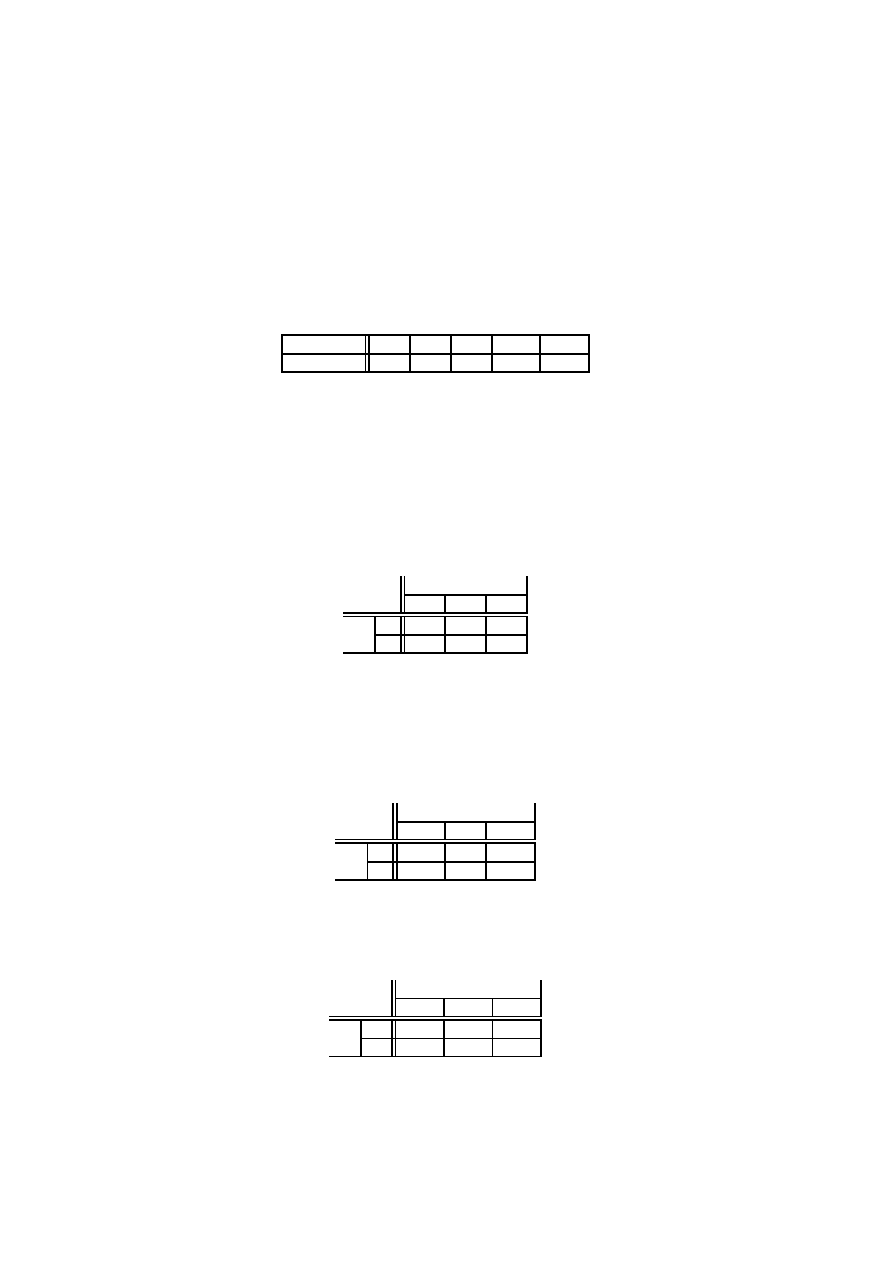
30

Rozdział 1. Rachunek prawdopodobie ´nstwa

16. Udowodnij, ˙ze je˙zeli zdarzenia

i

s¸a niezale˙zne, to niezale˙zne s¸a tak˙ze

i

oraz

i

.

17. Zmienna losowa

posiada rozkład:

1

2

3

4

5

'

-

#

!

#

!

Oblicz

'

-

,

'

-

.

Oblicz warto´s´c oczekiwan¸a

, wariancj¸e

'

-

oraz

'

-

.

18. Zmienna

'

-

jest okre´slona na przestrzeni

#

z jednostaj-

nym rozkładem. Podaj jej rozkład, warto´s´c oczekiwan¸a oraz

'

-

.

19. Podaj rozkład cz¸esto´sci wyst¸epowania liter w zdaniu:

"Podzbiory przestrzeni zdarze ´n losowych nazywamy zdarzeniami".

20. Ł¸aczny rozkład zmiennych losowych

i

przedstawiony jest w tabeli.

-1

0

1

0

1

!

!

!

Oblicz rozkłady zmiennych

,

,

,

.

Oblicz

,

,

'

-

,

'

-

,

'

-

,

'

-

.

Czy zmienne

i

s¸a niezale˙zne?

Oblicz prawdopodobie ´nstwa

'

-

,

'

-

.

21. Ł¸aczny rozkład zmiennych losowych

i

przedstawiony jest w tabeli.

0

1

2

0

(

!

(

1

Czy mo˙zna tak dobra´c liczby

,

i , aby zmienne

i

były niezale˙zne?

22. W dwóch tabelach przedstawiono ł¸aczny rozkład zmiennych

,

i

. Pierwsza

tabela zawiera warto´sci

'

-

, a druga warto´sci

'

-

.

Z=0

1

2

3

-1

#

!

(

1

#

1.14. Zadania

31

Z=1

1

2

3

-1

(

#

#

1

(

(

#

Oblicz rozkłady brzegowe zmiennych

,

i

. Oblicz

'

-

,

'

-

,

'

-

.

Czy zmienne

,

i

s¸a niezale˙zne? Je˙zeli nie, to zmie ´n prawdopodobie ´nstwa w

pierwszej tabeli tak, ˙zeby były niezale˙zne.

23. Na przestrzeni

#

z jednostajnym rozkładem okre´slamy trzy zmienne

'

-

,

'

-

,

'

-

. Czy zmienne te s¸a niezale˙zne?

24. Mamy trzy niezale˙zne zmienne losowe

,

i

(okre´slone na jakiej´s przestrzeni

probabilistycznej). Udowodnij, ˙ze ka˙zde dwie te˙z s¸a niezale˙zne.

25. Mamy

niezale˙znych zmiennych losowych

. Pokaza´c, ˙ze dla ka˙zdego

zmienne

te˙z s ˛

a niezale˙zne.

Podobnie ka˙zdy podzbiór tych zmiennych jest niezale˙zny.

26. Pokaza´c, ˙ze dla ka˙zdego

istnieje zmienna losowa

taka, ˙ze

'

-

oraz

'

-

.

27. Pokaza´c, ˙ze je˙zeli

ma rozkład symetryczny, tzn dla pewnego

,

'

-

'

-

dla ka˙zdego

, to

.

28. Pokaza´c, ˙ze jezeli mamy zmienna losow¸a

z rozkładem jednopunktowym i dowoln¸a

inn¸a zmienn¸a

, to

i

s¸a niezale˙zne

29. Poka˙z, ˙ze je˙zeli zmienne losowe

i

s¸a niezale˙zne, to dla dowolnych liczb

i ,

zdarzenia

oraz

s¸a niezale˙zne.

30. Poka˙z, ˙ze je˙zeli zmienne losowe

i

s¸a niezale˙zne, to dla dowolnych funkcji

i

, zmienne

i

te˙z s¸a niezale˙zne.

31. Pokaza´c, ˙ze

'

-

32. Poda´c przykład dwóch zmiennych

i

o ró˙znych rozkładach takich, ˙ze

i

.

33. Przypu´s´cmy, ˙ze zmienna losowa przyjmuje

warto´sci

ka˙zde z dodatnim prawdopodobie ´nstwem.

a) Czy jest mo˙zliwe

lub

?

b) Czy jest mo˙zliwe

lub

?

c) Czy b) jest mo˙zliwe je˙zeli

ma rozkład jednostajny?

32

Rozdział 1. Rachunek prawdopodobie ´nstwa

34. Kowariancja zmiennych losowych

i

równa si¸e

'

-

''

-

'

--

. Pokaza´c, ˙ze

a) je˙zeli

i

s¸a niezale˙zne to

'

-

;

b)

'

-

'

-

'

-

'

-

c)

'

,-

'

-

'

-

.

35. Rzucano monet¸a 10 razy. Jakie jest prawdopodobie ´nstwo, ˙ze orzeł wypadł co naj-

mniej raz?

36. Jakie jest prawdopodobie ´nstwo otrzymania parzystej liczby sukcesów w ci¸agu

prób Bernoulliego, je˙zeli prawdopodobie ´nstwo sukcesu w jednej próbie wynosi: a)
1/2, b)

.

37. Jakie jest prawdopodobie ´nstwo, ˙ze w serii sze´sciu rzutów kostk¸a suma oczek b¸edzie

parzysta.

38. Pokaza´c, ˙ze je˙zeli

)

+

, to

'

0)

-

'

0,+(-

; a je˙zeli

)

+

, to

'

0)

-

'

,+(-

, gdzie

'

)

-

to rozkład dwumianowy.

39. Niech zmienna losowa

ma rozkład dwumianowy z parametrami

,

. Oszacuj prawdopodobie ´nstwo

'

!

-

(za pomoc ˛

a nierówno´sci

Markowa, Czebyszewa i Chernoff’a).