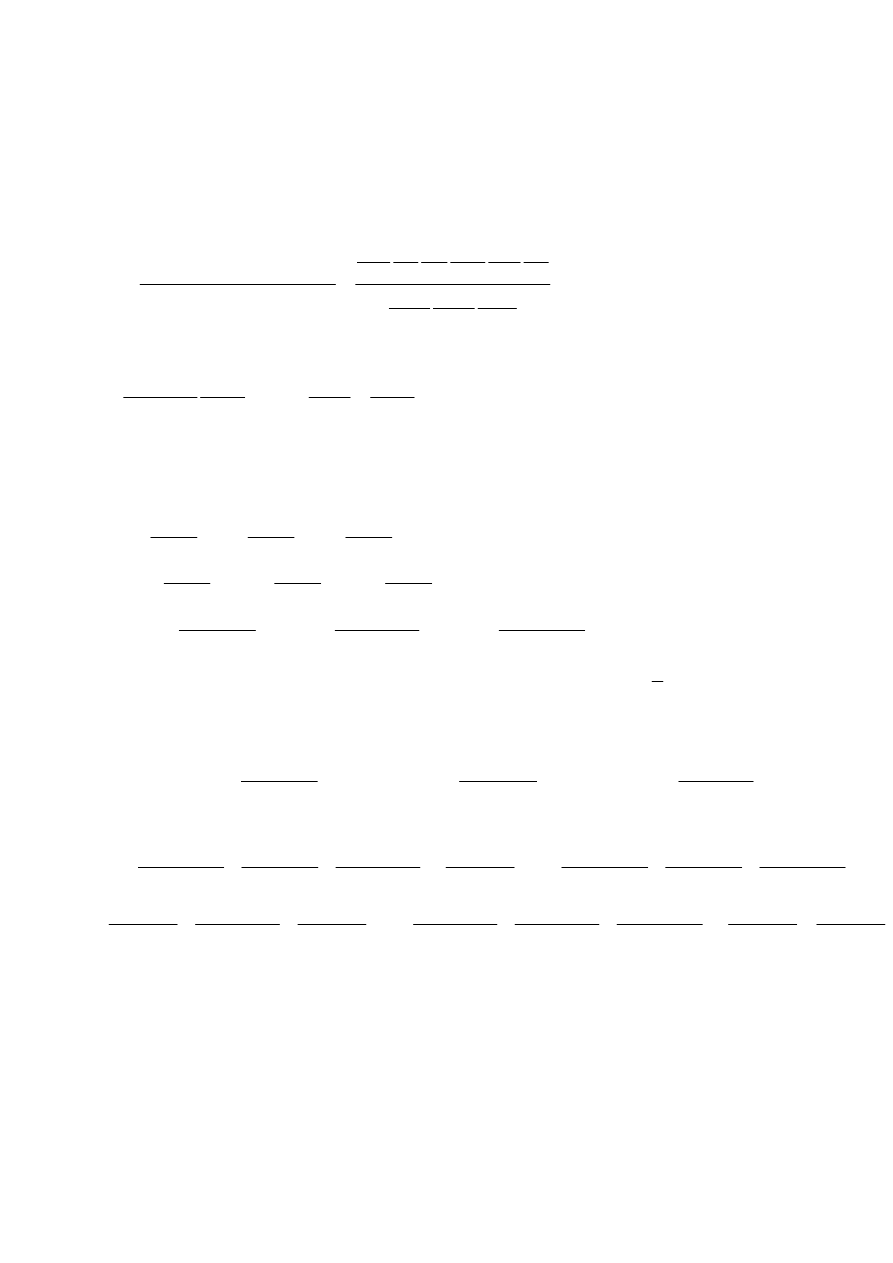
Egzamin dla Aktuariuszy z 13 kwietnia 2002 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
=
=
=
!
13
!
13
!
26
!
26
!
13
!
39
!
39
!
13
!
52
!
9
!
9
!
18
!
18
!
9
!
27
!
27
!
9
!
36
!
4
!
4
!
8
!
8
!
4
!
12
!
12
!
4
!
16
13
26
13
39
13
52
9
18
9
27
9
36
4
8
4
12
4
16
p
=
=
=
16
52
4
13
!
52
!
36
!
16
4
13
!
52
)
!
13
(
)
!
9
(
)
!
4
(
!
36
!
16
4
4
4
4
4
Zadanie 2
x
p
x
p
x
p
C
B
A
+
=
+
=
+
=
60
30
,
60
20
,
60
10
x
EN
x
EN
x
EN
C
B
A
+
=
+
=
+
=
60
210
,
60
140
,
60
70
2
2
2
)
60
(
)
30
(
210
var
,
)
60
(
)
40
(
140
var
,
)
60
(
)
50
(
70
var
x
x
N
x
x
N
x
x
N
C
B
A
+
+
=
+
+
=
+
+
=
(
)
(
)
(
)
(
)
B
A
B
A
B
A
B
A
B
A
B
A
EN
EN
N
N
N
N
EN
EN
N
N
N
N
E
+
−
−
+
=
+
=
2
1
var
var
var
,
cov
(
)
(
)
(
)
C
A
C
A
C
A
C
A
EN
EN
N
N
N
N
N
N
E
+
−
−
+
=
5
,
0
var
var
var
(
)
(
)
(
)
C
B
C
B
C
B
C
B
EN
EN
N
N
N
N
N
N
E
+
−
−
+
=
5
,
0
var
var
var
(
)
(
)
(
)
2
2
2
)
60
(
)
10
(
50
7
var
,
)
60
(
)
20
(
40
7
var
,
)
60
(
)
30
(
30
7
var
x
x
N
N
x
x
N
N
x
x
N
N
C
B
C
A
B
A
+
+
=
+
+
+
=
+
+
+
=
+
war:
(
)
(
)(
)
C
B
B
A
C
B
B
C
A
B
A
EN
EN
EN
EN
N
N
N
N
N
N
N
E
+
+
=
+
+
+
2
+
+
+
−
+
+
−
+
+
+
+
⋅
+
+
+
−
+
+
−
+
+
2
2
2
2
2
2
2
)
60
(
)
30
(
210
)
60
(
)
50
(
70
)
60
(
)
20
(
280
5
,
0
)
60
(
140
70
)
60
(
)
40
(
140
)
60
(
)
50
(
70
)
60
(
)
30
(
210
5
,
0
x
x
x
x
x
x
x
x
x
x
x
x
x
2
2
2
2
2
2
2
2
2
)
60
(
350
210
)
60
(
210
140
)
60
(
)
30
(
210
)
60
(
)
40
(
140
)
60
(
)
10
(
350
5
,
0
)
60
(
140
)
60
(
)
40
(
140
)
60
(
210
70
x
x
x
x
x
x
x
x
x
x
x
x
+
⋅
=
+
⋅
+
+
+
−
+
+
−
+
+
+
+
+
+
+
+
+
⋅
0,5(-2800)+9800+0,5(-4200)+14700+5600+140x+19600+0,5(-8400)+29400=73500
140x=2100
x=15
Zadanie 3
(
)
(
)
∑
∞
=
=
=
1
1
)
(
,...,
max
n
n
n
N
P
X
X
E
EM

1
max
+
=
n
n
E
∑
∑
∑
∑
∞
=
∞
=
∞
=
∞
=
−
−
−
−
−
−
−
=
−
−
=
−
−
=
=
+
=
+
=
1
2
2
2
1
1
1
!
)!
1
(
)!
1
(
1
1
!
1
n
t
t
t
λ
t
λ
t
λ
t
λ
n
e
t
λ
e
t
λ
e
t
λ
t
t
t
n
e
n
λ
n
n
ODP
(
)
λ
e
e
λ
e
λ
e
e
λ
e
λ
e
λ
λ
λ
λ
λ
λ
λ
−
−
−
−
−
−
−
−
−
=
+
+
−
−
=
−
−
−
−
=
1
1
1
1
1
1
1
Zadanie 4
Z CTG
)
1
,
0
(
N
n
σ
mn
X
i
≅
−
∑
(
)
∑
≅
−
n
σ
N
mn
X
i
2
,
0
(
)
∑
≅
n
σ
mn
N
X
i
2
,
(
)
2
, σ
n
m
N
n
X
i
≅
∑
∑
−
=
−
=
µ
K
S
Y
I
µ
X
I
Y
n
n
i
i
i
i
i
,
(
)
µ
p
X
I
E
i
i
=
( )
µ
p
I
µ
E
i
=
0
=
i
EY
(
) (
)
p
σ
p
µ
µ
p
µ
µ
σ
p
I
µ
X
I
µ
X
I
E
EY
i
i
i
i
i
i
2
2
2
2
2
2
2
2
2
2
2
2
=
+
−
+
=
+
−
=
(
)
p
σ
N
n
µ
K
S
n
n
2
,
0
→
−
Zadanie 5
(
)
(
)
(
)
(
)
=
=
<
=
+
=
<
=
=
X
W
P
W
W
X
W
W
E
X
W
P
W
W
X
W
W
E
ODP
2
1
2
2
1
1
2
1
1
1
,
,
(
)
=
>
+
=
4
4
4
4
8
4
4
4
4
7
6
A
X
W
W
W
W
E
X
2
2
1
1
,
2
1
(
)
λ
x
e
e
λ
xe
X
W
P
e
λ
t
A
x
λ
x
λ
x
λ
x
t
λ
1
1
1
+
=
+
=
>
=
−
−
−
∞
−
∫
λ
X
λ
X
X
ODP
2
1
1
2
1
+
=
+
+
=
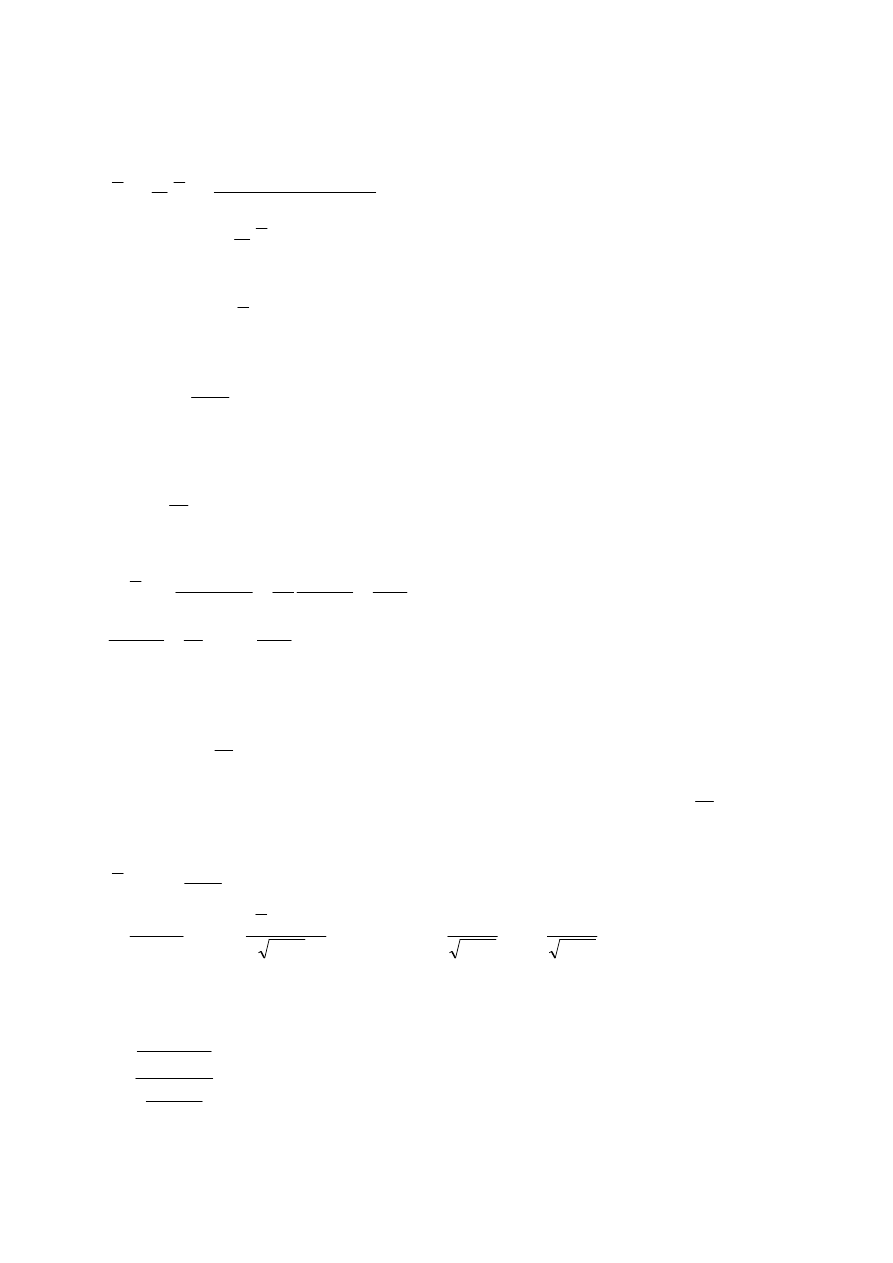
Zadanie 6
4
4
4
4
8
4
4
4
4
7
6
A
n
m
m
n
n
m
n
X
X
X
n
m
X
)
(
...
1
−
+
+
+
=
+
LICZNIK nzl od
m
X
n
m
LICZNIK nzl od A (oczywiste)
Z tego:
LICZNIK nzl od
n
X
nzl od MIANOWNIKA, z tego LICZNIK nzl od MIANOWNIKA
Z tego:
Ma rozkład F(m-1,n-1)
Czyli
1
1
−
−
=
n
m
Er
Zadanie 7
2
1
var
λ
X
=
∑
Γ
≅
)
,
(
λ
n
X
i
( )
(
)
2
2
2
2
2
2
1
)
1
(
1
λ
n
n
λ
n
n
n
n
X
E
X
E
i
+
=
+
=
=
∑
1
1
)
1
(
2
2
+
=
→
=
+
n
n
c
λ
λ
n
n
c
Zadanie 8
(
)
2
10
1
,
cov
σ
X
X
j
i
=
(
)
=
⋅
+
=
+
≅
+
+
2
2
2
100
1
10
1
9900
100
,
100
,
cov
2
100
2
100
;
100
...
σ
σ
µ
N
X
X
σ
µ
N
X
X
j
i
(
)
2
1090
,
100
σ
µ
N
=
≅
2
2
100
1090
,
σ
µ
N
X
(
)
45
,
0
1090
6
,
19
1090
6
,
19
...
96
,
1
1090
100
...
10
96
,
1
≈
≤
≤
−
=
≤
−
=
−
Y
P
σ
µ
X
P
σ
P
Zadanie 9
01
,
0
)
1
(
1
)
101
(
101
2
2
0
=
>
+
+
t
x
x
P

(
)
(
)
=
+
>
+
=
+
>
+
=
>
+
+
t
x
x
P
t
x
x
P
t
x
x
P
)
101
(
101
)
1
(
)
101
(
101
)
1
(
)
101
(
101
)
1
(
2
2
2
2
0
(
)
(
)
01
,
0
101
101
101
1
1
01
,
0
101
101
101
101
101
101
0
=
−
−
+
→
=
−
−
>
=
−
>
−
=
t
t
t
t
x
P
t
t
x
P
01
,
0
100
101
=
−
t
t
t
t
−
=
101
101
2
=
t
2
101
=
t
4
101
=
t
moc:
505
,
0
200
101
99
101
101
101
101
2
101
101
101
2
101
101
1
=
=
+
=
+
=
−
−
>
A
x
P
A
4
4 3
4
4 2
1
Zadanie 10
(
)
(
)
(
)
43
42
1
4
4
8
4
4
7
6
5
1
1
5
1
1
2
1
1
2
lim
→
→
∞
→
=
=
=
=
n
n
n
X
P
X
P
X
X
P
rozkład stacjonarny:
Π
=
Π
+
Π
Π
=
Π
Π
=
Π
+
Π
+
Π
3
3
2
2
1
1
3
2
1
3
2
3
2
2
1
3
1
3
1
2
1
Rozwiązujemy układ z warunkiem:
1
3
2
1
=
Π
+
Π
+
Π
i mamy:
5
2
,
5
1
,
5
2
3
2
1
=
Π
=
Π
=
Π
(
)
(
)
(
)
(
)
(
)
(
)
(
)
=
=
=
=
+
=
=
=
+
=
=
=
=
=
3
3
1
2
2
1
1
1
1
1
0
0
1
0
0
1
0
0
1
1
X
P
X
X
P
X
P
X
X
P
X
P
X
X
P
X
P
36
13
36
6
4
3
6
1
9
1
12
1
2
1
3
1
3
1
3
1
6
1
2
1
=
+
+
=
+
+
=
+
+
=
Wyszukiwarka
Podobne podstrony:
2002.04.13 prawdopodobie stwo i statystyka
2002 06 15 prawdopodobie stwo i statystykaid 21643
2002 10 12 prawdopodobie stwo i statystykaid 21648
2002 01 12 prawdopodobie stwo i statystykaid 21637
2010 12 13 prawdopodobie stwo i statystykaid 27016
2009.04.06 prawdopodobie stwo i statystyka
2002.01.12 prawdopodobie stwo i statystyka
2001.10.13 prawdopodobie stwo i statystyka
2000.04.08 prawdopodobie stwo i statystyka
2009 04 06 prawdopodobie stwo i statystykaid 26658
2002.06.15 prawdopodobie stwo i statystyka
1997.04.05 prawdopodobie stwo i statystyka
2001 10 13 prawdopodobie stwo i statystykaid 21609
2002.10.12 prawdopodobie stwo i statystyka
2010.12.13 prawdopodobie stwo i statystyka
2002 06 15 prawdopodobie stwo i statystykaid 21643
2002 10 12 prawdopodobie stwo i statystykaid 21648
2002 01 12 prawdopodobie stwo i statystykaid 21637
więcej podobnych podstron