Egzamin dla Aktuariuszy z 13 grudnia 2010 r.
Matematyka Ubezpieczeń Majątkowych
Zadanie 1
Y
t
P
≤ t = P( Y ≤ tX + tY )
= P Y ≤
X =
X + Y
1 − t
t
∞
x
−
1 t
1
= ∫ ∫
−
1 −
x 1
y
0,25
6
e
e
dydx =
4
6
0
0
t
∞
x
1
∞
y −
1
1
t
x
1
x
1 t
= ∫
−
−0,25
e
−
6
e
dx =
∫ −0,25
e
1 − ex
p −
x dx =
4
4
6 1 t
0
−
0
0
1
1
24 1
( − t) 1
6 1
( − t)
1
(
3 − t
= 4 −
= 1−
= 1−
= 1−
)
4
1
t
6 − t
6 + t
4 4
6 − t
2
3 − t
+
4
1
(
6 − t
)
3 ⋅ ,
0 4
,
1 2
F ( ,
0 6) = 1 −
= 1−
= 1− 5
,
0
= 5
,
0
→ ( B) Tak
3 − ,
0 6
,
2 4
Zadanie 2
σ
σ
Gdy µ znane to P : X
n − ε
;
α
X n + ε
i P
α
(N < εα )=1−α N ≅ N(0,1)
n
n
Gdy µ nieznane i σ nieznane:
X − µ
t
n
=
n −1 ≅ t S
. tud ( n − )
1 = T
Sn
S
S
t
n
n
α : P( T < tα ) = 1 − α i przedział: X n − t
; X
α
n + tα
n −1
n −1
1 − α = 9
,
0 5
U nas: εα = 9
,
1 6
tα = ,
2 262
S
S
10
P( LOLEK ) =
1
X
,
2 262 n ; X
,
2 262 n S
X
X
10 −
10 +
n =
∑( i − 10 )2
3
3
10 i=1
σ
σ
P( BOLEK ) = X
X
10 −
9
,
1 6
; 10 + 9
,
1 6
10
10
S
dl( LOLEK ) = 2 ⋅ ,
2 262
n
n −1
σ
dl( BOLEK ) = 2 ⋅ 9
,
1 6
n
S
σ
P X ⋅ 2 ⋅ ,
2 262
n
≤ 2 ⋅ 9
,
1 6
= 1
,
0
n −1
n
2
2
2
σ
S
S
2
3 ⋅ 9
,
1 6
n ⋅10
3⋅ 9
,
1 6
2
P S
P
n ≤
=
10
≤
=
1
,
0 a
n
≅ 2
χ 9
( ) →
10 ⋅ ,
2 262 x
2
σ
,
2 262 x
2
σ
2
3⋅ 9
,
1 6
3 ⋅ 9
,
1 6
→
= 1
,
4 68 → x =
≈ ,
1 27
,
2 262 x
1
,
4 68 ⋅ ,
2 262
Zadanie 3
To jest ciąg binarny złożony z n=7 liczb ujemnych i m=8 liczb dodatnich
n + m 15
Ilość takich ciągów Ω =
=
2
7
n −1
m −1
Ilość ciągów przy liczbie serii R=2k to A =
2
k −1
k −1
6
7
A =
2
2
2
2 ⋅15 ⋅ 21
3175200
14
= A
ODP
=
=
=
Ω
15
32432400
143
7
Zadanie 4
E( X Y )
σ1
= EX + ρ
( Y − EY)
σ 2
i ( X Y ) ma rozkład normalny
var( X Y ) = (
2
1 − ρ ) 2
σ1
U nas:
3
1
E( X Y ) = 1+ Y = 1+ Y
9
3
2
var( X Y )
3
= 1
−
⋅ 2 = 1
2 ⋅ 9
cov( 2
2
X , Y ) = E( 2 2
X Y )
2
2
− EX EY
E( X 2 Y 2 ) = EE( X 2 Y 2 Y ) = E[ Y 2 E( X 2 Y )]
E(
1
2
X Y ) = var( X Y )+ E ( X Y ) 2
2
= 1+ 1+ Y
3
E(
2
1
2
1
2
2
X Y )
= E 2
Y 1 + 1 + Y +
2
Y =
2
3
4
E 2 Y + Y + Y
3
9
3
9
Wiemy:
E( 2 k 1
+
Y
)= 0
E( 2 k
Y
)
k
= 1⋅3⋅⋅⋅ (2 k − 9
)
1
Czyli:
E( 2 2
X Y )
2
1
= 2 ⋅ 9 + ⋅ 0 + ⋅3⋅ 92 = 18 + 27 = 45
3
9
ODP = 45 − (2 + )
1 ⋅ 9 = 45 − 27 = 18
Zadanie 5
sup L(θ , x)
λ( x)
θ
=
sup L(θ , x)
θ θ
∈ H
2
4
f (θ ) =
−
x → max
2
θ θ
2
8
− 2θ + 8 x
f (
′ θ ) = −
+
x = 0 →
= 0 → θ = 4 x
2
3
3
θ
θ
θ
2
1
f (4 x ) =
−
=
2 (4 x
2 x ) 4 x
16 x
1
1
λ( x) =
=
4 x ⋅ (
2 1 − 2 x ) 8 x (1− 2 x ) P(
0
t
X < t ) = P(− t < X < t) = ∫ 2 4 x
2
4 x
+
+
2
∫
−
=
θ
θ
2
θ θ
− t
0
0
t
2
2
2
2
2
2
2 x
2
2 x
2 t
2 t
2 t
2 t
4 t
4 t
= x +
+ x −
=
−
+
−
=
−
2
2
2
2
2
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
− t
0
4
8 x
θ
→ f ( x) = −
d
l
a x ∈ ;
0
x
2
θ θ
2
1
1
1
P
> t = P8 Y 1
( − 2 Y ) < = ,
0
2 gdzi
e Y : f ( y) = 4 − 8
y y ∈ ;
0
8 Y 1
( − 2 Y )
t
2
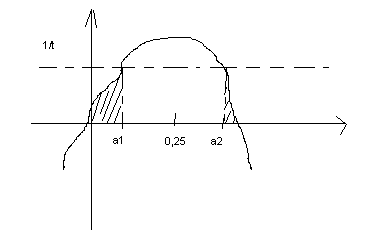
Szukamy:
a 1 = ,
0 25 − a
a 2 = ,
0 25 + a
0,5
∫ (4 − 8 x) dx + ∫(4 −8 x) dx = ,02
0
0,25+ a
[
a
4 x −
2
4 x ]0,25−
4 x
4 x
4( ,
0 25
a)
4( ,
0 25
a)
2 1 4( ,
0 25
a)
4( ,
0 25
a)
0
+ [ − 2 ]0,5
2
2
0,25+ a =
− −
−
+ − −
+ +
+
=
= −8 a +1+ 4 a = ,
0 2 → a = ,
0 2 → 1
a =
0
,
0
,
5 a 2 = ,
0 4
5
i K : { x < 0
,
0 5 ∧ x > ,
0 4 }
5
2
2
dl
a θ =
6 f ( x) =
−
x d
l
a x ∈ (
)
3
,
0
3
9
0,05
3
ODP = ∫ 2 2
2
2
− x + ∫
− x ≈ ,
0 76
3
9
3
9
0
0,45
Zadanie 6
N=1,2,3
P(
P S = N = k P N =
N = k S =
k
3)
( 3
) (
)
=
P( S = )
3
P( S = 3 N = ) 1
1 =
4
P( S = 3 N = 2) 1 1
1
=
⋅ 2 =
2 4
4
P( S = 3 N = 3) 1 1 1
1
= ⋅ ⋅ =
2 2 2
8
3
P( S = )
3 = ∑ P( S = 3 N = k ) 1 −
1 1
1 1
19
1
−1
−1
−
P( N = k) =
e
+
e
+
e
=
1
e
k =
4
4 2
8 6
48
1
1
1
−
P(
e
N = 1 S = 3)
1 48
12
4
=
=
=
19
1
−
4 19
19
e
48
1 1
1
−
P(
e
N = 2 S = 3)
1 48
6
4 2
=
=
=
19
1
−
8 19
19
e
48
1 1
1
−
P(
e
N = 3 S = )
1 48
1
8 6
3 =
=
=
19
1
−
48 19
19
e
48
3
ODP = ∑ P( N = k S = )⋅ k = 12
3
+ ⋅ 6
2
+ ⋅ 1
3
= 27
k =
19
19
19
19
1
Zadanie 7
Z danych wynika, że θ ≥ 1
0
i p ∈ (
)
1
,
0
A – zdarzenie, że 6 zmiennych większych od 5
L = P( )
A ⋅ ∏ f ( x x > 5)
i=1
t 1
1
∫
t −
f (
P
< X < t
θ
θ
t −
X < t X > 5)
(
)
5
5
(
)
5
5
=
=
=
=
P( X > )
5
θ
1
1
(
θ −
θ − 5)
5
∫θ θ
5
f
> =
∈
≅
x ( x x
) 1
5
d
l
a x
( ;5θ)
;
5
( θ )
θ
J
− 5
∞
P( )
A = ∑ P( A N = k ) P( N = k) k =6
θ
P(
k
A N = k )
6
−6
k
− 5 5
=
6
θ θ
∞
6
k −6
∞
6
m
k
θ
m
θ
P( )
A = ∑
− 5 5
1 7
k
5
5
m 6
p 1
( − p) = k − 6 = m = ∑ − +
−
+
p
1
( − p) =
θ
θ
m
θ
θ
k =
6
6
m=0
∞
7
m
7
6
= ∑ m −1+ 7
5 p θ − 5 p θ
θ − 5
6
p 1
( − p) =
m
θ
θ
θ
p
θ
m=
5
0
−
7
6
θ − 5 θ
6
= p 1
( − p)
θ θ − 5 p
1
6
L = p 1
( − p)θ (
θ − 5 p)7
ln L = 6 ln p + ln 1
( − p) + lnθ − 7 ln(θ − 5 p)
∂
1
7
θ − 5 p − 7θ − 6θ − 5
= −
=
=
p = → sprzeczno c
s
θ ≥
p ∈
∂θ θ θ − 5 p
θ (θ − 5 p)
θ(θ − 5 p) 0
b
o
1
0
i
(
)
1
,
0
θ
Czyli ustalamy ˆ
θ = 1
0 b
o (
funkcja malejąca θ (przy ustalonym p)
θ − p)7
5
Szukamy max:
6
10
f ( p) = p 1
( − p)
c
zyl
i g( p) = 6 ln p + ln 1
( − p) + ln10 − 7 ln 1
( 0 − 5 p)
1
( 0 − 5 p)7
∂ g( p)
6
1
35
6 1
( − p) 1
( 0 − 5 p) − p 1
( 0 − 5 p) + 35 p 1
( − p)
= −
+
=
= 0
∂ p
p
1 − p
10 − 5 p
p 1
( − p) 1
( 0 − 5 p)
2
2
2
60
12
licznik = 60 − 90 p + 30 p −10 p + 5 p + 35 p − 35 p = 6
− 5 p + 60 → ˆ p =
=
65
13
Zadanie 8
∫ L θ
( , a) f (θ X ,..., X d 1
5 ) θ → min
θ
Dla θ > max( X
i )
θ
θ
f (
f X ,..., X
f ( )
θ X ,..., X =
1
5 )
( 1
5
)
f ( X ,...., X
1
5 )
∞
f (
1
1
3
3
x ,..., x
3
θ
d
1
5 ) = ∫
⋅ ⋅
= −
=
5
4
8
θ
θ
8θ
8 2
1
⋅ 8
2
1
1
⋅
f (
8
5
4
θ
θ
⋅
θ x ,..., x =
=
θ >
1
5 )
3
8 2
dl
a
2
3
9
θ
8 ⋅ 28
∞
∫
8
2
θ − a
→ min
9
θ
2
dl
a a >
2 c
zyl
i a > 4
a
∞
8
8
2
4
2
2
a
Szukamy min: ∫ ( a −θ )
+ θ
( )
9
∫( − a) =
+
−
= f a
9
θ
θ
a 3
8
3
2
3 ⋅ 6
2
2
a
9
4
9
2
1
− 2 + a
4
9
4
4
f (
′ a) = −
+
= 0 →
= 0 → a = 2 → a = 2 = 4 2
4
8
8
4
a
2
2 a
Dla a ≤ 2
∞
8
4
a
Szukamy min: ∫ ( 2
θ − a) =
−
→min dla a=4
9
θ
3 ⋅ 6
8
2
2
2
Łącznie minimum jest dla
4
a = 4 2
Zadanie 9
n
nθ
θ λ
L =
∏ n(
θ
λ x 1
i ) +
+
i=1
n
ln L = n lnθ + nθ ln λ − (θ + ) 1 ∑ ln(λ + x
i )
i=1
∂
n
ln L = n + n lnλ − ∑ln(λ + x i )
∂θ
θ
i=1
∂
n
ln L = nθ − (θ + )∑ 1
1
∂λ
λ
λ
1
x
i=
( + i )
∂ ln L
n
= −
2
2
θ
∂
θ
∂
n
ln L
θ
= − n +
1
θ 1
2
2
( + )∑
∂
2
λ
λ
λ
i=1 (
+ xi )
∂
n
ln L = n − ∑ 1
∂λ
∂θ
λ
λ
1
x
i=
+ i
Z własności ENW (λˆ θˆ
,
ma asymptotycznie rozkład normalny ze średnią (λ,θ ) i n
n )
2
−1
∂ ln L
macierzą kowariancji I g
dzi
e I
ij = − E
∂λ∂θ
Dla λ =
1
i θ = 4 mamy:
1
I
E 4 n
5
1
,
1
= − ∑
(1+ xi )
2
n
n
I
= E =
2,2
16
16
1
I
,
1 2 = E ∑
− n
(1+ xi )
∞
1
1
4
4
E
= ∫
1 + X
1 +
5
x 1 x
5
0
[ ] =
+
2
∞
1
1
4
2
E
= ∫
=
1 + X
1
( +
2
x)
1
( +
5
x)
3
0
2
2
I
= 4 n − ⋅5 n = n
1
,
1
3
3
4
1
I
= n − n = − n
,
1 2
5
5
I ⋅ 3
2
1
n
3 2
1
2
2400
n
− n II+ I
II
n
n
n
10
−
I+80 II
0 ⋅ n 1 0
I = 3
5 → 3
5 → 3
→
− 1
n
n
n
n
0
0
0 1
5
16
400
400
75
120
Po tych samych operacjach na macierzy jednostkowej otrzymujemy −
I 1 = 2 n
n
120
400
n
n
75
(λ − )
λˆ
→
1
2 n
ma asymptotycznie rozkład N ,
1
c
zyl
i
m
a N (
)
1
,
0
n
2 n
75
ˆ
λ n −1 2
n
75
2 2 ztablic
→ lim P
> 2
= P N >
≈ 1− 2 ⋅ 1,
0 293 ≈ ,
0 741
n→∞
75
2
75
Zadanie 10
MSE = E(θ − )2
ˆ θ
MSE = E( aX + b −θ )2 = E( 2 2
a X + 2 abX + 2
b − 2θ aX − 2 bθ + 2
θ )=
2
2
2
2
= a EX + 2 abEX + b − 2 aθ EX − 2 bθ + θ
EX = nθ
2
EX
= nθ(1−θ )
2
2
2
2
2
+ n θ = nθ − nθ + n θ
MSE = 2
a ( nθ −
2
nθ + 2 2
n θ )+ 2 abnθ + 2
b − 2 aθ nθ − 2 bθ + 2
θ =
= ( 2 2
2
a n − a n − 2 an + )
1 + ( 2
a n + 2 abn − 2 b)
2
θ + b
1
4
4
4
2
4
4
4
3
1
4
4
4
2
4
4
4
3
1
A
A 2
Dla A1=0 mamy ( 2
n − n) 2
a − 2 na + 1 = 0
∆ = 4 n 2 − 4( n 2 − n)= 4 n n − n
n +
a =
n
, a =
a , a > 0 ok
1
2
2
2
1
2
n − n
n − n
A ponieważ aX + b ≥ 0 → b ≥ 0
a 2 n
Z A2=0 mamy: b =
2 − 2 an
( n− n)2
(
n
n − n)2
2
( n− n)2 n( n− )1 2 n( n − )1( n− )1 n −1
b =
=
=
=
>
1
2
2
2
n − n
2
( 2 n − n) ( n − )
0
2 n ( n − )
1
2( n − )
1
1
2 1
− n 2
n − n
( n+ n)2
(
n
n − n)2
2
n ( n + )2
2
1 n( n − )
1
b =
= −
< odpada
2
n + n
2 2
n ( n − )
1 2
n( + n ) 0
1
2 1
− n 2
n − n
( n − ) 2
2
1
n −1
→ ODP =
=
=
2( n − )
1
2( n −1)( n + )
1
1
4( n + )2
1