Egzamin dla Aktuariuszy z 9 grudnia 2000 r.

Prawdopodobieństwo i Statystyka

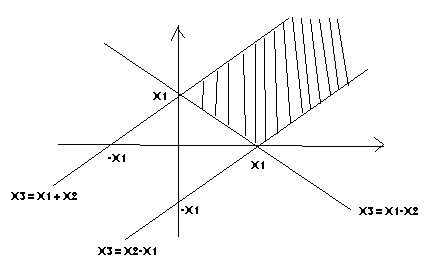
Zadanie 1



X

X

X

X

X

X

X

X

X

1 +

2 +

3

1 +

2 +

3

1 +

2 +



P X

X

X

1 ≤

,

2 ≤

,

3 ≤

3  =



2

2

2



= P( X ≤ X + X , X ≤ X + X , X ≤ X + X

X

∞

1

2

3

2

1

3

3

1

2 )

u

stalone (

0; )

1

WARUNKI: X ≥ X − X , X ≥ X − X , X ≤ X + X

3

1

2

3

2

1

3

1

2

∞  1

x 1

x + x 2

∞ 1

x + x 2



∫ ∫ ∫ 3 − λ 1 x − λx 2 − λ 3 x λ 1

x

λx 2

λ 3

x

λ e

e

e

dx dx dx

λ e

e

e

dx dx dx

3

2

1 + ∫

∫ 3 − −

−



3

2

1

=



0  0 1

x − x 2

1

x x 2 −



1

x



∞  1

x

∞



3 − λx

λx

1

λ x

x

1

λ x

x

λx

λx

1

λ x

x

1

1

−



2

− ( 1+ 2 )

− ( 1− 2 ) 

3 − 1 −



2

− ( 1+ 2 )

− λ( x 2− 1

x )

= ∫



∫ λ e e

 − e

+ e

 dx

λ e

e

e

e

dx

dx

2 + ∫

 −

+





2

1 =



 λ

λ



 λ

λ





0  0

1

x



∞  1

x

∞



= ∫ ∫ 2 −2 λx

2

1

−2 λ 1

x

−

λ e

−

2 λx 2

λx 2

λ 1

x

λx 2

λ e

e

dx

λ e

λ e

e

dx

dx

2 + ∫ 2 −2

2 −2

−

−

2



2

1 =





0  0

1

x



∞

= ∫ 2 −2 λx

2

λx

1

λx

1

λ

λx

λx

1

1

−



2

1

−



2

1

−2

2

1

−2 1

− λ 1

x λ e

λ e

e

e

λ e

e

x dx

1

−

 −

+

 +

−

2

1 =

 2 λ

2 λ 

2

2 λ

0

∞

= ∫ 2 −2 λx

λ 1

1

1

x λ e

1

=

=

2 2 λ

4

0

1

3

ODP = 1 −

=

4

4

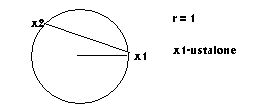
Zadanie 2

φ

a = 2 r sin

2

φ ≅ J ( ;

0 2Π)



φ

2 r sin φ ∈ ( ;

0 Π)



a = 

2



2Π − φ

2 r sin

φ ∈ (Π;2Π)



2

Π

2Π

ODP = ∫ 1

φ

φ

2 sin

dφ + ∫ 1

2Π −

2 sin

dφ = 2Π − φ = x =

2Π

2

2Π

2

0

Π

Π

Π

Π

1 

φ 

1

x

2

 1 

x 

=

− 2cos

+

2

2

4





∫ sin = +  − 2cos  = + =

Π 

2 

Π

2

Π

2

0

Π 



Π Π Π

0

0

Zadanie 3

Przy założeniu że µ ≠ 0 bo wtedy istnieje minimum nieobciążony → a + 2 a + 3 a + 4 a = 1

1

2

3

4

var( 2

2

2

2

a + a + a + a σ →

1

2

3

4 ) 2

min

2

2

2

2

L = a + a + a + a + λa + 2 λa + 3 λa + 4 λa − λ → min 1

2

3

4

1

2

3

4



1

 a 1 =

2 a

λ

1 +

= 0



30





2 a

λ

2 + 2

= 0

a 2 = 1





2 a

λ

3 + 3

= 0

→ 

15





2 a

λ

a

4 + 4

= 0

3 = 1





10

 a

a

a

a

1 + 2 2 + 3 3 + 4 4 − 1 = 0





 a 4 = 2



15

λ

 3 

− + 2(− λ) + 3− λ + 4(−2 λ) −1 = 0

2

 2 

1

λ = − 15

2

1

1

1

 2 

1 + 4 + 9 + 16

30

1

2

σ

Z tego: min =

+

+

+   =

=

=

→ min =

302

152

102

15 

302

302

30

30

Zadanie 4

k ≥ 1

P(

P S = N = k P N =

N = k S =

k

3)

( 3

) (

)

=

P( S = )

3

4 2

λ

− λ

8

3

λ

−

P( S = )

3 =

e

+

e λ

9 2

27 6

P( S = 3 N = )

1 = 0

P( N = 1 S = 3) = 0

P( S = 3 N = 2) 2 1

4

=

2 =

4 2

λ

3 3

9

− λ

P(

e

N = 2 S = 3)

9 2

=

P(

2

 

S = 3 N = 3)

2

8

=   =

P( S = )

3

 3 

27

8

3

λ

−

... = 0

λ

P(

e

N = 3 S = 3)

27 6

= P( S = )3

8 λ 2

3

−

24

4 2

4 3

4

4

e λ +

λ

−

e λ

λ +

λ

+

λ

ODP = 9 2

27 6

= 9

27

= 9 27 =

4 λ 2

3

−

2 2

4 3

2

4

8

e λ +

λ

− λ

λ

e

+

λ

+

λ

9

81

9

81

9 2

27 6

12 + 4 λ

81

36 + 12 λ

6 λ + 18

λ + 3

=

=

= 2

= 6

27

18 + 4 λ

18 + 4 λ

2 9

( + 2 λ)

2 λ + 9

Zadanie 5

1

1

1

−

= −

20

10

20

2







X

− X ≅

σ

N

;

0

 b

o :

20

10







20 

 X + ... + X

X

+ ... + X

X + ... + X



1

σ

1

10

11

20

1

10

2

1

2

var = var

+

−

 =

10

2

σ +

σ 10 =



20

20

10



400

400

20

9 2

S

X , X

n

zl o

d

S

≅ χ )

9

(

10

20

2

σ

P( X

10 − aS ≤ X 20 ≤ X 10 + aS ) = P(− aS ≤ X 20 − X 10 ≤ aS ) =



≅ N (0 )

1

,





6

4

4 7

4

4 8

 aS 20

( X 20 − X 10)



20

aS 20 

= P −

≤

≤

=







σ

σ

σ









≅ t(9)





6

4

4 7

4

4 8



(



X

− X



20

10 ) 20

,

2 262

= P− a 20 ≤

≤ a 20  → a 20 = ,

2 262 → a =

2



S



20



σ



2



σ



Zadanie 6

1

X =

µ + 5 = ...

1

X

( , )

2

0 ≅ N µ σ

X − wart.czek.

1  1



n

X =

 µ + 5 + 5

2

Y

2  2



n − wariancja



 





1

1 1 1

X =

X

X =

 µ + 5 + 5



 + 5

−

5

1 +

n

n



3

2  2  2







2

1

1

Y



= Y



−

1

Y =

σ + 1

1 +

n

n



1

4

4

n = ,

1 ... 1

, 0

1  1



Y =

 σ +1 +1

2

X

4  4



0 = µ

Y

1  1  1





0 = σ

Y =

 σ +1 +1



 + 1

3

4  4  4





Z tego:

1



1 

µ −10

X

µ

n =

+ 5⋅ 21−

 =

+10

2 n



2 n 

2 n



4 

 σ − 

1

4 

1 



3 

4

Y

σ

n =

+ 1−

 =

+

4 n

3 

4 n 

4 n

3

 µ −10



+10 = µ

10

 2



4

 σ −

4



3 + = σ

 410

3

10

10

µ −10 + 2 10 = µ 2

10(1− 210 )

µ =

= 10

1 − 210

4

4 10

10

σ −

+ 4 = σ 4

3

3

4 (1− 410) 4

3

σ =

=

1 − 410

3

Zadanie 7

E( K − K

K

= E K K

10

dr 5

10 )

( 5 10)

K

- ilość orłów w drugiej 5

dr 5

K

10 − X = X

X − E( K

K

= E K K - oczywiste

dr 5

10 )

( 5 10)

X = E(

K

K K

=

5

) 10

10

2

E(

dwum

K

var( K K

=

K −

E K K

=

K −

=

−

= −

=

=

5

10 )

var

var

5

( ( 5 10)

1

1 1

5

10

10

var

var

10

5

10

,

0 625

5

2

4

4 4

4

16

16

Zadanie 8



( x− )12





−

1



e

8



x 2

1

1 x 2









3

1

1

2



2Π 2



− + x− +

1



1

8

4

8

2



x + x−

8

4

8



P 

0

> t  = P e

> t = P e

> t =

2





x







−



1

 2



 2





e 2





2Π



 3



2

1

1

= P x + x − > ln(2 t) = P(3 2

x + 2 x −1 − 8ln(2 t) > 0)

 8

4

8



2

4

-2 jest pierwiastkiem z Vieta → −

= 2

− + x → x = b =

3

3



4



P x >

l

u

b x < 2

−  = 5

,

0 − ,

0 40824 + 5

,

0

− 07725 ≈ 1,

0 1 czyli odpowiedź (E) prawidłowa



3



Zadanie 9

P( X

X

P X

X

P X

X

P X

X

P X

X

n ≥ 3

n− <

=

n ≥

n− =

n− =

n− <

+

n ≥

n− =

n− =

n− <

1

)3 (

3

2

1

) (

2

1

1

)3 (

3

1

)1 (

1

1

1

)3

+ P(

P Y

P X

P Y

P X

X

X

P X

X

n ≥

3

2

3

1

3

n

n 1

n

n 1

n−1 = 0) (

n−1 = 0

n−1 <

) ( ≥ ) ( − = ) ( ≥ ) ( − = )

3 =

P( X

P X

n−1

)

+

< 3

( n−1 )

+

< 3

P( Y

P X

P X

n ≥

)3 ( n− = 0

n− =

1

)

(

,

1 0

,

2

1

)

+

P(

=

P Y

P Y

n ≥

=

n ≥

X

P X

n− <

n− <

1

)3

( 1 ) (

)3 (

)3

3

P(

9

P X

k

n 1 =

X

X

P X

X

P X

X

P Y

P Y

n < 3

n−

3

3

3

3

3

...

0

0

1 ≥

)= ( n < n−1 = ) ( n−1 = n−1 ≥ )+ = ( n = ) ( −

)

∑

=

n =

P X

k =

3

3

( n−1 ≥ )

(

)

P( X

P X

X

P X

P X

X

P X

n ≥

)3 = ( n ≥ 3 n−1 < )3 ( n−1 < )3+ ( n ≥ 3 n−1 ≥ )3 ( n−1 ≥ )3 =

= P( Y

P X

P Y

P X

P X

P X

P X

n ≥ 3)

(

7

1

n−1 < 3) + (1 −

( n = 0) ( n−1 ≥ 3) =

( n−1 < 3)+ ( n−1 ≥ 3)−

( n−1 ≥ 3) =

10

10

7

=

P( X

P X

P X

n− <

+

n− ≥

=

+

n− ≥

1

) 9

3

(

3

1

) 7 2 (

3

1

)

10

10

10

10

7

2

7

2

8

7

7 10

7

X

n =

+

X n− → x =

+

x →

x =

→ x =

=

1

10

10

10

10

10

10

10 8

8

Zadanie 10

P( )

A − P( A ∩ B) > 0

( C ∩ B)\ ( C ∩ ) A

P( B) − P( A ∩ B) > 0 BO: ( C ∩ B) \ ( C ∩ A ∩ C ∩ B) P( A ∩ B) > 0

Z nierówności z treści zadania:

P( A ∩ C) + P( B ∩ C) − P( A ∩ B ∩ C) P( A ∩ C)

>

b

o P( )

A + P( B) − P( A ∩ B) > 0

P( A ∪ B)

P( )

A

Z TEGO:

P( A ∩ C)

P( B ∩ C) − P( A ∩ B ∩ C) > P( A ∪ B) − P( A ∩ C) P( )

A

P( A ∩ C) P( A∪ B) − P( A∩ C) P( C B − A) P( C ∩ B) − P( A ∩ B ∩

=

C) > P( )

A

>

P( B) − P( A ∩ B) P( B) − P( A ∩ B) P( A ∩ C) P( A ∪ B) − P( ) A P( A ∩ C)

P( A ∩ C)( P( B) − P( A ∩ B))

>

=

= P C A

P( )

A ( P( B) − P( A ∩ B)) P( )

A ( P( B) − P( A ∩ B)) (

)