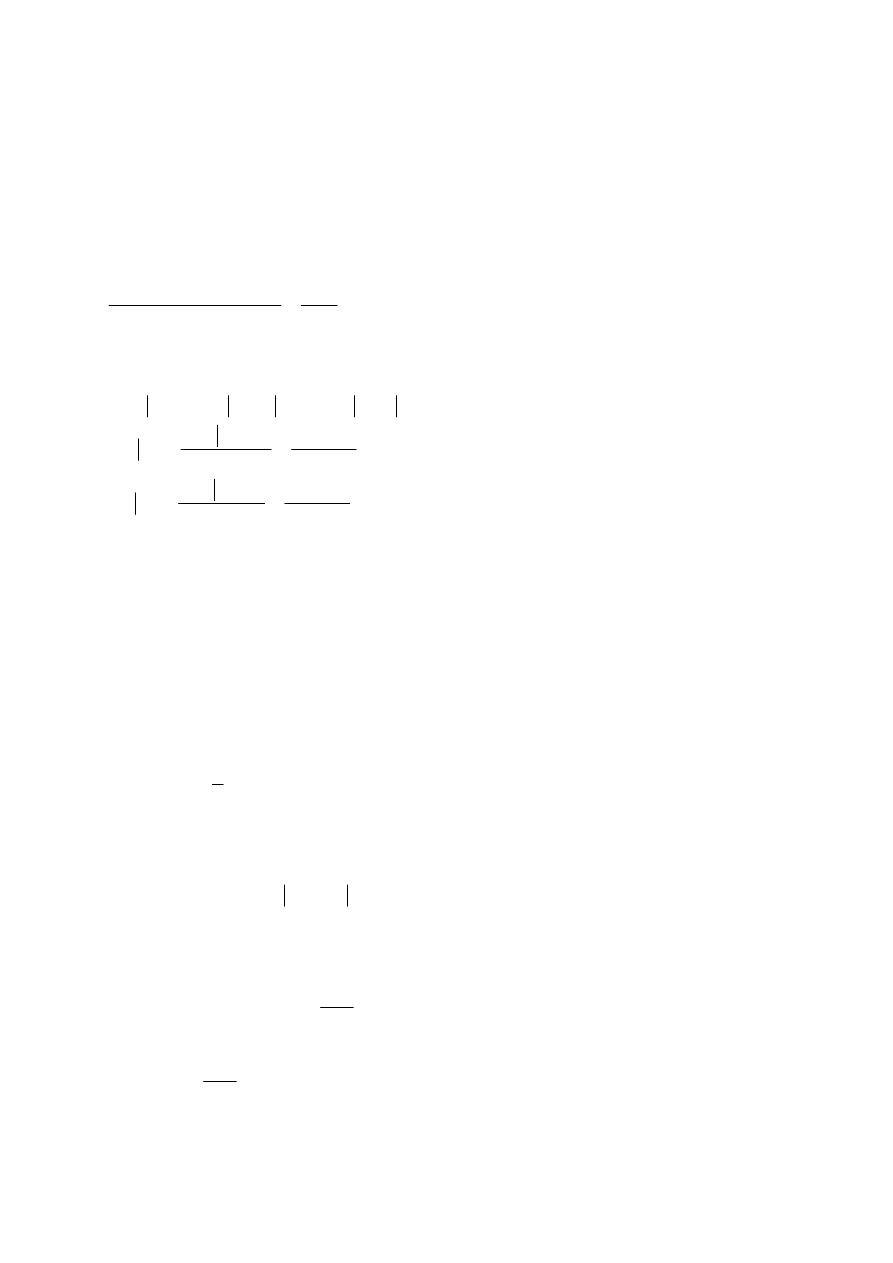
Egzamin dla Aktuariuszy z 5 grudnia 1998 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
4 – na jednej
1296
175
6
1
3
3
4
3
2
4
3
4
4
2
3
=
+
+
+
⋅
Zadanie 2
(
) ( ) ( ) ( ) ( )
28
,
0
4
,
0
4
,
0
6
,
0
2
,
0
1
2
1
2
1
2
=
⋅
+
⋅
=
+
=
S
z
P
z
S
P
S
d
P
d
S
P
S
S
P
( ) ( )
6
,
0
25
,
0
75
,
0
2
,
0
)
1
(
)
(
1
1
=
⋅
=
=
S
P
d
P
d
S
P
S
d
P
( ) ( )
4
,
0
25
,
0
25
,
0
4
,
0
)
1
(
)
(
1
1
=
⋅
=
=
S
P
z
P
z
S
P
S
z
P
25
,
0
25
,
0
4
,
0
75
,
0
2
,
0
)
(
4
,
0
)
(
2
,
0
)
1
(
=
⋅
+
⋅
=
+
=
z
P
d
P
S
P
Zadanie 3
Błąd bo:
(
)
2
3
)
(
3
P
A
P
C
B
A
P
−
=
∪
∪
(
)
2
2
P
P
B
A
P
−
=
∪
Z tego:
2
2
2
3
3
P
P
P
P
−
≥
−
P
P
−
≥
−
2
3
3
2
1
1
2
≤
→
≤
P
P
musi tak być i wynika odpowiedź (A)
Zadanie 4
∑
∑
∞
=
∞
=
−
=
+
⋅
=
=
−
=
⋅
⋅
1
0
1
)
1
(
75
,
0
125
,
0
1
75
,
0
25
,
0
5
,
0
k
n
n
k
n
n
k
k
12
3
25
,
0
75
,
0
...
75
,
0
75
,
0
25
,
0
...
75
,
0
2
75
,
0
75
,
0
...
75
,
0
2
75
,
0
2
3
2
2
=
=
=
+
+
=
⋅
+
⋅
+
=
⋅
+
⋅
+
=
X
X
X
X
2
16
125
,
0
25
,
0
1
12
125
,
0
=
⋅
=
+
=

Zadanie 5
95
,
0
1
)
(max
10
5
=
−
=
≤
−
x
e
x
P
1
,
0
5
95
,
0
1
=
−
−
x
e
1
,
0
5
95
,
0
1
−
=
−
x
e
(
)
1
,
0
95
,
0
1
ln
5
−
=
−
x
(
)
377
,
26
95
,
0
1
ln
5
1
,
0
≈
−
−
=
x
Zadanie 6
(
)
[
]
∫
∫
∫
≈
−
=
+
=
+
=
<
1
0
5
,
0
0
1
5
,
0
1
5
,
0
847
,
0
5
,
0
ln
5
,
0
5
,
0
ln
5
,
0
5
,
0
5
,
0
1
)
(
5
,
0
y
dy
y
dy
y
f
y
X
P
Zadanie 7
∑
≅
)
,
(
.
q
n
DWUM
UJ
X
i
∑
∞
=
=
−
−
+
+
0
!
)!
1
(
)!
1
(
k
k
n
p
q
p
k
n
k
n
k
a
a
∑
∞
=
−
=
=
−
−
+
+
0
1
1
-
n
r
gdzie
1
!
)!
1
(
)!
1
(
k
k
n
q
p
k
n
k
n
k
a
a
∑
∞
=
−
−
=
→
=
−
−
+
+
→
=
−
−
+
−
−
+
+
0
1
1
1
1
1
1
1
1
)!
2
(
!
)!
2
(
k
k
n
n
a
n
k
n
k
a
a
n
k
n
q
p
n
k
k
n
k
a
a
Zadanie 8
(
)
1
0
0
1
0
;
)
(max
φ
φ
t
φ
φ
φ
t
t
P
n
∈
−
−
=
≤
(
)
(
)
n
n
φ
φ
φ
t
n
f
0
1
1
0
max
−
−
=
−
(
)
1
0
0
1
1
;
1
)
(min
1
)
(min
φ
φ
t
φ
φ
t
φ
t
P
t
P
n
∈
−
−
−
=
≥
−
=
≤
(
)
(
)
n
n
φ
φ
t
φ
n
f
0
1
1
1
min
−
−
=
−
(
)
(
)
(
)
(
)
∫
∫
−
−
−
=
+
−
=
=
−
=
−
−
=
1
0
0
1
0
1
0
0
1
0
0
1
1
0
max
φ
φ
φ
φ
n
n
n
n
t
φ
t
φ
φ
n
t
φ
x
φ
φ
φ
x
xn
E
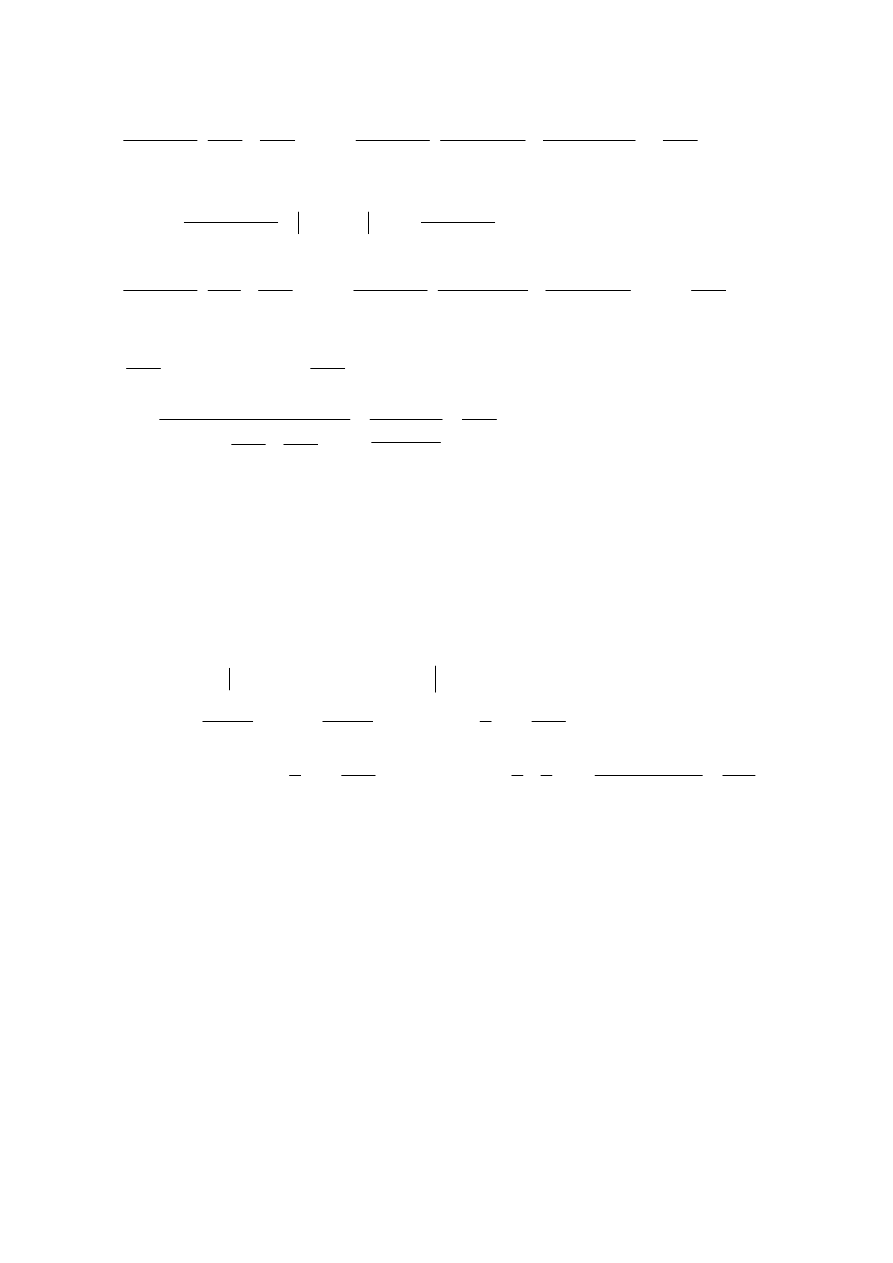
(
)
(
)
(
)
(
)
(
)
0
0
1
0
1
0
1
0
1
0
1
0
0
1
0
1
1
1
1
0
1
φ
φ
φ
n
n
n
φ
φ
φ
n
φ
φ
φ
φ
n
n
t
φ
n
t
φ
φ
n
n
n
n
φ
φ
n
n
n
+
−
+
=
−
+
+
−
−
=
+
+
−
=
+
−
+
(
)
(
)
(
)
(
)
∫
∫
−
−
−
=
−
−
=
=
−
=
−
−
=
1
0
0
1
0
1
1
0
1
1
0
1
1
1
min
φ
φ
φ
φ
n
n
n
n
t
t
φ
φ
φ
n
t
x
φ
φ
φ
x
φ
nx
E
(
)
(
)
(
) (
)
(
)
0
1
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
1
1
0
1
φ
φ
n
n
φ
n
φ
φ
n
φ
φ
φ
φ
φ
n
n
t
n
t
φ
φ
φ
n
n
n
n
φ
φ
n
n
n
−
+
−
=
+
−
−
−
−
=
+
−
−
=
+
−
+
(
)
(
)
→
−
=
−
+
+
−
+
−
+
0
1
0
1
1
0
0
1
1
1
φ
φ
φ
φ
n
n
φ
φ
φ
φ
n
n
a
(
)
1
1
1
1
2
1
1
1
1
0
1
0
1
−
+
=
+
−
−
=
−
+
+
+
−
−
=
→
n
n
n
n
n
n
n
n
n
φ
φ
φ
φ
a
Zadanie 9
Podane informacje są sprzeczne bo dodatkowe parametry powinny zwiększać m a jest
odwrotnie.
Zadanie 10
(
)
i
i
i
i
i
i
EZ
EX
Z
EX
Z
X
−
=
,
cov
(
)
(
)
(
)
(
)
=
=
=
+
=
=
=
j
i
j
i
j
i
i
i
i
i
i
i
i
i
Y
Z
P
Y
Z
Y
X
E
Y
Z
P
Y
Z
Y
X
E
Z
EX
(
)
(
)
n
n
µ
n
µ
p
σ
n
n
µ
n
n
µ
p
σ
1
1
!
)!
1
(
1
!
)!
1
(
2
2
2
2
2
2
−
−
+
=
−
−
+
−
+
=
(
)
(
)
(
)
n
p
σ
n
µ
µ
p
σ
µ
n
n
µ
p
σ
µ
n
n
µ
n
µ
p
σ
Z
X
i
i
2
2
2
2
2
2
2
2
2
2
2
1
1
1
1
,
cov
=
−
+
=
−
+
=
−
−
+
+
=
Wyszukiwarka
Podobne podstrony:
1998.12.05 prawdopodobie stwo i statystyka
2005.12.05 prawdopodobie stwo i statystyka
2005 12 05 prawdopodobie stwo i statystyka
1998 10 03 prawdopodobie stwo i statystykaid 18585
2000 12 09 prawdopodobie stwo i statystykaid 21582
2010 12 13 prawdopodobie stwo i statystykaid 27016
2007 12 03 prawdopodobie stwo i statystykaid 25662
2003.12.06 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2008 12 15 prawdopodobie stwo i statystykaid 26466
2007.12.03 prawdopodobie stwo i statystyka
1996.12.07 prawdopodobie stwo i statystyka
2008.12.15 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
2006 06 05 prawdopodobie stwo i statystykaid 25461
2009 10 05 prawdopodobie stwo i statystykaid 26670
1998.02.28 prawdopodobie stwo i statystyka
2000.12.09 prawdopodobie stwo i statystyka
więcej podobnych podstron