Egzamin dla Aktuariuszy z 28 lutego 1998 r.
Prawdopodobieństwo i Statystyka Zadanie 1
4
4 10
⋅ 2 ⋅ 2 ⋅ ⋅ 2
⋅ 2
P(
A ∩ A ∩ A =
1
2
3 )
2
2
5
20
⋅ 2
10
6 14
2
2
P(
A
=
2 )
3
7
20
⋅ 2
10
4
14
2
⋅ 2
⋅ 2
P(
A ∩ A
=
1
2 )
2
7
20
⋅ 2
10
6 4 10
2
2
2
P(
A ∩ A
=
3
2 )
3
2
5
202
10
2
4 10 20
4
14 20 6
4
10 20
1
6
8
2
8
2
2 5 10
2
7 10 3
2
5 10
=
20
6
14
20 6
14
20 6 14
4
2
4
2
4
10
3
7
10 3
7
10 3 7
2
4 10162
2 5
16
P =
=
..... = L → ( )
A
6
14
4
8 ⋅ 8
3
7
Zadanie 2
E(
1
x
1
x
X X
E X
X
X
P( N
k )
k
xdx
x
1
x
n
0 )
∞
∞ 1
∞
= ∑ ( N N > 0 )
=
= ∑ ∫
= ∑ −1
0
( − 0 ) + 0
+
=
0
k =
2
2
1
k =1 x
k =1
0
EX
N = EE ( X
X
N
= +
0 )
1
1
2
4
1
1
1
1
1
1
ODP =
+ − EX = + − =
0
2
4
2
4
2
4
Zadanie 3
Tu jest chyba błąd: wychodzi Be(0,5;0,5) Π
2
1
2
u
P
≤ t =
4
rd d
φ r
2
2
∫ ∫
=
u + v
Π
0 arccos t
bo:
u = r cos φ
= r
v = r sin φ
Π
φ ∈ ;
0
,
r ∈ ( )
1
,
0
2
cos2 φ ≤ t
cos φ ≤ t
Π
φ ∈ arccos t ;
2
1
= ∫ 4 Π
2 Π
2
r
− arccos t =
− arccos t = 1− arccos t Π 2
Π 2
Π
0
1 − 1
2
1
1
1
1
1
1
f ′
−
( t) =
=
1
( − t) 2
2
t
≅ Be(
)
5
,
0
;
5
,
0
b
o Γ
= Π
Π 1− t 2 t Π
2
Zadanie 4
k – liczba sukcesów
k+4 – liczba poraŜek
n=2k+4
k
k +4
2 k + 4
1 2
p
L
k =
=
k
3 3
k 1
+
k +5
k +4
p
(2
k +
k + )
6 !
1
2
k!( k + )
4 !
k
3
2 (2 k + )
5 (2 k + )
6
1 =
3
=
> 1
p
( k
k
+ )
1 !( k + )
5 ! 3
3
(2 k + )
4 !
2
9 ( k + )
5 ( k + )
1
4 2
k + 22 k + 30
9
>
2
k + 6 k + 5
2
8 2
k + 44 k + 60 − 9 2
k − 54 k − 45 > 2( 2
k + 6 k + )
0
5
2
− k −10 k +15 > 0 ∆ l icznika = 160
2( k + )
5 ( k + )
1
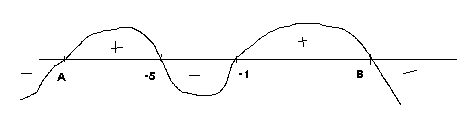
− 160 −10
A =
2
160 −10
B =
2
pk 1
+ > d
1
o ≈ 1,32 → max d
la k
= 2
pk
n = 2 ⋅ 2 + 4 = 8
Zadanie 5
MoŜna ograniczyć się do testu NM
2
2
1
1
xi − µ+
yi − µ−
2 n
2
2
1
−
−
2
2
∏ e
∏ e
2
P
Π
> t =
2
n
( xi− µ)2
( yi− µ)
,
0 05
2
1
−
−
2
2
e
e
∏
∏
2
Π
...
n
≅ N 0;
2
6 4
4 7 4
4 8
∑ y − ∑ x
i
i
1
n
1
P
− n > ln t = , 0 05 → ln t = ,
1 64
− n
H
0
2
4
2
4
1
n
≅ N n;
4 2
6
4
4
4
7
4
4
4
8
∑ yi − ∑ xi
1
n
1
moc: P
H
− n > ,
1 64
− n > 9
,
0 5
1
2
4
2
4
n
1
,
1 64
− n
2
2
< − ,
1 64
n
2
1 n 2
2 n
,
1 64 −
< − ,
1 64 →
> ,
3 28 → 2 n > 5
,
6 6 → 2 n > 4 ,
3 03 → n ≥ 21 5
, 1 → n ≥ 22
2
n
2
Zadanie 6
1
−
−
1
1
−
P(− ln X ≤ t) = P(ln X ≥ − t) = P(
t
X ≥ e )
θ
= ∫ x
θ
= [ θ
x ]
θ
t
− t = 1 − e
e
−
e t
f ( t) = θe− tθ ≅ wykl( θ)
− ∑ln X
;
5
(
)
i ≅ Γ
θ = S
c
c
c
θ θ 5
P θ <
= P( Sθ < c) = P S ≤ = ∫
4 − x
θ
x e
=
S
θ
24
0
u = 4
∫
x
4 −
x e θx =
...
u′ = 4 3
x ...
....
....
4
3
2
=
−
c
c
c
1 − e c
+
+
+ c +1 = ,
0 05
24
6
2
9
,
3 4
po wstawieniu wychodzi c ≈
2
c
c
18,31
tak samo P( θ > θ ) = P S > = 1− P S ≤ i wychodz
i
θ
θ
2
Zadanie 7
E( X
...
...
1 +
+ X Y
5
)+ E( X 6 + + X Y
15
)= Y
1
E( X + ... + X Y =
+ +
→ +
= →
+ +
=
6
15
) 2 E( X ... X Y
1
5
) X 2 X Y E( X ... X Y
1
5
) Y
3
1
2
ODP = E( X + ... + X Y +
+ +
−
+ +
= +
−
=
+
1
15
) E( X ... X Y
16
20
) E( X ... X Y
1
5
) Y 5 µ Y Y 5 µ
3
3
Zadanie 8
P( f ( X
P f X
n+ ) = )
1 =
n
= ⋅
1
( ( ) 2) 5,
0
P( f ( X
P f X
P f X
n+ ) = 2 =
n
= +
n
= ⋅
1
) ( ( ) )1 ( ( ) 2) 5,
0
E( f ( X
f X
P f X
P f X
P f X
n ) ⋅
( n+ ) = 2
n
= +
n
= ⋅
+
n
= ⋅
1
( ( ( ) )1 ( ( ) 2) 5,
0 ) 4 ( (
) 2) 5,
0
Ef ( X
P f X
P f X
n ) =
( ( n ) = )1+ 2 ( ( n ) = 2) Ef ( X
P f X
P f X
n+
=
n+
= +
n+
=
1 )
( ( 1) )1 2 ( ( 1) 2)
co [
v f ( X
f X
P f X
P f X
P f X
P f X
n ),
( n+1)]= 2 ( ( n ) = )1+ 3 ( ( n) = 2)−[ ( ( n) = )1+ 2 ( ( n ) = 2)]⋅
⋅[ 5
,
0 P( f ( X
P f X
P f X
n ) = 2) + 2
( ( n ) = )1+ ( ( n ) = 2)]
[
0
1
Π ,Π
= Π , Π
1
2 ]
[ 1 2]
5
,
0
5
,
0
Π
5
,
0
Π + Π = 1
2 = Π
1
1
2
Π
5
,
0
5
,
0 Π + Π = 1
1 +
Π2 = Π2
2
2
Π2 = 2
3
1
Π1 =
3
lim cov = 2Π
1 +
Π
3 2 − (Π1 + 2Π 2 )( Π
5
,
1
2 + 2Π1 )
1
2
1
2
3 2
1
= 2 ⋅ + 3⋅ − + 2 ⋅
+ 2 ⋅ =
n→∞
3
3
3
3
2 3
3
2
5 5
6 + 18 − 25
1
= + 2 −
=
= −
3
3 3
9
9
Zadanie 9
∞
x−
− c
EX = ∫ x
µ
e
= c + µ
µ
c
t − c
− n
n
µ
P(min ≤ t) = 1 − P ( X ≥ t) = 1 − e t − c
− n
n
µ
µ
f
t
( )
przesunięty wykładniczy → E min = c +
min
= e
µ
n
E∑ X
i = n( c + µ) n( c + µ) n
nc + µ
n − 1
( )
A
−
=
µ = µ → ( )
A
n −1
n −1
n
n − 1
Zadanie 10
E(
n
n
c X
...
2
2
1
1 +
+ c X
µ 2
E
c 2 X 2
c c X X
µ
c X
µ 2
n
n −
)
= ∑ i i + ∑ i j i j − ∑ i i + =
i=1
i< j
i=1
n
= 2∑ c c µ 2
c 2 γ 2 µ 2
µ 2
2 µ
c µ
µ 2
2 µ 2
c c
γ 2 µ 2
µ 2
c 2
2 µ 2
c
µ 2
i
j
+ ∑ i (
+
)− ∑ i + = ∑ i j +( + )∑ i − ∑ i +
i< j
i=1
i< j
∂ =2 µ 2∑ c 2 γ 2 µ 2 µ 2 c 2 µ 2 0
j +
( + ) i − =
∂ ci
j≠ i
1 s
. uma p
o i
2
:
2
µ ( n − )
1 ∑ c
i + 2( 2
2
γ µ + 2
µ )∑ ci − 2 2
nµ = 0
2
2
nµ
nµ
n
2 ∑
.
c
i =
2
2
2
2 µ ( n − )
1 + 2( 2 2
γ µ + 2
µ ) =
=
2
2 µ n +
2
2
2 γ µ
n + 2
γ
Z 1.
2
2 µ (∑ c − c +
+
=
i
i )
2( 2 2
2
γ µ
µ )
2
c
2 µ
i
2
2 µ (1− ∑ c
− ∑
i )
2
z
i
1
ci
1
c =
=
− czyli c
r
owne → c =
to daje min, moŜna sprawdzić
i
i
2
2
2
i
2
2 γ µ
γ
n + γ