Egzamin dla Aktuariuszy z 3 października 1998 r.

Prawdopodobieństwo i Statystyka Zadanie 1

X i − wynik n

a i

- tej k

ostce

W = X + X

1

2

1

f (2) = 36

Z = W + W

2

1

2

f

)

3

(

=

=

36

do z

1

0 wystarczy

3

1

f (4) =

f (4) =

2

36

36

4

4

f

)

5

(

=

f

)

5

(

=

36

2

36

5

10

f (6) =

f (6) =

36

2

36

6

8 + 12

20

f (7) =

f (7) =

=

36

2

2

36

36

5

10 + 16 + 9

35

f

)

8

(

=

f

)

8

(

=

=

36

2

2

36

36

4

+

+

f 9

( ) =

12

20

24

56

f 9

( ) =

=

36

2

2

36

36

3

f 1

( 0) =

10 + 24 + 30 + 16

80

f 1

( 0) =

=

36

2

2

36

36

2

f 1

( )

1 = 36

1

f 1

( 2) = 36

Z

X Y = Z + X

1 + 10 + 4 + 20 + 35 + 56

126

4

6

P( Y = 10) =

=

2

5

36 ⋅ 6

6

6

4

5

5

7

3

8

2

9

1

1

5

1

6

ODP =

=

126

126

65

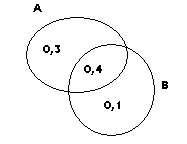
Zadanie 2

A ∩ B ∩ C = ZBIÓR PUSTY

przy min sumy A ∪ B przecięcie z C max – 0,4 możliwe tu max C można wcisnąć jako A+B- A ∩ B

a już nie można tego polepszyć P( C ∩ ( A ∪ B)

,

0 4

,

0 4

1

ODP

=

=

=

=

max

P( A ∪ B)

,

0 7 + 5

,

0 − ,

0 4

8

,

0

2

Zadanie 3

BŁĄD bo to znany fakt

Zad 4 z rozdziału 5.10 (Jakubowski) – ODPOWIEDŹ (A) Zadanie 4

x

x

f (

0

− ,5(5− )

−2

P X + Y =

X X + Y =

X f X

e

e

5)

(

5

) ( )

5

,

0

2

=

=

x ∈ (

)

5

;

0

P( X + Y = ) 5

5

∫ 5,

0

−0,5(5− x)

e

2 −2

e x

0

 2

2



MIAN = −2,5

e

 −

−7,5

e



 3

3



5

5

−2,5 − ,

1 5 x





−2,5

2

− ,

1 5 x

4 − ,15

xe

e

− ,

1 5

x

x

4

34

∫

u =

x

−7,5

v′ =

e

e

−

xe

− e



−



e

3

9



0

0

9

9

ODP =

=

2

=

=

≈

− ,

1 5

MIAN

u′ =

v = − e

x

−2,5 2

1

−7,5

−7,5

e

− e

−

3

(1

)

2 (1 e ) ,066

3

3

Zadanie 5

2

ENMW ( µ 2 ) 2

σ

= X −

n

2

4

∑( xi− µ)



1



−

8

L = 

 e

 2 2Π 

2

∑ xi − µ

ln L = 4

− ln(2 2Π )

(

)

−

8

∂

∑2( x − µ

i

) 1

=

= (∑ x − 4 µ) 2

2

= 0 → µ = X → µ = X

µ

i

∂

8

4

2

2

2

σ

4

ODP = X − X +

= = 1

n

4

Zadanie 6

K = { 2

2

2

x : x ≥ χ

1− α, n 1

− }

2

n − S

∑ x − X

2

(

)

1

( i )2

x =

=

2

2

σ

σ

0

0

kwantyl=7,815

wyszło: 2

x < 7 8

, 15

1 − ,

1 2 + 3 + ,

0 7

X =

= 8

,

0 75

4

∑( x

i −

)2

X

= 8

,

8 675

8

,

8 675 < 8,

7 15

2

→ σ > 1

,

1 34 ≈ 1

,

1 3

0

2

σ 0

Zadanie 7

Y ≅ N

i

( 2

x

θ ; σ

i

)

n

∑( iY− 1 θ ix )2



1



−

2

p(

σ

e

θ 1 )





2

 2Π σ 

( 1 θ− θ )(2∑ Xi iY−∑ 2

0

X )

θ

θ

i

e

rosnąca funkcja statystyki

1 >

0

p(

Y θ x

θ 0 ) =

=

n

∑( i− 0 i )2



1



−





2

2 σ

e

 2Π σ 

∑ X Y

X

więc też ∑ X Y

X

i i − ∑

2

i i − ∑

2

2

i

i

 ≅ N (

2

2

2

( θ − )

1 ∑ x ;

i σ ∑ i

x )= N (

2

2

2

−∑ x ;

i σ ∑ i

x )





6

4

4 7

4

4 8



2





P

θ =

∑ X Y

i i − ∑ X i

> c = 05

,

0

0 











 ≅ }

N (0 )

1

;

2 

2



c + ∑ X 

c + ∑ x

i

i

P

X

=

>

= ,

0 05 →

= u

θ 0

0,95

2

2



σ ∑ x 

σ ∑ x



i



i

odrzucamy gdy: ∑ X Y

X

u

σ

x

x

i i − ∑

2

i

> 0,

∑ 2

95

i

− ∑ 2 i

∑ x Y u σ

x

i i >

0,

∑ 2

95

i

Zadanie 8

P (max ≤ t) n

= t ( 0,1)

0

f max

n 1

=

−

nt

t ∈ (

)

1

,

0

0

n

 t 

P (max

)

1

≤ t = 



 3 2 

n 1

−

nt

f max =

t ∈ ;

0

2

1

n

( 3 )

3 2

1

n

n

P (max ≥ c) = , 0 2 → 1 − c = ,

0 2 → c = 8

,

0

0

3

3

2

2

0

n −1



0

n



n t

t

8

,

0

moc: ∫

0

= 



= 1−

> 9

,

0 5

1

0

n

0

n

0

n

3

3

3

1



2





2

 n 0

2

0,8

n 0

0,8

8

,

0

< ,

0 05

n

2 0

3

0

n

3

8

,

0

< ,

0 05 2

n

2 0

3

> 16

n ln 3 2 > ln16

0

ln16

n >

= 12 → n ≥ 13

0

0

ln 3 2

Zadanie 9

X

+ ... + X

X

+ ... + X

11

20

X

= X +

wiemy, że

11

20

X

n

z

l S

n

zl S

→ X n

zl S

20

10

10

10

10

20

10

20

20

przy µ = 0



2 

 σ 

X

N

20 ≅

 ;

0





20 

2

X

S

⋅ 9

20 ≅ N(

)

1

;

0

10

≅ χ 9

( )

2

σ

σ

20

20 X

1

20 X

Z tego:

20

20

≅ t →

≅ t

9

9

2

σ

S

S

10

10

2

σ

Zadanie 10

1. θ ≤ − 5

,

0 cały przedział ujemny

θ +

θ +

0,5



2  0,5

2

2

E X = ∫

x

( θ −

)

5

,

0

− ( θ +

− x =

)

5

,

0

−



=

= − θ → ob = − θ + θ = 0

θ −

2

2

0,5



 θ−0,5

.

2 θ ∈ (−

]5

,

0

;

5

,

0

0

θ +

0

θ +

0,5



2 

 2  0,5

2

2

E X = ∫ − x + ∫

x

x

( θ −

)

5

,

0

( θ +

x =

)

5

,

0

1

−



+  

=

+

= 2

θ +

θ −

2

2

2

2

4

0,5

0



 θ−





0,5

0

2

1

i) ob = θ +

+ θ d

l

a θ ∈ (−

0

;

5

,

0

]

4

2

1

= θ + − θ d l

a θ ∈ [

5

,

0

;

0

)

4

3. θ > 5

,

0

θ +

θ +

0,5

 2  0,5

2

2

E X = ∫

x

( θ +

)

5

,

0

− ( θ −

x =

)

5

,

0





=

= θ → ob = θ − θ = 0

θ −

2

2

0,5



 θ−0,5

z i) mamy:

2



1 

a) θ + 



2 

2



1 

b) θ − 



2 

2

 1 

Z tego: max ob =   = , 0 25

 2 