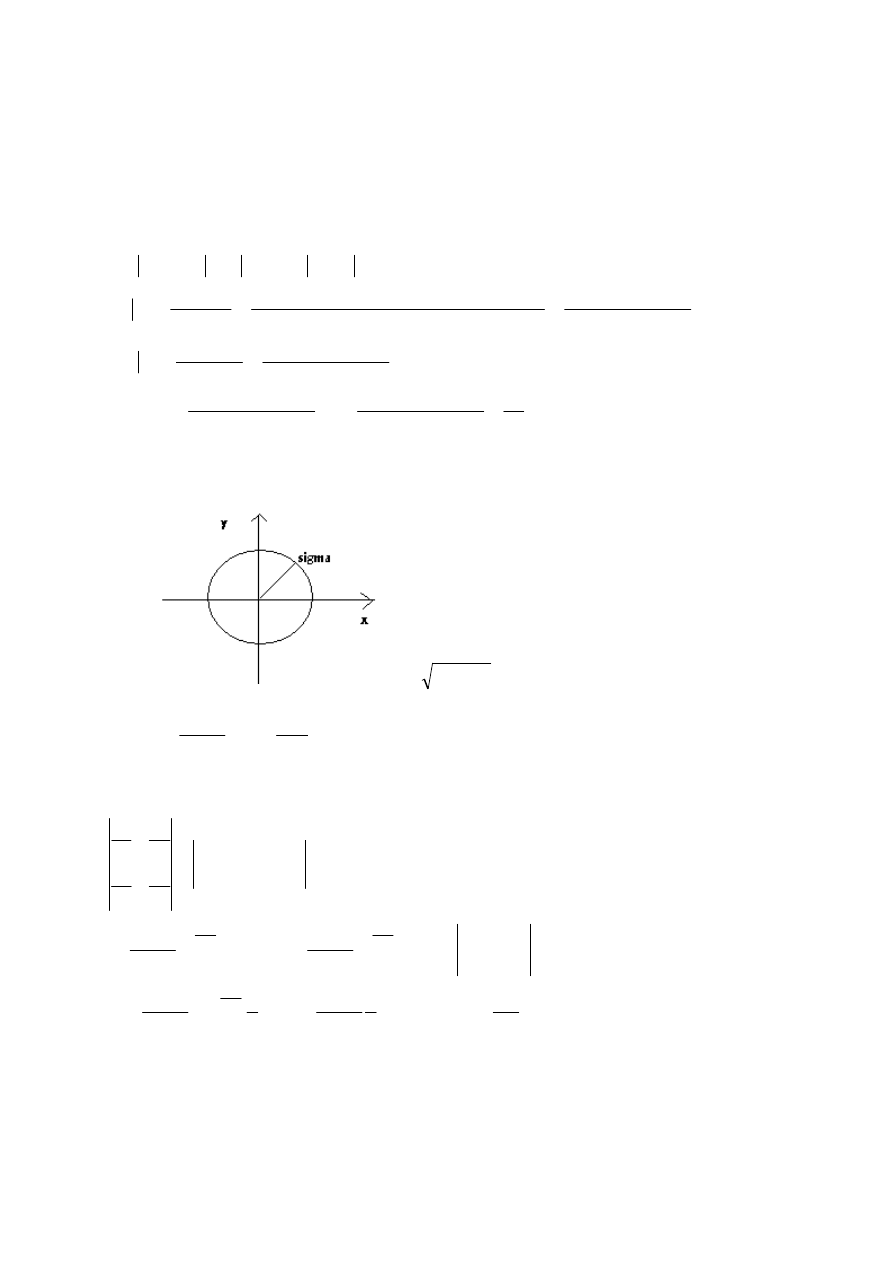
Egzamin dla Aktuariuszy z 26 października 1996 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
A – jeden trafi drugi nie + w (n-1) próbach albo obaj trafiają albo obaj nie
( ) ( ) ( ) ( ) ( )
A
g
P
g
T
P
A
l
P
l
T
P
A
T
P
+
=
( )
(
)
(
)
(
) (
)
2
,
0
4
,
0
6
,
0
8
,
0
6
,
0
8
,
0
2
,
0
4
,
0
6
,
0
8
,
0
6
,
0
2
,
0
4
,
0
8
,
0
6
,
0
8
,
0
6
,
0
2
,
0
4
,
0
8
,
0
)
(
1
1
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
+
⋅
⋅
⋅
+
⋅
=
∧
=
−
−
n
n
A
P
A
l
P
A
l
P
( )
(
)
2
,
0
4
,
0
6
,
0
8
,
0
2
,
0
4
,
0
)
(
⋅
+
⋅
⋅
=
∧
=
A
P
A
g
P
A
g
P
35
26
2
,
0
4
,
0
6
,
0
8
,
0
2
,
0
4
,
0
4
,
0
2
,
0
4
,
0
6
,
0
8
,
0
6
,
0
8
,
0
8
,
0
=
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
=
ODP
Zadanie 2
σ
y
x
<
+
2
2
(
)
+
−
Π
=
2
2
2
2
2
1
exp
2
1
)
,
(
y
x
σ
σ
y
x
f
=
=
φ
r
y
φ
r
x
sin
cos
r
φ
r
φ
φ
r
φ
φ
d
dy
dr
dy
φ
d
dx
dr
dx
=
−
=
cos
sin
sin
cos
(
)
∫ ∫
∫ ∫
Π
−
+
−
=
=
=
=
Π
=
Π
2
0 0
2
2
2
2
1
2
2
2
1
2
1
2
2
2
2
2
σ
σ
r
y
x
σ
dx
rdr
x
r
φ
rdrd
e
σ
e
σ
(
)
(
)
∫
∫
∫
Π
Π
−
−
−
−
−
=
−
Π
Π
=
−
Π
=
Π
=
2
0
0
2
0
5
,
0
5
,
0
2
2
2
2
2
2
)
5
,
0
exp(
1
1
2
2
1
2
2
1
2
1
2
1
2
1
σ
σ
x
e
e
σ
σ
dx
e
σ
Zadanie 3
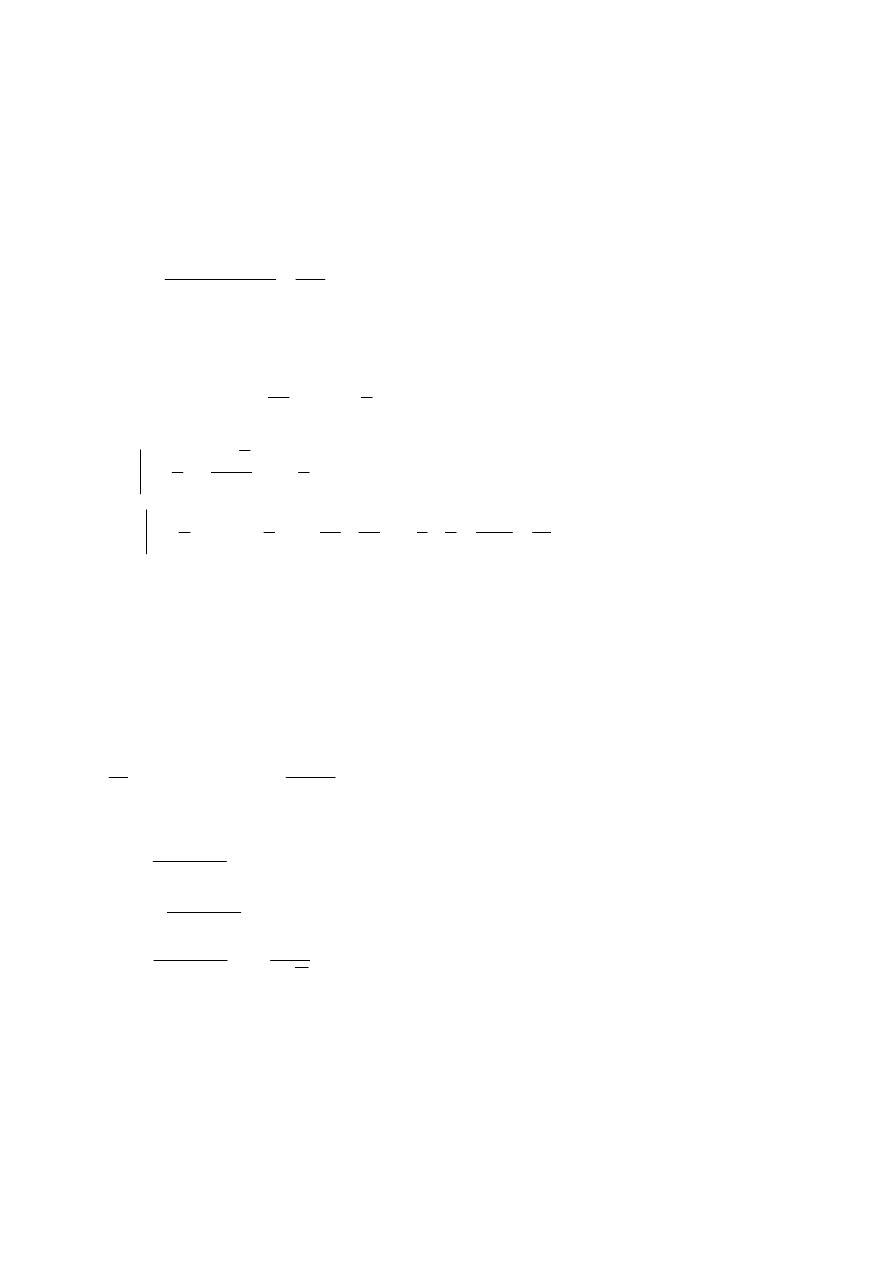
Jedna 3 reszta różne od 3 – (liczba możliwości)
}
3
3
3
trojki
dla
pozycja
⋅
⋅
(dwie ostatnie trójki – dla
pozostałych 4,5 lub 6)
x3 + jedna>3 -
}
3
3
trojek
ie
rozstawien
⋅
+ 3 trójki
216
37
6
6
6
1
3
3
3
3
3
=
⋅
⋅
+
⋅
+
⋅
⋅
=
ODP
Zadanie 4
∫
+
=
+
=
+
=
1
0
1
0
2
2
1
2
)
(
)
(
y
xy
x
dx
y
x
y
f
2
1
1
2
1
2
1
+
=
+
=
=
x
x
y
x
f
∫
=
+
=
+
=
+
=
+
=
=
1
0
1
0
2
3
12
7
12
3
4
4
1
3
1
4
3
2
1
2
1
x
x
x
x
Y
X
E
Zadanie 5
λ
e
M
P
−
=
=
)
0
(
λ
e
M
P
−
−
=
=
1
)
1
(
( )
(
)
∑
∑
−
−
−
−
=
i
i
M
λ
M
n
λ
e
e
L
1
(
)
(
)
∑
∑
−
−
+
−
−
=
λ
i
i
e
M
M
n
λ
L
1
ln
ln
(
)
(
)
(
)
∑
∑
∑
∑
−
−
−
−
=
−
−
→
=
−
+
−
−
=
∂
∂
λ
i
i
λ
λ
λ
i
i
e
M
M
n
e
e
e
M
M
n
L
λ
1
0
1
ln
(
)
∑
∑
∑
−
=
−
+
−
i
i
i
λ
M
n
M
n
M
e
n
M
n
e
i
λ
∑
−
=
−
n
M
n
λ
i
∑
−
=
−
ln
−
=
−
=
∑
m
M
n
n
λ
i
1
1
ln
ln
Zadanie 6
Bezpośrednio wynika z teorii: (n-1)(m-1)

Zadanie 7
)
,
(
0
λ
n
T
T
n
Γ
≅
−
∫
∫
∞
−
−
−
−
−
−
=
−
Γ
Γ
=
=
−
=
=
Γ
=
Γ
=
−
0
1
2
1
0
1
)
1
(
)
(
1
)
(
)
(
1
1
n
λ
λ
n
n
λ
λ
β
n
α
e
x
n
λ
e
x
n
λ
x
T
T
E
n
n
x
λ
n
n
x
λ
n
n
n
λ
n
λ
n
T
T
n
E
n
=
−
−
=
−
−
1
)
1
(
1
0
Zadanie 8
3
2
1
bX
aX
X
E
−
−
=
(
)
(
)
0
0
,
cov
0
,
cov
3
2
=
=
=
EE
X
E
X
E
(
)
(
)
=
=
→
0
0
3
2
EX
E
EX
E
(
)
(
)
(
)
(
)
=
−
−
=
−
−
0
0
3
2
1
3
3
2
1
2
bX
aX
X
X
E
bX
aX
X
X
E
=
−
−
⋅
=
−
−
0
5
,
0
1
2
0
5
,
0
5
,
1
b
a
b
a
=
−
−
=
−
−
0
5
,
0
1
0
2
3
b
a
b
a
i odejmujemy
2-1,5a=0
1,5a=2
3
4
3
2
2
=
⋅
=
a
Zadanie 9
(
)
2
10
;
10
σ
µ
N
y
i
≅
(
)
2
;
10
σ
µ
N
y
≅
(
)
(
)
[
]
(
)
∑
∑
∑
=
−
=
+
−
=
−
2
2
2
2
2
10
2
y
y
E
y
y
y
y
E
y
y
E
i
i
i
i
(
) (
)
90
1
90
1000
10
1000
100
100
10
100
10
10
2
2
2
2
2
2
2
2
2
=
→
=
−
−
+
=
+
−
+
=
const
σ
µ
σ
µ
σ
µ
σ
µ
σ
Zadanie 10
(
)
(
)
∫
−
−
=
+
−
+
=
+
=
+
=
≤
≤
−
=
≤
t
t
t
t
t
t
t
t
t
x
x
x
t
X
t
P
t
X
P
5
,
0
2
5
,
0
5
,
0
2
5
,
0
5
,
0
2
5
,
0
5
,
0
5
,
0
2
2
t
t
f
2
1
=
∂
∂
=
Wyszukiwarka
Podobne podstrony:
1996.10.26 prawdopodobie stwo i statystyka
1996.10.05 prawdopodobie stwo i statystyka
1996 10 05 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2002 10 12 prawdopodobie stwo i statystykaid 21648
2010.10.04 prawdopodobie stwo i statystyka
2001.10.13 prawdopodobie stwo i statystyka
2008.10.06 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2006.10.09 prawdopodobie stwo i statystyka
2004.10.11 prawdopodobie stwo i statystyka
1996.12.07 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
1999 10 23 prawdopodobie stwo i statystykaid 18598
2009 10 05 prawdopodobie stwo i statystykaid 26670
2000.10.14 prawdopodobie stwo i statystyka
1996.11.16 prawdopodobie stwo i statystyka
więcej podobnych podstron