Egzamin dla Aktuariuszy z 13 października 2001 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
P( B) = 4 P( A ∩ B) = 1− 3 P( ′
A ∩ B′)
P( B′) = 3 P( ′ A∩ B′) =1− 4 P( A∩ B)
1. P( )
A = 5 P( A ∩ B) = − 5
1
P( ′
A ∩ B′)
2
5
P( ′
A ) =
P( ′
A ∩ B′) = 1 − 5 P( A ∩ B)
2
( A ∪ B) ∩ ( A′ ∪ B′) = ( A ∪ B) ∩ (Ω \ ( A ∩ B)) = ( A ∪ B) \ ( A ∩ B (
i
)
A ∩ B) ∈ ( A ∪ B) z TEGO:
P( A ∪ B) − P( A ∩ B) 5 P( A ∩ B) + 4 P( A ∩ B) − 2 P( A ∩ B) 7 P( A ∩ B)
ODP =
=
=
P( A′) + P( B′) − P( A′ ∩ B′) 5
9
P( A′ ∩ B′) + 3 P( A′ ∩ B′) − P( A′ ∩ B′) P( A′ ∩ B′)
2
2
Z 1 mamy:
4 P( A ∩ B) = 1− 3 P( ′
A ∩ B′)
1
1
5
→ P ′
A ∩ B′ =
P A ∩ B =
5 P( A ∩ B) = 1
− P( ′
A ∩ B′)
(
) , (
)
5
10
2
1
7 ⋅
7 10
7
10
ODP =
=
=
9 1
10 9
9
2 5
Zadanie 2
Z=aX+bY
Chcemy: varZ=1, cov(Z,X)=0 Ŝeby nzl.
cov( aX + bY , X ) = a + bp = 0 → a = b
− p
2
2
2
2
2
2
2
2
1
var Z = 1 → a + b + 2 abp = 1 → b p + b − 2 b p = 1 → b =
2
1 − p
1
1
b =
, a = −
p
1 − p 2
1 − p 2
1
1
Z = −
pX +
Y
1 − p 2
1 − p 2
Z i X nzl → E( 2
Z X )
2
= EZ = 1
p 2
2
2 p
1
p 2
2
2
2 p
1
1 = E
X
−
XY +
Y
X =
X
−
XE
( Y X )+
E
2
2
2
2
2
2
( Y 2 X)
1 − p
1 − p
1 − p
1 − p
1 − p
1 − p
y
E( Y x)
σ
= m + ρ
−
=
y
( x mx ) px
σ x
2
2
2
p
2
2 p
2
p
2
−
+
+
−
−
−
E(
1
X
X
1
X
2
Y
X )
2
2
2
1
p
1
p
1
p
2
2
2
=
=
= 1− p + p X
1
1
2
2
1 − p
1 − p
E( 2 2
X Y ) = EE( 2 2
X Y
X ) = E( 2
X (
2
2
2
1 − p + p X ) = (
2
1 − p )
2
2
+ p 3 = 1+ 2 p
cov( 2
2
X , Y )
2
2
= 1+ 2 p −1⋅1 = 2 p
Zadanie 3
Rozkład stacjonarny
1 Π1 + 1Π2 = Π
2
1
2
3
Π1 = Π
→
2
3
1
2
Π1 + Π2 = Π2
Π1 + Π 2 =
1
2
3
2 Π + Π =1
2
2
3
3
2
Π = ,Π =
2
1
5
5
=12
6
4
4
4
7
4
4
4
8
P(⋅ ⋅)
P( X
X
P X
n+1 = 2
n =
)1 ( n = )
=
1
P( X
X
P X
P X
X
P X
n+1 = 2
n =
)1 ( n = )1+ ( n+1 = 2 n = 2) (
2
n
) =
=
2
→5
1
4
6
4
7 8
P( X n = )
1 2
1
1
1
15
3
1
2
2 5
5
=
→
=
=
= =
1 P( X
P X
n =
) 2 2
+ −
1 +
−
( n = ) 1 2 2 2 2 1 2 4 5 3 10 4 9 3
1
+ −
+ −
2
3
3
2 5
3
3 5
5
3
15
Zadanie 4
1
−∑( Xi − θ )/
L =
α
e
n
α
ln L = − n ln α − ∑ ( X
/
i − θ ) α
∂
ˆ
n
∑( X − θ
∑
−
i
)
( X θ
i
)
= − +
= 0 → αˆ =
α
∂
α
α 2
n
∑
1
X
,
,
i ≅ Γ n
nθ
α
− n( t− θ) / α
n − n( t− θ) / α
P(min ≤ t) = 1 − P(min ≥ t) = 1 − e
, f
= e
min
α
α
E min = θ +
n
1
α
nα − α
α( n − )
1
n
E ˆ
α =
nθ + nα − n θ − =
=
→ c =
n
n
n
n
n −1
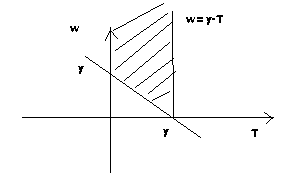
Zadanie 5
Tu jest chyba błąd bo wychodzi odpowiedź (D)
N
n
k
n!
1
k
n k
E
N = n = ∑
−
p q
=
N − N
1
1 !(
)!
1 +
n
k
k n
k
k =1
− +
−
n
n−1
= ∑ n
n
k
n− k
i 1
n i 1
p
n
p q
= k −1 = i = ∑ + − −
p q
= (1− p )
k
1
i
q
k =1
−
i=0
∞
n
= ∑ p
ODP
(
λ
p
1 − n
p )
− λ
e
= (
−
1 −
λq
e
)
q
n
q
n=
!
0
Zadanie 6
dla k ≥ 1 liczymy
P( N = )
1 = P( T
,
,...,
2 > Y T 3 > Y
T 1 ≤ Y )
P( N = 2) = P( T ≤ Y , T d owolne, T > Y , T > Y ,..
2
1
3
4
).
∞
P( N = k) = P( T
k ≤ Y , Tk +
Y
P T
Y , T
W
Y
P T
y, T
W
y y f ( y) dy
1 >
) = ( k ≤
k +
> ) = ∫ ( k ≤
k +
>
)
0
Korzystając z rysunku:
1
1
P(
y
y
k
k
λ
1
λ
T
y, T
w
y y
λe
T
e
dwdT
T 1 e
e (
)
k ≤
k +
>
) ∞
+
= ∫ ∫
− λw
k −
− λT
= ∫
k −
− λT
− λ y− T =
Γ( k)
Γ( k)
λ
0 y− T
0
k +
y
1
k
k
k
λ
1 −
=
λy
(
)
e
∫ k−1
λ
− λy y
λ
y
−
T
=
e
=
λy
e
Γ( k) λ
Γ( k)
k
k!
0
∞
k
k
∞
( λ
y )
λy
αy
λ
α = k +
k
λ α
λk
y
k
λk
P( N = k) = ∫
−
−
e
αe
dy =
α ∫
−
1
( + )
y e
=
=
!
α
=
k +
α
1
k +
k!
k!
β = λ + α
k!
( λ + α)
( λ +
1
α)
0
0
dla k=0 jako dopełnienie wychodzi i się zgadza
∞
k
∑ λ α
λ
α
=
→ P( N = )
0 =
OK. prawidłowa odpowiedź (A)
λ
α
λ
α
λ
α
λ
α
k =
1
+
+
+
+
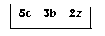
Zadanie 7
m – 3-ta statystyka pozycyjna
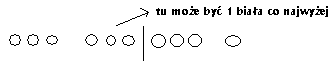
P( m ≤ µ + 1
,
1 503 σ
5 / n ∧ m ≥ µ − 1
,
1 503 σ
5 / n ) = P( m ∈ ( µ − 1
,
1 503 σ
5 / n; µ + 1
,
1 503 σ
5 / n ) =
= P( X ≤ µ + 1, 1 503 σ
5 / n −
≤ −
3
) P( X µ 1,1503 σ 5/ n 3
)
2
σ
X - pozycyjna dla
≅ N µ,
3
n
µ − 1
,
1 503 σ
5 / n - kwantyl rzędu 1/8
µ + 1
,
1 503 σ
5 / n - kwantyl rzędu 7/8
i
5− i
i
5−
i
7
1
5
5
c =
5
7
1
5
1
7
Q
,
5
,
3
− Q
,
5
,
3
= ∑
− ∑
=
8
8
i
i
i=
8
8
8
8
3
i=3
3
4
5
3
2
4
5
7 1
7 1 7
1 7
1 7 1
= 10
+ 5
+ −10 − 5 − ≈ 9
,
0 7
8 64
8 8 8
8 8
8 8 8
Zadanie 8
θ > θ
2
1
5
θ
θ
X
θ
2
∏
1
5
1 +
i
=
2
1
θ
θ 2
X
i
θ 2 +1
5
∏
−
∏ X
θ
θ
i
1
1
1
niemalejąca dla
→
∏
STATYSTYKA
X i
1
P
>
= ,
0 01
0
∏
c
X i
1
1
P
0
Π X
ln
ln
i <
= P
0
∑ Xi <
c
c
t
t
e
e
−1
1
1
1
1
P (ln X
)
( 2)
1
0
< t = P( X < te )
= ∫
t
= −
= − e 2 →≅ wykl
3
2
x
2
1
1
2 x 2
∑
1
ln X
χ
K
X
czyli (A) około
i ≅ Γ
2
1
,
5
=
1
( 0) → ln
= 5
,
2 58 →
{∑ln i < 5,
2 5 }
8
2
c
Zadanie 9
1-P(nie ma zielonej)
tzn Ŝe pierwszych kilka czerwonych + biała itd.
9
7
ilość kombinacji: 1 biała
2 białe na 9 sposobów i 2 zielone na 7 itd.
2
2
c, b,...
c, c, b,...
8
7
6
8
7
6
c }
cccc .
b .
9
7 8
6 7
5 6
4 5
3
4
+
+
+
+
+
2
2 2
2 2
2 2
2 2
2
2
36 ⋅ 21 + 28 ⋅15 + 15 ⋅ 6 + 10 ⋅ 3 + 6
=
= ,
0 6
10
5
1 !
0 10
!
5
!
5
5
3
4
1 4
23
pierwsze c
-
zerw..., d
rugie b
-
iala
2
ODP = 1 − ,
0 6 = ,
0 4 =
5
Zadanie 10
1
∞
∞
∞
n
P( X > N ) = ∑ P( X > n N = n) P( N = n) = ∑ − n −
2 2 n = ∑ 1
1 4
1
= 4 =
=
n=
4
1
4 3
3
1
n=1
n=
1
1 − 4