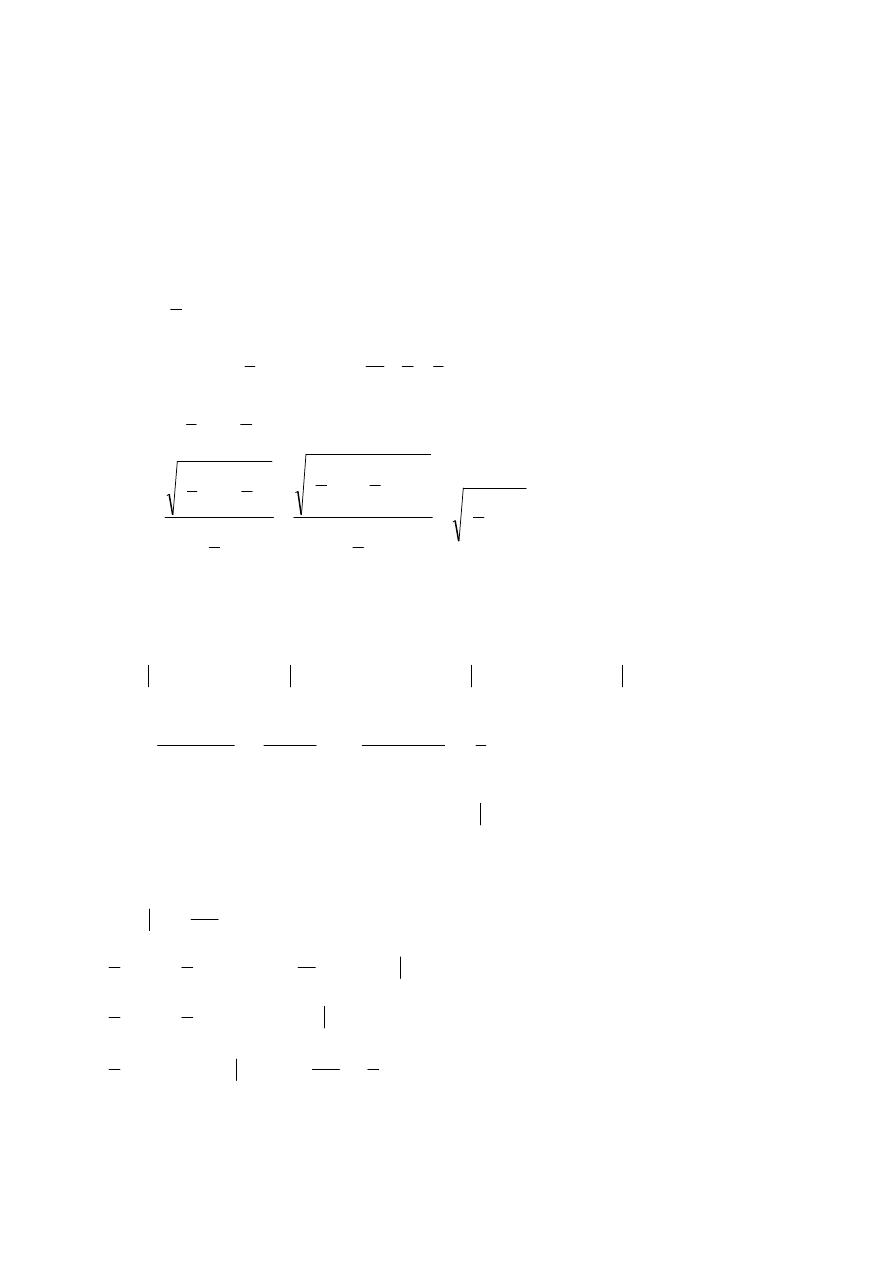
Egzamin dla Aktuariuszy z 12 stycznia 2002 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
J(0,1)
X
n
)
1
,
0
(
1
≅
−
≅
⋅
=
+
iloczyn
X
J
X
X
X
X
n
n
n
Z tego:
( )
n
n
n
n
n
n
n
n
X
EX
EX
EX
2
2
2
2
1
3
1
var
3
1
2
1
−
=
=
=
=
3
1
4
1
12
1
2
=
+
=
EX
1
3
4
2
1
1
3
4
2
1
2
1
4
1
3
1
2
−
=
−
=
−
=
n
n
n
n
n
n
n
ODP
Zadanie 2
Metodą eliminacji dla
2
=
A
N
(
)
(
)
(
)
(
)
=
=
=
+
=
=
⋅
+
=
=
+
=
=
2
2
1
2
2
1
1
1
6
2
6
2
1
1
A
A
A
A
N
A
P
N
A
P
N
A
E
N
N
E
3
1
7
66
28
2
4
8
6
2
12
8
8
2
8
2
2
12
8
8
1
4
1
8
1
6
=
⋅
+
⋅
+
=
+
+
=
i pasuje tylko odpowiedź (E)
można policzyć
A
EN
EN
i
1
i sprawdzić czy
(
)
1
1
EN
N
N
EE
A
=
Zadanie 3
( )
4
var
2
X
X
Y
≤
( )
(
)
=
+
=
+
X
Y
E
X
X
E
X
var
2
var
)
(
4
1
var
2
1
2
( )
(
)
X
Y
E
X
E
X
var
)
(
4
1
var
4
1
2
=
+
( )
(
)
→
=
<
=
2
2
2
4
1
4
var
4
1
EX
X
E
X
Y
E
EX
jesli
sprzeczność
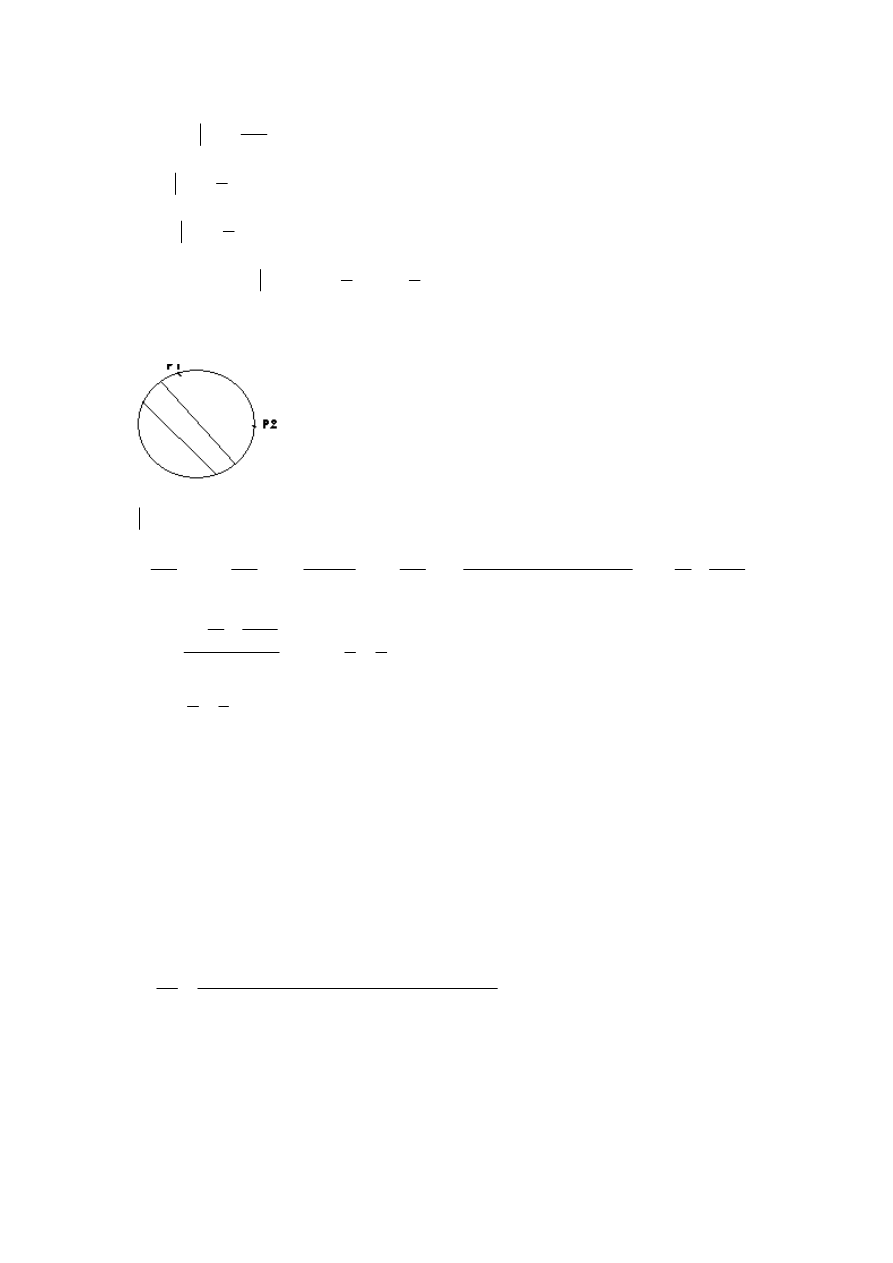
Z tego
( )
4
var
2
X
X
Y
=
a skoro tak to:
(
)
(
)
=
=
=
=
2
1
2
1
0
X
X
Y
P
X
Y
P
(
)
∫
∫
=
=
=
=
=
2
1
)
(
2
1
)
(
)
(
x
f
x
f
x
x
Y
P
x
Y
P
Zadanie 4
A
- nie przetną się
(
)
(
)
=
∈
∈
Π
∈
Π
∈
=
=
)
,
0
(
),
,
0
(
lub
)
2
,
(
),
2
,
(
4
3
4
3
2
x
P
x
P
x
P
x
P
P
x
P
A
P
2
2
2
2
2
2
2
2
2
0
2
2
2
1
)
2
(
4
)
2
(
2
2
2
2
1
2
1
Π
+
Π
−
=
Π
+
+
Π
−
Π
=
Π
+
Π
−
Π
=
Π
+
Π
=
∫
∫
Π
x
x
x
x
x
x
x
x
x
∫
Π
=
+
−
=
Π
Π
+
Π
−
=
2
0
2
2
3
2
3
2
1
1
2
2
1
)
(
x
x
A
P
3
1
3
2
1
=
−
=
ODP
Zadanie 5
(
)
(
)
(
)
=
+
−
+
−
=
+
−
−
+
=
−
2
0
1
2
0
1
0
1
2
)
1
(
)
1
(
)
1
(
ˆ
X
p
z
X
z
E
pX
X
X
z
zX
E
W
W
E
[
]
=
+
−
+
+
−
−
+
−
=
2
0
2
1
0
2
1
2
)
1
(
)
1
)(
1
(
2
)
1
(
X
p
z
X
X
p
z
z
X
z
E
(
)
(
)
(
)
(
)
=
+
−
+
+
−
+
−
−
+
−
+
+
−
=
2
0
2
2
1
0
2
2
1
2
2
2
2
1
2
2
2
2
4
1
2
EX
p
pz
p
z
z
X
X
E
p
zp
z
z
EX
z
z
(
)
(
)
(
)
(
)
c
pEX
EX
X
X
pE
X
X
E
EX
z
EX
X
X
E
EX
z
+
−
−
+
+
−
+
+
−
=
>
2
0
2
0
1
0
1
0
2
1
0
2
0
1
0
2
1
2
2
2
2
4
2
2
4
4
4
4
8
4
4
4
4
7
6
(
)
(
)
2
0
1
0
2
1
1
0
2
1
2
0
*
2
4
2
)
2
(
2
)
1
(
2
2
2
EX
X
X
E
EX
p
X
X
E
p
EX
EX
a
b
z
+
−
+
−
+
+
=
−
=
(
)
(
)
p
X
X
X
X
E
EX
EX
=
=
=
=
1
0
1
0
2
1
2
0
,
cov
1
1

2
1
)
1
(
4
)
1
)(
2
(
2
)
1
(
4
)
2
(
2
)
2
(
2
)
1
(
4
2
4
2
2
2
2
4
2
)
2
(
2
)
1
(
2
2
2
*
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
z
+
=
−
−
+
=
−
+
−
+
=
−
−
−
+
+
=
+
−
+
−
+
+
=
Zadanie 6
n
p
2
2
1
3
2
2
1
3
⋅
..
..
ORR
OROO
ROROO
k
1
2
1
2
2
1
−
=
⋅
k
k
ROO
RORR
ORORR
∑
∞
=
−
+
+
⋅
=
=
=
2
2
1
...
2
1
3
2
1
2
2
1
k
k
k
ODP
X
...
2
1
3
2
1
2
2
1
3
2
+
+
=
X
2
3
2
4
1
1
2
1
1
2
1
1
...
2
1
2
1
2
1
2
2
1
1
2
3
2
=
⋅
+
=
−
+
=
+
+
+
⋅
=
−
X
3
2
2
3
=
⋅
=
X
Zadanie 7
≅
n
σ
µ
N
X
2
,
≅
+
=
n
σ
N
Y
µ
Y
X
2
,
0
,
(
)
4
2
2
2
4
4
3
2
2
2
2
3
4
4
6
3
4
2
4
4
µ
n
σ
µ
n
σ
µ
Y
µ
µ
Y
Y
µ
Y
µ
Y
E
X
E
+
+
=
+
+
+
+
+
=
(
)
2
2
2
2
1
σ
ES
n
σ
X
X
E
i
=
→
−
=
−
∑
+
−
=
−
=
2
4
2
2
4
2
2
2
4
2
n
S
n
X
S
X
E
n
S
X
E
µ
E
(
)
+
=
=
2
2
2
2
2
2
2
µ
n
σ
σ
X
E
ES
X
S
E
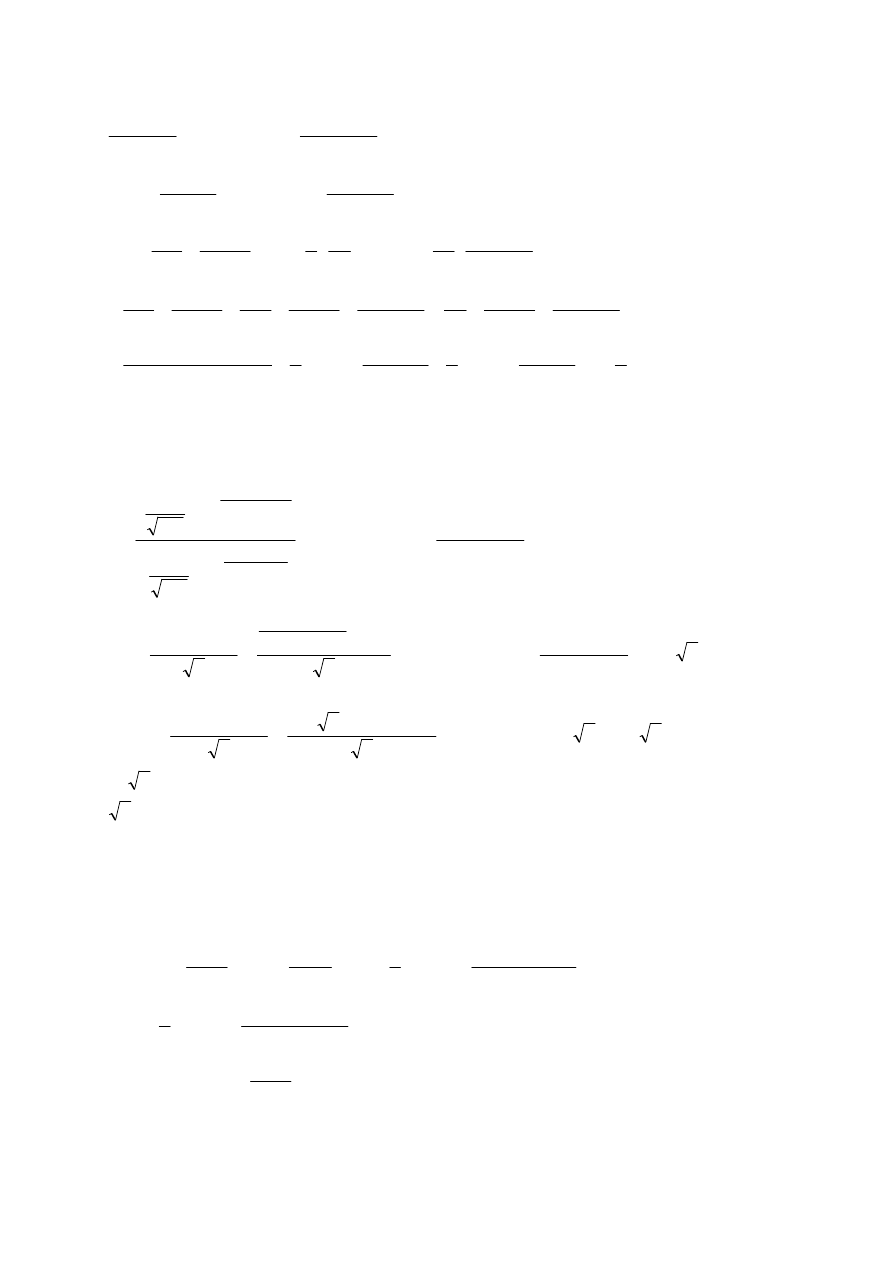
1
)
1
(
)
1
(
2
)
1
(
)
1
(
)
1
(
2
2
4
2
4
2
2
−
=
−
+
−
=
−
→
−
≅
−
n
n
n
σ
n
S
E
n
χ
σ
n
S
1
)
1
(
)
1
)(
1
(
)
1
(
4
2
4
4
−
+
=
+
−
−
=
n
n
σ
n
n
n
σ
ES
=
−
−
+
+
+
−
+
+
=
4
4
2
2
2
4
4
2
2
2
4
1
)
1
(
1
2
6
3
var
µ
n
n
σ
n
µ
σ
n
σ
n
µ
n
σ
µ
n
σ
=
−
+
+
+
=
−
+
+
−
−
+
=
)
1
(
)
1
(
4
)
1
(
)
1
(
2
2
6
3
2
4
2
2
2
4
2
4
2
2
2
4
2
2
2
4
n
n
n
σ
n
σ
µ
n
σ
n
n
n
σ
n
µ
σ
n
σ
n
σ
µ
n
σ
2
2
4
2
2
2
4
2
2
2
4
4
4
)
1
(
2
4
)
1
(
2
4
)
1
(
)
1
(
)
1
(
σ
µ
n
σ
n
n
σ
µ
n
n
n
σ
n
σ
µ
n
n
n
n
σ
σ
n
+
−
=
+
−
=
+
−
+
+
−
=
Zadanie 8
Innymi słowami: znaleźć n takie by test najmocniejszy istniał
(
)
(
)
05
,
0
1
,
0
005
,
1
ln
2
1
2
1
0
2
10
2
1
,
10
0
2
2
=
+
>
=
>
Π
Π
∑
∑
∑
−
−
−
−
n
t
X
P
t
e
e
P
i
X
n
X
n
i
i
n
n
n
t
n
n
n
t
n
n
X
P
i
10
64
,
1
1
,
0
005
,
1
ln
64
,
1
05
,
0
10
1
,
0
005
,
1
ln
10
0
+
=
+
→
→=
=
−
+
>
−
=
∑
moc:
0
1
,
10
10
64
,
1
5
,
0
1
,
10
10
64
,
1
1
,
10
≤
−
+
→
≥
−
+
>
−
∑
n
n
n
n
n
n
n
n
X
P
i
271
96
,
268
4
,
16
64
,
1
1
,
0
≈
≥
≥
≥
n
n
n
Zadanie 9
S: c-kwantyl rzędu 0,01 z chi(5), z tego c=0,554
∑
=
+
+
−
=
=
=
3
1
2
3
2
1
2
123
2
456
456
2
123
123
3
2
1
,
211
,
0
2
,
211
,
0
2
:
i
i
X
X
X
X
S
S
G
S
G
N
∑
=
+
+
−
=
6
4
2
6
5
4
2
456
3
2
1
i
i
X
X
X
X
S
≅
≅
)
2
(
2
od
nzl
2
2
123
2
456
2
123
χ
σ
S
S
S
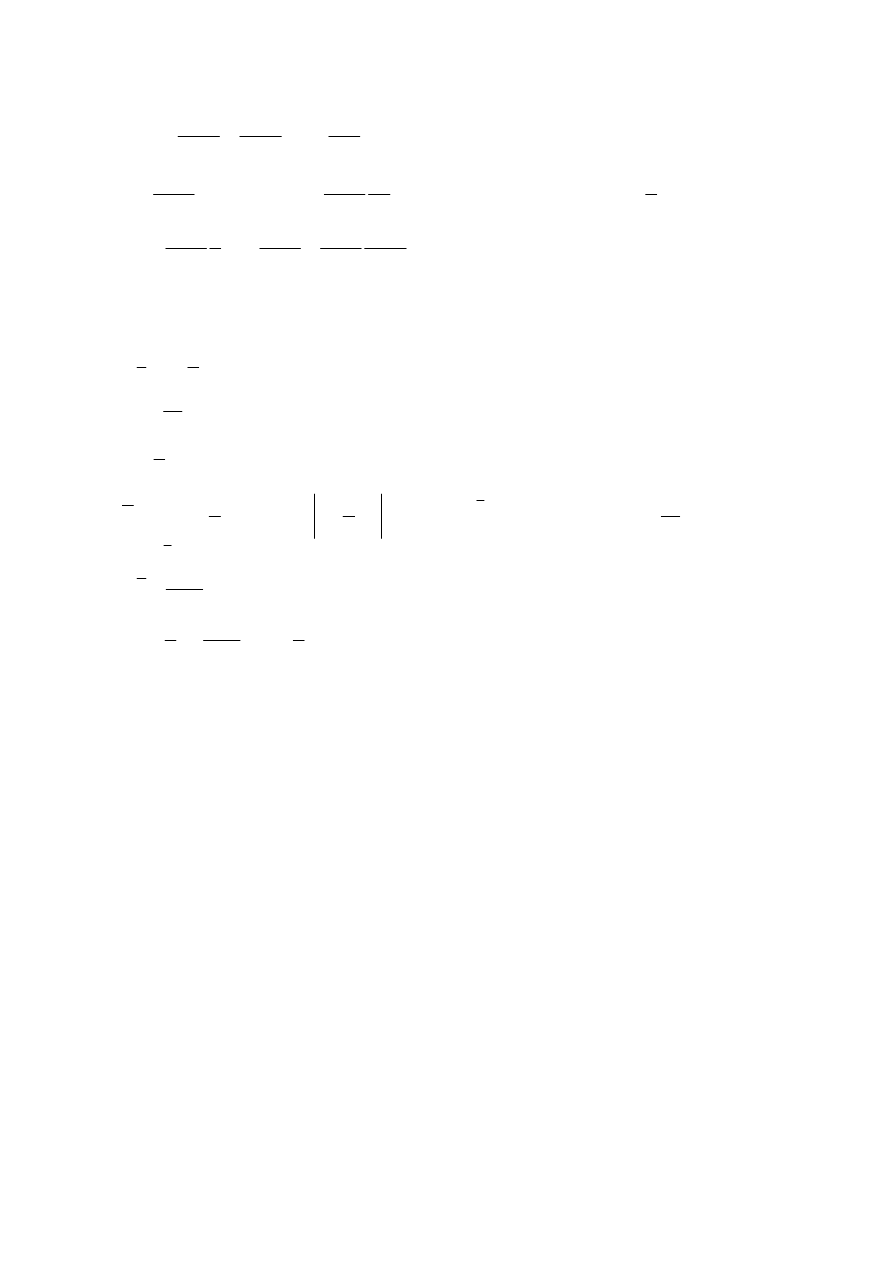
5
5
bo
554
,
0
5
554
,
0
5
2
2
2
2
=
=
=
σ
S
E
σ
S
E
EG
S
(
)
(
)
≅
=
=
2
1
wykl
(2)
nzl
,
max
2
211
,
0
2
,
max
211
,
0
2
2
1
2
2
456
2
123
χ
X
X
X
σ
S
S
G
i
N
( )
( )
S
S
N
G
E
G
E
σ
σ
EG
58
,
1
5
554
,
0
211
,
0
3
211
,
0
3
2
2
3
211
,
0
2
2
≈
=
=
⋅
=
Zadanie 10
2
var
EX
λ
S
=
2
var
X
E
λ
S
=
2
2
2
λ
EX
=
λ
EX
1
=
∫
∫
∫
∞
∞
∞
−
−
−
+
−
−
=
=
=
=
−
=
−
=
λ
a
a
t
λ
a
λ
a
t
λ
x
λ
λ
e
e
λ
t
e
dt
e
λ
t
t
λ
a
x
dx
e
λ
λ
a
x
X
E
0
0
2
2
2
2
2
2
λ
e
S
a
−
=
2
var
0217
,
1
36
,
0
ln
36
,
0
ln
2
36
,
0
2
2
var
≈
−
=
→
=
−
→
=
→
=
−
a
a
λ
λ
e
λ
S
a
Wyszukiwarka
Podobne podstrony:
2002.01.12 prawdopodobie stwo i statystyka
2002 10 12 prawdopodobie stwo i statystykaid 21648
2002.10.12 prawdopodobie stwo i statystyka
2002 10 12 prawdopodobie stwo i statystykaid 21648
2002 06 15 prawdopodobie stwo i statystykaid 21643
2003.01.25 prawdopodobie stwo i statystyka
2002.06.15 prawdopodobie stwo i statystyka
2000.01.15 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
1997.01.18 prawdopodobie stwo i statystyka
2002.04.13 prawdopodobie stwo i statystyka
2003 01 25 prawdopodobie stwo i statystykaid 21695
2000 01 15 prawdopodobie stwo i statystykaid 21565
2007 01 08 prawdopodobie stwo i statystykaid 25641
2005 01 17 prawdopodobie stwo i statystykaid 25338
2002 04 13 prawdopodobie stwo i statystykaid 21638
więcej podobnych podstron