Egzamin dla Aktuariuszy z 18 stycznia 1997 r.
Prawdopodobieństwo i Statystyka
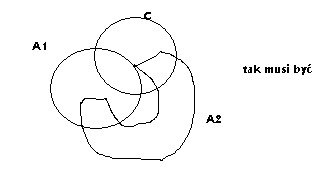
Zadanie 1
P( A ∩ C
P( A ∩ C
2
)
1
) 1
1
=
P(
=
A
P( A 2 )
2
1 )
3
1
P( A ∩ C) 1
= P( A ∩ C =
2
)
1
6
4
P( A ∩ A =
=
1
2 )
1 1
1
2 2
4
P( A ∩ A ∩ C =
1
) 0
2
Z tego wynika:
P A ∩ C + P A ∩ C
Z obrazka: P( C A ∪ A =
1
2 )
( 1
) ( 2
)
P( A + P A − P A ∩ A 1 )
( 2) ( 1
2 )
1
1
+
4 + 6 4
10
5
6
4
=
=
=
= → ( C)
1
1
1
24 3
18
9
+ −
2
2
4
Zadanie 2
2
− λ
− λ
8 λ
− λ
− λ
e
+ e
λ
=
e
: e
9 2
4 2
1 + λ =
λ
9
4 2
λ − 9 λ − 9 = 0
∆ = 225
∆ = 15
9 −15
λ =
∉ D
1
8
9 + 15
24
λ =
=
= 3
8
8
4
2
1
2
4
EX =
; EY = EY =
; EX
=
7
2
7
E[∑ X
Y
i − ∑ i ]
4
1
= 735 ⋅ − 880 ⋅ = 2
− 0
7
2
var[∑ X
Y
i − ∑ i ]
4
16
1
1
= 735 −
+ 880 − = 400
7
49
2
4
20
P( X < 0) = P Y <
= Φ )
1
(
≈ 8
,
0 4
20
Zadanie 4
=0
4
6
4
7 8
E( X X
= E X X = E X X + E X X + + E X X = E X X + → E X X = −
1
2 )
( 2 3) ( 1 2) ( 1 3) 1 ( 2 3) ( 1 3) 1
( 1 3) 1
ρ( X , X
= − → X = aX + b
<
1
3 )
1
a
l
e a
0
3
1
EX = a ⋅ 0 + b = 0 → b = 0
3
var
2
X = a ... → a = −1
3
z tego: P( X = − X
=
1
) 1
3
Zadanie 5
2
0,5
3
2 1
nzl
x
}
−
0,5
∞
1
ODP =
1
3
2
y
1
4
3 8
E X X ≤ + EY = ∫ 2 x
+ ye
1
1
4 1
0,5
∫ −
=
0
2
0,5
2
1
12
3
0
0
x
2 x
[ ] + = + = + =
∫
0
4
0
Zadanie 6
X −
t =
µ
n −1 ≅ t( n −
)
1 n = 10
S
.
1 P( t < u) = 9
,
0
5 kwantyl = ,
2 262 (
2 st
9
,
0
.
7 )
5
X −
−
µ
,
2 2622 <
3 < ,
2 2622
S
.......
,
2 2622 ⋅ S
,
2 2622 ⋅ S
u = X +
> µ > X −
= L
3
3
,
2 2622 ⋅ S
X −
= − ,
0 262
3
5
,
4 24 ⋅ 3
,
2 2622 ⋅ S
→ S =
, X = ,
4 262 −
,
2 2622 ⋅ S
2
⋅ ,
2 2622
3
X +
= ,
4 262
3
2 P( t < u =
=
2 )
0
,
0 1 k
wantyl 0
,99
-2,8215
X − µ 3 < − 8, 2 215
S
− 8
,
2 215 ⋅ S
X − µ <
3
8
,
2 215 ⋅ S
,
2 2622 ⋅ S
8
,
2 215 ⋅
µ > X +
= W =
S
,
4 262 −
+
≈ 8
,
4 21
3
3
3
Zadanie 7
− tn
µ
n
P(min ≤ t) = 1 − P(min > t) = 1 − e
≅ wykl
µ
1
µ
E ˆ1 = nµ = µ
n
oba nieobciąŜone
µ
µ
E ˆ 2 = nE min = n
= µ
n
2
1
2
µ
var ˆ µ =
nµ =
1
2
2
n
n
µ
poniewaŜ n>1
2
→
< µ → ( E)
2
n
2 µ
2
var ˆ µ = n
= µ
2
2
n
Zadanie 8
− x
αe
f ( x)
α
= ( + xe) α 1+
−
1
n
− xi
L = n ∏
e
α
α+
x
1
i=1 (
−
1 +
i
e
)
− ix
ln L = n ln α + ∑
e
−
ln (
= n ln α +
− x ( α
)
1 ln 1 e
i −
+
+
i
x
−
1
1 +
α
i
x
e
)
∑
+
(
(
)
∂ = n −∑ln(1+ − ix
e
)= 0
∂ α α
n − α∑ ln(1+ − ix e
)= 0
ˆ =
n
α
n
∑ln(
−
1 +
xi
e
)
i=1
Zadanie 9
4
Κ = 5 x
> t
1
P
4
5
> =
H 0 ( x
t ) α
1
4
t
t 4
P X
> =
0
∫ =1− = α
H
5
0,25
5
t
5
1
t
4 = 1− α
5
t
4
= 1
( − α)
5
4
t = 1
(
5 − α)
5
5
t
1
1
t
4
4
4
moc =
1
(
5
α)
P
4
X
x
x
H
> =
5
1
1
1
∫
4 = [ 5 ] 0,25 = −
−
= −
t
5
5
5
0,25
t
5
5
Zadanie 10
6
2
5
5
1
p =
=
, p =
, p =
1
2
3
36
12
12
6
2
2
2
5
5
1
45 −120 ⋅
50 −120 ⋅
25 −120 ⋅
2
12
12
6
χ
p =
+
+
= ,175
5
5
1
120 ⋅
120 ⋅
120 ⋅
12
12
6
dl
a α = 0,0
1 k
w 9
,21
α = 0,0
5 5
,991 2
χ
wszystkich → nie prowadzi do odrzucenia w Ŝadnym p >
α = 0,
1 4
,605
α = 0,00
5 1
0,597
wypadku czyli prawidłowa jest odpowiedź (D)