
Egzamin dla Aktuariuszy z 15 stycznia 2000 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
(
)
(
)
(
)
%
9
,
20
7
1
6
1
5
1
4
1
3
1
2
1
6
1
3
1
6
1
)
(
k
II
w
b
3
1
6
1
II)
w
(
II
w
b
2
II
w
b
2
6
1
≈
+
+
+
+
+
=
=
∧
=
∑
=
k
k
P
P
b
P
P
P
Zadanie 2
Długość cięciwy =
2
sin
2
φ
r
( )
∫
⋅
=
dr
r
f
r
E
ODP
)
(
( )
(
)
∫
Π
Π
Π
Π
−
Π
Π
=
⋅
2
0
1
1
1
2
1
2
2
,
max
sin
2
d
r
r
E
bo ustalamy kąt pierwszego jabłka i wtedy
drugie
)
2
;
0
(
Π
[
]
Π
=
+
Π
=
Π
−
Π
+
Π
−
Π
=
Π
−
Π
+
Π
Π
=
Π
Π
Π
Π
Π
Π
∫
∫
r
r
r
r
4
2
2
2
2
cos
2
2
cos
2
2
2
sin
2
sin
2
1
0
1
0
2
1
1
∫
∞
−
≈
Π
=
Π
=
Π
=
0
2
637
,
0
2
2
1
4
2
4
r
e
r
ODP
Zadanie 3
(
)
3
4
5
6
7
8
2160
3
2
4
3
4
1
5
4
6
5
7
2
8
6
6
4
3
2
1
⋅
⋅
⋅
⋅
⋅
=
+
=
∩
∩
∩
∩
B
B
B
C
B
P
(
)
3
4
5
6
7
8
2880
5
4
6
5
7
2
8
6
4
3
2
1
⋅
⋅
⋅
⋅
⋅
=
=
∩
∩
∩
B
B
C
B
P
( )
3
4
5
6
7
8
15120
4
2
5
3
6
4
7
5
8
6
4
3
5
2
6
4
7
5
8
6
4
3
5
4
6
2
7
5
8
6
4
3
5
4
6
5
7
2
8
6
4
3
5
4
6
5
7
6
8
2
3
1
3
2
4
2
5
3
6
4
7
5
8
6
1
czarna
ostatnia
i
wystapily
czarne
2
ze
uklady
6
⋅
⋅
⋅
⋅
⋅
=
+
+
+
+
−
−
=
→
4
4
4
4
4
4
4
4
4
4
4
4
8
4
4
4
4
4
4
4
4
4
4
4
4
7
6
B
P
układy że 2 czarne wystąpiły i ostatnia czarna: cbbbbc, bcbbbc, bbcbbc, bbbcbbc, bbbbcc
sprawdzamy A
3
4
5
6
7
8
15120
3
4
5
6
7
8
2880
3
4
5
6
7
8
2160
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
⋅
L=P

Zadanie 4
=
1
..
1
2
p
p
σ
WYNIK
)
1
;
1
(
1
2
−
∈
<
p
p
ale
( )
−
−
→
−
−
>
→
>
+
=
∑
1
;
1
1
1
1
0
2
2
var
n
n
p
p
n
n
Zadanie 5
(
)
2
5
5
;
5
σ
µ
N
S
≅
(
)
2
20
20
;
20
σ
µ
N
S
≅
(
)
2
15
15
;
15
σ
µ
N
S
≅
(
)
(
)
(
)
(
)
15
5
5
2
15
5
5
20
5
2
20
5
var
var
S
S
S
E
S
S
S
S
S
E
S
S
ODP
+
+
+
=
+
=
(
)
2
15
5
5
5
,
cov
σ
S
S
S
=
+
2
1
100
5
20
5
5
2
2
2
=
=
=
σ
σ
σ
p
(
)
(
)
20
20
20
15
5
5
25
,
0
5
25
,
0
5
20
20
5
5
,
0
5
S
µ
S
µ
µ
S
σ
σ
µ
S
S
S
E
=
−
+
=
−
+
=
+
(
)
(
)
2
2
2
2
20
5
4
15
4
3
5
5
5
,
0
1
var
σ
σ
σ
S
S
=
=
−
=
2
20
2
16
1
4
15
S
σ
ODP
+
=
Zadanie 6
Obliczenia pomocnicze:
...
3
2
3
2
2
2
1
+
+
+
=
−
−
−
e
e
e
u
...
3
2
4
2
3
2
2
1
+
+
+
=
−
−
−
−
e
e
e
ue
(
)
(
) (
)
...
5
3
...
2
3
1
2
1
3
2
1
3
2
2
2
2
2
1
1
+
+
+
=
+
−
+
−
+
=
−
−
−
−
−
−
−
−
e
e
e
e
e
e
e
u
(
)
...
5
3
1
4
3
2
1
1
+
+
+
=
−
−
−
−
−
−
e
e
e
e
e
u
(
)(
)
1
2
1
1
2
1
1
3
2
1
1
1
1
1
1
...
2
2
1
1
−
−
−
−
−
−
−
−
−
−
−
−
−
+
=
−
+
−
=
+
+
+
=
−
−
e
e
e
e
e
e
e
e
e
e
e
e
u
bo:
...
2
2
1
+
+
=
−
−
e
e
x
...
2
3
2
1
+
+
=
−
−
−
e
e
xe
(
)
(
)
2
1
1
1
1
2
1
1
1
1
...
1
−
−
−
−
−
−
−
−
=
→
−
=
+
+
=
−
e
e
x
e
e
e
e
e
x
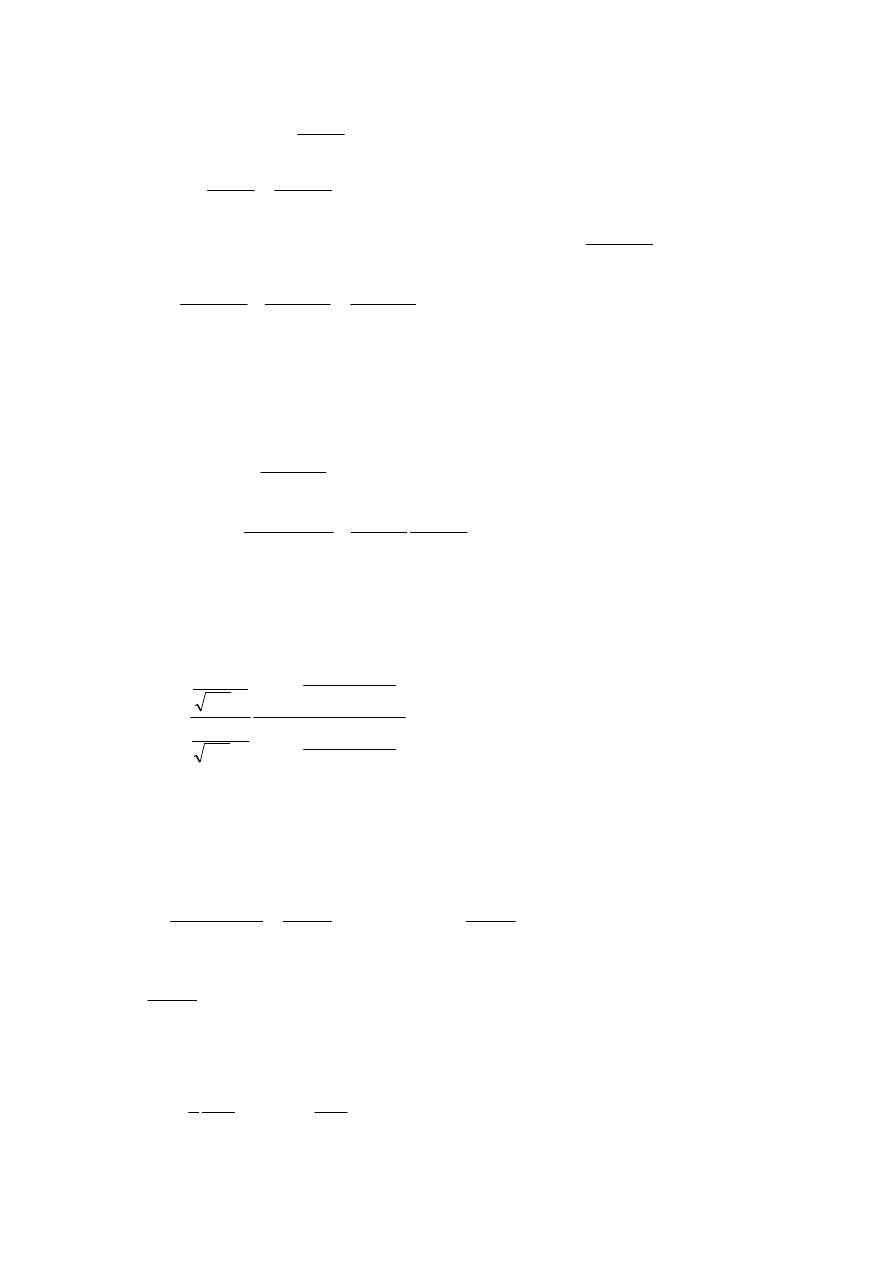
(
)
∑
∞
=
−
−
−
−
−
=
−
=
1
1
1
1
1
1
k
k
e
e
e
ke
X
E
1
1
1
1
1
2
1
1
1
−
−
−
−
−
−
=
−
−
>=
<
e
e
e
e
X
E
(
) ( )
∑ ∫
∑
∑
∞
=
+
∞
=
∞
=
−
−
−
−
−
+
−
−
−
−
+
=
−
=
−
=
=
1
1
1
1
2
1
2
1
1
2
)
1
(
2
2
2
2
1
1
k
k
k
k
k
k
k
k
x
e
e
e
e
e
k
e
k
e
k
e
k
X
E
(
) (
) (
)
2
1
1
2
1
2
2
1
2
1
1
1
1
var
−
−
−
−
−
−
−
−
=
−
−
−
+
=
e
e
e
e
e
e
e
X
(
)
X
X
X
X
X
,
cov
2
var
var
var
−
+
>=
<
.....
var
>=
<
X
(
)
[
]
(
)
∑ ∫
∑
∞
=
+
∞
=
−
−
−
−
−
−
−
−
−
−
−
−
=
−
−
−
−
−
+
=
−
=
>
<
⋅
1
1
1
1
2
1
1
1
)
(
k
k
k
k
k
k
k
k
k
k
k
x
e
e
e
k
e
e
e
e
e
ke
e
ke
k
e
k
x
k
X
X
E
(
) ( ) ( )
∑
∞
=
−
−
−
−
−
−
−
=
−
=
1
1
2
1
1
1
2
1
1
2
1
k
k
e
e
e
e
ke
(
)
(
)
(
) (
)
0
0
1
2
1
1
1
2
1
,
cov
1
1
1
1
2
1
1
1
=
→
=
−
−
−
−
−
−
=
>
<
−
−
−
−
−
−
−
corr
e
e
e
e
e
e
e
X
X
Zadanie 7
0
1
σ
σ
>
(
)
(
)
→
−
−
−
−
Π
Π
=
∑
∑
0
2
1
2
0
1
2
exp
2
exp
2
1
2
1
/
0
1
σ
µ
X
σ
µ
X
σ
σ
p
p
i
i
σ
σ
rosnące dla
(
)
∑
−
2
µ
X
i
(
)
307
,
18
05
,
0
)
10
(
2
1
2
=
→
=
>
−
≅
=
∑
c
c
µ
X
P
χ
i
σ
4
48
4
47
6
moc:
(
)
2
2
)
10
(
2
2
307
,
18
865
,
4
9
,
0
307
,
18
σ
σ
σ
µ
X
P
χ
i
≥
→
>
>
−
≅
∑
4
4 8
4
4 7
6
7628
,
3
865
,
4
307
,
18
2
≈
≥
σ
Zadanie 8
2
1
)
(
1
1
)
(
r
r
r
f
r
r
r
CBC
P
−
=
→
−
=
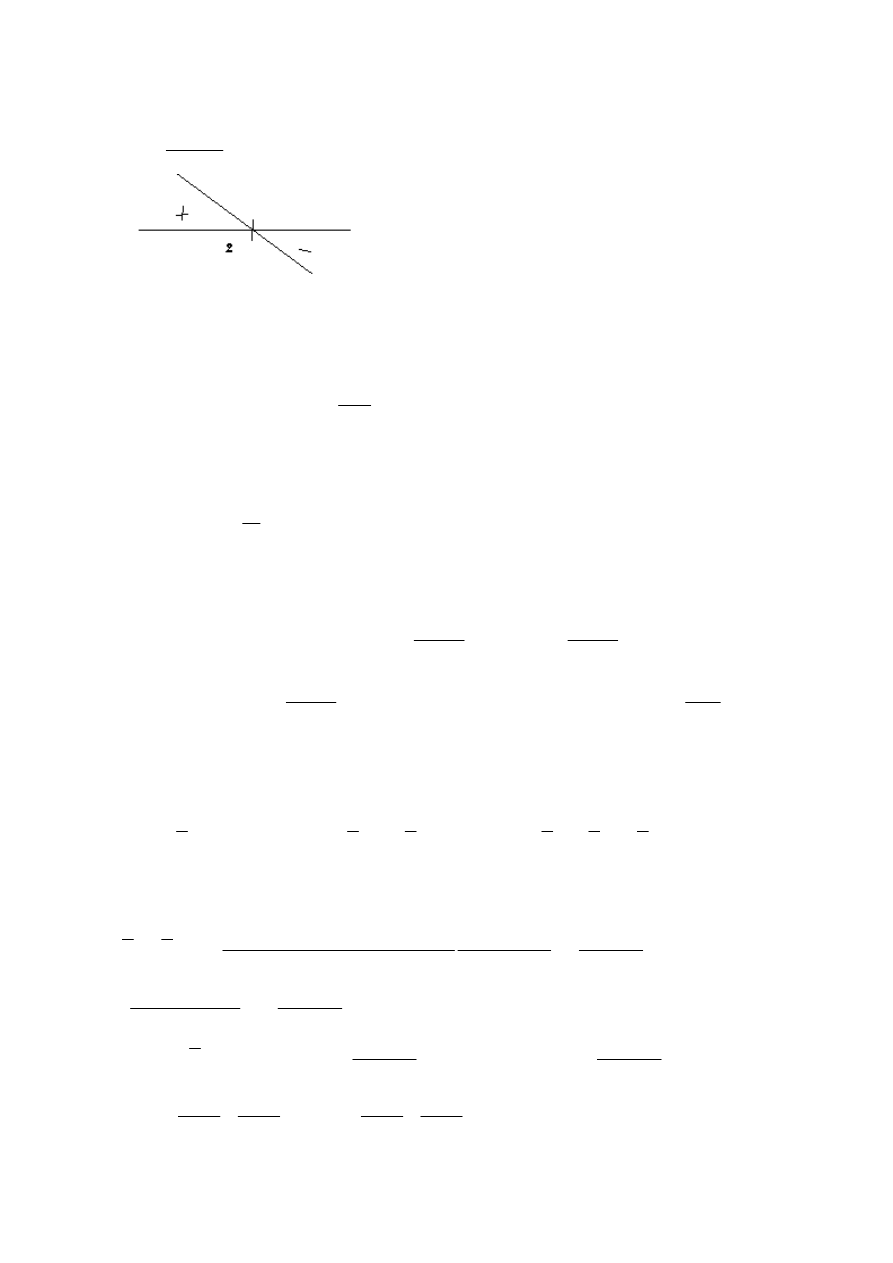
3
)
2
(
)
(
r
r
r
r
f
−
=
′
Z tego:
2
ˆ
=
r
Zadanie 9
)
1
,
0
(
J
X
i
≅
(
)
(
)
∑
∏
∏
+
−
≤
=
≤
=
≤
+
2
ln
)
1
(
ln
2
1
5
,
0
2
1
n
X
P
X
P
X
P
i
n
i
i
n
dla
)
0
;
(
−∞
∈
t
(
)
∫
=
=
<
=
<
t
e
t
t
e
e
X
P
t
X
P
0
..
)
(ln
(
)
∫
−
−
−
−
=
=
>
=
<
=
<
−
1
1
..
1
)
ln
(
t
e
t
t
t
e
e
X
P
e
X
P
t
X
P
t
e
X
f
−
=
−
)
ln
(
wykładniczy
)
1
;
(n
Y
n
Γ
≅
(
) (
)
∫
∫
∞
+
∞
−
−
−
−
=
−
≤
−
=
+
≥
=
≤
Π
2
ln
)
1
(
0
1
1
1
)!
1
(
1
)!
1
(
1
2
ln
)
1
(
5
,
0
n
x
n
x
n
n
n
dx
e
x
n
dx
e
x
n
n
Y
P
P
(
)
∫
∫
∫
+
+
∞
−
−
−
−
−
−
→
Γ
−
=
−
≥
−
≥
−
−
=
≤
Π
2
ln
)
1
(
0
2
ln
)
1
(
0
0
1
1
1
1
)
(
1
1
1
1
)!
1
(
1
1
5
,
0
n
n
x
n
x
n
x
n
n
n
e
x
e
x
e
x
n
P
czyli odpowiedź C jest prawidłowa
Zadanie 10
(
)
(
)
∑
∑
∑
=
=
=
+
+
+
+
+
+
−
=
+
−
=
−
n
i
n
i
n
i
m
n
n
m
n
i
m
n
m
n
i
i
m
n
i
X
n
X
n
X
X
X
X
X
X
X
X
1
1
1
2
2
2
2
2
2
2
(
)
∑
=
+
=
n
i
i
µ
σ
n
X
E
1
2
2
2
[
]
2
2
2
2
1
1
1
)
(
1
...
...
...
µ
nm
µ
n
σ
n
m
n
n
n
X
X
m
n
X
X
X
X
E
X
X
E
n
m
n
n
n
n
m
n
+
+
+
=
+
+
+
+
+
+
+
+
=
+
+
+
[
]
2
2
2
2
2
1
)
(
)
(
)
(
1
...
µ
m
n
σ
m
n
m
n
m
n
X
X
E
m
n
+
+
+
+
=
+
+
+
+
(
)
(
)
(
)
[
]
(
)
[
]
∑
=
+
+
+
+
+
+
+
+
−
+
=
−
+
2
2
2
2
2
2
2
2
2
2
)
(
)
(
1
)
(
2
µ
m
n
σ
m
n
m
n
n
µ
nm
µ
n
σ
n
m
n
n
n
µ
σ
n
X
X
E
m
n
i
=
+
+
−
+
−
+
+
+
+
−
=
n
m
n
nm
m
n
n
n
µ
m
n
n
m
n
n
n
σ
2
2
2
2
2
2

)
(
)
1
(
2
2
)
1
(
2
2
2
2
2
2
D
m
n
m
n
n
σ
m
n
nm
n
nm
n
nm
n
µ
m
n
m
n
n
σ
→
+
−
+
=
+
+
+
−
−
+
+
+
−
+
=
Wyszukiwarka
Podobne podstrony:
2000.01.15 prawdopodobie stwo i statystyka
2002 06 15 prawdopodobie stwo i statystykaid 21643
2000 12 09 prawdopodobie stwo i statystykaid 21582
2002 01 12 prawdopodobie stwo i statystykaid 21637
2002.01.12 prawdopodobie stwo i statystyka
2008 12 15 prawdopodobie stwo i statystykaid 26466
2000.04.08 prawdopodobie stwo i statystyka
2008.12.15 prawdopodobie stwo i statystyka
2003.01.25 prawdopodobie stwo i statystyka
2000.10.14 prawdopodobie stwo i statystyka
2002.06.15 prawdopodobie stwo i statystyka
2000.12.09 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
1997.01.18 prawdopodobie stwo i statystyka
2003 01 25 prawdopodobie stwo i statystykaid 21695
2007 01 08 prawdopodobie stwo i statystykaid 25641
2000 06 17 prawdopodobie stwo i statystykaid 21573
2005 01 17 prawdopodobie stwo i statystykaid 25338
więcej podobnych podstron