Egzamin dla Aktuariuszy z 25 stycznia 2003 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
Innymi słowami: losujemy do momentu pierwszej czarnej, ile średnio będzie białych (patrząc
z drugiej strony)
b,c i dalej
=
=
=
=
15
25
9
9
)
15
(
,
15
25
9
10
)
14
(
,...,
15
25
9
22
)
2
(
,
15
25
9
23
)
1
(
P
P
P
P
liczymy na piechotę:
11
15
=
EX
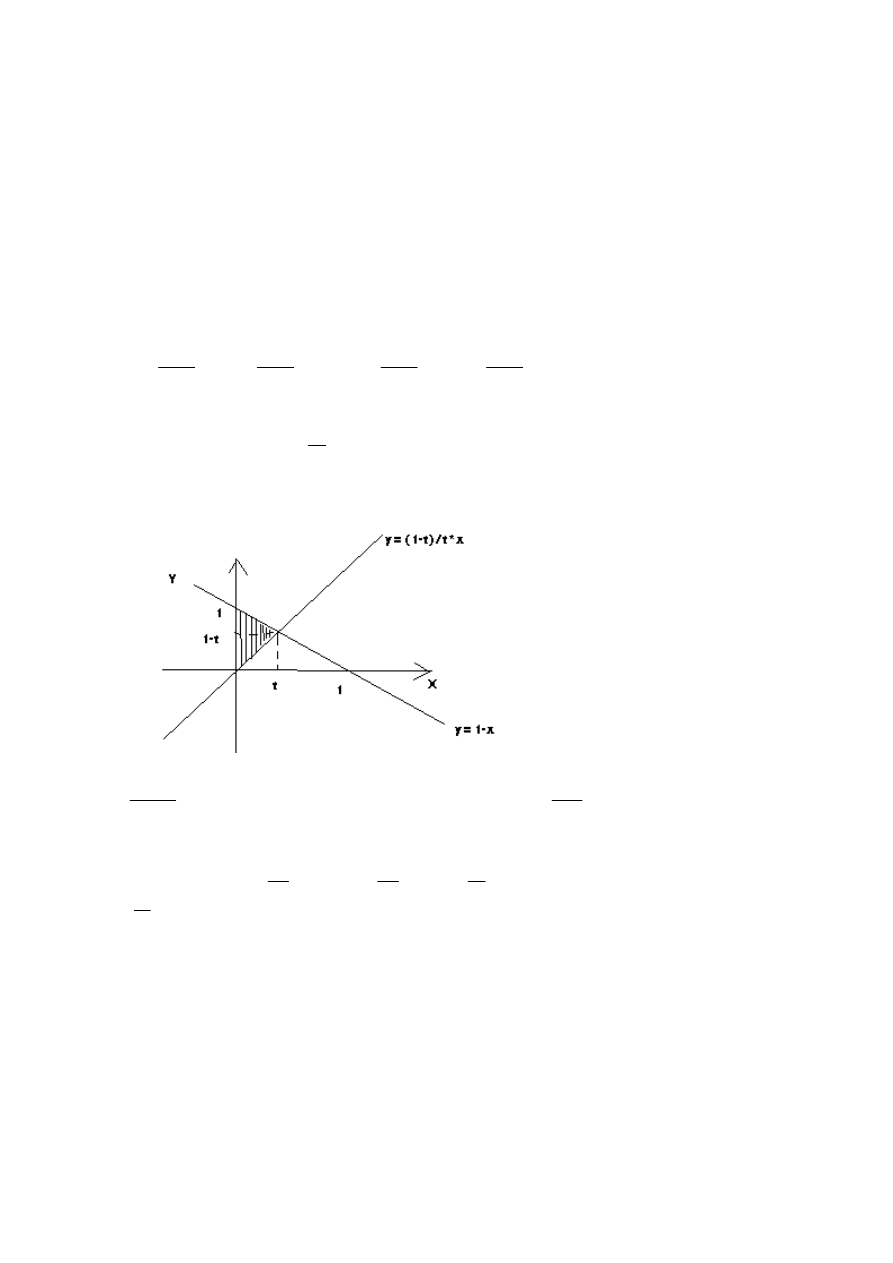
Zadanie 2
(
) (
)
=
−
≥
=
≤
−
=
+
≤
=
≤
+
∈
X
t
t
Y
P
tY
t
X
P
Y
X
t
X
P
t
Y
X
X
P
t
1
)
1
(
)
(
)
1
,
0
(
4
8
47
6
∫ ∫
∫
−
−
=
−
=
−
=
−
=
=
t
x
x
t
t
t
t
t
t
t
t
t
x
x
dx
t
x
dydx
0
1
1
0
2
0
2
2
2
2
2
2
g(z)=1 dla
1
0
≤
≤
z
Zadanie 3
0
3
=
µ
dla symetrycznych
3
2
3
3
2
3
µ
m
µ
m
µ
+
−
=
[
]
3
2
3
2
3
)
)(
2
)(
1
(
)
1
(
3
)
2
)(
1
(
)
1
(
3
EX
n
n
n
EXEX
n
n
nEX
X
X
X
n
n
n
X
X
n
n
nX
E
ODP
k
j
i
j
i
−
−
+
−
+
=
−
−
+
−
+
=
}
(
)
2
3
3
2
2
3
2
0
3
3
3
2
3
2
3
µσ
µ
µ
µ
σ
µ
µ
m
µ
µ
EX
+
=
−
+
=
−
+
=
=

2
2
2
µ
σ
EX
+
=
(
)
(
)
=
−
−
+
+
−
+
+
=
3
2
2
2
3
)
2
)(
1
(
)
1
(
3
3
µ
n
n
n
µ
σ
µ
n
n
µσ
µ
n
ODP
(
)(
) (
)
=
+
−
−
+
+
−
+
+
=
3
2
2
3
3
2
2
2
3
2
2
3
3
3
µ
n
n
n
n
µ
µσ
n
n
µσ
n
µ
n
(
)
2
2
2
3
3
2
3
3
3
2
3
2
2
2
2
3
3
2
3
3
3
3
3
3
µ
n
σ
µ
n
µ
n
µ
n
µ
n
µ
n
µσ
n
µ
n
µσ
n
µσ
n
µ
n
+
=
+
−
+
−
−
+
+
+
=
Zadanie 4
(
)
2
2
2
!
10
∑
−
−
Π
=
i
µ
X
i
e
L
(
)
2
2
!
10
ln
ln
2
∑
−
−
Π
=
i
µ
X
L
i
(
)
(
)
∑
∑
=
=
−
=
−
=
∂
∂
10
1
0
2
2
1
i
i
i
µ
X
i
µ
X
i
µ
max
0
2
→
<
∂
∂∂
µ
∑
=
−
0
55µ
iX
i
55
ˆ
∑
=
i
iX
µ
∑
=
=
µ
µ
i
µ
E
55
1
ˆ
∑
=
=
55
1
1
55
1
ˆ
var
2
2
i
i
µ
(
)
(
)
(
)
2643
,
0
55
96
,
1
95
,
0
55
ˆ
ˆ
ˆ
≈
→
=
→
=
≤
=
≤
−
=
+
≤
≤
−
d
d
d
X
P
d
µ
µ
P
d
µ
µ
d
µ
P
Zadanie 5
i
i
i
X
Z
Y
=
+
( ) ( )
cov
2
var
var
var
)
(
)
(
)
,
(
)
(
)
(
+
+
=
+
≅
Z
Y
X
λ
Poisson
Z
Y
S
S
S
S
48
47
6
2
)
(
var
EY
λ
S
Y
=
2
)
(
var
EZ
λ
S
Z
=
(
)
2
)
(
)
(
var
EX
λ
S
S
Z
Y
=
+
2
2
2
)
(
2
EY
XY
E
EX
EZ
+
−
=
∫
∫
∞
−
−
+
=
c
c
µ
x
µ
x
e
µ
c
e
µ
x
EY
0
2
2
2
1
1
∫
∫
∞
−
−
+
=
c
c
µ
x
µ
x
e
µ
cx
e
µ
x
XY
E
0
2
1
1
)
(
cov
2
1
2
1
2
2
2
2
+
+
−
=
→
∫
∫
∞
∞
−
−
c
c
µ
x
µ
x
EX
e
µ
cx
e
µ
c
λ
EX
λ
−
−
+
+
=
+
←
∫
∫
∫
∫
∫
∞
∞
∞
−
−
−
−
−
c
c
c
c
µ
x
µ
x
µ
x
µ
x
µ
x
Z
Y
e
µ
cx
e
µ
x
e
µ
x
e
µ
c
e
µ
x
λ
S
S
0
0
0
2
2
2
2
)
(
)
(
1
2
1
2
1
1
2
1
2
var
var
=
−
=
=
′
=
′
=
=
−
=
−
−
∞
∞
−
−
∫
∫
µ
x
µ
x
c
c
µ
x
µ
x
e
v
u
e
µ
v
x
u
e
µ
c
e
µ
cx
λ
1
1
1
1
cov
2
µ
c
µ
c
µ
c
µ
c
ce
λµ
e
c
ce
µ
e
c
λ
−
−
−
−
=
−
+
=
2
2
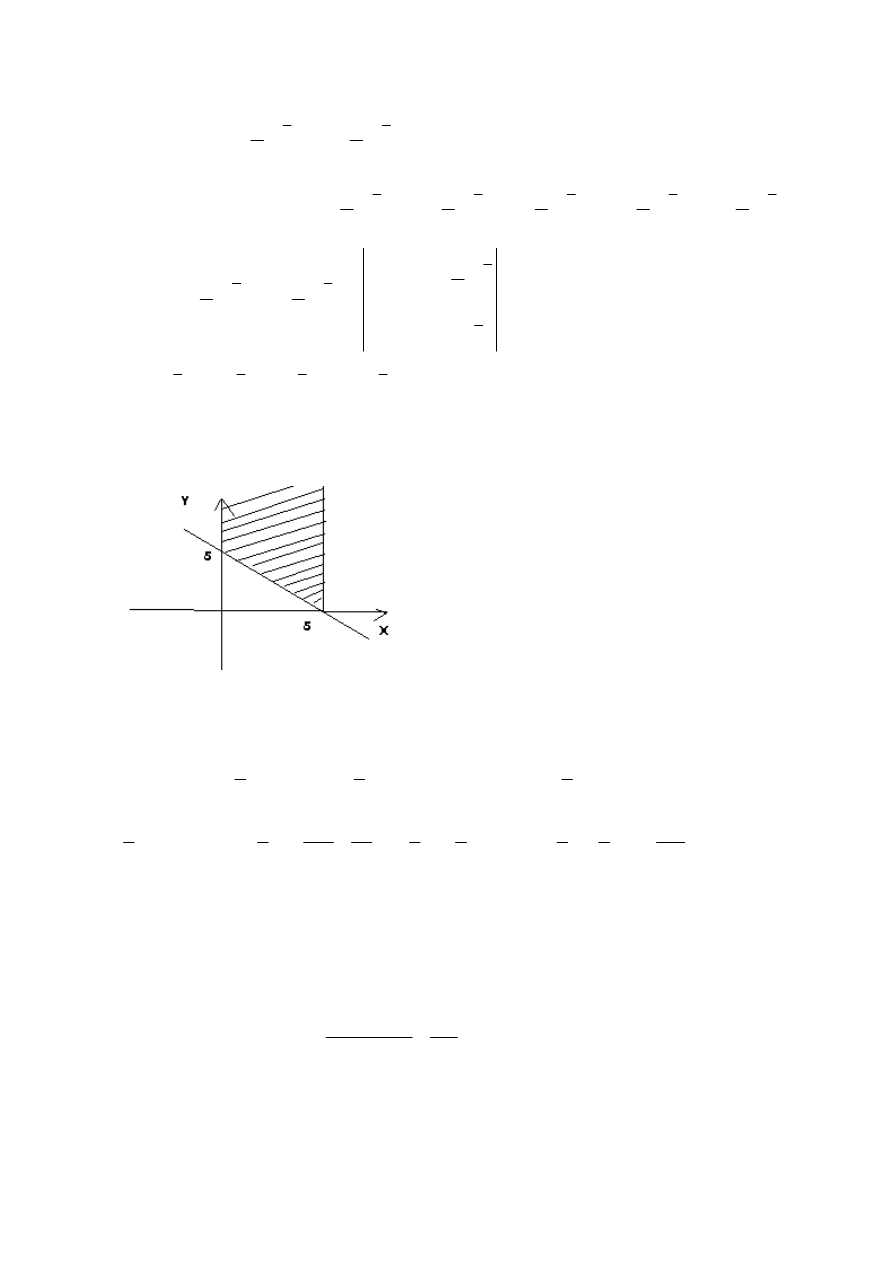
Zadanie 6
)
1
,
4
(
2
1
Γ
≅
+
=
X
X
X
)
1
,
2
(
3
Γ
≅
=
X
Y
(
)
5
,
5
3
2
1
2
1
>
+
+
≤
+
X
X
X
X
X
P
[
]
[
]
∫ ∫
∫
∫
∞
−
−
−
−
−
−
∞
−
−
−
−
−
−
=
+
−
=
−
−
=
=
5
0 5
5
0
5
0
)
5
(
)
5
(
3
5
3
3
)
5
(
6
1
6
1
6
1
x
x
x
x
x
y
y
x
x
y
e
e
x
e
x
e
ye
e
x
dydx
e
x
ye
ODP
∫
−
−
−
−
−
=
⋅
=
−
⋅
=
−
=
−
=
5
0
5
5
4
4
4
5
5
0
5
4
5
3
5
12
625
2
1
5
6
1
5
5
2
3
6
1
5
4
6
6
1
)
6
(
6
1
e
e
e
x
x
e
x
x
e
Zadanie 7
2
2
)
(
)
10
(
λ
λ
λ
m
λ
P
S
+
=
≅
2
2
100
10
λ
λ
ES
+
=
λ
ES
10
=
odpowiedź C prawidłowa bo:
2
2
2
9
,
0
1
,
0
10
100
9
100
100
10
λ
λ
λ
λ
λ
λ
λ
λ
+
=
+
+
=
⋅
+
+
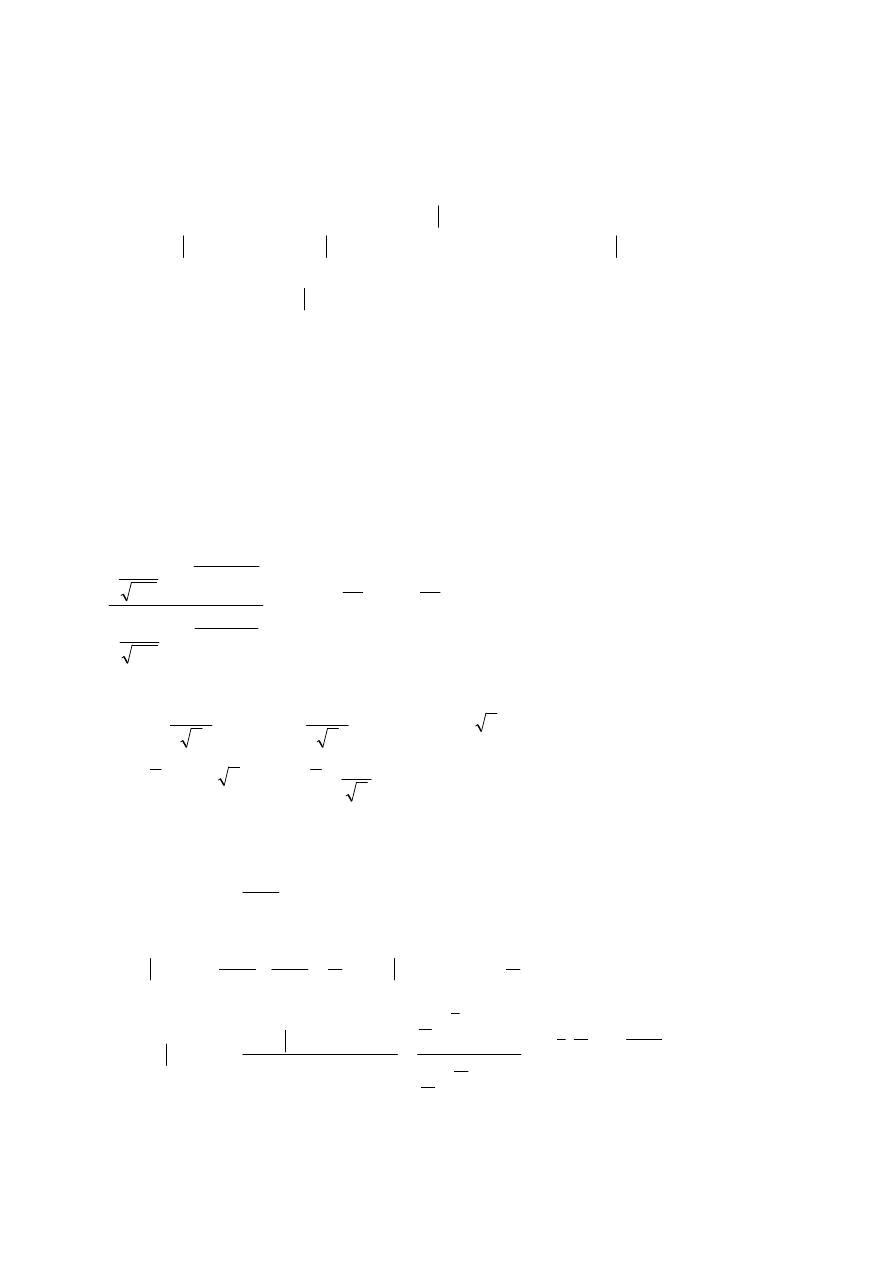
Zadanie 8
(
) (
) (
)
(
)
1
9
,
0
1
1
1
=
=
=
=
=
=
i
i
i
i
X
P
X
P
Z
P
Y
P
(
)
(
)
1
9
,
0
1
0
=
−
=
=
i
i
X
P
Y
P
(
) (
)
(
)
(
)
1
1
0
0
,
1
1
1
1
=
=
=
=
=
=
=
>
+
+
+
n
n
n
n
n
n
n
Y
P
Y
Y
P
Y
Y
P
Y
Y
P
(
) (
)
(
)
=
=
=
=
=
−
=
=
=
=
=
=
=
+
+
+
+
1
,
1
1
,
1
1
1
,
1
0
1
0
1
1
1
1
n
n
n
n
n
n
n
n
n
X
Z
X
Z
P
X
Z
Y
P
Y
Y
P
(
)
(
)
28
,
0
8
,
0
9
,
0
1
1
1
1
1
11
1
1
=
⋅
−
=
=
=
=
−
=
+
+
4
4
4
8
4
4
4
7
6
p
n
n
n
X
X
P
Z
P
(
) (
) (
)
(
)
1
9
,
0
1
1
1
=
=
=
=
=
=
n
n
n
n
X
P
X
P
Z
P
Y
P
(
)
126
,
0
5
,
0
9
,
0
28
,
0
1
9
,
0
28
,
0
lim
1
=
⋅
⋅
→
=
⋅
⋅
→
∞
→
4
8
47
6
p
n
n
X
P
1
bo
5
,
0
8
,
0
2
,
0
2
,
0
8
,
0
1
0
1
0
1
1
0
0
1
0
=
+
=
=
→
=
+
=
+
p
p
p
p
p
p
p
p
p
p
Zadanie 9
1
2
µ
µ
>
(
)
(
)
∑
=
→
=
Π
Π
+
−
−
−
−
−
−
∑
∑
∑
∑
i
n
µ
X
µ
n
µ
X
µ
µ
X
n
µ
X
n
X
STAT
e
e
e
i
i
i
i
2
2
2
2
2
1
1
2
2
2
2
1
2
2
2
1
2
1
(
)
025
,
0
.
1
0
=
>
∑
t
X
P
i
n
n
t
n
n
t
n
n
t
X
P
3
96
,
1
96
,
1
3
025
,
0
3
0
+
=
→
=
−
→
=
−
>
(
)
(
)
3
ˆ
3
96
,
1
3
96
,
1
>
=
+
>
=
+
>
=
−
µ
n
X
n
n
X
K
n
czyli (A) prawidłowa
Zadanie 10
µ
p
p
EX
EN
ES
N
−
=
⋅
=
1
p
N
P
N
P
−
=
=
−
=
>
1
)
0
(
1
)
0
(
(
)
(
)
≅
>
→
=
−
−
=
>
µ
p
wykl
N
S
p
µ
p
µ
p
p
N
S
E
n
N
0
1
1
1
0
(
) (
)
µ
p
s
µ
ps
µ
s
µ
ps
µ
s
S
N
N
e
e
p
e
µ
p
p
p
e
µ
s
f
N
P
N
S
f
s
S
N
P
N
)
1
(
)
1
(
)
1
(
1
)
(
)
1
(
1
1
−
−
+
−
−
−
=
=
−
−
=
=
=
=
=
=

(
)
)
1
(
)
0
(
0
)
(
p
e
µ
p
N
P
N
s
f
s
f
µ
ps
S
N
−
=
>
>
=
−
Wyszukiwarka
Podobne podstrony:
2003.01.25 prawdopodobie stwo i statystyka
2002 01 12 prawdopodobie stwo i statystykaid 21637
2003.05.17 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2002.01.12 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2003 05 17 prawdopodobie stwo i statystykaid 21698
2000.01.15 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
2003.10.11 prawdopodobie stwo i statystyka
1997.01.18 prawdopodobie stwo i statystyka
2000 01 15 prawdopodobie stwo i statystykaid 21565
2003 10 11 prawdopodobie stwo i statystykaid 21705
2007 01 08 prawdopodobie stwo i statystykaid 25641
2005 01 17 prawdopodobie stwo i statystykaid 25338
2002 01 12 prawdopodobie stwo i statystykaid 21637
więcej podobnych podstron