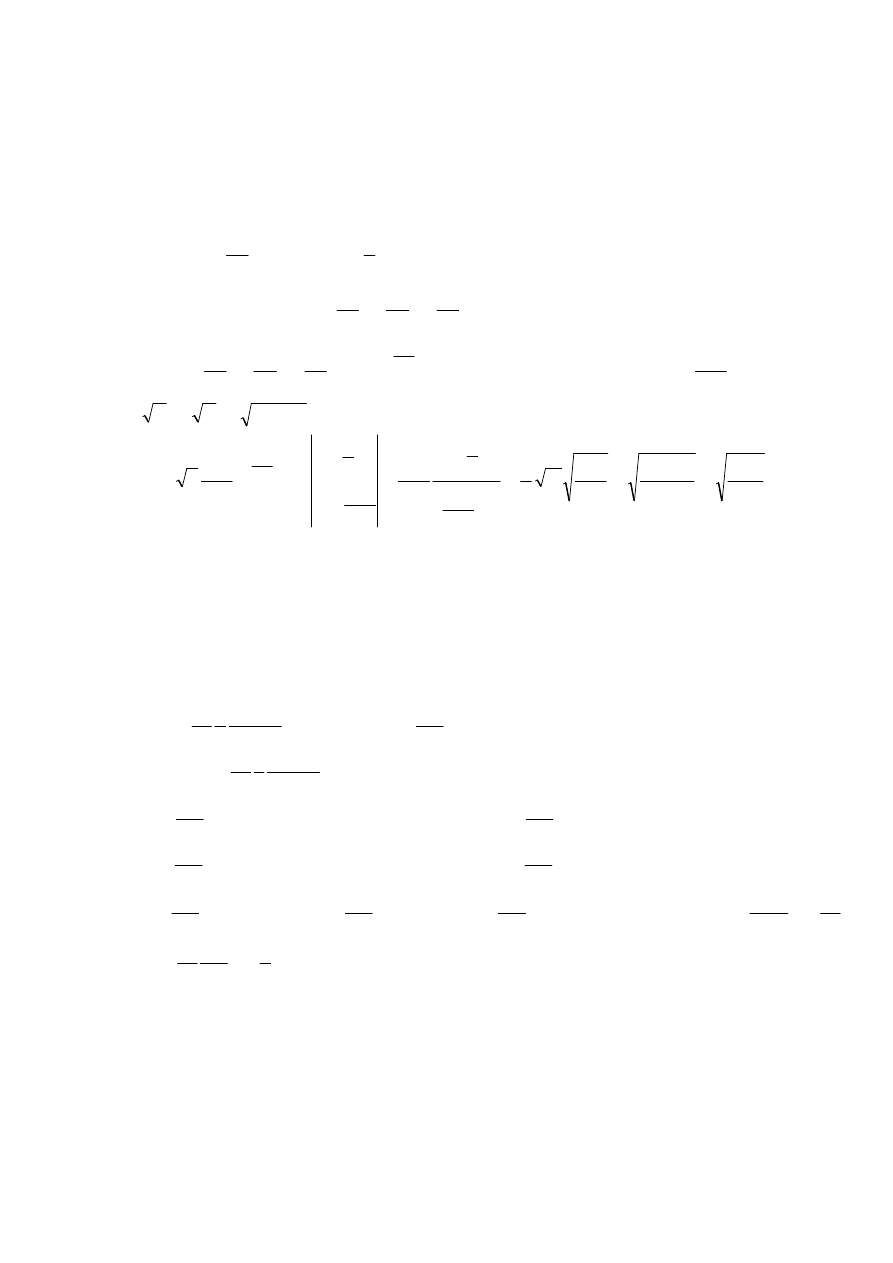
Egzamin dla Aktuariuszy z 17 maja 2003 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
≅
≅
+
=
2
1
)
2
(
2
2
2
wykl
χ
σ
Z
Y
X
Z
i
i
i
i
(
)
(
)
=
≤
=
<
2
2
2
1
1
,...,
min
,...,
min
σ
t
σ
Z
σ
Z
P
t
Z
Z
P
n
n
(
)
≅
+
+
→
−
=
>
−
=
−
2
2
2
2
1
2
1
2
2
2
2
1
2
,...,
min
1
,...,
min
1
2
σ
n
wykl
Y
X
Y
X
e
σ
t
σ
Z
σ
Z
P
n
n
σ
tn
n
(
)
min(...)
...
,...,
...
min
=
∫
∞
−
Π
=
⋅
Π
=
Π
=
Γ
=
=
=
=
=
0
2
2
2
5
,
1
2
2
2
2
2
2
4
2
2
2
1
2
2
3
2
2
2
3
2
2
n
σ
n
σ
n
σ
σ
n
σ
n
σ
n
β
α
dx
e
σ
n
x
ODP
σ
nx
Zadanie 2
1.0=varA+varB+varC+2cov(A,B)+2cov(B,C)+2cov(A,C)
2.0=varA+var(B+C)+2cov(A,B+C)
3.0=varB+var(A+C)+2cov(B,A+C)
A,B,C,A+C,B+C – mają odpowiednio hipergeometryczne rozkłady
Z tego:
87
144
var
var
29
12
30
3
2
30
10
12
var
=
=
=
−
⋅
=
C
B
A
A
C
B
C
A
B
A
var
)
var(
)
var(
29
12
30
3
1
30
20
12
)
var(
=
+
=
+
=
−
⋅
=
+
)
,
cov(
87
144
)
,
cov(
)
,
cov(
2
)
,
cov(
2
87
144
2
0
:
2
B
A
C
A
C
A
B
A
−
−
=
→
+
+
⋅
=
)
,
cov(
87
144
)
,
cov(
)
,
cov(
2
)
,
cov(
2
87
144
2
0
:
3
B
A
C
B
C
B
A
B
−
−
=
→
+
+
⋅
=
87
72
87
2
144
)
,
cov(
)
,
cov(
2
87
144
)
,
cov(
87
144
4
)
,
cov(
2
87
144
3
0
:
1
−
=
⋅
−
=
→
−
−
=
−
−
+
+
⋅
=
B
A
B
A
B
A
B
A
2
1
144
87
87
72
−
=
−
=
ODP
Zadanie 3
Można wypisać: (1,2,3,4) (1,2,3,5) (1,2,3,6) (1,2,4,5) (1,2,4,6) (1,2,5,6) (1,3,4,5) (1,3,4,6)
(1,3,5,6) (1,4,5,6) (2,3,4,5) (2,3,4,6) (2,3,5,6) (2,4,5,6) (3,4,5,6)
Jest 15 przypadków, z tego:
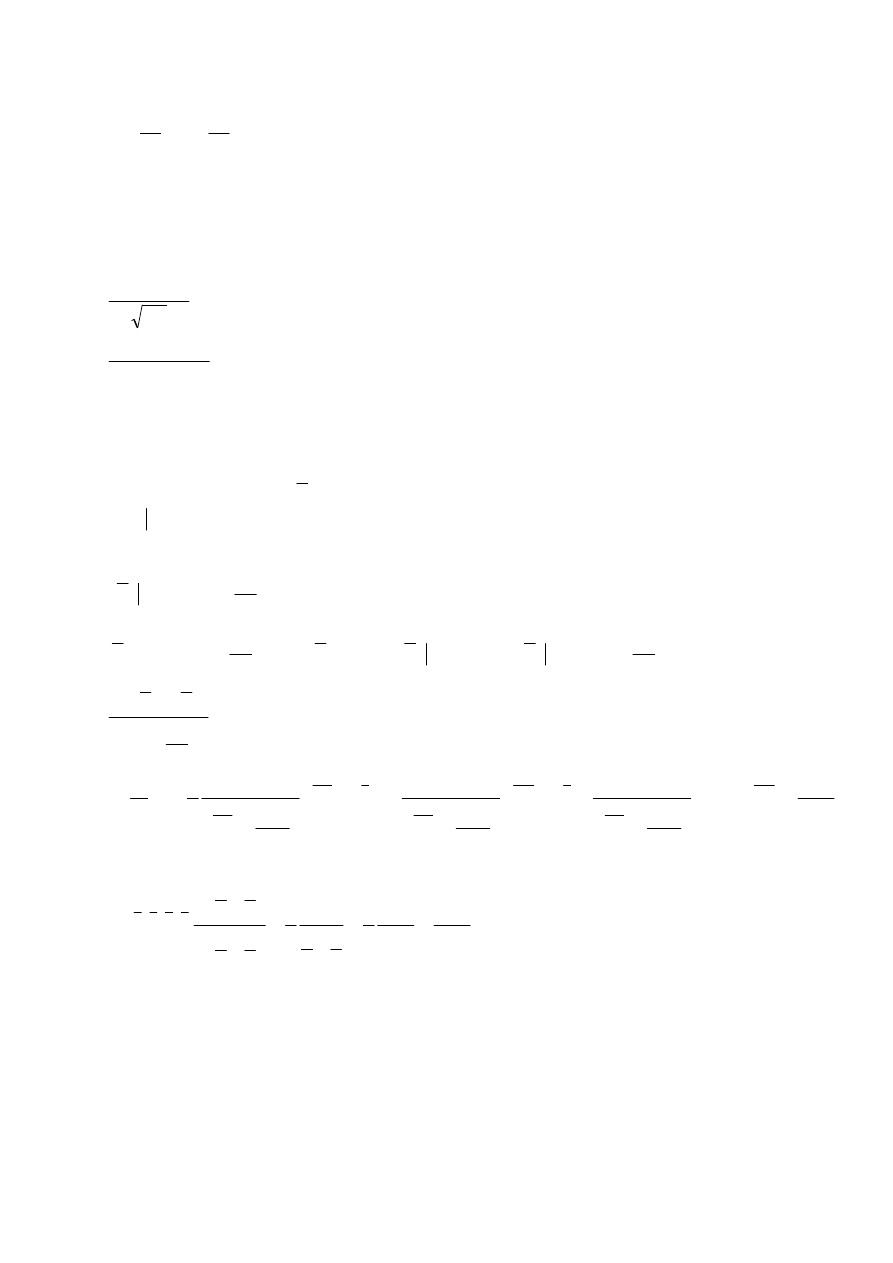
15
4
6
bo
6
1
4
6
6
15
4
4
=
=
=
P
Zadanie 4
(
)
∑
=
=
+
+
=
→
=
=
n
k
n
i
i
k
k
i
X
X
E
n
ES
λ
EX
X
n
S
1
1
..
...
)
(
)
(
)
1
,
0
(
)
(
N
n
λ
λ
n
n
S
CTG
i
i
i
→
−
(
)
)
1
(
)
(
2
2
χ
n
λ
λ
n
n
S
i
i
i
→
−
)
(
2
2
k
χ
χ
→
Zadanie 5
Chyba błąd w treści przy X
(
)
(
)
2
,
, σ
µ
N
µ
X
k
k
k
t
≅
( )
2
, a
µ
N
µ
k
≅
(
)
≅
T
σ
µ
N
µ
X
k
k
k
2
,
(
)
(
)
(
)
(
)
T
σ
a
µ
X
E
µ
X
E
X
T
σ
a
µ
N
X
k
k
k
k
k
k
2
2
2
2
var
var
var
bo
,
+
=
+
=
+
≅
(
)
)
1
(
2
2
2
−
≅
+
−
∑
k
χ
T
σ
a
X
X
k
ozn: X
∫
∫
∫
∞
∞
∞
−
−
−
−
−
−
−
−
−
−
=
−
Γ
⋅
−
Γ
=
−
Γ
=
−
Γ
=
0
0
0
2
3
2
1
2
1
2
3
2
1
2
1
2
1
2
1
2
3
2
...
2
1
2
1
2
1
2
1
2
1
2
1
1
1
k
dx
k
e
x
k
e
x
k
x
X
E
k
k
x
k
k
x
k
k
3
1
3
2
2
1
2
3
2
1
2
1
2
1
2
2
3
2
2
2
1
2
2
3
2
−
=
−
=
−
=
−
Γ
−
Γ
=
+
−
−
k
k
k
k
k
k
k
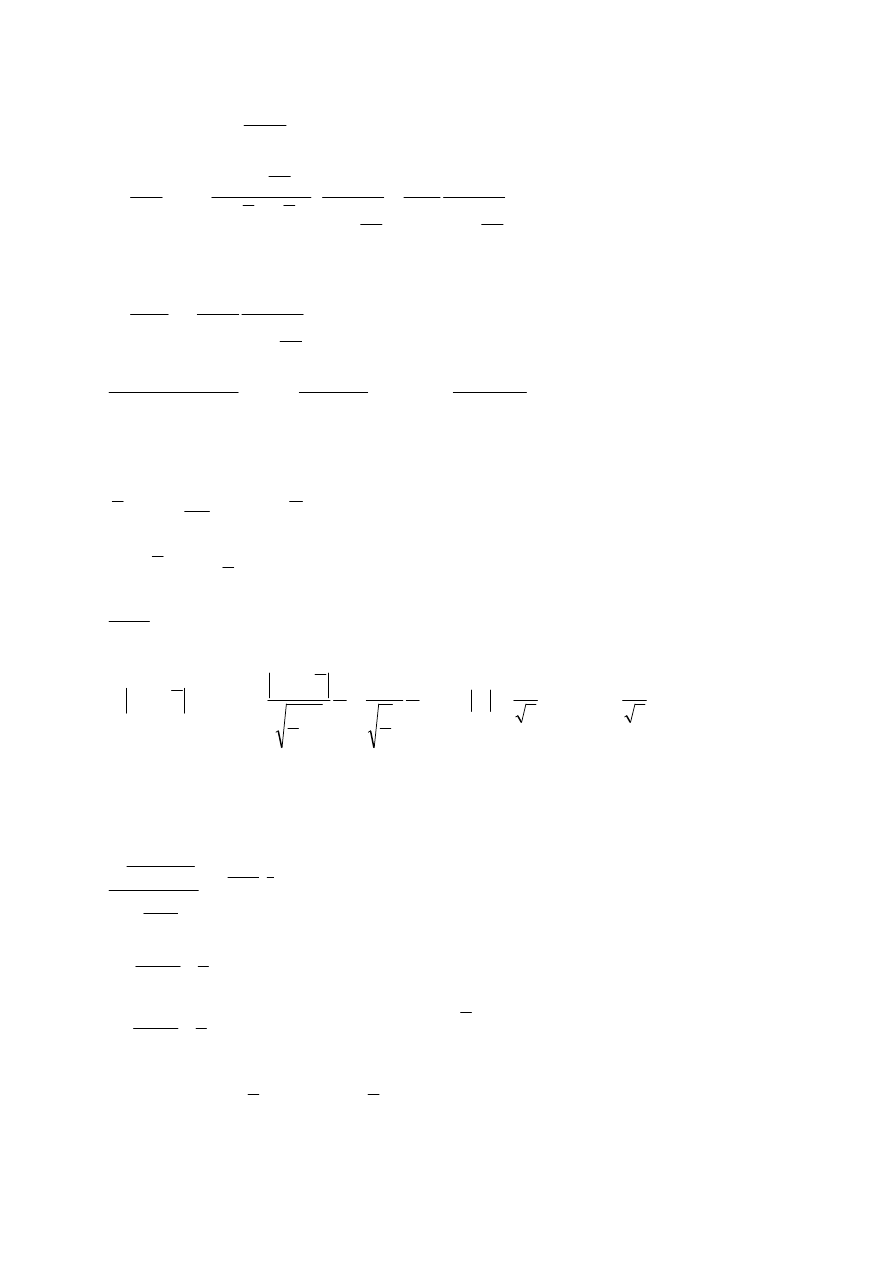
(
)
T
σ
a
k
T
σ
a
X
X
T
σ
a
E
SSB
E
k
χ
k
2
2
2
2
)
1
(
1
2
2
2
1
3
1
1
1
2
+
−
=
+
−
+
=
−
≅
∑
4
4 8
4
4 7
6
2
2
2
)
1
(
1
3
1
σ
T
K
T
σ
a
K
SSB
SSW
E
nzl
−
+
−
=
(
)
)
1
(
3
)
3
(
)
1
(
2
2
2
2
2
2
−
−
=
→
+
=
+
−
−
T
KT
K
const
σ
T
a
σ
const
σ
T
a
K
T
σ
T
K
Zadanie 6
5
2
2
X
nzl
X
nzl
4
,
S
σ
µ
N
X
≅
≅
−
2
5
4
5
;
0
σ
N
X
X
)
3
(
3
2
2
2
χ
σ
S
≅
⋅
(
)
}
558
,
3
182
,
3
5
2
95
,
0
5
2
4
5
4
5
)
3
(
)
3
(
2
5
5
≈
→
=
→
=
<
=
<
−
=
<
−
≅
≅
c
c
c
X
P
S
σ
σ
cS
S
σ
σ
X
X
P
cS
X
X
P
t
t
48
47
6
Zadanie 7
Budujemy test najmocniejszy bo wtedy β min przy ustalonym
α
(
)
8
9
2
2
2
5
,
0
2
2
−
−
−
−
∑
∑
∑
=
i
i
i
X
X
X
e
e
e
β
t
X
P
α
t
X
P
i
i
=
<
−
=
>
−
∑
∑
ln
8
9
2
ln
8
9
2
1
0
∑
∑
≅
≅
9
,
2
9
)
9
,
0
(
1
0
N
X
N
X
}
+
>
=
+
>
≅
∑
75
,
0
ln
3
2
4
9
ln
2
)
1
,
0
(
0
t
X
P
t
X
P
N
i

}
−
<
=
+
<
≅
∑
75
,
0
ln
3
2
4
9
ln
2
)
1
,
0
(
1
t
X
P
t
X
P
N
i
max
1
min
β
α
β
α
−
−
⇔
→
+
lnt=0
}
4533
,
0
75
,
0
1
)
1
,
0
(
≈
<
−
=
≅
N
X
P
ODP
Zadanie 8
3
2
1
3
2
1
25
)
1
(
4
3
4
3
4
1
)
1
(
4
1
X
X
X
X
X
X
θ
θ
θ
θ
L
−
−
−
−
−
=
)
1
,
2
(
:
)
2
,
1
(
:
)
1
,
1
(
:
3
2
1
X
X
X
3
2
3
2
2
1
25
25
25
)
1
(
4
3
X
X
X
X
X
X
θ
θ
L
+
−
−
−
−
−
=
(
)
(
)
(
)
θ
X
X
θ
X
X
X
X
L
ln
)
1
ln(
25
...
3
ln
25
ln
3
2
3
2
2
1
+
+
−
−
−
−
−
=
(
)
(
)
=
−
−
−
−
−
+
=
−
−
−
−
+
=
∂
∂
)
1
(
25
)
1
(
1
25
3
2
3
2
3
2
3
2
θ
θ
θ
X
X
θ
X
X
θ
X
X
θ
X
X
θ
25
ˆ
)
1
(
25
3
2
3
2
X
X
θ
θ
θ
θ
X
X
+
=
→
−
−
+
=
θˆ
=liczba (1,2) lub (2,1) w 25-próbce
prawdopodobieństwo sukcesu:
θ
θ
4
3
4
1
+
25
)
1
(
)
1
(
25
25
1
ˆ
var
2
θ
θ
θ
θ
θ
−
=
−
=
Zadanie 9
( ) ( )
)
(
)
(
y
f
N
f
N
y
f
y
N
f
=
(
)
)
(
1
N
α
wykl
e
N
x
Y
F
Nx
α
≅
−
=
<
−

( )
∑
∞
=
=
1
)
(
)
(
N
N
f
N
y
f
y
f
( )
Ny
α
Ne
α
N
y
f
−
=
( )
∑
∑
∞
=
∞
=
−
−
−
−
−
−
−
=
=
=
−
1
0
!
!
)
(
n
n
y
α
e
λ
λ
λ
e
λ
e
λ
n
y
α
λ
n
ny
α
e
λ
e
e
α
n
α
e
e
e
n
e
λ
e
n
λ
ne
α
y
f
y
α
y
α
y
α
(
)
∑
∑
∞
=
∞
=
−
−
−
−
−
−
=
=
=
=
1
1
2
!
1
!
n
n
n
ny
α
e
λ
y
α
e
λ
y
α
λ
λ
n
ny
α
n
λ
e
n
e
e
λ
e
e
λ
e
α
e
n
λ
ne
α
n
y
Y
N
E
y
α
y
α
( )
(
)
∑
∞
=
−
−
−
−
−
−
+
=
+
=
=
−
0
2
2
2
1
1
!
1
n
y
α
y
α
y
α
y
α
e
λ
n
y
α
e
λ
y
α
e
λ
e
λ
e
λ
e
λ
e
n
e
λ
n
e
e
λ
y
α
y
α
Zadanie 10
(
)
( ) ( )
p
C
P
C
P
p
C
C
P
=
=
=
∩
2
1
2
2
1
(
) (
)
rp
C
E
P
C
E
P
=
∩
=
∩
2
1
(
)
r
p
C
C
E
P
2
2
1
=
∩
∩
(
)
2
2
1
)
1
(
p
C
C
E
P
−
=
′
∩
′
∩
′
(
)
′
∪
∪
=
−
2
1
2
)
1
(
C
C
E
P
p
(
)
( ) ( ) (
) (
) (
) (
)
=
∩
∩
+
∩
−
∩
−
∩
−
+
+
=
∪
∪
2
1
2
1
2
1
2
1
2
1
)
(
C
C
E
P
C
C
P
C
E
P
C
E
P
C
P
C
P
E
P
C
C
E
P
→
−
+
+
−
−
=
−
→
+
−
−
+
=
r
p
p
rp
p
E
P
p
r
p
p
rp
p
E
P
2
2
2
2
2
2
2
)
(
1
)
1
(
2
2
)
(
r
p
rp
p
p
r
p
p
rp
p
E
P
2
2
2
2
2
2
1
2
2
1
)
(
−
=
−
+
−
−
+
+
−
=
→
(
)
p
p
rp
rp
r
p
rp
rp
E
P
E
C
P
ODP
−
=
−
=
−
=
∩
=
2
1
)
2
(
2
)
(
2
1
Wyszukiwarka
Podobne podstrony:
2003.05.17 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2008 03 17 prawdopodobie stwo i statystykaid 26449
2007 05 14 prawdopodobie stwo i statystykaid 25652
2007.05.14 prawdopodobie stwo i statystyka
2003.01.25 prawdopodobie stwo i statystyka
2005.05.16 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
2008.03.17 prawdopodobie stwo i statystyka
2003.10.11 prawdopodobie stwo i statystyka
2010.05.31 prawdopodobie stwo i statystyka
2003 01 25 prawdopodobie stwo i statystykaid 21695
1 1998.05.30 prawdopodobie stwo i statystyka
2003 10 11 prawdopodobie stwo i statystykaid 21705
2000 06 17 prawdopodobie stwo i statystykaid 21573
2005 01 17 prawdopodobie stwo i statystykaid 25338
2005 05 16 prawdopodobie stwo i statystykaid 25341
więcej podobnych podstron