Egzamin dla Aktuariuszy z 16 maja 2005 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
Założenie: że tworzą przedziały symetryczne czyli najlepsze (niedoprecyzowane zadanie
moim zdaniem)
28
,
1
8
,
0
/
1
.
1
=
→
=
<
−
a
a
n
m
X
P
28
,
1
8
,
0
/
2
.
2
=
→
=
<
−
b
b
n
m
Y
P
+
−
∈
n
X
n
X
m
28
,
1
;
28
,
1
.
1
⋅
+
⋅
−
∈
n
Y
n
Y
m
2
28
,
1
;
28
,
1
2
.
2
P(rozłączne)=
⋅
>
−
=
⋅
−
<
+
−
<
⋅
+
n
Y
X
P
n
Y
n
X
n
X
n
Y
P
28
,
1
3
28
,
1
2
28
,
1
lub
28
,
1
28
,
1
2
(
)
0
=
−
Y
X
E
(
)
n
n
n
n
n
n
Y
Y
n
X
X
Y
X
Y
X
n
n
3
2
1
2
1
1
2
4
1
...
;
...
cov
2
var
var
var
2
1
1
=
⋅
⋅
−
+
=
+
+
+
+
−
+
=
−
}
03
,
0
3
28
,
1
3
1
)
1
,
0
(
≈
⋅
<
−
=
≅
N
X
P
ODP
Zadanie 2
(
)
(
)
X
β
Y
β
X
X
y
X
X
β
i
i
i
1
0
2
1
ˆ
ˆ
,
ˆ
−
=
−
−
=
∑
∑
(
)
∑
=
+
=
−
=
20
10
10
,
2
2
X
X
X
i
dla
)
10
,...,
1
(
∈
i
1
0
)
10
(
β
β
EY
+
=
1
0
)
20
(
3β
β
EY
+
=
2
)
10
(
var
σ
Y
=
2
)
20
(
4
var
σ
Y
=
[
]
(
)
(
)
[
]
1
1
0
1
0
)
20
(
)
10
(
1
3
10
10
20
1
10
10
20
1
ˆ
β
β
β
β
β
EY
EY
β
E
=
+
+
+
−
=
+
−
=
[
]
[
]
8
4
10
10
400
1
var
10
var
10
400
1
ˆ
var
2
2
2
)
20
(
)
10
(
1
σ
σ
σ
Y
Y
β
=
⋅
+
=
+
=
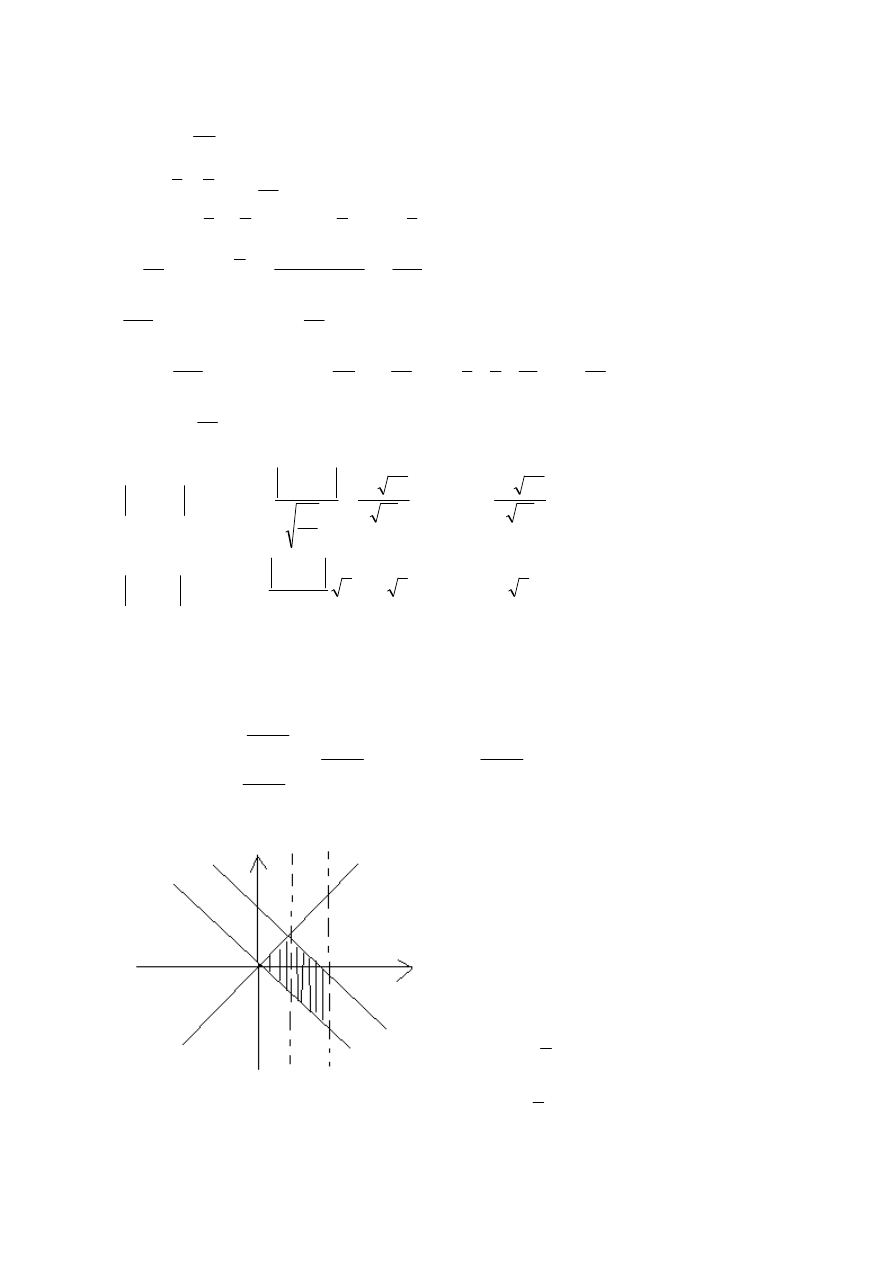
≅
8
;
ˆ
2
1
1
σ
β
N
β
(
)
(
)
(
)
0
1
1
0
1
0
1
0
2
3
10
10
20
1
ˆ
ˆ
β
β
β
β
β
β
β
E
X
Y
E
β
E
=
−
+
+
+
=
−
=
( )
( )
Y
β
X
β
X
Y
β
,
ˆ
cov
2
ˆ
var
var
ˆ
var
1
1
2
0
−
+
=
(
)
(
)
20
11
10
1
20
11
10
1
20
1
...
...
;
...
...
cov
400
1
20
...
;
20
1
cov
y
y
y
y
y
y
y
y
y
y
y
X
X
i
i
+
+
+
+
+
+
+
+
−
−
−
=
+
+
−
∑
[
]
2
2
2
40
3
4
10
10
400
1
σ
σ
σ
=
⋅
+
−
=
[
]
2
2
2
2
2
2
0
40
13
10
3
2
1
8
1
40
3
4
8
4
40
10
400
1
ˆ
var
σ
σ
σ
σ
σ
σ
β
=
−
+
=
⋅
−
+
+
=
≅
2
0
0
40
13
;
ˆ
σ
β
N
β
(
)
12
,
1
96
,
1
13
40
95
,
0
13
40
40
13
ˆ
ˆ
0
0
0
0
0
0
0
0
≈
→
=
→
=
<
−
=
<
−
z
z
z
σ
β
β
P
σ
z
β
β
P
(
)
69
,
0
96
,
1
8
95
,
0
8
8
ˆ
ˆ
1
1
1
1
1
1
1
1
≈
→
=
→
=
<
−
=
<
−
z
z
z
σ
β
β
P
σ
z
β
β
P
odpowiedź (D) jest najlepszym przybliżeniem
Zadanie 3
X
Y
V
Y
X
S
−
=
+
=
→
2
2
V
S
Y
V
S
X
+
=
−
=
V
S
V
S
>
>
−
,
0
2
S
V
V
S
−
>
→
>
+
0
2
S+V<1
V<1-S
)
1
,
(
,
1
,
2
1
lub
)
;
(
,
2
1
;
0
:
S
S
V
S
S
S
V
S
−
−
∈
∈
−
∈
∈
∆

∆
∈
=
−
)
,
(
2
1
2
1
2
1
2
1
2
1
v
s
)
(
2
3
2
1
2
6
)
,
(
v
s
v
s
v
s
f
−
=
−
=
∫
−
−
∈
=
+
+
−
=
−
=
−
=
s
s
s
s
s
s
s
s
s
s
v
sv
dv
v
s
s
f
2
2
2
2
2
2
2
1
;
0
3
4
3
2
3
4
3
2
3
4
3
2
3
)
(
2
3
)
(
∫
−
−
∈
−
=
−
=
s
s
s
s
dv
v
s
s
f
1
1
;
2
1
4
3
3
)
(
2
3
)
(
4
3
2
1
=
s
f
dla obu
−
∈
−
=
−
=
−
=
=
2
1
;
2
1
2
1
2
1
2
4
3
)
(
2
3
2
1
v
v
v
v
s
s
v
f
(
)
∫
−
−
−
=
−
=
−
=
=
5
,
0
5
,
0
5
,
0
5
,
0
3
2
2
6
1
3
2
2
2
2
1
x
x
x
x
S
V
E
∫
−
−
=
+
+
−
=
−
=
−
=
=
5
,
0
5
,
0
5
,
0
5
,
0
4
3
3
2
2
12
1
32
1
24
1
32
1
24
1
2
3
2
2
1
x
x
x
x
S
V
E
18
1
36
2
36
1
3
36
1
12
1
2
1
var
=
=
−
=
−
=
=
S
V
Zadanie 4
0
)
(
0
)
(
)
(
0
)
(
)
(
>
∩
>
∩
−
>
∩
−
C
B
P
C
B
P
B
P
B
C
P
C
P
(
)
→
∩
>
∩
−
∩
∩
−
∩
=
−
)
(
)
(
)
(
)
(
)
(
)
(
B
P
B
A
P
B
C
P
C
P
C
B
A
P
C
A
P
B
C
A
P
(
)
)
(
)
(
)
(
)
(
)
(
)
(
.
1
B
C
P
C
P
B
P
B
A
P
C
B
A
P
C
A
P
∩
−
∩
>
∩
∩
−
∩
→
Sprawdzamy (D)
(
)
=
∩
−
+
∩
−
∩
+
∩
>
∩
−
+
∩
∩
−
∩
+
∩
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
C
B
P
C
P
B
P
B
C
P
C
P
B
P
B
A
P
B
A
P
C
B
P
C
P
B
P
C
B
A
P
C
A
P
B
A
P
L
[
]
( )
B
A
P
B
P
B
A
P
B
C
P
C
P
B
P
B
C
P
C
P
B
P
B
P
B
A
P
=
∩
=
∩
−
+
∩
−
+
∩
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
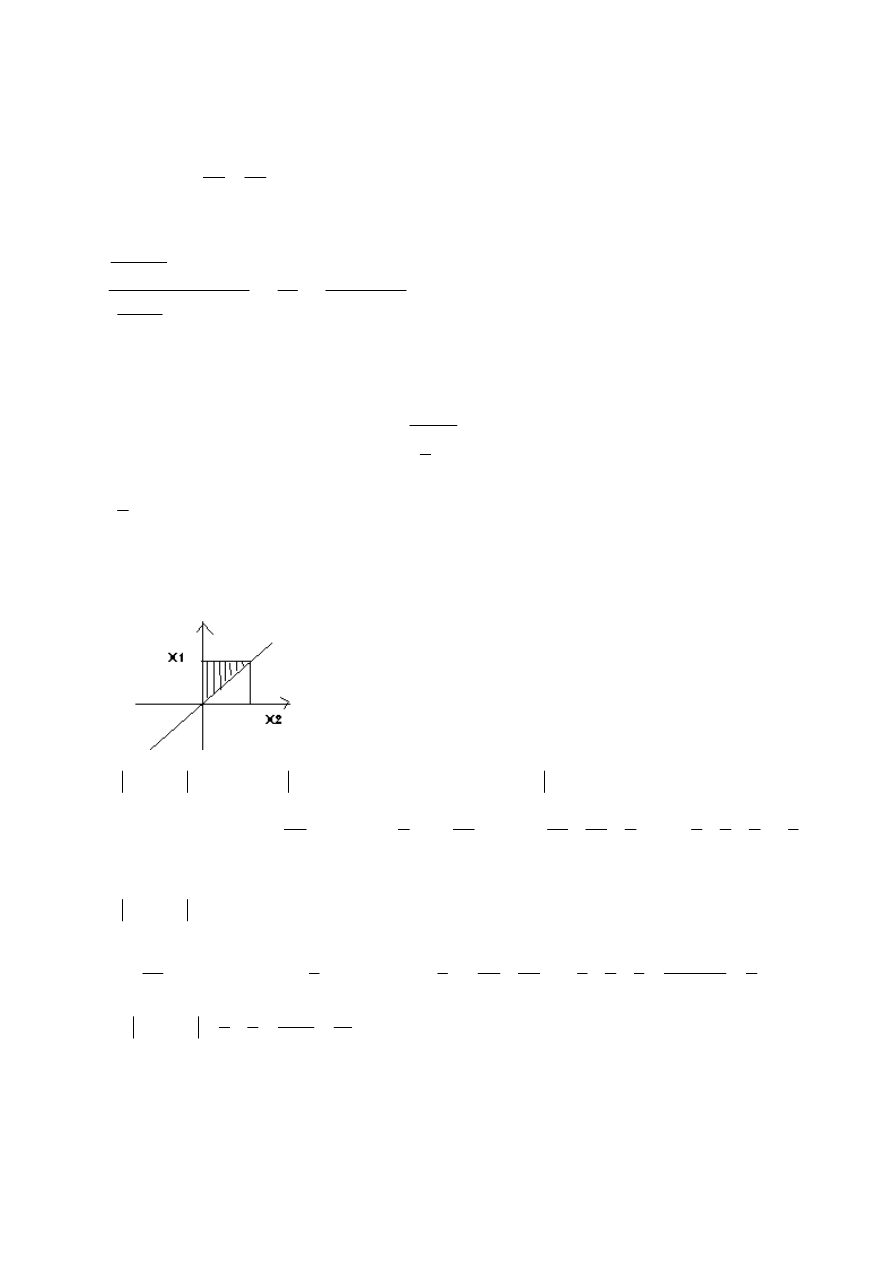
Zadanie 5
∫
=
=
<
t
θ
t
θ
x
t
X
P
0
2
2
2
2
)
(
1
2
θ
θ
>
(
)
( )
(
)
(
)
STAT
x
θ
χ
θ
χ
θ
θ
θ
χ
θ
X
θ
χ
θ
X
n
n
i
n
i
=
→
=
Π
∏
max
1
max
2
max
2
2
1
1
max
2
1
2
max
2
2
;
0
;
0
;
0
2
;
0
2
(
)
1
,
0
1
)
(max
1
2
0
max
0
=
−
=
<
−
=
>
n
t
t
P
t
x
P
9
,
0
2
=
n
t
9
,
0
2
3
9
,
0
1
)
(max
1
)
(max
2
1
1
≥
−
=
<
−
=
>
=
n
t
P
t
P
moc
9
4
9
≥
n
dla n=3 OK.
Zadanie 6
(
)
(
)
(
)
(
)
=
>
>
−
+
>
>
−
=
−
1
2
1
2
1
2
2
1
2
1
2
1
2
1
X
X
P
X
X
X
X
E
X
X
P
X
X
X
X
E
X
X
E
∫ ∫
∫
∫
=
+
−
=
+
−
=
+
−
−
=
−
=
−
=
1
0
1
1
0
1
0
1
0
2
3
2
2
1
2
3
1
2
1
2
1
6
1
2
2
2
6
2
2
2
1
2
2
2
)
(
2
x
x
x
x
x
x
x
x
xy
y
dydx
x
y
(
)
(
)
∫ ∫
∫ ∫
=
+
−
=
−
=
−
=
−
1
0
1
0
1
0
1
0
2
2
2
2
2
1
2
2
1
2
)
(
dxdy
y
xy
x
dxdy
y
x
X
X
E
X
X
E
∫
∫
=
+
−
=
+
−
=
+
−
=
+
−
=
+
−
=
1
0
1
0
1
0
3
2
2
1
0
2
2
3
6
1
6
2
3
2
3
1
2
1
3
1
3
2
3
1
3
1
3
y
y
y
dy
y
y
xy
y
x
x
18
1
18
2
3
9
1
6
1
var
2
1
=
−
=
−
=
−
X
X
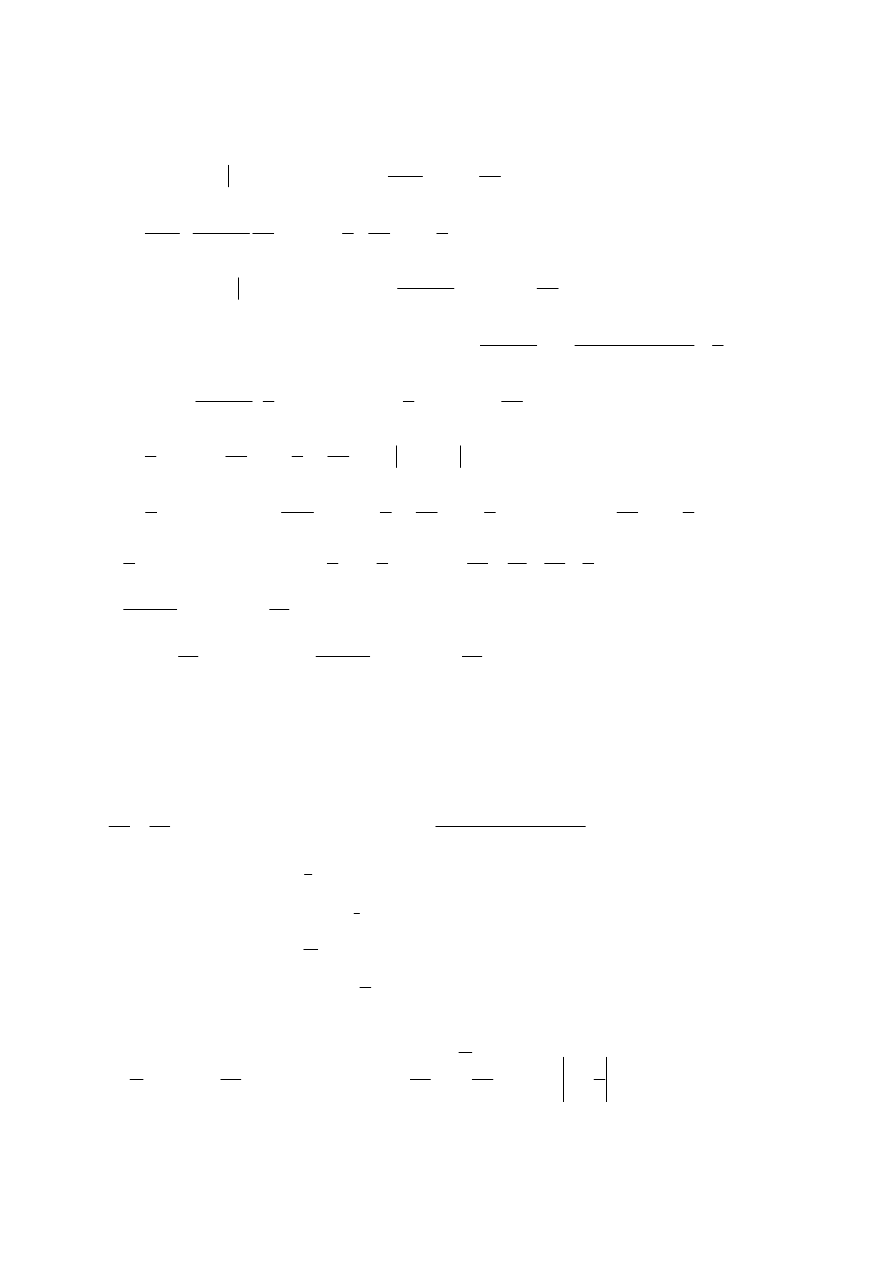
Zadanie 7
(
)
=
+
=
=
=
=
−
∞
=
∞
=
=
∑
∑
∑
2
1
1
1
!
2
3
1
1
)
(
e
k
i
k
k
N
P
k
N
Z
E
EZ
k
k
k
k
i
N
N
∑
∑
∞
=
∞
=
−
−
=
⋅
=
=
+
+
=
1
1
2
2
3
2
2
3
!
2
2
3
!
2
2
)
1
(
3
1
1
k
k
k
k
e
k
k
e
k
k
k
k
( )
(
)
(
)
∑
∑
∑
∞
=
∞
=
−
+
=
=
=
=
1
1
2
2
2
2
2
!
2
)
1
(
1
)
(
k
k
k
i
N
N
e
k
iX
E
k
k
N
P
k
N
Z
E
Z
E
(
)
(
)
(
)
∑
∑
∑
∑
=
+
+
+
+
=
+
+
=
+
=
k
i
i
i
i
k
k
k
k
k
k
k
i
iX
E
iX
i
X
E
1
2
2
2
2
2
2
)
1
(
4
9
6
)
1
2
)(
1
(
9
2
)
1
(
3
9
var
( )
∑
∞
=
−
=
+
+
+
+
+
=
1
2
2
2
2
2
!
2
)
1
(
4
9
)
1
2
)(
1
(
2
3
)
1
(
1
k
k
N
e
k
k
k
k
k
k
k
Z
E
(
)
∑
∞
=
−
−
=
=
+
=
+
+
=
1
2
2
2
2
1
!
2
4
9
!
2
2
2
3
k
k
k
n
k
e
k
k
e
k
k
k
[
]
(
)
∑
∑
∑
∞
=
∞
=
∞
=
−
−
−
−
=
+
+
+
−
=
+
−
+
−
=
2
1
2
2
2
2
2
2
1
2
)
4
2
(
4
9
!
2
1
3
2
4
3
!
2
4
9
!
2
1
)
1
(
2
2
3
n
k
n
n
k
n
e
n
n
n
e
k
k
e
n
n
n
[
]
(
)
=
−
+
=
+
−
=
⋅
+
−
+
⋅
−
+
=
−
−
−
2
2
2
4
3
2
27
4
21
2
27
7
4
3
6
4
9
1
2
3
)
4
2
(
2
4
3
e
e
e
2
2
75
,
0
4
75
75
,
0
4
54
21
−
−
−
=
−
+
=
e
e
2
2
2
2
75
,
0
75
,
9
75
,
0
4
39
75
,
0
4
36
75
9
75
,
0
4
75
var
−
−
−
−
−
=
−
=
−
−
=
−
−
=
e
e
e
e
Z
N
Zadanie 8
∏
∏
∏ ∏
−
−
−
−
=
=
1
2
1
20
10
1
2
10
10
1
10
2
2
θ
i
θ
i
θ
i
θ
i
y
x
θ
y
θ
X
θ
L
∑
∑
−
+
−
+
+
=
i
i
y
θ
x
θ
θ
L
ln
)
1
2
(
ln
)
1
(
ln
20
2
ln
10
ln
∑
∑
∑
∑
−
−
=
=
→
=
+
+
=
∂
∂
i
i
i
i
y
x
θ
T
y
x
θ
θ
ln
2
ln
20
ˆ
0
ln
2
ln
20
(
)
∫
−
≅
−
=
=
>
=
<
−
−
−
−
1
1
)
1
(
1
ln
θ
t
e
t
θ
θ
t
i
wykl
e
x
θ
e
X
P
t
x
θ
P
(
)
∫
−
≅
−
=
=
>
=
<
−
−
−
−
1
1
2
2
2
)
1
(
1
2
ln
2
θ
t
e
t
θ
θ
t
wykl
e
x
θ
e
y
P
t
y
θ
P
∑
∑
Γ
≅
−
−
)
1
;
20
(
ln
2
ln
i
i
y
θ
X
θ
∫
=
=
=
=
<
=
=
>
=
>
−
Γ
≅
a
x
X
t
x
e
x
a
X
P
a
X
P
a
θ
T
P
20
0
19
)
1
;
20
(
2
!
19
1
20
20
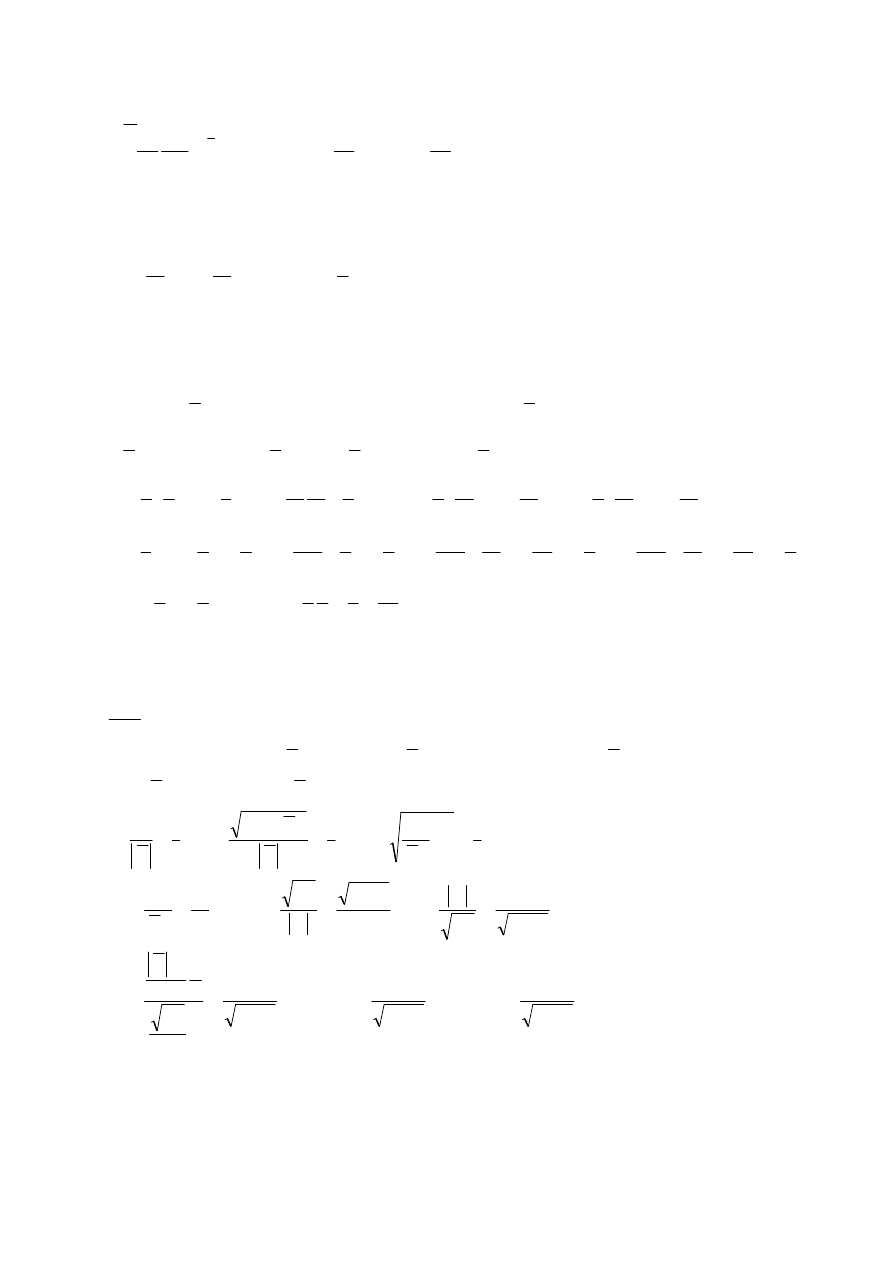
}
∫
≈
→
=
→
=
<
=
=
≅
−
a
χ
t
a
a
a
X
P
dt
e
t
40
0
)
40
(
2
20
19
772
,
0
805
,
51
40
9
,
0
40
2
!
19
1
2
Zadanie 9
p
p
p
p
p
p
−
=
=
=
=
3
2
,
,
15
4
,
15
1
4
3
2
1
(
)
(
)
=
−
+
−
−
=
−
+
+
4
3
2
4
3
4
3
2
2
1
,
cov
,
cov
N
N
N
N
N
n
N
N
N
N
N
(
)
(
)
(
)
(
)
=
+
−
−
+
−
−
=
4
4
3
4
2
4
3
3
3
2
var
,
cov
,
cov
,
cov
var
,
cov
N
N
N
N
N
N
N
N
N
N
(
)
(
)
=
−
−
−
=
3
2
3
4
2
4
,
cov
var
,
cov
var
N
N
N
N
N
N
(
)
[
]
(
)
[
]
=
−
−
+
−
−
−
−
+
−
=
3
2
3
2
3
4
2
4
2
4
var
var
var
2
1
var
var
var
var
2
1
var
N
N
N
N
N
N
N
N
N
N
(
)
(
)
=
+
−
+
−
−
+
=
3
2
4
2
3
2
4
var
2
1
var
2
1
var
2
1
var
var
2
3
N
N
N
N
N
N
N
=
−
+
−
+
−
−
−
−
+
+
−
=
p
p
p
p
p
p
p
p
n
15
11
15
4
2
1
15
1
15
14
2
1
)
1
(
2
1
15
11
15
4
3
1
3
2
2
3
=
+
−
+
−
+
+
−
−
+
−
+
−
−
+
=
2
2
2
2
2
1
30
11
15
2
225
22
2
1
30
1
15
7
225
7
2
1
2
1
225
44
2
3
2
1
3
1
p
p
p
p
p
p
p
p
p
p
p
n
75
45
5
3
2
3
5
2
0
5
2
3
2
=
=
=
→
=
+
−
=
p
p
n
Zadanie 10
)
9
(
9
2
2
2
9
χ
σ
S
≅
Z nie jest niezależne od X bo
∑
∑
+
=
=
−
2
2
2
2
2
2
9
9
,
9
X
S
X
nS
X
X
n
i
n
i
∑
→
≅
X
X
X
S
i
n
od
zl
2
=
<
+
=
<
+
=
<
t
X
S
P
t
X
X
S
P
t
X
Z
P
1
1
1
1
2
2
9
0
2
2
9
=
−
>
=
−
<
=
−
<
=
2
2
9
2
2
9
2
2
2
9
1
1
1
1
t
t
S
X
P
t
t
X
S
P
t
X
S
P
632
,
0
602
,
0
1
3
262
,
2
1
3
)
9
(
1
3
3
2
2
2
2
9
≈
≈
→
−
=
→
−
>
=
−
>
⋅
=
t
t
t
t
t
t
P
t
t
σ
σ
S
σ
σ
X
P
Wyszukiwarka
Podobne podstrony:
2005.05.16 prawdopodobie stwo i statystyka
2003.05.17 prawdopodobie stwo i statystyka
2003 05 17 prawdopodobie stwo i statystykaid 21698
2007 05 14 prawdopodobie stwo i statystykaid 25652
2007.05.14 prawdopodobie stwo i statystyka
1996.11.16 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
2010.05.31 prawdopodobie stwo i statystyka
1 1998.05.30 prawdopodobie stwo i statystyka
2005.10.10 prawdopodobie stwo i statystyka
2005 10 10 prawdopodobie stwo i statystykaid 25346
2005 01 17 prawdopodobie stwo i statystykaid 25338
1996 11 16 prawdopodobie stwo i statystykaid 18573
2010 05 31 prawdopodobie stwo i statystyka
więcej podobnych podstron