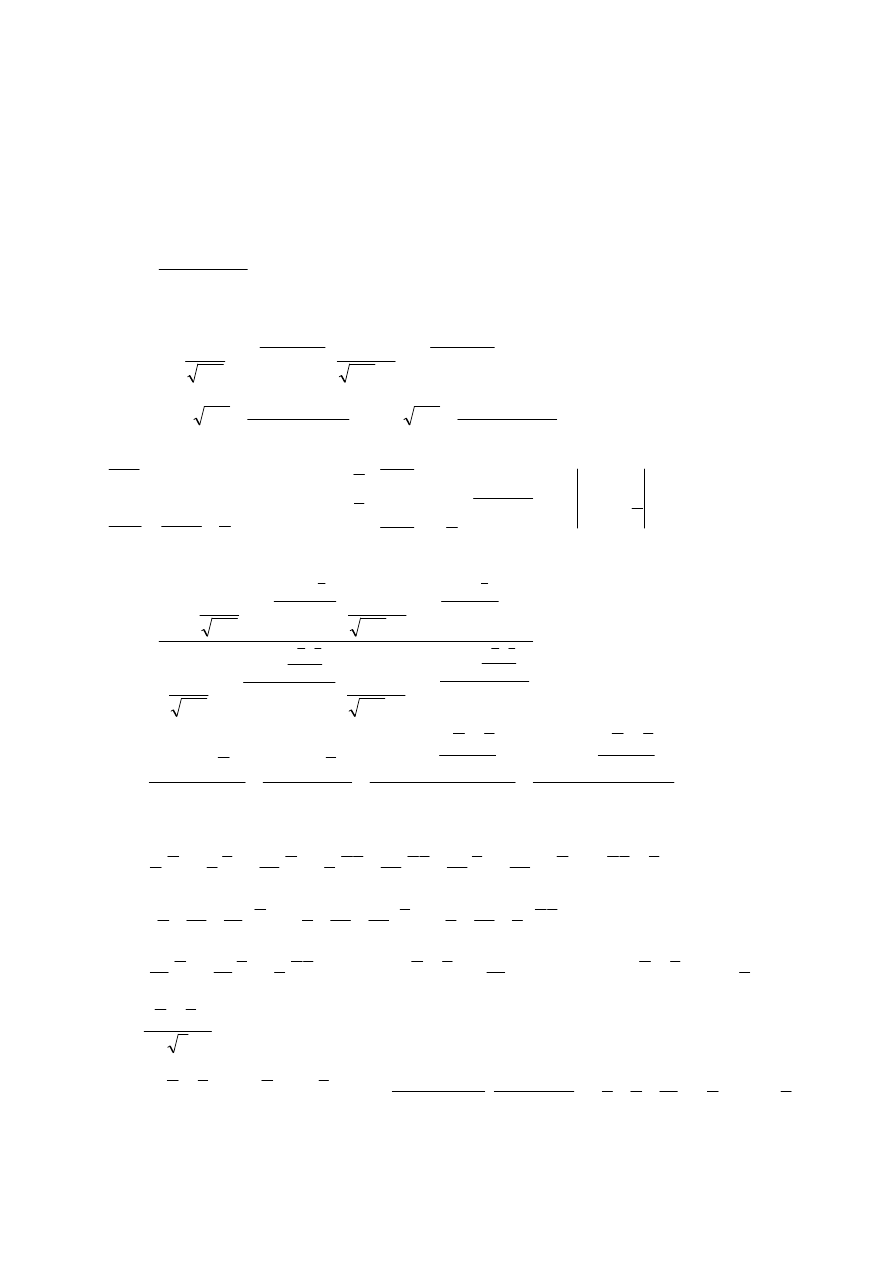
Egzamin dla Aktuariuszy z 10 października 2005 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
t
x
θ
L
x
θ
L
x
λ
m
m
m
m
m
m
>
=
≠
)
;
(
sup
)
;
(
sup
)
(
2
1
2
1
2
1
,
,
(
)
(
)
8
9
2
9
2
2
2
1
2
2
1
2
1
)
;
(
∑
∑
−
−
−
−
⋅
Π
Π
=
m
y
m
X
i
i
e
e
x
θ
L
(
)
(
)
8
2
2
ln
9
2
2
ln
9
ln
2
2
2
1
∑
∑
−
−
Π
−
−
−
Π
−
=
m
y
m
X
L
i
i
0
4
9
4
0
9
2
2
1
1
=
−
=
∂
∂
=
−
=
∂
∂
∑
∑
m
y
m
m
X
m
i
i
→
Y
m
X
m
=
=
2
1
4
9
9
2
2
2
2
1
2
−
=
∂
∂
−
=
∂
∂
m
m
0
2
1
2
=
∂
∂
∂
m
m
max
0
4
9
0
0
9
→
>
−
−
(
)
(
)
8
5
4
9
2
5
4
9
8
9
2
9
2
2
2
2
2
2
1
2
1
2
2
1
2
1
)
(
∑
∑
∑
∑
+
−
−
+
−
−
−
−
−
−
⋅
Π
Π
⋅
Π
Π
=
Y
X
y
Y
X
X
Y
y
X
X
i
i
i
i
e
e
e
e
x
λ
(
)
(
)
=
>
+
−
+
+
−
+
−
−
−
−
∑
∑
∑
∑
t
Y
X
y
Y
X
X
Y
y
X
X
P
i
i
i
i
ln
8
5
4
2
5
4
8
2
2
2
2
2
0
(
)
=
>
+
+
+
−
−
−
−
+
=
t
Y
Y
X
X
Y
Y
X
Y
X
X
Y
X
P
ln
8
16
40
9
20
9
20
36
5
9
5
36
8
9
2
9
2
2
2
2
2
2
0
=
>
−
+
−
+
−
+
+
−
=
t
Y
X
Y
X
P
ln
5
9
20
36
5
9
40
9
20
9
8
9
5
18
5
36
2
9
2
2
0
(
)
≅
−
>
−
=
>
−
+
=
9
5
;
0
ln
9
10
ln
5
9
10
9
10
9
2
2
2
0
N
Y
X
t
Y
X
P
t
Y
X
Y
X
P
841
,
3
ln
2
ln
2
5
3
)
(
2
0
=
→
>
−
t
t
Y
X
P
(
)
9
3
2
1
2
1
9
81
2
9
4
9
1
9
...
;
9
...
cov
2
var
var
var
:
9
1
9
1
=
⋅
⋅
⋅
−
+
=
+
+
+
+
−
+
=
−
Y
Y
X
X
Y
X
Y
X
II

(
)
01
,
0
2
841
,
3
3
10
)
1
(
ln
3
9
9
10
3
3
2
≈
>
=
>
−
χ
P
t
Y
X
P
moc:
≅
−
−
≅
≅
3
1
;
2
,
9
4
;
2
,
9
1
;
N
Y
X
m
N
Y
m
N
X
(
)
=
−
<
−
>
−
=
>
−
t
Y
X
t
Y
X
P
t
Y
X
P
ln
9
10
lub
ln
9
10
ln
9
10
2
(
)
(
)
=
−
−
<
−
−
−
>
−
−
=
3
2
ln
9
10
3
2
lub
3
2
ln
9
10
3
2
t
Y
X
t
Y
X
P
}
82
,
0
99
,
5
lub
93
,
0
)
1
,
0
(
≈
−
<
−
>
=
≅
X
X
P
N
Zadanie 2
(
)
(
)
=
−
−
−
=
∂
∂
=
−
−
−
=
∂
∂
∑
∑
0
var
2
0
var
2
1
0
1
1
0
0
i
i
i
i
i
i
i
x
β
β
y
ε
x
β
ε
x
β
β
y
β
=
−
−
=
−
−
∑
∑
∑
∑
∑
∑
0
var
var
var
0
var
var
1
var
2
1
0
1
0
i
i
i
i
i
i
i
i
i
i
i
i
ε
x
β
ε
x
β
ε
Y
x
ε
x
β
ε
β
ε
y
∑
∑
∑
−
=
i
i
i
i
i
ε
ε
x
β
ε
y
β
var
1
var
var
1
0
∑
∑
∑
∑
∑
∑
−
−
=
i
i
i
i
i
i
i
i
i
i
i
i
ε
x
ε
ε
x
β
ε
y
ε
x
ε
y
x
β
var
var
1
var
var
var
var
2
1
1
∑
∑
∑
∑
∑
∑
∑
−
−
=
2
2
1
var
var
var
1
var
var
var
var
1
i
i
i
i
i
i
i
i
i
i
i
i
i
ε
x
ε
x
ε
ε
y
ε
x
ε
y
x
ε
β
2
σ
się skraca, można założyć, że
i
ε
var
=1 lub 9
∑
∑
∑
=
=
=
+
=
+
=
5
1
5
1
2
2
2
2
2
9
50
9
5
5
9
1
1
var
1
i
i
i
σ
σ
σ
σ
σ
ε
∑
∑
∑
=
=
=
+
=
+
=
5
1
5
1
2
2
2
2
9
65
9
20
5
1
9
4
1
var
i
i
i
i
σ
σ
σ
σ
ε
x
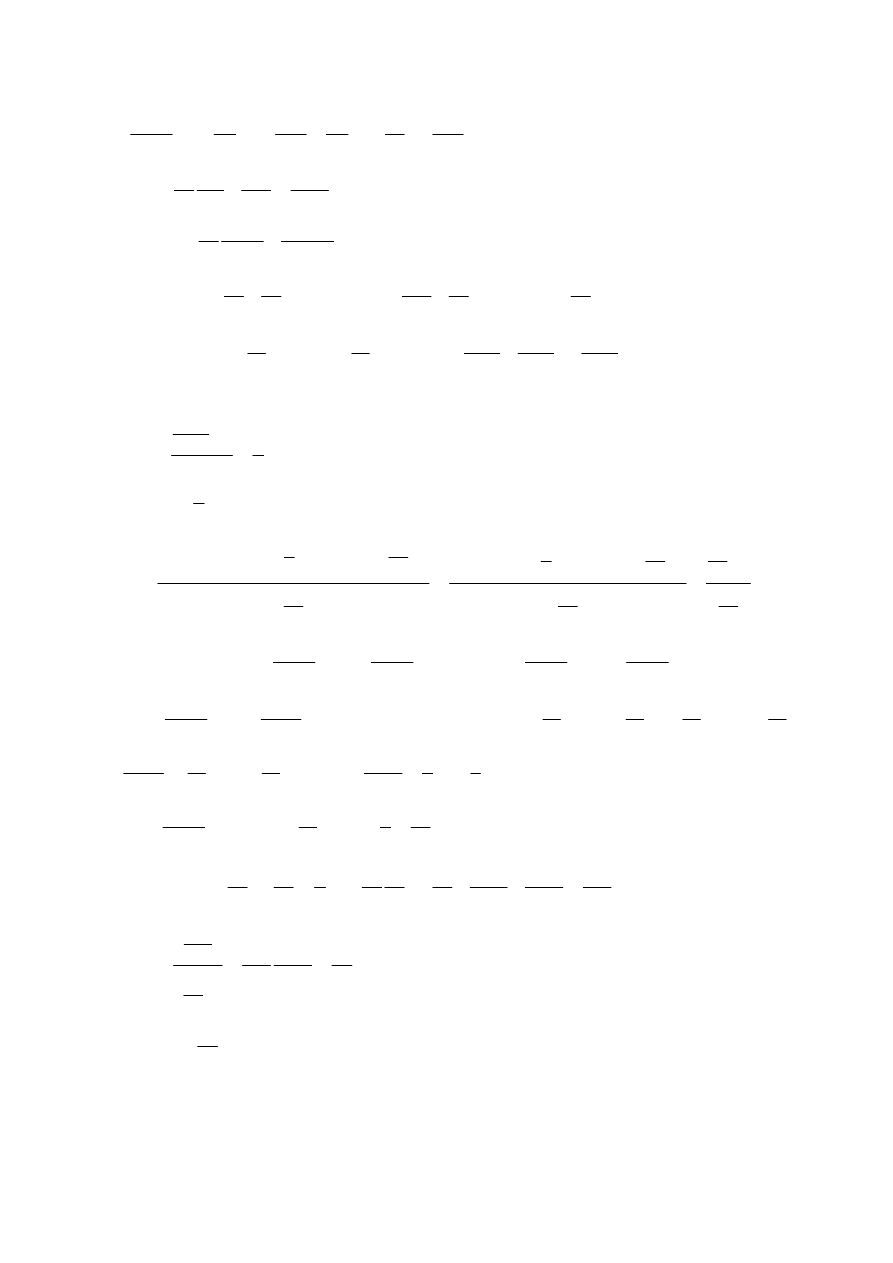
∑
∑
∑
=
=
=
+
=
+
=
5
1
5
1
2
2
2
2
2
9
125
9
80
5
1
9
16
1
var
i
i
i
i
σ
σ
σ
σ
ε
x
25
81
2025
81
65
9
125
9
50
2
=
=
−
=
MIAN
∑
−
=
i
i
i
i
y
ε
ε
x
LICZ
var
9
65
var
9
50
(
)
(
)
∑
∑
=
=
=
=
+
−
+
+
−
=
5
1
5
1
1
1
1
0
1
0
25
3
75
4
81
65
81
200
9
65
9
50
)
(
i
i
β
β
β
β
β
β
LICZ
E
∑
∑
=
=
=
+
=
+
−
=
5
1
5
1
2
2
2
2
2
2
9
1250
9
1125
81
1125
9
9
15
9
15
)
var(
i
i
σ
σ
σ
σ
LICZ
1
1
ˆ
β
β
E
=
2
2
1
9
2
625
9
1250
ˆ
var
σ
σ
β
=
=
≅
2
1
1
9
2
;
ˆ
σ
β
N
β
(
)
(
)
(
) (
)
0
0
1
1
0
1
0
5
1
5
1
1
1
0
1
0
0
9
50
9
50
9
50
9
65
4
9
5
5
9
50
9
65
4
9
1
ˆ
β
β
β
β
β
β
β
β
β
β
β
β
β
E
i
i
=
=
−
+
+
+
=
−
+
+
+
=
∑
∑
=
=
∑
∑
∑
∑
−
+
=
1
1
2
;
var
cov
var
2
var
var
var
var
)
(
var
0
β
ε
y
ε
x
β
ε
x
ε
y
LICZ
i
i
i
i
i
i
i
i
β
=
+
+
+
−
−
−
+
+
+
+
+
=
∑
10
6
5
1
10
6
5
1
2
1
9
15
...
9
15
9
15
...
9
15
;
...
...
cov
25
1
;
var
cov
y
y
y
y
y
y
y
y
σ
β
ε
y
i
i
3
8
3
9
8
25
9
75
8
9
5
9
15
5
9
15
25
1
2
2
2
=
⋅
=
⋅
⋅
=
⋅
⋅
+
⋅
−
=
σ
σ
σ
∑ ∑
∑
=
=
=
+
=
⋅
+
=
5
1
5
1
9
50
9
5
5
9
81
1
1
var
var
i
i
i
i
ε
y
27
800
81
6500
81
8450
9
50
9
50
9
65
2
9
2
9
65
9
50
)
(
var
2
0
=
−
+
=
⋅
−
+
=
LICZ
β
25
24
2500
81
27
800
9
50
27
800
ˆ
var
2
0
=
=
=
β
≅
2
0
0
25
24
;
ˆ
σ
β
N
β

(
)
=
→
=
→
<
−
=
<
−
0
0
0
0
0
0
0
0
24
5
96
,
1
24
5
24
5
ˆ
ˆ
z
z
z
σ
β
β
P
σ
z
β
β
P
(
)
=
→
=
→
<
=
<
−
1
1
1
1
1
1
2
3
96
,
1
2
3
ˆ
z
z
z
X
P
σ
z
β
β
P
Z tego wychodzi najbliżej odpowiedź C
Zadanie 3
∫
≅
≅
→
=
=
2
1
4
4
4
)
2
,
1
(
,
3
nzl
,
3
3
)
(
J
Y
x
X
Y
X
x
dy
x
x
f
(
) (
)
≥
∈
−
=
<
=
<
2
1
)
2
;
1
(
1
x
t
x
t
x
t
X
t
XY
P
X
t
S
P
( )
x
s
x
x
X
S
f
2
1
<
<
=
(
) (
)
∈
=
=
=
=
=
=
∫
wpp
0
]
3
;
5
,
1
[
5
108
3
3
1
)
3
(
)
(
3
3
5
3
2
3
5
4
x
x
x
x
x
S
f
x
f
x
S
f
S
x
g
Zadanie 4
i
i
A
S
X
=
>
2
- rozłączne
Z tego:
(
)
)
(
10
...
10
2
...
10
10
2
1
10
1
1
Y
X
P
X
X
X
P
X
X
X
P
ODP
>
=
+
+
>
=
+
+
>
=
gdzie
)
;
9
(
),
(
λ
Y
λ
wykl
X
Γ
≅
≅
∫ ∫
∫
∞ ∞
∞
−
−
−
−
=
=
=
0
0
8
10
8
9
1
!
8
10
!
8
10
y
y
λ
y
λ
y
λ
x
λ
dy
e
λ
e
y
λ
dxdy
e
y
λ
e
λ
ODP
256
5
512
10
2
10
)
2
(
!
8
!
8
10
2
9
!
8
10
9
9
9
0
2
8
9
=
=
=
=
=
=
=
=
∫
∞
−
λ
λ
λ
β
α
e
y
λ
y
λ
Zadanie 5
(
)
∑
−
Π
=
4
3
)
4
(
i
X
θ
i
n
e
X
θ
L
∑
∑
−
+
=
4
ln
3
)
4
ln(
ln
i
i
X
θ
X
θ
n
L

∑
∑
=
→
=
−
=
∂
∂
4
4
0
i
i
X
n
θ
X
θ
n
θ
n
X
n
T
e
θ
g
i
=
=
∑
−
4
)
(
4
2
3
2
8
)
(
x
e
x
x
f
−
=
(
)
∫
∫
≅
=
=
=
=
=
<
=
<
−
−
t
w
t
x
wykl
e
dw
dx
x
w
x
e
x
t
X
P
t
X
P
0
2
3
4
0
2
3
4
1
4
)
2
(
2
4
8
4
1
4
)
2
(
2
1
2
wykl
X
n
n
X
i
i
≅
Φ
→
−
∑
Sprawdzamy (B)
=
+
−
<
+
>
=
−
<
−
>
−
−
−
1
2
1
lub
1
2
1
2
lub
2
2
2
2
2
2
2
n
e
T
n
e
T
P
n
e
e
T
e
n
e
T
P
n
n
n
n
=
−
+
−
<
−
+
+
−
>
−
=
∑
∑
n
X
n
n
X
n
P
i
i
2
1
2
lub
1
2
ln
2
=
−
−
>
+
−
<
=
∑
∑
n
X
n
n
X
n
P
i
i
2
1
ln
2
lub
2
1
ln
2
=
−
−
<
+
−
>
=
∑
∑
n
n
X
n
n
X
P
i
i
2
1
ln
2
lub
2
1
ln
2
CTG
B
i
A
i
n
n
n
n
n
n
n
n
X
n
n
n
n
n
n
X
P
→
−
−
−
<
−
−
+
−
>
−
=
∑
∑
4
4
4
4
3
4
4
4
4
2
1
4
4
4
4
3
4
4
4
4
2
1
2
2
2
1
ln
2
2
1
2
lub
2
2
2
1
ln
2
2
1
2
(
) (
)
n
n
CTG
B
A
lim
lim
1
Φ
+
Φ
−
→
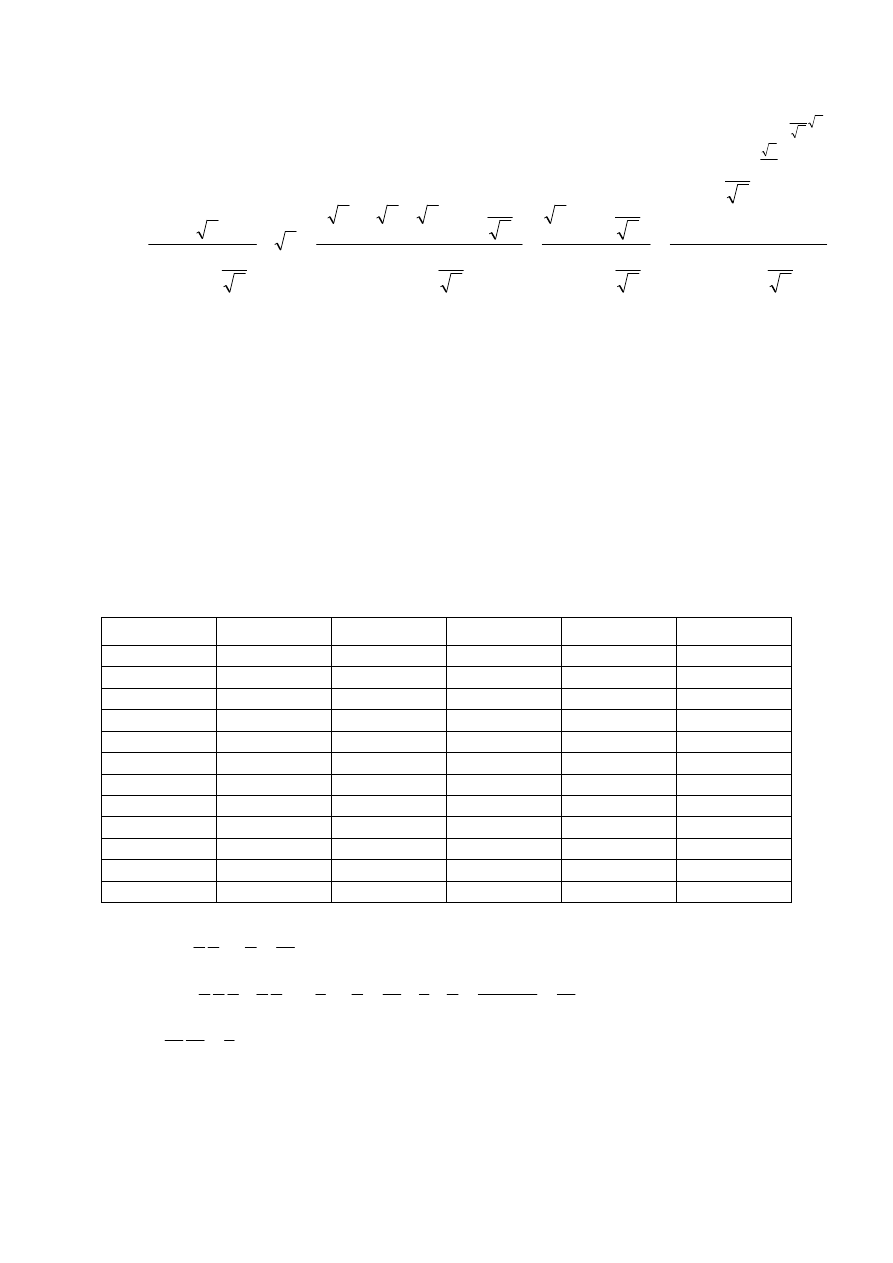
1
2
1
ln
2
2
1
ln
2
1
ln
2
2
1
ln
2
1
ln
2
2
1
ln
2
2
2
1
ln
2
2
0
2
2
→
+
−
+
=
+
−
+
=
+
−
+
+
−
=
−
+
−
=
→
→
43
42
1
48
47
6
n
n
n
n
n
n
n
n
n
n
n
n
n
A
n
n
e
n
n
1
−
→
n
B
analogicznie
32
,
0
)
1
(
2
2
)
1
(
1
)
1
(
1
)
1
(
)
1
(
1
≈
Φ
−
=
Φ
−
+
Φ
−
=
−
Φ
+
Φ
−
=
ODP
Zadanie 6
Teoria – odpowiedź (E) jest prawidłowa
Zadanie 7
Można wypisać wszystkie możliwości
+ oznacza, że istnieje prawdopodobieństwo
LICZ i MIAN to odpowiednio prawdopodobieństwo licznika i mianownika w
prawdopodobieństwie warunkowym
0
X
1
X
2
X
3
X
LICZ
MIAN
1
2
2
1
1
2
3
1
+
1
3
2
1
1
3
3
1
2
2
2
1
2
2
3
1
2
3
2
1
+
+
2
3
3
1
3
2
2
1
3
2
3
1
+
3
3
2
1
3
3
3
1
12
1
4
1
1
4
3
9
4
)
(
=
⋅
⋅
=
LICZ
P
12
8
12
3
4
1
4
1
3
1
12
1
4
3
1
3
1
1
4
3
9
4
4
3
2
1
9
2
)
(
=
+
+
=
+
+
=
⋅
⋅
+
⋅
+
=
MIAN
P
8
1
8
12
12
1
=
=
ODP
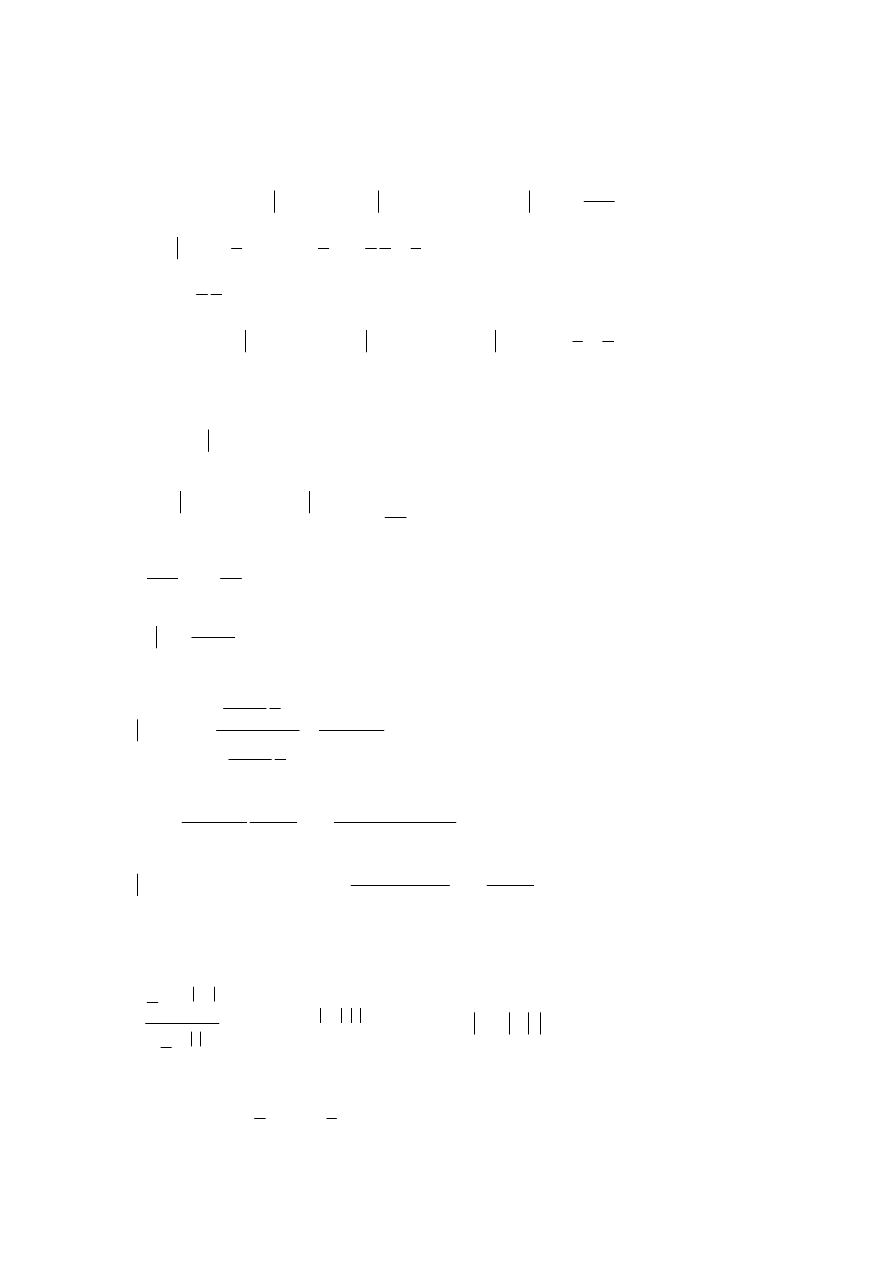
Zadanie 8
)
8
,
5
(
X
- ilość orłów w rzutach 5,6,7,8
(
)
(
)
(
)
3
3
12
12
4
12
12
4
12
)
12
,
9
(
)
8
,
5
(
4
X
X
X
E
X
X
X
E
X
X
X
X
E
=
→
=
=
+
+
(
)
3
1
2
1
2
1
12
9
1
var
9
1
var
12
12
4
=
⋅
⋅
=
=
X
X
X
E
1
2
1
2
1
4
var
4
=
⋅
=
X
(
)
(
)
(
)
3
2
3
1
1
var
var
var
var
12
4
12
4
12
4
4
=
−
=
→
+
=
X
X
E
X
X
E
X
X
E
X
Zadanie 9
Szukamy
(
)
1
min
=
θ
E
(
)
(
)
>
−
<
=
>
−
=
<
θ
t
t
θ
θ
t
θ
t
P
θ
t
P
n
1
0
min
1
min
2
2
bo:
∫
<
=
−
=
t
θ
t
θ
x
F
t
θ
x
θ
0
2
2
3
2
)
(
1
2
(
)
θ
t
t
n
θ
θ
f
n
n
>
−
=
−
1
2
min
2
1
2
dla
1
<
θ
(
)
:
bo
)
1
,
0
(
)
2
2
(
)
2
2
)(
1
2
(
2
)
1
2
(
2
2
1
1
2
2
1
1
2
1
min
1
2
1
2
1
0
2
2
∈
+
=
+
−
−
=
−
−
=
=
+
+
∫
θ
θ
n
n
n
n
θ
θ
n
θ
θ
n
θ
θ
f
n
n
n
n
)
2
2
)(
1
2
(
2
1
2
2
)
1
2
(
2
1
1
0
2
2
+
−
=
+
−
=
+
n
n
n
θ
n
MIAN
n
(
)
∫
+
+
=
+
+
=
+
=
=
+
+
1
0
1
0
3
2
2
2
3
2
2
2
3
2
)
2
2
(
)
2
2
(
1
min
n
n
n
n
θ
θ
n
θ
E
n
n
Zadanie 10
(
)
(
)
t
x
x
P
t
e
P
t
e
e
P
x
x
x
x
H
2
ln
1
5
,
0
2
2
1
4
1
1
5
,
0
1
5
,
0
0
>
+
+
−
=
>
=
>
+
+
−
−
+
−
)
2
ln(
2
1
)
2
ln(
)
1
(
5
,
0
1
.
1
t
x
t
x
x
x
−
<
→
>
−
−
−
−
−
<
3
1
)
2
ln(
3
2
)
0
;
1
(
.
2
−
−
<
−
∈
t
x
x

)
2
ln(
2
1
0
.
3
t
x
x
+
>
>
nie wiadomo jakie t ale jeżeli K:x>3....
na pewno
2
3
)
2
ln(
2
1
e
t
x
=
→
=
+
>
1
1
ln
2
1
.
1
−
<
−
=
−
<
x
e
x
też wchodzi do K
1
3
1
ln
3
2
)
0
;
1
(
.
2
−
<
−
−
<
−
∈
x
e
x
x
odpada
Z tego a=-1
∫
∫
∞
−
∞
−
−
−
−
≈
+
=
+
=
−
<
+
>
=
3
1
1
3
0
0
209
,
0
2
1
2
1
2
1
2
1
)
1
(
)
3
(
e
e
e
e
X
P
X
P
α
x
x
Wyszukiwarka
Podobne podstrony:
2005.10.10 prawdopodobie stwo i statystyka
2005.12.05 prawdopodobie stwo i statystyka
2005.05.16 prawdopodobie stwo i statystyka
2005.01.17 prawdopodobie stwo i statystyka
2005 01 17 prawdopodobie stwo i statystykaid 25338
2005 05 16 prawdopodobie stwo i statystykaid 25341
2005 12 05 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2002 10 12 prawdopodobie stwo i statystykaid 21648
1996 10 26 prawdopodobie stwo i statystykaid 18572
2010.10.04 prawdopodobie stwo i statystyka
2001.10.13 prawdopodobie stwo i statystyka
2008.10.06 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2006.10.09 prawdopodobie stwo i statystyka
więcej podobnych podstron