
Matematyka Dyskretna
Andrzej Szepietowski
25 marca 2004 roku


Rozdział 1
Rachunek prawdopodobie ´nstwa
1.1
Przestrze ´n zdarze ´n elementarnych
Podstawowym poj˛eciem rachunku prawdopodobie ´nstwa jest przestrze´n zdarze´n elemen-
tarnych, któr ˛
a najcz˛e´sciej b˛edziemy oznacza´c przez
Ω. W tej ksi ˛
a˙zce ograniczymy si˛e
do przypadków, gdy
Ω jest zbiorem sko ´nczonym. Dzi˛eki temu nasze rozwa˙zania b˛ed ˛
a
prostsze.
Elementy przestrzeni
Ω nazywamy zdarzeniami elementarnymi.
Przykład 1.1 Przypu´s´cmy, ˙ze rzucamy monet ˛
a. Przestrze´n zdarze´n elementarnych mo˙ze
by´c wtedy okre´slona jako
Ω =
{O, R}, gdzie O oznacza wypadni˛ecie orła, a R reszki.
Przykład 1.2 W przypadku dwukrotnego rzutu monet ˛
a przestrze´n zdarze´n elementarnych
mo˙ze by´c okre´slona jako
Ω =
{OO, OR, RO, RR}, gdzie OO oznacza, ˙ze dwa razy
wypadł orzeł;
OR, ˙ze za pierwszym razem wypadł orzeł, a za drugiem reszka; RO, ˙ze za
pierwszym razem reszka, a za drugim orzeł; a
RR, ˙ze dwa razy wypadła reszka.
Przykład 1.3 Przypu´s´cmy, ˙ze mamy urn˛e z pi˛ecioma ponumerowanymi kulami, i ˙ze kule
o numerach
2 i 4 s ˛
a białe, a kule o numerach
1, 3 i 5 s ˛
a czarne. Przestrze´n zdarze´n
elementarnych mo˙ze by´c zdefiniowana jako
Ω =
{1, 2, 3, 4, 5}.
Przykład 1.4 Przypu´s´cmy, ˙ze mamy urn˛e jak w poprzednim punkcie i ˙ze losujemy dwie
kule z tej urny. Przestrzeni ˛
a zdarze´n elementarnych mo˙ze tu by´c zbiór dwuelementowych
podzbiorów zbioru kul
Ω =
{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}}.
1.1.1
Zdarzenia
Dowolny podzbior
A przestrzeni zdarze ´n elementarnych Ω nazywamy zdarzeniem. Pa-
mi˛etajmy, ˙ze rozwa˙zamy tylko sko ´nczone przestrzenie zdarze ´n elementranych. W przy-
padku, gdy
Ω jest zbiorem niesko ´nczonym, konieczna jest inna definicja zdarzenia. Tak
3

4
Rozdział 1. Rachunek prawdopodobie ´nstwa
wi˛ec zdarzenia s ˛
a elementami zbioru
2
Ω
wszystkich podzbiorów zbioru
Ω, jest ich 2
|Ω|
.
Cały zbiór
Ω nazywamy zdarzeniem pewnym, a zbiór pusty
∅ zdarzeniem niemo˙zliwym.
Zdarzenia rozł ˛
aczne,
A
∩ B = ∅, nazywamy wykluczaj ˛
acymi si˛e. Zdarzenie
A
0
= Ω
− A
nazywamy zdarzeniem przeciwnym do zdarzenia
A.
Przykład 1.5 W przykładzie 1.2, z dwukrotnym rzutem monet ˛
a,
Ω =
{OO, OR, RO, RR},
mamy
16 = 2
4
zdarze´n. Zbiór
{OO, OR} jest zdarzeniem polegaj ˛acym na tym, ˙ze za
pierwszym razem wypadł orzeł. Zbiór
{OO, OR, RO}, ˙ze orzeł wypadł przynajmniej je-
den raz.
Przykład 1.6 W przykładzie 1.3, z kulami, zbiór
{2, 4} oznacza zdarzenie, ˙ze wylosowa-
no kul˛e biał ˛
a, a zbiór
{1, 2, 3}, ˙ze wylosowano kul˛e o numerze mniejszym od 4.
Przykład 1.7 W przykładzie 1.4, z losowaniem dwóch kul, zbiór
{{2, 4}} oznacza zda-
rzenie, ˙ze wylosowano dwie kule białe, a zbiór
{{1, 3}, {3, 5}, {3, 5}}, ˙ze wylosowano
dwie kule czarne.
1.1.2
Dalsze przykłady przestrzeni zdarze ´n elementarnych
Podamy teraz inne przykłady przestrzeni zdarze ´n elementarnych.
Przykład 1.8 Zbiór wszystkich czteroelementowych ci ˛
agów z warto´sciami
O lub R jako
przestrze´n dla czterokrotnego rzutu monet ˛
a. Zdarzenie, ˙ze za pierwszym i trzecim razem
wypadł orły to
{OOOO, OOOR, OROO, OROR}, a zdarzenie, ˙ze za pierwszym i trze-
cim razem wypadło to samo to
{OOOO, OOOR, OROO, OROR, RORO, RORR, RRRO, RRRR}.
Przykład 1.9 Zbiór wszystkich
n elementowych ci ˛
agów z warto´sciami
O lub R jako prze-
strze´n dla
n krotnego rzutu monet ˛
a. Podobnie jak w poprzednim przykładzie mo˙zemy roz-
patrywa´c zdarzenie, ˙ze za pierwszym i trzecim razem wypadł orzeł lub zdarzenie, ˙ze za
pierwszym i trzecim razem wypadło to samo.
Przykład 1.10 Niech
G = (V, E) b˛edzie wybranym ustalonym grafem z
|V | = n wierz-
chołkami i
|E| = m kraw˛edziami. Jako przestrze´n zdarze´n elementarnych we´zmy zbiór
wszystkich kolorowa´n dwoma kolorami wierzchołków grafu
G. Przestrze´n zdarze´n ele-
mentarnych jest zbiorem wszystkich funkcji ze zbioru wierzchołków
V w zbiór
{1, 2}, czy-
li
Ω =
{1, 2}
V
. Przykładem zdarzenia jest zbiór kolorowa´n, w których ko´nce wybranej z
góry kraw˛edzi
e =
{u, v} ∈ E maj ˛
a ró˙zne kolory
{f ∈ Ω | f(u) 6= f(v)}.
Przykład 1.11 Zbiór wszystkich funkcji ze zbioru
A w zbiór B, czyli Ω = B
A
. Przykła-
dem zdarzenia jest zbiór funkcji, które maj ˛
a tak ˛
a sam ˛
a warto´s´c dla dwóch z góry wybra-
nych punktów
a, b
∈ A, czyli {f ∈ Ω | f(a) = f(b)}.
Przykład 1.12 Mamy ustalony zbiór
V . Przestrze´n zdarze´n elementarnych to wszystkie
grafy ze zbiorem wierzchołków
V . Zdarzeniem jest zbiór grafów, w których dwa z góry
wybrane wierzchołki s ˛
a poł ˛
aczone kraw˛edzi ˛
a.

1.2. Prawdopodobie ´nstwo
5
Przykład 1.13 Zbiór liter lub słów wyst˛epuj ˛
acych w jakim´s tek´scie, ksi ˛
a˙zce lub li´scie.
Przykład 1.14 Grupa studencka. Zdarzeniem jest zbiór studentów, którzy otrzymali oce-
n ˛
a bardzo dobr ˛
a z egzaminu.
Przykład 1.15 Wyborcy. Zdarzeniem s ˛
a wyborcy, którzy nie brali udziału w ostatnich
wyborach.
1.2
Prawdopodobie ´nstwo
Definicja 1.16 Prawdopodobie´nstwo, lub rozkład prawdopodobie´nstwa, jest funkcj ˛
a
P : 2
Ω
→ R
okre´slon ˛
a na zbiorze zdarze´n (w naszym przypadku na zbiorze wszystkich podzbiorów
Ω).
Ka˙zdemu zdarzeniu
A
⊆ Ω przypisujemy liczb˛e rzeczywist ˛
a
P (A), jego prawdopodo-
bie´nstwo. Funkcja ta musi spełnia´c warunki:
Aksjomaty prawdopodobie ´nstwa
A1) Dla ka˙zdego
A
⊆ Ω, P (A) ≥ 0,
A2)
P (Ω) = 1,
A3) je˙zeli zdarzenia
A i B s ˛
a rozł ˛
aczne, to
P (A
∪ B) = P (A) + P (B).
Zbiór zdarze ´n elementarnych
Ω wraz z okre´slonym na nim prawdopodobie ´nstwem b˛e-
dziemy nazywa´c przestrzeni ˛
a probabilistyczn ˛
a. W przypadku, gdy przestrze ´n zdarze´n
elementarnych jest zbiorem sko ´nczonym, wystarczy okre´sli´c prawdopodobie ´nstwa dla
zdarze´n elementarnych. Musz ˛
a by´c tylko spełnione dwa warunki:
A4)
P (ω)
≥ 0, dla ka˙zdego ω ∈ Ω,
A5)
P
ω∈Ω
P (ω) = 1,
Prawdopodobie ´nstwo dowolnego zdarzenia
A jest wtedy równe
P (A) =
X
ω∈A
P (ω).
Łatwo mo˙zna sprawdzi´c, ˙ze tak zdefiniowane prawdopodobie ´nstwo spełnia aksjomaty
definicji 1.16.
Przykład 1.17 Dla dwukrotnego rzutu monet ˛
a (przykład 1.2) mo˙zemy okre´sli´c takie samo
prawdopodobie´nstwo dla wszystkich zdarze´n elementarnych
P (OO) = 0.25,
P (OR) = 0.25,
P (RO) = 0.25,
P (RR) = 0.25.
Ale oczywi´scie funkcja prawdopodobie´nstwa mo˙ze by´c dowoln ˛
a funkcj ˛
a spełniaj ˛
ac ˛
a wa-
runki A4 i A5. Na przykład
P (OO) = 0.27,
P (OR) = 0.24,
P (RO) = 0, 25,
P (RR) = 0, 24
lub
P (OO) = 0.5,
P (OR) = 0.3,
P (RO) = 0.2,
P (RR) = 0.
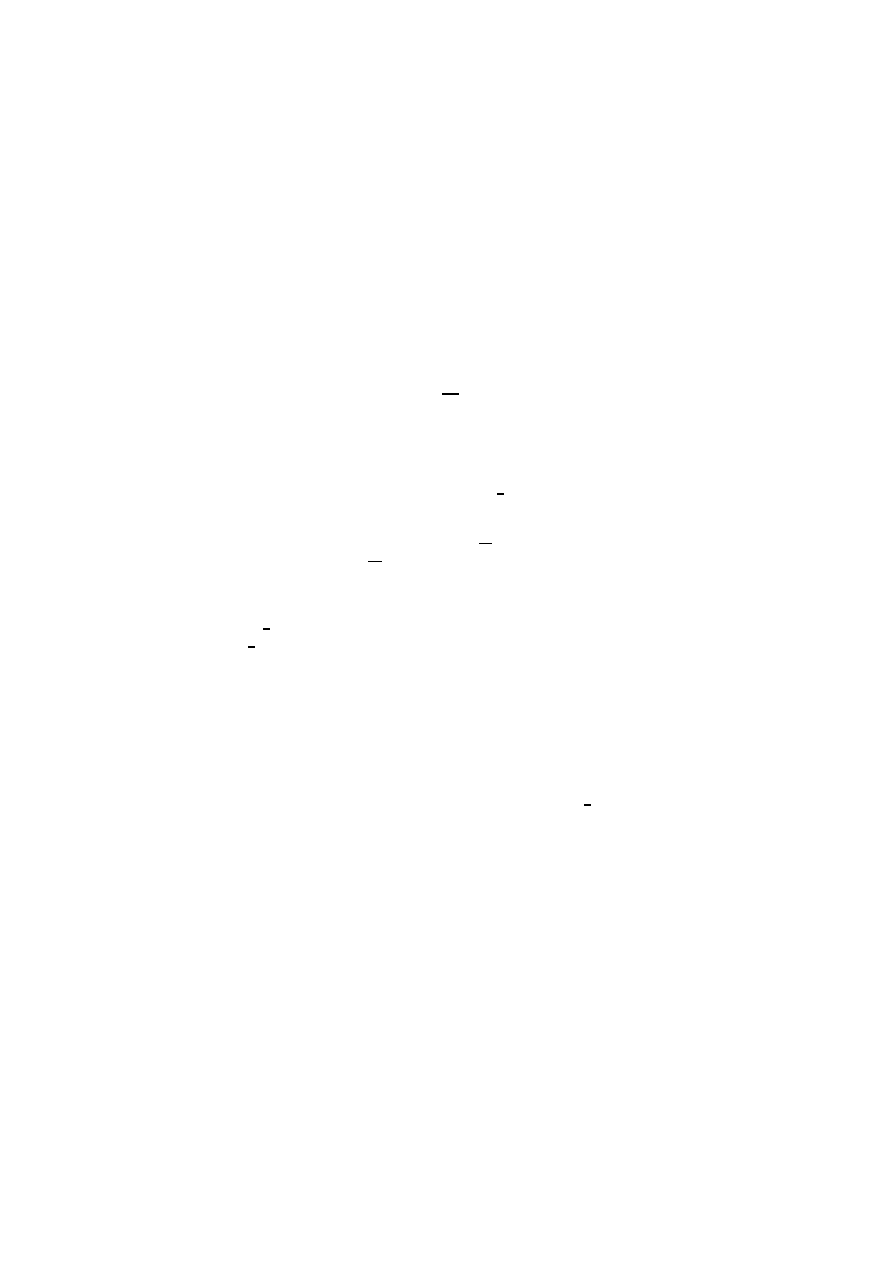
6
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.2.1
Klasyczna definicja prawdopodobie ´nstwa, rozkład jednostajny
W przypadku, gdy przestrze ´n zdarze´n elementarnych jest zbiorem sko ´nczonym najcz˛e-
´sciej przyjmuje si˛e, ˙ze funkcja prawdopodobie ´nstwa przypisuje, ka˙zdemu zdarzeniu ele-
mentarnemu tak ˛
a sam ˛
a warto´s´c. Mamy wtedy do czynienia z klasyczn ˛
a definicj ˛
a prawdo-
podobie´nstwa lub rozkładem jednostajnym.
Definicja 1.18 Rozkład prawdopodobie´nstwa, w którym ka˙zde zdarzenie elementarne
ω
∈
Ω ma takie samo prawdopodobie´nstwo P (ω) =
1
|Ω|
nazywamy rozkładem jednostajnym.
W dalszej cz˛e´sci ksi ˛
a˙zki b˛edziemy najcz˛e´sciej zakłada´c, ˙ze mamy jednostajny rozkład
prawdopodobie ´nstwa. W razie odst˛epstwa b˛edziemy to specjalnie zaznacza´c.
Przykład 1.19 (kontynuacja przykładów 1.3 oraz 1.6 z losowaniem jednej kuli) Prawdo-
podobie´nsto zdarzenia, ˙ze wylosowano kul˛e biał ˛
a wynosi
2
5
.
Przykład 1.20 (kontynuacja przykładów 1.4 oraz 1.7 z losowaniem pary kul). Prawdo-
podobie´nstwo ˙ze wylosowano par˛e kul białych wynosi
1
10
, a prawdopodobie´nstwo ˙ze wy-
losowano par˛e kul czarnych wynosi
3
10
.
Przykład 1.21 (kontynuacja przykładu 1.8 z czterokrotnym rzutem monet ˛
a). Je˙zeli zało-
˙zymy rozkład jednostajny, to prawdopodobie´nstwo ˙ze za pierwszym i trzecim razem wy-
padł orzeł wynosi
1
4
, a prawdopodobie´nstwo, ˙ze za pierwszym i trzecim razem wypadnie
to samo wynosi
1
2
.
Podobnie w przypadku, gdy
n krotnie rzucamy monet ˛
a
n > 3 (przykład 1.9). Prze-
strze´n zdarz˛e elementarnych zawiera
2
n
ci ˛
agów, z czego
2
n−2
sprzyja zdarzeniu, ˙ze za
pierwszym i trzecim razem wypadnie orzeł, a
2
n−1
sprzyja zdarzeniu, ˙ze za pierwszym i
trzecim razem jest to samo. Tak wi˛ec otrzymamy takie same prawdopodobie´nstwa jak w
przypadku czterokrotnego rzutu monet ˛
a.
Przykład 1.22 Powró´cmy do przypadku kolorowania dwoma kolorami wierzchołków gra-
fu
G = (V, E) z
|V | = n wierzchołkami (przykład 1.10). Prawdopodobie´nstwo, ˙ze ko´nce
wybranej z góry kraw˛edzi
e =
{u, v} ∈ E maj ˛
a ró˙zne kolory wynosi
1
2
. Rzeczywi´scie,
wszystkich kolorowa´n jest
2
n
. Kolorowa´n, w których
u i v maj ˛
a kolor biały, jest
2
n−2
(na
tyle sposobów mo˙zna pokolorowa´c pozostałe
n
− 2 wierzchołków). Tyle samo jest kolo-
rowa´n, w których
u i v maj ˛
a kolor czarny. Tak wi˛ec w połowie kolorowa´n
u i v maj ˛
a taki
sam kolor, a w połowie maj ˛
a ró˙zne kolory.
1.2.2
Własno´sci prawdopodobie ´nstwa
W nast˛epuj ˛
acym twierdzeniu zebrano kilka prostych wniosków wynikaj ˛
acych z aksjoma-
tów prawdopodobie ´nstwa.
Twierdzenie 1.23
a)
P (
∅) = 0.
b) Je˙zeli
A
⊆ B, to P (A) ≤ P (B) oraz P (B − A) = P (B) − P (A).
c)
P (A
∪ B) = P (A) + P (B) − P (A ∩ B).

1.3. Prawdopodobie ´nstwo warunkowe
7
d)
P (A
∪ B) ≤ P (A) + P (B).
Dowód:
a)
Z aksjomatu A3 mamy
P (
∅) = P (∅ ∪ ∅) = P (∅) + P (∅), a 0 jest jedyn ˛a liczb ˛a
spełniaj ˛
ac ˛
a równo´s´c
x = x + x.
b)
Je˙zeli
A
⊆ B, to B = (B − A) ∪ A oraz (B − A) ∩ A = ∅, a wi˛ec z aksjomatu A3
P (B) = P (B
− A) + P (A) ≥ P (A).
c)
Mamy
A
∪ B = A ∪ (B − (A ∩ B)) oraz A ∩ (B − (A ∩ B)) = ∅, a wi˛ec z aksjomatu
A3
P (A
∪ B) = P (A) + P (B − (A ∩ B)), a poniewa˙z A ∩ B ⊆ B, z wniosku 1.23b
mamy
P (B
− (A ∩ B)) = P (B) − P (A ∩ B).
d)
wynika bezpo´srednio z
c)
.
2
Twierdzenie 1.24 Niech
A
1
, . . . , A
n
b˛edzie rodzin ˛
a parami rozł ˛
acznych zdarze´n (to zna-
czy
A
i
∩ A
j
=
∅ dla ka˙zdej pary indeksów i < j). Wtedy
P
n
[
i=1
A
i
=
n
X
i=1
P (A
i
)
Dowód przez indukcj˛e: Dla
n = 1 twierdzenie zachodzi w sposób trywialny. Załó˙zmy,
˙ze twierdzenie jest prawdziwe dla dowolnej rodziny
n zbiorów. Rozpatrzmy
P
n+1
[
i=1
A
i
= P
n
[
i=1
A
i
∪ A
n+1
.
Poniewa˙z
S
n
i=1
A
i
∩ A
n+1
=
∅, z aksjomatu A3 i z zało˙zenia indukcyjnego wynika
P
n+1
[
i=1
A
i
= P
n
[
i=1
A
i
+ P (A
n+1
) =
n
X
i=1
P (A
i
) + P (A
n+1
) =
n+1
X
i=1
P (A
i
).
2
1.3
Prawdopodobie ´nstwo warunkowe
Definicja 1.25 Prawdopodobie´nstwo warunkowe zaj´scia zdarzenia
A pod warunkiem, ˙ze
zaszło zdarzenie
B oznaczane przez P (A
|B) okre´slamy jako
P (A
|B) =
P (A
∩ B)
P (B)
.
Ma to sens tylko wtedy gdy
P (B) > 0.
Mo˙zemy powiedzie´c, ˙ze jest to prawdopodobie ´nstwo zaj´scia zdarzenia
A w sytuacji, gdy
mamy pewno´s´c, ˙ze zaszło zdarzenie
B. Przy klasycznej definicji, gdy prawdopodobie ´n-
stwo oznacza cz˛esto´s´c wyst ˛
apienia, to prawdopodobie ´nstwo
P (A
|B) oznacza jaka cz˛e´s´c
elementów zbioru
B nale˙zy do zbioru A.

8
Rozdział 1. Rachunek prawdopodobie ´nstwa
Przykład 1.26 Niech w urnie b˛edzie sze´s´c kul o numerach od 1 do 6, i niech kule o
numerach parzystych b˛ed ˛
a białe, a kule o numerach nieparzystych czarne. Przypu´s´c-
my, ˙ze losujemy jedn ˛
a kul˛e. Jako przestrze´n zdarze´n elementarnych wybieramy zbiór
Ω =
{1, 2, 3, 4, 5, 6} z jednostajnym rozkładem prawdopodobie´nstwa. Rozwa˙zmy zdarze-
nie
A =
{1, 2} polegaj ˛ace na wylosowaniu kuli o numerze mniejszym od 3 oraz zdarzenie
B =
{2, 4, 6} polegaj ˛ace na wylosowaniu kuli białej. Prawdopodobie´nstwo P (A|B) zaj-
´scia zdarzenia
A pod warunkiem, ˙ze zaszło zdarzenie A wynosi P (A
|B) =
P (A∩B)
P (B)
=
1
6
:
1
2
=
1
3
. Mówi ˛
ac inaczej, w´sród białych kul
1
3
ma numer mniejszy od 3.
Zauwa˙zmy, ˙ze
P (A
|B) = P (A), czyli
1
3
kul ma numer mniejszy od 3 zarówno w
całym zbiorze
Ω jak i w´sród białych kul. Mo˙zemy wi˛ec powiedzie´c, ˙ze zaj´scie zdarzenia
A nie zale˙zy od tego, czy zaszło zdarzenie B, czy nie.
Zauwa˙zmy, ˙ze tak˙ze zdarzenie
B nie zale˙zy od zdarzenia A, poniewa˙z P (B
|A) =
P (B) =
1
2
.
To co zauwa˙zyli´smy w powy˙zszym przykładzie jest ogóln ˛
a prawidłowo´sci ˛
a. Mianowicie,
je˙zeli
A i B s ˛
a zdarzeniami o niezerowych prawdopodobie ´nstwach i
P (A) = P (A
|B)
(zdarzenie
A jest niezale˙zne od B), to P (B) = P (B
|A) (zdarzenie B jest niezale˙zne od
A). Rzeczywi´scie P (A
|B) = P (A) poci ˛aga P (A ∩ B) = P (A) · P (B), a to poci ˛aga
P (B) =
P (A
∩ B)
P (A)
= P (B
|A).
Czyli relacja niezale˙zno´sci zbiorów jest symetryczna. Zwykle jednak u˙zywa si˛e troch˛e
innej definicji niezale˙zno´sci.
1.4
Zdarzenia niezale˙zne
Definicja 1.27 Zdarzenia
A i B s ˛
a niezale˙zne, je˙zeli
P (A
∩ B) = P (A) · P (B).
Zauwa˙zmy, ˙ze je˙zeli
P (A) = 0 lub P (B) = 0, to poniewa˙z A
∩ B ⊂ A oraz A ∩ B ⊂ B,
na podstawie twierdzenia 1.23, mamy
P (A
∩B) = 0, czyli zdarzenia A i B s ˛aniezale˙zne.
Wniosek 1.28
P (A
∩ B) = P (A|B) · P (B).
Definicja 1.29 Zdarzenia
A
1
, . . . , A
n
, s ˛
a:
• parami niezale˙zne, je˙zeli ka˙zde dwa zdarzenia s ˛
a niezale˙zne, to znaczy gdy
P (A
i
∩
A
j
) = P (A
i
)
· P (A
j
) dla ka˙zdej pary i < j.
• niezale˙zne, je˙zeli dla ka˙zdego podzbioru I ⊆ {1, . . . , n} mamy
P
\
i∈I
A
i
=
Y
i∈I
P (A
i
).

1.5. Prawdopodobie ´nstwo całkowite
9
Przykład 1.30 (Kontynuacja przykładu 1.2, z dwukrotnym rzutem monet ˛
a). Niech
A
1
b˛e-
dzie zdarzeniem, ˙ze za pierwszym razem wypadł orzeł,
A
2
, ˙ze za drugim razem wypadł
orzeł, a
A
3
, ˙ze w obu rzutach wypadło to samo. Mamy
P (A
1
) = P (A
2
) = P (A
3
) =
1
2
P (A
1
∩ A
2
) = P (A
1
∩ A
3
) = P (A
2
∩ A
3
) = P (A
1
∩ A
2
∩ A
3
) =
1
4
.
Jak wida´c zdarzenia te s ˛
a parami niezale˙zne, poniewa˙z dla ka˙zdej pary indeksów
1
≤ i <
j
≤ 3 mamy P (A
i
∩ A
j
) = P (A
i
)
· P (A
j
) =
1
4
. Ale zdarzenia te nie s ˛
a niezale˙zne,
poniewa˙z
1
4
= P (A
1
∩ A
2
∩ A
3
)
6= P (A
1
)
· P (A
2
)
· P (A
3
) =
1
8
.
Przykład 1.31 W przypadku
n krotnego rzutu monet ˛
a, niech
A
i
oznacza, ˙ze za
i-tym
razem wypadł orzeł. Wtedy zdarzenia
A
1
, . . . , A
n
s ˛
a niezale˙zne. Łatwo sprawdzi´c, ˙ze
• dla ka˙zdego i, P (A
i
) =
1
2
,
• dla ka˙zdej pary i < j, P (A
i
∩ A
j
) =
1
4
• dla ka˙zdej trójki i < j < k, P (A
i
∩ A
j
∩ A
k
) =
1
8
,
• i ogólnie, dla ka˙zdego podzbioru zbioru indeksów I ⊆ {1, . . . , n} mamy
P
\
i∈I
A
i
=
1
2
|I|
1.5
Prawdopodobie ´nstwo całkowite
Twierdzenie 1.32 (wzór na prawdopodobie ´nstwo całkowite.) Niech
A
1
, . . . , A
n
⊆ Ω,
b˛ed ˛
a zdarzeniami takimi, ˙ze:
• P (A
i
) > 0, dla ka˙zdego 1
≤ i ≤ n,
• A
i
∩ A
j
=
∅, dla 1 ≤ i < j ≤ n (zdarzenia s ˛
a parami rozł ˛
aczne),
•
S
1≤i≤n
A
i
= Ω (zdarzenia daj ˛
a w sumie cał ˛
a przestrze´n).
Wtedy prawdopodobie´nstwo dowolnego zdarzenia
B
⊆ Ω wynosi
P (B) =
n
X
i=1
P (B
|A
i
)
· P (A
i
)

10
Rozdział 1. Rachunek prawdopodobie ´nstwa
Dowód: Mamy
B = B
∩ Ω = B ∩
[
1≤i≤n
A
i
=
[
1≤i≤n
(B
∩ A
i
).
Ponadto
(B
∩ A
i
)
∩ (B ∩ A
j
) =
∅ dla i 6= j, wi˛ec na mocy twierdzenia 1.24 mamy
P (B) =
n
X
i=1
P (B
∩ A
i
).
Z wniosku 1.28 mamy
P (B
∩ A
i
) = P (B
|A
i
)
· P (A
i
); co daje tez˛e twierdzenia.
2
W przypadku dwóch zdarze ´n uzupełniaj ˛
acych si˛e
A i A
0
= Ω
− A wzór z twierdze-
nia 1.32 wygl ˛
ada nast˛epuj ˛
aco:
P (B) = P (B
|A) · P (A) + P (B|A
0
)
· P (A
0
).
(1.1)
Przykład 1.33 Wyobra´zmy sobie dwie urny z kulami. W pierwszej urnie mamy kule o nu-
merach 1,2, w drugiej kule o numerach 3,4,5. Zakładamy, ˙ze kule o numerach parzystych
s ˛
a białe, a kule o numerach nieparzystych s ˛
a czarne. Rzucamy monet ˛
a. Je˙zeli wypadnie
orzeł, to losujemy kul˛e z pierwszej urny, je˙zeli reszka, to losujemy z drugiej urny.
Jakie jest prawdopodobie´nstwo, ˙ze wylosujemy kul˛e biał ˛
a? Niech
B oznacza wyloso-
wanie kuli białej, a
A wypadni˛ecie orła na monecie, wtedy A
0
oznacza, ˙ze na monecie
wypadła reszka. Mamy
P (A) = P (A
0
) =
1
2
oraz
P (B
|A) =
1
2
— jest to prawdopodobie´nstwo wylosowania kuli białej pod warunkiem,
˙ze wypadł orzeł i losowali´smy z pierwszej urny.
P (B
|A
0
) =
1
3
— jest to prawdopodobie´nstwo wylosowania kuli białej pod warun-
kiem, ˙ze wypadła reszka i losowali´smy z drugiej urny.
Rysunek 1.1: Prawdopodobie ´nstwo całkowite
O
1
2
1
1
2
2
1
2
R
1
2
3
1
3
4
1
3
5
1
3
Korzystaj ˛
ac teraz ze wzoru (1.1) mamy
P (B) =
1
2
·
1
2
+
1
3
·
1
2
=
5
12
.

1.5. Prawdopodobie ´nstwo całkowite
11
Rozwi ˛
azanie tego zadania mo˙zna przedstawi´c za pomoc ˛
a drzewa (rysunek 1.1). Na po-
cz ˛
atku jeste´smy w korzeniu drzewa. Dwaj synowie korzenia odpowiadaj ˛
a dwóm wynikom
rzutu monet ˛
a. Jak wypadnie orzeł, to idziemy w lewo do wierzchołka
O, jak wypadnie
reszka, to idziemy w prawo do wierzchołka
R. Etykiety przy kraw˛edziach oznaczaj ˛
a praw-
dopodobie´nsta z jakimi te kraw˛edzie s ˛
a wybierane. Synowie wierzchołka
O odpowiadaj ˛
a
wynikom losowania kul pod warunkiem, ˙ze na monecie wypadł orzeł i losujemy z pierw-
szej urny. Etykiety przy kraw˛edziach oznaczaj ˛
a prawdopodobie´nsta warunkowe z jakimi
te kraw˛edzie s ˛
a wybierane. Podobnie synowie wierzchołka
R odpowiadaj ˛
a wynikom lo-
sowania kul pod warunkiem, ˙ze na monecie wypadła reszka i losujemy z drugiej urny.
Ka˙zdy li´s´c w drzewie odpowiada jakiemu´s wynikowi ko´ncowemu (wylosowaniu kon-
kretnej kuli). Prawdopodobie´nsto, ˙ze b˛edzie taki wynik jest równe iloczynowi etykiet na
drodze prowadz ˛
acej od korzenia do tego li´scia. Prawdopodobie´nstwo wylosowania kuli
białej (z parzystym numerem) jest równe
1
2
·
1
2
+
1
2
·
1
3
=
5
12
.
Przykład 1.34 Wyobra´zmy sobie, ˙ze mamy jedn ˛
a urn˛e z trzema kulami o numerach
2, 3
i
4 oraz ˙ze kule o numerach 2 i 4 s ˛
a białe, a kula
3 jest czarna. Przypu´s´cmy, ˙ze pierwsza
osoba wylosowała jedn ˛
a kul˛e i schowała j ˛
a. Jakie jest prawdopodobie´nstwo, ˙ze druga
osoba wylosuje kul˛e biał ˛
a?
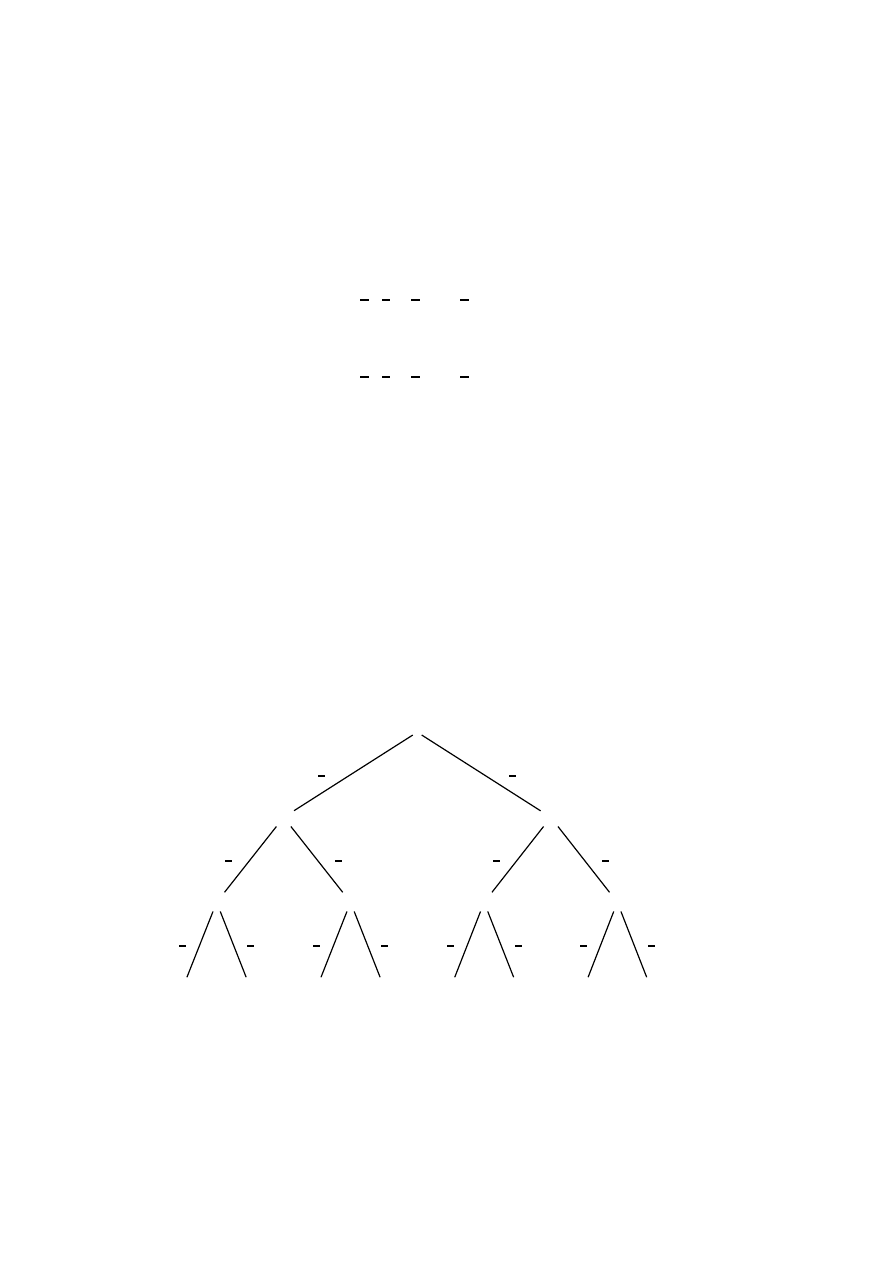
Rysunek 1.2:
B
2
3
BB
1
2
BC
1
2
C
1
3
CB
1
CC
0
Rozwi ˛
azanie tego zadania jest przedstawione na drzewie z rysunku 1.2. Synowie ko-
rzenia odpowiadaj ˛
a wynikowi losowania pierwszej osoby. Losuje ona kul˛e biał ˛
a, wierz-
chołek
B, z prawdopodobie´nstwem
2
3
, a kul˛e czarn ˛
a, wierzchołek
C, z prawdopodobie´n-
stwem
1
3
. Synowie wierzchołka
B odpowiadaj ˛
a losowaniom drugiego gracza pod warun-
kiem, ˙ze pierwszy gracz wylosował kułe biał ˛
a. W tej sytuacji drugi gracz wylosuje kul˛e
biał ˛
a, wierzchołek
BB, lub czarn ˛
a, wierzchołek
BC, obie z prawdopodobie´nstwem wa-
runkowym
1
2
. Etykieta
BB oznacza, ˙ze obaj gracze wylosowali kule białe, a etykieta BC
oznacza, ˙ze pierwszy gracz wylosował kul˛e biał ˛
a, a drugi kul˛e czarn ˛
a. Synowie wierz-
chołka
C odpowiadaj ˛
a losowaniom drugiego gracza pod warunkiem, ˙ze pierwszy gracz
wylosował kułe czarn ˛
a. Teraz drugi gracz wylosuje kul˛e biał ˛
a, wierzchołek
CB, z prawdo-
podobie´nstwem warunkowym
1, a kul˛e czarn ˛
a, wierzchołek
CC, z prawdopodobie´nstwem
12
Rozdział 1. Rachunek prawdopodobie ´nstwa
0. Prawdopodobie´nstwo wylosowania kuli białej przez drug ˛
a osob˛e wynosi
2
3
·
1
2
+
1
3
· 1 =
2
3
.
Zauwa˙zmy, ˙ze prawdopodobie´nstwo, ˙ze po drugim losowaniu w urnie zostanie biała kula
jest równe
2
3
·
1
2
+
1
3
· 1 =
2
3
.
Jak wida´c prawdopodobie´nstwo wylosowania białej kuli jest takie samo dla pierwszego,
drugiego i trzeciego losuj ˛
acego.
1.6
Schemat dwumianowy (Bernouliego)
W schemacie dwumianowym (Bernouliego) mamy seri˛e
n do´swiadcze´n losowych (na
przykład rzutów monet ˛
a). W ka˙zdym do´swiadczeniu mo˙zliwe s ˛
a dwa wyniki: sukces (wy-
padni˛ecie orła) lub pora˙zka (wypadnie´cie reszki). Wyniki do´swiadcze´n s ˛
a niezale˙zne i w
ka˙zdym mamy takie samo prawdopodobie ´nstwo sukcesu równe
p.
1.6.1
Rzut symetryczn ˛
a monet ˛
a
Rozpatrzmy trzykrotny rzut symetryczn ˛
a monet ˛
a. Rysunek 1.3 ilustruje jak w tym przy-
Rysunek 1.3: Trzykrotny rzut symetryczn ˛
a monet ˛
a
O
1
2
OO
1
2
OOO
1
2
OOR
1
2
OR
1
2
ORO
1
2
ORR
1
2
R
1
2
RO
1
2
ROO
1
2
ROR
1
2
OR
1
2
RRO
1
2
RRR
1
2
padku rozkłada si˛e prawdopodobie ´nstwo. W korzeniu rzucamy pierwszy raz monet ˛
a, je-
˙zeli wypadnie orzeł, to idziemy do wierzchołka
O, je˙zeli reszka, to do R. W wierzchołku

1.6. Schemat dwumianowy (Bernouliego)
13
O rzucamy drugi raz, id ˛
ac albo do
OO lub do OR. Etykieta OO oznacza, ˙ze w obu rzutach
wypadł orzeł, a etykieta
OR oznacza, ˙ze za pierwszym razem wypadł orzeł, a za drugim
reszka. Podobnie w wierzchołku
R. Poniewa˙z drugi rzut jest niezale˙zny od pierwszego,
etykiety na kraw˛edziach wychodz ˛
acych z
O s ˛
a takie same jak na kraw˛edziach wycho-
dz ˛
acych z
R. Kraw˛edzie wychodz ˛
ace z wierzchołków z dwoma etykietami odpowiadaj ˛
a
trzeciemu rzutowi. Tak˙ze tutaj etykiety kraw˛edzi wychodz ˛
acych z wierzchołków s ˛
a takie
same, poniewa˙z trzeci rzut jest niezale˙zny od dwóch pierwszych.
Li´scie odpowiadaj ˛
a wynikom trzech rzutów. Wyst˛epuj ˛
a tutaj wszystkie 8 ci ˛
agów dłu-
go´sci 3. Ka˙zdy z nich jest przyjmowane z prawdopodobie ´nstwem
1
8
. Otrzymali´smy wi˛ec
jednostajny rozkład prawdopodobie ´nstwa na zbiorze
Ω =
{OOO, OOR, ORO, ORR, ROO, ROR, RRO, RRR}.
Podobnie, przy
n krotnym rzucie monet ˛
a, je˙zeli rzuty s ˛
a niezale˙zne i w ka˙zdym rzucie
prawdopodobie ´nstwa wypadni˛ecia orła i reszki wynosz ˛
a
1
2
,
1
2
, otrzymamy jednostajny
rozkład na zbiorze wszystkich ci ˛
agów długo´sci
n z elementami O i R.
1.6.2
Kolorowanie wierzchołków grafu
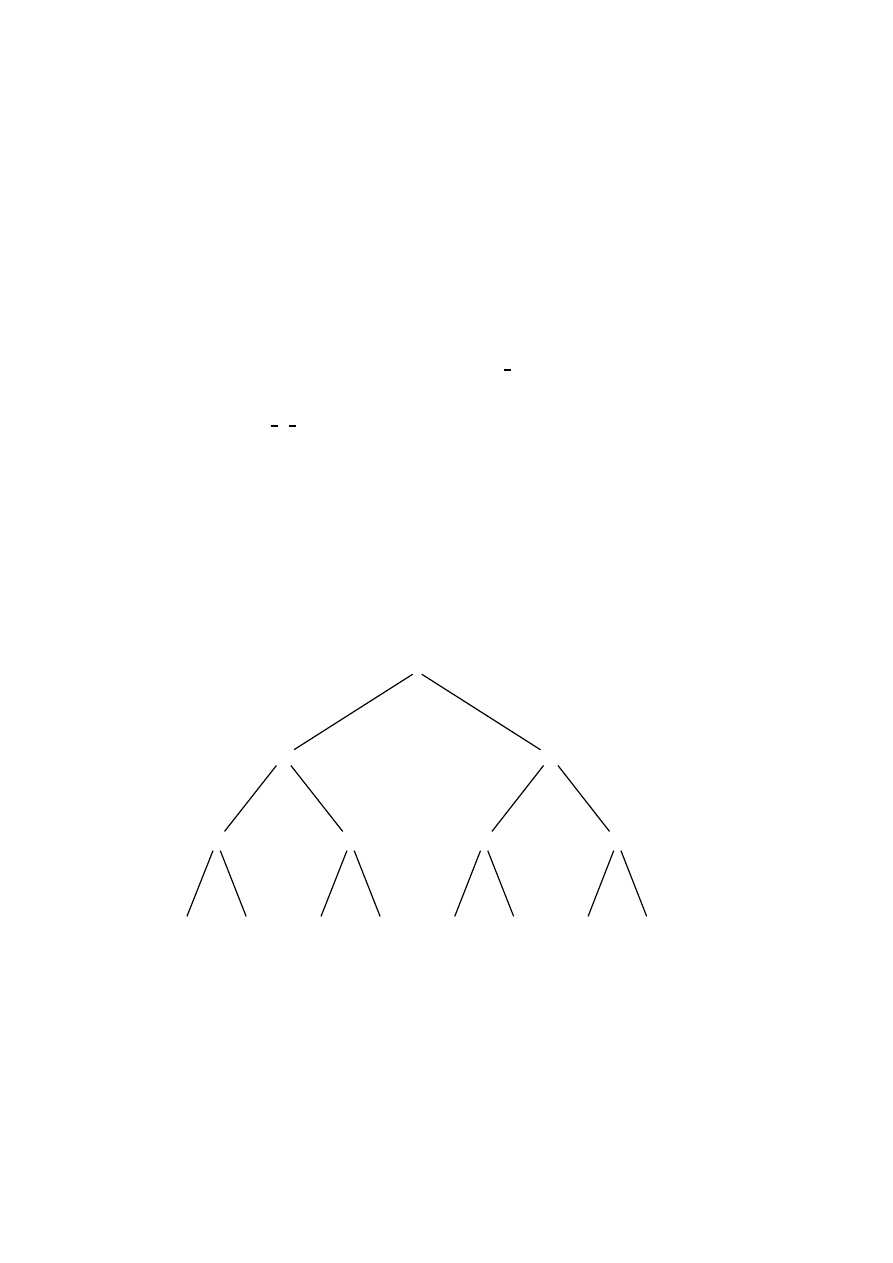
Rysunek 1.4: Kolorowanie wierzchołków grafu
B
1
2
BB
1
2
BBB
1
2
BBC
1
2
BC
1
2
BCB
1
2
BCC
1
2
C
1
2
CB
1
2
CBB
1
2
CBC
1
2
BC
1
2
CCB
1
2
CCC
1
2
Przypu´s´cmy, ˙ze mamy graf z trzema wierzchołkami
a, b i c, i ˙ze jego wierzchoł-
ki kolorujemy po kolei niezale˙znie na biało lub czarno z pawdopodobie ´nstwami
1
2
,
1
2
.
Do´swiadczenie to mo˙zna zilustrowa´c za pomoc ˛
a drzewa z rysunku 1.4. W korzeniu wy-
bieramy kolor dla wierzchołka
a, je˙zeli biały, to idziemy do wierzchołka B, je˙zeli czarny,
to do
C. W wierzchołku B wybieramy kolor dla wierzchołka b, id ˛
ac albo do
BB lub do
14
Rozdział 1. Rachunek prawdopodobie ´nstwa
BC. Etykieta BB oznacza, ˙ze oba wierzchołki a i b s ˛
a białe, a etykieta
BC oznacza, ˙ze
wierzchołek
a jest biały, a wierzchołek b czarny. Podobnie w wierzchołku C. Kraw˛edzie
wychodz ˛
ace z wierzchołków z dwoma kolorami odpowiadaj ˛
a kolorowaniom wierzchołka
c. Tak˙ze tutaj etykiety kraw˛edzi wychodz ˛
acych z wierzchołków s ˛
a takie same, ponie-
wa˙z wybór koloru dla
c jest niezale˙zny od wyboru kolorów dla a i b. Li´scie odpowiadaj ˛
a
ostatecznym kolorowaniom trzech wierzchołków. Wyst˛epuje tutaj wszystkie 8 kolorowa ´n.
Ka˙zdy z nich jest przyjmowane z prawdopodobie ´nstwem
1
8
. Otrzymali´smy wi˛ec jedno-
stajny rozkład prawdopodobie ´nstwa na zbiorze wszystkich kolorowa ´n.
Podobnie, koloruj ˛
ac po kolei niezale˙znie
n wierzchołków, na biało lub czarno z praw-
dopodobie ´nstwami
1
2
,
1
2
, otrzymamy jednostajny rozkład na zbiorze wszystkich mo˙zli-
wych kolorowa ´n.
1.6.3
Trzykrotny rzut niesymetryczn ˛
a monet ˛
a
Rozpatrzmy teraz trzykrotny rzut niesymetryczn ˛
a monet ˛
a, gdy prawdopobie ´nstwo wy-
padni˛ecia orła wynosi
p, a prawdopobie ´nstwo wypadni˛ecia reszki wynosi q = 1
− p.
Nadal zakładamay, ˙ze wyniki poszczególnych rzutów s ˛
a od siebie niezale˙zne.
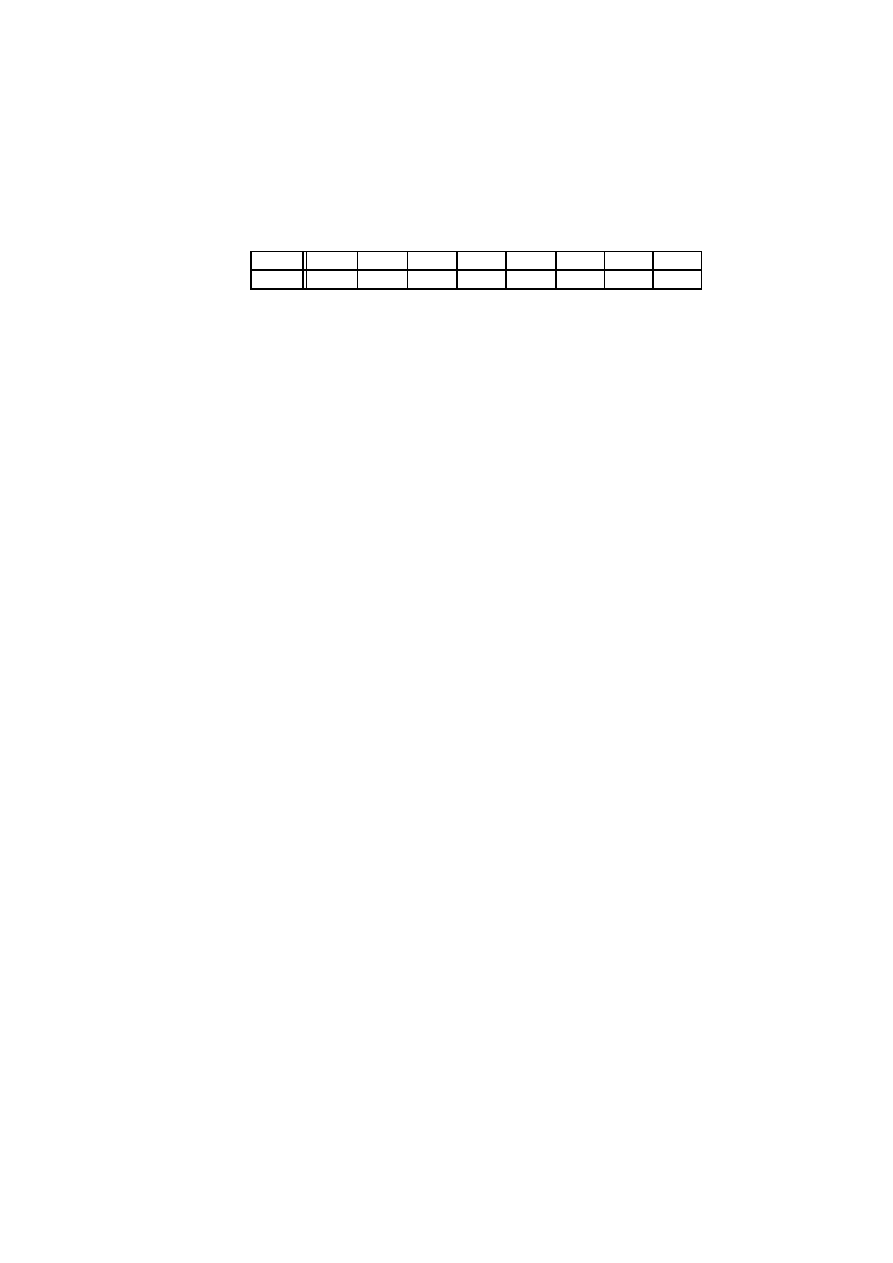
Rysunek 1.5: Trzykrotny rzut niesymetryczn ˛
a monet ˛
a
O
p
OO
p
OOO
p
OOR
q
OR
q
ORO
p
ORR
q
R
q
RO
p
ROO
p
ROR
q
OR
q
RRO
p
RRR
q
Rysunek 1.5 ilustruje jak rozkłada si˛e prawdopodobie ´nstwo w takim przypadku. Ety-
kiety wierzchołków maj ˛
a takie same znaczenie jak w przypadku rzutu symetryczn ˛
a mo-
net ˛
a, Zmieniły si˛e tylko etykiety kraw˛edzi. Kraw˛edzie odpowiadaj ˛
ace wypadni˛eciu orła
maj ˛
a etykiet˛e
p, a odpowiadaj ˛
ace reszce etykiet˛e
q.
Otrzymali´smy teraz inny rozkład prawdopodobie ´nstwa na zbiorze
Ω.
1.6. Schemat dwumianowy (Bernouliego)
15
ω
OOO
OOR
ORO
ORR
ROO
ROR
RRO
RRR
P (ω)
p
3
p
2
q
p
2
q
pq
2
p
2
q
pq
2
pq
2
q
3
Zauwa˙zmy, ˙ze prawdopodobie ´nsto, ˙ze za pierwszym (drugim lub trzecim) razem wy-
padnie orzeł wynosi
p
3
+ p
2
q + p
2
q + pq
2
= p(p
2
+ 2pq + q
2
) = p(p + q)
2
= p,
a prawdopodobie ´nsto, ˙ze za pierwszym (drugim lub trzecim) razem wypadnie reszka wy-
nosi
p
2
q + pq
2
+ pq
2
+ q
3
= q(p
2
+ 2pq + q
2
) = q(p + q)
2
= q.
1.6.4
Ogólny schemat — n krotny rzut niesymetryczn ˛
a monet ˛
a
Ogólnie w schemacie dwumianowym mamy seri˛e
n niezale˙znych do´swiadcze´n. W ka˙z-
dym do´swiadczeniu prawdopodobie ´nstwo sukcesu wynosi
p, a prawdopodobie ´nstwo po-
ra˙zki
q = 1
− p. Bez straty ogólno´sci mo˙zemy nasze rozwa˙zania ograniczy´c do n krot-
nego rzutu niesymetryczn ˛
a monet ˛
a. Zakładamy, ˙ze rzuty s ˛
a niezale˙zne i w ka˙zdym rzucie
prawdopodobie ´nstwa wypadni˛ecia orła wynosi
p, a reszki q. Otrzymamy wtedy rozkład
na zbiorze wszystkich ci ˛
agów długo´sci
n z elementami O i R, w którym prawdopodo-
bie´nstwo ci ˛
agu
ω
∈ Ω jest równe
p
k
q
n−k
,
gdzie
k oznacza liczb˛e symboli O w ci ˛
agu
ω.
Zauwa˙zmy, ˙ze ci ˛
agów z
k orłami jest
n
k
, wi˛ec je˙zeli pogrupujemy te prawdopodo-
bie´nstwa według liczby orłów i zsumujemy, to otrzymamy
n
X
k=0
n
k
p
k
q
n−k
= (p + q)
n
= 1
n
= 1.
Je˙zeli rozwa˙zymy tylko ci ˛
agi z
O na pierwszej (lub na dowolnej i tej) pozycji, to znowu
mo˙zemy je pogrupowa´c według liczby symboli
O. Dla ka˙zdego k od 0 do n
− 1, ci ˛agów
z
k + 1 symbolami O jest
n−1
k
(trzeba wybra´c k pozycji spo´sród n − 1, na których b˛ed ˛a
orły). Je˙zeli pogrupujemy te prawdopodobie ´nstwa według liczby orłów i zsumujemy, to
otrzymamy prawdopodobie ´nstwo wypadni˛ecia orła za pierwszym (lub dowolnym
i tym
razem) równe
n−1
X
k=0
n − 1
k
p
k+1
q
n−1−k
= p
·
n−1
X
k=0
n − 1
k
p
k
q
n−1−k
= p(p + q)
n−1
= p.
Podobnie, je˙zeli rozwa˙zymy ci ˛
agi z
R na pierwszej (lub na dowolnej i tej) pozycji, to
znowu mo˙zemy je pogrupowa´c według liczby symboli
O. Dla ka˙zdego k od 0 do n
− 1
ci ˛
agów z
k symbolami O jest
n−1
k
, wi˛ec je˙zeli pogrupujemy te prawdopodobie ´nstwa
według liczby orłów to, zgodnie ze wzorem na dwumian Newtona, otrzymamy
n−1
X
k=0
n − 1
k
p
k
q
n−k
= q
·
n−1
X
k=0
n − 1
k
p
k
q
n−1−k
= q(p + q)
n−1
= q.
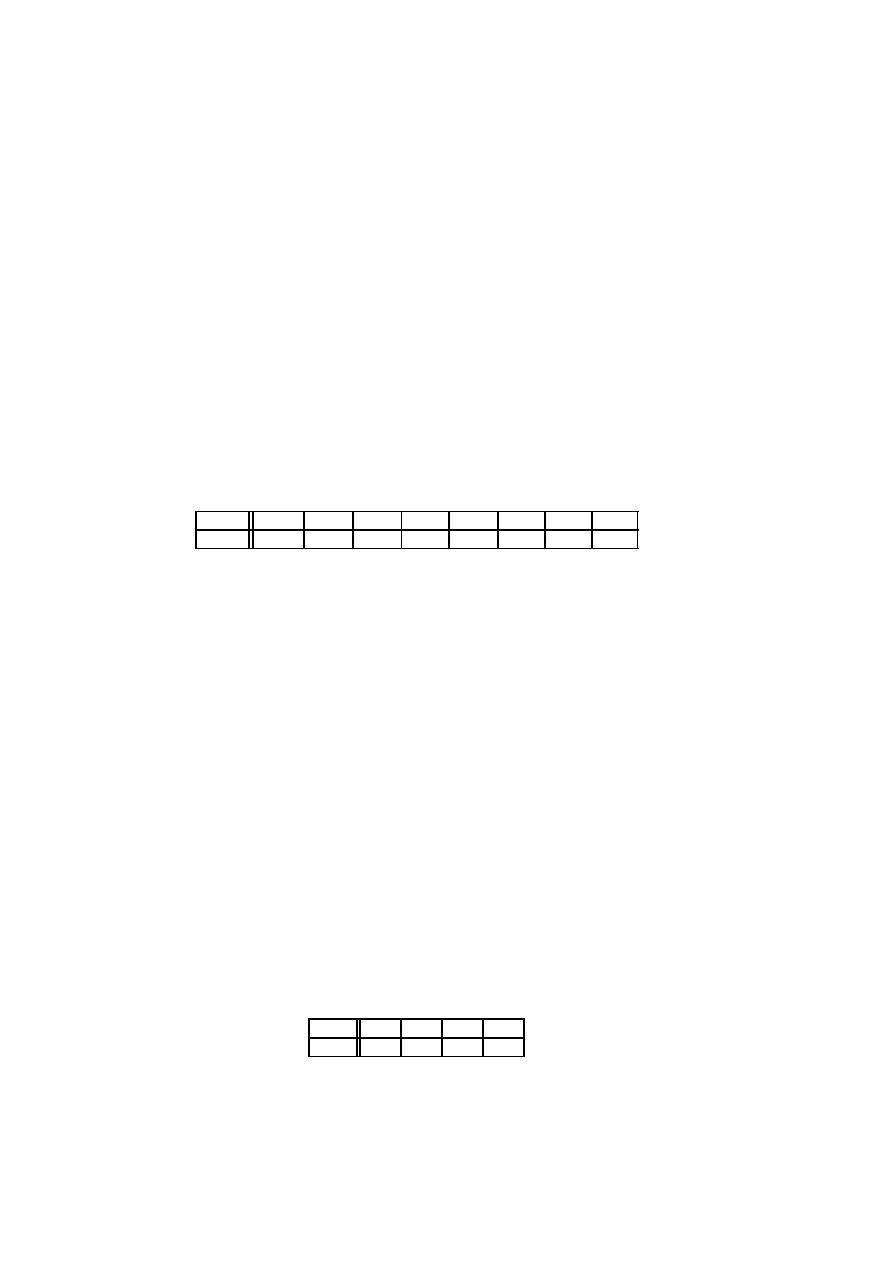
16
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.7
Zmienna losowa
Definicja 1.35 Zmienna losowa
X jest to dowolna funkcja z przestrzeni zdarze´n elemen-
tarnych
Ω w zbiór liczb rzeczywistych R.
Trzeba tutaj przypomnie´c, ˙ze w tej ksi ˛
a˙zce rozwa˙zamy tylko sko ´nczone przestrzenie zda-
rze´n elementarnych. W przypadku, gdy
Ω jest zbiorem niesko ´nczonym definicja zmiennej
losowej jest inna.
Przykład 1.36 Rozwa˙zmy trzykrotny rzut symetryczn ˛
a monet ˛
a,
Ω =
{OOO, OOR, ORO, ORR, ROO, ROR, RRO, RRR}.
Zmienna losowa
X oznacza ile razy wypadł orzeł. Jej warto´sci podane s ˛
a w nast˛epuj ˛
acej
tabeli:
ω
OOO
OOR
ORO
ORR
ROO
ROR
RRO
RRR
X(ω)
3
2
2
1
2
1
1
0
Maj ˛
ac zmienn ˛
a losow ˛
a
X i dowoln ˛
a liczb˛e rzeczywist ˛
a
x definiujemy zdarzenie (X = x)
jako
(X = x) =
{ω ∈ Ω | X(ω) = x}.
Zauwa˙zmy, ˙ze je˙zeli liczba
x nie nale˙zy do zbioru warto´sci X(Ω) zmiennej X, to zdarze-
nie
(X = x) jest zdarzeniem niemo˙zliwym.
Przykład 1.37 Dla zmiennej losowej
X z przykładu 1.36 mamy:
(X = 0) =
{RRR},
(X = 1) =
{0RR, ROR, RRO},
(X = 2) =
{OOR, ORO, OOR},
(X = 3) =
{OOO},
Je˙zeli
x
6= 0, 1, 2, 3, to (X = x) = ∅.
1.7.1
G˛esto´s´c rozkładu prawdopodobie ´nstwa zmiennej losowej
Definicja 1.38 Funkcj˛e
f (x) = P (X = x)
nazywamy funkcj ˛
a g˛esto´sci (rozkładu) prawdopodobie´nstwa zmiennej losowej
X.
Przykład 1.39 (Kontynuacja przykładu 1.36) Je˙zeli zało˙zymy, ˙ze ka˙zde zdarzenie elemen-
tarne jest równo prawdopodobne, to zmienna losowa
X posiada rozkład
x
0
1
2
3
f (x)
1/8
3/8
3/8
1/8

1.7. Zmienna losowa
17
Poniewa˙z, jak zało˙zyli´smy
Ω jest zbiorem sko´nczonym, to zbiór warto´sci X(Ω) zmiennej
X te˙z jest sko´nczony. Dla x /
∈ X(Ω) mamy f(x) = P (X = x) = P (∅) = 0. Tak wi˛ec
funkcja g˛esto´sci przyjmuje warto´sci niezerowe tylko dla sko ´nczenie wielu argumentów.
Zauwa˙zmy, ˙ze je˙zeli
x
1
6= x
2
, to zdarzenia
(X = x
1
) i (X = x
2
) wykluczaj ˛
a si˛e.
Lemat 1.40 Je˙zeli
f jest funkcj ˛
a g˛esto´sci zmiennej losowej
X, to
• f(x) ≥ 0 dla ka˙zdego x ∈ R.
•
P
x
f (x) = 1.
Sum˛e
P
x
f (x) rozumiemy jako sko´nczon ˛
a sum˛e po zbiorze warto´sci zmiennej
X, czyli
P
x
f (x) =
P
x∈X(Ω)
f (x)
Dowód.
X
x∈X(Ω)
f (x) =
X
x∈X(Ω)
P (X = x) =
X
x∈X(Ω)
X
X(ω)=x
P (ω).
Zauwa˙zmy, ˙ze ostatnia podwójna suma jest sum ˛
a po wszystkich elementach
ω
∈ Ω po-
grupowanych według warto´sci zmiennej
X. Mamy wi˛ec
X
x
f (x) =
X
ω∈Ω
P (ω) = 1.
2
W dalszej cz˛e´sci przedstawiaj ˛
ac funkcj˛e g˛esto´sci zmiennej losowej
X b˛edziemy roz-
wa˙za´c tylko te
x, dla których f (x) > 0.
Maj ˛
ac funkcj˛e g˛esto´sci rozkładu zmiennej
X mo˙zemy okre´sla´c prawdopodobie´nstwa
zdarze´n opisywanych za pomoc ˛
a zmiennej
X.
Przykład 1.41 Dla zmiennej losowej
X z przykładu 1.38. mamy
P (X < 2) = P (X = 0 lub X = 1) = P (X = 0) + P (X = 1) =
1
8
+
3
8
=
1
2
,
pami˛etajmy, ˙ze zdarzenia
X = 0 oraz X = 1 s ˛
a rozł ˛
aczne.
1.7.2
Dalsze przykłady zmiennych losowych
Przykład 1.42 Przypu´s´cmy, ˙ze mamy urn˛e z czteroma ponumerowanymi kulami
{1, 2, 3, 4},
i ˙ze kule o numerach parzystych s ˛
a białe, a kule o numerach nieparzystych czarne. Losu-
jemy dwie kule bez zwracania. Jako przestrze´n zdarze´n elementarnych wybieramy zbiór
dwuelementowych podzbiorów zbioru kul
Ω =
{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}
z jednostajnym rozkładem prawdopodobie´nstwa.
Niech zmienna losowa
X oznacza liczb˛e białych kul w wylosowanej parze. Jej warto-
´sci podane s ˛
a w nast˛epuj ˛
acej tabeli:
18
Rozdział 1. Rachunek prawdopodobie ´nstwa
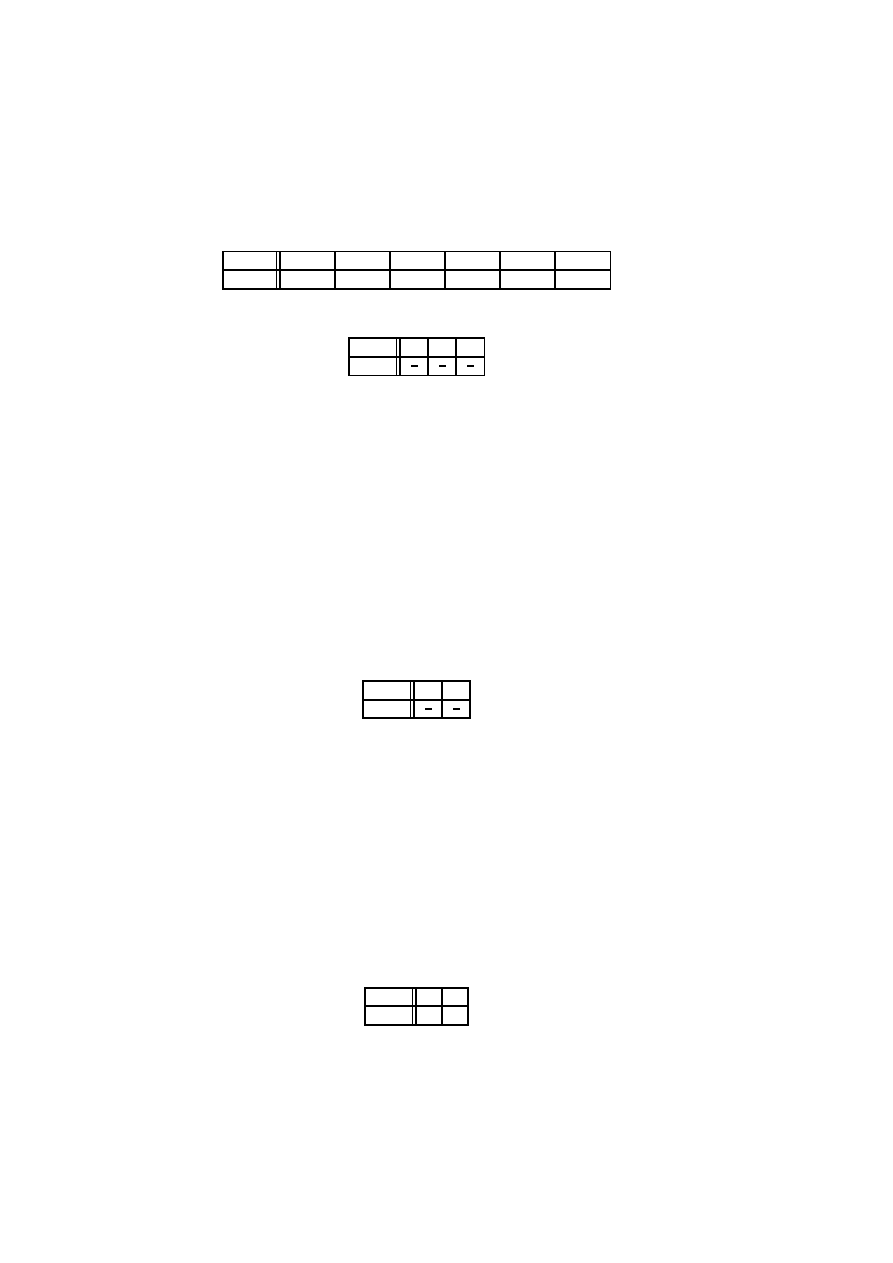
ω
{1, 2}
{1, 3}
{1, 4}
{2, 3}
{2, 4}
{3, 4}
X(ω)
1
0
1
1
2
1
G˛esto´s´c rozkładu prawdopodobie´nstwa zawiera tabela
x
0
1
2
f (x)
1
6
4
6
1
6
Przykład 1.43 Rozwa˙zmy zmienn ˛
a losow ˛
a
X oznaczaj ˛
ac ˛
a liczb˛e ró˙znobarwnych kraw˛e-
dzi w kolorowaniu wierzchołków dowolnego grafu
G = (V, E) (przykład 1.10). Przestrze-
ni ˛
a zdarze´n losowych to zbiór
Ω =
{1, 2}
V
wszystkich funkcji ze zbioru wierzchołków
V
w zbiór
{1, 2} dwóch kolorów. Dla ka˙zdego kolorowania ω ∈ Ω warto´s´c X(ω) oznacza
ile kraw˛edzi ma ko´nce w ró˙znych kolorach w kolorowaniu
ω.
W szczególnym przypadku, gdy graf
G = (V, E) jest trójk ˛
atem z wierzchołkami
V =
{a, b, c} i kraw˛edziami E = {{a, b}, {a, c}, {b, c}}. Mamy 8 jednakowo praw-
dopodobnych kolorowa´n (porównaj podrozdział 1.6.2).
Ω =
{BBB, BBC, BCB, BCC, CBB, CBC, CCB, CCC}.
Przypominamy, ˙ze na przykład,
CBB oznacza, ˙ze wierzchołek a jest pokolorowany na
czarno, a wierzchołki
b i c na biało. Łatwo zauwa˙zy´c, ˙ze zmienna X przyjmuje warto´s´c 0
dla dwóch kolorowa´n
BBB oraz CCC. Dla wszystkich innych kolorowa´n X przyjmuje
warto´s´c
2. Wi˛ec jej rozkład ma posta´c
x
0
2
f (x)
2
8
6
8
1.7.3
Rozkład jednopunktowy
Z rozkładem jednopunktowym mamy do czynienia, wtedy gdy całe prawdopodobie ´nstwo
jest skupione w jednym punkcie. Mówi ˛
ac inaczej zmienna losowa
X ma rozkład jedno-
punktowy, je˙zeli dla jekiego´s
m
P (X = m) = 1.
1.7.4
Rozkład zero-jedynkowy
Zmienna losowa
X ma rozkład zero-jedynkowy, je˙zeli prawdopodobie ´nstwo jest skupio-
ne tylko w dwóch punktach 0 i 1. G˛esto´s´c rozkładu prawdopodobie ´nstwa ma wtedy posta´c
x
0
1
f (x)
q
p
dla pewnych dodatnich
p, q spełniaj ˛
acych warunek
p + q = 1.
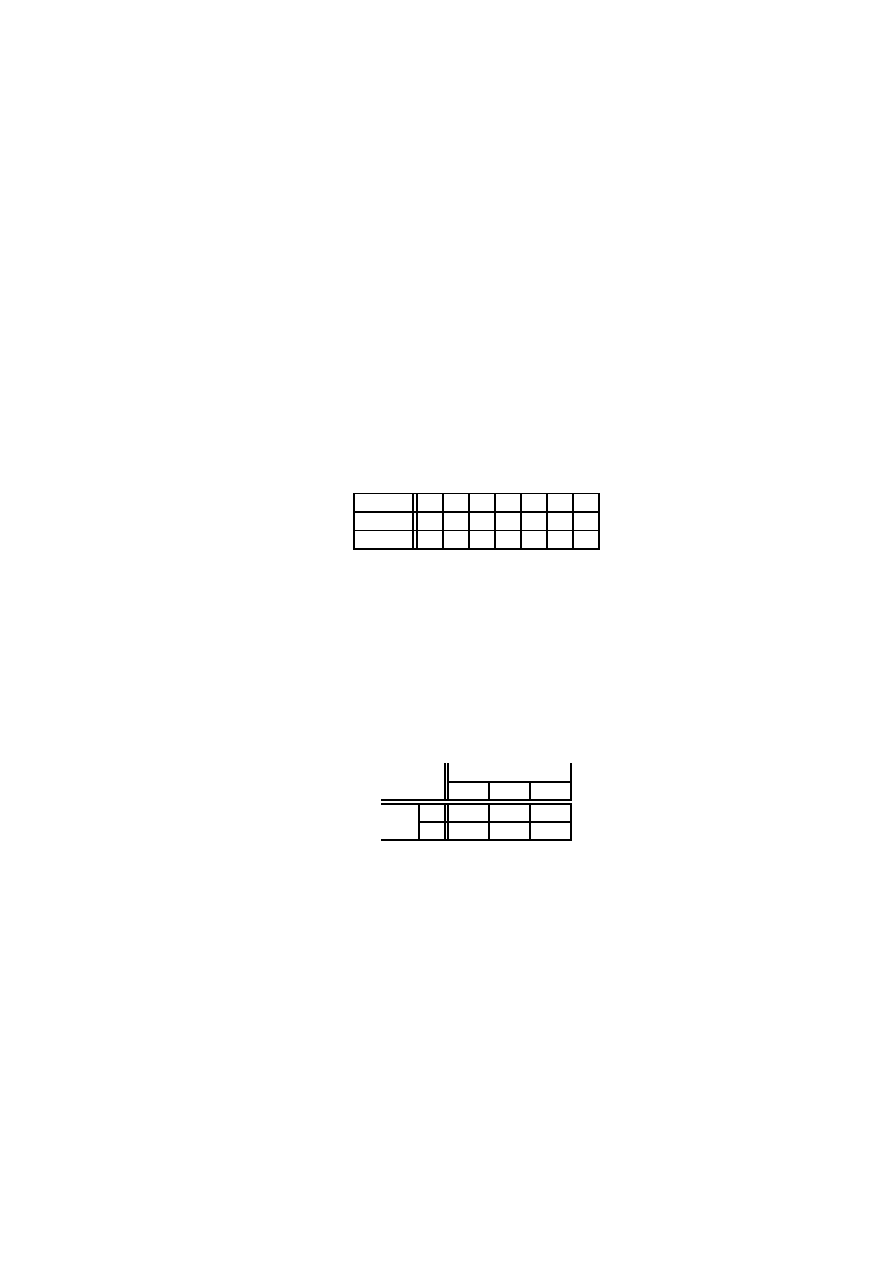
1.8. Ł ˛
aczny rozkład prawdopodobie ´nstwa
19
1.8
Ł ˛
aczny rozkład prawdopodobie ´nstwa
Mo˙ze si˛e zda˙zy´c, ˙ze na tej samej przestrzeni zdarze ´n elementarnych mamy okre´slone
dwie lub wi˛ecej zmiennych losowych.
Przykład 1.44 Rozwa˙zmy losowanie jednej kuli z urny zawieraj ˛
acej siedem ponumero-
wanych kul.
Ω =
{1, 2, 3, 4, 5, 6, 7}. Niech zmienna losowa X
2
bedzie zdefiniowana jako
X
2
(ω) = ω mod 2,
a zmienna losowa
X
3
jako
X
3
(ω) = ω mod 3.
(
X
2
(ω) jest reszt ˛
a z dzielenia numeru kuli przez 2, a
X
3
(ω) reszt ˛
a z dzielenia przez 3).
Warto´sci tych dwóch zmiennych zebrane s ˛
a w tabeli.
ω
1
2
3
4
5
6
7
X
2
(ω)
1
0
1
0
1
0
1
X
3
(ω)
1
2
0
1
2
0
1
1.8.1
G˛esto´s´c ł ˛
acznego rozkładu
W przypadku dwóch zmiennych losowych
X i Y okre´slonych na tej samej przestrzeni
zdarze´n elementarnych
Ω mamy tak zwany ł ˛
aczny rozkład prawdopodobie ´nstwa, którego
g˛esto´s´c jest okre´slona jako
f (x, y) = P (X = x i Y = y).
(X = x i Y = y) jest innym zapisem zdarzenia (X = x)
∩ (Y = y).
Przykład 1.45 Dla zmiennych
X
2
i
X
3
z przykładu 1.44 g˛esto´s´c ł ˛
acznego rozkładu praw-
dopodobie´nstwa przedstawiona jest w tabeli:
X
3
0
1
2
X
2
0
1/7
1/7
1/7
1
1/7
2/7
1/7
Mo˙zemy teraz oblicza´c prawdopodobie´nstwa zdarze´n opisywanych przez te zmienne. Na
przykład
P (X
2
= X
3
) = P (X
2
= 0 i X
3
= 0 lub X
2
= 1 i X
3
= 1) =
P (X
2
= 0 i X
3
= 0) + P (X
2
= 1 i X
3
= 1) = 1/7 + 2/7 = 3/7
lub
P (X
2
< X
3
) = P (X
2
= 0 i X
3
= 1 lub X
2
= 0 i X
3
= 2 lub X
2
= 1 i X
3
= 2) =
= 1/7 + 1/7 + 1/7 = 3/7
Łatwo mo˙zna zauwa˙zy´c, ˙ze sumuj ˛
ac wiersze tabeli ł ˛
acznego rozkładu mo˙zna otrzyma´c
g˛esto´s´c rozkładu zmiennej
X
2
, a sumuj ˛
ac kolumny g˛esto´s´c rozkładu
X
3
.
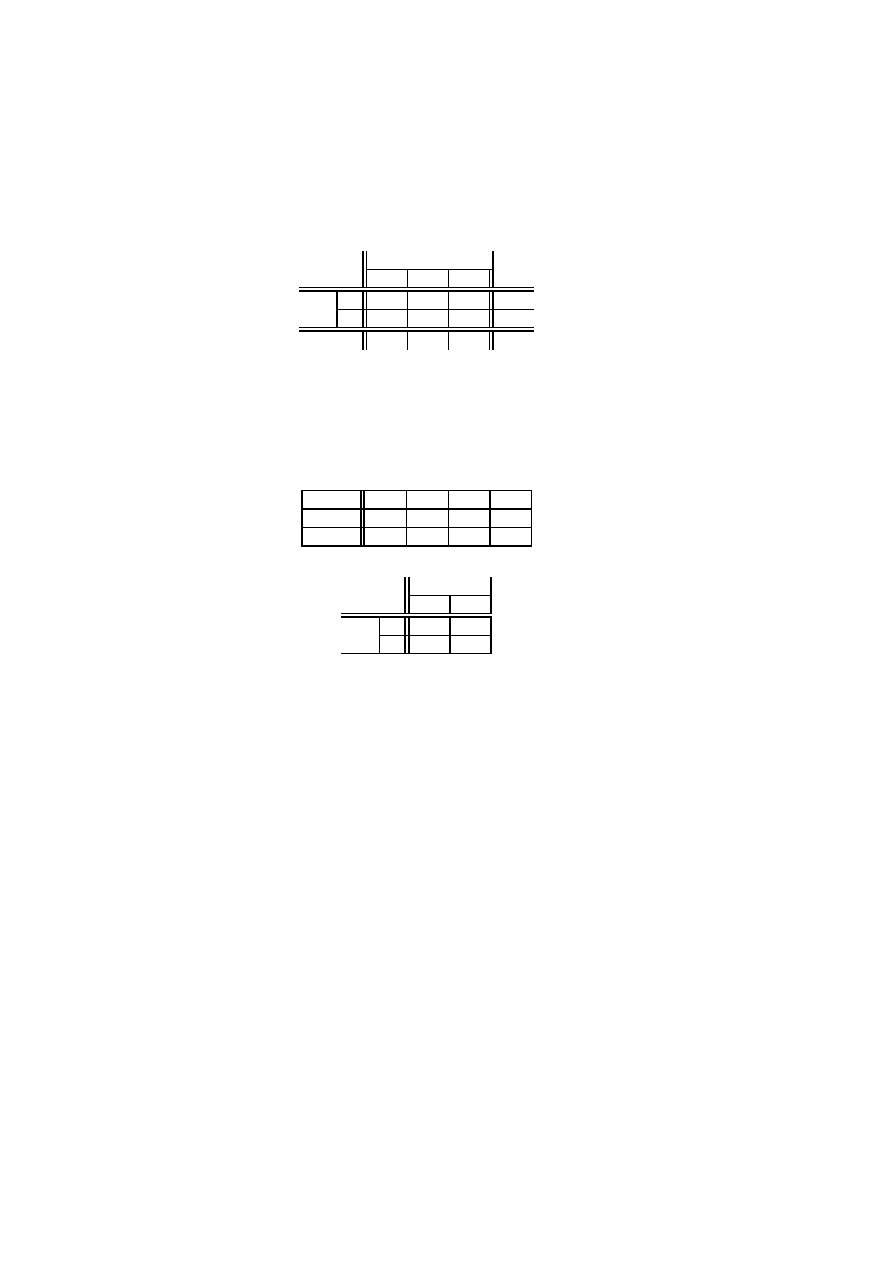
20
Rozdział 1. Rachunek prawdopodobie ´nstwa
X
3
0
1
2
X
2
0
1/7
1/7
1/7
3/7
1
1/7
2/7
1/7
4/7
2/7
3/7
2/7
Przykład 1.46 Rozwa˙zmy dwie zmienne losowe
X
1
i
X
2
okre´slone na przestrzeni
Ω =
{OO, OR, RO, RR}
opisuj ˛
acej wyniki dwukrotnego rzutu monet ˛
a.
Zmienna
X
1
przyjmuje warto´s´c
1, je˙zeli za pierwszym razem wypadnie orzeł, oraz
warto´s´c
0, je˙zeli za pierwszym razem wypadnie reszka. Podobnie zmienna X
2
opisuje
wynik drugiego rzutu. Warto´sci tych dwóch zmiennych zebrane s ˛
a w tabeli.
ω
OO
OR
RO
RR
X
1
(ω)
1
1
0
0
X
2
(ω)
1
0
1
0
Ł ˛
aczny rozkład prawdopodobie´nstwa przedstawiony jest w tabeli:
X
2
0
1
X
1
0
1/4
1/4
1
1/4
1/4
1.9
Niezale˙zno´s´c zmiennych losowych
Definicja 1.47 Zmienny losowe
X i Y s ˛
a niezale˙zne je˙zeli dla ka˙zdej pary liczb
x, y
mamy
P (X = x i Y = y) = P (X = x)
· P (Y = y)
lub inaczej, gdy
f
XY
(x, y) = f
X
(x)
· f
Y
(y),
gdzie
f
XY
oznacza g˛esto´s´c rozkładu ł ˛
acznego,
f
X
g˛esto´s´c zmiennej
X, a f
Y
g˛esto´s´c
zmiennej
Y .
Przykład 1.48 Zmienne losowe
X
1
i
X
2
z przykładu 1.46 s ˛
a niezale˙zne, a zmienne loso-
we
X
2
i
X
3
z przykładu 1.45 nie s ˛
a niezale˙zne.
Oczywi´scie mo˙ze by´c wi˛ecej zmiennych losowych okre´slonych na jednej przestrzeni
Dla trzech zmiennych losowych
X, Y , Z g˛esto´s´c ł ˛
acznego rozkładu prawdopodobie ´n-
stwa, zdefiniowana jest jako
f (x, y, z) = P (X = x i Y = y i Z = z).
W ogólnym przypadku
n zmiennych losowych X
1
, . . . , X
n
g˛esto´sc ich ł ˛
acznego rozkładu
okre´slona jest jako
f (x
1
. . . , x
n
) = P (X
1
= x
1
, . . . , X
n
= x
n
).

1.9. Niezale˙zno´s´c zmiennych losowych
21
Definicja 1.49 Zmienne losowe
X, Y , Z s ˛
a niezale˙zne je˙zeli dla ka˙zdej trójki liczb
x, y i
z mamy
f (x, y, z) = P (X = x)
· P (Y = y) · P (Z = z).
Podobnie mamy w przypadku
n zmiennych losowych
Definicja 1.50 Zmienne losowe
X
1
, . . . , X
n
s ˛
a niezale˙zne je˙zeli dla ka˙zdej
n-tki liczb
x
1
, . . . , x
n
zachodzi
P
n
\
i=1
(X
i
= x
i
)
=
n
Y
i=1
P (X
i
= x
i
),
czyli
f (x
1
, . . . , x
n
) =
n
Y
i=1
f
i
(x
i
),
gdzie
f oznacza g˛esto´s´c rozkładu ł ˛
acznego, a
f
i
g˛esto´s´c rozkładu zmiennej
X
i
.
Przykład 1.51 Rozwa˙zmy
n krotny rzut symetryczn ˛
a monet ˛
a. Przestrze´n zdarze´n elemen-
tarnych zawiera ci ˛
agi długo´sci
n o elementach ze zbioru
{O, R} i ka˙zdy ci ˛
ag jest równie
prawdopodobny. Dla ka˙zdego
i od 1 do n okre´slmy zmienn ˛
a losow ˛
a
X
i
:
X
i
(ω) =
1, je˙zeli za i-tym razem wypadł orzeł
0, je˙zeli za i-tym razem wypadła reszka
Zmienne
X
1
, . . . , X
n
s ˛
a niezale˙zne. Prze´sled´zmy to dla
n = 3 (patrz podrozdział 1.6.1).
Dla ka˙zdej trójki liczb
x
1
,
x
2
,
x
3
zdarzenie
(X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
)
zawiera tylko jeden ci ˛
ag. Na przykład zdarzenie
(X
1
= 1 i X
2
= 0 i X
3
= 0) =
{ORR}.
Czyli dla ka˙zdej trójki
x
1
,
x
2
,
x
3
prawdopodobie´nstwo
P (X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
) =
1
8
.
Z drugiej strony, dla ka˙zdego
i
∈ {1, 2, 3} mamy P (X
i
= x
i
) =
1
2
, czyli
P (X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
) = P (X
1
= x
1
)
· P (X
2
= x
2
)
· P (X
3
= x
3
).
Zmienne
X
1
, . . . , X
n
s ˛
a niezale˙zne tak˙ze w przypadku rzutu niesymetryczn ˛
a monet ˛
a.
Znowu poka˙zemy to dla
n = 3. W ogólnym przypadku dowód jest podobny. Tak jak dla
rzutu symetryczn ˛
a monet ˛
a dla ka˙zdej trójki liczb
x
1
,
x
2
,
x
3
zdarzenie
(X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
)
zawiera tylko jeden ci ˛
ag. Jego prawdopodobie´nstwo
P (X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
) = p
k
q
3−k
,

22
Rozdział 1. Rachunek prawdopodobie ´nstwa
gdzie
k oznacza liczb˛e jedynek w ci ˛
agu
(x
1
, x
2
, x
3
).
Z drugiej strony zdarzenie
(X
i
= 1) zawiera wszystkie ci ˛
agi, które na
i-tej pozycji
maj ˛
a
O. W podrozdziale 1.6.3 pokazano, ˙ze prawdopodobie´nstwo takiego zdarzenia wy-
nosi
p. Podobnie (X
i
= 0) zawiera wszystkie ci ˛
agi, które na
i-tej pozycji maj ˛
a
R, a jego
prawdopodobie´nstwo wynosi
q. Tak wi˛ec
P (X
1
= x
1
i
X
2
= x
2
i
X
3
= x
3
) = P (X
1
= x
1
)
· P (X
2
= x
2
)
· P (X
3
= x
3
).
1.9.1
Własno´s´c niezale˙znych zmiennych losowych
Poka˙zemy teraz, ˙ze je˙zeli zmienne losowe
X i Y s ˛
a niezale˙zne, to niezale˙zne s ˛
a te˙z zmien-
ne
X
− a i Y − b. Dokładniej
Lemat 1.52 Niech
X i Y b˛ed ˛
a niezale˙znymi zmiennymi losowymi, a
a i b dowolnymi
liczbami rzeczywistymi. Wtedy zmienne
X
− a i Y − b s ˛
a niezale˙zne.
Dowód: Niech
X
1
= X
− a oraz Y
1
= Y
− b. Zaywa˙zmy, ˙ze X
1
(ω) = x
1
wtedy i
tylko wtedy, gdy
X(ω) = a + x
1
, czyli zdarzenie
X
1
= x
1
pokrywa si˛e ze zdarzeniem
X = a + x
1
. Podobnie zdarzenie
Y
1
= y
1
pokrywa si˛e ze zdarzeniem
Y = a + y
1
.
Mamy wi˛ec
P (X
1
= x
1
i
Y
1
= y
1
) = P (X = a + x
1
i
Y = b + y
1
) =
P (X = a + x
1
)
· P (Y = b + y
1
) = P (X
1
= x
1
)
· P (Y
1
= y
1
).
´Srodkowa równo´s´c wynika z niezale˙zno´sci zmiennych X i Y .
2
1.10
Rozkład dwumianowy — Bernoulliego
Przypomnijmy sobie schemat dwumianowy z seri ˛
a
n do´swiadcze´n (rzutów monet ˛
a) i z
prawdopodobie ´nstwem sukcesu (wypadni˛ecia orła) w pojedy ´nczym do´swiadczeniu rów-
nym
p (podrozdział 1.6.4) Przestrze ´n zdarze´n elementarnych jest zbiorem wszystkich ci ˛
a-
gów długo´sci
n z elementami O i R, w którym prawdopodobie ´nstwo ci ˛
agu
ω
∈ Ω jest
równe
p
k
q
n−k
,
gdzie
k oznacza liczb˛e symboli O w ci ˛
agu
ω.
Niech zmienna losowa
X oznacza liczb˛e sukcesów (orłow) w serii. Mówimy, ˙ze
zmienna losowa
X posiada rozkład dwumianowy (Bernouliego) z parametrami: długo-
´sci ˛
a serii
n i prawdopodobie´nstwem sukcesu p. Zmienna losowa X przyjmuje warto´sci k
od
0 do n. Prawdopodobie´nstwo, ˙ze zmienna X posiada warto´s´c k wynosi
P (x = k) =
n
k
p
k
q
n−k
.
Przykładem zminnej losowej z rozkładem dwumianowym jest zmienna opisana w
przykładzie 1.36, która okre´sla liczb˛e orłów w serii 3 rzutów.
Dla
n = 4 rozkład zmiennej X wygl ˛
ada nast˛epuj ˛
aco:
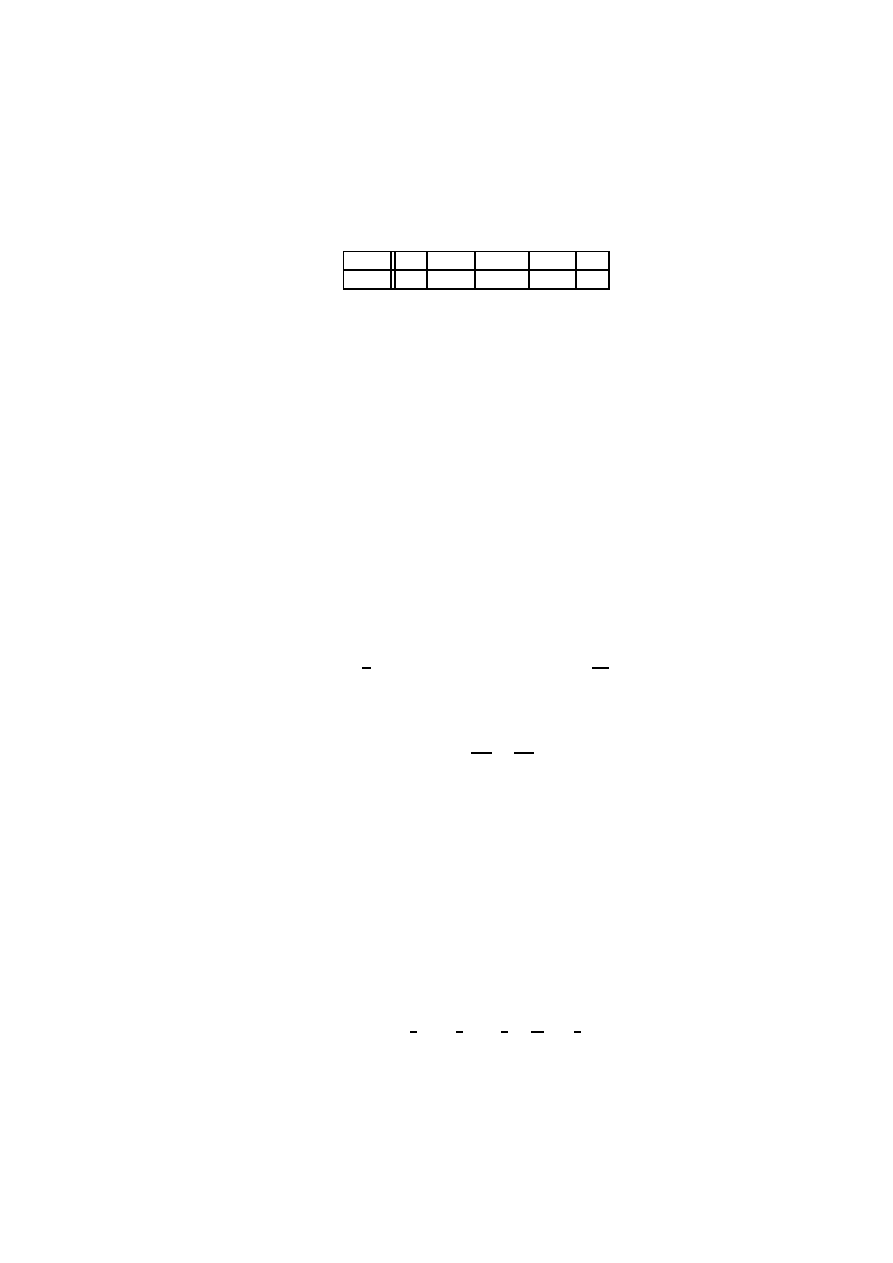
1.11. Warto´s´c oczekiwana, ´srednia
23
x
0
1
2
3
4
f (x)
q
4
4pq
3
6p
2
q
2
4p
3
q
p
4
Zauwa˙zmy, ˙ze zmienna losowa
X jest sum ˛
a zmiennych
X(ω) =
n
X
i=1
X
i
(ω),
gdzie, dla ka˙zdego
i zmienna X
i
oznacza wynik
i tego rzutu i jest równa
X
i
(ω) =
1, je˙zeli za i-tym razem wypadł orzeł
0, je˙zeli za i-tym razem wypadła reszka
Rzeczywi´scie, dla ka˙zdego ci ˛
agu
ω suma
P
n
i=1
X
i
(ω) jest równa liczbie indeksów i
∈
{1, . . . , n}, dla których X
i
(ω) = 1, czyli liczbie pozycji, na których w ci ˛
agu
ω stoi orzeł.
1.11
Warto´s´c oczekiwana, ´srednia
Definicja 1.53 Warto´s´c oczekiwana (´srednia) zniennej losowej
X to liczba
E(X) =
X
ω∈Ω
X(ω)
· P (ω).
Przykład 1.54 Dla zmiennej losowej
X z przykładu 1.36 warto´s´c oczekiwana wynosi
E(X) =
1
8
(3 + 2 + 2 + 1 + 2 + 1 + 1 + 0) =
12
8
= 1.5
Je˙zeli zmienna posiada jednostajny rozkład prawdopodobie ´nstwa, to jej warto´s´c oczeki-
wana jest zwykł ˛
a ´sredni ˛
a arytmetyczn ˛
a jej warto´sci.
E(X) =
X
ω∈Ω
X(ω)
·
1
|Ω|
=
1
|Ω|
·
X
ω∈Ω
X(ω).
W ogólnym przypadku warto´s´c oczekiwana jest nazywana ´sredni ˛
a wa˙zon ˛
a. Je˙zeli mamy
rozkład zmiennej losowej, to warto´s´c oczekiwan ˛
a obliczamy według wzoru.
Lemat 1.55
E(X) =
P
x∈X(Ω)
x
· P (X = x).
Dowód: Je˙zeli pogrupujemy wyrazy sumy
P
ω∈Ω
X(ω)
·P (ω) według warto´sci zmiennej
X, to otrzymamy
E(X) =
X
ω∈Ω
X(ω)
· P (ω) =
X
x∈X(Ω)
x
X
X(ω)=x
P (ω) =
X
x∈X(Ω)
x
· P (X = x).
Przykład 1.56 Przypu´s´cmy, ˙ze mamy informacj˛e, ˙ze w jakiej´s grupie studenckiej połowa
studentów otrzymała ocen˛e 5 z matematyki dyskretnej, jedna trzecia otrzymała ocen˛e 4,
a jedna szósta ocen˛e 3. Jaka jest ´srednia ocena w tej grupie? Przyjmujemy, ˙ze grupa jest
przestrzeni ˛
a losow ˛
a, a zmienna losowa
X jest ocen ˛
a studenta. Wtedy warto´s´c oczekiwana
zmiennej
X wynosi E(X) = 5
·
1
2
+ 4
·
1
3
+ 3
·
1
6
=
26
6
= 4
1
3
i jest ´sredni ˛
a ocen ˛
a w tej
grupie.

24
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.11.1
Własno´sci warto´sci oczekiwanej
W poni˙zszym twierdzeniu zebrano podstawowe własno´sci warto´sci oczekiwanej.
Twierdzenie 1.57
a)
E(X + Y ) = E(X) + E(Y ).
b) Je˙zeli
a jest liczb ˛
a rzeczywist ˛
a, to
E(a
· X) = a · E(X).
c) Je˙zeli zmienne
X i Y s ˛
a niezale˙zne, to
E(X
· Y ) = E(X) · E(Y ).
d) Je˙zeli
X
≥ 0, to E(X) ≥ 0.
Dowód:
a)
E(X + Y ) =
X
ω∈Ω
(X + Y )(ω)
· P (ω) =
X
ω∈Ω
(X(ω) + Y (ω))
· P (ω) =
X
ω∈Ω
X(ω)
· P (ω) +
X
ω∈Ω
Y (ω)
· P (ω) = E(X) + E(Y ).
b)
E(a
·X) =
X
ω∈Ω
(a
·X)(ω)·P (ω) =
X
ω∈Ω
a
·X(ω)·P (ω) = a·
X
ω∈Ω
X(ω)
·P (ω) = a·E(X).
c)
E(X
· Y ) =
X
ω∈Ω
XY (ω)P (ω).
Pogrupujmy składniki sumy według warto´sci zmiennych
X i Y .
E(X
· Y ) =
X
x
X
y
x
· y ·
X
X
(ω)=x
Y
(ω)=y
P (ω)
=
X
x
X
y
x
· y · P (X = x i Y = y) =
X
x
X
y
x
· y · P (X = x) · P (Y = y)
=
X
x
x
· P (X = x)
·
X
y
y
· P (Y = y)
= E(X) · E(Y ).
d)
Je˙zeli dla ka˙zdego
ω, X(ω)
≥ 0, to
P
ω∈Ω
X(ω)
· P (ω) ≥ 0.
2
Punkt a) powy˙zszego twierdzenia mo˙zna uogólni´c (za pomoc ˛
a indukcji) na sume
n
zmiennych.
Twierdzenie 1.58 Warto´s´c oczekiwana sumy
k zmiennych X
1
, . . . , X
k
jest równa
E(
k
X
i=1
X
i
) =
k
X
i=1
E(X
i
).

1.11. Warto´s´c oczekiwana, ´srednia
25
1.11.2
Warto´s´c oczekiwana rozkładu jednopunktowego
Warto´s´c oczekiwana zmiennej
X z rozkładem jednopunktowym wynosi
E(X) = m.
Z definicji warto´sci oczekiwanej wynika nast˛epuj ˛
acy fakt:
Lemat 1.59 Je˙zeli jaka´s zmienna
X przyjmuje warto´sci nieujemne i E(X) = 0, to ma
ona rozkład jednopunktowy.
Zało˙zenie, ˙ze zmienna
X przyjmuje tylko warto´sci nieujemne jest istotne we wnio-
sku 1.59. Pokazuje to nast˛epuj ˛
acy przykład.
Przykład 1.60 Zmienna losowa
Z z funkcj ˛
a g˛esto´sci:
z
i
-1
1
f (z
i
)
1
2
1
2
ma warto´s´c oczekiwan ˛
a
E(Z) = 0.
1.11.3
Warto´s´c oczekiwana rozkładu zero-jedynkowego
Warto´s´c oczekiwana zmiennej
X z rozkładem zero-jedynkowym wynosi
E(X) = 0q + 1p = p
1.11.4
Warto´s´c oczekiwana rozkładu dwumianowego
Warto´s´c oczekiwana zmiennej losowej
X maj ˛
acej rozkład dwumianowy z długo´sci ˛
a serii
n i prawdopodobie´nstwem sukcesu p wynosi E(X) = np.
Wynika to z twierdzenia 1.58 oraz z faktu, ˙ze jak zauwa˙zyli´smy w podrozdziale 1.10,
zmienna
X jest sum ˛
a
n zmienych o rozkładzie zero-jedynkowym X =
P
n
i=1
X
i
.
1.11.5
Warto´s´c oczekiwana liczby ró˙znokolorowych kraw˛edzi
Policzymy teraz warto´s´c oczekiwan ˛
a zmiennej
X okre´slaj ˛
acej liczb˛e ró˙znokolorowych
kraw˛edzi w grafie
G = (V, E) z n =
|V | wierzchołkami (przykład 1.43). W tym celu dla
ka˙zdej kraw˛edzi
e =
{u, v} ∈ E okre´slmy zmienn ˛a losow ˛a X
e
w nast˛epuj ˛
acy sposób:
X
e
(ω) =
1, je˙zeli w kolorowaniu ω oba ko´nce kraw˛edzi e
maj ˛
a ró˙zne kolory,
0, w przeciwnym przypadku.
W przykładzie 1.22 pokazano, ˙ze prawdopodobie ´nstwo tego, ˙ze dowolna kraw˛ed´z ma
ko´nce w ró˙znych kolorach wynosi
1
2
, czyli
E(X
e
) =
1
2
.
Zauwa˙zmy teraz, ˙ze
X =
X
e∈E
X
e
.

26
Rozdział 1. Rachunek prawdopodobie ´nstwa
Rzeczywi´scie dla dowolnego kolorowania
ω suma X =
P
e∈E
X
e
(ω) jest równa liczbie
kraw˛edzi; dla których
X
e
(ω) = 1, czyli liczbie kraw˛edzi z róznymi kolorami na ko ´ncach.
Tak wi˛ec mamy
E(X) =
X
e∈E
E(X
e
) =
m
2
.
E(X), czyli ´srednia liczba ró˙znokolorowych kraw˛edzi w kolorowaniu mo˙ze by´c obliczo-
na bez u˙zywania terminologii rachunku prawdopodobie ´nstwa. Policzmy ile we wszyst-
kich kolorowaniach jest ró˙znokolorowych kraw˛edzi. Z jednej strony jest to
X
ω∈Ω
(liczba ró˙znokolorowych kraw˛edzi w kolorowaniu ω).
Z drugiej strony
X
e∈E
(liczba kolorowa´n, w których kraw˛ed´z e jest ró˙znokolorowa) =
X
e∈E
2
n−1
= m
·2
n−1
.
Przedostatnia równo´s´c wynika z tego, ˙ze liczba kolorowa ´n, w których
e jest ró˙znoko-
lorowa wynosi
2
n−1
(połowa wszystkich). ´Srednia liczba ró˙znokolorowych kraw˛edzi w
kolorowaniu wynosi wi˛ec
m
· 2
n−1
2
n
=
m
2
.
1.11.6
Własno´sci warto´sci oczekiwanej c.d.
Cz˛esto wykorzystywana własno´s´c warto´sci oczekiwanej mówi, ˙ze zawsze istnieje przy-
najmniej jedna warto´s´c mniejsza od lub równa warto´sci ´sredniej oraz warto´s´c wi˛eksza od
lub równa ´sredniej.
Lemat 1.61 Dla ka˙zdej zmiennej losowej
X istnieje zdarzenie elementarne ω
∈ Ω takie,
˙ze
P (ω) > 0 oraz X(ω)
≥ E(X).
Podobnie istnieje zdarzenie
ω
∈ Ω takie, ˙ze P (ω) > 0 oraz X(ω) ≤ E(X).
Dowód: Udowodnimy tylko pierwsz ˛
a cz˛e´s´c twierdzenia, drug ˛
a mo˙zna udowodni´c w po-
dobny sposób. Przypu´s´cmy, ˙ze dla ka˙zdego
ω
∈ Ω z dodatnim prawdopodobie´nstwem
mamy
X(ω) < E(X). Ale to prowadzi do sprzeczno´sci
E(X) =
X
ω∈Ω
X(ω)
· P (ω) <
X
ω∈Ω
E(X)
· P (ω) = E(X)
X
ω∈Ω
P (ω) = E(X).
2
Przykład 1.62 Wierzchołki dowolnego grafu mo˙zna pokolorowa´c dwoma kolarami (bia-
łym i czarnym) w taki sposób, ˙ze przynajmniej połowa kraw˛edzi ma swoje ko´nce w ró˙z-
nych kolorach. Niech
X oznacza liczb˛e ró˙znokolorowych kraw˛edzi w grafie. W podroz-
dziale 1.11.5 pokazano, ˙ze warto´s´c oczekiwana zmiennej
X wynosi
m
2
, czyli musi istnie´c
kolorowanie z co najmniej połow ˛
a ró˙znokolorowych kraw˛edzi.
1.12. Nierówno´s´c Markowa
27
1.12
Nierówno´s´c Markowa
Twierdzenie 1.63 (Nierówno´s´c Markowa) Je˙zeli zmienna losowa
X przyjmuje warto´sci
nieujemne, to dla dowolnej liczby rzeczywistej
d > 0
P (X
≥ d) ≤
E(X)
d
.
Dowód:
E(X) =
X
x
x
· P (X = x) =
X
x≥d
x
· P (X = x) +
X
x<d
x
· P (X = x) ≥
X
x≥d
x
· P (X = x) ≥
X
x≥d
d
· P (X = x) = d
X
x≥d
P (X = x) = d
· P (X ≥ d),
czyli
E(X)
≥ d · P (X ≥ d). Po podzieleniu tej nierówno´sci stronami przez d otrzymu-
jemy tez˛e twierdzenia.
2
Zauwa˙zmy, ˙ze nierówno´s´c Markowa jest u˙zyteczna tylko kiedy
d > E(X). Je˙zeli
bowiem
d
≤ E(X), to mamy trywialne oszacowanie P (X ≥ d) ≤ 1 ≤
E(X)
d
.
Przykład 1.64 Nierówno´s´c Markowa wyra˙za do´s´c prosty fakt. Przypu´s´cmy, ˙ze
X okre´sla
liczb˛e pieni˛edzy posiadan ˛
a przez studenta. Je˙zeli warto´s´c ´srednia zmiennej
X wynosi 100
złotych, to tylko połowa studentów mo˙ze mie´c 200 lub wi˛ecej złotych. Przypu´s´cmy bowiem
˙ze
0.5 + cz˛e´s´c studentów posiada 200 (lub wi˛ecej) złotych. Wtedy udział tej bogatej
cz˛e´sci studentów w ´sredniej wynosi co najmniej
200
· (0.5 + ) = 100 + 200 · > 100, i
warto´s´c ´srednia nie mo˙ze wynosi´c 100 złotych.
Przykład 1.65 Niech zmienna losowa
X posiada rozkład dwumianowy z długo´sci ˛
a serii
n = 1000 oraz prawdopodobie´nstwem sukcesu p =
1
2
. Spróbujmy oszacowa´c prawdo-
podobie´nstwo
P (X
≥ 600). Warto´s´c oczekiwana E(X) = np = 500. Z nierówno´sci
Markowa otrzymamy oszacowanie
P (X
≥ 600) ≤
500
600
=
5
6
.
Oszacowanie to jest bardzo grube. Zauwa˙zmy, ˙ze
P (X
≥ 500) =
1
2
, poniewa˙z rozkład
jest symetryczny
P (X = k) = P (X = 1000
− k) dla ka˙zdego k.
1.13
Wariancja
Definicja 1.66 Wariancj ˛
a zmiennej losowej
X o warto´sci oczekiwanej E(X) = m
X
nazywamy liczb˛e
V ar(X) = E((X
− m
X
)
2
)
Wariancja
V ar(X) jest miar ˛
a tego jak bardzo warto´sci zmiennej
X s ˛
a oddalone od ´sred-
niej. Im wi˛eksze rozrzucenie warto´sci tym wi˛eksza wariancja. W poni˙zszym twierdzeniu
zebrano podstawowe własno´sci wariancji

28
Rozdział 1. Rachunek prawdopodobie ´nstwa
Twierdzenie 1.67
a)
V ar(X)
≥ 0.
b)
V ar(X) = E(X
2
)
− m
2
X
c)
V ar(aX) = a
2
V ar(X).
d) Je˙zeli zmienne
X i Y s ˛
a niezale˙zne, to
V ar(X + Y ) = V ar(X) + V ar(Y ).
e) Je˙zeli zmienne
X
1
, . . . , X
k
s ˛
a parami niezale˙zne, to
V ar
k
X
i=1
X
i
=
k
X
i=1
V ar(X
i
)
Dowód:
a)
wynika z faktu, ˙ze zmienna
(X
− m
X
)
2
przyjmuje tylko nieujemne warto´sci,
b)
V ar(X) = E((X
− m
X
)
2
) = E(X
2
− 2m
X
· X + m
2
X
) = E(X
2
)
− 2m
X
E(X) +
m
2
X
= E(X
2
)
− 2m
2
X
+ m
2
X
= E(X
2
)
− m
2
X
c)
V ar(aX) = E(aX
− E(aX))
2
= E(a
2
(X
− EX)
2
) = a
2
V ar(X).
d)
Pami˛etajmy, ˙ze
E(X + Y ) = m
X
+ m
Y
. Mamy
(X+Y
−E(X+Y ))
2
= (X
−m
X
+Y
−m
Y
)
2
= (X
−m
X
)
2
+(y
−m
Y
)
2
+2(X
−m
X
)(Y
−m
Y
)
czyli
V ar(X+Y ) = E(X
−m
X
)
2
+E(Y
−m
Y
)
2
+2E(X
−m
X
)E(Y
−m
Y
) = V ar(X)+V ar(Y ).
Przedstatnia równo´s´c wynika z faktu, ˙ze na podstawie lematu 1.52 zmienne
X
−m
X
oraz
Y
− m
Y
s ˛
a niezale˙zne, a ostatnia równo´s´c z faktu, ˙ze
E(X
− m
X
) = m
X
− m
X
= 0.
e)
Podobnie jak w przypadku d) korzystaj ˛
ac z faktu, ˙ze
k
X
i=1
X
i
−
k
X
i=1
m
X
i
2
=
k
X
i=1
(X
i
− m
X
i
)
2
+ 2
k
X
i=1
k
X
j=i+1
(X
i
− m
X
i
)(X
j
− m
X
j
)
oraz z faktu, ˙ze zmienne
X
1
− m
X
1
, .... ,
X
k
− m
X
k
s ˛
a parami niezale˙zne.
2
1.13.1
Wariancja rozkładu jednopunktowego
Wariancja zmiennej losowej
X z rozkładem jednopunktowym wynosi
V ar(X) = E(X
2
)
− (E(X))
2
= m
2
− m
2
= 0.
Ale i na odwrót
Lemat 1.68 Je˙zeli
V ar(X) = 0, to zmienna losowa X posiada rozkład jednopunktowy.
Dowód: Poniewa˙z
V ar(X) = E((X
− m
X
)
2
) = 0, to z lematu 1.59 wynika, ˙ze 1 =
P (X
− m
X
= 0) = P (X = m
X
).
2
1.13. Wariancja
29
1.13.2
Wariancja rozkładu zero-jedynkowego
Je˙zeli
X ma rozkład zero-jedynkowy to jego wariancvja wynosi
V ar(X) = E(X
2
)
− (E(X))
2
= p
− p
2
= p(1
− p) = pq.
1.13.3
Wariancja rozkładu dwumianowego
Je˙zeli zmienna losowa
X ma rozkład dwumianowy z długo´sci ˛
a serii
n i prawdopodobie´n-
stwem sukcesu
p, to jest sum ˛
a
X =
P
n
i=1
X
i
niezale˙znych zmiennych
X
i
o rozkładach
zero-jedynkowych. Wariancja ka˙zdej zmiennej
X
i
wynosi
V ar(X
i
) = pq. Wariancja
zmiennej losowej
X wynosi wi˛ec
V ar(X) = npq.
1.13.4
Wariancja liczby ró˙znokolorowych kraw˛edzi
Obliczmy variancj˛e zmiennej losowej
X oznaczaj ˛
acej liczb˛e kraw˛edzi dwukolorowych w
kolorawaniu grafu
G (patrz podrozdział 1.11.5). Najpierw zauwa˙zmy, ˙ze zmienne losowe
X
e
s ˛
a parami niezale˙zne. Dokładniej, je˙zeli
e
1
i
e
2
s ˛
a dwoma ró˙znymi kraw˛edziami grafu
G, to zmienne X
e
1
i
X
e
2
s ˛
a niezale˙zne. Niech
e
1
=
{u
1
, v
1
} i e
2
=
{u
2
, v
2
}. Poniewa˙z
kraw˛edzie s ˛
a ró˙zne, to mog ˛
a mie´c tylko jeden wspólny koniec. Załó˙zmy, ˙ze wierzchołek
v
2
/
∈ e
1
. W przykładzie 1.6.2 pokazali´smy, ˙ze jednostajny rozkład pokolorowa ´n otrzy-
mamy koloruj ˛
ac po kolei wierzchołki niezale˙znie i ze stałym prawdopodobie ´nstwem:
1
2
dla koloru białego i
1
2
dla czarnego. Mo˙zemy zało˙zy´c, ˙ze wierzchołek
v
2
jest kolorawny
ostatni. Łatwo teraz zauwa˙zy´c, ˙ze przy jednym wyborze koloru dla
v
2
mamy
X
e
1
= X
e
2
,
a przy drugim
X
e
1
6= X
e
2
. Ł ˛
aczny rozkład prawdopodobie ´nstwa zmiennych
X
e
1
i
X
e
2
wygl ˛
ada wi˛ec nast˛epuj ˛
aco:
X
e
2
0
1
X
e
1
0
1/4
1/4
1
1/4
1/4
czyli zmienne te s ˛
a niezałe˙zne.
Dla ka˙zdej kraw˛edzi
e mamy V ar(X
e
) =
1
4
i na podstawie twierdzenia 1.67e mamy
V ar(X) =
m
4
.
Zauwa˙zmy, ˙ze cały komplet zmiennych
X
e
dla wszystkich kraw˛edzi grafu nie musi
by´c niezale˙zny. Na przykład, je˙zeli trzy kraw˛edzie
e
1
,
e
2
i
e
3
tworz ˛
a trójk ˛
at, to zmienne
X
e
1
,
X
e
2
,
X
e
3
nie s ˛
a niezale˙zne. Rzeczywi´scie, je˙zeli
X
e
1
(ω) = X
e
2
(ω) = 0, to w
kolorowaniu
ω ko´nce obu kraw˛edzi e
1
i
e
2
maja taki sam kolor, ale wtedy, tak˙ze ko ´nce
kraw˛edzi
e
3
s ˛
a w tym samym kolorze i
X
e
3
(ω) = 0.
30
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.14
Nierówno´s´c Czebyszewa
Twierdzenie 1.69 (Nierówno´s´c Czebyszewa) Dla zmiennej losowej
X z warto´sci ˛
a ocze-
kiwan ˛
a
E(X) = m
X
oraz liczby rzeczywistej
> 0 mamy
P (
|X − m
X
| ≥ ) ≤
V ar(X)
2
.
Dowód: Rozwa˙zmy zmienn ˛
a losow ˛
a
Y = X
− m
X
. Poniewa˙z
|Y (ω)| ≥ ⇔ Y
2
(ω)
≥
2
,
to
P (
|Y | ≥ ) = P (Y
2
≥
2
).
Stosuj ˛
ac nierówno´s´c Markowa dla zmiennej
Y
2
mamy
P (
|Y | ≥ ) = P (Y
2
≥
2
)
≤
E(Y
2
)
2
ale
E(Y
2
) = E((X
− m
X
)
2
) = V ar(X)
2
Przykład 1.70 (Kontynuacja przykładu 1.65). Dla zmienneja losowej
X z rozkładem
dwumianowy z parametrami
n = 1000 oraz p =
1
2
spróbujmy oszacowa´c prawdo-
podobie´nstwo
P (X
≥ 600). Warto´s´c oczekiwana E(X) = np = 500, a wariancja
V ar(X) = npq = 250. Z symetrii rozkładu wynika, ˙ze
P (X
≥ 600) =
1
2
P (
|x − 500| ≥ 100)
i z nierówno´sci Czebyszewa otrzymamy
P (X
≥ 600) ≤
1
2
·
250
10000
=
1
80
= 0.0125.
1.15
Kra ´nce rozkładu dwumianowego
Dla zmiennej losowej
X z rozkładem dwumianowym istniej ˛
a oszacowania, które w nie-
których przypadkach s ˛
a lepsze od nierówno´sci Czebyszewa.
Twierdzenie 1.71 (Nierówno´sci Chernoff’a) Niech zmienna losowa
X posiada rozkład
dwumianowy z długo´sci ˛
a serii
n i prawdopodobie´nstwem sukcesu p. Oznaczmy warto´s´c
oczekiwan ˛
a tego rozkładu przez
m = np. Wtedy dla dowolnej liczby rzeczywistej , 0
≤
≤ 1, mamy
P (X
≥ (1 + )m) ≤ e
−
2
m/3
oraz
P (X
≤ (1 − )m) ≤ e
−
2
m/2
1.16. Problem dnia urodzin
31
Przykład 1.72 Je˙zeli zastosujemy pierwsz ˛
a nierówno´s´c Chernoffa do przykładu 1.70, to
otrzymamy oszacowanie
P (X
≥ 600) = P (X ≥ (1 +
1
5
)500)
≤ e
−20/3
≤
1
786
Je˙zeli skorzystamy z symetrii rozkładu i z drugiej nierówno´s´c Chernoffa, to otrzymamy
du˙zo lepsze oszacowanie
P (X
≥ 600) = P (X ≤ 400) = P (X ≤ (1 −
1
5
)500)
≤ e
−10
≤
1
22027
1.16
Problem dnia urodzin
Przypu´s´cmy, ˙ze na przyj˛eciu jest
k osób. Wtedy prawdopodobie ´nstwo, ˙ze nowo przybyła
osoba ma urodziny tego samego dnia, co jaka´s z osób ju˙z obecnych jest nie wi˛eksze ni˙z
k
365
. Tak wi˛ec,
k musi by´c wi˛eksze ni˙z
365
2
, aby prawdopodobie ´nstwo to przekroczyło
1
2
.
Zastanówmy si˛e teraz ile osób musi znajdowa´c si˛e w pokoju, aby była du˙za szansa
(wi˛eksza od
1
2
), ˙ze dwie osoby maj ˛
a urodziny tego samego dnia.
Dla prostoty przyjmujemy, ˙ze problem dnia urodzin jest równowa˙znu problemowi
wylosowania ci ˛
agu
k liczb u
1
, . . . , u
k
, ka˙zda spo´sród
n = 365 mo˙zliwo´sci, tak aby wy-
st ˛
apiło w nim jakie´s powtórzenie.
Oznaczmy przez
B
k
zdarzenie przeciwne, ˙ze wszystkie wylosowane liczby s ˛
a ró˙zne.
Je˙zeli zało˙zymy, ˙ze wszystkie ci ˛
agi s ˛
a równo prawdopodobne, to prawdopodobie ´nstwo,
˙ze otrzymamy ci ˛
ag ró˙znowarto´sciowy wynosi
P (B
k
) =
n(n
− 1) · · · (n − k + 1)
n
k
= 1
· (
n
− 1
n
)
· (
n
− 2
n
)
· · · (
n
− k + 1
n
) =
= 1
· (1 −
1
n
)
· (1 −
2
n
)
· · · (1 −
k
− 1
n
).
Skorzystamy teraz z nierówno´sci
1 + x
≤ e
x
P (B
k
)
≤ e
−1/n
e
−2/n
· · · e
−(k−1)/n
= e
−
P
k−1
i
=1
i/n
=
= e
−k(k−1)/2n
≤ e
−(k−1)(k−1)/2n
= e
−(k−1)
2
/2n
.
Prawdopodobie ´nstwo to jest mniejsze od
1
2
wtedy gdy
(k
− 1)
2
≥ 2n ln 2, a to zachodzi
wtedy gdy
k
≥ 1 +
√
2 ln 2
√
n. Dla n = 365, zachodzi to dla k
≥ 24.
Tak wi˛ec je´sli w pokoju znajduj ˛
a si˛e co najmniej 24 osoby, to z prawdopodobie ´nstwem
wi˛ekszym od
1
2
dwie spo´sród nich maj ˛
a urodziny w tym samym dniu.
1.17
Algorytmy probabilistyczne
Algorytmy probabilistyczne to algorytmy, które w trakcie obliczenia dokonuj ˛
a losowych
wyborów. Prze´sledzimy teraz kilka prostych przykładów.

32
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.17.1
Algorytm z jednostronnym bł˛edem
Wyobra˙zmy sobie, ˙ze mamy urny z kulami. Urny s ˛
a dwojakiego rodzaju. Urny pierwszego
rodzaju zawieraj ˛
a wył ˛
acznie kule białe. W urnach drugiego rodzaju s ˛
a kule białe i czarne
po połowie. Celem algorytmu jest rozpoznanie jakiego rodzaju jest dana urna. Zakładamy
przy tym, ˙ze nie mo˙zemy obejrze´c wszystkich kul z urny.
Nasz pierwszy algorytm polega na wylosowaniu jednej kuli z danej urny. Je˙zeli wy-
losowana kula jest biała, to orzekamy, ˙ze urna jest pierwszego rodzaju, a je˙zeli kula jest
czarna, to orzekamy, ˙ze urna jest drugiego rodzaju. Je˙zeli urna naprawd˛e jest pierwszego
rodzaju, to nasz algorytm na pewno, z prawdopodobie ´nstwem równym 1 da poprawn ˛
a
odpowied´z. Je˙zeli natomiast urna jest drugiego rodzaju, to poprawn ˛
a odpowied´z uzyska-
my z prawdopodobie ´nstwem równym
1
2
. Prawdopodobie ´nswto bł˛edu mo˙zna zmniejszy´c
powtarzaj ˛
ac losowanie kilka razy.
Drugi algorytm składa si˛e z
t rund. W ka˙zdej rundzie losujemy jedn ˛
a kul˛e i po obej-
rzeniu zwracamy j ˛
a spowrotem do urny. Je˙zeli w które´s rundzie wylosowano kul˛e czarn ˛
a,
to algorytm orzeka, ˙ze urna jest drugiego rodzaju. Je˙zeli we wszystkich losowaniach wy-
padła kula biała, to algorytm orzeka, ˙ze urna jest pierwszego rodzaju. Je˙zeli urna jest
pierwszego rodzaju, to drugi algorytm na pewno da poprawn ˛
a odpowied´z. Je˙zeli urna jest
drugiego rodzaju, to bł ˛
ad popełnimy wtedy, gdy
t razy z rz˛edu wylosujemy kul˛e biał ˛
a.
Zakładaj ˛
ac, ˙ze losowania kul s ˛
a niezale˙zne, prawdopodobie ´nstwo bł˛edu wynosi
1
2
t
.
1.17.2
Algorytm sprawdzaj ˛
acy mno˙zenie wielomianów
Przypu´s´cmy, ˙ze mamy trzy wielomiany
P (x), Q(x) i R(x) i mamy sprawdzi´c, czy R(x) =
P (x)
· Q(x), zachodzi dla ka˙zdego rzeczywistego x. Załó˙zmy, ˙ze P (x) i Q(x) s ˛a stopnia
n, a R(x) jest stopnia 2n. Jednym ze sposobów jest pomno˙zenie wielomianów P (x) i
Q(x) i porównanie współczynników iloczynu z wielomianem R(x). Ta metoda wymaga
około
n
2
mno˙ze´n. Przedstawimy teraz szybszy algorytm probabilistyczny sprawdzaj ˛
acy,
czy dwa wielomiany s ˛
a dobrze wymno˙zone.
Algorytm probabilistyczny sprawdzaj ˛
acy mno˙zenie wielomianów.
Dane wej´sciowe: trzy wielomiany:
P (x), Q(x) oraz R(x).
Dane wyj´sciowe: odpowied´z, czy
P (x)
· Q(x) = R(x).
Losuj liczb˛e naturaln ˛
a
x
0
z przedziału od
0 do 4n,
oblicz waro´sci
u
0
= P (x
0
), v
0
= Q(x
0
) oraz w
0
= R(x
0
).
porównaj
w
0
z iloczynem
u
0
· v
0
.
Je˙zeli
w
0
6= u
0
· v
0
, to
orzekaj, ˙ze
P (x)
· Q(x) 6= R(x).
Je˙zeli
w
0
= u
0
· v
0
, to
orzekaj, ˙ze
P (x)
· Q(x) = R(x).
W rozdziale pierszym pokazano, ˙ze warto´s´c wielomianu
P (x) stopnia n w punkcie x
0
mo˙zna obliczy´c w czasie proporcjonalnym do
n. Je˙zeli równo´s´c P (x)
· Q(x) = R(x) jest
to˙zsamo´sci ˛
a, to dla ka˙zdej wylosowanej warto´sci
x
0
otrzymamy
P (x
0
)
· Q(x
0
) = R(x
0
),
czyli nasz algorytm udzieli poprawnej odpowiedzi z prawdopodobie ´nstwem równym 1.
Je˙zeli
P (x)
·Q(x) = R(x) nie jest to˙zsamo´sci ˛a, to wielomian W (x) = P (x)·Q(x)−R(x)

1.17. Algorytmy probabilistyczne
33
nie jest to˙zsamo´sciowo równy 0, i algorytm mo˙ze wylosowa´c
x
0
, które jest pierwiastkiem
wielomianu
W (x), i da´c bł˛edn ˛
a odpowied´z. Ale jak pokazano w rozdziale pierwszym
wielomian stopnia
2n nie ma wi˛ecej ni˙z 2n pierwiastków, wi˛ec prawdopodobie ´nstwo
bł˛edu jest nie wi˛eksze ni˙z
1
2
.
1.17.3
Algorytmy z bł˛edem obustronnym
W przykładach z poprzedniego podrozdziału tylko jedna z odpowiedzi typu TAK/NIE
mo˙ze by´c udzielana bł˛ednie. Czasami mamy do czynienia z sytuacj ˛
a kiedy bł˛edy s ˛
a mo˙z-
liwe w obu przypadkach.
Wyobra´zmy sobie teraz, ˙ze oba rodzaje urn zawieraj ˛
a kule białe i czarne. Urny pierw-
szego rodzaju zawieraj ˛
a
2
3
kul białych i
1
3
kul czarnych, a urny drugiego rodzaju zawieraj ˛
a
1
3
kul białych i
2
3
kul czarnych.
Jak poprzednio algorytm losuje jedn ˛
a kul˛e i orzeka ˙ze urna jest pierwszego rodza-
ju, je˙zeli wylosuje kul˛e biała, oraz orzeka, ˙ze urna jest drugiego rodzaju, je˙zeli wylosuje
kul˛e czarn ˛
a. Algorytm mo˙ze teraz popełni´c bł ˛
ad w obu przypadkach. Pradwopodobie ´n-
stwo złej odpowiedzi wynosi
1
3
. Aby zmniejszy´c prawdopodobie ´nstwo bł˛edu losujemy
ze zwracaniem
t razy. Je˙zeli wi˛ecej było kul białych, to algorytm orzeka, ˙ze urna jest
pierwszego rodzaju, a je˙zeli wi˛ecej było czarnych, to orzeka, ˙ze drugiego rodzaju.
Zastanówmy si˛e teraz jakie jest prawdopodobie ´nstwo bł˛edu je˙zeli losujemy z urny
pierwszego rodzaju. Niech
X oznacza liczb˛e wylosowanych kul czarnych. X posiada
rozkład dwumianowy długo´sci
t z prawdopodobie´nstwem sukcesu
1
3
. Algorytm popełni
bł ˛
ad, je˙zeli liczba sukcesów b˛edzie wi˛eksza od
t
2
. Z nierówno´sci Chernoffa prawdopodo-
bie´nstwo to mo˙zna oszacowa´c w nast˛epuj ˛
acy sposób:
P (X
≥
t
2
) = P (X
≥ (1 +
1
2
)
t
3
)
≤ e
−
t
36
.
Z nierówno´sci Czebyszewa mo˙zna to oszacowa´c przez
P (X
≥
t
2
) = P (X
−
t
3
≥
t
6
)
≥ P (|X −
t
3
| ≥
t
6
)
≥
2t
9
:
t
2
36
=
8
t
.
1.17.4
Algorytm kolorownia wierzchołków grafu
Wyobra´zmy sobie algorytm, który niezale˙znie i ze stałym prawdopodobie ´nstwem
1
2
kolo-
ruje na biało lub czarno wierzchołki wybranego grafu
G = (V, E). Chcemy go wykorzy-
sta´c do takiego pokolorowania grafu aby mie´c du˙zo kraw˛edzi dwukolorowych. Niech
X
oznacza liczb˛e kraw˛edzi dwukolorowych. Pami˛etamy, ˙ze
EX =
m
2
oraz
V ar(X) =
m
4
.
Za pomoc ˛
a nierówno´sci Czebyszewa poka˙zemy, ˙ze
P (X >
m
2
−
√
m)
≥
3
4
. W tym celu
oszacujemy prawdopodobie ´nstwo zdarzenia przeciwnego
P (X
≤
m
2
−
√
m)
≤ P (|X −
m
2
| ≤
√
m)
≤
m
4m
=
1
4
.

34
Rozdział 1. Rachunek prawdopodobie ´nstwa
1.18
Zadania
1. Zaproponuj przestrze ´n zdarze´n elementarnych dla rzutu dwiema (rozró˙znialnymi)
kostkami. Przedstaw zdarzenie, ˙ze suma oczek na obu kostkach wynosi 5.
2. Zaproponuj przestrze ´n zdarze´n elementarnych dla losowania dwóch kul z urny za-
wieraj ˛
acej 3 kule białe i 4 czarne. Przedstaw zdarzenie, ˙ze wylosowano:
a) dwie kule białe, b) kule w ró˙znych kolorach.
3. Zaproponuj przestrze ´n zdarze´n elementarnych dla ustawienia czterech liter
a, b, c
i
d w ci ˛
ag. Przedstaw zdarzenie, ˙ze:
a)
a i b stoj ˛
a obok siebie;
b)
a i b s ˛
a
rozdzielone jedn ˛
a liter ˛
a.
4. Zaproponuj przestrze ´n zdarze´n elementarnych dla nast˛epuj ˛
acych do´swiadcze´n: a)
Rzut monet ˛
a i kostk ˛
a. b) Losowanie 13 kart z talii 52 kart. c) Wypełnienie kuponu
totolotka. d) Wypełnienie kuponu totalizatora piłkarskiego.
5.
A, B i C s ˛
a zdarzeniami. Zapisa´c za pomoc ˛
a działa ´n na zbiorach zdarzenia:
a) zachodz ˛
a wszystkie trzy zdarzenia;
b) zachodzi dokładnie jedno ze zdarze ´n
A, B lub C;
c) zachodz ˛
a dokładnie dwa ze zdarze ´n
A, B, C;
d) zachodz ˛
a co najmniej dwa spo´sród zdarze ´n
A, B, C.
6. Cyfry
0, . . . , 9 ustawiono losowo. Jakie jest prawdopodobie ´nstwo: a) ˙ze 1 i 2 stoj ˛
a
obok siebie; b) ˙ze pomi˛edzy
1 i 2 stoj ˛
a dwie cyfry; c) ˙ze
0, 1 i 2 stoj ˛
a obok siebie.
7. Pokaza´c, ˙ze
P (A
∩ B) ≥ P (A) + P (B) − 1
8. Dane s ˛
a
P (A
0
) =
1
3
,
P (A
∩ B) =
1
4
i
P (A
∪ B) =
2
3
. Obliczy´c
P (B
0
), P (A
∩ B
0
)
i
P (B
− A).
9. Dane s ˛
a
P (A
∩ B) =
1
4
i
P (A
∪ B) =
1
2
, wiadomo te˙z, ˙ze
P (A
− B) = P (B − A).
Obliczy´c
P (B) oraz P (B
− A).
10. Udowodnij, ˙ze dla dowolnej rodziny zbiorów
A
1
, . . . , A
n
(niekoniecznie parami
rozł ˛
acznych) mamy
P
n
[
i=1
A
i
≤
n
X
i=1
P (A
i
)
11. W urnie s ˛
a 4 kule białe i 3 czarne. Losujemy dwie. Jakie jest prawdopodobie ´nstwo,
˙ze wylosowane kule b˛ed ˛
a w ró˙znych kolorach?
12. Jakie jest prawdopodobie ´nstwo, ˙ze przy okr ˛
agłym stole wybrane na pocz ˛
atku dwie
osoby usi ˛
ad ˛
a obok siebie?

1.18. Zadania
35
13. Niech przestrze ´n zdarze´n elementarnych b˛edzie zbiorem 3 elementowych ci ˛
agów
zero-jedynkowych. Wypisz zdarzenia: a) na pierwszej współrz˛ednej jest zero; b) na
pierwszej i trzeciej współrz˛ednej s ˛
a zera; c) na pierwszej i trzeciej współrz˛ednej
mamy ró˙zne warto´sci; d) na wszystkich współrz˛ednych jest to samo.
14. Oblicz prawdopodobie ´nstwa zdarze ´n z poprzedniego zadania (rozkład jednostaj-
ny).
15. Niech przestrze ´n zdarze´n elementarnych b˛edzie zbiorem
n elementowych ci ˛
agów
zero-jedynkowych (rozkład jednostajny). Oblicz prawdopodobie ´nstwa zdarze ´n z
zadania 13.
16. Policz jakie jest prawdopodobie ´nstwo, ˙ze losowo wybrana funkcja posiada takie
same warto´sci dla dwóch z góry wybranych punktów
a i b (patrz przykład 1.11).
17. Dwukrotnie rzucamy monet ˛
a. Niech zdarzenie
A oznacza, ˙ze wypadł dokladnie
jeden orzeł, a zdarzenie
B oznacza, ˙ze w pierwszym rzucie wypadł orzeł. Oblicz
P (B
|A). Czy zdarzenia A i B s ˛a niezale˙zne?
18. Rzucamy trzema kostkami. Jakie jest prawdopodobie ´nstwo, ˙ze na ˙zadnej kostce nie
wypada szóstka, je˙zeli na ka˙zdej kostce wypada inna liczba oczek.
19. Mamy dwie urny z kulami. W pierwszej urnie s ˛
a dwie kule białe i cztery czarne, a
w drugiej urnie trzy białe i trzy czarne. Rzucamy kostk ˛
a do gry. Je˙zeli wypadnie 1
lub 2, to losujemy kul˛e z pierwszej urny, je˙zeli 3,4,5 lub 6, to losujemy z drugiej
urny. Jakie jest prawdopodobie ´nstwo, ˙ze wylosujemy kul˛e biał ˛
a?
20. W urnie jest
n kul w tym k białych. n osób po kolei losuje jedn ˛
a kul˛e bez zwracania.
a) Ile wynosi prawdopodobie ´nstwo wylosowania kuli białej dla trzeciej osoby? b)
Ile wynosi prawdopodobie ´nstwo wylosowania kuli białej dla ka˙zdej z losuj ˛
acych
osób?
21. Udowodnij, ˙ze je˙zeli zdarzenia
A i B s ˛
a niezale˙zne, to niezale˙zne s ˛
a tak˙ze zdarzenia
A i B
0
oraz
A
0
i
B
0
.
22. Zmienna
X
5
(x) = x mod 5 jest okre´slona na przestrzeni
{1, . . . , 30} z jednostaj-
nym rozkładem. Podaj jej rozkład, warto´s´c oczekiwan ˛
a oraz
P (X < 3).
23. Zmienna losowa
X posiada rozkład:
x
1
2
3
4
5
P (X = x)
1
2
1
4
1
8
1
16
1
16
Oblicz
P (Xparzyste), P (X < 3), warto´s´c oczekiwan ˛
a
EX, wariancj˛e V ar(X)
oraz
P (X
≥ EX).
24. Mamy urn˛e z czteroma białymi i trzema czarnymi kulami. Losujemy bez zwraca-
nia trzy kule i niech zmienna losowa
X oznacza ile w´sród wylosowanych jest kul
białych. Podaj g˛esto´s´c rozkładu zmiennej losowej
X oraz jej warto´s´c oczekiwan ˛
a.

36
Rozdział 1. Rachunek prawdopodobie ´nstwa
25. W urnie znajduje si˛e pi˛e´c monet, trzy pi˛eciozłotowe i cztery dwuzłotowe. Losujemy
dwie monety i niech zmienna losowa
Y oznacza sum˛e nominałów wylosowanych
monet. Oblicz g˛esto´s´c rozkładu zmiennej losowej
Y oraz jej warto´s´c oczekiwan ˛
a.
26. Rzucamy monet ˛
a a˙z do wypadni˛ecia orła, ale nie wi˛ecej ni˙z cztery razy. Niech
zmienna losowa
Z oznacza liczb˛e wykonanych rzutów. Podaj g˛esto´s´c rozkładu
zmiennej losowej
Z oraz jej warto´s´c oczekiwan ˛
a.
27. W urnie znajduje si˛e sze´s´c monet, dwie pi˛eciozłotowe, dwie dwuzłotowe oraz dwie
jednozłotowe. Losujemy jedn ˛
a monet˛e, a je´sli jest to złotówka to losujemy jeszcze
jedn ˛
a. Niech zmienna losowa
Z oznacza sum˛e nominałów wylosowanych monet.
Oblicz g˛esto´s´c rozkładu zmiennej losowej
Z oraz jej warto´s´c oczekiwan ˛
a.
28. Rzucamy dwukrotnie monet ˛
a. Okre´slamy dwie zmienne losowe
X
1
oraz
X
2
. Zmien-
na
X
1
przyjmuje warto´s´c
1, je˙zeli za pierwszym razem wypadnie orzeł, oraz war-
to´s´c
0, je˙zeli za pierwszym razem wypadnie reszka. Podobnie zmienna X
2
opisuje
wynik drugiego rzutu. Niech zmienna
C b˛edzie okre´slona wzorem C = X
1
+ X
2
.
Podaj rozkład zmiennej losowej
C. Czy zmienne C i X
1
s ˛
a niezale˙zne?
29. W urnie znajduje si˛e pi˛e´c kul z numerami 1,2,3,4,5. Losujemy ze zwracaniem dwie
kule. Niech zmienna losowa
X oznacza sum˛e numerów obu kul. Oblicz g˛esto´s´c
rozkładu zmiennej losowej
X oraz jej warto´s´c oczekiwan ˛
a.
30. Zmienna losowa
Y posiada rozkład:
x
−2
−1
0
1
2
P (X = x)
1
12
1
6
1
2
1
6
1
12
Oblicz warto´s´c oczekiwan ˛
a
EX, wariancj˛e V ar(X) oraz P (
|X − EX| ≥ 1).
Porównaj ostatni ˛
a liczb˛e z warto´sci ˛
a otrzyman ˛
a z oszacowania Czebyszewa.
31. Podaj przykład nieujemnej zmiennej losowej
X oraz liczby d, dla których zachodzi
P (X
≥ d) =
EX
d
.
32. Podaj przykład zmiennej losowej
X oraz liczby , dla których zachodzi
P (
|X − EX| ≥ ) =
V arX
2
.
33. Mamy graf z czteroma wierzchołkami
{a, b, c, d} i kraw˛edziami {{a, b}, {b, c}, {c, d}, {a, d}, }.
Rozwa˙zmy przestrze ´n wszystkich kolorowa ´n wierzchołków tego grafu dwoma ko-
lorami. Nich zmienna losowa
X oznacza liczb˛e kraw˛edzi z ró˙znymi kolorami na
ko´ncach. Podaj rozkład zmiennej losowej
X oraz jej warto´s´c oczekiwan ˛
a.
34. Ł ˛
aczny rozkład zmiennych losowych
X i Y przedstawiony jest w tabeli.

1.18. Zadania
37
Y
-1
0
1
X
0
1
8
1
4
1
8
1
1
6
1
6
1
6
Oblicz rozkłady zmiennych
X, Y , Z = X + Y , W = 2X
− Y .
Oblicz
EX, EY , V ar(X), V ar(Y ), E(X + Y ), V ar(X + Y ).
Czy zmienne
X i Y s ˛
a niezale˙zne?
Oblicz prawdopodobie ´nstwa
P (X = Y ), P (X < Y ).
35. Na przestrzeni
{1, . . . , 30} z jednostajnym rozkładem okre´slamy trzy zmienne X
5
(x) =
x mod 5, X
3
(x) = x mod 3, X
2
(x) = x mod 2. Czy zmienne te s ˛
a niezale˙zne?
36. Pokaza´c, ˙ze dla ka˙zdego
0 < e < 1 istnieje zmienna losowa X taka, ˙ze E(X) = 1
oraz
P (X < 0.5) = 1
− e.
37. Pokaza´c, ˙ze je˙zeli
X ma rozkład symetryczny, tzn dla pewnego m, P (X = m
−
x) = P (X = m + x) dla ka˙zdego x, to EX = m.
38. Pokaza´c, ˙ze
V arX = V ar(X + c)
39. Poda´c przykład dwóch zmiennych
X i Y o ró˙znych rozkładach takich, ˙ze EX =
EY i V arX = V arY .
40. Przypu´s´cmy, ˙ze zmienna losowa przyjmuje
n > 2 warto´sci x
1
< x
2
< . . . < x
n
ka˙zde z dodatnim prawdopodobie ´nstwem.
a) Czy jest mo˙zliwe
EX = x
1
lub
EX = x
n
?
b) Czy jest mo˙zliwe
EX < x
2
lub
EX > x
n−1
?
c) Czy b) jest mo˙zliwe je˙zeli
X ma rozkład jednostajny?
41. Rzucano symetryczn ˛
a monet ˛
a 9 razy. Jakie jest prawdopodobie ´nstwo, ˙ze:
a) orzeł
wypadł co najmniej raz,
b) orzeł wypadł parzyst ˛
a liczb˛e razy?
42. Jakie jest prawdopodobie ´nstwo, ˙ze w serii sze´sciu rzutów kostk ˛
a suma oczek b˛edzie
parzysta.
43. Poka˙z, ˙ze je˙zeli
i < j < np, to B(n, p, i) < B(n, p, j); a je˙zeli np < i < j, to
B(n, p, i) > B(n, p, j), gdzie B(n, p, i) =
n
i
p
i
q
n−i
to rozkład dwumianowy.
44. Niech zmienna losowa
X ma rozkład dwumianowy z parametrami n = 2000,
p =
1
2
. Oszacuj prawdopodobie ´nstwo
P (X > 1500) (za pomoc ˛
a nierówno´sci
Markowa, Czebyszewa i Chernoff’a).
45. Rozwa˙zmy przestrze ´n wszystkich grafów ze zbiorem wierzchołków
{1, . . . , n} z
jednostajnym rozkładem prawdopodobie ´nstwa. Jakie jest prawdopodobie ´nstwo, ˙ze
wierzchołki 1 i 2 s ˛
a poł ˛
aczone kraw˛edzi ˛
a?

38
Rozdział 1. Rachunek prawdopodobie ´nstwa
46. Podobnie jak w poprzednim zadaniu rozwa˙zmy przestrze ´n grafów z czteroma wierz-
chołkami
{1, 2, 3, 4}. Jake jest prawdopodobie´nstwo, ˙ze graf jest spójny (ka˙zde dwa
jego wierzchołki s ˛
a poł ˛
aczone ´scie˙zk ˛
a)?
47. Rozwa˙zmy kolorowanie dowolnego grafu
G = (V, E) trzema kolorami. Niech
zmienna losowa
X oznacza liczb˛e ró˙znokolorowych kraw˛edzi. Oblicz E(X) oraz
V ar(X).
1.19
Problemy
1.19.1
Niezale˙zno´s´c zmiennych losowych
1. Mamy trzy niezale˙zne zmienne losowe
X, Y i Z (okre´slone na jakiej´s przestrzeni
probabilistycznej). Udowodnij, ˙ze ka˙zde dwie te˙z s ˛
a niezale˙zne.
2. Poka˙z, ˙ze je˙zeli zmienne losowe
X i Y s ˛
a niezale˙zne, to dla dowolnych funkcji
g i
h, zmienne g
◦ X i h ◦ Y te˙z s ˛a niezale˙zne.
3. Udowodnij, ˙ze je˙zeli
A i B s ˛
a dowolnymi podzbiorami zbioru liczb rzeczywistych,
to zdarzenia
A
X
=
{ω | X(ω) ∈ A}
oraz
B
Y
=
{ω | Y (ω) ∈ B}
s ˛
a niezale˙zne.
4. Pokaza´c, ˙ze je˙zeli mamy zmienna losow ˛
a
X z rozkładem jednopunktowym i do-
woln ˛
a inn ˛
a zmienn ˛
a
Y , to X i Y s ˛
a niezale˙zne
1.19.2
Suma kwadratów
Niech
x
1
, . . . , x
k
b˛ed ˛
a dowolnymi liczbami rzeczywistymi i niech
m =
1
k
k
X
i=1
x
i
.
Udowodnij, ˙ze
1
k
k
X
i=1
x
2
i
≥ m
2
,
przy czym równo´s´c zachodzi wtedy i tylko wtedy, gdy
x
i
= m dla ka˙zdego i.
Wskazówka: Niech
Ω =
{1, . . . , k} b˛edzie przestrzeni ˛a z jednostajnym rozkładem praw-
dopodobie ´nstwa i niech
X b˛edzie zmienn ˛
a losow ˛
a okre´slon ˛
a wzorem
X(i) = x
i
. Oblicz
wariancj˛e tej zmiennej losowej.
Wyszukiwarka
Podobne podstrony:
Matematyka dyskretna 2004 04 Rachunek prawdopodobieństwa
Matematyka dyskretna 2002 04 Rachunek prawdopodobieństwa
Matematyka dyskretna 2002 04 Rachunek prawdopodobieństwa
Matematyka dyskretna 2004 01 Podstawowe pojęcia, oznaczenia
PK-I-06, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Test 2, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
TPI CH 2, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
PK-WE Z E, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
PK-WE Z E 2, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Matematyka dyskretna 2004 06 Teoria liczb
Test 3, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
E 0, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Test a, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
PK-WE M test 2, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2
Test-06, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Test 1, 1 STUDIA - Informatyka Politechnika Koszalińska, Matematyka dyskretna i TPI, 04-10-2012
Matematyka dyskretna 2004 01 Podstawowe pojęcia, oznaczenia
Matematyka dyskretna 2004 06 Teoria liczb
więcej podobnych podstron