Matematyka dyskretna 2002 02 Arytmetyka

Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Arytmetyka

1.1

System dziesi˛etny

Najpowszechniej u˙zywanym sposobem przedstawiania liczb naturalnych jest system dzie-
si˛etny, gdzie na przykład zapis:

przedstawia liczb˛e składaj ˛

ac ˛

a si˛e z jednej setki, siedmiu dziesi ˛

atek i o´smiu jedno´sci. Mo-

˙zemy to zapisa´c w postaci:

albo inaczej:

Tak wi˛ec w systemie dziesi˛etnym kolejne cyfry oznaczaj ˛

a współczynniki przy kolejnych

pot˛egach liczby dziesi˛e´c, zaczynaj ˛

ac od najwi˛ekszej, a ko ´ncz ˛

ac na najmniejszej pot˛edze.

Mówimy, ˙ze liczba dziesi˛e´c jest podstaw ˛

a lub baz ˛

a systemu dziesi˛etnego. W systemie

dziesi˛etnym u˙zywamy dziesi˛eciu cyfr:

!#"$&%')(*&+'-,'./&'-0

a zapis:

243

oznacza liczb˛e:

2!3

243

(1.1)

któr ˛

a mo˙zemy te˙z zapisa´c w postaci:

(1.2)

Rozdział 1. Arytmetyka

gdzie

s ˛

a cyframi nale˙z ˛

acymi do zbioru

'!4-0

Liczby mo˙zna te˙z zapisywa´c w systemach z inn ˛

a baz ˛

a. Je˙zeli za baz˛e systemu wybie-

rzemy liczb˛e

, to potrzebujemy

cyfr, a zapis:

2!3

oznacza w systemie z baz ˛

liczb˛e:

243

2!3

5!!

(1.3)

któr ˛

a mo˙zemy te˙z zapisa´c w postaci:

(1.4)

1.2

System dwójkowy

W informatyce bardzo wa˙znym systemem jest system dwójkowy (binarny), gdzie pod-
staw ˛

a jest liczba

i gdzie mamy tylko dwie cyfry, 0 i 1 (cyfry w systemie dwójkowym

nazywa si˛e bitami). Zapis:

2!3

oznacza liczb˛e:

243

2!3

lub:

Przykład 1.1 Zapis

oznacza w systemie dwójkowym liczb˛e:

5""

czemu w systemie dziesi˛etnym odpowiada

. Podobnie zapis:

oznacza w systemie dziesi˛etnym liczb˛e

Poni˙zej w pierwszej tabeli przedstawiono siedemna´scie kolejnych liczb w postaci dwój-
kowej i dziesi˛etnej, a w drugiej jedena´scie pierwszych pot˛eg liczby 2 w postaci dwójkowej
i dziesi˛etnej.

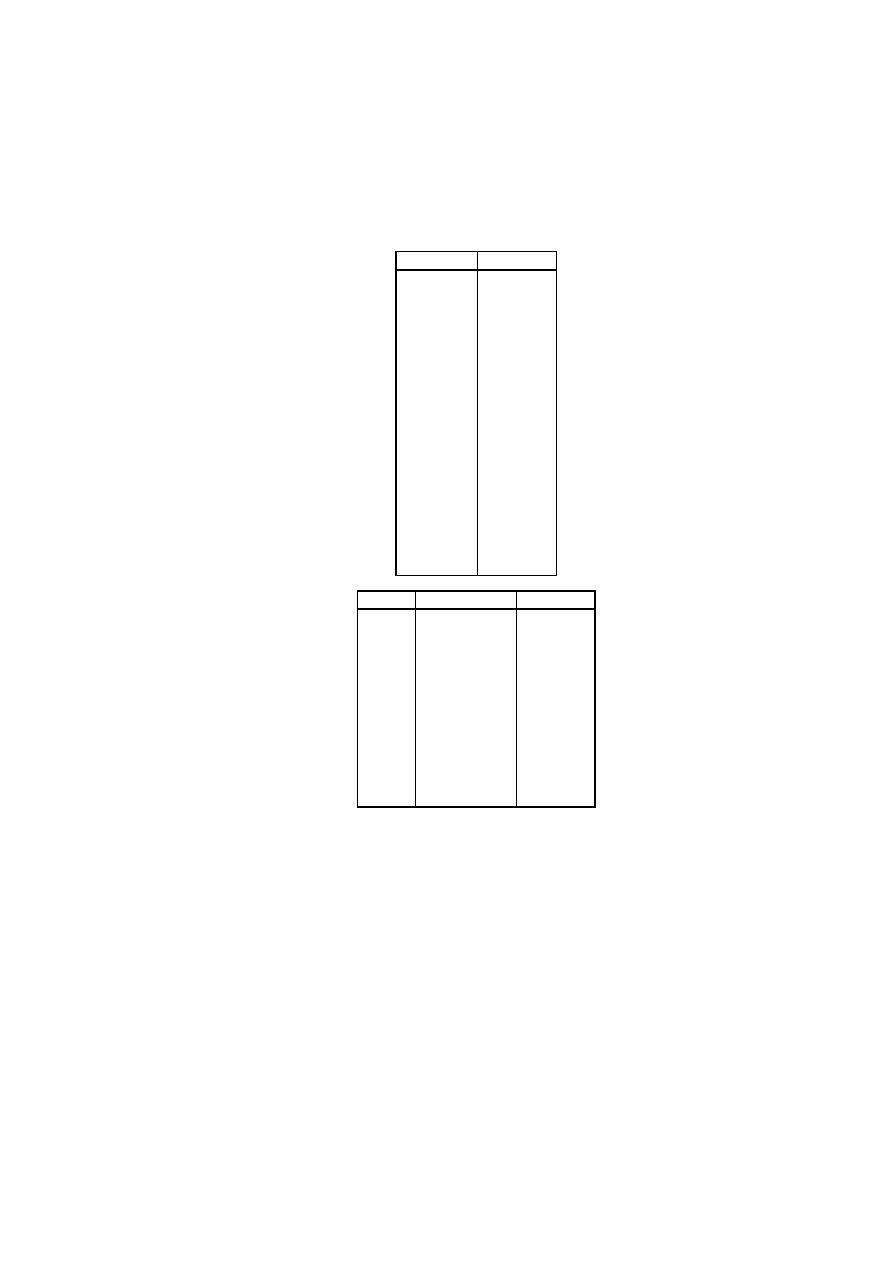
1.3. Zwi˛ekszanie liczby o jeden

dwójkowy

dziesi˛etny

100

101

110

111

1000

1001

1010

1011

1100

1101

1110

1111

10000

pot˛ega

dwójkowy

dziesi˛etny

100

1000

10000

100000

1000000

10000000

128

100000000

256

1000000000

512

10000000000

1024

1.3

Zwi˛ekszanie liczby o jeden

Algorytm zwi˛ekszania liczby o jeden. Aby zwi˛ekszy´c o jeden liczb˛e zapisan ˛

a w syste-

mie dwójkowym:

wskazujemy na ostatni bit,

powtarzamy, co nast˛epuje:

je˙zeli wskazany bit jest zerem, to zamieniamy go na jedynk˛e i ko ´nczymy

algorytm,

je˙zeli jest on równy jeden, to zamieniamy go na zero i wskazujemy nast˛epny

bit w lewo; je˙zeli nie ma nast˛epnego bitu w lewo, to stawiamy jedynk˛e na pocz ˛

atku

liczby i ko´nczymy algorytm.

Rozdział 1. Arytmetyka

Mówi ˛

ac inaczej, szukamy pierwszego zera od prawej strony, zamieniamy go na jedynk˛e,

a wszystkie jedynki stoj ˛

ace za nim zamieniamy na zera.

Przykład 1.2 Liczba o jeden wi˛eksza od liczby

Je˙zeli liczba nie zawiera zer, tylko same jedynki, to zamieniamy te jedynki na zera i
stawiamy jedynk˛e na pocz ˛

atku.

Przykład 1.3 Po liczbie

jest liczba

Zauwa˙zmy, ˙ze podobnie działa algorytm zwi˛ekszania o jeden liczb w systemie dziesi˛et-
nym (lub dowolnym innym systemie). Szukamy pierwszej od prawej cyfry ró˙znej od dzie-
wi ˛

atki (najwi˛ekszej cyfry w systemie), zwi˛ekszamy t˛e cyfr˛e o jeden, a wszystkie stoj ˛

ace

za ni ˛

a dziewi ˛

atki zamieniamy na zera.

1.4

Porównywanie liczb

Algorytm porównywania liczb. Aby stwierdzi´c, która z dwóch liczb w postaci dwójko-
wej jest wi˛eksza, post˛epujemy w nast˛epuj ˛

acy sposób:

je˙zeli zapisy liczb nie s ˛

a tej samej długo´sci, to wi˛eksz ˛

a jest liczba z dłu˙zszym zapi-

sem (zakładamy tu, ˙ze zapis liczby ró˙znej od zera nie ma zer na pocz ˛

atku),

je˙zeli zapisy liczb s ˛

a równej długo´sci, to porównujemy bit po bicie od lewej strony

do prawej:

je˙zeli bity s ˛

a takie same, to przechodzimy do nast˛epnego bitu w prawo,

je˙zeli bity s ˛

a ró˙zne, to ko ´nczymy i stwierdzamy, ˙ze wi˛eksza jest ta liczba,

która ma wi˛ekszy bit na tej pozycji,

je˙zeli wszystkie bity s ˛

a takie same, to porównywane liczby s ˛

a równe.

Przykład 1.4

. Liczby te s ˛

a tej samej długo´sci, maj ˛

a takie same trzy

pierwsze bity, a ró˙zni ˛

a si˛e dopiero czwartym bitem — czwarty bit pierwszej liczby jest

wi˛ekszy od czwartego bitu drugiej liczby.

1.5

Operacje arytmetyczne w systemie dwójkowym

Operacje dodawania, mno˙zenia, odejmowania i dzielenia w systemie dwójkowym mo˙zna
wykonywa´c podobnie do tak zwanych szkolnych pisemnych działa ´n arytmetycznych w
systemie dziesi˛etnym. Działania w systemie dwójkowym s ˛

a prostsze, poniewa˙z mamy tu

tylko dwie cyfry, 0 i 1, i prostsze s ˛

a operacje na pojedynczych cyfrach.

Zacznijmy od tabliczki dodawania i mno˙zenia. Wygl ˛

adaj ˛

a one tak:

1.5. Operacje arytmetyczne w systemie dwójkowym

Przypu´s´cmy, ˙ze chcemy doda´c dwie liczby w postaci dwójkowej. Zakładamy tu, ˙ze obie
liczby s ˛

a tej samej długo´sci. Je˙zeli nie s ˛

a, to krótsz ˛

a z nich uzupełniamy na pocz ˛

atku

zerami.

Algorytm dodawania. Aby doda´c dwie liczby w postaci binarnej:

243

2!3

dla kolejnych pozycji

od 0 do

obliczamy bit sumy

oraz

— tak zwany bit przenie-

sienia do nast˛epnej pozycji:

najpierw obliczamy

oraz

(czyli

jest reszt ˛

a z dzielenia

przez 2),

nast˛epnie po kolei, dla ka˙zdego

od 1 do

, obliczamy:

, je˙zeli co najmniej dwa spo´sród bitów

oraz

s ˛

a jedynkami,

na ko´ncu obliczamy najbardziej znacz ˛

acy bit sumy

Wynikiem dodawania jest liczba

(mo˙ze si˛e zdarzy´c, ˙ze

Przykład 1.5 Dodawanie liczb

wygl ˛

ada nast˛epuj ˛

aco:

Aby odj ˛

a´c od siebie dwie liczby w systemie dwójkowym, odejmujemy bit po bicie

od prawej do lewej, a w przypadku gdy trzeba odj ˛

a´c bit wi˛ekszy od mniejszego, „po˙zy-

czamy” dwójk˛e z nast˛epnej (w lewo) pozycji (szczegóły algorytmu pozostawiono jako

´cwiczenie).

Przykład 1.6 Odejmowanie liczb

wygl ˛

ada nast˛epuj ˛

aco:

Rozdział 1. Arytmetyka

Aby pomno˙zy´c dwie liczby, mno˙zymy pierwsz ˛

a liczb˛e przez poszczególne cyfry dru-

giej liczby, a wyniki podpisujemy pod spodem odpowiednio przesuni˛ete wzgl˛edem siebie.
Ka˙zdy kolejny wynik jest przesuni˛ety o jedn ˛

a kolumn˛e w lewo. Nast˛epnie sumujemy te

iloczyny.

Przykład 1.7 Oto przykład mno˙zenia liczb

Zauwa˙zmy, ˙ze pomno˙zenie liczby w postaci dwójkowej przez 2 oznacza dopisanie

jednego zera na ko ´ncu liczby. Podobnie pomno˙zenie liczby przez

-t ˛

a pot˛eg˛e 2 oznacza

dopisanie na ko ´ncu liczby

zer.

Przykład 1.8

pomno˙zone przez

daje wynik

Równie˙z dzielenie wykonuje si˛e podobnie jak w systemie dziesi˛etnym. Na przykład:

1
1

Je˙zeli liczba jest podzielna przez 2, to ma w postaci binarnej zero na ko ´ncu, a je˙zeli dzieli
si˛e przez

-t ˛

a pot˛eg˛e dwójki, to ma na ko ´ncu

zer. Podzielenie liczby przez 2 oznacza

skre´slenie w jej postaci binarnej jednego zera z ko ´nca.

Przykład 1.9

podzielone przez 2 daje

1.6

Zamiana systemu

Zastanówmy si˛e teraz, jak przechodzi´c od jednego sposobu przedstawiania liczby do dru-
giego. Poniewa˙z b˛edziemy u˙zywa´c ró˙znych systemów zapisu liczb, wi˛ec zapis w systemie
z baz ˛

oznaczymy przez:

243

B˛edziemy rezygnowa´c z tego zapisu, je˙zeli nie b˛edzie w ˛

atpliwo´sci, jakiego systemu u˙zy-

wamy. Przedyskutujmy to na przykładach. Aby przedstawi ´c liczb˛e

1.6. Zamiana systemu

w postaci dziesi˛etnej, korzystamy ze wzoru (1.3):

"5"

i wykonujemy wszystkie rachunki w systemie dziesi˛etnym:

(

%"5,

(

Podobnie mo˙zemy post˛epowa´c przy zamianie w odwrotn ˛

a stron˛e, z systemu dziesi˛etnego

na dwójkowy. Najpierw korzystamy ze wzoru (1.1):

nast˛epnie przedstawiamy cyfry i podstaw˛e systemu 10 w postaci dwójkowej i wykonuje-
my wszystkie działania w systemie dwójkowym:

Ten sposób zamiany liczb z postaci dziesi˛etnej na dwójkow ˛

a jest analogiczny do sposobu,

w jaki wy˙zej zamieniali´smy liczby z postaci dwójkowej na dziesi˛etn ˛

a. Byłby to naturalny

sposób dla kogo´s, kto swobodnie liczy w systemie dwójkowym. Sposób ten ma t˛e wad˛e,

˙ze wolno działa. Zobaczymy na przykładach dwa szybsze algorytmy zamiany postaci

liczby z dziesi˛etnej na dwójkow ˛

We´zmy liczb˛e 178. Pierwszy sposób polega na tym, ˙ze wyszukujemy najwi˛eksz ˛

a po-

t˛eg˛e liczby 2, która jeszcze jest mniejsza od naszej liczby (w przykładzie

nast˛epnie odejmujemy t˛e pot˛eg˛e od naszej liczby i z ró˙znic ˛

a post˛epujemy tak samo. Na

ko´ncu mamy liczb˛e w postaci sumy pot˛eg dwójki. W naszym przykładzie wygl ˛

ada to tak:

"+"%"

,"'

Teraz ju˙z łatwo zapisa´c nasz ˛

a liczb˛e w postaci dwójkowej:

)

Drugi sposób polega na kolejnym dzieleniu liczby w sposób całkowity przez 2 i za-

pami˛etywaniu reszt z dzielenia. Reszty te zapisane w odwrotnej kolejno´sci tworz ˛

a zapis

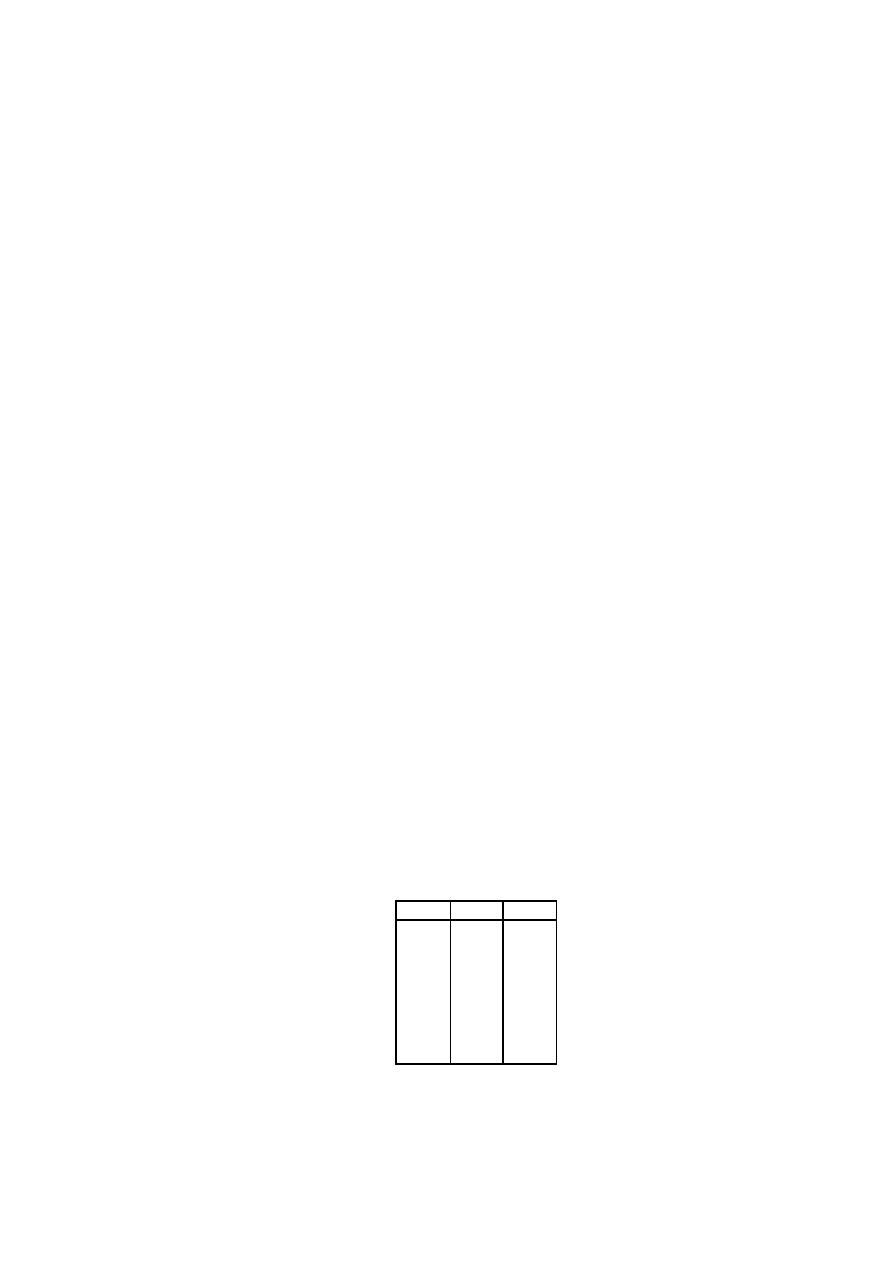
binarny liczby. Na przykład, we´zmy znowu liczb˛e 178. W poni˙zszej tabeli przedstawiono
kolejne ilorazy i reszty.

liczba

iloraz

reszta

178

Rozdział 1. Arytmetyka

Reszty zapisane w odwrotnej kolejno´sci:

tworz ˛

a binarny zapis liczby

)

. Poprawno´s´c działania tego algorytmu wynika z fak-

tu, ˙ze je˙zeli podzielimy liczb˛e

przez 2, to reszta z dzielenia wyniesie

, a iloraz całkowitoliczbowy wyniesie:

nast˛epne dzielenie przez 2 da reszt˛e

oraz iloraz:

i tak dalej.

Ostatni sposób mo˙zna łatwo uogólni´c na algorytm zamiany liczb z systemu dziesi˛et-

nego na system z inn ˛

a baz ˛

. Nale˙zy tylko dzieli´c przez

. Je˙zeli chcemy, na przykład,

przedstawi´c liczb˛e

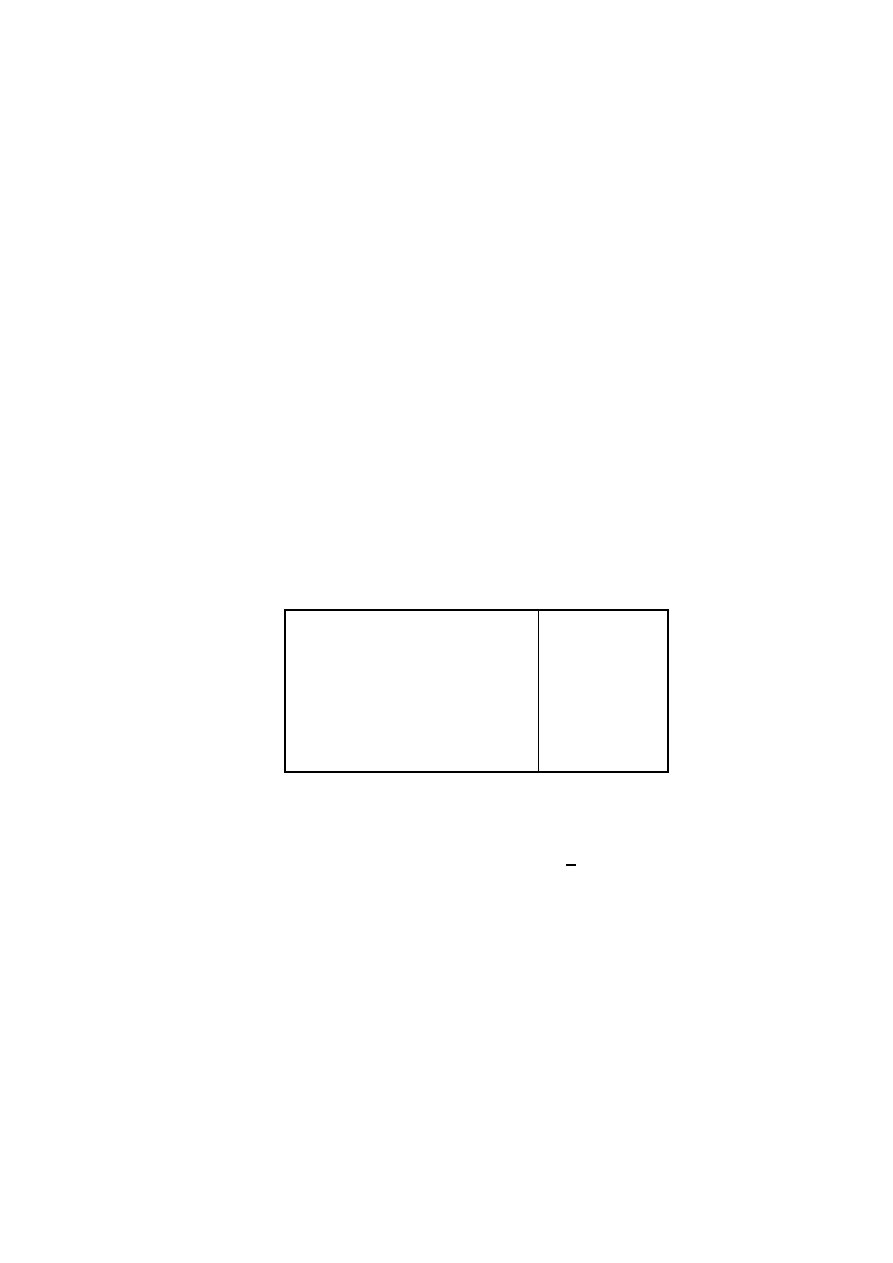
w systemie trójkowym, to dzielimy j ˛

a kolejno przez 3 i spisujemy

reszty z dzielenia:

liczba

iloraz

reszta

W wyniku otrzymamy:

1.7

Długo´s´c liczby

Zastanówmy si¸e ile cyfr zawiera zapis dziesi¸etny liczby naturalnej

. Cztery cyfry w

systemie dziesi¸etnym posiadaj¸a liczby od

0000

, a

cyfr

posiadaj¸a liczby od

. Tak wi¸ec liczba

cyfr wtedy i tylko wtedy

gdy

, czyli gdy

. Mamy wi˛ec

Lemat 1.10 Liczba naturalna

ma w systemie dziesi¸etnym

(w przybli˙zeniu

) cyfr.

Podobnie w systemie z podstaw¸a

, liczba

cyfr wtedy i tylko wtedy gdy

, czyli:

1.8. Du˙ze liczby

Lemat 1.11 W systemie o podstawie

liczba naturalna

(w przybli˙zeniu

) cyfr.

Korzystaj¸ac z tego faktu mo˙zemy ustala´c przybli˙zon¸a liczb¸e cyfr potrzebn¸a do zapisu
liczb.

Wniosek 1.12 Liczba, posiadaj¸aca

cyfr w systemie dziesi¸etnym ma około

bitów w systemie dwójkowym, a liczba maj¸aca

bitów w postaci dwójkowej ma

około

cyfr w postaci dziesi¸etnej.

Dowód: Je˙zeli liczba

ma w postaci dziesi˛etnej

cyfr, to

. W postaci dwój-

kowej

ma około

bitów, a

poniewa˙z

% "000,5%/

Podobnie, je˙zeli liczba

ma w postaci dwójkowej

bitów, to w postaci dziesi˛etnej

ma około

!%/

1.8

Du˙ze liczby

Aby si¸e zorientowa´c jak du˙ze mog¸a by´c liczby przedstawione za pomoc¸a systemu dziesi¸etnego
lub dwójkowego przypatrzmy si¸e poni˙zszej tabeli:

Liczba sekund w roku

Wiek układu słonecznego w latach

Wiek układu słonecznego w sekundach

Liczba cykli w roku (100 MHz)

Liczba ci¸agów 64 bitowych

Liczba ci¸agów 128 bitowych

(

Liczba ci¸agów 256 bitowych

Liczba atomów na Ziemi

Liczba atomów w naszej galaktyce

Dane do tabeli zaczerpni¸eto z ksi¸a˙zki A. Menezes, P. van Oorschot and S. Vanstone,
Handbook of Applied Cryptography. oraz z ksi¸a˙zki B. Schneier, Applied Cryptography.

Tabela ta pozwala oceni´c niektóre algorytmy.

Przykład 1.13 Rozwa˙zmy prosty algorytm sprawdzaj¸acy, czy liczba naturalna

jest pierw-

sza. Algorytm ten dzieli

przez kolejne liczby od 2 do

. Je˙zeli

ma 120 bitów, to

potrzeba

dziele´n. Je˙zeli zało˙zymy, ˙ze komputer potrafi wykona´c

milionów

dziele´n w ci¸agu sekundy i

w ci¸agu roku, to b¸edzie liczył około 300 lat. W rozdziale

o teorii liczb b¸edziemy mówi´c o szybszych algorytmach sprawdzaj¸acych pierwszo´s´c liczb
maj¸acych po kilkaset bitów.

Przykład 1.14 Przypu´s´cmy, ˙ze chcemy zaprojektowa´c tablic¸e, która dla ka˙zdego ci¸agu
zło˙zongo z o´smiu liter przechowuje jak¸a´s informacj¸e (jeden bajt). W przypadku 26 liter
takich ci¸agów mamy

!"$#&%/

zatem potrzebowaliby´smy wi¸ecej ni˙z 100 gigabajtów pami¸eci.

Rozdział 1. Arytmetyka

1.9

Ułamki

Przypomnijmy najpierw krótko, jak przedstawia si˛e ułamek w systemie dziesi˛etnym. Na
przykład,

"%(

oznacza:

(

U˙zyli´smy kropki do oddzielania cz˛e´sci całkowitej od ułamkowej. Jest to cz˛esto u˙zywany
w informatyce sposób, stosowany mi˛edzy innymi w j˛ezyku Pascal. Ogólniej, zapis:

oznacza liczb˛e:

któr ˛

a mo˙zemy te˙z zapisa´c w postaci:

Podobnie mo˙zemy zapisywa´c ułamki w systemie dwójkowym. Jedyna ró˙znica polega na
tym, ˙ze w systemie binarnym podstaw ˛

a pot˛eg jest dwójka i ˙ze u˙zywamy tylko dwóch cyfr,

0 i 1. Tak wi˛ec w systemie dwójkowym zapis:

oznacza liczb˛e:

lub inaczej:

Przykład 1.15

,"+

W poni˙zszej tabeli przedstawiono kilka pierwszych ujemnych pot˛eg liczby 2 w systemie
dwójkowym i dziesi˛etnym.

"/3

,"+

"/3

%'"+

"/3

)

'+,"+

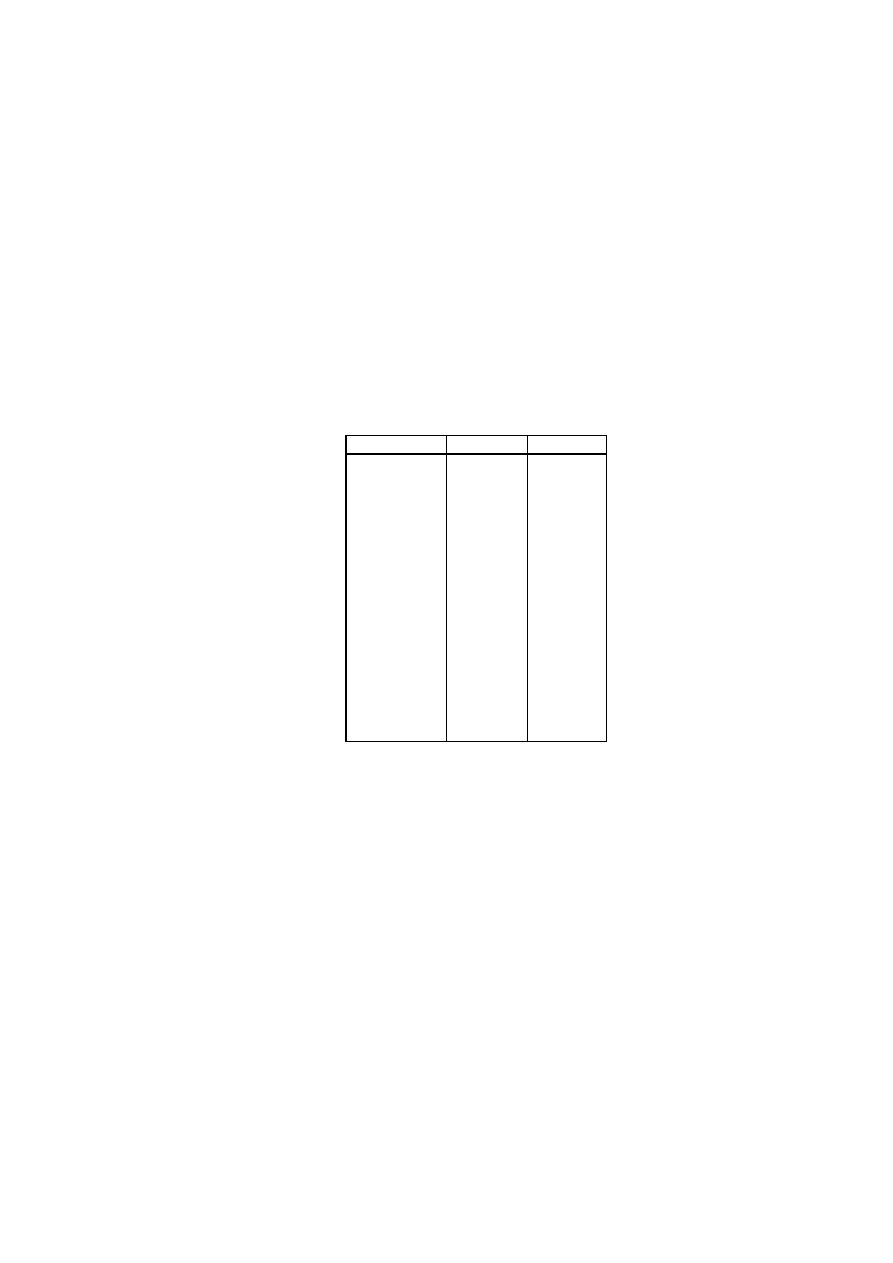
1.10. System szesnastkowy

1.10

System szesnastkowy

W informatyce u˙zywa si˛e te˙z systemu szesnastkowego, gdzie podstaw ˛

a jest liczba 16. Do

systemu szesnastkowego potrzebujemy szesnastu cyfr. Zwykle u˙zywa si˛e nast˛epuj ˛

acych

„cyfr”:

"$'% $( *+'','*$'' 0

W poni˙zszej tabeli zestawiono cyfry systemu szesnastkowego z odpowiadaj ˛

acymi im licz-

bami w systemie dwójkowym i dziesi˛etnym.

szesnastkowy

dwójkowy

dziesi˛etny

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

W j˛ezyku Pascal liczby w systemie szesnastkowym poprzedza si˛e znakiem dolara

, a w

j˛ezyku

znakami

Przykład 1.16 Zapis

oznacza liczb˛e w systemie szesnastkowym, która w systemie

dziesi˛etnym ma posta´c

Dzi˛eki temu, ˙ze 16 jest pot˛eg ˛

a dwójki, prosta jest zamiana postaci liczby z systemu dwój-

kowego na szesnastkowy, i na odwrót. Przy zamianie z systemu szesnastkowego na dwój-
kowy wystarczy zamienia´c kolejne cyfry przedstawienia na grupy odpowiednich czterech
bitów według powy˙zszej tabeli.

Przykład 1.17 Liczba, która w systemie szesnastkowym wygl ˛

ada tak

w systemie

dwójkowym ma posta´c

Przy zamianie z postaci dwójkowej na posta´c szesnastkow ˛

a post˛epujemy odwrotnie. Za-

st˛epujemy grupy po cztery bity pojedynczymi cyframi.

Przykład 1.18

)

Rozdział 1. Arytmetyka

Je˙zeli liczba cyfr w postaci dwójkowej nie dzieli si˛e przez 4, to uzupełniamy j ˛

a zerami na

pocz ˛

atku.

Przykład 1.19

W ten sposób mo˙zemy u˙zywa´c zapisu szesnastkowego do zwi˛ezłego przedstawiania dłu-
gich ci ˛

agów bitów.

1.11

Reprezentacja liczb w komputerze

W wielu j˛ezykach ka˙zda zmienna ma swój typ, który jest deklarowany na pocz ˛

atku pro-

gramu. Sposób przechowywania warto´sci zmiennej zale˙zy od jej typu.

1.11.1

Integer

Zmienne typu integer przechowywane s ˛

a zwykle w dwóch bajtach. Jeden bajt (ang. by-

te) zawiera osiem bitów, tak wi˛ec warto´s´c zmiennej typu integer przechowywana jest w
szesnastu bitach. Pierwszy bit oznacza znak. Je˙zeli jest on zerem, to liczba jest dodatnia,
je˙zeli jedynk ˛

a, to ujemna.

Je˙zeli liczba jest dodatnia, to pozostałe pi˛etna´scie bitów stanowi binarny zapis tej

liczby. Na przykład liczba

jest przechowywana jako:

Najwi˛eksz ˛

a liczb˛e dodatni ˛

a, jak ˛

a mo˙zna przechowa´c w zmiennej typu integer, jest:

czyli zero i pi˛etna´scie jedynek. Jest to:

%",/

Liczby ujemne s ˛

a przechowywane w tak zwanym systemie uzupełnieniowym. Liczba

ujemna o warto´sci bezwzgl˛ednej

jest przedstawiana jako liczba:

w postaci binarnej. Na przykład liczba

jest przedstawiona jako:

czyli szesna´scie jedynek. A liczba

jako:

Najmniejsza liczba ujemna, któr ˛

a mo˙zna zmie´sci´c do zmiennej typu integer, to:

1.11. Reprezentacja liczb w komputerze

czyli jedynka i pi˛etna´scie zer, która koduje liczb˛e:

%",

Cz˛esto nie ma ˙zadnego zabezpieczenia przed przekroczeniem maksymalnego lub mini-
malnego zakresu liczb typu integer. Je˙zeli, na przykład, do liczby

%",

, która jest prze-

chowywana jako:

dodamy jedynk˛e, to otrzymamy:

która koduje liczb˛e

%",

, i komputer nie zakomunikuje tego przekroczenia.

1.11.2

Real

Liczby typu real s ˛

a zapisywane w dwóch notacjach:

stałopozycyjnej,

zmiennopozycyjnej.

Liczby w notacji stałopozycyjnej to, na przykład:

czyli notacja dziesi˛etna. Zwró´cmy uwag˛e, ˙ze kropka oddziela cz˛e´s´c całkowit ˛

a liczby od

cz˛e´sci ułamkowej.

W notacji zmiennopozycyjnej liczba przedstawiona jest w postaci:

gdzie

jest mantys ˛

a, liczb ˛

a w postaci dziesi˛etnej z przedziału

lub

, a

, zwana cech ˛

a, jest liczb ˛

a całkowit ˛

a. Zapis

oznacza liczb˛e:

W poni˙zszej tabeli mamy kilka liczb w postaci stało- i zmiennopozycyjnej.

4837.92

(

%/0"

0.034

(

Sposób przechowywania warto´sci zmiennych typu real jest skomplikowany i nie b˛edzie
przedstawiony szczegółowo.

Rozdział 1. Arytmetyka

1.11.3

Inne typy całkowite

W j˛ezyku Pascal, oprócz integer, mo˙zna u˙zywa´c innych typów całkowitych; s ˛

a to:

shortint, zawiera liczby całkowite z przedziału od

byte, zawiera liczby całkowite z przedziału od

"++

word, zawiera liczby całkowite z przedziału od

,++%+

longint, zawiera liczby całkowite z przedziału od

"$(/(%,(

"$!($(%,(/

Elementy typu byte i shortint przechowywane s ˛

a w jednym bajcie (osiem bitów) pa-

mi˛eci, typu word — w dwóch bajtach, a typu longint — w czterech bajtach pami˛eci.
Liczby typu shortint i longint mog ˛

a by´c dodatnie lub ujemne i s ˛

a zapami˛etywane w po-

staci uzupełnieniowej z pierwszym bitem oznaczaj ˛

acym znak (podobnie jak liczby typu

integer). Elementy typu byte i word mog ˛

a by´c tylko dodatnie i s ˛

a przechowywane w po-

staci dwójkowej.

1.12

Wyra˙zenia arytmetyczne w j˛ezyku Pascal

W j˛ezyku Pascal wyra˙zeniami arytmetycznymi s ˛

a stałe liczbowe, na przykład:

"%(

"%'

(+'

oraz zmienne typów liczbowych (np. integer lub real). Wyra˙zenia mo˙zna tak˙ze budowa ´c
za pomoc ˛

a operatorów arytmetycznych i nawiasów. Je˙zeli

oraz

s ˛

a dwoma wyra˙zenia-

mi arytmetycznymi, to wyra˙zeniami arytmetycznymi s ˛

a tak˙ze:

U+W, U-W, U*W, U/W, (U), U div V, U mod V.

Gwiazdka

reprezentuje tutaj znak mno˙zenia, a operacje

div

oraz

mod

to iloraz i reszta

z dzielenia całkowitoliczbowego (s ˛

a one opisane dokładnie w rozdziale o teorii liczb).

Na przykład, wyra˙zeniami arytmetycznymi s ˛

-(2-3)/2+7*4, (2-3)/(3*2), 7 div 2, 7 mod 2.

Je˙zeli

oraz

s ˛

a zmiennymi liczbowymi, to wyra˙zeniami arytmetycznymi s ˛

a tak˙ze:

2*x, x*x-2/y.

Dla danego wyra˙zenia mo˙zemy obliczy´c jego warto´s´c. Robi si˛e to według zwykłych reguł
znanych ze szkoły. Najpierw oblicza si˛e wyra˙zenia w nawiasach, potem mno˙zenie i dzie-
lenie (od lewej do prawej), a na ko ´ncu dodawanie i odejmowanie (od lewej do prawej).

1.13

Poszukiwania binarne (binary search)

Znana jest gra w dwadzie´scia pyta´n. W tej grze za pomoc ˛

a dwudziestu pyta ´n, na które

odpowiedzi ˛

a mo˙ze by´c „tak” lub „nie”, nale˙zy odgadn ˛

a´c pomy´slan ˛

a przez przeciwnika

rzecz. Zobaczymy, jak mo˙zna wykorzysta´c binarny system zapisu liczb do opracowania
strategii wygrywaj ˛

acej w tej grze.

1.13. Poszukiwania binarne (binary search)

Najpierw upro´s´cmy nieco t˛e gr˛e. Załó˙zmy, ˙ze mo˙zemy zada´c tylko cztery pytania i ˙ze

odgadujemy liczb˛e naturaln ˛

ze zbioru:

'!&"'-%'-( #+$-, #$-'&0'$"$!%'4( +

Wtedy nale˙zy zada´c nast˛epuj ˛

ace cztery pytania:

Czy liczba

nale˙zy do zbioru

-0' !!"$!%'4( 4+

Czy

nale˙zy do zbioru

(*&+'-,'./"$% !!(*4+

Czy

nale˙zy do zbioru

"'-% -,'./'!!(*4+

Czy

nale˙zy do zbioru

-% &+$./&0'!%'+

Dlaczego te cztery pytania wystarcz ˛

a? Sprawa stanie si˛e jasna, je˙zeli przedstawimy liczby

w postaci binarnej. Ka˙zd ˛

a za pomoc ˛

a czterech bitów (z zerami na pocz ˛

atku). Wtedy nasz

zbiór wygl ˛

ada tak:

'&'& '&$- !'-''&'$-

'' '$!!'!'$!

A pytania wygl ˛

adaj ˛

a teraz tak:

Czy

nale˙zy do zbioru

'! !'! !! '!$!!'

Czy

nale˙zy do zbioru

'- - ! -$'!$!!'

Czy

nale˙zy do zbioru

''-'- ! -$!''!'!!'

Czy

nale˙zy do zbioru

-'- $-$!'!'!$

Zauwa˙zmy, ˙ze zbiór

zawiera wszystkie liczby z pierwszym bitem równym jedynce,

s ˛

a wszystkie liczby z drugim bitem równym jedynce, i tak dalej. Tak wi˛ec nasze

pytania s ˛

a w rzeczywisto´sci pytaniami o kolejne bity odgadywanej liczby. Na przykład w

pierwszym pytaniu pytamy, czy pierwszy bit odgadywanej liczby jest jedynk ˛

Ale mo˙zna do tych pyta ´n podej´s´c inaczej. Najpierw dzielimy zbiór na połowy: na

liczby mniejsze od o´smiu i na liczby wi˛eksze lub równe o´smiu, i pytamy, do której połowy
nale˙zy odgadywana liczba (dokładniej pytamy, czy liczba nale˙zy do górnej połowy). Po
uzyskaniu odpowiedzi mamy dwa razy w˛e˙zszy przedział poszukiwa ´n. Przypu´s´cmy, ˙ze
odgadywan ˛

a liczb ˛

a jest 11. W drugim etapie dzielimy przedział

-0 ! !!"$%'!('+

na połowy, górn ˛

"'!%'!( +

i doln ˛

-0 ! !

Rozdział 1. Arytmetyka

i pytamy, do której połowy nale˙zy szukana liczba. Po drugiej odpowiedzi przedział po-
szukiwa´n jest ju˙z cztery razy krótszy. Po dwóch kolejnych pytaniach przedział zaw˛e˙za si˛e
do jednej liczby. Drugi sposób jest całkowicie równowa˙zny pierwszemu, tutaj te˙z pytamy
o kolejne bity i otrzymujemy takie same odpowiedzi.

Potrzeba cztery razy kolejno dzieli´c zbiór na połowy, aby z pocz ˛

atkowej długo´sci

16 przej´s´c na ko´ncu do długo´sci 1. A ile trzeba podziałów, je˙zeli na pocz ˛

atku mamy

elementów? Po pierwszym podziale nasz zbiór b˛edzie miał długo´s´c

, po

drugim

, a po

-tym

. Jak wida´c, potrzeba

kolejnych podziałów, aby

doj´s´c do 1. Tak wi˛ec je˙zeli mamy do dyspozycji

pyta ´n, to mo˙zemy odnale´z´c jedn ˛

spo´sród

)

liczb całkowitych z przedziału od

(++

Metod˛e poszukiwa ´n binarnych mo˙zna zastosowa´c do stwierdzenia, czy jaka´s liczba

naturalna

jest kwadratem (lub jak ˛

a´s inn ˛

a ustalon ˛

a pot˛eg ˛

a) innej liczby naturalnej. Ina-

czej, czy istnieje liczba naturalna

taka, ˙ze

, lub ogólniej, czy istnieje liczba

naturalna

taka, ˙ze

Poni˙zej przedstawiamy taki algorytm. Algorytm ten u˙zywa dwoch dodatkowych zmien-

nych

, warto´sci tych zmiennych przybli˙zaj ˛

a pierwiastek stopnia

od dołu i od

góry. W trakcie wykonywania algorytmy przybli˙zeniaa te s ˛

a coraz lepsze

Algorytm sprawdzaj ˛

acy, czy dana liczba naturalna

jest pot˛eg ˛

a o wykładniku

jakiej´s

liczby naturalnej.

Dane wej´sciowe: liczba naturalna .

Dane wyj´sciowe: pierwiastek stopnia

, (liczba naturalna

, taka ˙ze

) lub

informacja, ˙ze

nie ma pierwiastka stopnia

Powtarzaj a˙z do skutku:

je˙zeli

, to koniec,

nie ma pierwiastka.

je˙zeli

, to koniec,

jest pot˛eg ˛

je˙zeli

, to

je˙zeli

, to

1.14

Zadania

1. Zwi˛eksz o jeden nast˛epuj ˛

ace liczby zapisane w postaci dwójkowej: a)

2. Porównaj nast˛epuj ˛

ace pary liczb: a)

3. Dodaj (odejmij, pomnó˙z) w postaci dwójkowej nast˛epuj ˛

ace pary liczb: a)

1.15. Problem: Waga

4. Napisz dokładny algorytm odejmowania dwóch liczb w postaci dwójkowej.

5. Liczby 81, 126 przedstaw w postaci dwójkowej. Jak b˛ed ˛

a one reprezentowane w

komputerze jako stałe typu integer (byte, word)?

6. Nast˛epuj ˛

ace liczby przedstaw w postaci dwójkowej: 6.75, 5.625, $B1, $FF.

7. Nast˛epuj ˛

ace liczby przedstaw w postaci trójkowej: 80, 120.

8. Nast˛epuj ˛

ace liczby w postaci dwójkowej, 10001101, 100101, przedstaw w postaci:

a) dziesi˛etnej,

b) szesnastkowej.

9. Opisz algorytm zamiany ułamka z postaci dziesi˛etnej na posta ´c dwójkow ˛

10. Ile maksymalnie pyta ´n z odpowiedziami TAK/NIE trzeba zada´c, aby odgadn ˛

a´c licz-

b˛e z przedziału od 0 do 100 000?

11. Zastosuj algorytm wyznaczania pierwiastków do znalezienia pierwiastka stopnia 3

z liczby 512.

1.15

Problem: Waga

Wyobra´zmy sobie wag˛e szalkow ˛

a. Na jednej szalce, lewej, kładziemy jaki´s przedmiot do

zwa˙zenia, a nast˛epnie na obu szalkach kładziemy odwa˙zniki. Je˙zeli waga jest w równowa-
dze, to wa˙zony przedmiot ma wag˛e równ ˛

a sumie (nominałów) odwa˙zników poło˙zonych

na prawej szalce minus suma odwa˙zników poło˙zonych na lewej szalce, obok wa˙zonego
przedmiotu. Na przykład, je˙zeli na prawej szalce le˙z ˛

a odwa˙zniki

gramowe, a na

lewej odwa˙zniki

(

gramowe, to przedmiot wa˙zy

(

gramów.

Interesuj ˛

ace nas pytanie brzmi: jakie powinny by´c nominały poszczególnych odwa˙z-

ników, aby mo˙zna było zwa˙zy´c ka˙zdy ci˛e˙zar o wadze od

, przy jak najmniejszej

liczbie odwa˙zników. Zakładamy, ˙ze wa˙zymy tylko przedmioty o całkowitych wagach.

Poka˙z, ˙ze

(a) Za pomoc ˛

odwa˙zników mo˙zna zwa˙zyc co najwy˙zej

ró˙znych ci˛e˙zarów.

(b) Je˙zeli nominały odwa˙zników s ˛

a kolejnymi pot˛egami trójki, to znaczy

dla

, to za ich pomoc ˛

a mo˙zna zwa˙zy´c ka˙zdy (całkowity) ci˛e˙zar o nominale

od 1 do

Wskazówki:
(a) Poniewa˙z ka˙zdy odwa˙znik mo˙ze si˛e znajdowa´c na prawej lub lewej szalce, lub na stole,
to mamy

ró˙znych poło˙ze ´n odwa˙zników. W´sród tych poło˙ze ´n jest takie, gdzie wszystkie

odwa˙zniki le˙z ˛

a na stole (wtedy wa˙zymy zerowy ci˛e˙zar). Ponadto je˙zeli odwa˙zniki le˙z ˛

na szalkach i odwa˙zaj ˛

a ci˛e˙zar

, to zamieniwszy poło˙zenia odwa˙zników na szalkach

(odwa˙zniki z lewej przekładamy na praw ˛

a szalk˛e, i na odwrót), b˛edziemy odwa˙za ´c ci˛e˙zar

Rozdział 1. Arytmetyka

(b) Rozło˙zenie odwa˙zników przy wa˙zeniu ci˛e˙zaru

odpowiada przedstawieniu

postaci

(1.5)

gdzie

- !

. Aby przedstawi´c ci˛e˙zar

w postaci (1.5), najpierw przedstawia-

my liczb˛e

w systemie trójkowym:

a nast˛epnie od ka˙zdej cyfry odejmujemy jedynk˛e: