Matematyka Dyskretna

Andrzej Szepietowski

25 czerwca 2002 roku

Rozdział 1

Funkcje boolowskie

1.1

Algebra Boole’a

Przykładem algebry Boole’a jest zbiór dwuelementowy:

z trzema operacjami: alternatyw¸a, koniunkcj¸a i negacj¸a.

Alternatywa, któr¸a b¸edziemy te˙z nazywa´c po prostu sum¸a, jest operacj¸a dwuargumentow¸a,

oznaczan¸a przez:

lub

i okre´slon¸a przez tabel¸e:

p

q

p+q

0

0

0

0

1

1

1

0

1

1

1

1

Koniunkcja (lub iloczyn) jest drug¸a operacj¸a dwuargumentow¸a, oznaczan¸a przez:

lub

i okre´slon¸a przez tabel¸e:

p

q

0

0

0

0

1

0

1

0

0

1

1

1

3

4

Rozdział 1. Funkcje boolowskie

Podobnie jak w arytmetyce, kropk¸e b¸edziemy opuszcza ´c, je˙zeli nie b¸edzie to prowadzi´c
do niejednoznaczno´sci.

Operacje alternatywy i koniunkcji mo˙zna te˙z zdefiniowa´c za pomoc¸a nast¸epuj¸acych

wzorów:

Negacja jest operacj¸a jednoargumentow¸a, oznaczan¸a przez:

lub

i okre´slon¸a przez tabel¸e:

p

0

1

1

0

Algebr¸e

mo˙zemy interpretowa´c jako logik¸e zdaniow¸a. Zmienne s¸a zdaniami,

które mog¸a przyjmowa´c warto´sci prawda lub fałsz. Je˙zeli oznaczymy prawd¸e przez

i

fałsz przez

, to powy˙zej zdefiniowane operacje odpowiadaj¸a znanym operacjom z logiki

zda´n.

Lemat 1.1 Operacje alternatywy, koniunkcji i negacji spełniaj¸a nast¸epuj¸ace to˙zsamo´sci:

(a)

(alternatywa i koniunkcja s¸a przemienne),

(b)

(alternatywa i koniunkcja s¸a

ł¸aczne),

(c)

(alternatywa jest rozdzielna wzgl¸edem koniunkcji),

(d)

(koniunkcja jest rozdzielna wzgl¸edem alternatywy),

(e)

,

,

,

,

(f)

,

,

,

,

(g)

,

(prawa pochłaniania),

(h)

,

(prawa de’Morgana),

(i)

(prawo podwójnego przeczenia).

Najprostsze dowody powy˙zszych to˙zsamo´sci polegaj¸a na sprawdzeniu, ˙ze zachodz¸a one
dla ka˙zdego mo˙zliwego podstawienia za zmienne warto´sci 1 lub 0. Na przykład, udowod-
nimy to˙zsamo´s´c:

Wszystkie mo˙zliwe podstawienia zebrane s¸a w tabeli:

1.1. Algebra Boole’a

5

p

q

0

0

0

0

1

0

1

0

1

1

1

1

Poniewa˙z trzecia kolumna jest identyczna z pierwsz¸a, wi¸ec równo´s´c

jest

prawdziwa dla ka˙zdego podstawienia, czyli jest to˙zsamo´sci¸a.

Innym przykładem algebry Boole’a jest zbiór wszystkich podzbiorów jakiego´s zbioru

z operacjami okre´slonymi w nast¸epuj¸acy sposób:

jest sum¸a mnogo´sciow¸a

jest iloczynem

jest uzupełnieniem zbioru,

,

1

jest zbiorem

,

0

jest zbiorem pustym

.

Tak˙ze te operacje spełniaj¸a to˙zsamo´sci z lematu 1.1.

Udowodnimy, dla przykładu, to˙zsamo´s´c

. Je˙zeli element

nale˙zy do

zbioru

, to nale˙zy tak˙ze do sumy

. Je˙zeli za´s

nie nale˙zy do

, to nie nale˙zy

tak˙ze do iloczynu

, a wi¸ec

nie nale˙zy do ˙zadnego składnika sumy

, czyli nie

nale˙zy do

. Tak wi¸ec zbiory

i

zawieraj¸a dokładnie te same elementy,

a wi¸ec s¸a równe.

Oprócz trzech podstawowych, w algebrze Boole’a definiuje si¸e inne operacje. Dla nas

wa˙zna b¸edzie operacja xor (ang. exclusive or) albo alternatywa wykluczaj¸aca. xor jest
operacj¸a dwuargumentow¸a, oznaczan¸a przez:

i okre´slon¸a przez tabel¸e:

p

q

0

0

0

0

1

1

1

0

1

1

1

0

Operacja ta jest nazywana alternatyw¸a wykluczaj¸ac¸a, poniewa˙z w logice zdaniowej

zdanie

jest prawdziwe, je˙zeli albo

, albo

jest prawdziwe, ale nie jest prawdziwe,

gdy

i

naraz s¸a prawdziwe. Operacja

ma nast¸epuj¸ace własno´sci:

Lemat 1.2

(a)

(jest przemienna),

6

Rozdział 1. Funkcje boolowskie

(b)

(jest ł¸aczna),

(c)

(xor jest rozdzielne wzgl¸edem koniunkcji),

(d)

,

,

,

,

(e) Je˙zeli

, to

.

(f) zbiór

z działaniami xor i koniunkcji tworzy ciało.

Ł¸aczno´s´c operacji

zapewnia, ˙ze mo˙zemy opuszcza´c nawiasy w wyra˙zeniach typu

, bez spowodowania niejednoznaczno´sci.

Operacj¸e xor mo˙zna zdefiniowa´c poprzez alternatyw¸e, koniunkcj¸e i negacj¸e:

W algebrze podzbiorów operacja xor odpowiada ró˙znicy symetrycznej:

1.2

Wyra˙zenia boolowskie

Podobnie jak wyra˙zenia arytmetyczne, mo˙zemy budowa ´c wyra˙zenia boolowskie. Wyra-

˙zeniami boolowskimi s¸a stałe

i

oraz zmienne boolowskie (typu boolean). Bardziej

zło˙zone wyra˙zenia mo˙zna budowa´c za pomoc¸a operatorów boolowskich i nawiasów. Je-

˙zeli

i

s¸a dwoma wyra˙zeniami boolowskimi, to wyra˙zeniami boolowskimi s¸a tak˙ze

nast¸epuj¸ace wyra˙zenia:

1.2.1

Wyra˙zenia boolowskie w j¸ezyku Pascal

W j¸ezyku Pascal wyra˙zeniami boolowskimi s¸a stałe

true

i

false

oraz zmienne ty-

pu

boolean

. Wyra˙zenia boolowskie mo˙zna te˙z budowa´c z wyra˙ze´n arytmetycznych za

pomoc¸a tak zwanych operatorów relacyjnych. Je˙zeli

U

i

W

s¸a dwoma wyra˙zeniami aryt-

metycznymi, to wyra˙zeniem boolowskim jest wyra˙zenie:

U op W,

gdzie

op

oznacza dowolny operator relacyjny. Operatory relacyjne s¸a zestawione w tabeli:

operator

znaczenie

=

równe

<

mniejsze

>

wi¸eksze

<>

ró˙zne

<=

mniejsze lub równe

>=

wi¸eksze lub równe

1.3. Funkcje boolowskie

7

Wyra˙zenia boolowskie mo˙zna tak˙ze budowa´c za pomoc¸a operatorów boolowskich i na-
wiasów. Je˙zeli

U

i

W

s¸a dwoma wyra˙zeniami boolowskimi, to wyra˙zeniami boolowskimi

s¸a tak˙ze nast¸epuj¸ace wyra˙zenia:

U or W

(suma lub alternatywa),

U and W

(koniunkcja),

not W

(negacja),

U xor W

(exclusive or lub alternatywa wykluczaj¸aca),

(U)

(wyra˙zenie

U

wzi¸ete w nawias).

Przykładami wyra˙ze ´n boolowskich w j¸ezyku Pascal s¸a:

true or b

,

b and not(x>=0)

,

(0<=x) and (x<=10)

,

(0<x) or (x>10)

.

gdzie

b

jest zmienn¸a typu boolean, a

x

— zmienn¸a liczbow¸a.

Wyra˙zenia boolowskie wyst¸epuj¸a w j¸ezyku Pascal w instrukcjach warunkowych lub

w p¸etlach while i repeat.

1.3

Funkcje boolowskie

Funkcje boolowskie

zmiennych to funkcje:

gdzie

. Mamy cztery funkcje boolowskie jednej zmiennej:

funkcj¸e stał¸a

równ¸a 0,

identyczno´s´c

,

negacj¸e

,

funkcj¸e stał¸a

równ¸a 1.

Warto´sci tych funkcji zestawiono w tabeli:

x

0

0

0

1

1

1

0

1

0

1

8

Rozdział 1. Funkcje boolowskie

S¸a to wszystkie funkcje boolowskie jednej zmiennej, poniewa˙z s¸a to funkcje ze zbioru
w zbiór

, a takich funkcji jest:

Funkcji boolowskich dwóch zmiennych jest:

Ich warto´sci zestawiono w tabeli:

x

y

0

0

0

0

0

0

0

0

0

0

1

1

1

1

1

1

1

1

0

1

0

0

0

0

1

1

1

1

0

0

0

0

1

1

1

1

1

0

0

0

1

1

0

0

1

1

0

0

1

1

0

0

1

1

1

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0

1

Zauwa˙zmy, ˙ze ci¸ag warto´sci ka˙zdej z tych funkcji czytany od góry do dołu stanowi zapis
binarny jej numeru. Przyjrzyjmy si¸e bli˙zej tym funkcjom:

jest funkcj¸a stał¸a równ¸a 0,

jest funkcj¸a stał¸a równ¸a 1,

jest koniunkcj¸a,

jest alternatyw¸a,

jest xorem,

jest implikacj¸a z

do

,

jest implikacj¸a z

do

,

jest równowa˙zno´sci¸a,

jest rzutem na pierwsz¸a współrz¸edn¸a,

jest rzutem na drug¸a współrz¸edn¸a,

jest negacj¸a drugiej współrz¸ednej,

jest negacj¸a pierwszej współrz¸ednej,

jest zaprzeczeniem koniunkcji, tak zwany nand,

jest zaprzeczeniem alternatywy, tak zwany nor,

jest zaprzeczeniem implikacji z

do

,

jest zaprzeczeniem implikacji z

do

.

1.3. Funkcje boolowskie

9

Jak wida´c, ka˙zd¸a z tych funkcji mo˙zna przedstawi´c za pomoc¸a koniunkcji, alternatywy i
negacji.

Funkcji boolowskich trzech zmiennych jest:

nie b¸edziemy ich wszystkich wypisywa´c.

Nasuwa si¸e pytanie, czy ka˙zd¸a funkcj¸e

zmiennych mo˙zna przedstawi ´c za pomoc¸a

koniunkcji, alternatywy i negacji. Odpowied´z jest pozytywna. Najpierw przykład. Roz-
patrzmy funkcj¸e boolowsk¸a trzech zmiennych:

x

y

z

f(x,y,z)

0

0

0

0

0

0

1

1

0

1

0

0

0

1

1

1

1

0

0

1

1

0

1

1

1

1

0

0

1

1

1

0

Rozwa˙zmy wyra˙zenie:

Przyjmuje ono warto´s´c 1 tylko dla jednego wektora

, czyli dla podstawienia

,

,

. Podobnie, wyra˙zenie

przyjmuje warto´s´c 1 tylko dla wektora

,

wyra˙zenie

— tylko dla

, a wyra˙zenie

— tylko dla

. Suma tych

wyra˙ze´n:

(1.1)

przyjmuje warto´s´c 1 tylko dla wektorów

,

,

,

, czyli jest

równowa˙zna naszej funkcji

. Wyra˙zenie (1.1) jest w tak zwanej dysjunkcyjnej postaci

normalnej (DNF).

Funkcj¸e

mo˙zna te˙z opisa´c w innej formie. Rozwa˙zmy wyra˙zenie:

Przyjmuje ono warto´s´c 0 tylko dla jednego wektora

, czyli dla podstawienia

,

,

. Podobnie, wyra˙zenie

przyjmuje warto´s´c 0 tylko dla wektora

, wyra˙zenie

— tylko dla

, a wyra˙zenie

— tylko

dla

. Iloczyn tych wyra˙ze ´n:

przyjmuje warto´s´c zero tylko dla wektorów

,

,

, i

, czy-

li jest równowa˙zny funkcji

. Jest to tak zwana koniunkcyjna posta´c normalna (CNF)

funkcji

.

10

Rozdział 1. Funkcje boolowskie

Metod¸e t¸e mo˙zna uogólni´c na funkcje

zmiennych. Wprowadzimy oznaczenie:

Dla dowolnego wektora

, niech

oznacza

-t¸a współrz¸edn¸a wektora .

Rozwa˙zmy teraz wyra˙zenie:

Zauwa˙zmy, ˙ze

jest równe 1 tylko wtedy, gdy podstawimy

, dla ka˙zdego

, czyli dla

. Wida´c z tego, ˙ze:

Jest to dysjunkcyjna posta´c normalna (DNF) funkcji

(sumowanie oznacza tutaj alternatyw¸e).

Aby otrzyma´c posta´c koniukcyjn¸a, zaczynamy od wyra˙zenia:

Zauwa˙zmy, ˙ze

jest równe 0 tylko wtedy, gdy podstawimy:

, dla ka˙zdego

, czyli dla

. Wida´c z tego, ˙ze:

Jest to koniunkcyjna posta´c normalna (CNF) funkcji

.

1.4

Sieci boolowskie

Najpierw przykład. Na rysunku 1.1 przedstawiono pewn¸a sie ´c boolowsk¸a. Jest to graf
skierowany z sze´scioma wierzchołkami (bramkami) i pi¸ecioma kraw¸edziami ł¸acz¸acymi
niektóre bramki. W tym i nast¸epnych przykładach przyjmujemy, ˙ze kraw¸edzie s¸a skiero-
wane od góry do dołu. Bramki maj¸a etykiety. Jedna etykietowana jest stał¸a

, dwie ety-

kietowane s¸a zmiennymi

i

, a trzy etykietowane s¸a operatorami logicznymi,

,

i

.

Bramki oznaczone stałymi lub zmiennymi s¸a bramkami wej´sciowymi i ˙zadne kraw¸edzie
nie prowadz¸a do nich. Bramka

ma jedn¸a kraw¸ed´z wchodz¸ac¸a, a bramki

i

po dwie.

Bramka

jest bramk¸a wyj´sciow¸a, bo nie wychodzi z niej ˙zadna kraw¸ed´z. Z ka˙zd¸a bramk¸a

w sieci mo˙zemy zwi¸aza´c wyra˙zenie boolowskie. W przypadku bramki etykietowanej stał¸a
lub zmienn¸a, tym wyra˙zeniem jest ta stała lub ta zmienna. Z bramk¸a

zwi¸azane jest wy-

ra˙zenie

, z bramk¸a

wyra˙zenie

, a z bramk¸a

wyra˙zenie

.

Ogólnie, sie´c boolowska to graf składaj¸acy si¸e z wierzchołków, nazywanych bramka-

mi, i skierowanych kraw¸edzi ł¸acz¸acych niektóre bramki. Ka˙zda bramka ma swoj¸a etykiet¸e,
któr¸a mo˙ze by´c stała 1 lub 0, zmienna lub operator boolowski. W naszych rozwa˙zaniach
ograniczymy si¸e do czterech operatorów:

,

,

i

, ale mo˙zna rozwa˙za ´c sieci z innym

zbiorem operatorów. Do bramek oznaczonych stałymi lub zmiennymi nie prowadz¸a ˙zadne

1.4. Sieci boolowskie

11

Rysunek 1.1: Przykład sieci boolowskiej

kraw¸edzie, s¸a to bramki wej´sciowe. Bramki oznaczone przez

maj¸a po jednej kraw¸edzi

wej´sciowej, a bramki z pozostałymi operatorami maj¸a po dwie kraw¸edzie wchodz¸ace. W
sieci boolowskiej nie mo˙ze by´c cyklu, czyli ci¸agu kraw¸edzi

takiego ˙ze

, i dla ka˙zdego

spełniaj¸acego warunek

w sieci istnieje

kraw¸ed´z od wierzchołka

do wierzchołka

. Wierzchołek, z którego nie wychodz¸a

˙zadne kraw¸edzie, nazywamy wyj´sciowym. W sieci mo˙ze by´c kilka bramek wyj´sciowych.

Z ka˙zd¸a bramk¸a

w sieci mo˙zemy zwi¸aza´c wyra˙zenie boolowskie

. Robimy to

przez indukcj¸e ze wzgl¸edu na struktur¸e sieci:

Najpierw przypisujemy wyra˙zenia bramkom wej´sciowym. W tym wypadku wyra-

˙zeniem tym jest etykieta bramki

: stała lub zmienna.

Je˙zeli bramka

jest etykietowana negacj¸a

i dochodzi do niej kraw¸ed´z od bramki

oraz bramka

ma ju˙z przypisane wyra˙zenie

, to bramce

przypisujemy

wyra˙zenie

.

Je˙zeli etykiet¸a bramki

jest operator dwuargumentowy

, to do

prowadz¸a kraw¸edzie

od dwóch bramek,

i

. Je˙zeli przypisano ju˙z wyra˙zenia

i

bramkom

i

, to bramce

przypisujemy wyra˙zenie

.

Liczb¸e wszystkich bramek w sieci nazywamy kosztem sieci, a długo´s´c najdłu˙zszej ´scie˙zki
w sieci nazywamy gł¸eboko´sci¸a sieci. Je˙zeli w sieci istnieje bramka wyj´sciowa

, to mo-

˙zemy powiedzie´c, ˙ze sie´c oblicza wyra˙zenie

. Z faktu, ˙ze ka˙zd¸a funkcj¸e boolowsk¸a

mo˙zna przedstawi´c w postaci normalnej, wynika, ˙ze ka˙zd¸a funkcj¸e boolowsk¸a mo˙zna
przedstawi´c za pomoc¸a sieci. Jednak konstrukcja sieci dla funkcji boolowskiej

poprzez

wyznaczanie postaci normalnej zazwyczaj prowadzi do sieci o du˙zym koszcie (liczbie
bramek). Poni˙zej omówiono przykłady sieci o stosunkowo małym koszcie.

12

Rozdział 1. Funkcje boolowskie

1.4.1

Suma (alternatywa) kilku zmiennych

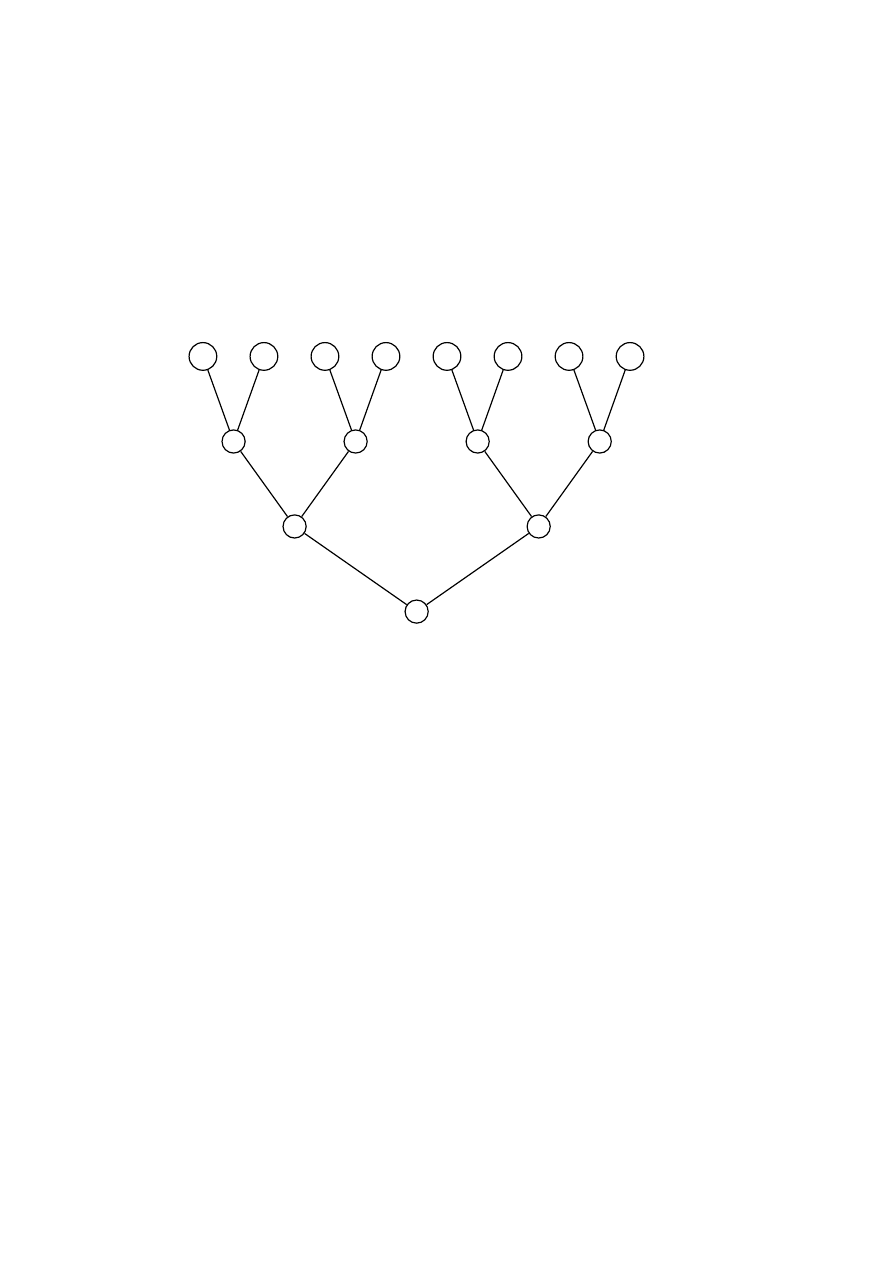
Rysunek 1.2: Sie´c boolowska obliczaj¸aca alternatyw¸e o´smiu zmiennych

Na rysunku 1.2 przedstawiono sie´c obliczaj¸ac¸a alternatyw¸e o´smiu zmiennych:

Gł¸eboko´s´c tej sieci wynosi 3.

Podobnie mo˙zna skonstruowa´c sie´c licz¸ac¸a alternatyw¸e

zmiennych, gdzie

jest

jak¸a´s pot¸eg¸a dwójki. Gł¸eboko´s´c takiej sieci wynosi

. Oczywi´scie tak samo mo˙zemy

zbudowa´c sie´c dla uogólnionej koniunkcji lub operatora

.

1.4.2

Funkcje progowe

Funkcja

gdy liczba jedynek w´sród

jest

równa lub wi¸eksza od

w przeciwnym wypadku,

jest funkcj¸a progow¸a o

zmiennych z progiem

. B¸edziemy zakłada ´c, ˙ze

.

Sieci funkcji progowych dwóch zmiennych s¸a proste, poniewa˙z:

Przedstawiono je na rysunku 1.3.

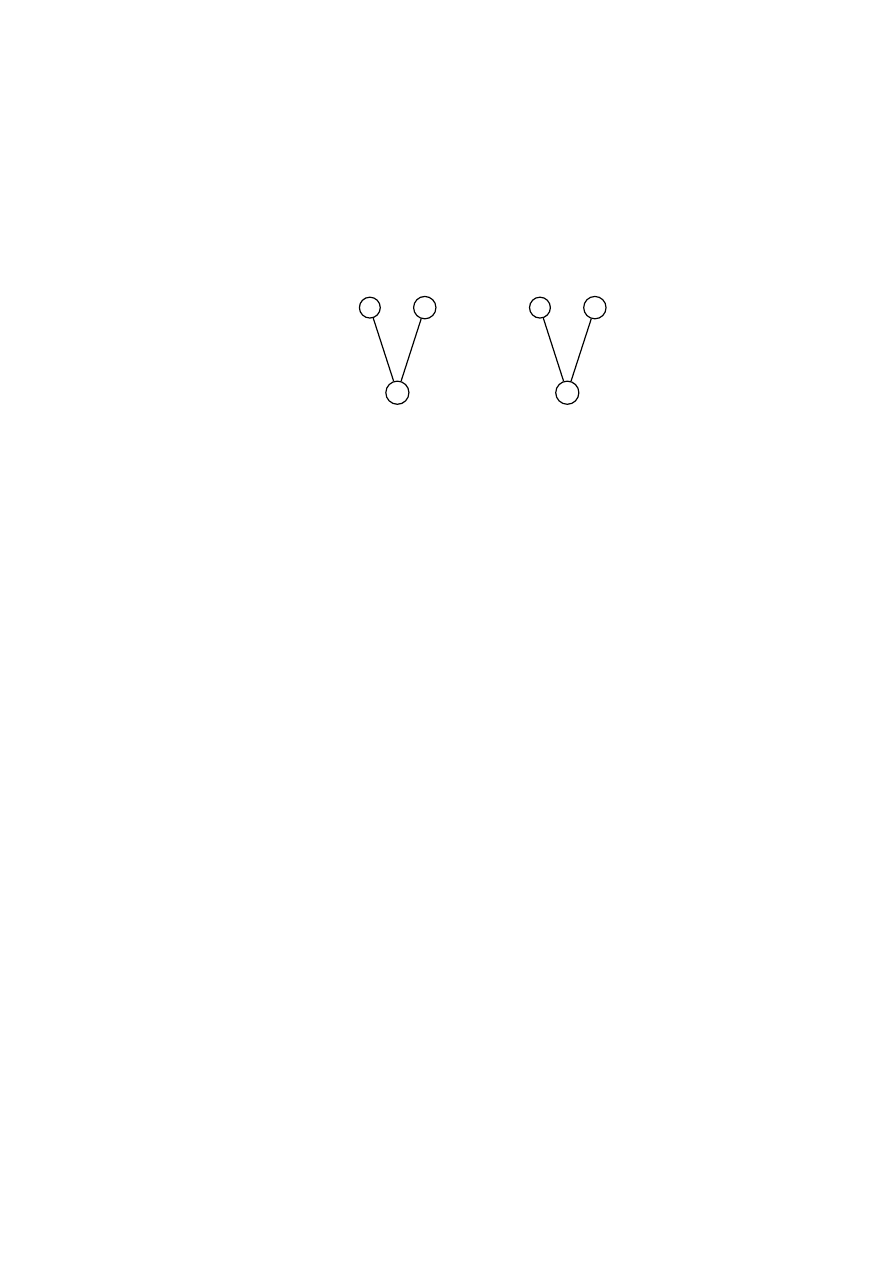
1.4. Sieci boolowskie

13

Rysunek 1.3: Sieci funkcji progowych dwóch zmiennych

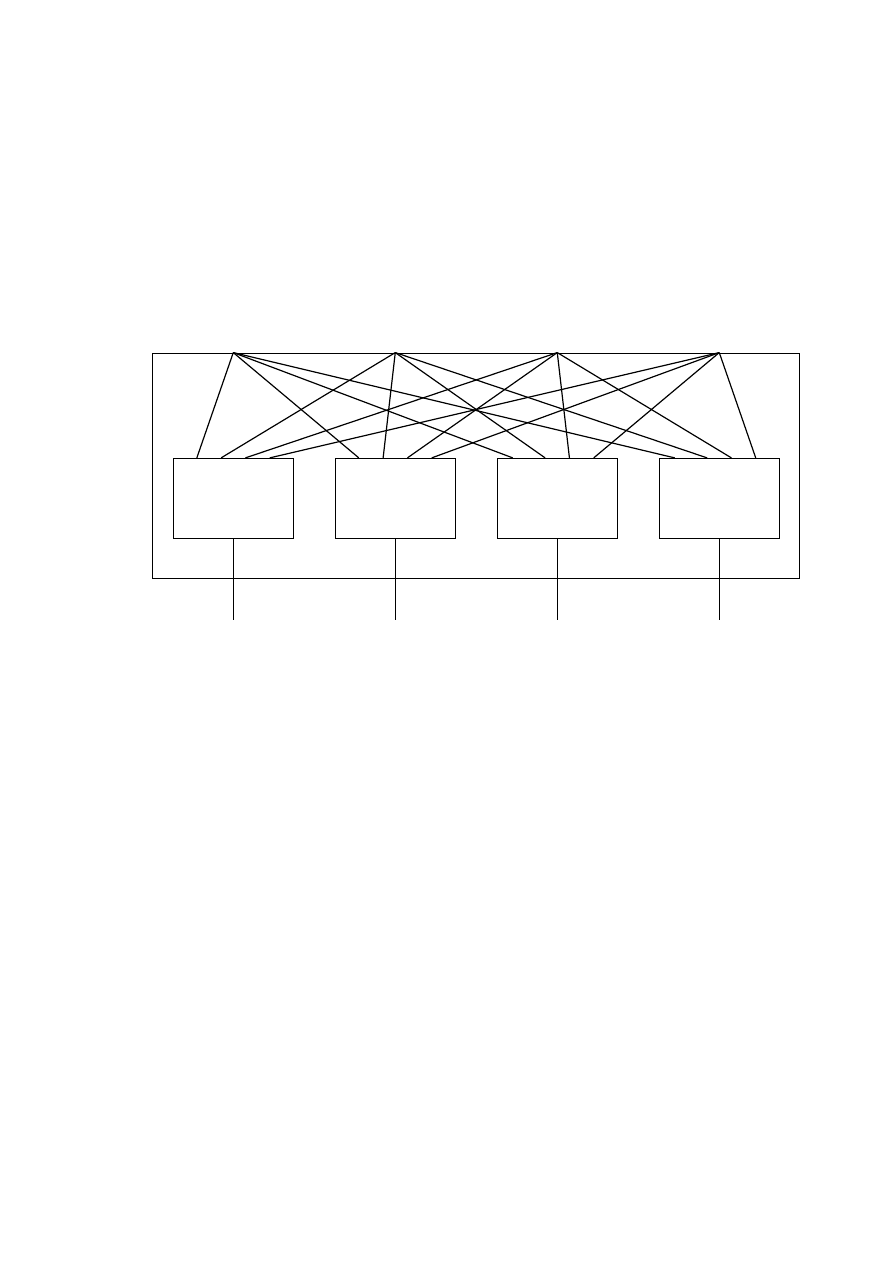
Przypu´s´cmy, ˙ze mamy ju˙z sieci funkcji progowych

zmiennych. Za ich pomoc¸a

mo˙zemy skonstruowa´c funkcje progowe

zmiennych (rysunek 1.4). Zrobimy to

posługuj¸ac si¸e nast¸epuj¸acymi zale˙zno´sciami:

Je˙zeli

, to:

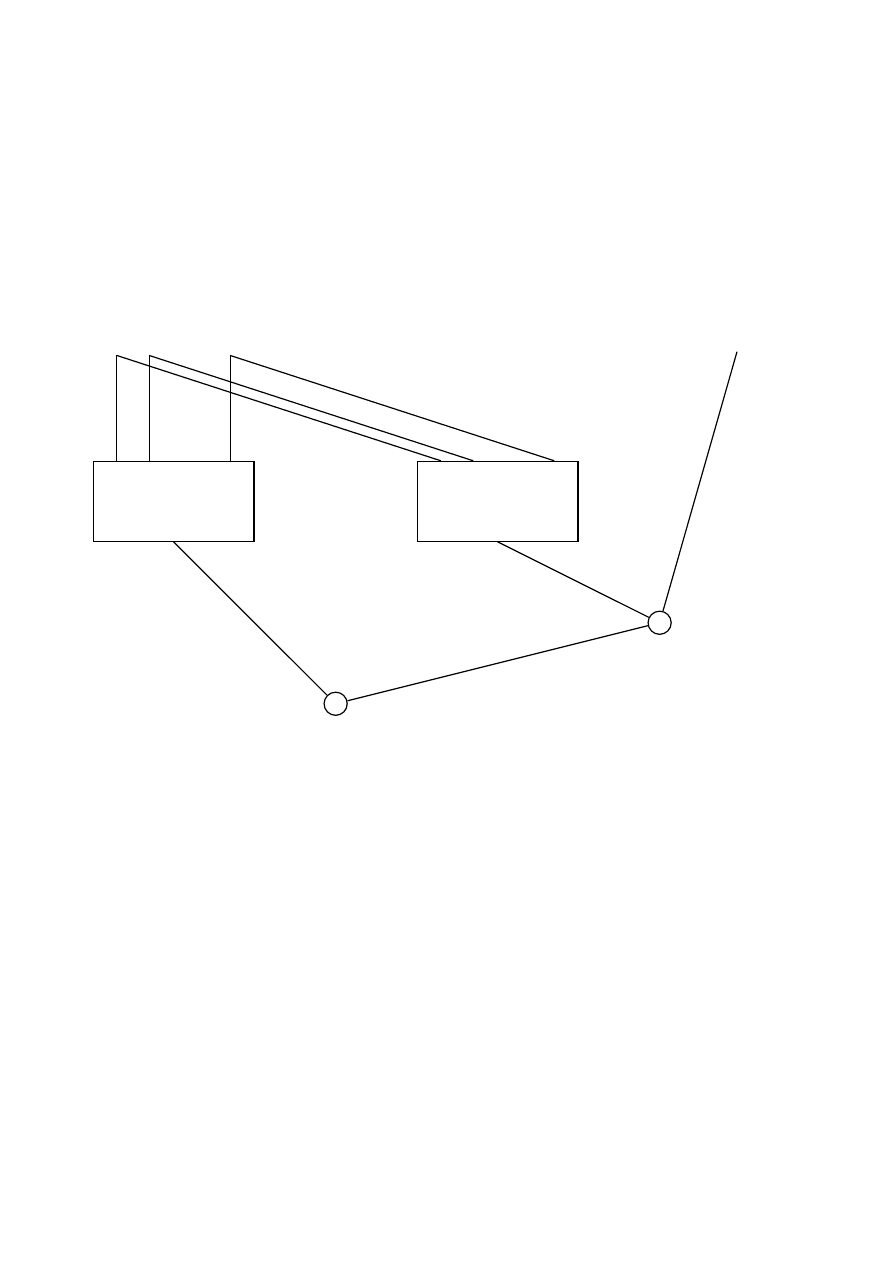
Je˙zeli zestawimy równolegle sieci funkcji progowych, tak jak zrobiono to na rysun-

ku 1.5, to otrzymamy sie´c sortuj¸ac¸a. Sie´c ta bierze na wej´sciu ci¸ag czterech bitów:

i zwraca na wyj´sciu te same bity w porz¸adku nierosn¸acym:

Na przykład gdy na wej´sciu b¸edzie ci¸ag

, wówczas na wyj´sciu pojawi si¸e ci¸ag

.

1.4.3

Sumator

Zastanówmy si¸e teraz, jak skonstruowa´c sumator, czyli sie´c, która b¸edzie dodawa´c dwie
liczby -bitowe:

oraz

i da w wyniku

bitów sumy:

14

Rozdział 1. Funkcje boolowskie

Rysunek 1.4: Sie´c funkcji progowej

Na wej´sciu sumatora mamy

bitów pierwszej liczby,

, ... ,

, oraz

bitów drugiej

liczby,

, ... ,

, a na wyj´sciu

bitów sumy arytmetycznej

, ... ,

. Nasz sumator

na´sladuje szkolne dodawanie opisane w rozdziale o arytmetyce. Najpierw dodaje bity

i

i oblicza ostatni bit sumy

oraz przeniesienie

, które ma by´c dodane do nast¸epnego

bitu. Potem dla kolejnych pozycji

od

do

dodaje bity

,

oraz przeniesienie

z poprzedniej pozycji i oblicza

-ty bit sumy

oraz przeniesienie

do nast¸epnej

pozycji.

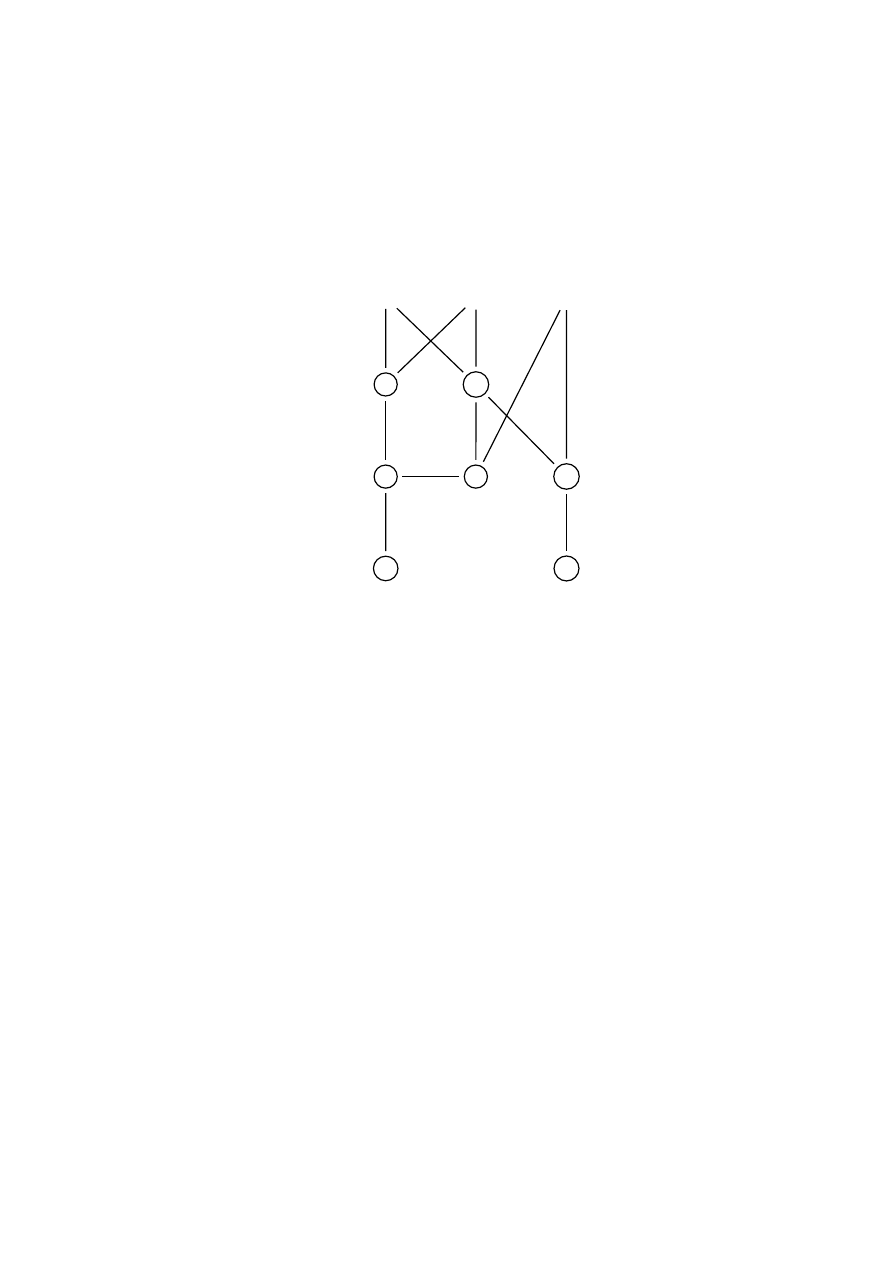
Na rysunku 1.6 przedstawiono sie´c HA (ang. half adder — półsumator), która ma na

wej´sciu dwa bity,

i

, a na wyj´sciu — bit sumy

oraz bit przeniesienia

.

Na rysunku 1.7 przedstawiono sie´c FA (ang. full adder), która ma na wej´sciu trzy

bity,

,

oraz

, a na wyj´sciu bit sumy

oraz bit przeniesienia

.

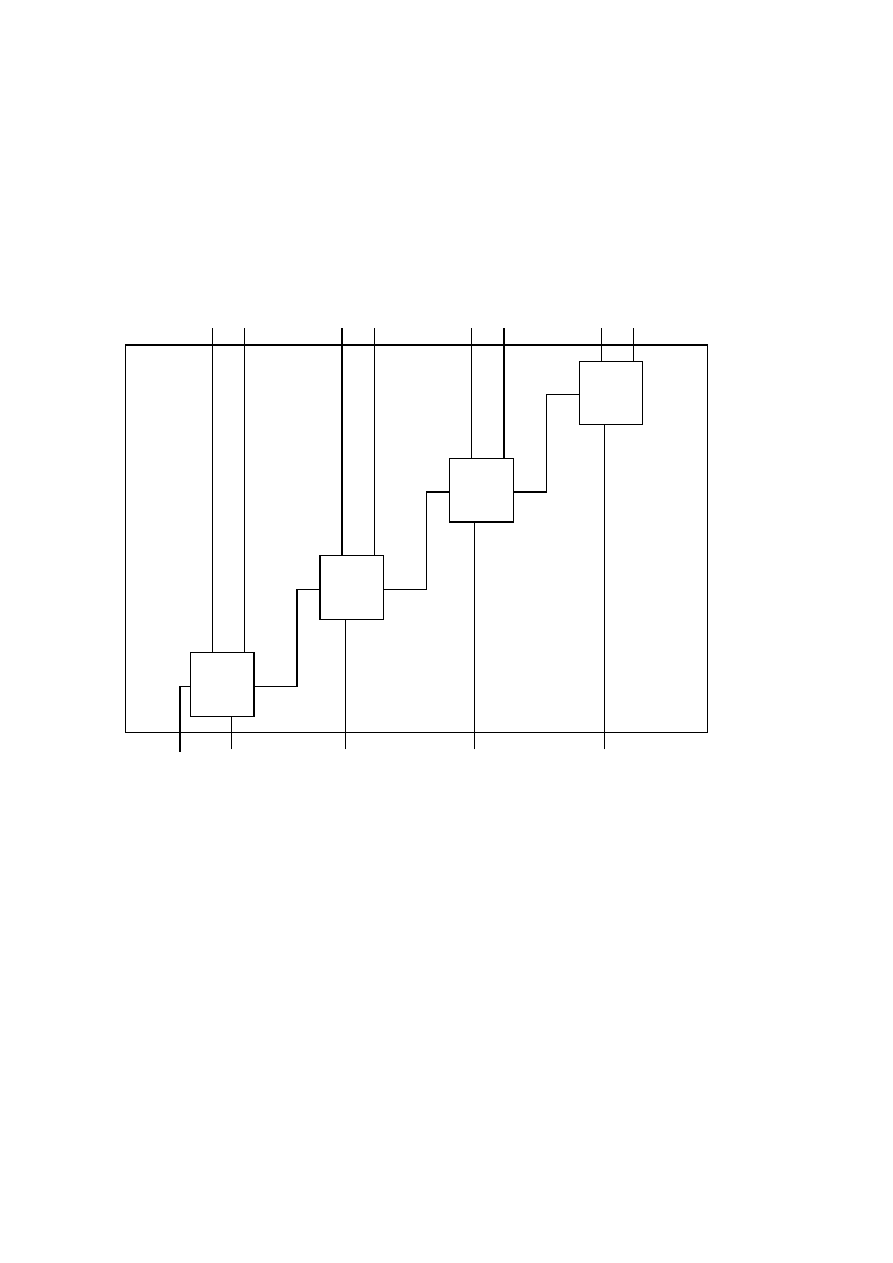
Na rysunku 1.8 przedstawiono schemat konstrukcji sumatora dla

. Podobnie

mo˙zna skonstruowa´c sumator dla dowolnego

. Taki sumator b¸edzie zawierał

1.5. Operacje boolowskie na wektorach

15

Rysunek 1.5: Schemat sieci sortuj¸acej

bramek i miał gł¸eboko´s´c

.

1.5

Operacje boolowskie na wektorach

Operacje boolowskie mo˙zna wykonywa´c tak˙ze na ci¸agach bitów okre´slonej długo´sci, czy-
li na elementach zbioru

Dla dwóch ci¸agów:

oraz

operacje koniunkcji, alternatywy, xor i negacji wykonywane s¸a po współrz¸ednych:

Je˙zeli wektor zerowy

oznaczymy przez 0, a wektor zło˙zony z samych jedy-

nek

— przez 1, to zachodz¸a wszystkie to˙zsamo´sci lematu1.1 oraz to˙zsamo-

´sci (a)—(e) z lematu 1.2. Nie jest natomiast na ogół spełniona własno´s´c (e) lematu 1.2,

16

Rozdział 1. Funkcje boolowskie

Rysunek 1.6: Sie´c obliczaj¸aca HA (półsumator)

poniewa˙z je˙zeli

, to

z działaniami

i

nie jest ciałem (nie ma elementu prze-

ciwnego do

). Zbiór

jest przestrzeni¸a liniow¸a nad ciałem

, z

jako

dodawaniem oraz mno˙zeniem przez skalar zdefiniowanym przez:

(tutaj zero po lewej stronie jest zerem z ciała, a zero po prawej stronie jest

wektorem zerowym),

.

1.5.1

Operacje na wektorach w j¸ezyku Pascal

W j¸ezyku Pascal (i w wielu innych j˛ezykach) operacje boolowskie:

and, or, xor,

neg

, mo˙zna stosowa´c do liczb typu integer lub innych typów całkowitych (byte, shor-

tint, word lub longint). Liczba traktowana jest wtedy jako ci¸ag bitów jej przedstawienia
binarnego. Na przykład:

13 and 6=4

poniewa˙z 13 jest reprezentowane przez:

6 przez:

oraz:

(0000 0000 0000 1101)

and

(0000 0000 0000 0110) =(0000 0000 0000 0100),

a ten ostatni ci¸ag reprezentuje 4 w typie integer. Podobnie zachodzi:

13 or 6=15; 13 xor 6=11; not 0=-1.

1.5. Operacje boolowskie na wektorach

17

Rysunek 1.7: Sie´c obliczaj¸aca FA

1.5.2

Reprezentacja zbioru

Ci¸agi bitów z

mog¸a słu˙zy´c do reprezentacji podzbiorów zbioru

Ci¸ag

nale˙zy traktowa´c jako funkcj¸e charakterystyczn¸a pewnego podzbioru.

Wtedy operacje boolowskie na ci¸agach odpowiadaj¸a operacjom na zbiorach. Alternaty-
wa odpowiada sumie zbiorów, koniunkcja cz¸e´sci wspólnej, a negacja uzupełnieniu zbio-
ru. Operacja xor odpowiada ró˙znicy symetrycznej. Taka reprezentacja ma dwie zalety.
Zajmuje mało pami¸eci i operacje na zbiorach s¸a wykonywane bardzo szybko, poniewa˙z
operacje boolowskie s¸a operacjami niskiego poziomu.

Na przykład je˙zeli chcemy reprezentowa´c w pami¸eci komputera uło˙zenie kamieni w

grze w warcaby na 64-polowej szachownicy, to wystarcz¸a dwie liczby typu longint (po 32
bity). W jednej liczbie reprezentujemy poło˙zenie czarnych, a w drugiej poło˙zenie białych
kamieni (w grze w warcaby kamienie mog¸a le˙ze´c tylko na 32 czarnych polach).

1.5.3

Szyfrowanie w systemie one-pad

Operacje boolowskie na wektorach mo˙zna wykorzysta´c do szyfrowania. W systemie szy-
frowania „one-pad” wiadomo´s´c

i klucz

s¸a ci¸agami bitów

(Je˙zeli wia-

domo´s´c jest ci¸agiem znaków, to kodujemy ka˙zdy znak jako 8 bitów i cały ci¸ag mo˙ze by ´c
traktowany jako ci ˛

ag bitów). Zaszyfrowana wiadomo´s´c ma posta´c:

18

Rozdział 1. Funkcje boolowskie

Rysunek 1.8: Schemat sumatora

HA

FA

FA

FA

Zauwa˙zmy, ˙ze deszyfrowa´c mo˙zna według tego samego wzoru:

poniewa˙z

gdzie 0 reprezentuje wektor zerowy. Zalet¸a tego systemu jest to, ˙ze jest on absolutnie bez-
pieczny. Zróbmy nast¸epuj¸acy eksperyment. Przypu´s´cmy, ˙ze kto´s ma zaszyfrowan¸a wia-
domo´s´c

i chce j¸a odszyfrowa´c przez odgadni¸ecie samej wiadomo´sci

. Zastanówmy si¸e,

dla jakich ci¸agów

istnieje klucz

, taki ˙ze

, czyli inaczej, jakie wiadomo´sci

mog¸a by´c zaszyfrowane w

. Okazuje si¸e, ˙ze dla ka˙zdego ci¸agu

istnieje klucz

, taki ˙ze

. Wystarczy wzi¸a´c

. Mamy wtedy:

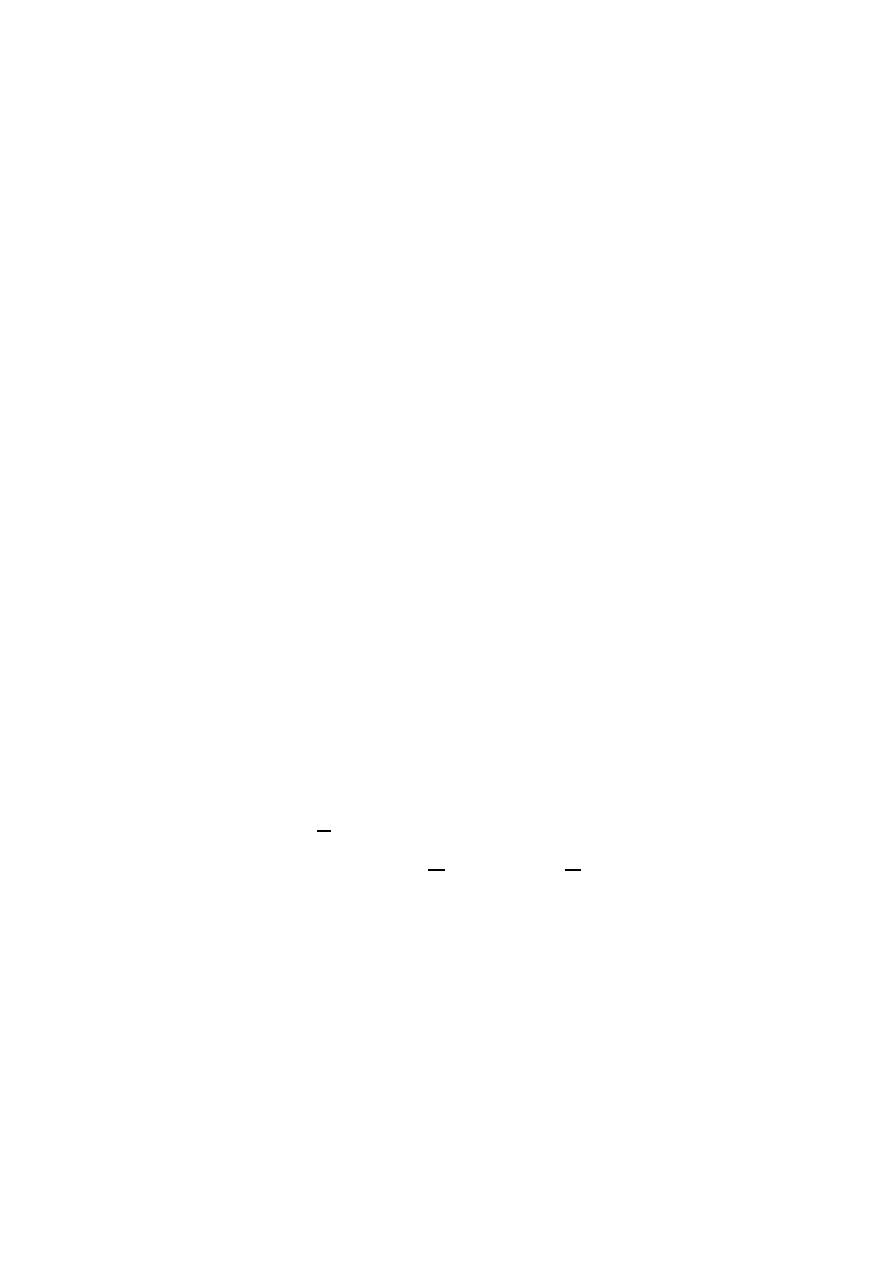
1.6. Funkcja parzysto´sci (parity)

19

Wad¸a tego systemu jest to, ˙ze klucze musz¸a by´c tej samej długo´sci co sama wiadomo´s´c i
musz¸a by´c trzymane w sekrecie. Powoduje to kłopoty z przesyłaniem i przechowywaniem
kluczy.

System one-pad mo˙zna stosowa´c w nast¸epuj¸acy sposób: Najpierw przesyła si¸e bezpieczn¸a

poczt¸a (na przykład kuriersk¸a) zapasy kluczy, na przykład notesy z kartkami, gdzie ka˙zda
strona zawiera jeden klucz. Nast¸epnie szyfrowane depesze mog¸a by ´c przesyłane mniej
bezpiecznymi kanałami. Trzeba tylko przestrzega´c zasady, ˙ze jedna kartka mo˙ze by´c u˙zy-
ta tylko raz (st¸ad angielska nazwa systemu). Same klucze powinny by ´c losowane, aby
przeciwnik nie mógł ich odgadn¸a´c.

Łami¸ac szyfry cz¸esto korzysta si¸e z faktu, ˙ze wiadomo´sci, lub ich fragmenty, wyst¸epuj¸a

z ró˙zn¸a cz¸esto´sci¸a (prawdopodobie ´nstwem). Przypu´s´cmy dla prostoty, ˙ze szyfrujemy po-
jedyncze znaki i niech

b¸edzie zbiorem wiadomo´sci (kody ASCII). Dla normal-

nych tekstów (listów) rozkład cz¸esto´sci poszczególnych znaków jest bardzo niejednostaj-
ny. Kody jednych liter wyst¸epuj¸a du˙zo cze´sciej, ni˙z innych, a pewne znaki nie wyst¸epuj¸a
wcale. Gdyby´smy teraz zastosowali jaki´s prymitywny sposób kodowania bez klucza,
gdzie ka˙zdy znak

zawsze jest szyfrowany za pomoc¸a

, to w zaszyfrowanej wia-

domo´sci rozkład cz¸esto´sci b¸edzie podobny (przepermutowany). Najcz¸e´sciej wyst¸epuj¸acy
znak w wiadomo´sci zaszyfrowanej odpowiada najcz¸e´sciej wyst¸epuj¸acemu znakowi w tek-
´scie, itd. Mo˙zna to wykorzysta´c przy łamaniu szyfrów.

Jak zaraz zobaczymy w przypadku szyfrów one-pad tak nie jest. Znaki w zaszyfro-

wanej wiadomo´sci posiadaj¸a rozkład jednostajny, tak jakby´smy losowali kolejne znaki i
dlatego analiza statystyczna jest tutaj bezu˙zyteczna.

Niech

b¸edzie zbiorem wiadomo´sci z dowolnym rozkładem prawdopo-

dobie´nstwa, a

zbiorem kluczy z jednostajnym rozkładem prawdopodobie ´n-

stwa. Losujemy wiadomo´s´c

i klucz

i obliczamy wiadomo´s´c

. Niech

oznacza zdarzenie, ˙ze wylosowano wiadomo´s´c

,

, ˙ze wylosowano

klucz

, a

zdarzenie, ˙ze otrzymano zaszyfrowan¸a wiadomo´s´c

. Zgodnie ze wzorem

na prawdopodobie ´nstwo całkowite mamy

ale

bo tylko dla jednego klucza

,

. Dlatego

1.6

Funkcja parzysto´sci (parity)

Zdefiniujmy funkcj¸e boolowsk¸a parzysto´sci (parity):

20

Rozdział 1. Funkcje boolowskie

Funkcja

jest addytywna, to znaczy:

co wynika z faktu, ˙ze operacja

jest ł¸aczna i przemienna.

jest równa 1, je˙zeli liczba jedynek w ci¸agu

jest nieparzysta, oraz jest równa

0, je˙zeli w ci¸agu

liczba jedynek jest parzysta. Je˙zeli b¸edziemy uto˙zsamia ´c wektor

ze

zbiorem, to

jest równe parzysto´sci mocy zbioru

.

Twierdzenie 1.3

dla dokładnie połowy wej´s´c. To znaczy:

Pierwszy dowód. Twierdzenie wynika z faktu, ˙ze dokładnie połowa podzbiorów zbioru

jest nieparzystej mocy.

Drugi dowód. We´zmy wektor:

który ma jedynk¸e tylko na pierwszej współrz¸ednej. Zdefiniujemy teraz funkcj¸e

:

Funkcja

ł¸aczy elementy ze zbioru

w pary, poniewa˙z je˙zeli

, to

. Rzeczywi´scie:

Ponadto:

a st¸ad wynika, ˙ze dla ka˙zdej pary

,

dokładnie jedna z dwóch liczb

,

jest jedynk¸a, czyli dla dokładnie połowy

,

1.7

Zabezpieczanie danych

Funkcja

jest wykorzystywana do kontroli, czy dane nie zostały przekłamane podczas

przesyłania lub przechowywania. Przypu´s´cmy, ˙ze Małgosia chce przesła´c Jasiowi wiado-
mo´s´c

i chce cho´c troch¸e zabezpieczy´c

przed przekłamaniem. Wtedy Mał-

gosia wysyła

razem z bitem

— jego podpisem. Przypu´s´cmy teraz, ˙ze Ja´s dostał

wiadomo´s´c

z podpisem

. Dla prostoty zakładamy, ˙ze podpis

nie został

przekłamany, na przykład Małgosia i Ja´s mog¸a si¸e umówi´c, ˙ze przesyłaj¸a sobie tylko ta-
kie wiadomo´sci

, dla których

. Aby sprawdzi´c, czy wiadomo´s´c nie została

przekłamana, Ja´s oblicza

i porównuje go z

. Je˙zeli

, to

Ja´s ma pewno´s´c, ˙ze

. Je˙zeli

, to Ja´s przyjmuje, ˙ze

, cho´c

1.7. Zabezpieczanie danych

21

w tym przypadku nie mo˙ze mie´c pewno´sci. Zauwa˙zmy, ˙ze je˙zeli

i

ró˙zni¸a si¸e tylko na

jednym bicie, to

ma tylko jedn¸a jedynk¸e, wi¸ec:

Z drugiej strony:

z czego wynika:

Tak wi¸ec je˙zeli w przesyłanych danych zostanie zmieniony (przekłamany) jeden bit, b¸edzie
mo˙zna to wykry´c porównuj¸ac

z

.

Jest to bardzo stary system kontroli danych. Działa on dobrze, je˙zeli przekłamania s¸a

przypadkowe i prawdopodobie ´nstwo przekłamania dwóch bitów jest du˙zo mniejsze ni˙z
prawdopodobie ´nstwo przekłamania jednego bitu. Funkcja

jest jednak zbyt prosta,

aby zabezpieczy´c dane przed zło´sliwym przekłamywaniem. Wystarczy bowiem zawsze
przekłamywa´c parzyst¸a liczb¸e bitów, aby rzecz si¸e nie wykryła.

Poka˙zemy teraz bardziej zło˙zony sposób zabezpieczania danych przed przekłama-

niem. Dla dowolnego wektora

zdefiniujmy funkcj¸e:

Funkcja

oblicza parzysto´s´c liczby bitów wektora

, ale liczone s¸a tylko bity na

pozycjach wyznaczonych przez wektor

, inaczej —

to parzysto´s´c przekroju

i

.

Funkcja

jest addytywna:

Twierdzenie 1.4 Je˙zeli

oraz

, to dla dokładnie połowy

zachodzi

.

Dowód. Je˙zeli

, to istnieje wektor

z jedn¸a jedynk¸a, taki ˙ze:

Wektor

powinien mie´c jedynk¸e na pozycji, na której

te˙z ma jedynk¸e. Podobnie jak w

dowodzie twierdzenia 1.3, mo˙zemy teraz okre´sli´c funkcj¸e:

która „zlepia” wektory z

w pary. Ponadto mamy:

22

Rozdział 1. Funkcje boolowskie

Z tego wynika, ˙ze:

a st¸ad — ˙ze dla ka˙zdej pary,

,

, dokładnie jedna z dwóch liczb

,

jest jedynk¸a.

Wykorzystuj¸ac funkcje

, mo˙zna zbudowa´c lepszy system zabezpieczania da-

nych. Na pocz¸atku Małgosia i Ja´s zaopatruj¸a si¸e w ci¸ag wylosowanych kluczy:

Klucze te powinny by´c trzymane w sekrecie. Je˙zeli teraz Małgosia chce przesła´c Jasio-
wi wiadomo´s´c

, to bierze kolejny klucz

z ci¸agu

i wysyła

razem z

podpisem

. Ja´s po odebraniu wiadomo´sci

razem z podpisem

(tak

jak poprzednio zakładamy, ˙ze

nie jest przekłamywane) porównuje

i

.

Je˙zeli

, to dla ka˙zdego

:

Je˙zeli za´s

, to

i dla połowy wektorów

mamy:

a wi¸ec dla połowy wektorów

mamy:

Tak wi¸ec z prawdopodobie ´nstwem jedna druga Ja´s wykryje, ˙ze

.

Aby zwi¸ekszy´c to prawdopodobie ´nstwo mo˙zna bra´c kilka kolejnych kluczy

.

Wtedy prawdopodobie ´nstwo, ˙ze w przypadku, gdy

, mamy

,

dla ka˙zdego

, jest równe

.

1.8

Zadania

1. Udowodnij lematy 1.1 i 1.2.

2. Udowodnij, ˙ze to˙zsamo´sci lematu 1.1 s¸a to˙zsamo´sciami w algebrze podzbiorów

zbioru

.

3. Które z poni˙zszych równo´sci s¸a to˙zsamo´sciami w algebrze

:

a) p+qr=q+pr,

b) (p+q)r=p+qr,

c) (r+q)r=r+qr,

d) (p+q)r=p(q+r)+qr.

4. Udowodnij, ˙ze wszystkie funkcje boolowskie dwóch zmiennych mo˙zna przedsta-

wi´c za pomoc¸a dwóch operatorów, koniunkcji i negacji (lub alternatywy i negacji).

1.9. Problemy

23

5. Udowodnij, ˙ze wszystkie funkcje boolowskie dwóch zmiennych mo˙zna przedsta-

wi´c za pomoc¸a jednego operatora nand (lub nor).

6. Ile funkcji

spełnia równanie

7. Funkcja

przyjmuje warto´s´c 1 tylko dla wektorów

,

oraz

. Przedstaw funkcj¸e

w postaciach normalnych (dysjunkcyjnej i ko-

niunkcyjnej).

8. Narysuj sie´c boolowsk¸a dla funkcji z poprzedniego zadania.

9. Zaprojektuj sie´c odejmuj¸ac¸a od siebie dwie liczby w postaci dwójkowej.

10. Zaprojektuj sie´c, która mno˙zy dwie liczby dwubitowe.

11. Opisz schemat sumatora dla liczb

-bitowych, którego gł¸eboko´s´c jest proporcjo-

nalna do

.

12. Oblicz warto´s´c wyra˙ze´n

x or y, x and y, not x, x xor y

:

a) je˙zeli zmienne

x

i

y

s¸a typu shortint i przyjmuj¸a warto´sci:

x=6, y=-3

,

b) je˙zeli zmienne

x

i

y

s¸a typu byte i przyjmuj¸a warto´sci:

x=6, y=3

.

13. Dany jest wektor

. Dla jakich wektorów

,

?

14. Dane s¸a dwa wektory:

oraz

. Dla jakich wektorów

,

.

1.9

Problemy

1.9.1

System one-pad

System „one-pad” mo˙ze by´c stosowany do ci¸agów liter alfabetu łaci ´nskiego. Wtedy uto˙z-
samiamy litery z liczbami od 0 do 25 i zamiast operacji

stosujemy:

czyli reszt¸e z dzielenia

przez 26. Jak wygl¸ada wtedy operacja deszyfrowania?

Poka˙z, ˙ze system one-pad z literami jest równie bezpieczny jak system z dwoma cyframi
0 i 1.

1.9.2

Zabezpieczanie

Zaproponuj zmiany w systemie podpisów opisanym pod koniec rozdziału, tak aby praw-
dopodobie ´nstwo wykrycia bł¸edu zwi¸ekszy´c do 0.75.

24

Rozdział 1. Funkcje boolowskie

1.9.3

Posta´c normalna

Udowodnij, ˙ze dla ka˙zdej funkcji funkcji

istnieje dokładnie jeden wektor:

taki ˙ze: