1. Wstęp.

Celem eksperymentu było zbadanie skuteczności algorytmu symulowanego

wyżarzania zastosowanego do rozwiązywania problemu n-komiwojażerów – należało n-
komiwojażerom przydzielić takie cykle, aby maksymalna z n dróg była najmniejsza.

2. Opis algorytmu.

Badany algorytm był oparty na losowym ruchu typu insert:

• Losujemy wierzchołek grafu, oraz miejsce w uporządkowanym zbiorze wierzchołków

tworzących drogi.

• Obliczamy jakie zmiany w długości dróg wprowadzi wylosowany ruch
• Jeżeli nowe rozwiązanie jest lepsze to wykonaj ten ruch
• W przeciwnym wypadku przyjmujemy wylosowane rozwiązanie z

prawdopodobieństwem określonym przez funkcję f(numer iteracji).

• Kończymy algorytm po określonej ilości iteracji.

W moim eksperymencie sprawdziłem działanie programu dla następujących funkcji

wyznaczających prawdopodobieństwo przyjęcie gorszego rozwiązania:

• funkcja ekspotencjalnie malejąca (parametrem jest współczynnik w wykładniku)
• funkcja liniowo malejąca (parametrem jest współczynnik kierunkowy prostej)
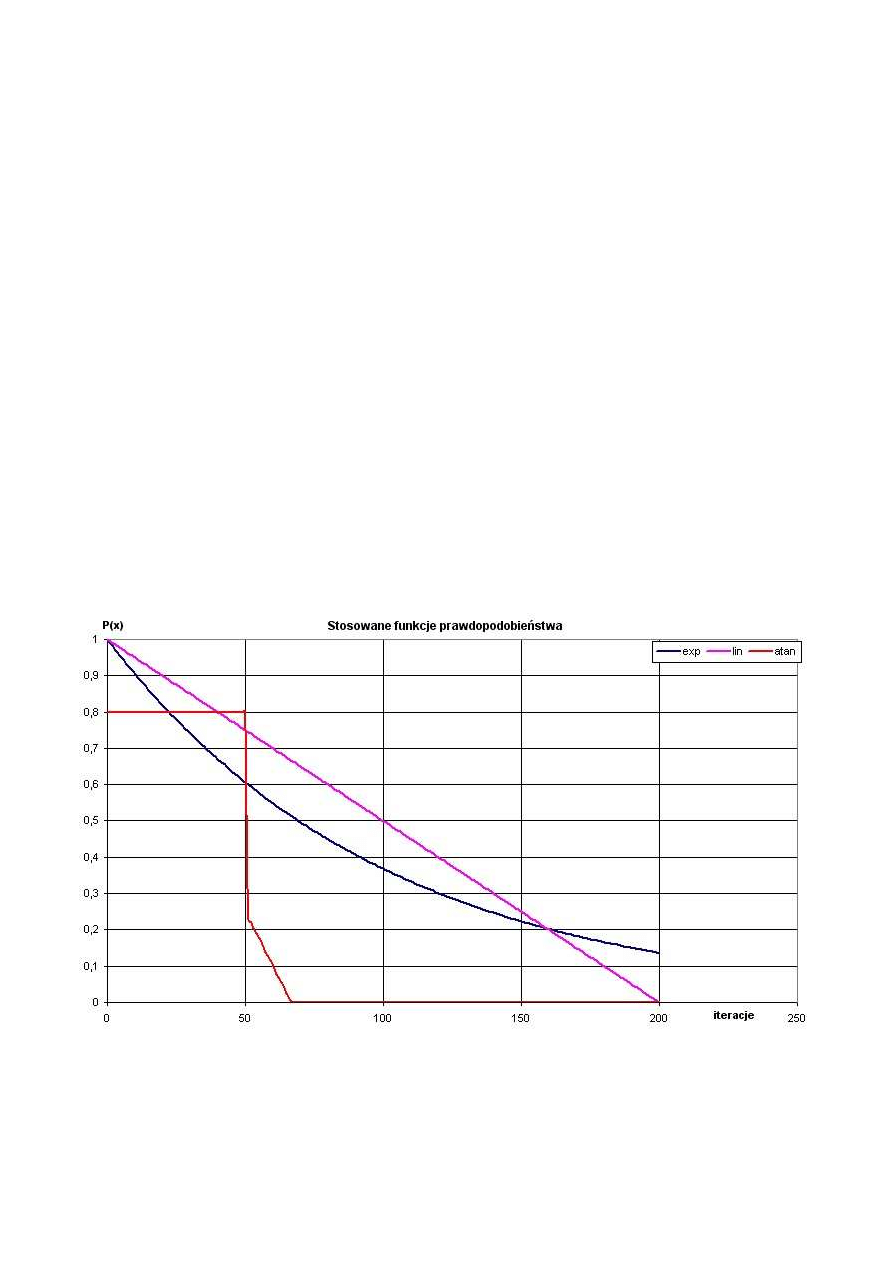
• funkcja do pewnego momentu stała, następnie gwałtownie opadająca (parametrem jest

przy której iteracji funkcja zaczyna opadać)

Wykres 1: Stosowane podczas symulacji funkcje prawdopodobieństwa (przykładowe parametry).

Każda z funkcji przyjmowała wartości poprawnie określające prawdopodobieństwo,

czyli przedział [0,1]. Losowanie z prawdopodobieństwem zaimplementowałem losując liczbę
z przedziału [0,1] i sprawdzając czy jest ona większa od wartości funkcji f dla aktualnego
numeru iteracji.

3. Badanie kształtowania się rozwiązania w zależności od ilości iteracji dla różnych

parametrów funkcji prawdopodobieństwa.

Wylosowałem po 3 różne instancje dla każdej z funkcji określającej

prawdopodobieństwo oraz uruchomiłem 500 razy dla metodę insert() rejestrując wartość
kryterium, co 50 iteracji. Wyniki zostały zobrazowane na wykresach.

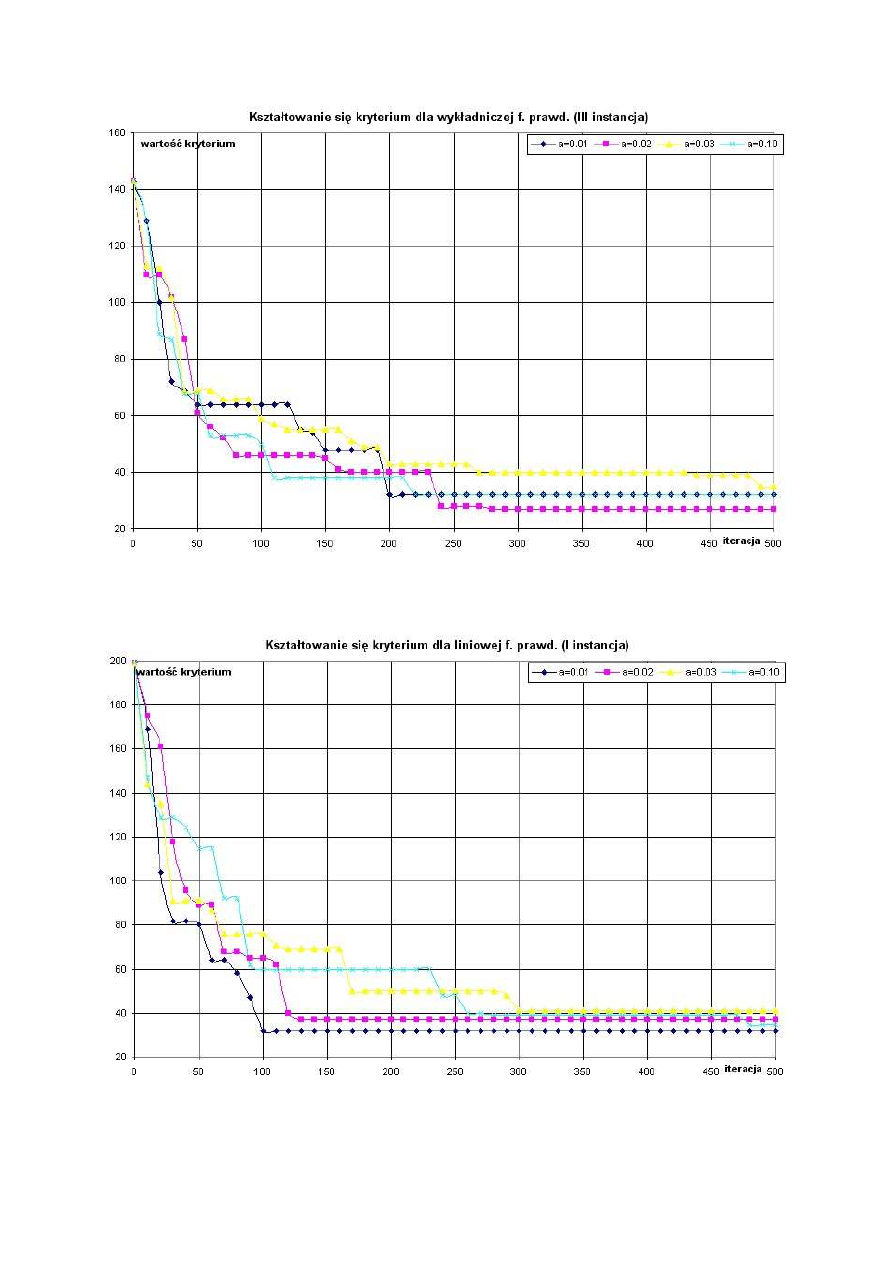
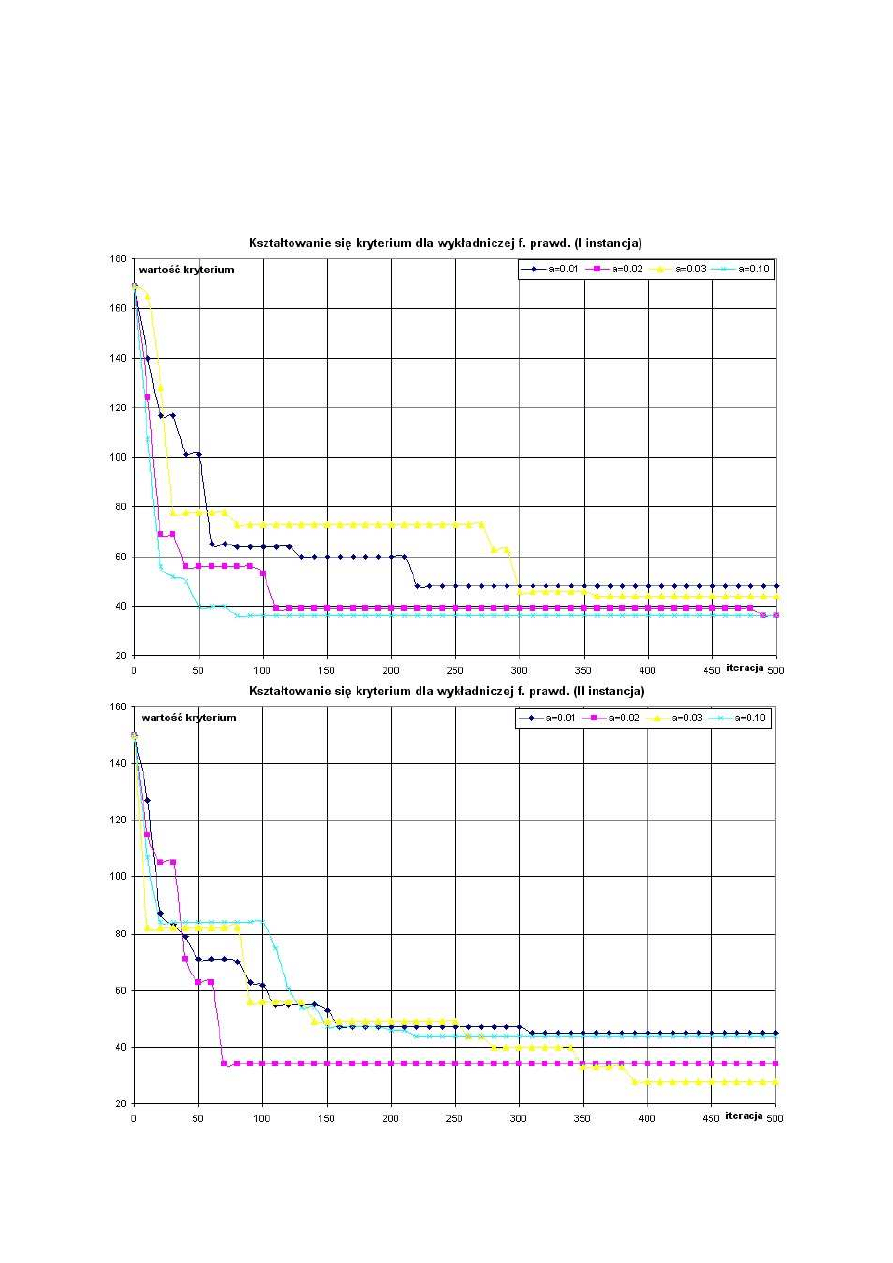
Wykresy 2,3,4: Wartość kryterium w funkcji numeru iteracji dla ekspotencjalnej funkcji
prawdopodobieństwa.

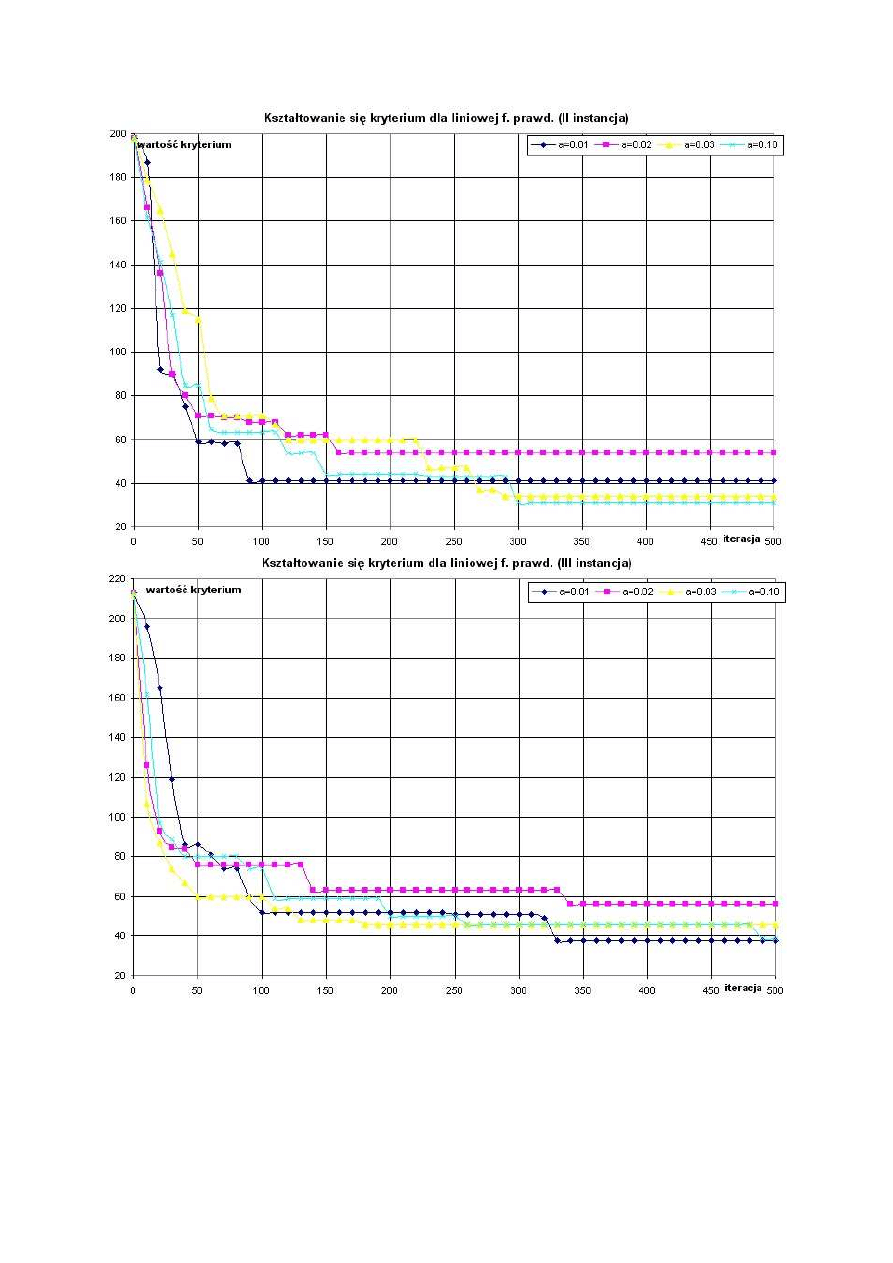
Wykresy 5,6,7: Wartość kryterium w funkcji numeru iteracji dla liniowej funkcji
prawdopodobieństwa.

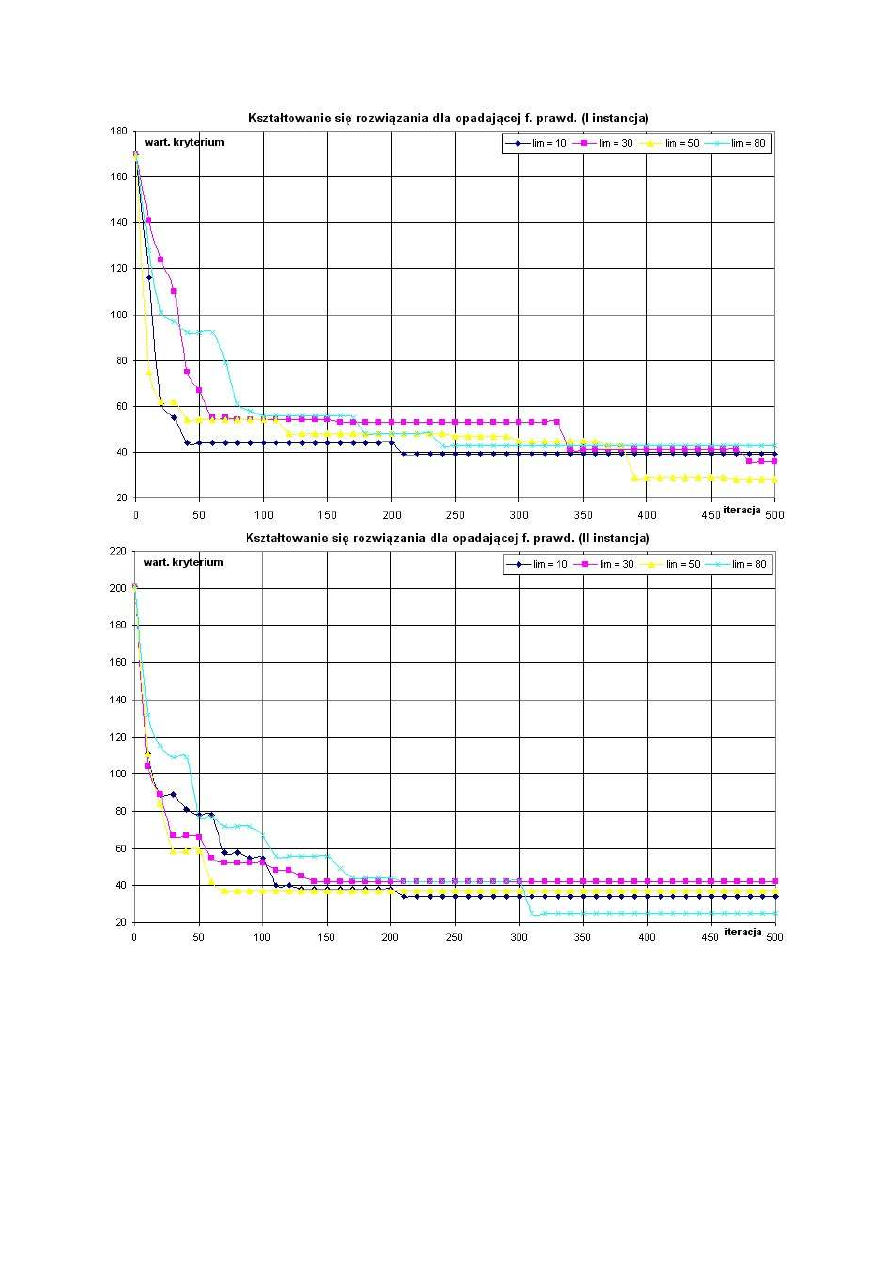
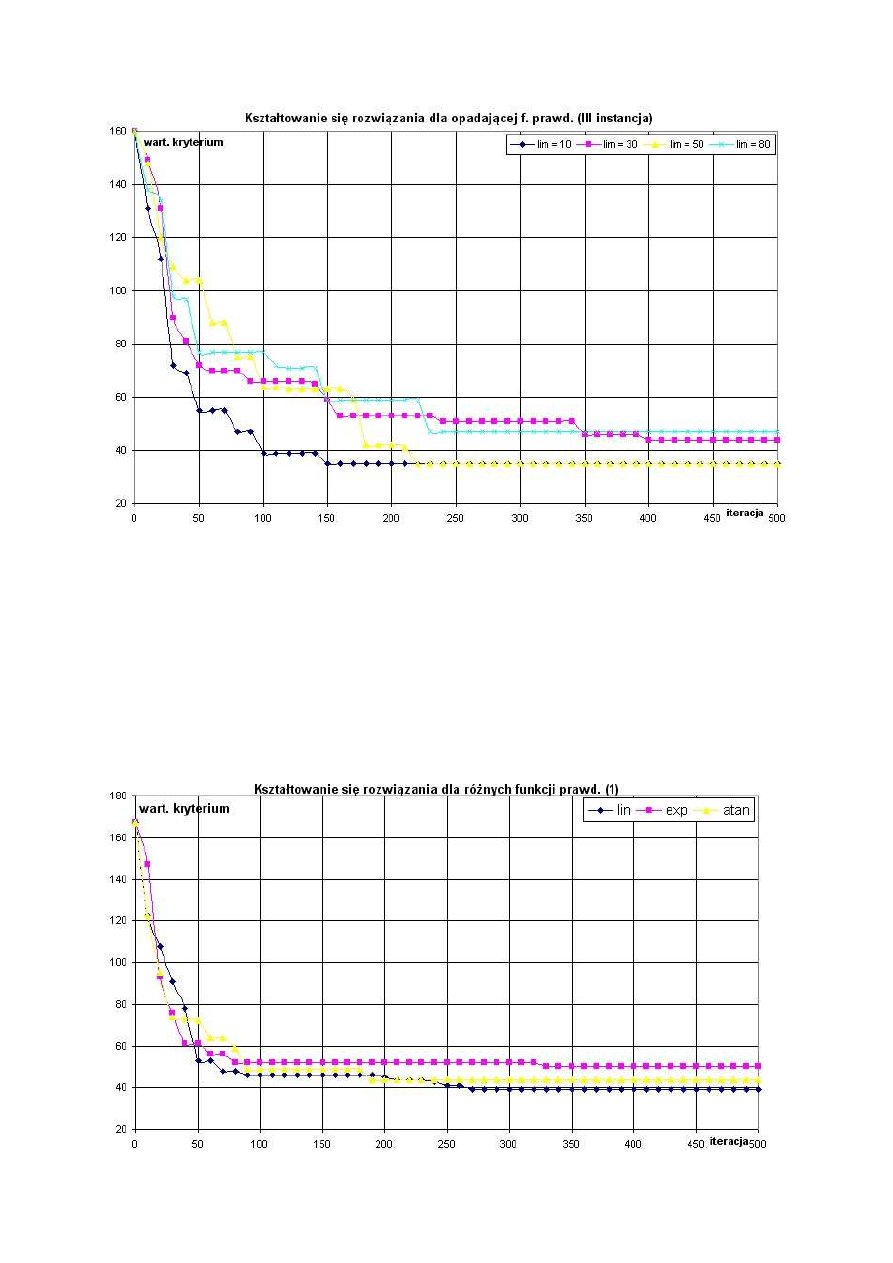
Wykresy 8,9,10: Wartość kryterium w funkcji numeru iteracji dla nieliniowo opadającej
funkcji prawdopodobieństwa.

4. Badanie kształtowania się rozwiązania w zależności od zastosowanej funkcji określającej

prawdopodobieństwo.

Następnie

przeprowadziłem

podobne

badania

lecz

dla

różnych

funkcji

prawdopodobieństwa w których przyjąłem stałe parametry (0,1 dla eksponenty i f. liniowej
oraz 50 dla funkcji opadającej). Wyniki również zostały zobrazowane na poniższych
wykresach.

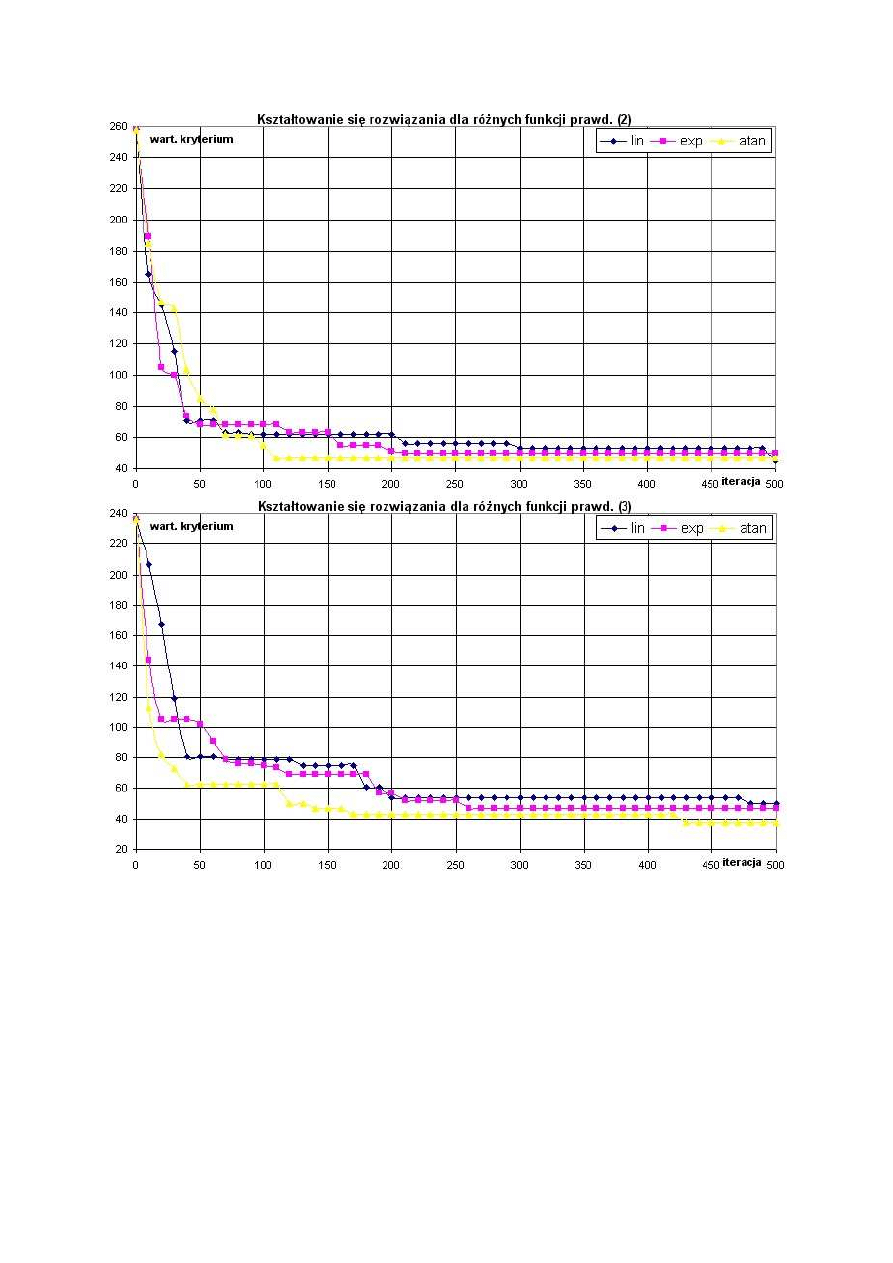
Wykresy 11, 12, 13: Kształtowanie się rozwiązania dla różnych funkcji prawdopodobieństwa
(porównanie skuteczności).

5. Porównanie algorytmu z optymalnym algorytmem rozwiązywania problemu

komiwojażera.

Do

porównania

skuteczności

algorytmów

zastosowałem

metodę

analizy

eksperymentalnej. Liczyłem średnie błędy względne 100 instancji dla ilości miast w zakresie
od 4 do 14. Zależności przedstawione zostały na wykresie.

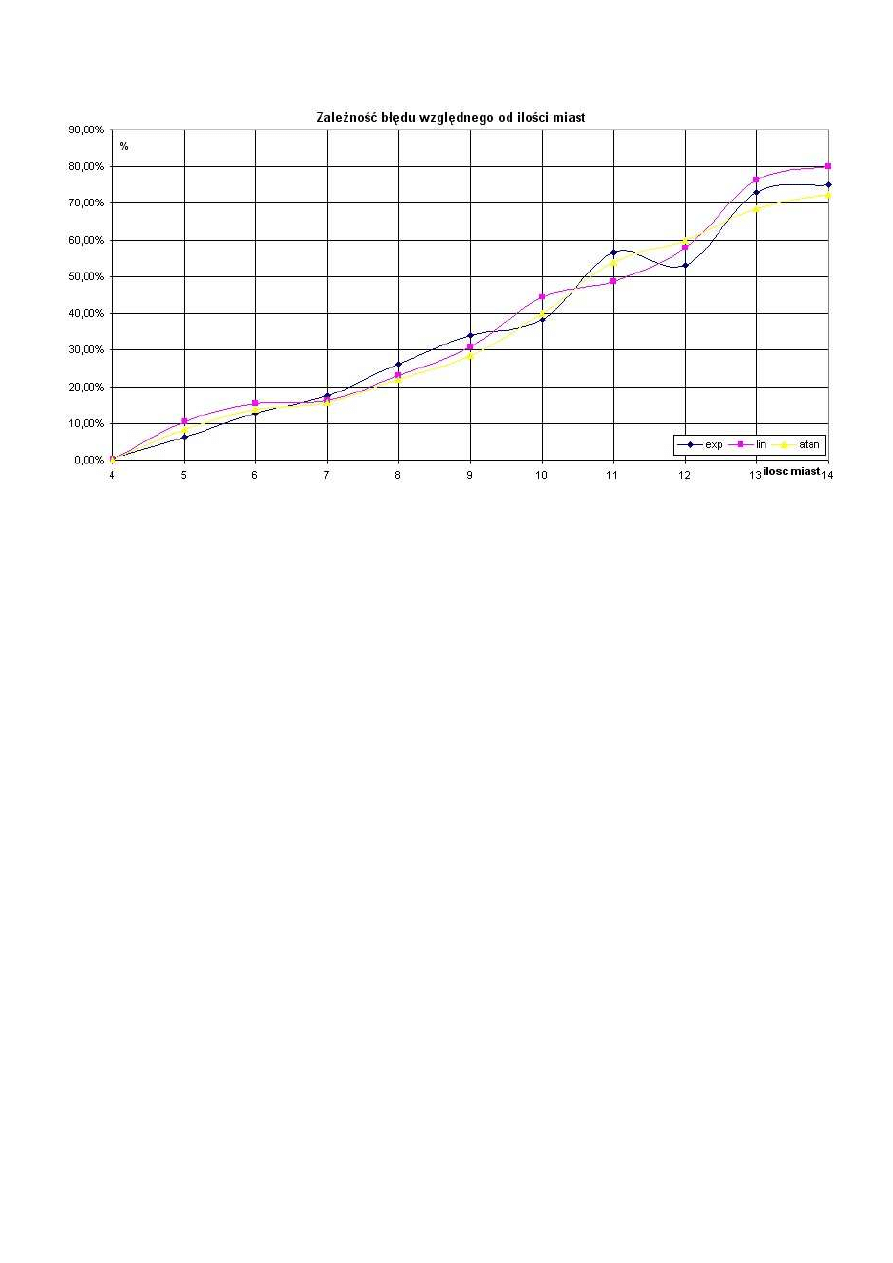
Wykres 14: Zależność względnych błędów algorytmu metaheurystycznego od ilości miast.