Analiza danych jako´sciowych

Andrzej D ¾abrowski

2

Spis tre´sci

1 Dane

7

Skale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8

2 Statystyczne modele danych jako´sciowych

11

Rozk÷ady prawdopodobie´nstwa dla liczno´sci w tablicach . . . . . . . . .

13

Testowanie zgodno´sci modelu z danymi . . . . . . . . . . . . . . . . . .

15

Testowanie jednorodno´sci . . . . . . . . . . . . . . . . . . . . . . . . .

18

Test niezalezno´sci Â

2

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

21

Iloraz krzyzowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

23

3 Modele logitowe

31

Modele logitowe dla zmiennych liczbowych . . . . . . . . . . . . . . . .

32

Regresja logitowa ze zmiennymi nominalnymi . . . . . . . . . . . . . .

34

Regresja logitowa ze zmiennymi porz ¾

adkowymi . . . . . . . . . . . . . .

36

4 Modele logarytmiczno-liniowe

39

Modele hierarchiczne . . . . . . . . . . . . . . . . . . . . . . . . . . . .

47

A Skale dla prawdopodobie´nstw

59

B Metoda IPF

63

C ´

Cwiczenia

67

Zadania na ´cwiczenia w laboratorium . . . . . . . . . . . . . . . . . . .

68

Zadania egzaminacyjne . . . . . . . . . . . . . . . . . . . . . . . . . . .

71

Egzamin poprawkowy . . . . . . . . . . . . . . . . . . . . . . . . .

73

3

4

SPIS TRE´SCI

Wst ¾ep

5

6

Wst ¾ep

Skrypt ten zawiera zapis wyk÷adów z analizy danych jako´sciowych, wyg÷oszonych

przeze mnie na Uniwersytecie Wroc÷awskim w semestrze zimowym roku aka-
demickiego 2002/2003.

Wyk÷ad ten rozszerza w istotny sposób wyk÷ady ze statystyki, które na ogó÷ za-

wieraj ¾a opis metod dla danych ilo´sciowych. Praktyczne zastosowania statystyki w

naukach biologicznych, medycznych czy w naukach spo÷ecznych wymagaj ¾a wiedzy
z tego szczególnego dzia÷u statystyki.

Andrzej D ¾abrowski
luty 2003

Rozdzia÷ 1

Dane

7

8

Dane

Dane s ¾a efektem pomiarów i obserwacji, dokonywanych w do´swiadczeniach

planowanych i takich, które polegaj ¾a na zebraniu informacji o badanym zjawisku.
Temu samemu obiektowi mog ¾a by´c przypisane rózne dane. Na przyk÷ad, danymi,
kóre mog ¾a by´c przypisane choremu s ¾a: diagnoza, stopie´n zaawansowania choroby,

wiek, ci´snienie krwi, temperatura.

Skale

Dane wyrazaj ¾a swoje warto´sci w róznych skalach.

Skala nominalna. Skal ¾e nominaln ¾a stosuje si ¾e w celu klasy…kacji (nazwania)

obiektów w populacji. Kazdej klasie nadaje si ¾e odr ¾ebne oznaczenie (nazw ¾e) w ten
sposób, aby rózne klasy mia÷y rózne oznaczenia. Cz ¾esto te oznaczenia b ¾edziemy
nazywa´c poziomami. Na przyk÷ad w skali nominalnej wyrazona moze by´c diag-

noza (grypa, katar), stopie´n zaawansowania choroby (lekko chory, ci ¾ezko chory,
bardzo ci ¾ezko chory), temperatura (ponizej 37

±

, mi ¾edzy 38

±

a 40

±

), temperatura

(37

±

;38

±

;40

±

). Struktura skali nominalnej nie zmieni si ¾e, je´sli dokonamy zmiany

oznacze´n za pomoc ¾a przekszta÷cenia róznowarto´sciowego. Na przyk÷ad, diagnoza
moze by´c zapisana za pomoc ¾

a numeru statystycznego choroby

1

, stan chorego jako

A,B,C itp.

Skala porz ¾

adkowa. Jest to szczególny rodzaj skali nominalnej. Pozwala ona

uporz ¾adkowa´c klasy wed÷ug stopnia intensywno´sci opisywanej cechy. Na przyk÷ad,
stopie´n zaawansowania choroby (lekko chory, ci ¾ezko chory, bardzo ci ¾ezko chory),
temperatura (ponizej 37

±

, mi ¾edzy 38

±

a 40

±

), temperatura (37

±

;38

±

;40

±

) wyrazaj ¾a

si ¾e w skali porz ¾adkowej, natomiast diagnoza (grypa, katar) nie jest wyrazona w
skali porz ¾

adkowej. Struktura skali porz ¾adkowej zachowa si ¾e, gdy dokonamy zmi-

any oznacze´n przez przekszta÷cenie, zachowuj ¾ace porz ¾adek. Tradycyjnie, je´sli
skal ¾e porz ¾

adkow ¾a koduje si ¾e za pomoc ¾a liczb, to porz ¾adek naturalny tych liczb

2

odzwierciedla

porz ¾adek skali. Podobnie, koduj ¾ac za pomoc ¾a liter alfabetu A,B,... porz ¾adek skali
odzwierciedla si ¾e w porz ¾adku alfabetycznym. I tak system ocen: niedostateczny,
dostateczny, dobry bardzo dobry wyrazaj ¾acy si ¾e w skali porz ¾

adkowej koduje si ¾e

3

w Polsce za pomoc ¾a liczb 2,3,4,5. Analogiczny system ocen w USA koduje si ¾e za

pomoc ¾a liter alfabetu A,B,...

Skala przedzia÷owa. Skala ta pozwala nie tylko klasy…kowa´c i porz ¾adkowa´c

obiekty ale i porównywa´c je ilo´sciowo. Wymaga ona ustalenia jednostki pomiaru

i punktu zerowego skali. W tej skali naturaln ¾a operacj ¾a porównania jest róznica.
Skala zachowuje si ¾e tak samo przy przekszta÷ceniach a…nicznych x

0

= ax +b (a >

0), których efektem jest zmiana jednostek. Na przyk÷ad temperatura (37

±

;38

±

;40

±

)

jest wyrazona w skali przedzia÷owej a jednostki, w których jest wyrazona to skala

1

ale wtedy pe÷ni on wy÷ ¾

acznie funkcje opisow ¾a

2

ale nie ich warto´s´c!

3

co nie oznacza, ze oceny ma j ¾a jakakolwiek warto´s´c liczbow ¾a

Dane

9

Celsjusza. Przej´scie do skali Fahrenheita odbywa si ¾e przez przekszta÷cenie F =

9
5

C + 32. Zero skali Fahrenheita jest w punkcie, odpowiadaj

¾

acym ¡17: 778

±

C .

Skala ilorazowa. Rózni si ¾e ona od skali przedzia÷owej tym, ze wyst ¾epuje w

niej absolutny pocz ¾

atek skali (absolutne zero). W skali ilorazowej wyraza si ¾e wiele

parametrów biologicznych (wzrost, waga cia÷a, ci´snienie krwi). Struktura skali

nie zmieni si ¾e, je´sli zastosujemy przekszta÷cenie x

0

= ax (a > 0). Na przyk÷ad,

wag ¾e cia÷a mozemy wyrazi´c w gramach, ale równiez w kilogramach, funtach itp.
Naturaln ¾

a operacj ¾a porównania dla skali ilorazowej jest iloraz dwóch wielko´sci.

Skale: nominalna i porz ¾adkowa opisuj ¾a charakterystyki jako´sciowe danych i

dane, wyrazone w takich skalach nazywaj ¾a si ¾e jako´sciowymi. Dane, wyrazone w
skalach: przedzia÷owej i ilorazowej nazywamy danymi ilo´sciowymi .

Materia÷, przedstawiony w dalszej cz ¾e´sci skryptu, dotyczy´c b ¾edzie metod statysty-

cznych zwi ¾azanych z analiz ¾a danych jako´sciowych.

10

Dane

Rozdzia÷ 2

Statystyczne

modele

danych jako´sciowych

11

12

Statystyczne modele danych jako´sciowych

Przypu´s´cmy, ze dana jest zmienna nominalna lub porz ¾adkowa X o warto´sciach

x

1

; x

2

; :::; x

I

. Prawdopodobie´nstwo, ze X = x

i

oznaczymy przez p

i

:

Dane wynikaj ¾ace z obserwacji w n-elementowej próbce, powstaj ¾

acej z nieza-

leznego losowawania warto´sci cechy X; b ¾edziemy zapisywa´c w tablicy kontyn-
gencji

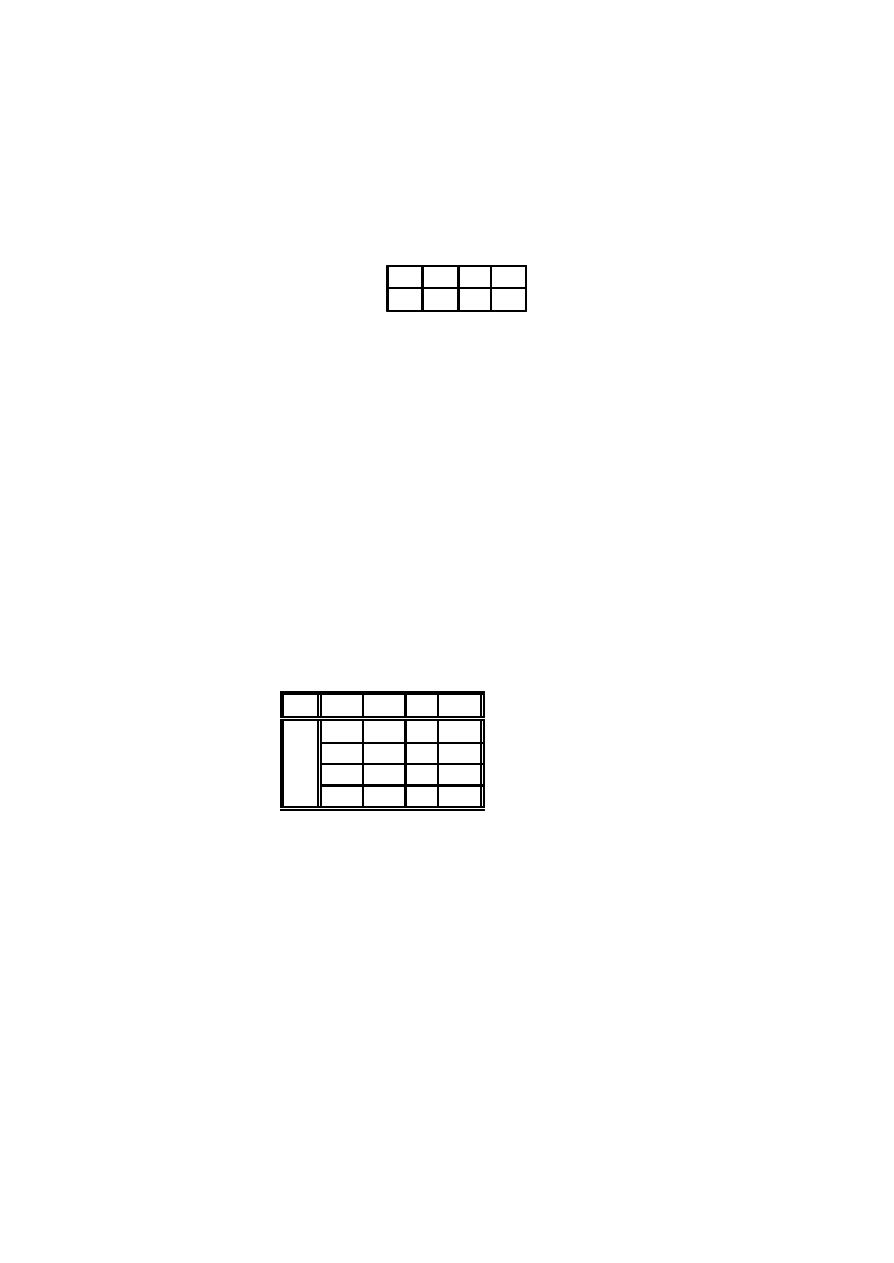
x

1

x

2

::: x

I

n

1

n

2

::: n

I

(2.1)

Parametr n

i

okre´sla, ile razy zaobserwowano w próbce warto´s´c x

i

:

Problemem, z jakim mozemy si ¾e spotka´c w przypadku takich danych, to spre-

cyzowanie rozk÷adu prawdopodobie´nstwa zmiennej X; czyli uk÷adu liczb fp

1

; p

2

; ::::p

I

g ;

spe÷niaj ¾

acych warunki

I

X

i=1

p

i

= 1; p

i

¸ 0 i = 1; 2; :::I

Rozk÷adem, zwi ¾azanym z jednowymiarow ¾a tablic ¾a (2.1) jest rozk÷ad zmiennej

losowej N

i

okre´slaj ¾acej, ile wyników cechy X na poziomie x

i

wyst ¾api w próbce.

Rozk÷ad ten zalezy od rozk÷adu prawdopodobie´nstwa zmiennej X:

Jezeli kazdemu obiektowi przypisujemy dwie lub wi ¾ecej zmiennych nominal-

nych albo porz ¾adkowych X; Y; Z; ::: to dane, uzyskane z obserwacji tych zmien-
nych zapisuje si ¾e w postaci tablicy kontyngencji. Tablica kontyngencji dla pary
zmiennych (X; Y ) o warto´sciach X = fx

1

; x

2

; ::::x

I

g i Y = fy

1

; y

2

; ::::y

J

g ma

posta´c:

y

1

y

2

... y

J

x

1

n

11

n

12

... n

1J

x

2

n

21

n

22

... n

2J

...

...

...

... ...

x

I

n

I1

n

I2

... n

IJ

,

gdzie n

ij

jest liczb ¾a obserwacji w n-elementowej próbce takich, ze X = x

i

oraz

Y = y

j

. N

ij

niech b ¾edzie zmienn ¾a, okre´slajac ¾a ile wyst ¾api÷o w próbce wyników

zmiennej X na poziomie x

i

i jednocze´snie wyników zmiennej Y na poziomie

y

j

: Prawdopodobie

´nstwo P (X = x

i

; Y = y

j

) oznaczymy symbolem p

ij

. Praw-

dopodobie´nstwa p

ij

spe÷niaj ¾a warunki

I

X

i=1

J

X

j=1

p

ij

= 1; p

ij

¸ 0

Podobnie, tablica kontyngencji dla trójki zmiennych (X; Y; Z) o warto´sciach

X = fx

1

; x

2

; ::::x

I

g ; Y = fy

1

; y

2

; ::::y

J

g i Z = fz

1

; z

2

; ::::z

K

g ma posta´c:

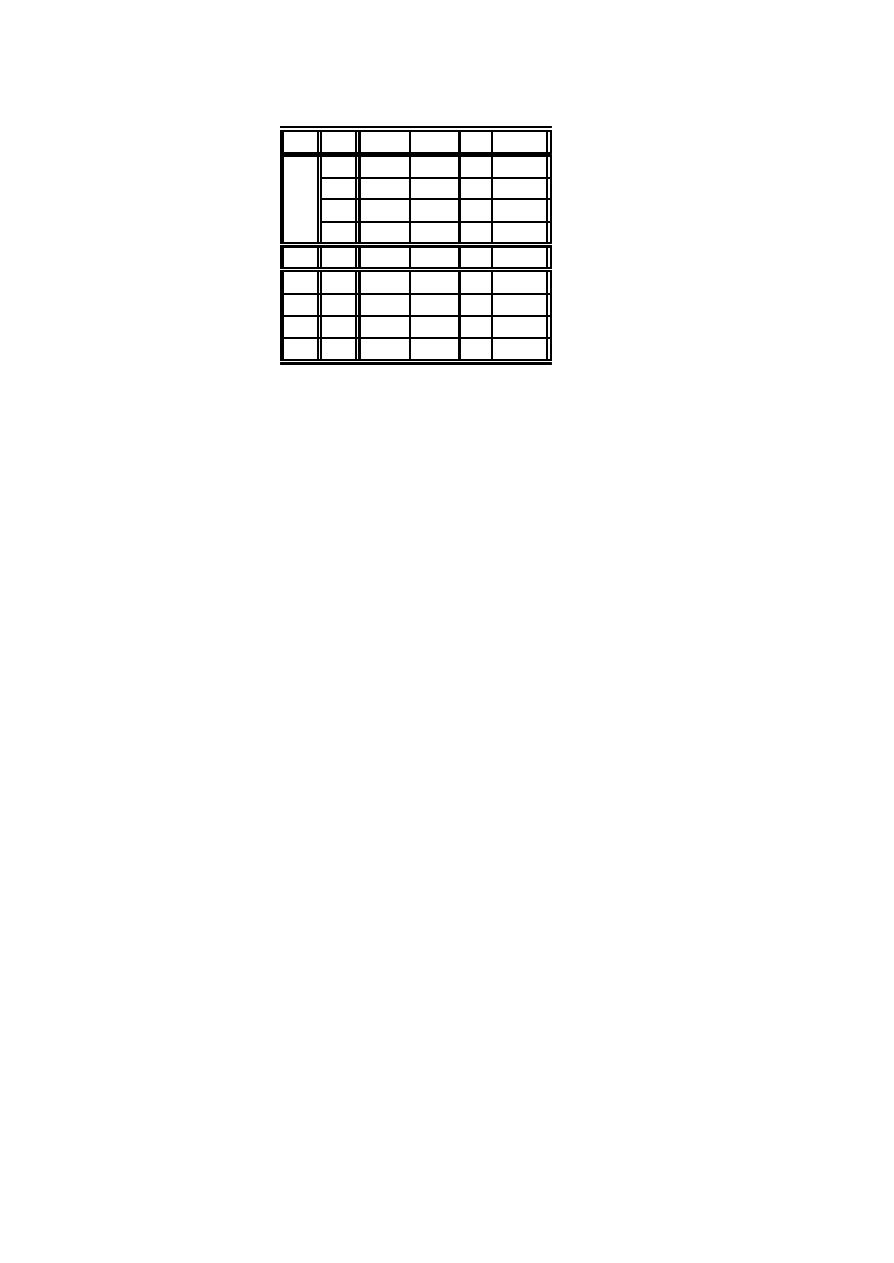
Statystyczne modele danych jako´sciowych

13

z

1

z

2

... z

K

x

1

y

1

n

111

n

112

... n

11K

y

2

n

121

n

122

... n

12K

...

...

...

... ...

y

J

n

1J1

n

1J2

... n

1JK

...

...

...

...

... ...

x

I

y

1

n

I11

n

I12

... n

I1K

y

2

n

I21

n

I22

... n

I2K

...

...

...

...

... ...

y

J

n

IJ1

n

IJ 2

... n

IJK

Oznaczenia uzyte w ostatniej tablicy s ¾

a analogiczne do uzytych w opisie tabl-

icy dwuwymiarowej: n

ijk

jest liczb ¾a obserwacji w próbce takich, ze X = x

i

,

Y = y

j

i Z = z

k

, natomiast liczba p

ijk

jest prawdopodobie´nstwem tego zdarzenia,

a N

ijk

zmienn ¾

a o warto´sciach n

ijk

.

Analogiczne sposoby zapisu danych i oznaczenia s ¾a uzywane dla uk÷adu wi ¾ecej

niz trzech zmiennych.

Oznaczenie 2.1 Zast ¾

apienie symbolem + w indeksie zmiennej oznacza operacj ¾e

sumowania po tym indeksie. Na przyk÷ad

n

+j

=

X

i

n

ij

; n

++

=

X

i;j

n

ij

;

n

i+k

=

X

;j

n

ijk

Rozk÷ady prawdopodobie´nstwa dla liczno´sci

w tablicach

Rózne sposoby uzyskania informacji w próbce maj ¾a wp÷yw na rozk÷ad zmiennych
losowych N

i

; N

ij

; N

ij k

:

Rozk÷ad dwumianowy (Bernoullego) B(p)
Powtarzamy n-krotnie eksperyment, polegaj ¾acy na wykonaniu n

0

niezaleznych

powtórze´n zmiennej o dwóch poziomach: sukces, porazka z prawdopodobie´nst-
wem sukcesu p: Zmienna X mierzy liczb ¾e sukcesów w n

0

powtórzeniach, natomi-

ast n

i

jest liczb ¾a eksperymentów w której wyst ¾

api÷o x

i

sukcesów.

P (N

1

= n

1

; N

2

= n

2

; :::; N

I

= n

I

) =

I

Y

i=1

ÃÃ

n

0

x

i

!

p

x

i

(1 ¡ p)

n

0

¡x

i

!

n

i

Rozk÷ad Poissona P (¸)

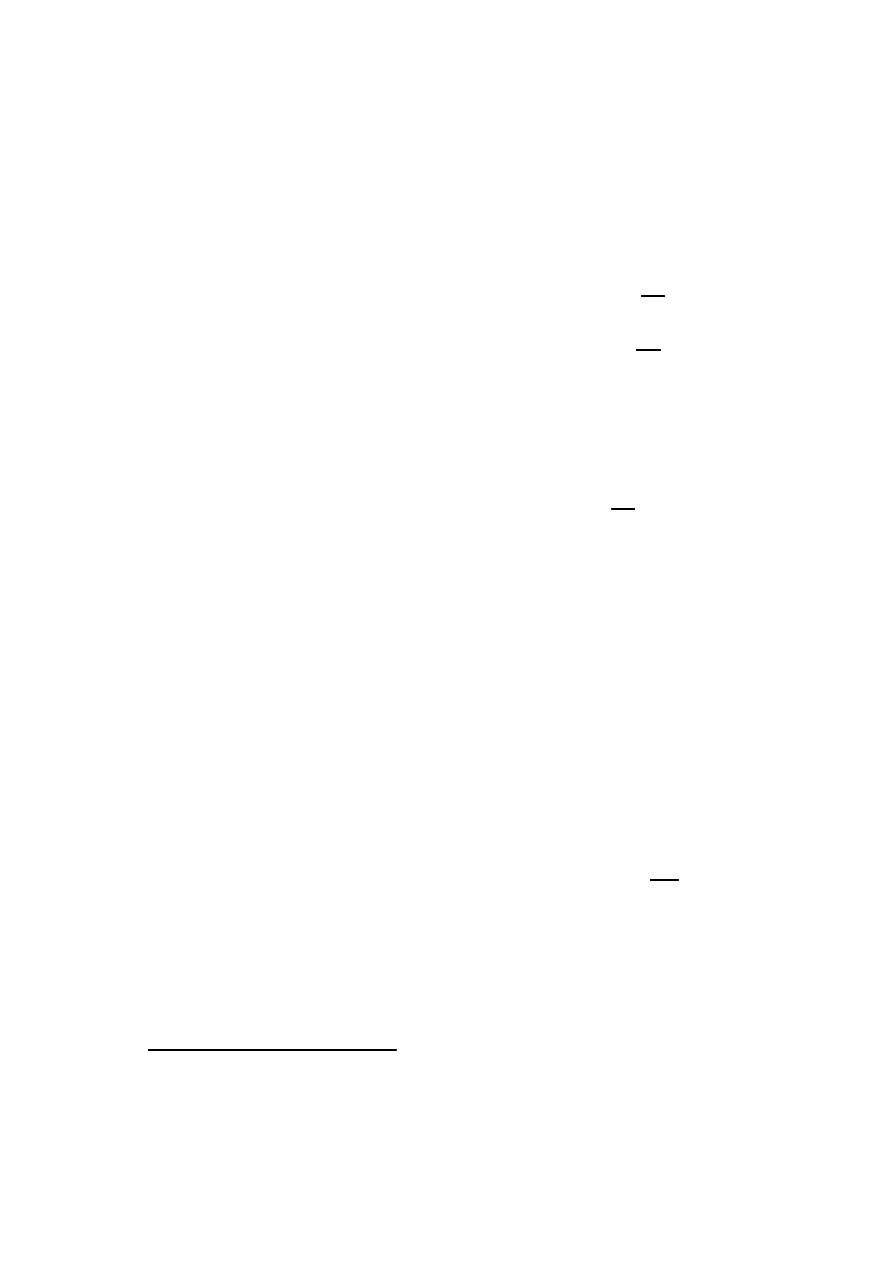
14

Statystyczne modele danych jako´sciowych

Rozk÷ad Poissona jest przypadkiem granicznym w rozk÷adzie dwumianowym

1

.

Wyst ¾api on w tej sytuacji, gdy n-krotnie, niezaleznie powtarzamy pewien ekspery-
ment o wynikach sukces, porazka z ma÷ym prawdopodobie´nstwem sukcesu i oczeki-
wan ¾a liczb ¾a sukcesów ¸ w jednym eksperymencie. Przypu´s´cmy, ze w tablicy (2.1)

poziom x

i

oznacza liczb ¾e sukcesów w jednym eksperymencie, a n

i

liczb ¾e ekspery-

mentów w której wyst ¾api÷o x

i

sukcesów.

P (N

1

= n

1

; N

2

= n

2

; :::; N

I

= n

I

) =

I

Y

i=1

exp (¡¸n

i

)

Ã

¸

x

i

x

i

!

!

n

i

= exp (¡¸n)

I

Y

i=1

Ã

¸

x

i

x

i

!

!

n

i

(2.2)

Rozk÷ad wielomianowy W (p

1

; p

2

; ::::; p

I

)

Przypu´s´cmy, ze zmienna X ma poziomy x

1

; x

2

; :::; x

I

, prawdopodobie´nstwo,

ze X jest na poziomie x

i

jest równe p

i

. Elementy próbki utworzone s ¾a z n nieza-

leznych obserwacji zmiennej X .

P (N

1

= n

1

; N

2

= n

2

; :::; N

I

= n

I

) = n

+

!

I

Y

i=1

p

n

i

i

n

i

!

(2.3)

Stwierdzenie 2.2 Rozk÷ad wielomianowy ma nast ¾epuj ¾

ace w÷asno´sci

1. N

i

» B (p

i

) ;

2. (N

1

; N

2

; :::; N

r

; N

0

) » W (p

1

; p

2

; ::::; p

r

; p

0

), gdzie

N

0

=

I

X

i=r+1

N

i

; p

0

=

I

X

i=r+1

p

i

Rozk÷ad produktowo-wielomianowy V (p

11

; p

12

; ::::; p

IJ

)

Niezalezne zmienne X

i

maj ¾a poziomy x

i1

; x

i2

; :::; x

iJ

, prawdopodobie´nstwo,

ze X

i

jest na poziomie x

ij

jest równe p

ij

. Powtarzamy n

i+

-krotnie niezaleznie

eksperyment obserwacji zmiennej X

i

i t ¾a operacj ¾e, niezaleznie powtarzamy dla

i = 1; 2; :::; I. Wielko´s´c n

ij

oznacza liczb ¾e powtórze´n, kiedy osi ¾agni ¾eto poziom

x

ij

:

P (N

11

= n

11

; N

12

= n

12

; :::; N

IJ

= n

IJ

) =

I

Y

i=1

n

i+

!

J

Y

j=1

p

n

ij

ij

n

ij

!

;

(2.4)

p

i+

=

J

X

j=1

p

ij

= 1

Stwierdzenie 2.3 Dla kazdego i = 1; 2; :::; I wektory losowe (N

i1

; N

i2

; :::; N

iJ

)

1. s ¾

a niezalezne,

2. maj ¾

a rozk÷ady wielomianowe W (p

i1

; p

i2

; ::::; p

iJ

)

1

jezeli liczba powtórze´n n

0

jest duza a prawdopodobie´nstwo sukcesu jest ma÷e; parametr ¸

jest oczekiwan ¾a liczb ¾

a sukcesów

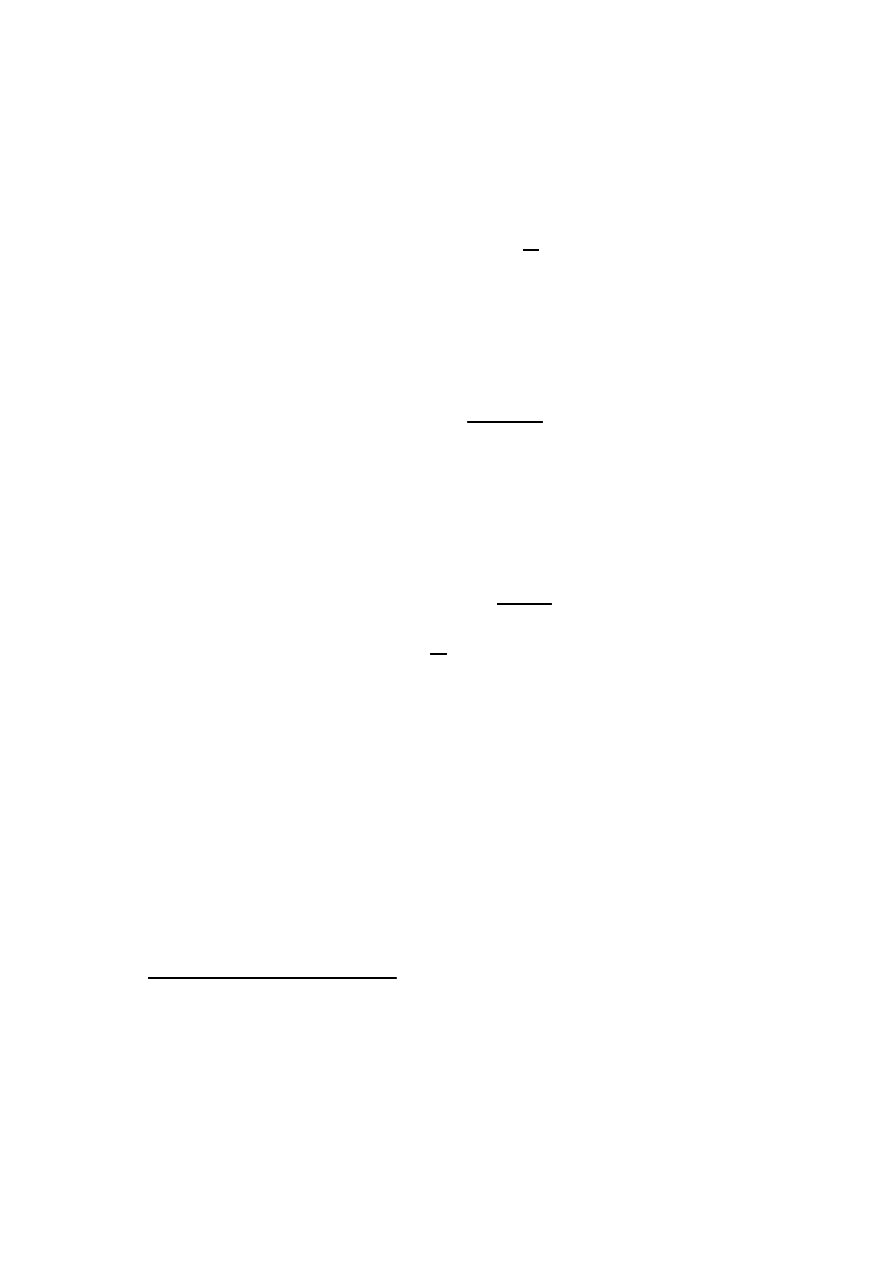
Statystyczne modele danych jako´sciowych

15

Testowanie zgodno´sci modelu z danymi

De…nicja 2.4 Odchyleniem danych fn

1;

n

2

; :::; n

I

g od modelu M nazywamy liczb ¾e

G

2

(M ) = 2

I

X

i=1

n

i

ln

n

i

b

n

i

;

gdzie

b

n

i

= n

b

p

i

oraz

b

p

i

jest estymatorem najwi ¾ekszej wiarygodno´sci p

i

w modelu

M

De…nicja 2.5 Odleg÷o´sci ¾

a Â

2

Pearsona

2

danych fn

1;

n

2

; :::; n

I

g od modelu M nazy-

wamy liczb ¾e

Â

2

(M ) =

I

X

i=1

(n

i

¡

b

n

i

)

2

b

n

i

;

gdzie

b

n

i

= n

b

p

i

oraz

b

p

i

jest estymatorem najwi ¾ekszej wiarygodno´sci p

i

w modelu

M;

Twierdzenie 2.6 Odleg÷o´s´c Â

2

(M ) Pearsona jest, pomnozonym przez n; oczeki-

wanym kwadratowym b÷ ¾edem wzgl ¾ednym danych wzgl ¾edem modelu M :

3

Â

2

(M) = n

I

X

i=1

b

p

i

µ

n

i

¡

b

n

i

b

n

i

¶

2

;

b

p

i

=

b

n

i

n

Twierdzenie 2.7 Odleg÷o´s´c Â

2

(M ) Pearsona jest asymptotycznie, przy n ! 1

równa odchyleniu G

2

(M)

Twierdzenie 2.8 Dla modelu M Poissona, dwumianowego lub wielomianowego
(równiez produktowo-wielomianowego) odchylenie G

2

jest proporcjonalne do pod-

wojonego logarytmu ilorazu wiarygodno´sci hipotezy zgodno´sci z modelem M prze-
ciwko hipotezie niezgodno´sci z tym modelem.

Twierdzenie 2.9 Zmienne losowe G

2

(M ) i Â

2

(M ) maj

¾

a asymptotycznie, przy

n ! 1 rozk÷ad Â

2

: Liczba stopni swobody tego rozk÷adu jest róznic

¾

a liczby stopni

swobody hipotezy H

1

orzekaj ¾

acej, ze do danych nie mozna stosowa´c modelu M i

liczby stopni swobody hipotezy H

0

orzekaj ¾

acej, ze do danych mozna stosowa´c model

M:

2

Odleg÷o´s´c ta zosta÷a zaproponowana przez Karla Pearsona w artykule z 1900 pod tytu÷em

On the Criterion that a Given System of Deviations from the Probable in the Case of a Cor-
related System of Variables is such that it Can be Reasonably Supposed to Have Arisen from
Random Sampling. Motywacj ¾a tego artyku÷u by÷o sprawdzenie m.in. jednorodno´sci pojawiania
si ¾e wyników ruletki w Monte Carlo.

3

Oczekiwany b÷ ¾

ad wzgl ¾edny danych wzgl ¾edem modelu nazywany jest inercj ¾

a

16

Statystyczne modele danych jako´sciowych

Twierdzenie 2.10 Warto´sci

d

i

=

n

i

¡

b

n

i

p

b

n

i

; i = 1; 2; :::; I

maj ¾

a asymptotycznie, przy n ! 1 rozk÷ad standardowy normalny.

Uwaga 2.11 (praktyczna) Na poziomie istotno´sci ® = 0:05 istotnie rózne od
0 s

¾

a te komórki tabeli dla których jd

i

j > 1:96 (d

2

i

> 3:84); na poziomie istotno

´sci

® = 0:01 istotnie rózne od 0 s

¾

a te komórki tabeli dla których jd

i

j > 2:58 (d

2

i

>

6:66)

Uwaga 2.12 (praktyczna) Dobre przyblizenie dla zgodno´sci z rozk÷adem Â

2

uzyskuje si ¾e dla odleg÷o´sci G

2

(M ) gdy wszystkie warto´sci

b

n

i

s ¾

a nie mniejsze niz

1. Analogiczny warunek dla Â

2

(M ) jest wyrazony przez nierówno

´s´c

b

n

i

¸ 5

Lemat 2.13 Problem maksymalizacji

X

i

c

i

ln q

i

= max;

X

i

q

i

= 1

ma rozwi ¾

azanie

b

q

i

=

c

i

P

i

c

i

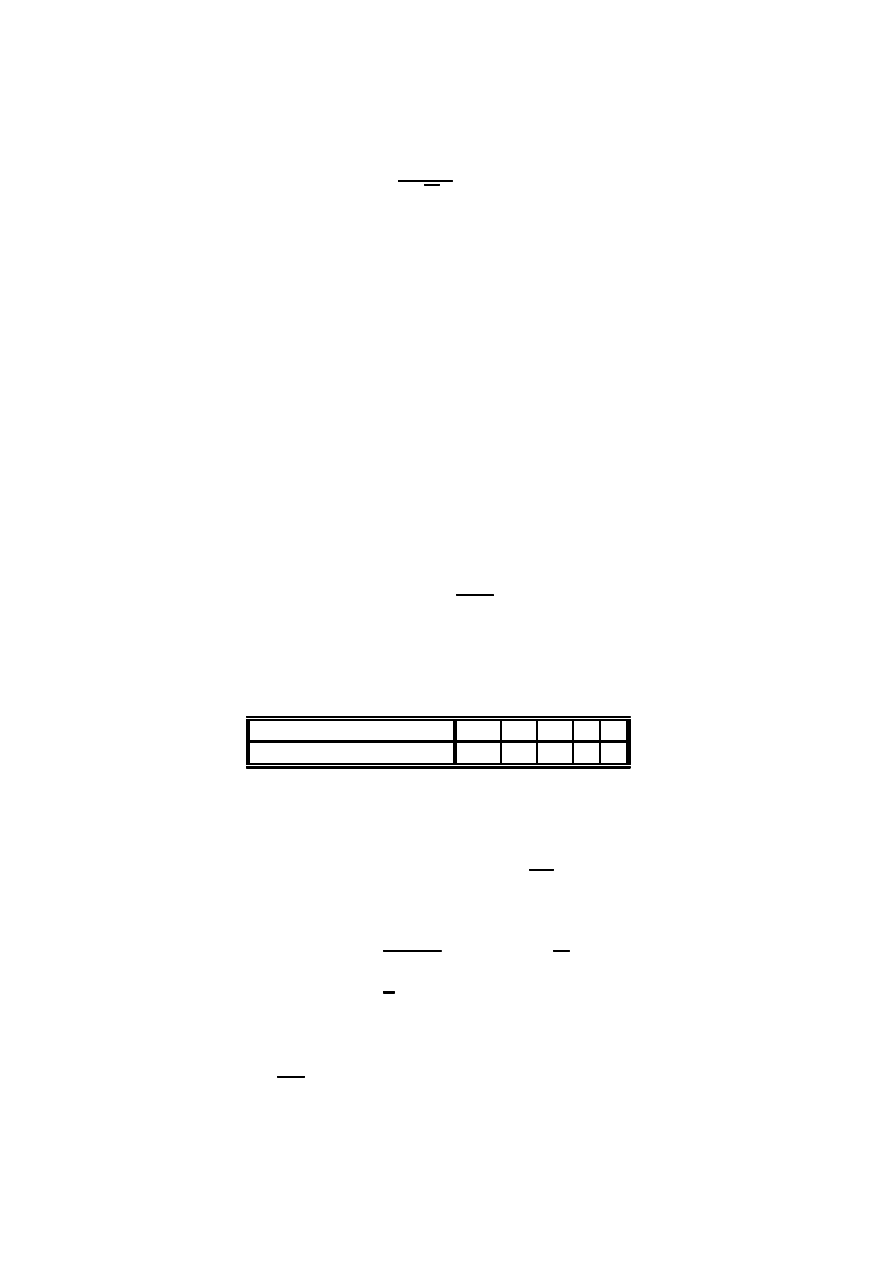
Przyk÷ad 2.14 (dane von Bortkiewicza) Statystyk niemiecki Ladislaus von
Bortkiewicz przytoczy÷ w 1898 dane, dotycz ¾

ace rocznej liczby wypadków ´smiertel-

nych, spowodowanych kopni ¾eciem przez konia w´sród zo÷nierzy 10 korpusów armii
pruskiej w ci ¾

agu 20 lat:

Liczba wypadków w roku

0

1

2

3 4

Liczba korpusów i lat

109 65 22 3 1

Sprawdzimy, czy dane te mog ¾

a by´c opisane rozk÷adem Poissona.

Wyznaczymy najpierw estymator najwi ¾ekszej wiarygodno´sci dla parametru ¸:

Logarytm funkcji wiarygodno´sci (2.2) ma posta´c

ln (L) = ln

Ã

exp (¡¸n)

I

Y

i=1

Ã

¸

x

i

x

i

!

!

n

i

!

=

= ¡¸n +

X

n

i

(x

i

ln ¸ ¡ ln (x

i

!))

0 =

@ ln (L)

@¸

= ¡n +

X

n

i

x

i

¸

()

b

¸ =

1

n

X

n

i

x

i

co w naszym przypadku daje warto´s´c estymatora

b

¸ =

1

200

(0 ¤ 109 + 1 ¤ 65 + 2 ¤ 22 + 3 ¤ 3 + 4 ¤ 1) = 0:61

Statystyczne modele danych jako´sciowych

17

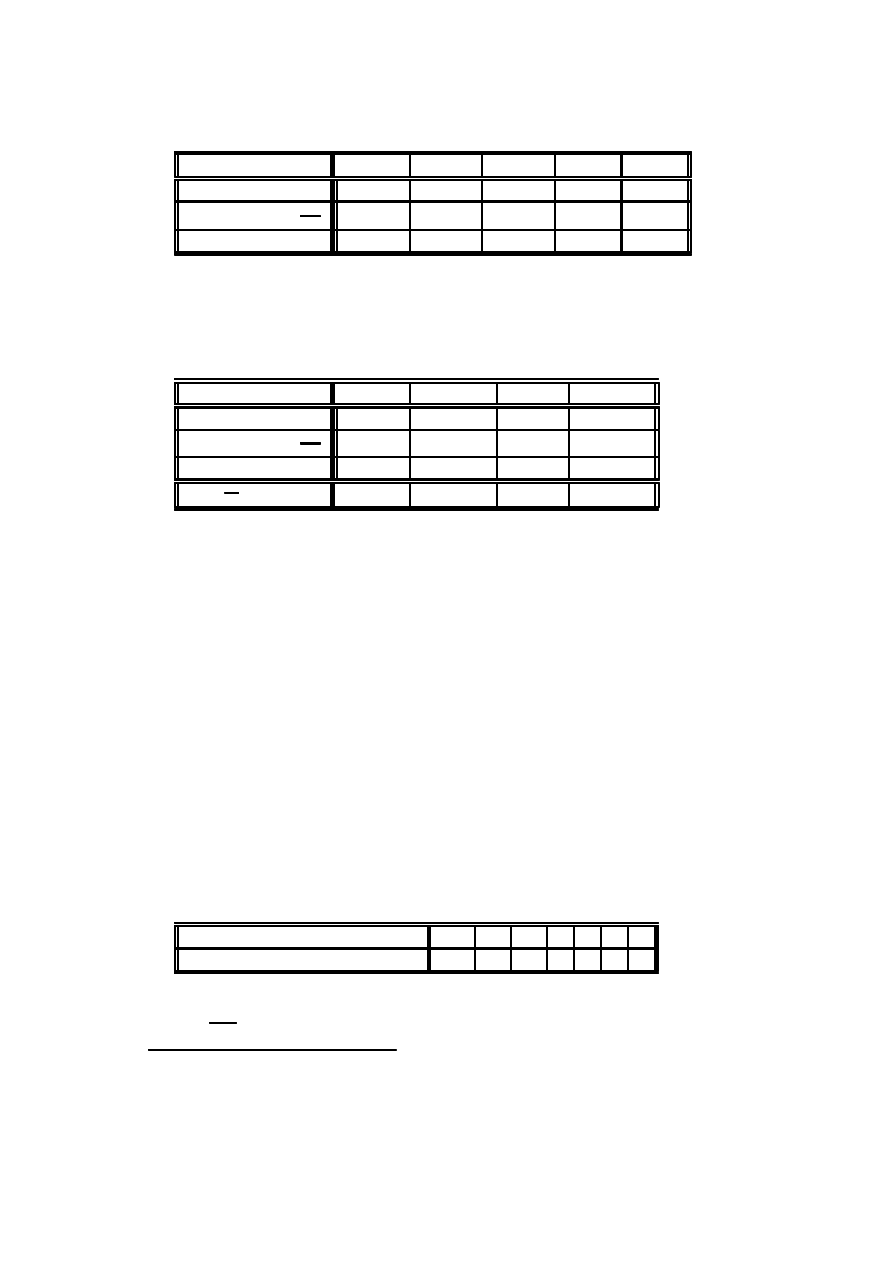
Przygotujemy tabel ¾e do oblicze´n statystyki testowej G

2

(lub Â

2

)

x

i

0

1

2

3

4

n

i

109

65

22

3

1

b

p

i

= exp

³

¡

b

¸

´

¸

xi

x

i

!

: 543 35 : 331 44

: 101 09 :02056

:00313

c

n

i

= n

b

p

i

108: 67

66: 29

20: 22

4: 11

: 63

W ostatniej kolumnie oczekiwana liczebno´s´c wynosi

c

n

i

= : 63, co wskazuje

na to, ze szukanie poziomu krytycznego rozk÷adu Â

2

moze by´c niedok÷adne (zbyt

ma÷a warto´s´c - patrz Uwaga 2.12). W takich przypadkach zaleca si ¾e ÷ ¾

aczenie

s ¾

asiednich kategorii, tak aby warto´s´c

c

n

i

by÷a dostatecznie duza. Po po÷ ¾

aczeniu

dwóch ostatnich kategorii otrzymamy tablic ¾e, dla której mozemy obliczy´c warto´s´c
G

24

x

i

0

1

2

3 lub 4

n

i

109

65

22

4

b

p

i

= exp

³

¡

b

¸

´

¸

xi

x

i

!

: 543 35

: 331 44

: 101 09

:0 236 9

c

n

i

= n

b

p

i

108: 67

66: 29

20: 22

4: 74

n

i

ln

n

i

b

n

i

: 330 5

¡1: 277 4 1: 856 1 ¡: 678 97

Warto´s´c G

2

= : 460 46. Hipoteza H

1

ma 3 stopnie swobody, gdyz nieznanymi

parametrami s ¾

a p

0

; p

1

; p

2

; p

3

, oznaczaj ¾

ace prawdopodobie´nstwa warto´sci x

i

; spe÷-

niaj ¾

ace jedno równanie

3

X

i=0

p

i

= 1

Hipoteza H

0

ma 1 stopie´n swobody, gdyz ¸ jest jedynym nieznanym parametrem.

G

2

ma wi ¾ec rozk÷ad Â

2

z 2 stopniami swobody. Poziom krytyczny dla modelu

Poissona wynosi wi ¾ec

P

³

G

2

> : 460 46

´

= 0:79435

Wynika st ¾

ad, ze z duzym przekonaniem mozemy przyj ¾

a´c model Poissona dla

danych von Bortkiewicza.

Przyk÷ad 2.15 (listy federalistów) W historii Stanów Zjednoczonych wazn ¾

a

rol ¾e odegra÷o ustalenie autorstwa tzw ”Listów federalistów”. Zazwyczaj w ta-
kich przypadkach charakteryzuje si ¾e styl autora poprzez podanie rozk÷adu praw-
dopodobie´nstwa wyst ¾epowania charakterystycznych s÷ów danego j ¾ezyka. Zbadano
262 bloki tekstu, zawieraj ¾

ace po 200 s÷ów kazdy. Zbadamy, czy s÷owo ”may”

5

moze

by´c opisane modelem Poissona. Zmienna X podaje liczbe wyst ¾

apie´n tego s÷owa w

bloku.

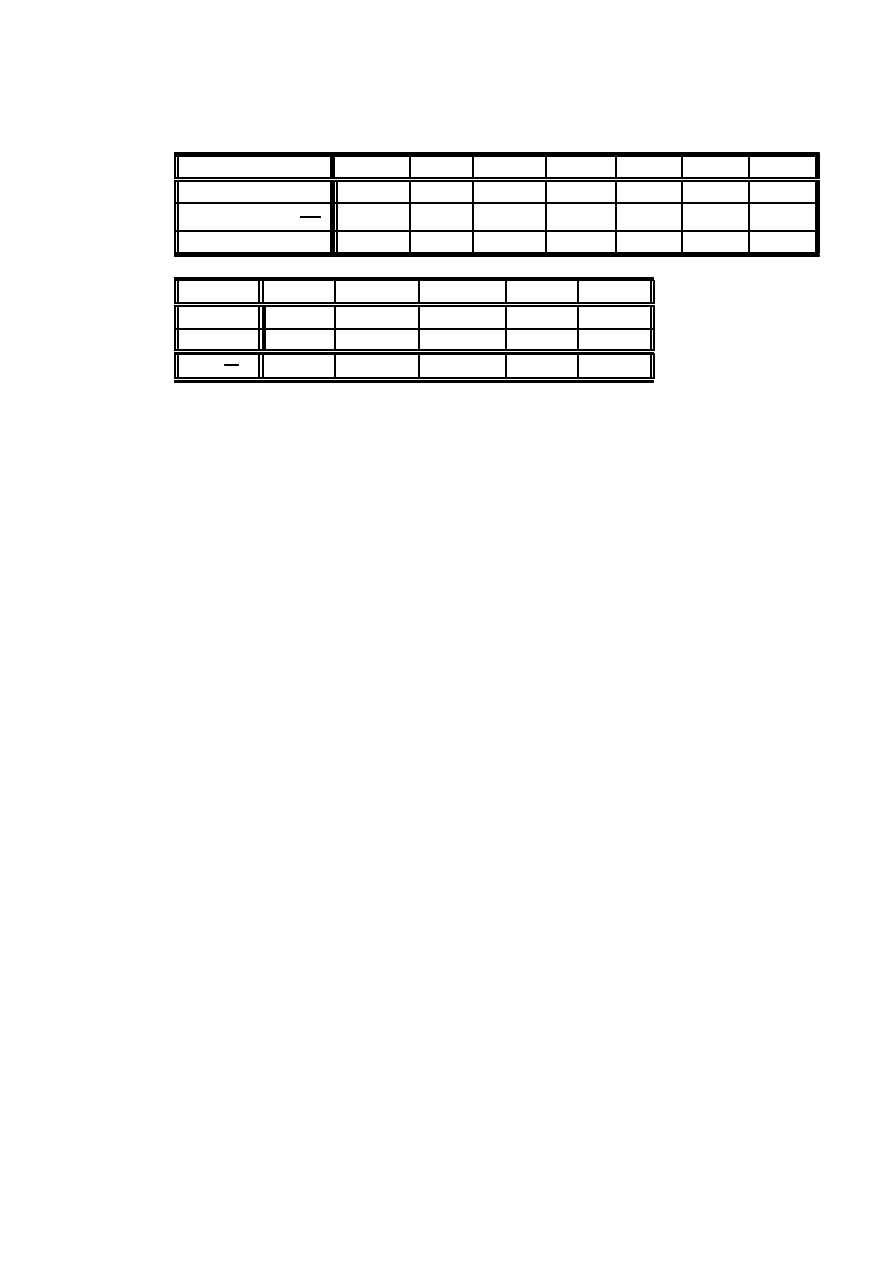
Liczba wyst ¾

apie´n s÷owa ”may”

0

1

2

3 4 5 6

Liczba fragmentów

156 63 29 8 4 1 1

Warto´s´c estymatora parametru ¸ wynosi

b

¸ =

1

262

(0 ¤ 156 + 1 ¤ 63 + 2 ¤ 29 + 3 ¤ 8 + 4 ¤ 4 + 5 ¤ 1 + 6 ¤ 1) = : 656 49

4

Ale nie Â

2

!

5

Ma j ¾ace dwa znaczenia: miesi ¾ac maj lub czasownik moze (od móc)

18

Statystyczne modele danych jako´sciowych

Tabela do oblicze´n statystyki testowej G

2

(lub Â

2

)

x

i

0

1

2

3

4

5

6

n

i

156

63

29

8

4

1

1

b

p

i

= exp

³

¡

b

¸

´

¸

xi

x

i

!

: 518 67 : 340 5

: 111 77

:02 446

:00401

:00053

:00006

c

n

i

= n

b

p

i

135: 89

89: 21

29: 28

6: 41

1: 05

: 14

:0 2

Po po÷ ¾

aczeniu trzech ostatnich poziomów otrzymamy tablic ¾e

x

i

0

1

2

3

4,5,6

n

i

156

63

29

8

6

c

n

i

= n

b

p

i

135: 89

89: 21

29: 28

6: 41

1: 21

n

i

ln

n

i

b

n

i

21: 53

¡21: 915 ¡: 278 66 1: 772 7 9: 606 8

Warto´s´c G

2

= 21: 432. Hipoteza H

1

ma 4 stopnie swobody, H

0

ma 1 stopie´n

swobody. G

2

ma wi ¾ec rozk÷ad Â

2

z 3 stopniami swobody. Poziom krytyczny dla

modelu Poissona wynosi wi ¾ec

P

³

G

2

> 21: 432

´

= 0:00009

Wynika st ¾

ad, ze z duzym przekonaniem mozemy odrzuci´c model Poissona dla

tych danych. Otwartym zagadnieniem pozostaje, jakim rozk÷adem mozna opisa´c
te dane.

Testowanie jednorodno´sci

Gdy dane, zawarte w tabeli kontyngencji dla pary zmiennych (X; Y ) mozna
opisa´c rozk÷adem produktowo-wielomianowym, to naturalnym pytaniem o relacj ¾e

mi ¾edzy X i Y jest hipoteza jednorodno´sci. Rozk÷ad produktowo-wielomianowy

narzuca interpretacj ¾e roli, jak ¾a odgrywaj ¾a zmienne X i Y :

² zmienna X jest grupuj ¾aca, to znaczy na kazdym poziomie x

i

tej zmiennej

obserwujemy niezaleznie warto´sci zmiennej Y ,

² zmienna Y jest wynikowa, co oznacza, ze interesujemy si ¾e jej warto´sciami

w zalezno´sci od róznych kon…guracji przyczyn (tu pogrupowania poprzez
zmienn ¾a X)

Hipoteza jednorodno´sci g÷osi, ze rozk÷ad zmiennej Y jest taki sam w kazdej

grupie, odpowiadaj ¾acej innemu poziomowi zmiennej X .

T÷umacz ¾ac to na j ¾ezyk rozk÷adu produktowo-wielomianowego:

H

0

: 8

j=1;2;:::;j

p

1j

= p

2j

= ::: = p

Ij

def

= q

j

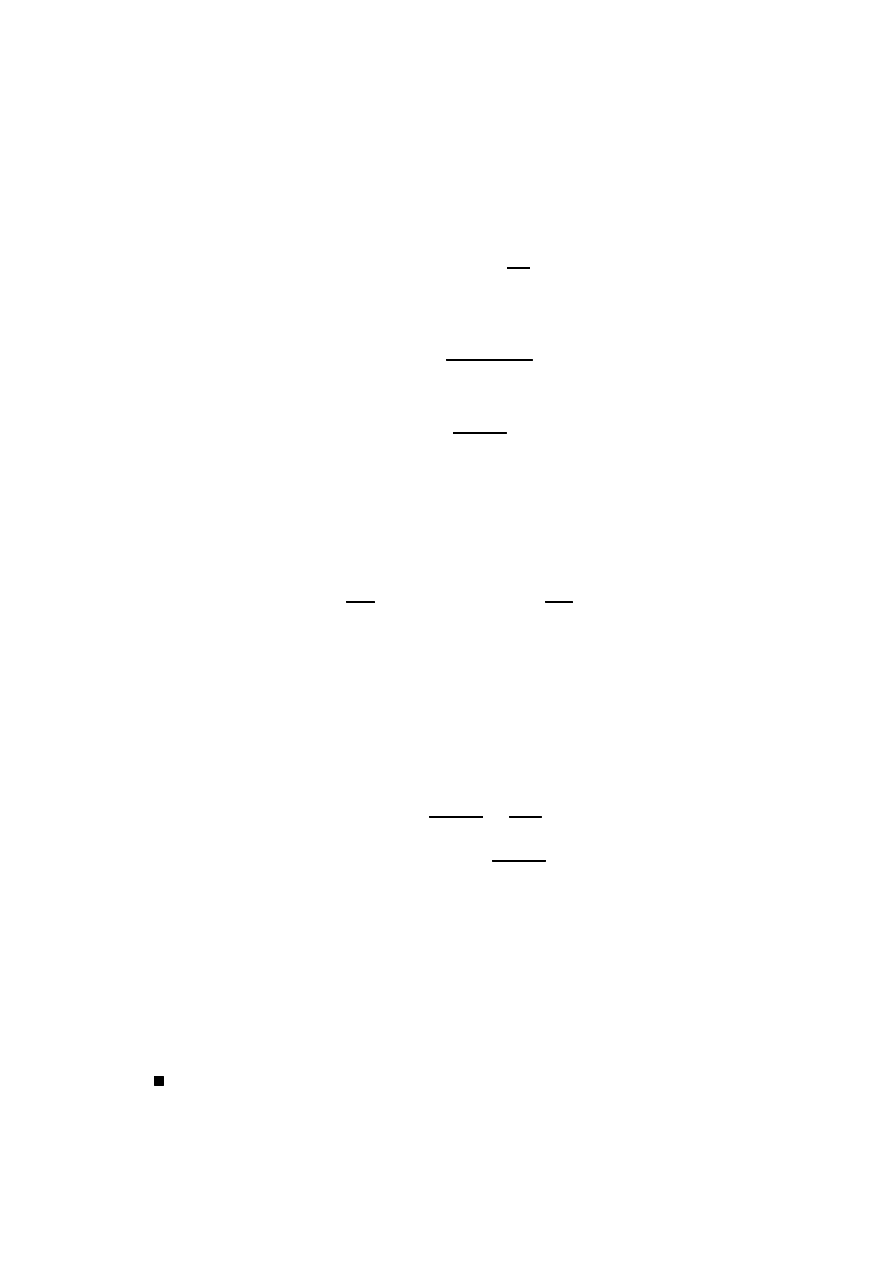
Statystyczne modele danych jako´sciowych

19

Twierdzenie 2.16 Test hipotezy

H

0

: 8

j=1;2;:::;J

p

1j

= p

2j

= ::: = p

Ij

= q

j

jest oparty na statystyce testowej G

2

G

2

= 2

X

ij

n

ij

ln

n

ij

c

n

ij

lub Â

2

Â

2

=

X

ij

(n

ij

¡

c

n

ij

)

2

c

n

ij

gdzie

c

n

ij

=

n

i+

n

+j

n

++

Statystyki te maj ¾

a asymptotycznie rozk÷ad Â

2

z (I ¡ 1) (J ¡ 1) stopniami swobody.

Dowód. Estymatory najwi ¾ekszej wiarygodno´sci dla nieznanych parametrów

q

j

uzyskamy minimalizuj ¾ac logarytm funkcji wiarygodno´sci (2.4):

ln

0

@

I

Y

i=1

n

i+

!

J

Y

j =1

p

n

ij

ij

n

ij

!

1

A

= ln

0

@

I

Y

i=1

n

i+

!

J

Y

j=1

q

n

ij

j

n

ij

!

1

A

=

= c +

X

ij

n

ij

ln q

j

= c +

X

j

n

+j

ln q

j

przy warunku

X

j

q

j

= 1

Korzystaj ¾ac z lematu 2.13 otrzymamy rozwi ¾

azanie

b

q

j

=

n

+j

P

j

n

+j

=

n

+j

n

++

;

c

n

ij

= n

i+

b

q

j

=

n

i+

n

+j

n

++

Liczba stopni swobody dla hipotezy H

1

wynosi IJ ¡ I; gdyz mamy IJ niez-

nanych parametrów, ale I dodatkowych warunków p

i+

= 1; i = 1; 2; :::; I. Liczba

stopni swobody dla hipotezy H

0

wynosi J ¡1; gdyz w tym przypadku nieznanymi

parametrami s ¾a q

j

, j = 1; 2; :::; J z jednym warunkiem

P

j

q

j

= 1: Liczba stopni

swobody dla rozk÷adu Â

2

, zgodnie z twierdzeniem 2.9, wynosi

DF (H

1

) ¡ DF (H

0

) = I J ¡ I ¡ (J ¡ 1) = (I ¡ 1) (J ¡ 1)

20

Statystyczne modele danych jako´sciowych

Przyk÷ad 2.17 (preferencje klientów) (´zród÷o [[4], str. 447]). Mieszka´ncy
po÷udniowej dzielnicy pewnego miasta zostali podzieleni na 4 grupy: mieszkaj ¾

acych

na pó÷nocy dzielnicy (N), po÷udniu (S), wschodzie (E) i zachodzie (W ). Z kazdej z
tych grup wylosowano niezaleznie po 100 osób i kazdej osobie zadano pytanie, czy
w ci ¾

agu ostatniego tygodnia odwiedzili centrum handlowe, umieszczone w ´srodku

osiedla. Celem tej ankiety by÷o rozstrzygni ¾ecie, czy klienci w jednakowym stopniu
korzystaj ¾

a z centrum dzielnicowego.

Zmienna grupuj ¾

aca X o poziomach N; S; W; E wskazuje, sk ¾

ad pochodz ¾

a anki-

etowani mieszka´ncy dzielnicy. Zmienna Y ma dwa poziomy: T (tak, odwiedzi÷em
centrum handlowe), N (nie odwiedzi÷em centrum handlowego). Wyniki ankiety
umieszczone s ¾

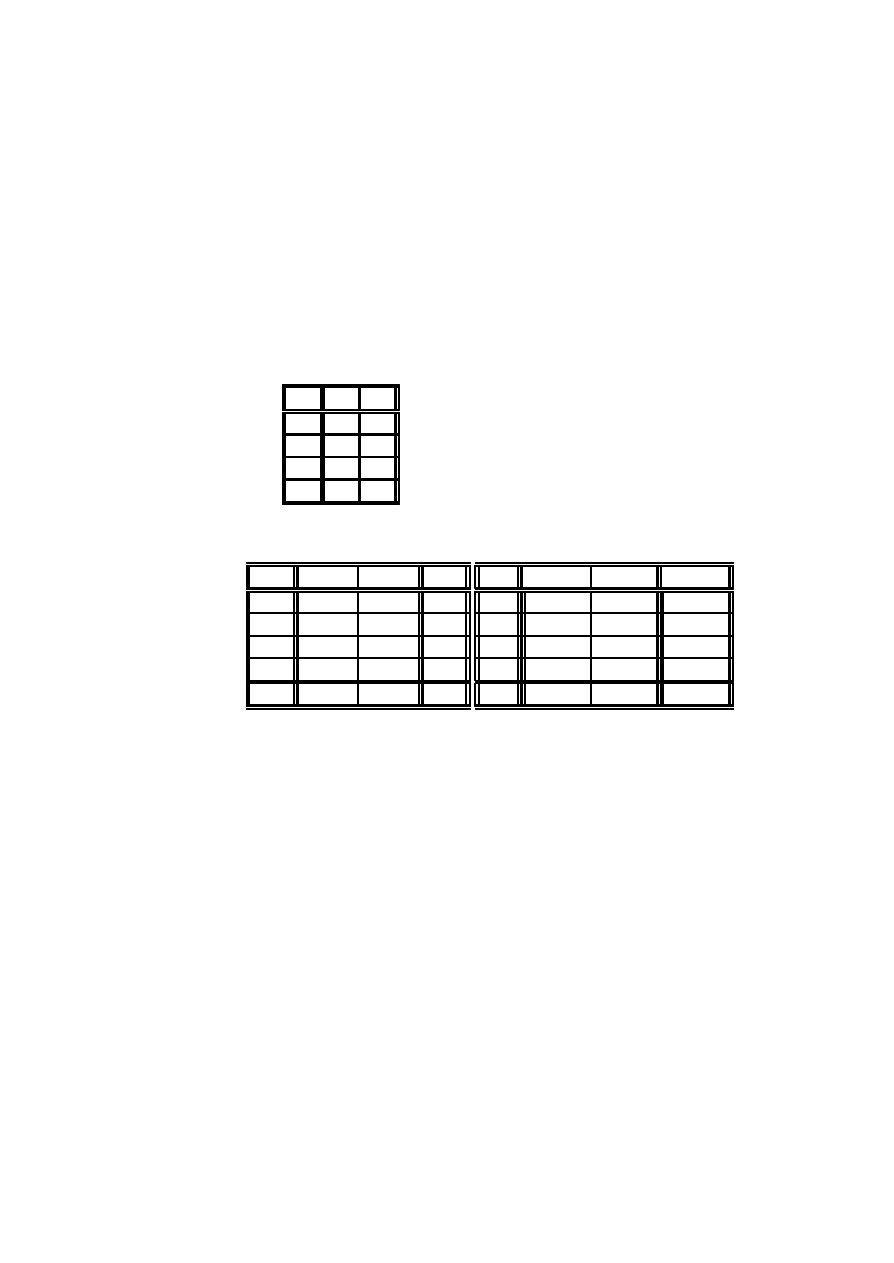
a w tablicy kontyngencji:

T

N

N

28 72

S

56 44

W

43 57

E

34 66

Zgodnie z twierdzeniem 2.16 musimy wyznaczy´c tablic ¾e liczno´sci oczekiwanych

i warto´sci Â

2

:

c

n

ij

T

N

d

n

i+

N

40: 25

59: 75

100

S

40: 25

59: 75

100

W

40: 25

59: 75

100

E

40: 25

59: 75

100

d

n

+j

161

239

400

Â

2

ij

T

N

Â

2

i+

N

3: 728

2: 512

6:240

S

6: 163

4: 152

10:305

W

: 188

: 125

:313

E

: 970

: 654

1:624

Â

2

ij

11:049

7:433

18:482

Poniewaz liczebno´sci oczekiwane s ¾

a wi ¾eksze od 5, uzyli´smy statystyki Â

2

. Liczba

stopni swobody wynosi 3*1=3. Poziom krytyczny wyliczamy z dystrybuanty rozk÷adu
Â

2

z 3 stopniami swobody wynosi

p = P

³

Â

2

> 18:482

´

= :00035

co jest zdecydowanym argumentem za odrzuceniem hipotezy jednorodno´sci. Spo-
jrzenie na tablic ¾e warto´sci Â

2

pokazuje, gdzie realizuje si ¾e to odchylenie od jed-

norodno´sci - w grupie S, gdzie warto´sci Â

2

ij

s ¾

a wi ¾eksze od 3.84, co oznacza is-

totnie duze (na poziomie 0.05) odchylenie od hipotezy jednorodno´sci. Liczba
odpowiedzi T (tak, korzystam z centrum handlowego) s ¾

a zdecydowanie wyzsze

niz liczba odpowiedzi T, gdyby wszyscy odpowiadali tak samo. Podobnie, liczba
odpowiedzi N (nie korzystam z centrum) jest zdecydowanie mniejsza. Mozna to
interpretowa´c tak, ze mieszka´ncy po÷udniowej cz ¾e´sci dzielnicy ch ¾etniej korzystaj ¾

a

z centrum, usytuowanego w kierunku ich przejazdu do centrum miasta.

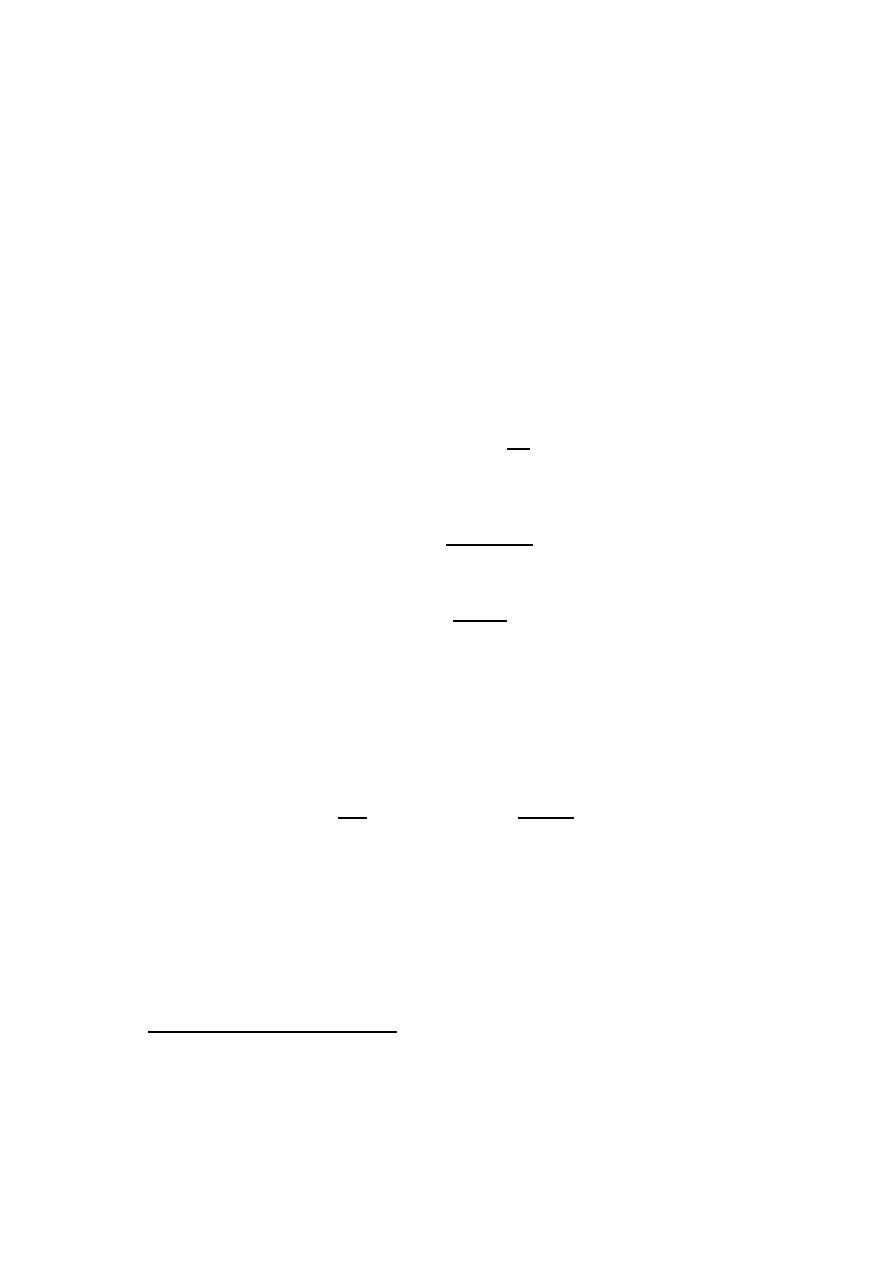
Statystyczne modele danych jako´sciowych

21

Test niezalezno´sci Â

2

Drugim waznym problemem, który dotyczy dwuwymiarowych tablic kontyngencji
jest testowanie niezalezno´sci. Naturalnym rozk÷adem, który wyst ¾epuje w tym
zagadnieniu jest rozk÷ad wielomianowy.

Test niezalezno´sci jest szczególnym przypadkiem twierdzenia 2.9.

Twierdzenie 2.18 Test hipotezy niezalezno´sci

H

0

: 8

i=1;2;:::;I

8

j =1;2;:::;J

p

ij

= p

i+

p

+j

jest oparty na statystyce testowej G

2

G

2

= 2

X

ij

n

ij

ln

n

ij

c

n

ij

lub Â

2

Â

2

=

X

ij

(n

ij

¡

c

n

ij

)

2

c

n

ij

gdzie

c

n

ij

=

n

i+

n

+j

n

++

Statystyki te maj ¾

a asymptotycznie rozk÷ad Â

2

z (I ¡ 1) (J ¡ 1) stopniami swo-

body

6

.

Dowód. Estymatory najwi ¾ekszej wiarygodno´sci dla nieznanych parametrów

p

i+

; p

+j

uzyskamy minimalizuj ¾ac logarytm funkcji wiarygodno´sci (2.3):

ln

0

@

n

++

!

Y

i;j

p

n

ij

ij

n

ij

!

1

A

= ln

0

@

n

++

!

Y

i;j

p

n

ij

i+

p

n

ij

+j

n

ij

!

1

A

= c +

X

ij

n

ij

ln (p

i+

p

+j

)

= c +

X

i

n

i+

ln p

i+

+

X

j

n

+j

ln p

+j

przy warunku

X

i

p

i+

= 1;

X

j

p

+j

= 1

6

Pearson w swojej oryginalnej pracy z 1900 b÷ ¾ednie podawa÷ liczbe stopni swobody jako

IJ ¡ 1. Dopiero Fisher wyja´sni÷ w 1922 poprawnie, na gruncie geometrii , poj ¾ecie stopni

swobody i poda÷ regu÷y ich obliczania.

22

Statystyczne modele danych jako´sciowych

Korzystaj ¾ac z lematu 2.13 otrzymamy rozwi ¾azanie

d

p

i+

=

n

i+

P

i

n

i+

=

n

i+

n

++

;

d

p

+j

=

n

+j

P

j

n

+j

=

n

+j

n

++

;

c

n

ij

= n

++

d

p

i+

d

p

+j

= n

++

n

i+

n

+j

(n

++

)

2

=

n

i+

n

+j

n

++

Liczba stopni swobody dla hipotezy H

1

wynosi IJ ¡1; gdyz mamy IJ nieznanych

parametrów, ale 1 dodatkowy warunek

P

ij

p

ij

= 1. Liczba stopni swobody dla

hipotezy H

0

wynosi I ¡ 1 +J ¡ 1 = I + J ¡ 2; gdyz w tym przypadku nieznanymi

parametrami s ¾a p

i+

, i = 1; 2; :::; I z jednym warunkiem

P

i

p

i+

= 1 oraz p

+j

, j =

1; 2; :::; J z jednym warunkiem

P

j

p

+j

= 1: Liczba stopni swobody dla rozk÷adu

Â

2

, zgodnie z twierdzeniem 2.9, wynosi

DF (H

1

) ¡ DF (H

0

) = IJ ¡ 1 ¡ (I + J ¡ 2) = (I ¡ 1) (J ¡ 1)

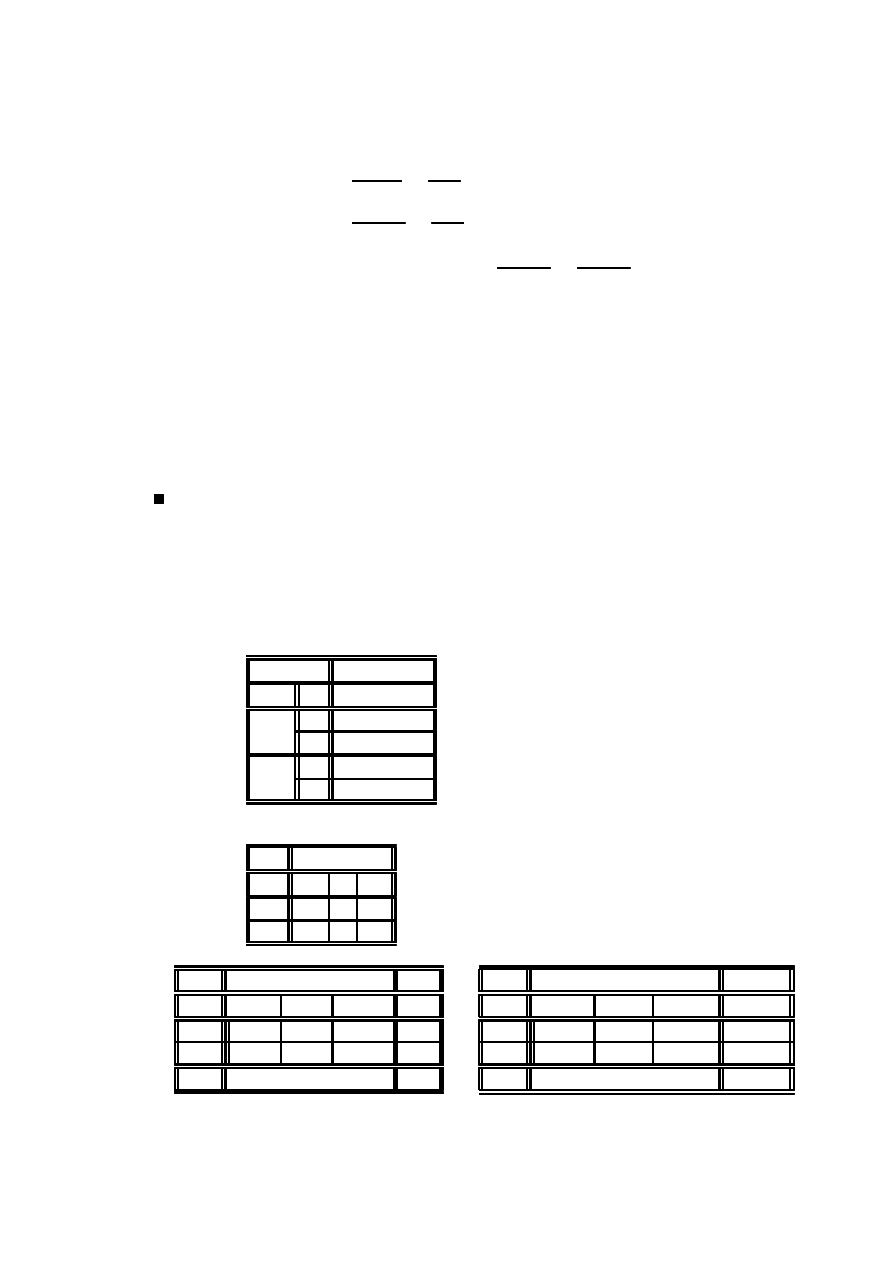
Przyk÷ad 2.19 (artretyzm, terapia, p÷e´c) (´zród÷o [[3]]), Tabela przedstawia
wyniki obserwacji 84 pacjentów, chorych na artretyzm. Cechy, obserwowane w
eksperymencie to:

W : wyniki leczenia (z - zadne, u - umiarkowane, l - lepsze);
P : p÷e´

c (k - kobieta, m - m ¾ezczyzna),

T : zastosowana terapia (a - aktywna, p - placebo).

n

ijk

W

P

T

z

u l

k

a

6

5 16

p

19 7 6

m

a

7

2 5

p

10 0 1

Zbadamy, czy zastosowana terapia mia÷a wp÷yw na wyniki leczenia. × ¾

acz ¾

ac

dane dla kobiet i m ¾ezczyzn, otrzymamy tabel ¾e

n

ij

W

T

z

u l

a

13 7 21

p

29 7 7

Zbudujemy tabel ¾e liczebno´sci oczekiwanych i odleg÷o´sci Â

2

c

n

ij

W

T

z

u

l

n

i+

a

20: 5

6: 83

13: 67

41

p

21: 5

7: 17

14: 33

43

n

+j

42

14

28

84

Â

2

ij

W

T

z

u

l

Â

2

i+

a

2: 744

:0042

3: 930

6.678

p

2: 616

:0040

3: 749

6.369

Â

2

+j

5.360

.0082 7.679

13.047

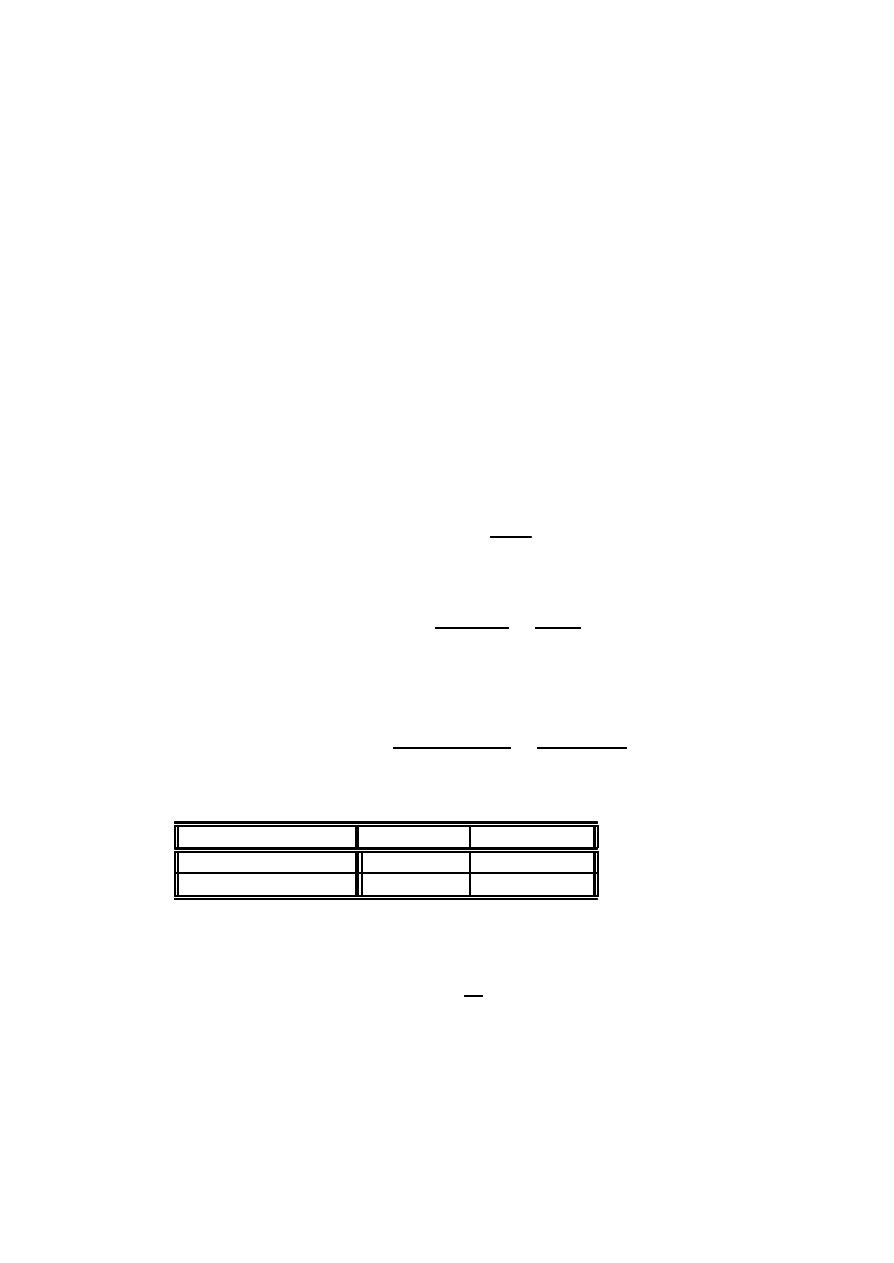
Statystyczne modele danych jako´sciowych

23

Liczba stopni swobody wynosi 1*2=2 a poziom krytyczny

p = P

³

Â

2

> 13:047

´

= :0015

co pozwala na odrzucenie hipotezy o niezalezno´sci wyników od zastosowanej ter-
apii. Pogrubione pole w tablicy Â

2

ij

pokazuje na istotn ¾

a róznic ¾e w liczbie lepszych

wyników przy zastosowanej aktywnej terapii w stosunku do hipotetycznej liczby,
odpowiadaj ¾

acej niezalezno´sci.

Iloraz krzyzowy

Inna koncepcja opisania zwi ¾azku mi ¾edzy cechami opiera si ¾e na poj ¾eciu stosunku
szans.

De…nicja 2.20 (stosunek szans) Prawdopodobie´nstwo zaj´scia zdarzenia A jest
równe p. Stosunkiem szans dla tego zdarzenia nazywamy iloraz

$ = $ (A) =

p

1 ¡ p

Dobrym estymatorem stosunku szans jest wielko´s´c

c

$ =

c

$ (A) =

n (A)

n ¡ n (A)

=

n (A)

n (A

0

)

;

gdzie n (A) jest liczb ¾a obserwacji w próbie, dla których zasz÷o zdarzenie A, n jest
wielko´sci ¾a próby. Gdy próba nie jest wielka zaleca si ¾e stosowanie nieco innego
estymatora

f

$ =

f

$ (A) =

n (A) + 0:5

n ¡ n (A) + 0:5

=

n (A) + 0:5

n (A

0

) + 0:5

Przyk÷ad 2.21 Dane o wykszta÷ceniu i dochodzie rocznym zebrano w´sród 300
osób:

dochód niski dochód wysoki

wykszta÷cenie ´srednie

70

30

wykszta÷cenie wyzsze

80

120

Niech A b ¾edzie zdarzeniem, ze osoba ma wykszta÷cenie ´srednie, B - ze ma niski

dochód. Gdy ograniczymy si ¾e do osób z niskim dochodem to stosunek szans dla
zdarzenia A mozna oszacowa´c, jako

c

$ (A jB ) =

70
80

= : 875

co oznacza, ze w´sród osób z niskim dochodem jest prawie taka sama liczba osób
o wykszta÷ceniu ´srednim i wyzszym z lekk ¾

a przewag ¾

a liczby osób z wykszta÷ceniem

wyzszym.

24

Statystyczne modele danych jako´sciowych

Gdy ograniczymy si ¾e do osób z wyzszym dochodem to stosunek szans dla

zdarzenia A mozna oszacowa´c, jako

c

$ (A jB

0

) =

30

120

= : 25

co oznacza, ze w´sród osób z wysokim dochodem jest ma÷a liczba osób o wykszta÷ce-
niu ´srednim a duza z wyzszym (4 razy wi ¾eksza).

Z kolei, gdy ograniczymy si ¾e do osób z wykszta÷ceniem ´srednim to stosunek

szans dla zdarzenia B mozna oszacowa´c, jako

c

$ (B jA ) =

70
30

= 2:33

a w´sród osób z wykszta÷ceniem wyzszym

c

$ (B jA

0

) =

80

120

= :67

Zauwazmy, ze

c

$ (A jB )

c

$ (A jB

0

)

=

c

$ (B jA )

c

$ (B jA

0

)

=

70 ¤ 120

30 ¤ 80

= 3:5

Pierwszy stosunek mówi, ze iloraz szans dla ´sredniego wykszta÷cenia jest 3.5

raza wi ¾ekszy w grupie zarabiaj ¾

acych ma÷o od takiego ilorazu w grupie zarabiaj ¾

a-

cych duzo. Drugi stosunek mówi, ze iloraz szans dla niskiego dochodu jest 3.5
raza wi ¾ekszy w grupie osób o ´srednim wykszta÷ceniu od takiego ilorazu dla osób z
wyzszym wykszta÷ceniem. Podsumowuj ¾

ac, jest silny zwi ¾

azek mi ¾edzy niskim wyk-

szta÷ceniem a niskim dochodem. Liczba 3.5 jest miar ¾

a si÷y tego zwi ¾

azku.

Z poprzedniego przyk÷adu wynika potrzeba zde…niowania nowego poj ¾ecia.

De…nicja 2.22 (iloraz krzyzowy) Dana jest para cech binarnych (X; Y ) : Ilo-

razem krzyzowym dla tych cech nazywamy liczb ¾e

µ = µ (X; Y ) =

p

11

p

22

p

12

p

21

;

gdzie p

ij

= P (X = x

i

; Y = y

j

) ; i; j = 1; 2

Estymator ilorazu krzyzowego z tablicy kontyngencji

y

1

y

2

x

1

n

11

n

12

x

2

n

21

n

22

b ¾edzie postaci

b

µ =

b

µ (X; Y ) =

n

11

n

22

n

12

n

21

lub, gdy dysponujemy ma÷ ¾a liczba obserwacji

e

µ =

e

µ (X; Y ) =

(n

11

+ 0:5) (n

22

+ 0:5)

(n

12

+ 0:5) (n

21

+ 0:5)

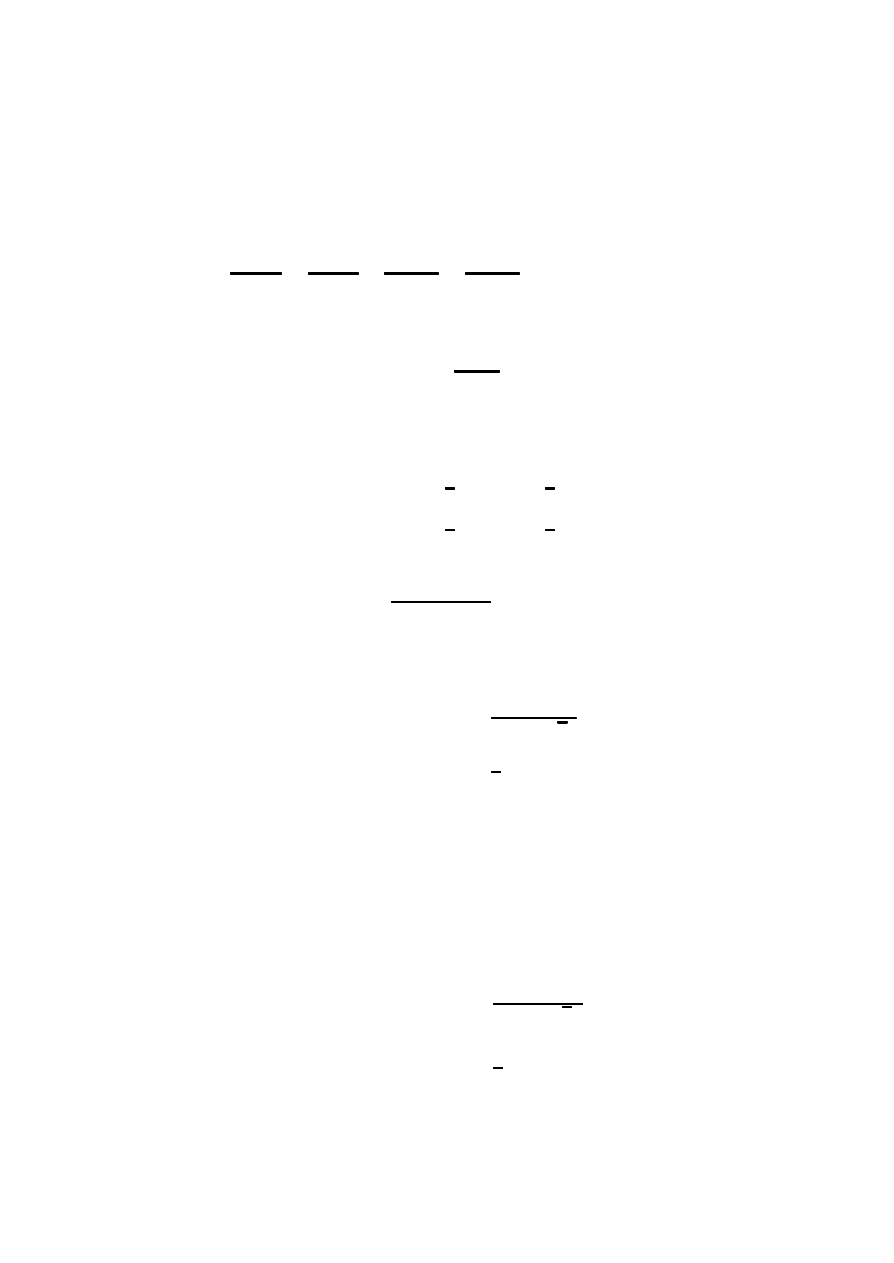
Statystyczne modele danych jako´sciowych

25

Twierdzenie 2.23 Niech dana b ¾edzie para cech binarnych (X; Y ): Oznaczmy:

p

ij

= P (X = x

i

; Y = y

j

) ; i; j = 1; 2

A = fX = x

1

g ; B = fY = y

1

g

Zachodz ¾

a wtedy równo´sci:

1. µ =

$(A

jB )

$(A

jB

0

)

=

$(B

jA)

$(B

jA

0

)

=

$(A

0

jB

0

)

$(A

0

jB )

=

$(B

0

jA

0

)

$(B

0

jA )

2. Niech p

¤

1j

= c

1

p

1j

; p

¤

2j

= c

2

p

2j

; c

1

p

1+

+ c

2

p

2+

= 1. Wtedy p

¤

ij

jest

rozk÷adem prawdopodobie´nstwa dla pary (X; Y ) takim, ze odpowiadaj ¾

acy mu iloraz

krzyzowy

µ

¤

=

p

¤

11

p

¤

22

p

¤

12

p

¤

21

jest równy iloczynowi krzyzowemu µ:

3. Dla kazdego µ istnieje uk÷ad prawdopodobie´nstw p

ij

(µ) taki, ze

p

1+

(µ) =

1
2

; p

2+

(µ) =

1
2

;

p

+1

(µ) =

1
2

; p

+2

(µ) =

1
2

oraz

p

11

(µ) p

22

(µ)

p

12

(µ) p

21

(µ)

= µ

Uk÷ad taki nazywamy standardow ¾a reprezentacj ¾a ilorazu krzyzowego µ

Reprezentacja standardowa jest wyznaczona jednoznacznie ze wzoru

p

12

(µ) = p

21

(µ) =

1

2

³

1 +

p

µ

´

;

p

11

(µ) = p

22

(µ) =

1
2

¡ p

12

(µ)

Reprezentacja standardowa przedstawia sytuacj ¾e, gdyby do´swiadczenie wyko-

nano tak, ze zarówno cecha X jak i Y maj ¾a swoje warto´sci reprezentowane z
tak ¾a sam ¾a cz ¾esto´sci ¾

a (nie preferujemy zadnych warto´sci tych cech). Wtedy praw-

dopodobie´nstwa wyst ¾epuj ¾ace w tablicy standardowej odzwierciedlaj ¾a si÷ ¾e zwi ¾azku

mi ¾edzy tymi cechami.

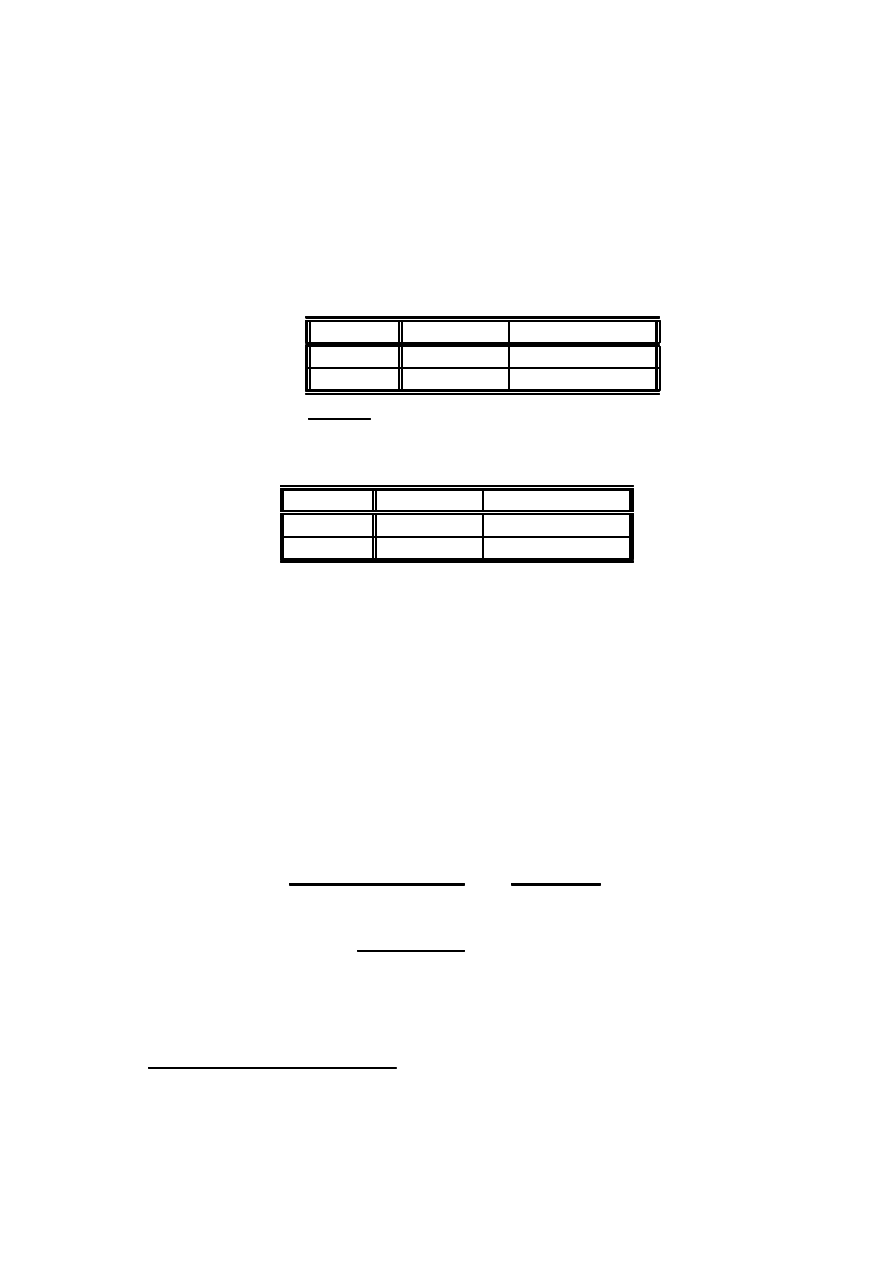
Reprezentacja standardowa dla estymatora ilorazu krzyzowego

b

µ wynika z

powyzszych wzorów:

p

12

³

b

µ

´

= p

21

³

b

µ

´

=

1

2

µ

1 +

q

b

µ

¶

;

p

11

³

b

µ

´

= p

22

³

b

µ

´

=

1
2

¡ p

12

³

b

µ

´

26

Statystyczne modele danych jako´sciowych

Przyk÷ad 2.24 Cecha X wskazuje, czy osoba jest czy nie jest chora na rzadko
wyst ¾epuj ¾

ac ¾

a chorob ¾e a Y czy wyst ¾epuje, czy nie wyst ¾epuje u badanej osoby spadek

wagi cia÷a. Ze wzgl ¾edu na ma÷e prawdopodobie´nstwa spadku czy braku spadku
wagi w´sród osób u których wyst ¾epuje ta choroba, mogliby´smy nie zauwazy´c rzeczy-
wistych rozmiarów wzajemnych relacji mi ¾edzy warto´sciami tych cech. Wady tej
jest pozbawiona reprezentacja standardowa.

Przypu´s´cmy, ze uda÷o nam si ¾e zebra´c dane tylko od 18 osób chorych na t ¾

a

chorob ¾e

spadek wagi brak spadku wagi

chory

10

8

nie chory

300

600

b

µ =

10 ¤ 600

8 ¤ 300

= 2: 5

Reprezentacja standardowa tej tabeli ma posta´c

spadek wagi brak spadku wagi

chory

:306

:194

nie chory

:194

:306

co ujawnia, ze gdyby chorych by÷o tyle samo, co zdrowych to iloraz szans dla
spadku wagi by÷by równy 1.58 (= :306=:194) a nie 1.25 jak to by÷o w naszej z
trudem zebranej próbie.

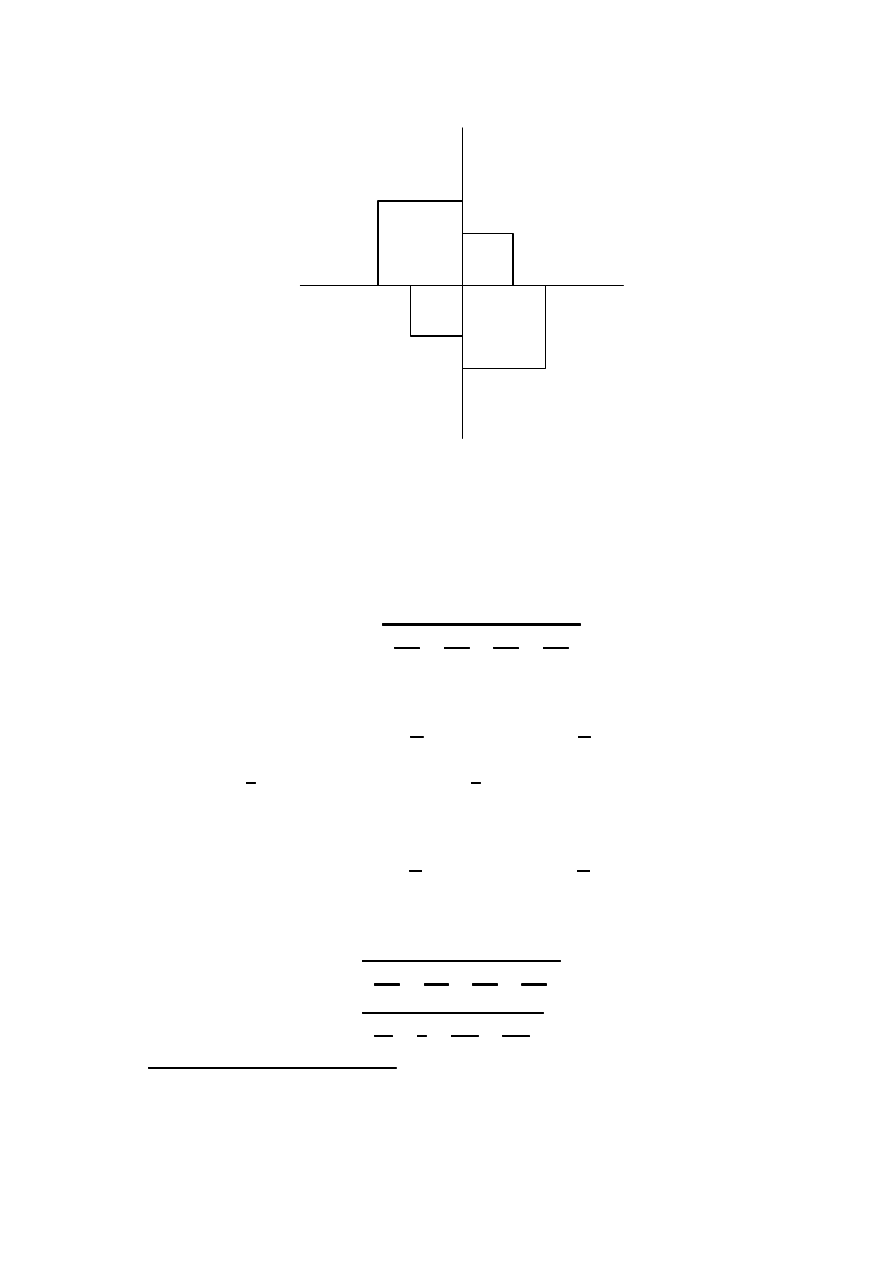
Warto´s´c ilorazu krzyzowego µ (

b

µ) mozna przedstawi´c za pomoc ¾

a wykresu

ko÷owego, czy kwadratowego, pozwalaj ¾

acego zobrazowa´c si÷ ¾e zwi ¾

azku mi ¾edzy cechami,

reprezentowan ¾a przez iloraz krzyzowy. Na osi pionowej, odpowiadajacej osobom

chorym i osi poziomej, odpowiadaj ¾acej spadkowi wagi rysujemy kwadrat

7

o boku

p

11

³

b

µ

´

, na osi pionowej, odpowiadajacej osobom chorym i osi poziomej, odpowiada-

j ¾acej brakowi spadku wagi rysujemy kwadrat o boku p

12

³

b

µ

´

itd. Stosunek sumy

pól kwadratów lewy- górny, prawy-dolny do sumy pól prawy-górny, lewy_dolny
wynosi

³

p

11

³

b

µ

´´

2

+

³

p

22

³

b

µ

´´

2

³

p

12

³

b

µ

´´

2

+

³

p

21

³

b

µ

´´

2

=

2

³

p

11

³

b

µ

´´

2

2

³

p

12

³

b

µ

´´

2

=

p

11

³

b

µ

´

p

22

³

b

µ

´

p

12

³

b

µ

´

p

21

³

b

µ

´

=

b

µ

Zgodnie z teori ¾

a percepcji ogl ¾adaj ¾ac obiekty na p÷aszczy´znie porównujemy ich

wielko´sci poprzez porównanie pól. Tak wi ¾ec nasz wykres, poprzez porównanie
pól kwadratów, dobrze ilustruje wielko´s´c ilorazu krzyzowego.

7

Mozo to by´c ´cwiartka ko÷a o tym promieniu

Statystyczne modele danych jako´sciowych

27

nie spadek

spadek

nie chory

chory

Kiedy obliczamy estymator

b

µ ilorazu krzyzowego µ interesowa´c nas musi rozk÷ad

prawdopodobie´nstwa tego estymatora. Pozwoli nam to na zbudowanie przedzia÷u

ufno´sci, co umozliwi testowanie hipotezy o prawdziwej warto´sci ilorazu krzyzowego.

Twierdzenie 2.25 W tablicy kontyngencji dla binarnych cech (X; Y ) o rozk÷adach
dwumianowym, Poissona lub wielomianowym, zmienna losowa ln

³

b

µ

´

ma, asymp-

totycznie przy n ! 1 rozk÷ad N (ln (µ) ;

b

¾), gdzie

b

¾ =

sµ

1

n

11

+

1

n

12

+

1

n

21

+

1

n

22

¶

Wniosek 2.26 Przedzia÷ ufno´sci na poziomie 1 ¡ ® dla ln (µ) ma posta´c:

µ

ln

³

b

µ

´

¡ z

µ

1 ¡

®

2

¶

b

¾; ln

³

b

µ

´

+ z

µ

1 ¡

®

2

¶

b

¾

¶

;

gdzie z

³

1 ¡

®

2

´

jest kwantylem rz ¾edu 1 ¡

®
2

dla standardowego rozk÷adu normal-

nego

8

.

Stwierdzenie to jest równowazne temu, ze przedzia÷ ufno´sci dla µ jest postaci

µ

b

µ exp

µ

¡z

µ

1 ¡

®

2

¶

b

¾

¶

;

b

µ exp

µ

z

µ

1 ¡

®

2

¶

b

¾

¶¶

Przyk÷ad 2.27 (kontynuacja przyk÷adu 2.24).

Warto´s´c

b

¾ obliczamy ze wzoru

b

¾ =

sµ

1

n

11

+

1

n

12

+

1

n

21

+

1

n

22

¶

=

=

sµ

1

10

+

1
8

+

1

300

+

1

600

¶

= : 479 58

8

Dla ® = 0:05 kwantyl ten wynosi 1:96 a dla ® = 0:01 kwantyl ten wynosi 2:58

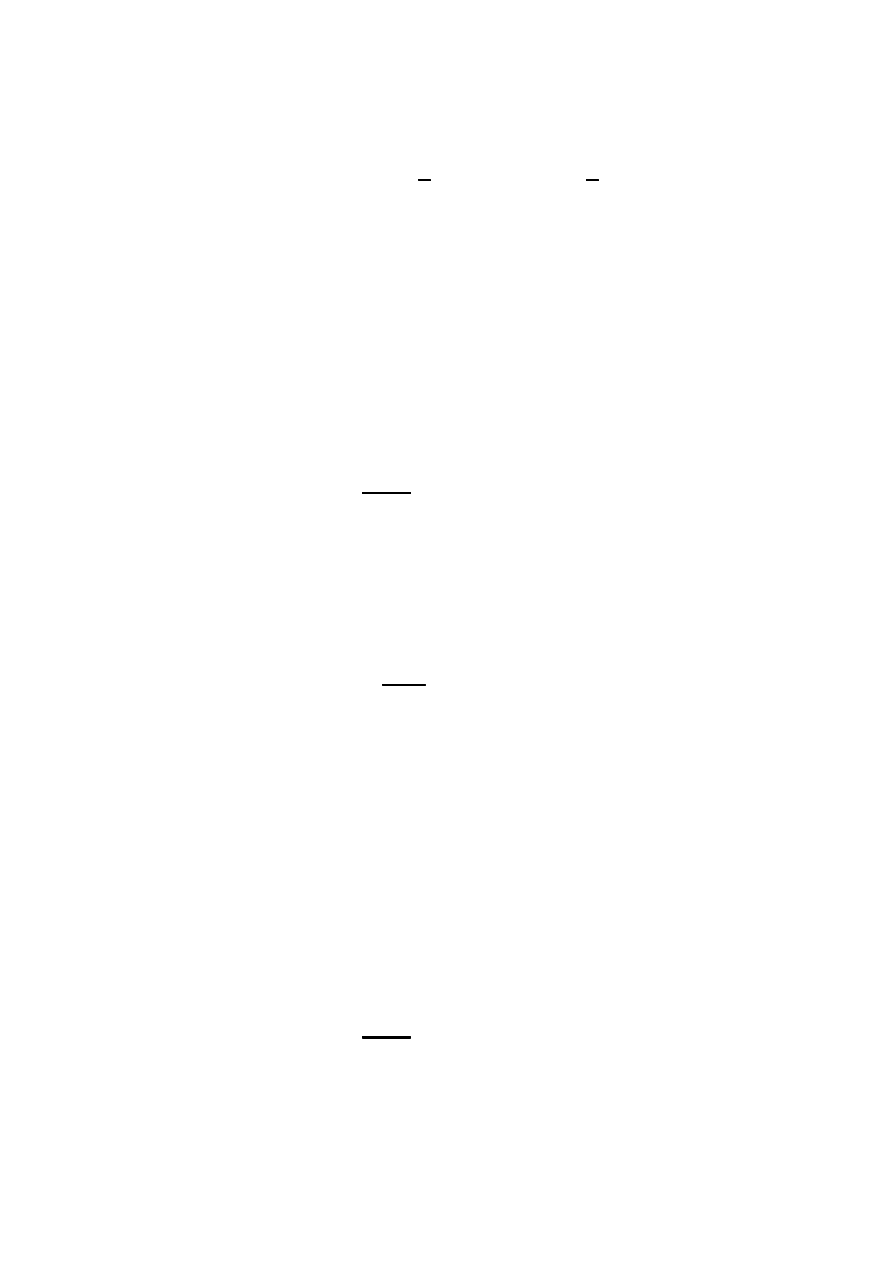
28

Statystyczne modele danych jako´sciowych

Przedzia÷ ufno´sci dla µ na poziomie 0:95 b ¾edzie mia÷ posta´c:

µ

b

µ exp

µ

¡z

µ

1 ¡

®

2

¶

b

¾

¶

;

b

µ exp

µ

z

µ

1 ¡

®

2

¶

b

¾

¶¶

= (2:5 exp (¡1:96 ¤ : 479 58) ; 2:5 exp (1:96 ¤ : 479 58))
= (: 976 59; 6: 399 8)

Wskazuje to na olbrzymi zakres mozliwych warto´sci ilorazu krzyzowego. Odpowiedzialne
za to s ¾

a nadzwyczaj ma÷e ilo´sci obserwacji zwi ¾

azanych z osobami chorymi.

Niezalezno´s´c i jednorodno´s´c cech mozna ÷atwo wyrazi´c poprzez iloraz krzyzowy.

Twierdzenie 2.28 Cechy X o poziomach fx

1

; x

2

; :::; x

I

g i Y o poziomach fy

1

; y

2

; :::; y

J

g ;

maj ¾

acych ÷ ¾

aczny rozk÷ad prawdopodobie´nstwa

p

ij

= P (X = x

i

; Y = y

j

) ; i = 1; 2; :::; I; j = 1; 2; :::; J

s ¾

a niezalezne wtedy i tylko wtedy, gdy kazdy iloraz krzyzowy

µ (i; j; i0; j

0

) =

p

ij

p

i

0

j

0

p

i

0

j

p

ij

0

; i; i

0

= 1; 2; :::; I; j; j

0

= 1; 2; :::; J

jest równy 1.

Sprawdzenie niezalezno´sci za pomoc ¾a ilorazów krzyzowych wymaga wi ¾ec sprawdzenia

(IJ )

2

warunków. Uci ¾azliwo´s´c tej procedury mozna znacz ¾aco zmniejszy´c.

Twierdzenie 2.29 Cechy X i Y s ¾

a niezalezne wtedy i tylko wtedy, gdy kazdy

iloraz krzyzowy

µ (1; 1; i; j) =

p

11

p

ij

p

1j

p

i1

; i = 2; 3; :::; I; j = 2; 3; :::; J

jest równy 1.

W szczególno´sci, gdy X i Y s ¾

a cechami binarnymi to ich niezalezno´s´c jest

równowazna temu, ze ich iloraz krzyzowy jest równy 1.

Analogiczne wyniki dotycz ¾a jednorodno´sci rozk÷adów

Twierdzenie 2.30 Cecha X o poziomach fx

1

; x

2

; :::; x

I

g jest grupuj ¾

aca. Rozk÷ad

cechy Y o poziomach fy

1

; y

2

; :::; y

J

g ; ma rozk÷ad prawdopodobie´nstwa

p

ij

= P (Y = y

j

j X = x

i

; ) ; i = 1; 2; :::; I; j = 1; 2; :::; J

Rozk÷ad cechy Y jest jednorodny wzgl ¾edem X to znaczy taki, ze

8

j=1;2;:::;J

p

1j

= p

2j

= ::: = p

Ij

wtedy i tylko wtedy, gdy kazdy iloraz krzyzowy

µ (i; j; i0; j

0

) =

p

ij

p

i

0

j

0

p

i

0

j

p

ij

0

; i; i

0

= 1; 2; :::; I; j; j

0

= 1; 2; :::; J

jest równy 1.

Statystyczne modele danych jako´sciowych

29

Twierdzenie 2.31 Rozk÷ad cechy Y jest jednorodny wzgl ¾edem X wtedy i tylko
wtedy, gdy kazdy iloraz krzyzowy

µ (1; 1; i; j) =

p

11

p

ij

p

1j

p

i1

; i = 2; 3; :::; I; j = 2; 3; :::; J

jest równy 1.

Iloraz krzyzowy estymujemy na podstawie tablicy kontyngencji. W takim

razie wazny jest problem, czy estymator ilorazu krzyzowego wskazuje na danym
poziomie istotno´sci, ze prawdziwa warto´s´c tego ilorazu jest równa 1. Odpowied´z

na to pytanie wynika natychmiast z twierdzenia 2.25.

Twierdzenie 2.32 Statystyka testowa do testowania hipotez

H

0

:

µ = 1;

H

1

:

µ 6= 1 (µ < 1) (µ > 1)

oparta jest na statystyce testowej

z =

ln

b

µ

b

¾

maj ¾

acej asymptotycznie standardowy rozk÷ad normalny.

Hipotez ¾e H

0

odrzucamy na rzecz hipotezy H

1

gdy zachodz ¾

a odpowiednie nierówno´sci

jzj > z

µ

1 ¡

®

2

¶

;

z < ¡z (1 ¡ ®) ;
z > z (1 ¡ ®)

gdzie z (u) jest kwantylem rz ¾edu u standardowego rozk÷adu normalnego.
Przyk÷ad 2.33 (kontynuacja przyk÷adu 2.24)

Zbadamy, czy zachorowanie na analizowan ¾

a chorob ¾e i spadek wagi s ¾

a od siebie

niezalezne. Obliczyli´smy, ze estymator ilorazu krzyzowego ma w tym przypadku
warto´s´c

b

µ = 2:5;

b

¾ = : 479 58. Warto

´s´c statystyki z jest równa

z =

ln

b

µ

b

¾

=

ln 2:5

: 479 58

= 1: 910 6

Poziom krytyczny dla hipotez

H

0

:

µ = 1;

H

1

:

µ 6= 1

jest równy

p = P (jZj > 1: 910 6) = :0561

co prowadzi do konkluzji, ze dysponujemy s÷abymi argumentami za odrzuceniem
hipotezy zerowej a wi ¾ec s÷abymi argumentami za uznaniem zalezno´sci mi ¾edzy za-
chorowaniem na analizowan ¾

a chorob ¾e i spadkiem wagi, mimo wydawa÷oby si ¾e

duzej warto´sci

b

µ:

30

Statystyczne modele danych jako´sciowych

Rozdzia÷ 3

Modele logitowe

31

32

Modele logitowe

W dwóch kolejnych rozdzia÷ach b ¾edziemy rozwaza´c modele prawdopodobie´nstw

lub liczebno´sci zdarze´n jako funkcji innych zmiennych. Stworzenie takich mod-
eli jest o tyle k÷opotliwe, ze zastosowanie klasycznej teorii regresji z b÷ ¾edami
modelu, maj ¾acymi rozk÷ad normalny nie jest w tym przypadku mozliwe. Praw-
dopodobie´nstwa bowiem ograniczone s ¾a do przedzia÷u (0; 1) a warto´sci bliskie

kra´ncom skali maj ¾a szczególne znaczenie. Znacznie trudniej jest uzyska´c wzrost
prawdopodobie´nstwa o 0:01 gdy obserwujemy zdarzenie o prawdopodobie´nstwie
0:95 niz wtedy, gdy obserwujemy zdarzenie o prawdopodobie

´nstwie 0:6. Rozwi ¾azanie

tego zagadnienia moze u÷atwi´c przedstawienie prawdopodobie´nstwa w innej skali(
patrz Dodatek A)

Modele logitowe dla zmiennych liczbowych

Modele logitowe s ¾a modelami regresyjnymi, opisuj ¾acymi relacj ¾e mi ¾edzy zmienn ¾a
wynikow ¾a dychotomiczn ¾

a

1

a zmiennymi obja´sniaj ¾acymi. W modelu tym in-

teresuje nas regresja, najlepiej liniowa, mi ¾edzy prawdopodobie´nstwem sukcesu,

wyrazonym w skali logitowej a zmiennymi obja´sniaj ¾acymi

2

.

Przyk÷ad 3.1 (Ci´snienie) (´zród÷o, [1] str. 93)

Mieszka´ncy Framingham (Massachusetts), m ¾ezczy´zni w wieku 40-60 lat, byli

obserwowani przez 6 kolejnych lat. Notowano, czy w tym czasie zachorowali na
wie´ncow ¾

a chorob ¾e serca. Zbadamy, jaki wp÷yw na prawdopodobie´nstwo zachorowa-

nia moze mie´c poziom ci´snienia krwi

ci´snienie chorzy zdrowi probit
112

3

153

ln

3

153

= ¡3: 93

122

17

235

ln

17

235

= ¡2: 63

132

12

272

ln

12

272

= ¡3: 12

142

16

255

ln

16

255

= ¡2: 77

152

12

127

ln

12

127

= ¡2: 36

162

8

77

ln

8

77

= ¡2: 26

177

16

83

ln

16
83

= ¡1: 65

192

8

35

ln

8

35

= ¡1: 48

Regresja liniowa okaza÷a si ¾e dobrym modelem relacji ci´snienie - logit:

1

tzn, majac ¾a dwie warto´sci; jedna z nich tradycyjnie nazywa si ¾e sukcesem

2

Dla niektórych danych zamiast skali logitowej trzeba uzy´c innej skali prawdopodobie´nstw,

na przyk÷ad probitowej czy tez podwójnie logarytmicznej.

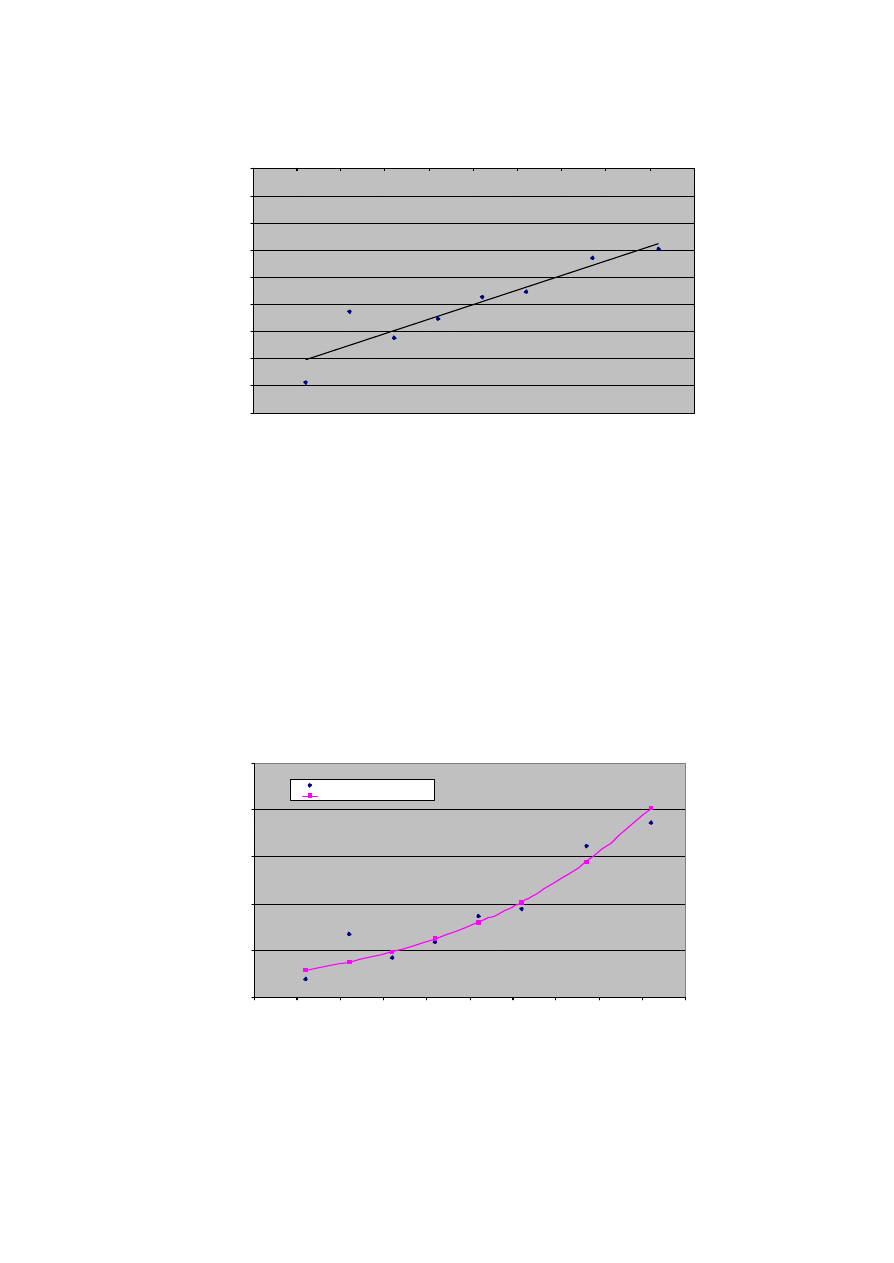
Modele logitowe

33

REGRESJA LOGITOWA

y = 0,0267x - 6,503

R

2

= 0,8572

-4,50

-4,00

-3,50

-3,00

-2,50

-2,00

-1,50

-1,00

-0,50

0,00

100

110

120

130

140

150

160

170

180

190

200

CISNIENIE

LOGIT

Wspó÷czynnik determinacji modelu wynosi 0:8572 co wskazuje na dobre jego

dopasowanie do danych. Jak wida´c z wykresu, jedynie dwa punkty, odpowiadaj ¾

ace

dwom najnizszym warto´sciom ci´snienia odbiegaj ¾

a istotnie od prostej logitowej.

Model, który uzyskali´smy ma posta´c

lgt = ¡6:503 + 0:0237 c

gdzie c oznacza ci´snienie krwi. Wzrost tego ci´snienia o 1 jednostk ¾e powoduje
wzrost logitu o 0:0237 co oznacza, ze iloraz krzyzowy dla zachorowania i dla danego
ci´snienia przy jego wzro´scie o 1 jednostk ¾e wynosi exp (0:0237) = 1: 024:Zwi ¾ekszenie
ci´snienia o 1 jednostk ¾e powoduje zwi ¾ekszenie ilorazu szans zachorowania o 2%.

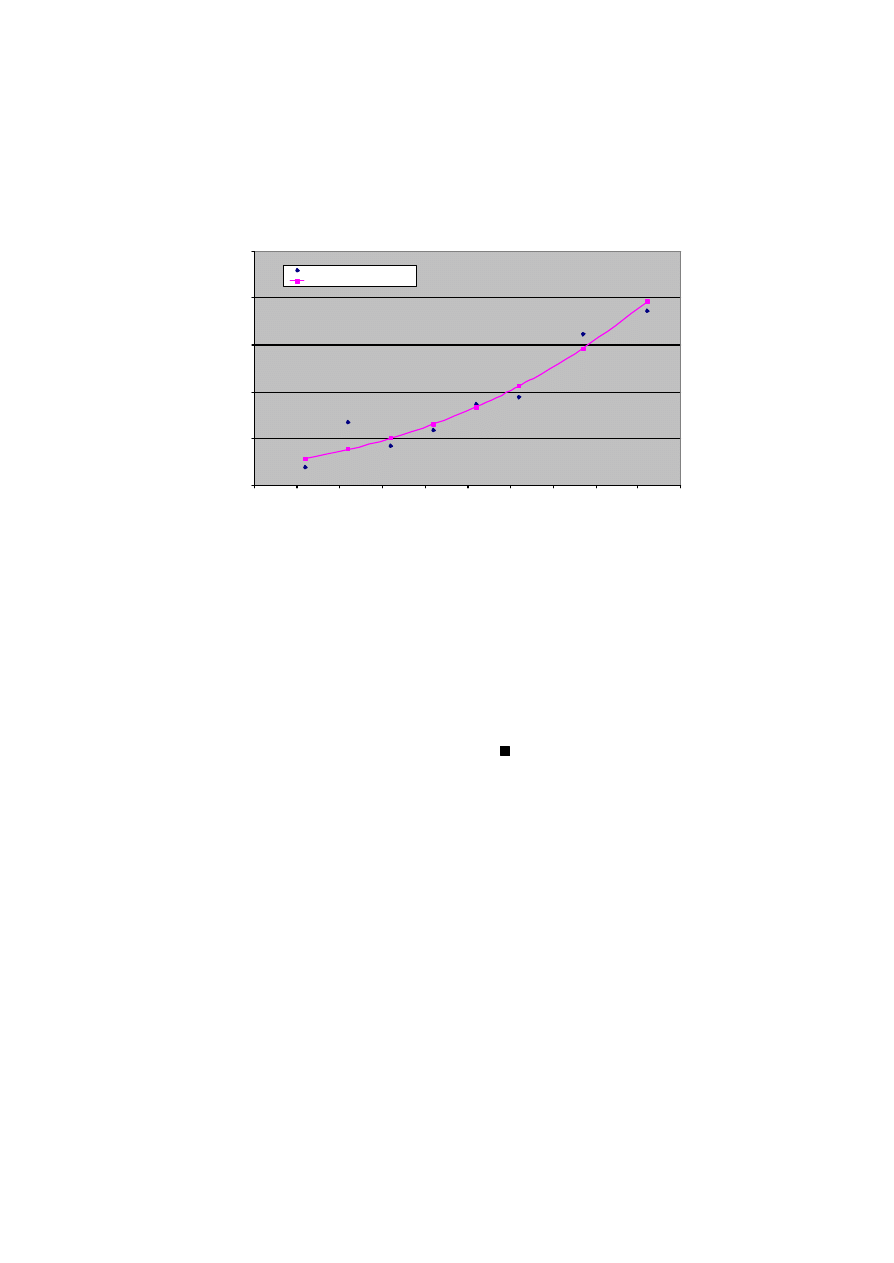
Maj ¾

ac model logitowy odwracaj ¾

ac skal ¾e mozemy narysowa´c relacj ¾e mi ¾edzy cis-

nieniem a prawdopodobie´nstwem zachorowania

REGRESJA LOGITOWA

0,000

0,050

0,100

0,150

0,200

0,250

100

110

120

130

140

150

160

170

180

190

200

CIŒNIENIE

PRAWDOPODOBIEÑSTWO

prawdopodobieñstwa rzeczywiste

prawdopodobieñstwa oszacowane

Mogliby´smy w tej sytuacji zastosowa´c regresj ¾e probitow ¾

a. Jest ona nawet

nieco lepiej dopasowana do danych (wspó÷czynnik determinacji jest równy 0:8781).

34

Modele logitowe

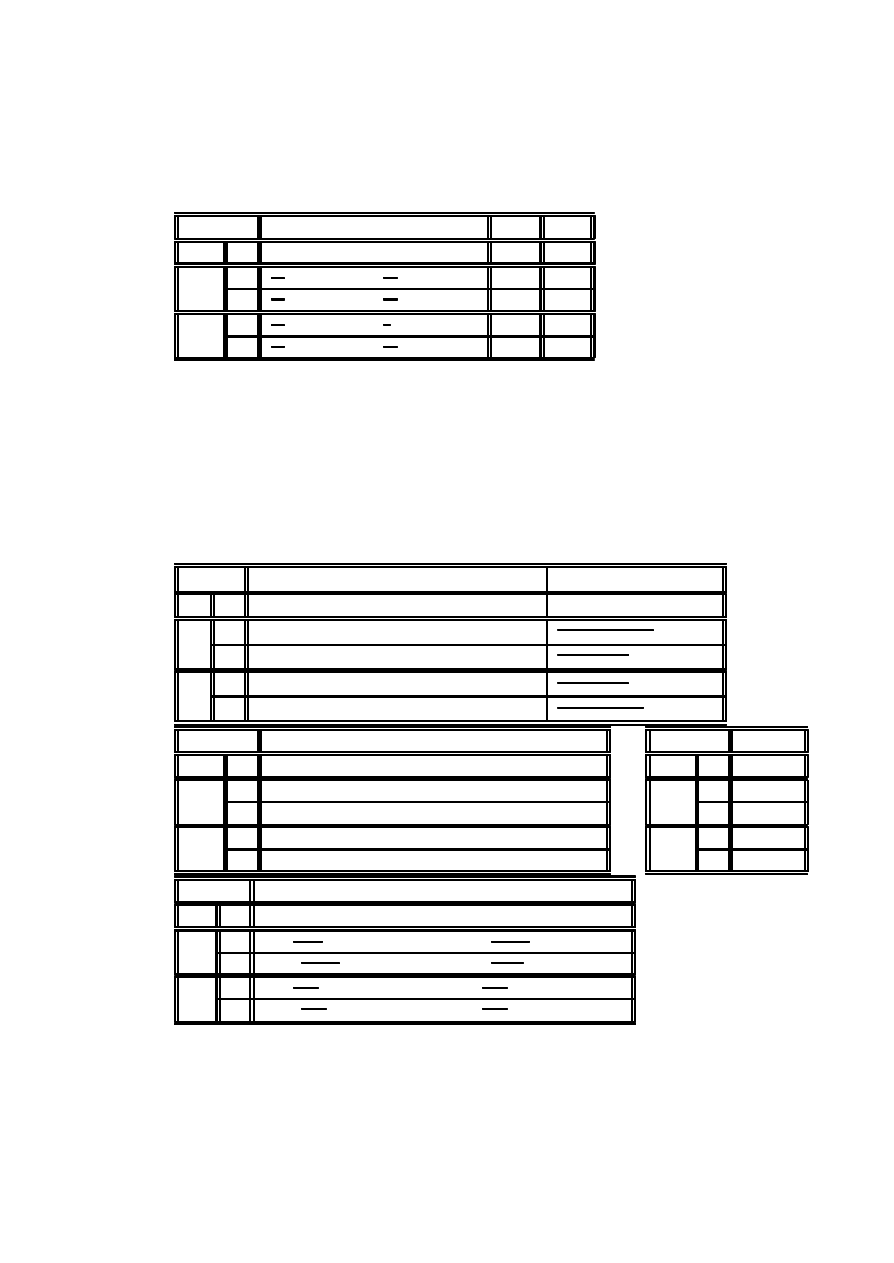
Praktyczna jednak ÷atwo´s´c wykorzystania regresji logitowej rekompensuje nieco
lepszy model probitowy. Dla ilustracji pokazemy relacj ¾e mi ¾edzy ci´snieniem a praw-
dopodobie´nstwem, uzyskanym z modelu probitowego.

REGRESJA PROBITOWA

0,000

0,050

0,100

0,150

0,200

0,250

100

110

120

130

140

150

160

170

180

190

200

CIŒNIENIE

PRAWDOPODOBIEÑSTWO

prawdopodobieñstwa rzeczywiste

prawdopodobieñstwa oszacowane

Twierdzenie 3.2 W regresji logitowej liczba stopni swobody w te´scie zgodno´sci
G

2

lub Â

2

jest równa liczbie wyst ¾epuj ¾

acych w danych logitów minus liczba parametrów

w modelu regresyjnym.

Dowód. Zgodnie z technik ¾a wyznaczania liczby stopni swobody w testach

zgodno´sci, jest ona równa liczbie wolnych parametrów w hipotezie konkurencyjnej
minus liczba wolnych parametrów w hipotezie zerowej. W naszym przypadku
w hipotezie konkurencyjnej jest tyle parametrów, ile jest logitów do oszacowa-
nia. W hipotezie zerowej, opisuj ¾acej dane za pomoc ¾a równania regresji jest tyle

parametrów, ile wyst ¾epuje w tym równaniu.

Regresja logitowa ze zmiennymi nominal-

nymi

Regresja logitowa moze znale´z´c zastosowanie równiez wtedy, gdy niektóre zmi-

enne obja´sniaj ¾ace s ¾a nominalne. Kazdej zmiennej nominalnej przyporz ¾adku-

jemy tyle zmiennych indykatorowych, ile róznych warto´sci ma dana zmienna.

Po wprowadzeniu takich zmiennych budujemy zwyk÷y model regresji logitowej

De…nicja 3.3 Niech zmienna nominalna X ma warto´sci fx

1

; x

2

; :::; x

I

g. Zmien-

nymi indykatorowymi, odpowiadaj ¾

acymi X; nazywamy zmienne liczbowe X

(1)

; X

(2)

; :::;

X

(I

¡1)

o warto´sciach f0; 1g, takie, ze X

(i)

= 1 () X = x

i

Modele logitowe

35

Przyk÷ad 3.4 (kontynuacja przyk÷adu 2.19)

Interesuje nas jak prawdopodobie´nstwo uzyskania lepszego wyniku zalezy od

p÷ci i zastosowanej terapii. Przekszta÷´cmy tabel ¾e tak, aby przygotowa´c dane do
oblicze´n

n

ij k

prawdop

lg t

P

(k)

T

(a)

P

T

p

ij

k

a

21
27

= : 778

ln

21

6

= 1: 253

1

1

p

13
32

= : 406

ln

13
19

= ¡: 379

1

0

m

a

7

14

= : 500

ln

7
7

= :000

0

1

p

1

11

= :091

ln

1

10

= ¡2: 303

0

0

Równanie regresji logitowej b ¾edzie mia÷o posta´c

lgt (p

ij

) = ® + ¯

(P)

P

(k)

ij

+ ¯

(T )

T

(a)

ij

Po zastosowaniu metody najmniejszych kwadratów otrzymamy nast ¾epuj ¾

ace esty-

matory

b

® = ¡1:9037;

d

¯

(P )

= 1:4687;

d

¯

(T )

= 1:7817

(3.1)

Z tych estymatorów mozemy oszacowa´c logity i prawdopodobie´nstwa oraz oczeki-
wane liczebno´sci

c

lgt

d

prawdop

P

T

c

p

ij

k

a

¡1:9037 + 1:4687 + 1:7817 = 1: 346 7

1

1+exp(

¡1: 346 7)

= : 794

p

¡1:9037 + 1:4687 = ¡: 435

1

1+exp(: 435)

= : 393

m

a

¡1:9037 + 1:7817 = ¡: 122

1

1+exp(: 122)

= : 470

p

¡1:9037 = ¡1: 903 7

1

1+exp(1: 903 7)

= : 130

d

n

ij k

W

P

T

z

l

k

a

27 ¡ 21: 438 = 5: 562

27 ¤ : 794 = 21: 438

p

32 ¡ 12: 576 = 19: 424 32 ¤ : 393 = 12: 576

m

a

14 ¡ 6: 58 = 7: 42

14 ¤ : 470 = 6: 58

p

11 ¡ 1: 43 = 9: 57

11 ¤ : 130 = 1: 43

n

ij k

W

P

T

z

l

k

a

6

21

p

19 13

m

a

7

7

p

10 1

G

2

W

P

T

z

l

k

a

6 ln

6

5:562

= : 454 81

21 ln

21

21: 438

= ¡: 433 49

p

19 ln

19

19: 424

= ¡: 419 34 13 ln

13

12: 57

= : 437 27

m

a

7 ln

7

7: 42

= ¡: 407 88

7 ln

7

6: 58

= : 433 13

p

10 ln

10

9: 57

= : 439 52

1 ln

1

1: 43

= ¡: 357 67

G

2

= : 292 7. Dla 1 stopni swobody (1 = 4 ¡ 3) poziom krytyczny, odpowiada-

j ¾

acy G

2

= : 292 7 wynosi 0:5885 co oznacza niez÷e dopasowanie do danych.

Parametry równania regresji 3.1 pozwalaj ¾

a odpowiedzie´c na niektóre pytania

36

Modele logitowe

² Jaki wp÷yw ma p÷e´c na prawdopodobie´nstwo wyleczenia?

Róznica logitów dla kobiet i m ¾ezczyzn przy tej samej terapii wynosi

d

¯

(P)

=

1:4687, co oznacza ze stosunek szans lepszego wyniku jest dla kobiet exp (1:4687) =
4: 3 raza wi ¾

ekszy niz dla m ¾ezczyzn

² Jaki wp÷yw ma terapia na prawdopodobie´nstwo wyleczenia?

Róznica logitów dla terapii aktywnej i placebo dla tej samej p÷ci chorego
wynosi

d

¯

(T )

= 1:7817, co oznacza ze stosunek szans lepszego wyniku jest dla

terapii aktywnej exp (1:7817) = 5: 9 raza wi ¾ekszy niz dla placebo.

Regresja logitowa ze zmiennymi porz ¾ad-

kowymi

Cz ¾esto zmienna wynikowa ma wi ¾ecej niz dwie warto´sci. Je´sli te warto´sci wys-
t ¾epuj ¾

a w skali porz ¾

adkowej, to do opisania ich zaleznosci stosuje si ¾e model pro-

porcjonalnych szans.

Model ten jest seri ¾a modeli logitowych, uporz ¾

adkowanych wed÷ug stopnia

narastania intensywno´sci cechy wynikowej. Na przyk÷ad, gdy cecha wynikowa
X ma warto

´sci ma÷y, ´sredni, duzy, olbrzymi uporz ¾adkowane to modele logitowe

by÷yby utworzone wed÷ug narastaj ¾acych poziomów dychotomicznych: ma÷y/wi ¾ecej
niz ma÷y; co najwyzej ´sredni/wi ¾ecej niz ´sredni;co najwyzej duzy/wi ¾ecej niz duzy;
mniej niz olbrzymi/olbrzymi

Proporcjonalno´s´c szans polega na tym, ze wszystkie te modele tworz ¾a równoleg÷e

hiperp÷aszczyzny regresji. Oznacza to taki sam wp÷yw zmiennych obja´sniaj ¾

a-

cych w kazdej klasie intensywno´sci cechy wynikowej. Zmiany prawdopodobie´nstw
cechy wynikowej w tych klasach s ¾

a niezalezne od cech obja´sniaj ¾acych.

Dzia÷anie modelu proporcjonalnych szans wyja´snimy na przyk÷adzie.

Przyk÷ad 3.5 (kontynuacja przyk÷adu 2.19) Przypomnimy dane:

n

ij k

W

P

T

z

u

i

k

a

6

5 16

p

19 7 6

m

a

7

2 5

p

10 0 1

Rozbijemy t ¾e tablic ¾e na dwie, zawieraj ¾

ace dychotomiczne podzia÷y zmiennej W :

z=l; ¡u=i, gdzie l oznacza wyniki lepsze (umiarkowane lub istotne), ¡u wyniki co

najwyzej umiarkowane.

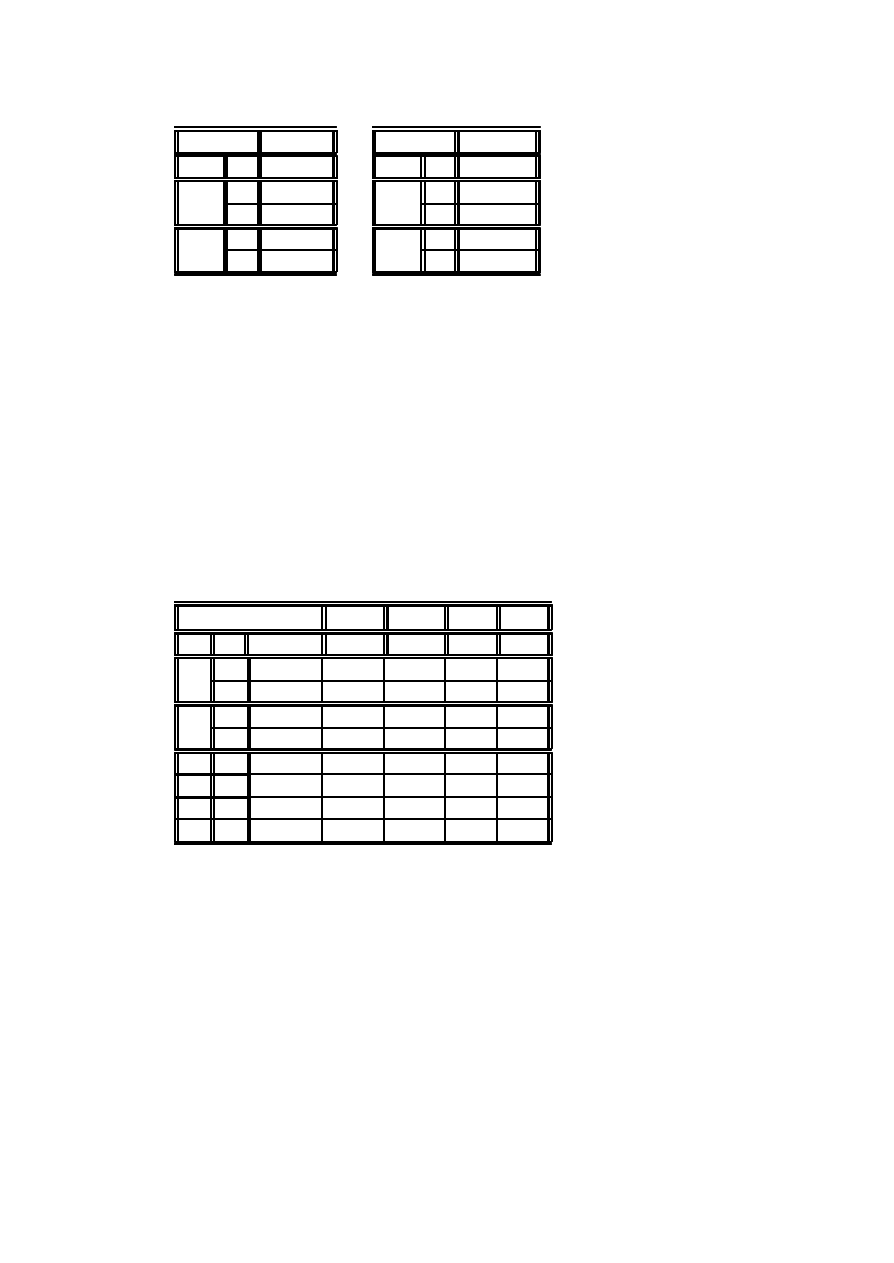
Modele logitowe

37

n

ij k

W

P

T

z

l

k

a

6

21

p

19 13

m

a

7

7

p

10 1

n

ijk

W

P

T

¡u i

k

a

11

16

p

26

6

m

a

9

5

p

10

1

Napiszemy model proporcjonalnych szans dla tych tablic

lgt

³

p

(1)
ij

´

= ®

1

+ ¯

(P )

P

(k;1)

ij

+ ¯

(T )

T

(a;1)

ij

lgt

³

p

(2)
ij

´

= ®

2

+ ¯

(P )

P

(k;2)

ij

+ ¯

(T )

T

(a;2)

ij

W tych wzorach p

(1)
ij

; p

(2)
ij

oznaczaj ¾

a prawdopodobie´nstwa odpowiednio wyniku z i

¡u w tablicach 1 i 2; P

(k;1)

ij

; P

(k;2)

ij

zmienne (indykatorowe) odpowiadaj ¾

ace p÷ci w

tablicach; T

(a;1)

ij

; T

(a;2)

ij

zmienne odpowiadaj ¾

ace terapii.

Wprowadzaj ¾

ac dwie zmienne indykatorowe C

(1)

; C

(2)

wskazuj ¾

ace na numer

tablicy mozna oba równania zapisa´c za pomoc ¾

a jednego, co umozliwia wykorzys-

tanie standardowego oprogramowania

lgt

³

p

(r)
ij

´

= ®

1

C

(1)

+ ®

2

C

(2)

+ ¯

(P)

P

(k;r)

ij

+ ¯

(T )

T

(a;r)

ij

Dane z tablicy, które umozliwiaj ¾

a estymacj ¾e modelu przyjm ¾

a teraz posta´c:

lgt

P

(k;r)

ij

T

(a;r)

ij

C

(1)

C

(2)

P

T

k

a

¡1:253 1

1

1

0

p

:379

1

0

1

0

m

a

:000

0

1

1

0

p

2:303

0

0

1

0

k

a

¡:375

1

1

0

1

p

1:466

1

0

0

1

m

a

:588

0

1

0

1

p

2:303

0

0

0

1

Parametry wyznaczone z tych danych metod ¾

a najmniejszych kwadratów s ¾

a

nast ¾epuj ¾

ace

®

1

= 1:91575; ®

2

= 2:55400; ¯

(P )

= ¡1:24425; ¯

(T )

= ¡1:87275

Model regresyjny dobrze pasuje do danych - jego wspó÷czynnik determinacji wynosi
0:9502.

Co mozna odczyta´c z danych?
Dla m ¾ezczyzn leczonych placebo, iloraz szans z÷ych do lepszych wyników wynosi

exp (1:91575) = 6:8, natomiast iloraz szans wyników co najwyzej umiarkowanych
do istotnych wynosi exp (2:55400) = 12:9: Obie te wielko´sci nalezy pomnozy´c przez
exp (¡1:24425) = : 29 gdy badan ¾

a osob ¾

a jest kobieta, a przez exp (¡1:87275) = :

38

Modele logitowe

15 gdy zastosowano terapi

¾e aktywn ¾

a. Na przyk÷ad, gdy zastosuje si ¾e terapi ¾e akty-

wn ¾

a u m ¾ezczyzn to iloraz szans z÷ych do lepszych wyników wynosi 6:8 ¤ : 15 = 1: 0

natomiast iloraz szans wyników co najwyzej umiarkowanych do istotnych wynosi
2:9 ¤ : 15 = 1: 9, co jak wida´c dobrze ´swiadczy o zastosowanej terapii. Dla kobiet,

leczonych aktywnie, te wyniki s ¾

a jeszcze lepsze: w pierwszym przypadku wynosz ¾

a

1: 0 ¤ : 29 = :29 a w drugim 1: 9 ¤ : 29 = : 55 co wskazuje na przewag ¾e praw-

dopodobie´nstwa wyników lepszych nad gorszymi na kazdym poziomie oczekiwa´n.

Rozdzia÷ 4

Modele logarytmiczno-liniowe

39

40

Modele logarytmiczno-liniowe

W poprzednich rozdzia÷ach rozwazali´smy sytuacje, w których interesowa÷a

nas zalezno´s´c czy niezalezno´s´c pary cech. Jezeli do pary cech do÷ ¾aczy trzecia,
to powstaje uk÷ad, który jest bardziej skomplikowany, niz by to si ¾e z pozoru
wydawa÷o. Jednym z przejawów tej komplikacji jest tzw paradoks Simpsona

1

.

Paradoks ten polega na tym, ze dla trzech zdarze´n A; B;C jest mozliwy uk÷ad

nierówno´sci

P (A jB \ C ) < P (A jB

c

\ C ) ; P (A jB \ C

c

) < P (A jB

c

\ C

c

)

ale P (A jB ) > P (A jB

c

)

Paradoks ten ostrzega nas, ze w rozwazaniu relacji zdarze´n nie wystarczy

udowodni´c, ze dana relacja zachodzi dla wszystkich przypadków (tu C i C

c

).

Konkluzja, jak wida´c moze by´c inna.

Przyk÷ad 4.1 (Paradoks Simpsona) (zród÷o:[1] str.136)

Obro´nca O…ara

Kara

´smierci

Tak

Nie

Bia÷y

Bia÷y

19

132

Murzyn

0

9

Murzyn

Bia÷y

11

52

Murzyn

6

97

Tabela 4.1 Kara ´smierci i rasa

Niech A=”orzeczono kar ¾e ´smierci”, B=”Obro´nca jest Bia÷y”, C=”O…ar ¾

a jest

Bia÷y”. ×atwo obliczy´c odpowiednie prawdopodobie´nstwa

P (A jB ) =

19

160

= : 119; P (A jB

c

) =

17

166

= : 102 ; P (A jB ) > P (A jB

c

)

P (A jB \ C ) =

19

151

= : 126; P (A jB

c

\ C ) =

11
63

= : 175;

P (A jB \ C

c

) =

0
9

= 0; P (A jB

c

\ C

c

) =

6

103

= : 059;

P (A jB \ C ) < P (A jB

c

\ C ) ; P (A jB \ C

c

) < P (A jB

c

\ C

c

)

De…nicja 4.2 Dana jest tablica wyników obserwacji trzech cech X; Y; Z:

Niech p

ijk

= P (X = x

i

; Y = y

j

; Z = z

k

), oraz niech m

ijk

= n p

ijk

(m

ijk

jest

oczekiwan ¾

a liczb ¾

a obserwacji w komórce tabeli)

De…nicja 4.3 (Model logarytmiczno-liniowy) Modelem logarytmiczno-liniowym
nazywamy taki, w którym

ln m

ijk

= ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XZ
ik

+ ¸

XY
ij

+ ¸

Y Z
jk

+ ¸

X Y Z
ijk

(4.1)

1

Nazwa tego paradoksu pochodzi od artyku÷u, opublikowanego przez E.H. Simpsona w 1951,

cho´c zjawisko to by÷o znane wcze´sniej, np by÷o omawiane przez Yule’a w 1903.

Modele logarytmiczno-liniowe

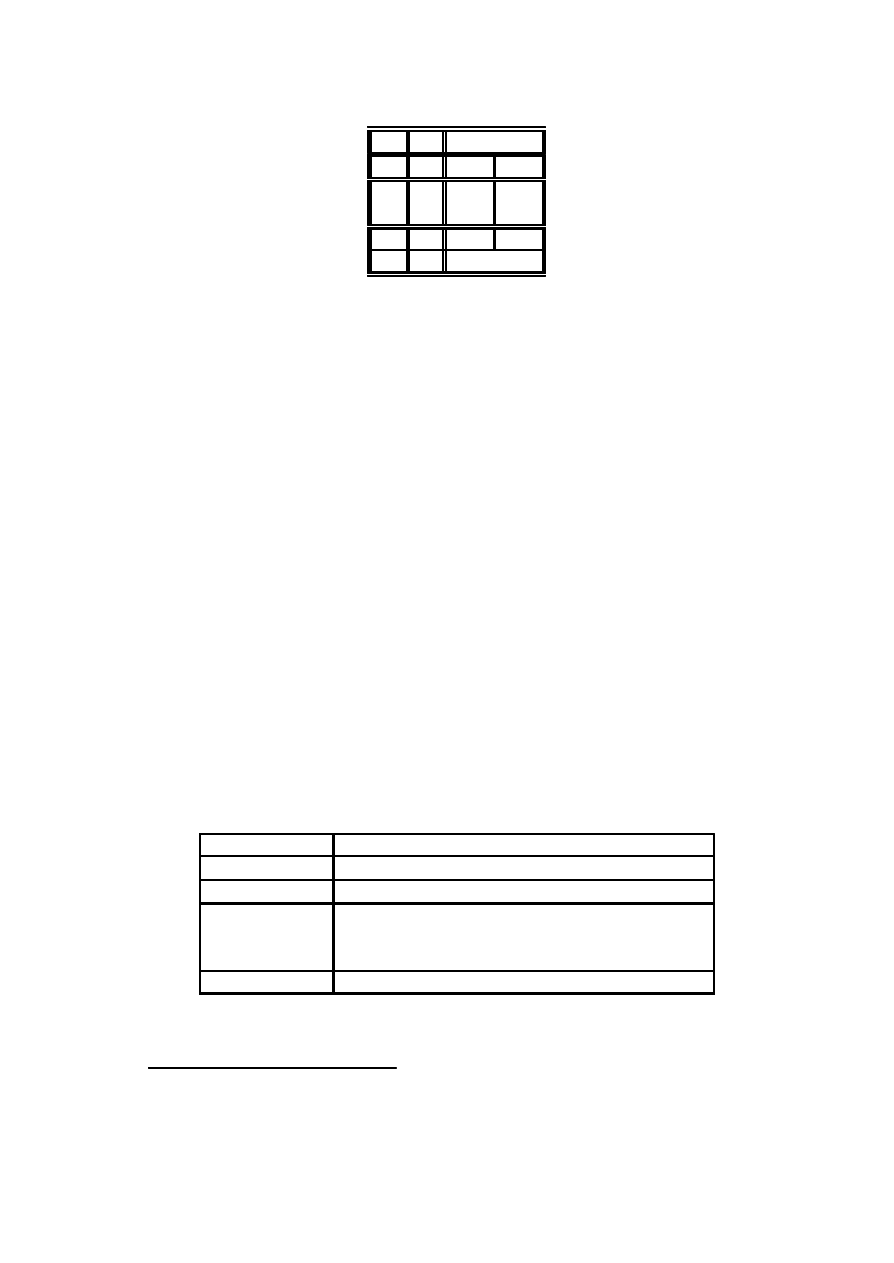
41

X

Y

Z
z

1

z

2

x

1

y

1

n

111

n

112

y

2

n

121

n

122

x

2

y

1

n

211

n

212

y

2

n

221

n

222

Tabela 4.2 Tablica wyników obserwacji

oraz

X

i

¸

X
i

= 0;

X

j

¸

Y
j

= 0;

X

k

¸

Z
k

= 0;

(4.2)

X

i

¸

XY

ij

= 0;

X

j

¸

XY

ij

= 0;

X

j

¸

Y Z
j k

= 0;

X

k

¸

Y Z
jk

= 0;

X

i

¸

XZ
ik

= 0;

X

k

¸

XZ
ik

= 0;

X

i

¸

XY Z

ijk

= 0;

X

j

¸

XY Z

ijk

= 0;

X

k

¸

XY Z

ijk

= 0;

Wielko´sci ¸

X
i

; ¸

Y
j

; ¸

Z
k

nazywamy efektami g÷ównymi, ¸

XZ
ik

; ¸

XY
ij

; ¸

Y Z
jk

efektami in-

terakcji ( interakcjami) rz ¾edu 2, ¸

XY Z
ijk

efektami interakcji ( interakcjami) rz ¾edu

3.

Zapis ln m

ijk

w postaci równa´n 4.1 i 4.2 nazywamy zapisem bilansowym. Zapis

bilansowy jest uk÷adem równa´n liniowych.

Twierdzenie 4.4 Dla kazdego uk÷adu fm

ijk

g istnieje dok÷adnie jeden zapis bi-

lansowy.

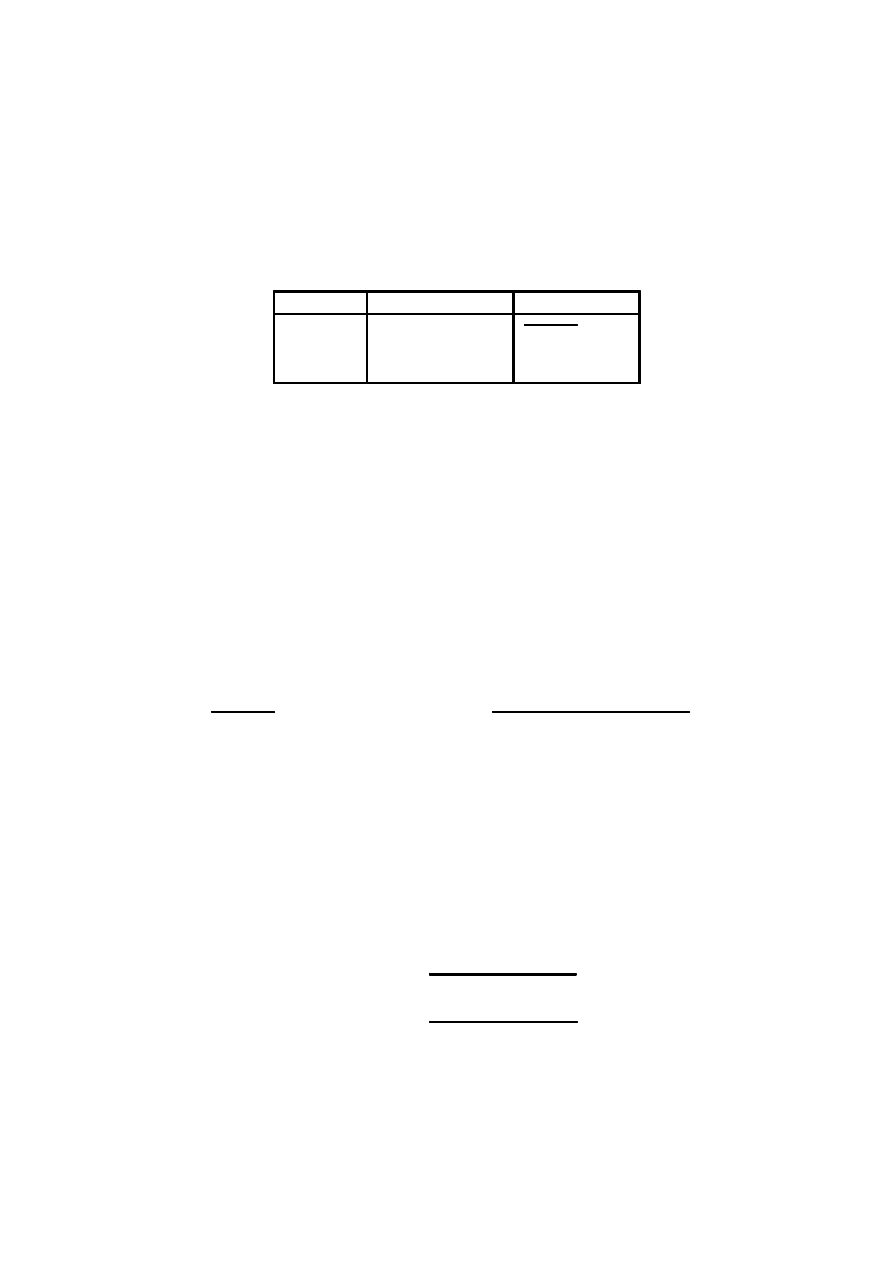
De…nicja 4.5 Rozróznia si ¾e modele logarytmiczno-liniowe:

Model

ln m

ijk

[XY Z]

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XZ
ik

+ ¸

XY
ij

+ ¸

Y Z
j k

+ ¸

XY Z
ijk

[XZ][X Y ][Y Z]

¹ + ¸

X

i

+ ¸

Y

j

+ ¸

Z

k

+ ¸

XY

ij

+ ¸

XZ

ik

+ ¸

Y Z

j k

[XZ][Y Z]

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XZ
ik

+ ¸

Y Z
jk

[XY ][Z]

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

[X][Y ][Z]

¹ + ¸

X

i

+ ¸

Y

j

+ ¸

Z

k

[]

¹

Tabela 4.3 Modele logarytmiczno-liniowe

Model [XY Z] nazywa si ¾e modelem nasyconym, model [] - sta÷ym

2

.

2

W modelu sta÷ym wszystkie prawdopodobie´nstwa p

ijk

s ¾

a równe.

42

Modele logarytmiczno-liniowe

Modele logarytmiczno liniowe, w przeciwie´nstwie do modeli logitowych, nie

wyrózniaj ¾a zadnej z cech. Ich zadaniem jest stworzenie jak najprostszego modelu,
obja´sniaj ¾acego zwi ¾azki mi ¾edzy wyst ¾epuj ¾

acymi cechami.

Twierdzenie 4.6 Rózne modele logarytmiczno-liniowe reprezentuj ¾

a rózne typy

zalezno´sci mi ¾edzy cechami

Model

Typ zalezno´sci p

ijk

[XZ][Y Z] X?Y jZ

p

i+k

p

+jk

p

++k

[XY ][Z]

(X; Y ) ?Z

p

ij+

p

++k

[X][Y ][Z]

X?Y ?Z

p

i++

p

+j +

p

++k

Tabela 4.4 Modele zalezno´sci

Dowód. [XZ][Y Z] :

ln m

ijk

= ¹ + ¸

X

i

+ ¸

Y

j

+ ¸

Z

k

+ ¸

XZ

ik

+ ¸

Y Z

jk

()

n p

ijk

= ® ¯

X
i

¯

Y
j

¯

Z
k

¯

XZ
ik

¯

Y Z
jk

np

i+k

= ® ¯

X
i

¯

Z
k

¯

XZ
ik

X

j

¯

Y
j

¯

Y Z
jk

;

np

+jk

= ®¯

Y
j

¯

Z
k

¯

Y Z
jk

X

i

¯

X
i

¯

XZ
ik

;

np

++k

= ®¯

Z
k

X

j

¯

Y
j

¯

Y Z
jk

X

i

¯

X
i

¯

X Z
ik

;

n

p

i+k

p

+jk

p

++k

= ® ¯

X
i

¯

Z
k

¯

XZ
ik

X

j

¯

Y
j

¯

Y Z
jk

®¯

Y
j

¯

Z
k

¯

Y Z
jk

P

i

¯

X
i

¯

XZ
ik

®¯

Z
k

P

j

¯

Y
j

¯

Y Z
jk

P

i

¯

X
i

¯

XZ
ik

=

= ® ¯

X

i

¯

Y

j

¯

Z

k

¯

XZ

ik

¯

Y Z

jk

= n p

ijk

[XY ][Z] :

ln m

ijk

= ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

() n p

ijk

= ® ¯

X
i

¯

Y
j

¯

Z
k

¯

XY
ij

n p

ij +

= ® ¯

X
i

¯

Y
j

¯

Z
+

¯

XY
ij

; n p

++k

= ® ¯

Z
k

X

ij

¯

X
i

¯

Y
j

¯

XY
ij

;

n = n p

+++

= ® ¯

Z
+

X

ij

¯

X
i

¯

Y
j

¯

X Y
ij

n p

ij+

p

++k

= ® ¯

X
i

¯

Y
j

¯

Z
+

¯

XY
ij

® ¯

Z
k

P

ij

¯

X
i

¯

Y
j

¯

XY
ij

n

=

= ® ¯

X
i

¯

Y
j

¯

Z
+

¯

XY
ij

® ¯

Z
k

P

ij

¯

X
i

¯

Y
j

¯

XY
ij

® ¯

Z
+

P

ij

¯

X
i

¯

Y
j

¯

XY
ij

= n p

ijk

[X][Y ][Z] :

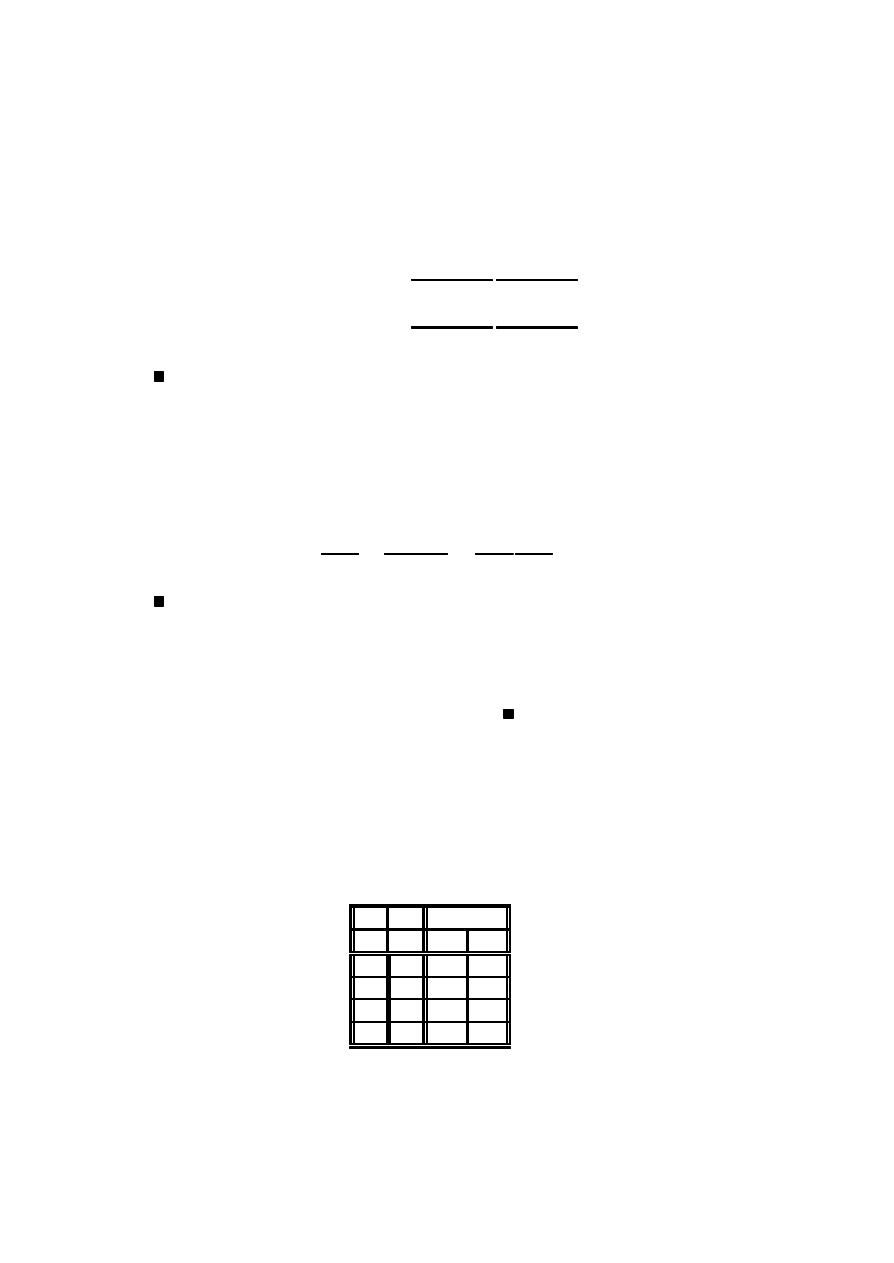
Modele logarytmiczno-liniowe

43

ln m

ij k

= ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

() n p

ijk

= ® ¯

X
i

¯

Y
j

¯

Z
k

n p

i++

= ® ¯

X
i

¯

Y
+

¯

Z
+

; n p

+j+

= ® ¯

X
+

¯

Y
j

¯

Z
+

; n p

++k

= ® ¯

X
+

¯

Y
+

¯

Z
k

n = n p

+++

= ® ¯

X
+

¯

Y
+

¯

Z
+

n p

i++

p

+j+

p

++k

= ® ¯

X
i

¯

Y
+

¯

Z
+

® ¯

X
+

¯

Y
j

¯

Z
+

n

® ¯

X
+

¯

Y
+

¯

Z
k

n

=

= ® ¯

X
i

¯

Y
+

¯

Z
+

® ¯

X

+

¯

Y

j

¯

Z

+

® ¯

X
+

¯

Y
+

¯

Z
+

® ¯

X

+

¯

Y

+

¯

Z

k

® ¯

X
+

¯

Y
+

¯

Z
+

= ® ¯

X
i

¯

Y
j

¯

Z
k

= n p

ijk

Wniosek 4.7 W modelu [XZ][Y Z] cechy X i Y s ¾

a niezalezne warunkowo, to

znaczy

p

ij

jk

= p

i+

jk

p

+j

jk

Dowód.

p

ij

jk

=

p

ijk

p

++k

=

p

i+k

p

+jk

(p

++k

)

2

=

p

i+k

p

++k

p

+jk

p

++k

= p

i+

jk

p

+j

jk

Wniosek 4.8 W modelu [XY ][Z] zachodz ¾

a relacje: X?Z; Y ?Z

Dowód. p

i+k

=

P

j

p

ijk

=

P

j

p

ij+

p

++k

= p

i++

p

++k

. Podobnie,

p

+jk

=

P

i

p

ijk

=

P

i

p

ij+

p

++k

= p

+j +

p

++k

Uwaga 4.9 Relacja Y ?Z jX nie implikuje relacji Y ?Z

Dowód. Dla dowodu wystarczy poda´c przyk÷ad .
Tablica przedstawia prawdopodobie´nstwa dla uk÷adu trzech cech:
X wykszta÷cenie {s -

´scis÷e, h - humanistyczne},

Y p÷e

´c {k - kobieta, m -m ¾ezczyzna}

Z zarobki {w - wysokie, n - niskie}

X

Y

Z
w

n

s

k

:08 :02

m

:32 :08

h

k

:12 :18

m

:08 :12

Y ?Z jX = s gdyz w tym przypadku tablica prawdopodobie´nstw sprowadza

si ¾e do tablicy

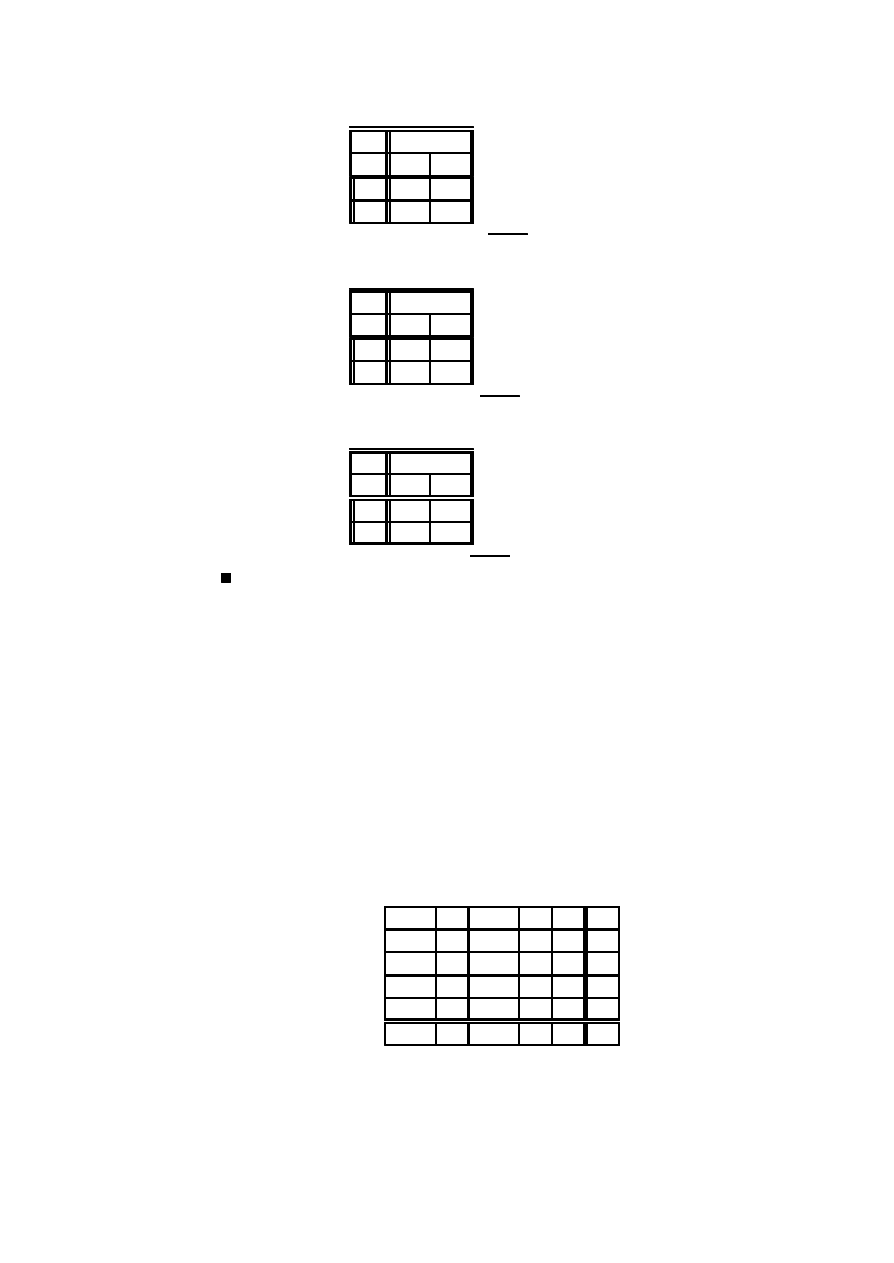
44

Modele logarytmiczno-liniowe

Y

Z
w

n

k

:16 :04

m

:64 :16

,

dla której iloraz krzyzowy wynosi µ =

:16

¤:16

:64

¤:04

= 1 co oznacza niezalezno´s´c.

Podobnie,

Y ?Z jX = h. W tym przypadku tablica prawdopodobie´nstw ma posta´c

Y

Z
w

n

k

:24 :36

m

:16 :24

’

dla której iloraz krzyzowy wynosi µ =

:24

¤:24

:16

¤:36

= 1 co równiez oznacza nieza-

lezno´s´c. Natomiast tabela prawdopodobie´nstw dla pary cech (Y; Z), gdy nie
znamy warto´sci X przedstawia si ¾e nast ¾epuj ¾aco:

Y

Z
w

n

k

:20 :20

m

:40 :20

,

dla której iloraz krzyzowy wynosi µ =

:20

¤:20

:40

¤:20

= :50; co oznacza, ze te cechy s

¾a

zalezne.

Lemat 4.10 Stopnie swobody dla modeli prostych:

P

1

: ln (m

ij k

) = ¹;

P

2

: ln (m

ij k

) = ¸

X
i

;

P

3

: ln (m

ij k

) = ¸

XY

ij

;

P

4

: ln (m

ij k

) = ¸

XY Z
ij k

wynosz ¾

a odpowiednio: 1; I ¡ 1; (I ¡ 1) (J ¡ 1) ; (I ¡ 1)(J ¡ 1)(K ¡ 1)

Dowód. Liczba wolnych parametrów w modelu P

1

wynosi 1; gdyz w tym

przypadku nie ma zadnych ogranicze´n na warto´s´c ¹:

W modelu P

2

liczba wolnych parametrów wynosi I ¡ 1 gdyz mamy jedno

ograniczenie

P

I

i=1

¸

X
i

= 0:

W modelu P

3

liczba wolnych parametrów moze by´c wyznaczona z tabeli

¸

XY
11

... ¸

XY
1j

... *

0

...

... ...

... ...

...

¸

XY
i1

... ¸

XY
ij

... *

0

...

... ...

... ...

...

*

*

*

... *

0

0

... 0

... 0

0

pami ¾etaj ¾ac, ze suma ¸

XY
ij

w wierszach i kolumnach jest równa 0, sk ¾

ad wynika,

ze wystarczy wype÷ni´c pola w miejscach nie zaznaczonych *. Pola z * musz ¾a byc

Modele logarytmiczno-liniowe

45

wype÷nione tak ¾a warto´sci ¾a, aby suma warto´sci ¸

XY
ij

w wierszach i kolumnach by÷a

równa 0. Takich pól jest (I ¡ 1) (J ¡ 1) :

Podobnie w modelu P

4

, tylko w tym przypadku mamy tablic ¾e trójwymiarow ¾a,

z ostatnimi wierszami/kolumnami/warstwami wype÷nionymi *, st ¾

ad liczba stopni

swobody równa (I ¡ 1) (J ¡ 1) (K ¡ 1).

Twierdzenie 4.11 Estymatory najwi ¾ekszej wiarygodno´sci dla liczby obserwacji
w polach tablic wielodzielczych, odpowiadaj ¾

acych efektom w modelu M o rozk÷adzie

wielomianowym lub Poissona s ¾

a równe obserwowanej liczbie obserwacji dla efek-

tów. Estymatory te s ¾

a wyznaczone jednoznacznie.

Dowód. Dowód przeprowadzimy na przyk÷adzie rozk÷adu wielomianowego i

modelu [XY ][Y Z]. Dowód w kazdym innym przypadku jest analogiczny. Nasz
model oznacza zachodzenie równo´sci

ln m

ijk

= ln (np

ijk

) = ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

Y Z
j k

Funkcja logarytmu wiarygodno´sci w rozk÷adzie wielomianowym z dok÷adno´s-

ci ¾a do sta÷ych ma posta´c

X

ijk

n

ijk

ln p

ijk

co, z dok÷adno´sci ¾a do sta÷ych jest równe

X

ij k

n

ijk

ln np

ijk

=

X

ijk

n

ijk

³

¹ + ¸

X

i

+ ¸

Y

j

+ ¸

Z

k

+ ¸

XY

ij

+ ¸

Y Z

jk

´

W zagadnieniu estymacji nalezy obliczy´c maksimum powyzszej funkcji przy ograniczeni-
ach

1 =

X

ijk

p

ijk

=

1

n

X

ijk

m

ijk

;

X

i

¸

X

i

= 0;

X

j

¸

Y

j

= 0;

X

k

¸

Z

k

= 0;

X

i

¸

X Y
ij

= 0;

X

j

¸

XY
ij

= 0;

X

j

¸

Y Z
jk

= 0;

X

k

¸

Y Z
jk

= 0

Potraktujemym

ijk

jako funkcj ¾e zmiennych ¹; ¸

X
i

; ¸

Y
j

; ¸

Z
k

; ¸

XY
ij

; ¸

Y Z
jk

. Niech u

b ¾edzie jedn ¾a z tych zmiennych. Wtedy

@m

ijk

@u

=

@ exp

³

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

Y Z
j k

´

@u

=

m

ijk

@

³

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

Y Z
j k

´

@u

Wyrazenie

@

(

¹+¸

X

i

+¸

Y

j

+¸

Z
k

+¸

XY

ij

+¸

Y Z
j k

)

@u

jest równe 1 lub 0 w zalezno´sci od tego,

czy u wyst ¾epuje, czy tez nie wyst ¾epuje w´sród ¹; ¸

X
i

; ¸

Y
j

; ¸

Z
k

; ¸

XY
ij

; ¸

Y Z
jk

:

46

Modele logarytmiczno-liniowe

Uzywaj ¾ac metody mnozników Lagrange’a nalezy znale´z´c maksimum funkcji

F =

X

ijk

n

ijk

³

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

Y Z
jk

´

+

+®

X

ijk

m

ijk

+

+¯

X
1

X

i

¸

X
i

+ ¯

Y
1

X

j

¸

Y
j

+ ¯

Z
1

X

k

¸

Z
k

+

+

X

j

¯

2j

X

i

¸

XY
ij

+

X

i

¯

3i

X

j

¸

XY
ij

+

+

X

k

¯

4k

X

j

¸

Y Z
jk

+

X

j

¯

5j

X

k

¸

Y Z
jk

Obliczamy pochodne wzgl ¾edem nieznanych parametrów i przyrównamy je do

0

0 =

@F

@¹

=

=

X

ij k

n

ijk

+ ®

X

ij k

m

ijk

=

= n + ®

X

ijk

(np

ijk

) = n (® + 1) =) ® = ¡1

Dla ¸

X
i

0 =

@ F

@¸

X

i

=

=

X

jk

n

ijk

+ ®

X

ijk

m

ij k

+ ¯

X

1

=

= n

i++

¡ m

i++

+ ¯

X

1

Dodaj ¾ac stronami po i powyzsz ¾a równo´s´c, otrzymamy

0

=

X

i

³

n

i++

¡ m

i++

+ ¯

X
1

´

= n ¡

X

i

(np

i++

) + n¯

X
1

= n¯

X
1

=) ¯

X
1

= 0

St ¾ad otrzymamy, ze dla efektu ¸

X

i

zachodzi równo´sc

3

d

n

i++

= n

i++

:

Podobnie,dla efektu ¸

Y
j

zachodzi równo´sc

d

n

+j +

= n

+j+

;dla efektu ¸

Z
k

zachodzi

równo´sc

d

n

++k

= n

++k

Analogiczne rachunki przeprowadzimy dla efektu ¸

XY
ij

0 =

@F

@¸

XY

ij

=

X

k

n

ijk

+ ®

X

k

m

ijk

+ ¯

2j

+ ¯

3i

=

(4.3)

= n

ij+

¡ m

ij+

+ ¯

2j

+ ¯

3i

3

Zawsze symbolem bµ oznacza´c b ¾edziemy estymator parametru µ, uzyskany z maksymali-

zowania funkcji wiarygodno´sci

Modele logarytmiczno-liniowe

47

Sumuj ¾ac jak powyzej, najpierw po i, potem po j otrzymamy

0 = n

+j+

¡ m

+j+

+ I ¯

2j

+ ¯

3+

= I¯

2j

+ ¯

3+

;

(4.4)

0 = n

i++

¡ m

i++

+ ¯

2+

+ J¯

3i

= ¯

2+

+ J¯

3i

Sumuj ¾ac teraz najpierw po j, potem po i otrzymamy

0 = I¯

2+

+ J¯

3+

;

(4.5)

Z równa´n 4.4 mnozonych: pierwsze przez J, drugie przez I oraz dodanych

stronami uzyskamy

IJ

³

¯

3i

+ ¯

2j

´

+ I¯

2+

+ J ¯

3+

= 0;

co w po÷ ¾aczeniu z 4.5 daje, ze ¯

2j

+ ¯

3i

= 0 oraz, ze w 4.3 zachodzi równo

´s´c

d

n

ij +

= n

ij+

:

W analogiczny sposób mozna pokaza´c, ze dla efektu ¸

Y Z
jk

,

d

n

+j k

= n

+j k

Wniosek 4.12 W modelu nasyconym estymatory najwi ¾ekszej wiarygodno´sci

d

n

ijk

spe÷niaj ¾

a równo´s´c

b

n

ijk

= n

ijk

dla kazdego i; j; k:

Wniosek 4.13 Zachodz ¾

a nast ¾epuj ¾

ace implikacje:

8

i;j;k

(

b

n

ijk

= n

ijk

) =) 8

i;j

b

n

ij+

= n

ij +;

8

i;k

b

n

i+k

= n

i+k

; 8

j;k

b

n

+jk

= n

+jk

; =)

=) 8

i

b

n

i++

= n

i++;

8

j

b

n

+j+

= n

+j+;

8

k

b

n

++k

= n

++k;

=)

=)

b

n

+++

= n

+++;

Dowód. Oczywisty

Modele hierarchiczne

Niech M

1

b ¾edzie danym modelem logarytmiczno liniowym.

De…nicja 4.14 Model M

2

nazwiemy hierarchicznie podporz ¾

adkowanym modelowi

M

1

(w skrócie - podporz ¾

adkowanym M

1

; M

2

Á M

1

) gdy zbiór efektów w modelu

M

2

jest podzbiorem zbioru efektów M

1

.

De…nicja 4.15 Odchyleniem modelu M

2

od M

1

nazywamy liczb ¾e

G

2

(M

2

jM

1

) = 2

X

i

X

j

X

k

b

n

(1)
ij k

ln

b

n

(1)
ij k

b

n

(2)
ij k

;

gdzie

b

n

(r)
ijk

jest estymatorem najwi ¾ekszej wiarygodno´sci n

ijk

w modelu M

r

(r = 1; 2).

48

Modele logarytmiczno-liniowe

Zauwazmy, ze odchylenie danych od modelu logarytmiczno-liniowego jest równe

odchyleniem tego modelu od modelu nasyconego.

Twierdzenie 4.16 Gdy model M

1

jest prawdziwy to

G

2

(M

2

jM

1

) = G

2

(M

2

) ¡ G

2

(M

1

)

Co wi ¾ecej,

DF

³

G

2

(M

2

jM

1

)

´

= DF

³

G

2

(M

2

)

´

¡ DF

³

G

2

(M

1

)

´

Wniosek 4.17 Jezeli dany jest ci ¾

ag hierarchicznie podporz ¾

adkowanych modeli

M

0

 M

1

 :::  M

k

¡1

 M

k

gdzie M

0

jest modelem nasyconym oraz modele M

0

; M

1

; :::; M

k

¡1

s ¾

a prawdziwe, to

zachodzi wzór

G

2

(M

k

) =

k

X

r=1

G

2

(M

r

jM

r

¡1

)

z liczb ¾

a stopni swobody równ ¾

a

DF

³

G

2

(M

k

)

´

=

k

X

r=1

DF

³

G

2

(M

r

jM

r

¡1

)

´

Dowód twierdzenia. Dowód przeprowadzimy w szczególnym przypadku,

gdy

ln

³

m

(1)
ijk

´

= ¹ + ¸

X

i

+ ¸

Y

j

+ ¸

X Y

ij

+ ¸

XZ

ik

;

ln

³

m

(2)
ijk

´

= ¹ + ¸

Y
j

+ ¸

XZ
ik

Wtedy

G

2

(M

2

jM

1

) = 2

X

i;j;k

b

n

(1)
ij k

ln

b

n

(1)
ij k

b

n

(2)
ij k

(4.6)

= 2

X

i;j;k

b

n

(1)
ij k

³³

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

XY
ij

+ ¸

XZ
ik

´

¡

³

¹ + ¸

Y
j

+ ¸

XZ
ik

´´

= 2

X

i;j;k

b

n

(1)
ij k

³

¸

X
i

+ ¸

XY
ij

´

= 2

X

i

b

n

(1)
i++

¸

X
i

+ 2

X

i;j

b

n

(1)
ij+

¸

XY
ij

:

Z twierdzenia 4.11 wynika, ze gdy model M

1

jest prawdziwy to estymatory na-

jwi ¾ekszej wiarygodno´sci dla liczby obserwacji, odpowiadaj ¾acych efektom ¸

X

i

oraz

¸

X Y
ij

s ¾a równe obserwowanej liczbie obserwacji. St ¾

ad

b

n

(1)
i++

= n

i++

oraz

b

n

(1)
ij+

= n

ij+

dla dowolnych i; j.

Modele logarytmiczno-liniowe

49

Wstawiaj ¾ac ostatnie równo´sci do wzoru 4.6 i zwijaj ¾ac ten wzór od ty÷u, otrzy-

mamy

2

X

i

b

n

(1)
i++

¸

X
i

+ 2

X

i;j

b

n

(1)
ij+

¸

XY
ij

= 2

X

i

n

i++

¸

X
i

+ 2

X

i;j

n

ij+

¸

XY
ij

= 2

X

i;j;k

n

ij k

³³

¹ + ¸

X
i

+ ¸

Y
j

+ ¸

XY
ij

+ ¸

XZ
ik

´

¡

³

¹ + ¸

Y
j

+ ¸

XZ
ik

´´

= 2

X

i;j;k

n

ij k

ln

n

ijk

b

n

(2)
ijk

¡ 2

X

i;j;k

n

ijk

ln

n

ijk

b

n

(1)
ijk

= G

2

(M

2

) ¡ G

2

(M

1

) :

Liczba stopni swobody w modelu M

2

jM

1

jest równa (patrz Lemat 4.10) (I ¡

1) + (I ¡ 1)(J ¡ 1), czyli róznicy

1 + (I ¡ 1) + (J ¡ 1) + (I ¡ 1)(J ¡ 1) + (I ¡ 1)(K ¡ 1)

i

1 + (J ¡ 1) + (I ¡ 1)(K ¡ 1)

co dowodzi drugiej cz ¾e´sci tezy twierdzenia.
Dowód w kazdym innym przypadku jest analogiczny.

Twierdzenie 4.18 Utwórzmy ci ¾

ag hierarchicznie podporz ¾

adkowanych modeli:

M

0

: [XY Z]

M

1

: [XY ][XZ][Y Z]

M

2

: [XY ][Y Z]

M

3

: [XY ][Z]

M

4

: [X][Y ][Z]

Wtedy

DF (M

1

jM

0

) = (I ¡ 1) (J ¡ 1) (K ¡ 1)

DF (M

2

jM

1

) = (I ¡ 1) (K ¡ 1)

DF (M

3

jM

2

) = (J ¡ 1) (K ¡ 1)

DF (M

4

jM

3

) = (I ¡ 1) (J ¡ 1)

gdzie I; J; K jest liczb ¾

a róznych warto´sci cech X; Y; Z:

Dowód. Model M

0

(nasycony) jest postaci [XY Z], co oznacza, ze

ln

³

m

(0)
ijk

´

= ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

X Z
ik

+ ¸

Y Z
jk

+ ¸

X Y Z
ijk

50

Modele logarytmiczno-liniowe

Model M

1

postaci [XY ][XZ][Y Z] ma posta´c:

ln

³

m

(1)
ij k

´

= ¹ + ¸

X
i

+ ¸

Y
j

+ ¸

Z
k

+ ¸

XY
ij

+ ¸

XZ
ik

+ ¸

Y Z
jk

Odchylenie G

2

(M

1

jM

0

) jest statystyk

¾

a testow ¾a w uk÷adzie hipotez:

H

0

:

prawdziwy jest model M

1

;

H

1

:

prawdziwy jest model M

0

Liczba stopni swobody dla takiego uk÷adu hipotez jest róznic ¾

a DF (H

1

) ¡

DF (H

0

).

Liczba stopni swobody modelu M

0

wynosi

1 + I ¡ 1 + J ¡ 1 + K ¡ 1 + (I ¡ 1)(J ¡ 1) + (I ¡ 1)(K ¡ 1) + (J ¡ 1)(K ¡ 1)
+(I ¡ 1)(J ¡ 1)(K ¡ 1)

Podobnie, liczba stopni swobody modelu M

1

wynosi

1 + I ¡ 1 + J ¡ 1 + K ¡ 1 + (I ¡ 1)(J ¡ 1) + (I ¡ 1)(K ¡ 1) + (J ¡ 1)(K ¡ 1):

Jak ÷atwo zobaczy´c, róznica tych liczb wynosi (I ¡ 1)(J ¡ 1)(K ¡ 1), czyli

jest liczb ¾a stopni swobody prostego modelu ¸

XY Z
ij k

, który wyst ¾epuje w M

0

a nie

wyst ¾epuje w M

1

. W podobny sposób mozna uzasadni´c pozosta÷e wzory w tezie

twierdzenia.

Uwaga 4.19 (praktyczna) Liczba stopni swobody w modelu warunkowym M

r+1

jM

r

jest

liczb ¾

a stopni swobody w modelu prostym, który wyst ¾epuje w M

r

a nie wyst ¾epuje

w M

r+1

:

Twierdzenie 4.20 Estymatory najwi ¾ekszej wiarygodno´sci n

(r+1)
ijk

w modelach hi-

erarchicznych M

r+1

jM

r

(patrz Twierdzenie 4.18) wyrazaj ¾

a si ¾e wzorami

n

(2)
ijk

=

n

(1)
ij+

n

(1)
+jk

n

(1)
+j+

n

(3)
ijk

=

n

(2)
ij+

n

(2)
++k

n

(2)
+++

n

(4)
ijk

=

n

(3)
i++

n

(3)
+j+

n

(3)
++k

³

n

(3)
+++

´

2

Estymatory n

(1)
ij k

mozna wyznaczy´c metod ¾

a iteracyjnego oszacowania propor-

cjonalnego (Dodatek A)

Modele logarytmiczno-liniowe

51

Dowód. Model M

2

jM

1

;postaci [XY ][Y Z], jest modelem warunkowej nieza-

lezno´sci X ? Z jY (Twierdzenie 4.6), co oznacza, ze

p

(2)
ik

jj

= p

(2)
i+

jj

p

(2)
+k

jj

czyli równowaznie

p

(2)
ijk

p

(2)
+j +

=

p

(2)
ij +

p

(2)
+j+

p

(2)
+jk

p

(2)
+j+

Mnoz ¾ac obie strony tego równania przez n

(2)
+++

otrzymamy, po uproszczeniach

n

(2)
ijk

= n

(2)
ij +

p

(2)
+jk

p

(2)
+j+

Mnoz ¾ac teraz licznik i mianownik u÷amka po prawej stronie przez n

(2)
+++

; otrzy-

mamy równo´s´c:

n

(2)
ijk

=

n

(2)
ij+

n

(2)
+jk

n

(2)
+j+

Korzystaj ¾ac z twierdzenia4.11 mamy, ze n

(2)
ij+

= n

(1)
ij+

; n

(2)
+jk

= n

(1)
+jk

; n

(2)
+j+

=

n

(1)
+j +

Analogicznie, model M

3

jM

2

;postaci [XY ][Z], jest modelem niezalezno

´sci pary

(X; Y ) i Z. Korzystaj ¾

ac znów z twierdzenia 4.6 mamy

p

(3)
ijk

= p

(3)
ij+

p

(3)
++k

co po analogicznych operacjach, jak wyzej (mnozenie obustronne przez n

(3)
+++

,

potem mnozenie i dzielenie po prawej stronie przez n

(3)
+++

i wykorzystanie twierdzenia

??) daje

n

(3)
ijk

=

n

(2)
ij +

n

(2)
++k

n

(2)
+++

Ostatni ¾a równo´s´c w tezie twierdzenia uzyskuje si ¾e w analogiczny sposób.

Uwaga 4.21 (praktyczna) Wyniki, uzyskane w tym punkcie mozemy podsumowa´c
w tabeli

Model

M

0

: [XY Z]

M

1

: [XY ][XZ][Y Z]

M

2

: [XY ][Y Z]

M

3

: [XY ][Z]

M

4

: [X][Y ][Z]

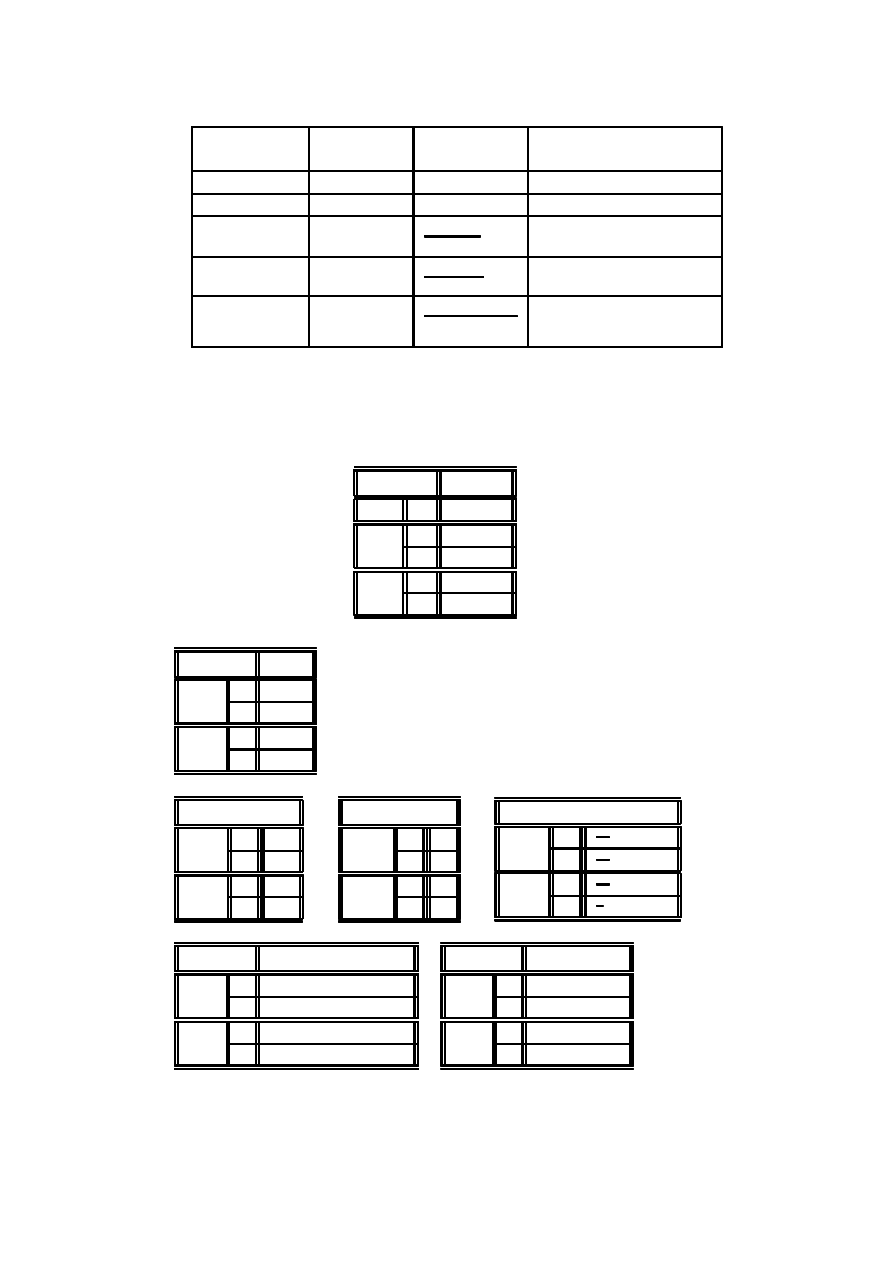
52

Modele logarytmiczno-liniowe

Model

Typ

Estymacja

DF

warunkowy zalezno´sci

-

nasycony

0

M

1

jM

0

-

IPF

(I ¡ 1) (J ¡ 1) (K ¡ 1)

M

2

jM

1

X?Z jY

n

(1)
ij+

n

(1)
+jk

n

(1)
+j +

(I ¡ 1) (K ¡ 1)

M

3

jM

2

(X; Y ) ?Z

n

(2)
ij+

n

(2)
++k

n

(2)
+++

(J ¡ 1) (K ¡ 1)

M

4

jM

3

X?Y ?Z

n

(3)
i++

n

(3)
+j+

n

(3)
++k

³

n

(3)
+++

´

2

(I ¡ 1) (J ¡ 1)

Tabela 4.5 Dopasowanie modelu hierarchicznego

Przyk÷ad 4.22 (artretyzm, terapia, p÷e´c) (c.d. przyk÷adu 2.19)

Zbadamy struktur ¾e tych danych, stosuj ¾

ac model logarytmiczno-liniowy na poziomie

istotno´sci 0,05

n

(0)
ijk

W

P

T

z

l

k

a

6

21

p

19 13

m

a

7

7

p

10 1

Oszacujemy, metod ¾

a IPF liczebno´sci n

(1)
ijk

dla modelu [P W][T W ][P T ]

w

(0)

ij k

z

l

k

a

1 1

p

1 1

m

a

1 1

p

1 1

Najpierw dopasujemy model [P W ]

n

(0)
i+k

k

z

25

l

34

m

z

17

l

8

w

(0)

i+k

k

z

2

l

2

m

z

2

l

2

®

i+k

k

z

25

2

= 12: 5

l

34

2

= 17: 0

m

z

17

2

= 8: 5

l

8
2

= 4: 0

Po uwzgl ¾ednieniu wspó÷czynnika skaluj ¾

acego otrzymamy now ¾

a macierz:

w

(1)

ij k

z

l

k

a

1 ¤ 12: 5 1 ¤ 17: 0

p

1 ¤ 12: 5 1 ¤ 17: 0

m

a

1 ¤ 8: 5

1 ¤ 4: 0

p

1 ¤ 8: 5

1 ¤ 4: 0

=

w

(1)
ij k

z

l

k

a

12: 5

17: 0

p

12: 5

17: 0

m

a

8: 5

4: 0

p

8: 5

4: 0

W drugim kroku pierwszego cyklu dopasujemy model [T W]

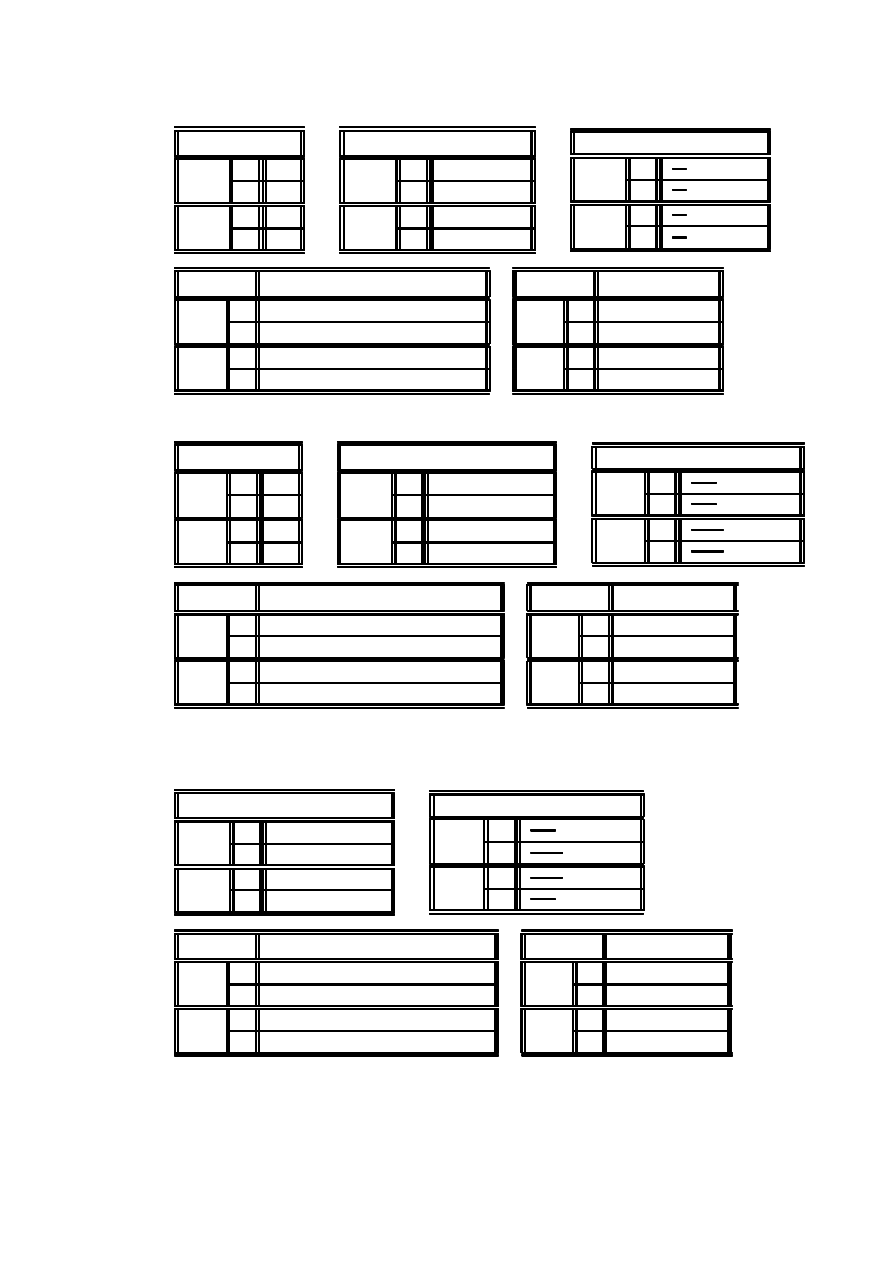
Modele logarytmiczno-liniowe

53

n

(0)
+j k

a

z

13

l

28

p

z

29

l

14

w

(1)

+jk

a

z

12: 5 + 8: 5

l

17: 0 + 4: 0

p

z

12: 5 + 8: 5

l

17: 0 + 4: 0

®

+jk

a

z

13
21

= : 619

l

28
21

= 1: 333

p

z

29
21

= 1: 381

l

14
21

= : 667

w

(2)

ij k

z

l

k

a

12: 5 ¤ : 619

17: 0 ¤ 1: 333

p

12: 5 ¤ 1: 381 17: 0 ¤ : 667

m

a

8: 5 ¤ : 619

4: 0 ¤ 1: 333

p

8: 5 ¤ 1: 381

4: 0 ¤ : 667

=

w

(2)
ijk

z

l

k

a

7: 74

22: 66

p

17: 26 11: 34

m

a

5: 26

5: 32

p

11: 74 2: 67

W trzecim kroku pierwszego cyklu dopasujemy model [P T ]

n

(0)
ij +

k

a

27

p

32

m

a

14

p

11

w

(2)

ij+

k

a

7: 74 + 22: 66

p

17: 26 + 11: 34

m

a

5: 26 + 5: 32

p

11: 74 + 2: 67

®

ij+

k

a

27

30: 4

= : 889

p

32

28: 6

= 1: 119

m

a

14

10: 58

= 1: 323

p

11

14: 41

= : 763

w

(3)

ij k

z

l

k

a

7: 74 ¤ : 889

22: 66 ¤ : 889

p

17: 26 ¤ 1: 119 11: 34 ¤ 1: 119

m

a

5: 26 ¤ 1: 323

5: 32 ¤ 1: 323

p

11: 74¤ : 763

2: 67¤ : 763

=

w

(3)
ijk

z

l

k

a

6: 89

20: 14

p

19: 31 12: 69

m

a

6: 96

7: 04

p

8: 96

2: 04

Rozpoczynamy drugi cykl iteracji

Model [P W ]

w

(3)

i+k

k

z

6: 89 + 19: 31

l

20: 14 + 12: 69

m

z

6: 96 + 8: 96

l

7: 04 + 2: 04

®

i+k

k

z

25

26: 2

= : 954

l

34

32: 83

= 1: 036

m

z

17

15: 92

= 1: 068

l

8

9: 08

= : 881

w

(4)

ij k

z

l

k

a

6: 89 ¤ : 954

20: 14 ¤ 1: 036

p

19: 31 ¤ : 954 12: 69 ¤ 1: 036

m

a

6: 96 ¤ 1: 068 7: 04¤ : 881

p

8: 96 ¤ 1: 068 2: 04¤ : 881

=

w

(4)
ijk

z

l

k

a

6: 57

20: 86

p

18: 42

13: 15

m

a

7: 43

6: 20

p

9: 57

1: 80

Model [T W ]

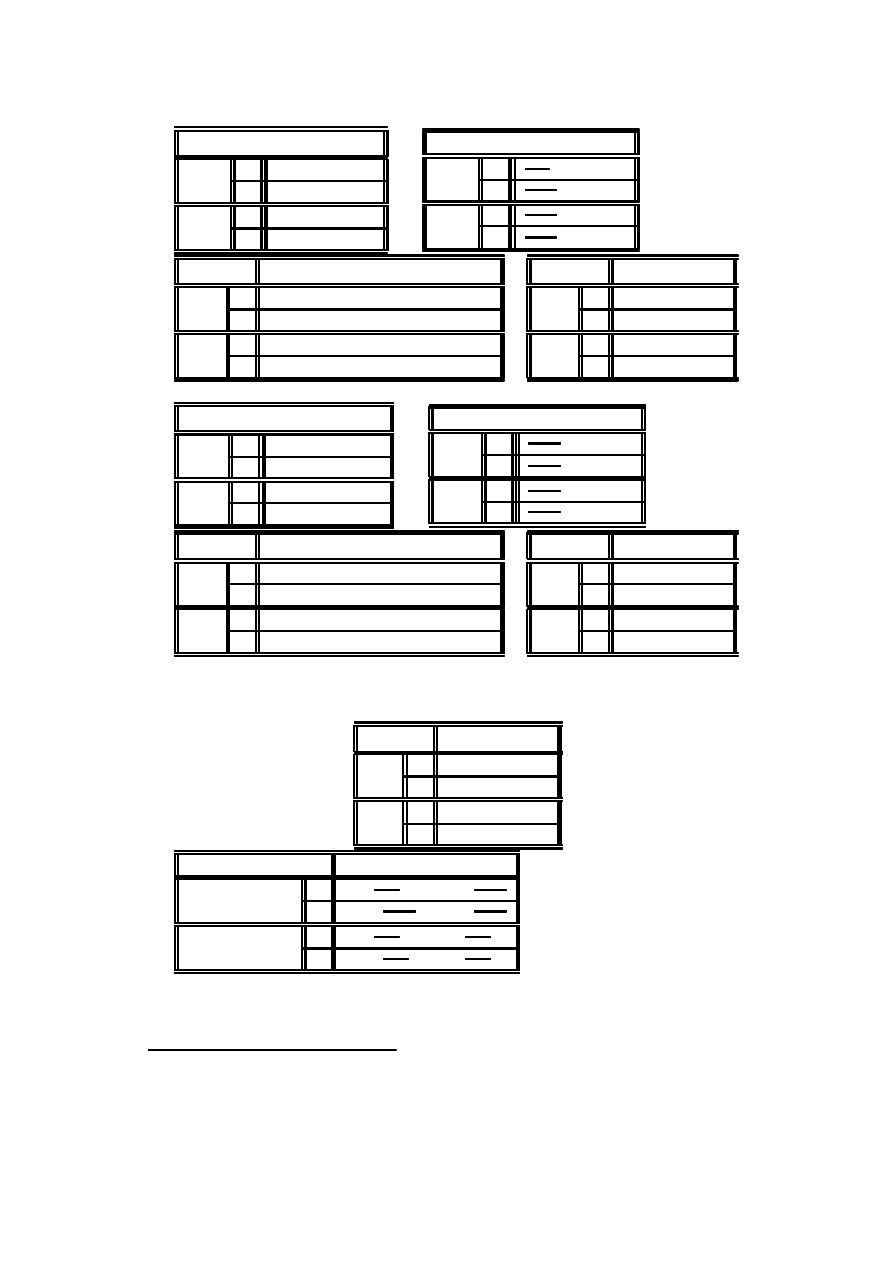
54

Modele logarytmiczno-liniowe

w

(4)

+jk

a

z

6: 57 + 7: 43

l

20: 86 + 6: 20

p

z

18: 42 + 9: 57

l

13: 15 + 1: 80

®

+jk

a

z

13

14:0

= : 929

l

28

27: 06

= 1: 035

p

z

29

27: 99

= 1: 036

l

14

14: 95

= : 936

w

(5)

ij k

z

l

k

a

6: 57 ¤ : 929

20: 86 ¤ 1: 035

p

18: 42 ¤ 1: 036 13: 15 ¤ : 936

m

a

7: 43 ¤ : 929

6: 20 ¤ 1: 035

p

9: 57 ¤ 1: 036

1: 80¤ : 936

=

w

(5)
ijk

z

l

k

a

6: 10

21: 59

p

19: 08 12: 31

m

a

6: 90

6: 42

p

9: 91

1: 68

Model [P T ]

w

(5)

ij +

k

a

6: 10 + 21: 59

p

19: 08 + 12: 31

m

a

6: 90 + 6: 42

p

9: 91 + 1: 68

®

ij+

k

a

27

27: 69

= : 975

p

32

31: 39

= 1: 019

m

a

14

13: 32

= 1: 051

p

11

11: 59

= : 949

w

(6)

ij k

z

l

k

a

6: 10 ¤ : 975

21: 59 ¤ : 975

p

19: 08 ¤ 1: 019 12: 31 ¤ 1: 019

m

a

6: 90 ¤ 1: 051

6: 42 ¤ 1: 051

p

9: 91 ¤ : 949

1: 68¤ : 949

=

w

(6)
ijk

z

l

k

a

5: 95

21: 05

p

19: 44 12: 54

m

a

7: 25

6: 75

p

9: 40

1: 59

Obliczenia w tym modelu zatrzymujemy po dwóch cyklach

4

.

Przyjmiemy wi ¾ec tabel ¾e warto´sciami w

(6)
ijk

jako tabel ¾e z estymatorami n

(1)
ijk

dla

modelu [P W ][T W ][P T ]:

n

(1)
ijk

z

l

k

a

5: 95

21: 05

p

19: 44 12: 54

m

a

7: 25

6: 75

p

9: 40

1: 59

G

2

ij k

(M

1

jM

0

)

z

l

k

a

6 ln

6

5: 95

21 ln

21

21: 05

p

19 ln

19

19: 44

13 ln

13

12: 54

m

a

7 ln

7

7: 25

7 ln

7

6: 75

p

10 ln

10

9: 40

1 ln

1

1: 59

=) G

2

ijk

(M

1

jM

0

) = : 395 16

Poziom krytyczny, odpowiadaj ¾

acy warto´sci : 395 16 dla rozk÷adu Â

2

z 1 stop-

niem swobody ( (I ¡ 1) (J ¡ 1)(K ¡ 1) = 1 ) wynosi 0; 5296 co upowaznia nas

do zaakceptowania modelu M

1

:

4

Kryteria stopu zalez ¾

a od wybranej opcji. Moze to by´c dok÷adno´s´c liczno´sci brzegowych czy

tez, jak w naszym przyk÷adzie, liczba cykli oblicze´n.

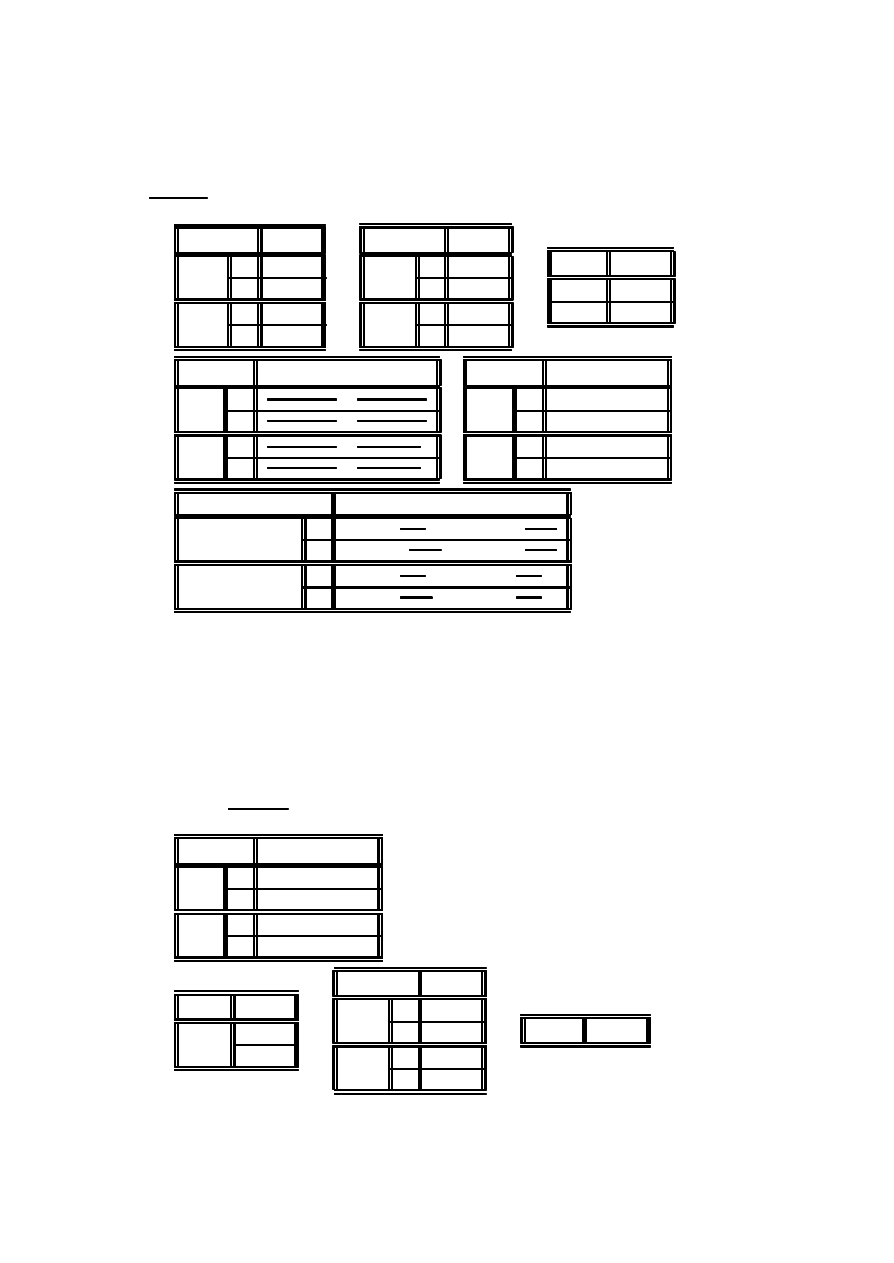
Modele logarytmiczno-liniowe

55

Oszacujemy teraz parametry modelu M

2

jM

1

gdzie M

2

: [P W][T W ]: Od razu

mozemy obliczy´c estymatory n

(2)
ijk

w tym modelu (patrz tabela 4.5) ze wzoru n

(2)
ijk

=

n

(1)
i+k

n

(1)
+j k

n

(1)
++k

:

n

(1)
i+k

k

z

25: 39

l

33: 59

m

z

16: 65

l

8: 34

n

(1)
+jk

a

z

13: 20

l

27: 80

p

z

28: 84

l

14: 13

n

(1)
++k

z

42: 04

l

41: 93

n

(2)
ij k

z

l

k

a

25: 39

¤13: 20

42: 04

33: 59

¤27: 80

41: 93

p

25: 39

¤28: 84

42: 04

33: 59

¤14: 13

41: 93

m

a

16: 65

¤13: 20

42: 04

8: 34

¤27: 80

41: 93

p

16: 65

¤28: 84

42: 04

8: 34

¤14: 13

41: 93

=

n

(2)
ijk

z

l

k

a

7: 97

22: 27

p

17: 42

11: 32

m

a

5: 23

5: 53

p

11: 42

2: 81

G

2

ij k

(M

2

jM

1

)

z

l

k

a

5: 95 ln

5: 95
7: 97

21: 05 ln

21: 05
22: 27

p

19: 44 ln

19: 44
17: 42

12: 54 ln

12: 54
11: 32

m

a

7: 25 ln

7: 25
5: 23

6: 75 ln

6: 75
5: 53

p

9: 40 ln

9: 40

11: 42

1: 59 ln

1: 59
2: 81

=) G

2

ijk

(M

2

jM

1

) = 2: 938 8 =) G

2

ijk

(M

2

) = G

2

ijk

(M

2

jM

1

) + G

2

ijk

(M

1

jM

0

)

= : 39516 + 2: 938 8 = 3: 334

Poziom krytyczny, odpowiadaj ¾

acy warto´sci 3: 334 dla rozk÷adu Â

2

z 2 stopni-

ami swobody ( (I ¡ 1)(J ¡ 1) (K ¡ 1) + (I ¡ 1)(K ¡ 1) = 2 ) wynosi 0; 1888 co

upowaznia nas do zaakceptowania modelu M

2

:

Oszacujemy teraz parametry modelu M

3

jM

2

gdzie M

3

: [P ][T W]: Mozemy

obliczy´c estymatory n

(3)
ijk

w tym modelu (patrz tabela 4.5) ze wzoru

n

(3)
ijk

=

n

(2)
i++

n

(2)
+jk

n

(2)
+++

n

(2)
ij k

z

l

k

a

7: 97

22: 27

p

17: 42

11: 32

m

a

5: 23

5: 53

p

11: 42

2: 81

n

(2)
i++

k

58: 98

m

24: 99

n

(2)
+jk

a

z

13: 20

l

27: 80

p

z

28: 84

l

14: 13

n

(2)
+++

83: 97

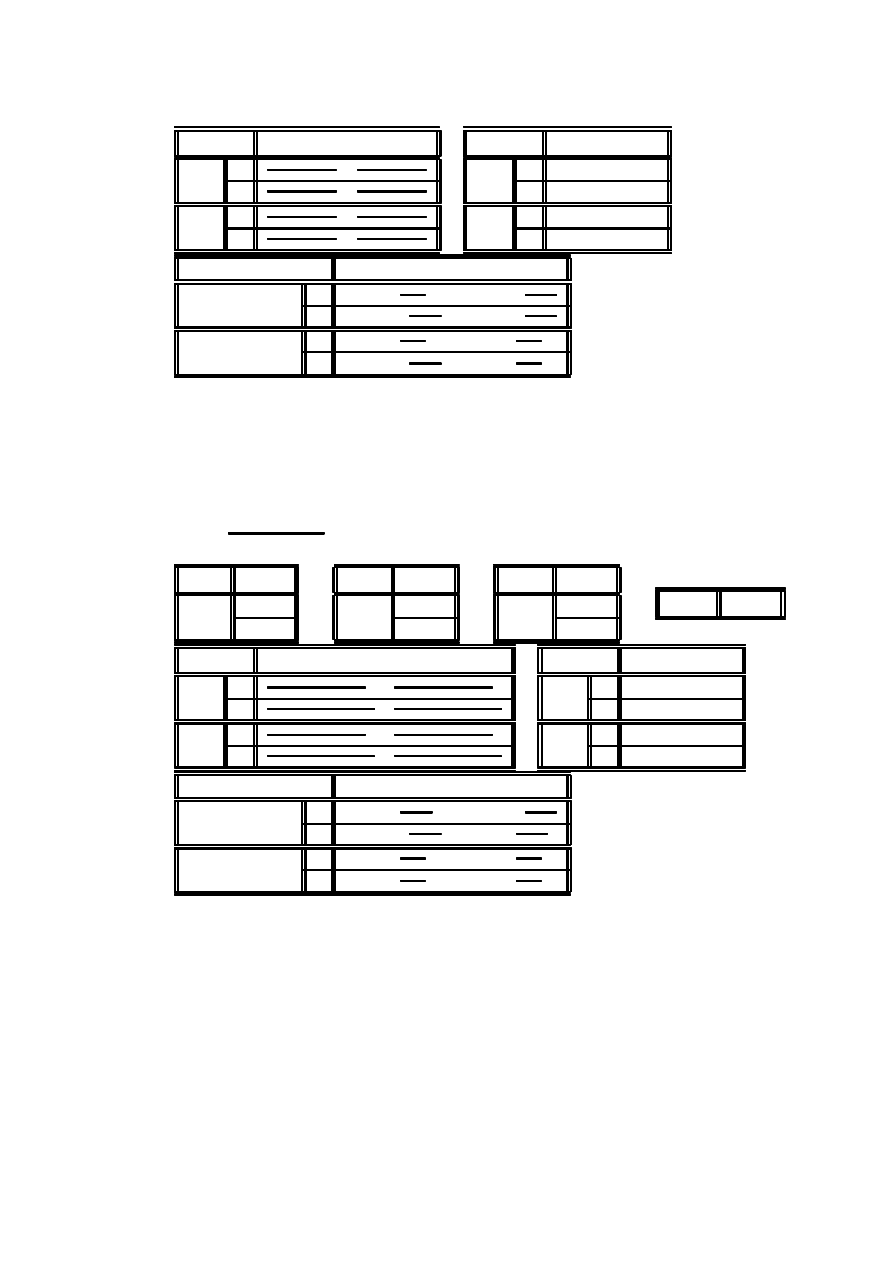
56

Modele logarytmiczno-liniowe

n

(3)
ij k

z

l

k

a

58: 98

¤13: 20

83: 97

58: 98

¤27: 80

83: 97

p

58: 98

¤28: 84

83: 97

58: 98

¤14: 13

83: 97

m

a

24: 99

¤13: 20

83: 97

24: 99

¤27: 80

83: 97

p

24: 99

¤28: 84

83: 97

24: 99

¤14: 13

83: 97

=

n

(3)
ijk

z

l

k

a

9: 27

19: 53

p

20: 26

9: 92

m

a

3: 93

8: 27

p

8: 58

4: 21

G

2

ij k

(M

3

jM

2

)

z

l

k

a

7: 97 ln

7: 97
9: 27

22: 27 ln

22: 27
19: 53

p

17: 42 ln

17: 42
20: 26

11: 32 ln

11: 32

9: 92

m

a

5: 23 ln

5: 23
3: 93

5: 53 ln

5: 53
8: 27

p

11: 42 ln

11: 42

8: 58

2: 81 ln

2: 81
4: 21

=) G

2

ijk

(M

3

jM

2

) = 3: 962 8 =) G

2

ijk

(M

3

) = 3: 962 8 + 3: 334 = 7: 296 8

Poziom krytyczny, odpowiadaj ¾

acy warto´sci 7: 296 8 dla rozk÷adu Â

2

z 3 stop-

niami swobody ( 2 + (I ¡ 1) (K ¡ 1) = 3) wynosi 0; 06302 co upowaznia nas do

zaakceptowania modelu M

3

:

Oszacujemy teraz parametry modelu M

4

jM

3

gdzie M

3

: [P ][T ][W ]: Estymatory

n

(4)
ij k

mozemy obliczy´c ze wzoru

n

(4)
ijk

=

n

(3)
i++

n

(3)
+j+

n

(3)
++k

³

n

(3)
+++

´

2

n

(3)
i++

k

58: 98

m

24: 99

n

(3)
+j+

a

41:0

p

42: 97

n

(3)
++k

z

42: 04

l

41: 93

n

(3)
+++

83: 97

n

(4)
ij k

z

l

k

a

58: 98

¤41:0¤42: 04

83: 97

2

58: 98

¤41:0¤41: 93

83: 97

2

p

58: 98

¤42: 97¤42: 04

83: 97

2

58: 98

¤42: 97¤41: 93

83: 97

2

m

a

24: 99

¤41:0¤42: 04

83: 97

2

24: 99

¤41:0¤41: 93

83: 97

2

p

24: 99

¤42: 97¤42: 04

83: 97

2

24: 99

¤42: 97¤41: 93

83: 97

2

=

n

(4)
ijk

z

l

k

a

14: 42 14: 38

p

15: 11 15: 07

m

a

6: 11

6: 09

p

6: 40

6: 39

G

2

ij k

(M

4

jM

3

)

z

l

k

a

9: 27 ln

9: 27

14: 42

19: 53 ln

19: 53
14: 38

p

20: 26 ln

20: 26
15: 11

9: 92 ln

9: 92

15: 07

m

a

3: 93 ln

3: 93
6: 11

8: 27 ln

8: 27
6: 09

p

8: 58 ln

8: 58
6: 40

4: 21 ln

4: 21
6: 39

=) G

2

ijk

(M

4

jM

3

) = 10: 462

=) G

2

ijk

(M 4) = 10: 462 + 7: 2968 = 17: 759

Poziom krytyczny, odpowiadaj ¾

acy warto´sci 17: 759 dla rozk÷adu Â

2

z 4 stop-

niami swobody ( 3 + (J ¡ 1) (K ¡ 1) = 4) wynosi 0; 0014 co upowaznia nas do

odrzucenia modelu M

4

:

Ostatecznie mozemy przyj ¾

a´c, ze na poziomie istotno´sci 0:05 modelem, opisu-

j ¾

acym dane jest [P ][T W ], co oznacza , ze zwi ¾

azane ze sob ¾

a s ¾

a wyniki leczenia i

zastosowana terapia. Wybór pacjentów wg kryteriów p÷ci ani nie by÷ zwi ¾

azany z

wyborem zastosowanej terapii, ani z uzyskanymi wynikami.

Modele logarytmiczno-liniowe

57

Gdyby´smy przeprowadzili rozumowanie na poziomie 0:1

5

to ostatnim zaakcep-

towanym modelem by÷by [P W ][T W ] z poziomem krytycznym 0; 1661: Model taki
oznacza, ze przy kazdych danych wynikach leczenia nie ma zwi ¾

azku mi ¾edzy p÷ci ¾

a a

wyborem terapii, natomiast zarówno p÷e´c jak i terapia mog ¾

a mie´c wp÷yw na wyniki

leczenia

6

.

Oszacowany przez nas model danych nie musi by´c jedynym. Poszli´smy jedn ¾a

z mozliwych ´sciezek w drzewku modeli hierarchicznych. Przypu´s´cmy, jak to ro-

bi ¾a pakiety statystyczne, ze oszacowali´smy wszystkie dopuszczalne modele na
wybranym poziomie istotno´sci. Który z nich wybra´c? Jednym z uzywanych w
statystyce kryteriów jest kryterium AI C, podane przez Akaike czy tez kryterim
bayesowskie BIC. Pozwalaj ¾a one wybra´c ten model, który jednocze´snie najlepiej

pasuje do danych i jest najoszcz ¾edniejszy w swoim opisie. Wybiera si ¾e wi ¾ec ten
model, który ma wi ¾eksz ¾a warto´s´c kryterium.Dla modeli logarytmiczno - liniowych
(p.[1] str. 251) mozna te kryteria wyrazi´c wzorami

AI C (M) = G

2

(M ) ¡ 2DF (M ) ;

BI C (M) = G

2

(M ) ¡ ln (n

M

) DF (M) ;

gdzie n

M

jest liczb ¾a obserwacji dla modelu M

W rozwazanym przyk÷adzie warto´s´c kryterium Akaike zmienia÷a si ¾e nast ¾epu-

j ¾aco:

AIC (M

1

) = 0:39516 ¡ 2 ¤ 1 = ¡1: 6048;

AIC (M

2

) = 3:334 ¡ 2 ¤ 2 = ¡: 666

AIC (M

3

) = 7:2968 ¡ 2 ¤ 3 = 1: 2968

5

co cz ¾esto jest przyjmowane w programach statystycznych jako warto´s´c domy´slna (np. w

programie Statistica)

6

Patrz tez wyniki modelu logitowego dla tych danych

58

Modele logarytmiczno-liniowe

Dodatek A

Skale dla prawdopodobie´nstw

59

60

Skale dla prawdopodobie´nstw

De…nicja A.1 Przypu´s´cmy, ze obserwowana wielko´s´c X jest wyrazona w jakiej´s
skali liczbowej. Skal ¾

a dla wielko´sci X nazywamy kazd ¾

a rosn ¾

ac ¾

a i ci ¾

ag÷ ¾

a funkcj ¾e

H. Warto´sci X w nowej skali s ¾

a równe H (X)

Wymóg´scis÷ego wzrostu skali jest zrozumia÷y - warto´sci obserwowanego zjawiska

wyrazone w nowej skali powinny zachowa´c porz ¾adek skali pocz ¾atkowej. Podob-

nie, ci ¾ag÷o´s´c oznacza, ze warto´sci bliskie w skali pocz ¾atkowej b ¾ed ¾a bliskie w nowej
skali. Róznowarto´sciowo´s´c funkcji H umozliwia powrót z nowej skali do skali
pocz ¾

atkowej.

Uwaga A.2 Z÷ozenie skal H

1

i H

2

jest skal ¾

a. W szczególno´sci z÷ozenie skali

liniowej H

1

= ® + ¯u (¯ > 0) jest skal

¾

a. Na÷ozenie skali liniowej umozliwia

wybór zera i jednostki kazdej skali.

De…nicja A.3 Skala prawdopodobie´nstw to funkcja rosn ¾

aca i ci ¾

ag÷a

1

H : (0; 1) ¡! R

De…nicja A.4 Skala prawdopodobie´nstw jest symetryczna gdy H (1 ¡ p) = ¡H (p)

Uwaga A.5 Dla skali symetrycznej H

³

1
2

´

= 0

Twierdzenie A.6 Kazd ¾

a skal ¾e mozna zsymetryzowa´c

H

0

(p) = H (p) ¡ H (1 ¡ p)

Dowód. 1. H

0

jest funkcj ¾a ci ¾ag÷ ¾a, bo jest róznic ¾a funkcji ci ¾ag÷ych.

2. Niech p

1

< p

2

: H

0

(p

1

) = H (p

1

) ¡ H (1 ¡ p

1

) < H (p

2

) ¡ H (1 ¡ p

2

) =

H

0

(p

2

) (funkcja ¡H (1 ¡ p) jest rosn ¾aca)

3. H

0

jest symetryczna: H

0

(1 ¡ p) = H (1 ¡ p) ¡ H (1 ¡ (1 ¡ p)) = ¡H

0

(p)

Przyk÷ad A.7 (Skale kwantylowe) Niech F b ¾edzie rosn ¾

ac ¾

a i ci ¾

ag÷ ¾

a dystry-

buant ¾

a rozk÷adu zmiennej losowej.

Lewostronna skala kwantylowa oparta na F jest funkcj ¾

a

H

L

(p) = F

¡1

(p)

Prawostronna skala kwantylowa oparta na F jest funkcj ¾

a

H

P

(p) = ¡F

¡1

(1 ¡ p)

Uwaga A.8 Niech F b ¾edzie rosn ¾

ac ¾

a i ci ¾

ag÷ ¾

a dystrybuant ¾

a rozk÷adu prawdopodobie´nstwa,

symetrycznego w zerze. Wtedy:

1. lewostronna i prawostronna skala kwantylowa jest symetryczna,
2. dla kazdego p ; H

L

(p) = H

P

(p)

1

Zazwycza j de…niuje si ¾e skal ¾e dla przedzia÷u otwartego, wyklucza j ¾ac z rozwaza´n zdarzenia

niemozliwe i pewne

Skale dla prawdopodobie´nstw

61

Dowód. 1. Niech H

L

(p) = u; H

L

(1¡p) = v. Wtedy F (u) = p; F (v) = 1¡p.

Z de…nicji rozk÷adu symetrycznego w 0 mamy, ze v = ¡u. Podobnie, niech
H

P

(p) = u; H

P

(1 ¡ p) = v. Wtedy F (¡u) = 1 ¡ p; F (¡v) = p co implikuje

równo´s´c v = ¡u:

2. Niech H

L

(p) = u; H

P

(p) = v. Wtedy F (u) = p; F (¡v) = 1 ¡ p. Z tej

równo´sci i symetrii wynika, ze v = u:

De…nicja A.9 Skal ¾e kwantylow ¾

a opart ¾

a na dystrybuancie © rozk÷adu normalnego

standardowego

2

nazywamy skal ¾

a probitow ¾

a

Skal ¾e probitow ¾a stosujemy dla zjawisk o rozk÷adzie prawdopodobie´nstwa symetrycznie

roz÷ozonym wokó÷ warto´sci

1
2

i niezbyt daleko odbiegaj ¾

acym od tej warto´sci.

Dla zjawisk, w których obserwujemy zjawiska ekstremalne (np. ´smiertel-

no´s´c owadów na skutek stosowania ´srodków chemicznych) stosuje si ¾e prawo i
lewostronn ¾a skal ¾e kwantylow ¾a opart ¾

a na rozk÷adzie Gumbela

3

o dystrybuancie

F (u) = exp (¡ exp (¡u))

Wtedy H

L

(p) = ¡ ln (¡ ln (p)) ; H

P

(p) = ln (¡ ln (1 ¡ p)). Takie przekszta÷cenie

nazywane jest skal ¾

a podwójnie logarytmiczn ¾

a. Jak ÷atwo zauwazy´c skala pod-

wójnie logarytmiczna nie jest symetryczna.

Najcz ¾e´sciej, ze wzgl ¾edu na swoj ¾a prostot ¾e i dopasowanie do cz ¾esto wyst ¾epu-

j ¾acych w praktyce zjawisk asymetrycznych

4

jest skala logitowa.

De…nicja A.10 Skala logitowa jest symetryzacj ¾

a skali logarytmicznej dla praw-

dopodobie´nstw

lgt (p) = ln (p) ¡ ln (1 ¡ p) = ln

Ã

p

1 ¡ p

!

Jak wida´c, skala logitowa jest równa logarytmowi stosunku szans dla zdarzenia o
prawdopodobie´nstwie p.

Maj ¾

ac warto´s´c logitu, ÷atwo obliczy´c prawdopodobie´nstwo ze wzoru

lgt

¡1

(u) =

1

1 + exp (¡u)

Przyk÷ad A.11 (Kennedy i Nixon) W rywalizacji o fotel prezydenta USA w
listopadzie 1960 wygra÷ Kennedy. Dane przedstawiaj ¾

a procent poparcia dla Kennedy’ego

2

Dystrybuanta ta jest ci ¾ag÷a i rosn ¾aca, a rozk÷ad jest symetryczny w 0.

3

Rozk÷ad Gumbela jest jednym z trzech mozliwych rozk÷adów granicznych dla warto´sci

najwi ¾ekszej z ci ¾agu niezaleznych zmiennych losowych. To ciekawe twierdzenie udowodni÷
Gniedenko w 1943.

4

wyst ¾epuj ¾a ma÷o prawdopodobne zjawiska, ale z jednego ko´nca skali, np bardzo praw-

dopodobne s ¾a stany zdrowia i lekkiego stanu choroby a ma÷o prawdopodobne stany ci ¾ezkiej
choroby

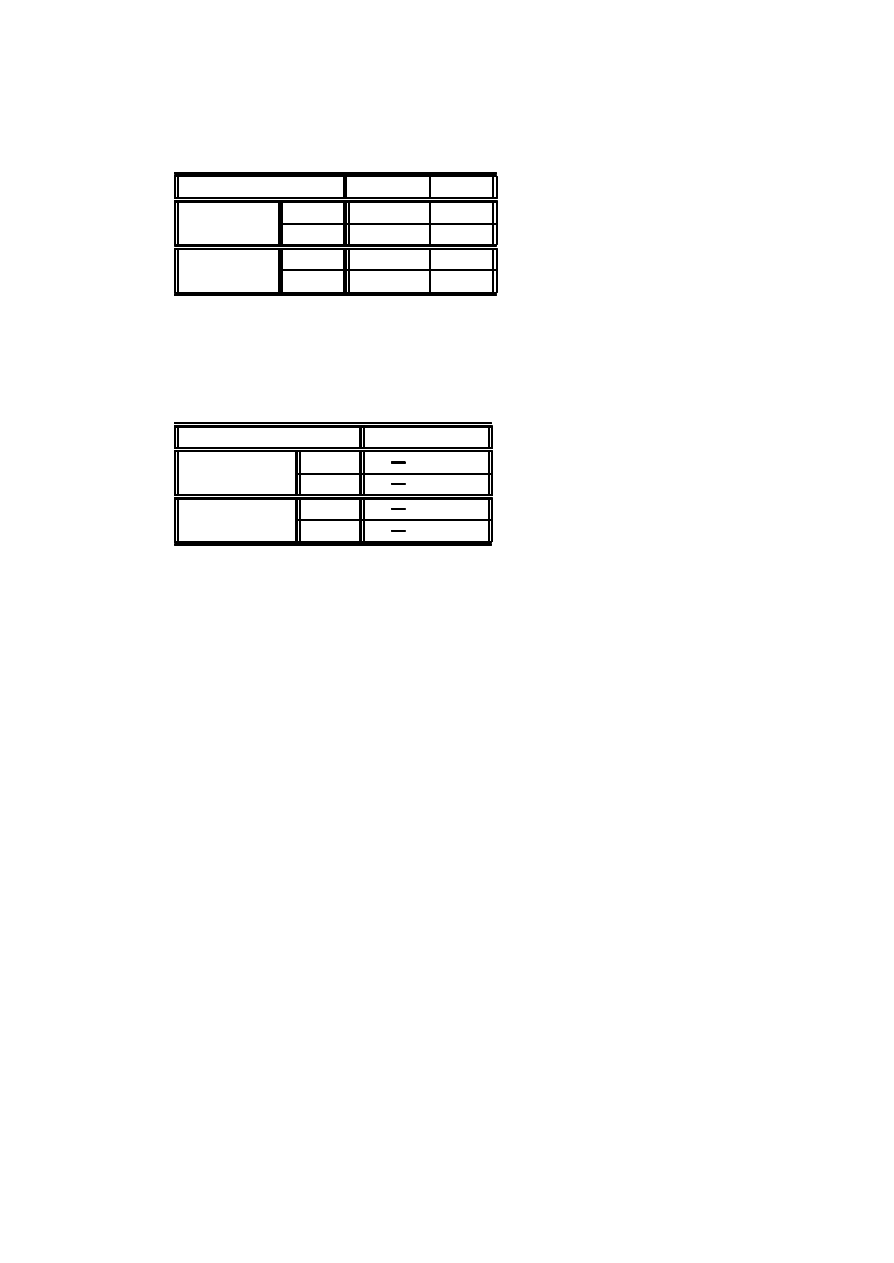
62

Skale dla prawdopodobie´nstw

i Nixona w listopadzie 1960 i styczniu 1962 (w po÷owie kadencji) w´sród katolików
(elektorat Kennedy’ego) i protestantów (elektorat Nixona)

% poparcia

Kennedy Nixon

protestanci

XI,60

38

62

I,62

59

41

katolicy

XI,60

78

22

I,62

89

11

Czytaj ¾

ac bezpo´srednio procenty poparcia dla Kennedy’ego widzimy, ze w´sród

protestantów poparcie wzros÷o w po÷owie kadencji o 21 punktów procentowych, a
w´sród katolików o 11 punktów procentowych. Czyzby Kennedy zas÷uzy÷ sobie w´sród
protestantów na wi ¾ekszy wzrost poparcia? Pami ¾etaj ¾

ac, jak trudno zdoby´c cho´c

jeden procent poparcia w grupie wysokiego poziomu poparcia wyra´zmy poparcie dla
Kennedy’ego w skali logitowej

logit poparcia

Kennedy

protestanci

XI,60

ln

38
62

= ¡: 490

I,62

ln

59
41

= : 364

katolicy

XI,60

ln

78
22

= 1: 266

I,62

ln

89
11

= 2: 091

Przyrost poparcia dla Kennedy’ego w skali logitowej wynosi w´sród protestantów

: 854 a w

´sród katolików : 825. Wskazuje to na równomierny wzrost poparcia dla

Kennedy’ego w obu grupach.

Dodatek B

Metoda IPF

63

64

Metoda IPF

Metoda iteracyjnego oszacowania proporcjonalnego (metoda

Iterative Proportional

Fitting) zosta÷a opracowana przez Deminga i Stephana w 1940 [2]. Metoda ta jest
przydatna w znajdowaniu estymatorów n

(r)
ijk

w hierarchicznych modelach warunk-

owych. Procedur ¾e t ¾a mozna opisa´c w kilku krokach

1. Iteracja zerowa w

(0)

ijk

estymatorów n

(r)
ijk

powinna by´c tak wybrana, aby odpowiada÷a

modelowi podporz ¾adkowanemu modelowi, dla którego wyznaczamy estyma-

tory n

(r)
ijk

. Takim modelem jest model sta÷y, dla którego w

(0)

ijk

= 1

2. Mnoz ¾ac przez odpowiednie wspó÷czynniki skaluj ¾ace sukcesywnie dopasuj

w

(0)

ijk

tak, aby zachowane zosta÷y liczebno´sci brzegowe dla efektów, wyst ¾epu-

j ¾acych w estymowanym modelu; w ten sposób otrzymamy kolejne przyblize-
nia w

(1)

ijk

; w

(2)

ijk

; w

(3)

ijk

; :::

3. Proces kontynuuj tak d÷ugo, az róznica mi ¾edzy liczbno´sciami brzegowymi

w

(s)

ijk

i liczbno´sciami brzegowymi n

(r)
ij k

dla efektów, wyst ¾epuj ¾acych w modelu

b ¾edzie mniejsza od zadanej warto´sci ":

Wspó÷czynniki skaluj ¾ace s ¾a obliczane w specy…czny sposób dla kazdego efektu

. Przypu´s´cmy, ze jeste´smy w s ¡ 1 iteracji w

(s

¡1)

ijk

i chcemy dopasowa´c nowe

warto´sci w

(s)

ijk

tak, aby zachowane by÷y liczebno´sci, odpowiadaj ¾ace efektowi ¸

X Y
ij

z modelu M

r

. Wiadomo (twierdzenie

??), ze wtedy n

(r)
ij+

= n

(r

¡1)

ij+

. Wspó÷czyn-

nikiem skaluj ¾acym b ¾edzie wtedy

®

ij

=

n

(r

¡1)

ij+

w

(s

¡1)

ij+

Nowe warto´sci w

(s)
ijk

otrzymujemy ze wzoru

w

(s)
ijk

= ®

ij

w

(s

¡1)

ij k

Zauwazmy, ze wtedy

w

(s)

ij+

=

K

X

k=1

w

(s)

ijk

=

K

X

k=1

®

ij

w

(s

¡1)

ijk

= ®

ij

w

(s

¡1)

ij+

= n

(r

¡1)

ij+

Analogicznie mozemy wyznaczy´c wspó÷czynniki skaluj ¾ace dla dowolnych efek-

tów oraz wykona´c kolejne kroki iteracyjne.

Anderson, Fienberg i Haberman pokazali, ze w

(s)
ij k

s ¾a zbiezne do estymatorów

najwi ¾ekszej wiarygodno´sci n

(r)
ijk

.

Przyk÷ad B.1 Dopasujmy model [XY ][Y Z] do danych n

(r

¡1)

ij k

:

Metoda IPF

65

n

(r

¡1)

ij k

z

1

z

2

x

1

y

1

1

2

y

2

3

4

x

2

y

1

5

6

y

2

7

8

w

(0)

ijk

z

1

z

2

x

1

y

1

1

1

y

2

1

1

x

2

y

1

1

1

y

2

1

1

Dopasujemy macierz dla efektu ¸

XY

ij

, gdyz wyst ¾epuje on w naszym modelu

[XY ][Y Z]

n

(r

¡1)

ij +

x

1

y

1

3

y

2

7

x

2

y

1

11

y

2

15

w

(0)
ij+

x

1

y

1

2

y

2

2

x

2

y

1

2

y

2

2

®

ij

x

1

y

1

3
2

= 1: 5

y

2

7
2

= 3: 5

x

2

y

1

11

2

= 5: 5

y

2

15

2

= 7: 5

Po uwzgl ¾ednieniu wspó÷czynnika skaluj ¾

acego otrzymamy now ¾

a macierz:

w

(1)

ij k

z

1

z

2

x

1

y

1

1 ¤ 1: 5 1 ¤ 1:5

y

2

1 ¤ 3: 5 1 ¤ 3:5

x

2

y

1

1 ¤ 5: 5 1 ¤ 5:5

y

2

1 ¤ 7: 5 1 ¤ 7:5

=

w

(1)
ijk

z

1

z

2

x

1

y

1

1: 5

1: 5

y

2

3: 5

3: 5

x

2

y

1

5: 5

5: 5

y

2

7: 5

7: 5

Teraz wyliczymy kolejne przyblizenie odpowiadaj ¾

ace efektowi ¸

Y Z
jk

dla modelu

[XY ][Y Z]:

n

(r

¡1)

+j k

z

1

z

2

y

1

6

8

y

2

10

12

w

(1)
+jk

z

1

z

2

y

1

7

7

y

2

11

11

®

jk

z

1

z

2

y

1

6
7

= : 857

8
7

= 1: 143

y

2

10
11

= : 909

12
11

= 1: 091

I kolejne przyblizenie estymatorów:

w

(2)

ij k

z

1

z

2

x

1

y

1

1: 5 ¤ : 857 1: 5 ¤ 1: 143

y

2

3: 5 ¤ : 909 3: 5 ¤ 1: 091

x

2

y

1

5: 5 ¤ : 857 5: 5 ¤ 1: 143

y

2

7: 5 ¤ : 909 7: 5 ¤ 1: 091

=

w

(2)
ijk

z

1

z

2

x

1

y

1

1: 286

1: 714

y

2

3: 182

3: 815

x

2

y

1

4: 714

6: 286

y

2

6: 818

8: 182

W ten sposób zako´nczyli´smy pierwszy cykl przyblize´n. Warto´sci brzegowe dla

efektu ¸

XY
ij

wynosz ¾

a

w

(2)

ij +

x

1

y

1

1: 286 + 1: 714

y

2

3: 182 + 3: 815

x

2

y

1

4: 714 + 6: 286

y

2

6: 818 + 8: 182

=

w

(2)
ij+

x

1

y

1

3:0

y

2

6: 997

x

2

y

1

11:0

y

2

15:0

która juz jest idealnie zblizona do n

(r

¡1)

ij +

, nie ma wi ¾ec potrzeby wprowadza´c

poprawki na ten efekt. Trzeba jeszcze sprawdzi´c warto´sci brzegowe dla efektu ¸

Y Z
jk

66

Metoda IPF

w

(2)

+jk

y

1

z

1

1: 286 + 4: 714

z

2

1: 714 + 6: 286

y

2

z

1

3: 182 + 6: 818

z

2

3: 815 + 8: 182

=

w

(2)
+jk

y

1

z

1

6:0

z

2

8:0

y

2

z

1

10:0

z

2

11: 997

Tu tez warto´sci brzegowe s ¾

a bardzo bliskie n

(r

¡1)

+j k

, co oznacza, ze znale´zli´smy

estymatory najwi ¾ekszej wiarygodno´sci dla n

(r)
ijk

, równe w

(2)

ijk

:

w

(2)

ijk

z

1

z

2

x

1

y

1

1: 286 1: 714

y

2

3: 182 3: 815

x

2

y

1

4: 714 6: 286

y

2

6: 818 8: 182

Tutaj zbiezno´s´c uzyskali´smy po dwóch iteracjach w jednym cyklu, obejmuja-

cym wszystkie efekty modelu

1

. W przypadku ogólnym takich iteracji trzeba b ¾edzie

wykona´c wi ¾ecej.

1

Nie jest to przypadek. Haberman w 1974 pokaza÷, ze je´sli liczba nieznanych parametrów

modelu nie przekracza 6, to metoda IPF jest zbiezna w jednym cyklu.

Dodatek C

´

Cwiczenia

67

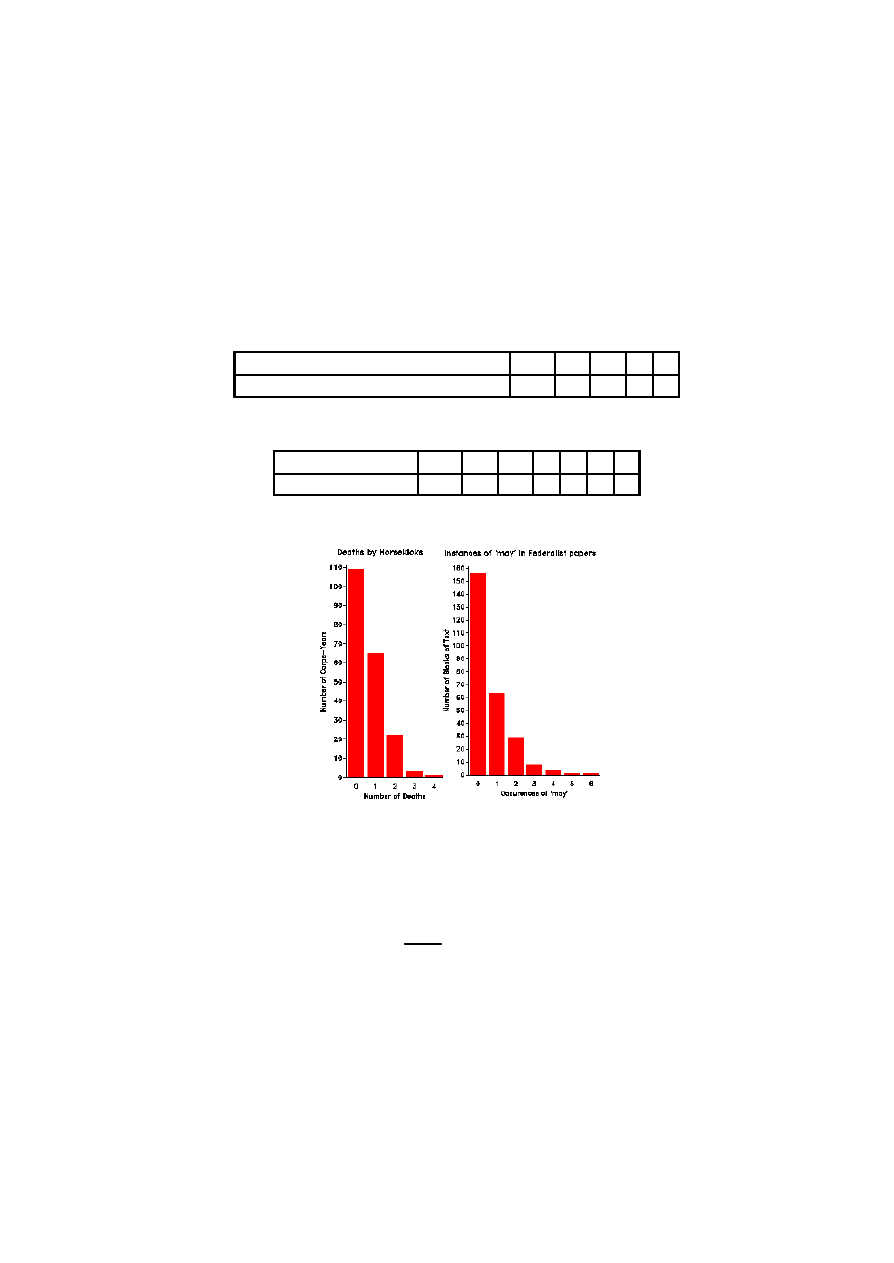
68

´Cwiczenia

Zadania na ´cwiczenia w laboratorium

Materia÷y na ´cwiczenia:

http://www.math.yorku.ca/SCS/Courses/grcat/
1.

Dopasowywanie rozk÷adów.

1.1

Wykres poisonness

Dane:
Dane von Bortkiewicza (1898). Liczba wypadków ´smiertelnych w 10 kor-

pusach armii pruskiej w ci ¾

agu 20 lat:

liczba wypadków

0

1

2

3 4

liczba obserwacji (korpusy x lata) 109 65 22 3 1

Listy Federalistów. Wyst ¾epowanie s÷owa may w 262 blokach po 200 s÷ów.

liczba wyst ¾

apie´n 0

1

2

3 4 5 6

liczba bloków

156 63 29 8 4 1 1

Metoda.
1.1.1 Pokaz, ze gdy w n

k

próbach wyst ¾api÷o k sukcesów i gdy rozk÷ad liczby

sukcesów jest rozk÷adem Poissona z parametrem ¸ to dla duzej liczby n obserwacji
zachodzi w przyblizeniu równo´s´c

u

k

df

= ln

Ã

k! n

k

n

!

= ¡¸ + (ln ¸) k

Wielko´s´c u

k

nazywamy pseudolicznikiem (ang. count metameter)

1.1.2. Napisz za pomoc ¾a najwygodniejszego dla ciebie narz ¾edzia (np. Excela)

procedur ¾e, która rysuje wykres punktowy f(k; u

k

) : k = 0; 1; :::g oraz wpisuje w

ten uk÷ad prost ¾a regresji, oblicza jej równanie i drukuje warto´s´c wspó÷czynnika
determinacji R

2

.

´Cwiczenia

69

1.1.3. Oce´n wizualnie, na podstawie sporz ¾adzonych wykresów czy mozna

przyj ¾a´c, ze Dane von Bortkiewicza pochodz ¾a z rozk÷adu Poissona.

1.1.4. Zrób zadanie 1.1.3. Dla Listów Federalistów.
1.2.

Wykresy Orda.

Metoda (Ord,1967) zapoznaj si ¾e z metod ¾a w [3]
2. Sprawd´z metod ¾a Orda typ rozk÷adu dla poznanych przyk÷adów. Napisz

odpowiedni ¾a procedur ¾e w znanym ci j ¾ezyku programowania.

3.

W÷asno´sci ilorazu krzyzowego µ

Dana jest tablica prawdopodobie´nstw 2 £ 2

Y

X

y

1

y

2

x

1

p

11

p

12

x

2

p

21

p

22

i odpowiadaj ¾acy jej iloraz krzyzowy µ =

p

11

p

22

p

12

p

21

.

3.1 Pokaz, ze prawdziwe s ¾a nierówno´sci:

µ > 1 () P (Y = y

1

jX = x

1

) > P (Y = y

1

jX = x

2

) ;

µ > 1 () P (X = x

1

jY = y

1

) > P (X = x

1

jY = y

2

) ;

µ < 1 () P (Y = y

1

jX = x

1

) < P (Y = y

1

jX = x

2

) ;

µ < 1 () P (X = x

1

jY = y

1

) < P (X = x

1

jY = y

2

)

3.2 Udowodnij, ze dla kazdego µ > 0 i dla kazdych 0 < p < 1 i 0 < q < 1

istnieje tablica prawdopodobie´nstw 2 £ 2

Y

X

y

1

y

2

x

1

p

11

p

12

x

2

p

21

p

22

taka, ze jej iloraz krzyzowy jest równy µ i taka, ze p

1

¢

df

= p

11

+ p

12

= p oraz

p

¢2

df

= p

12

+ p

22

= q.

Wskazówka. Oznaczmy p

12

df

= x. Pokaz, korzystaj ¾

ac z w÷asno´sci Darboux,

ze równanie f (x) = µ ma zawsze rozwi ¾azanie. Funkcja f (x) jest zde…niowana

wzorem

f (x) =

(p ¡ x) (q ¡ x)

x (x + 1 ¡ p ¡ q)

3.3 Spróbuj wyznaczy´c tak ¾

a tablic ¾e dla µ = 1:5; p = 0:2; q = 0:6

4.

Test Â

2

i test oparty na ilorazie krzyzowym µ

4.1 Oblicz iloraz krzyzowy µ dla danych Pearsona o rozwoju umys÷owym i

…zycznym uczniów. Zilustruj na podstawie tych danych nierówno´sci, opisane w

70

´Cwiczenia

zadaniu 3.1, zast ¾epuj ¾ac odpowiednie prawdopodobie´nstwa przez ich cz ¾esto´sci. Co

te nierówno´sci oznaczaj ¾a?

4.2 Przedstaw t ¾e tablic ¾e w postaci standaryzowanej i narysuj odpowiadaj ¾

acy

jej wykres ko÷owy. Jak wygl ¾

ada w tablica w postaci standaryzowanej i odpowiada-

j ¾acy jej wykres ko÷owy dla przypadku niezalezno´sci i jednorodno´sci?

4.3 Zastosuj test Â

2

i test oparty na ilorazie krzyzowym µ dla testowania

hipotezy niezalezno´sci dla tych danych. Zapoznaj si ¾e z metod ¾a oblicze´n testu
Â

2

w programach Excel i Statistica

4.4 Znajd´z 95% przedzia÷ ufno´sci dla µ:
4.5 Dla lewego i prawego ko´nca tego przedzia÷u zbuduj tablice w postaci

standaryzowanej i narysuj odpowiadaj ¾ace im wykresy ko÷owe. Porównaj wykresy,

otrzymane w punktach 4.2 i 4.5. Jak z tych wykresów odczyta´c zalezno´s´c (nieza-
lezno´s´c) wierszy i kolumn?

Dane: Rozwój umys÷owy i …zyczny uczniów.

Rozwój umys÷owy

Rozwój …zyczny

dobry

z÷y

dobry

581

561

z÷y

209

351

´Zród÷o. Pearson, K., (1906) On the relationship of inteligence to size and shape of head,

and to other physical and mental characters, Biometrica, 5, 105-146

4.4 Wykonaj to samo dla danych:
Dane: Liczba dobrze rozwi ¾

azanych zada´n z matematyki

Zadania

P÷e´c

geometryczne niegeometryczne

uczennice

21

29

uczniowie

22

32

´Zród÷o. Wyniki matury próbnej z matematyki (poziom podstawowy) w III LO w Wa÷brzy-

chu w 2001 (informacja od nauczyciela)

5.

Test symetrii

5.1 Próba z rozk÷adu wielomianowego o prawdopodobie´nstwie
P (X = x

i

; Y = y

j

) = p

ij

; (i; j = 1; 2; :::; I ) umieszczona jest w tablicy N =

[n

ij

] (n

ij

jest liczb ¾

a obserwacji w próbie takich, ze X = x

i

oraz takich, ze

Y = y

j

).

Znajd´z test Â

2

do testowania hipotezy

H

0

:

p

ij

= p

ji

dla wszystkich i; j = 1; 2; :::; I.
5.2 Uzyj tego testu do testowania hipotezy H

0

w tablicy danych:

Dane: Porównanie wzrostu 205 par ma÷ze´nskich.

´Cwiczenia

71

Zona

M ¾az

wysoka ´srednia niska

wysoki

18

28

14

´sredni

20

51

28

niski

12

25

9

Co oznacza hipoteza H

0

dla wzrostu par ma÷ze´nskich?

´Zród÷o. Wyniki zebrane przez Galtona, Christensen [59]

5.3 Zbadaj symetri ¾e rozwoju umys÷owego i …zycznego uczniów
6.

Eksperyment przedszkolny. W 1962 roku przeprowadzono ekspery-

ment, w którym wzi ¾a÷o udzia÷ 123 dzieci z 3 i 4-letnich z ubogich rodzin w Ypsi-

lanti w stanie Michigan. Cz ¾e´s´c dzieci, wybranych losowo, ucz ¾eszcza÷a przez dwa
lata do przedszkola. Pozosta÷e dzieci do przedszkola nie ucz ¾eszcza÷y.

Zadania egzaminacyjne

1. Na ponizszym drzewku podane s ¾

a wyniki oblicze´n dla hierarchicznych model

logliniowych trzech zmiennych X; Y; Z. Na kraw ¾edzi, ÷ ¾acz ¾acej dwa modele

podane s ¾a warto´sci G

2

(M

r

jM

r

¡1

) :

Na przyk÷ad G

2

([X Z][Y Z] j[XY ][Y Z][XZ]) = 8: Pocz ¾atkowa warto´s´c, nie

zaznaczona na drzewku, oznaczaj ¾aca G

2

(M

1

jM

0

) = G

2

([XY ][Y Z][X Z] j[XY Z )

wynosi 10. Liczba róznych warto´sci cechy X jest równa I = 3;cechy Y jest
równa J = 4; cechy Z jest równa K = 2:

[XY][XZ][YZ]

[XZ][YZ]

[XY][XZ]

[XZ][Y]

[XZ][Y]

[X][Y][Z]

[XY][YZ]

[XY][Z]

[X][YZ]

4

4

8

4

8

4

12

10

14

8

4

2

2

Podaj wzór na ostateczny model, wynikaj ¾

acy z tych oblicze´n.

2. Tablica zawiera prawdopodobie´nstwa P (X = x

i

; Y = y

j

; Z = z

k

). Wybierz,

jaki typ zalezno´sci

(a) [XZ][Y Z]

72

´Cwiczenia

(b) [XY ][Z]

(c) [X][Y ][Z]

(d) zaden z nich

wyst ¾epuje w danych. Dla u÷atwienia, wystarczy sprawdzi´c czy warunek,

okre´slaj ¾acy typ zalezno´sci zachodzi dla p

111

z

1

z

2

y

1

0,060

0,240

y

2

0,040

0,060

y

1

0,240

0,160

y

2

0,160

0,040

x

1

x

2

3. Zmienna X ma dwie warto´sci: w wysokie zarobki, n niskie zarobki, zmi-

enna Y warto´sci - k kobieta, m m ¾ezczyzna, Z: s wykszta÷cenie ´srednie, z
wykszta÷cenie wyzsze. Model logitowy, ÷ ¾acz ¾acy te zmienne ma posta´c:

L = ¡1 ¡ Y

(m)

+ 2 Z

(w)

;

gdzie L jest logitem prawdopodobie´nstwa uzyskania wysokich zarobków,
Y

(m)

jest równe 1 gdy Y ma warto´s´c m, 0 gdy Y ma warto´s´c k; Z

(w)

jest

równe 1 gdy Z ma warto´s´c w, 0 gdy Z ma warto´s´c s.

(a) Kto ma wi ¾eksze prawdopodobie´nstwo wysokich zarobków: kobieta z

wykszta÷ceniem wyzszym, czy m ¾ezczyzna ze ´srednim?

(b) Ile to wi ¾eksze prawdopodobie´nstwo wynosi?

(c) Oblicz iloraz krzyzowy dla par zmiennych (Y; X)

4. Napisz uk÷ad równa´n w modelu logitowym proporcjonalnych szans, w którym

zmienna wynikowa P oznacza stosunek danej osoby do palenia: nie pali,
troch ¾e pali, duzo pali. Zmiennymi obja´sniaj ¾acymi s ¾a P p÷e´c: kobieta, m ¾ezczyzna,
R stosunek rodziców do palenia: oboje pal

¾

a, jedno z nich pali, zadne nie pali.

Jakie znaki b ¾ed ¾a mia÷y wspó÷czynniki przy zaprojektowanych przez ciebie
zmiennych obja´sniaj ¾

acych, je´sli dzieci obojga pal ¾acych rodziców wi ¾ecej pal ¾a

niz dzieci rodziców, z których jedno pali, a ci pal ¾a wi ¾ecej niz dzieci rodziców

niepal ¾acych. Podobnie, je´sli m ¾ezczy´zni pal ¾a wi ¾ecej od kobiet?

5. Cechy X i Y s ¾a niezalezne. Uzupe÷nij tabel ¾e z liczebno´sciami

?

?

4

8

12 16

28 ?

?

´Cwiczenia

73

6. W´sród studentów ADJ uzyskano nast ¾epuj ¾ace wyniki

ocena

2

3

4

5

Kobiety

10

40

120

10

M ¾ezczy´zni 10 10 80

20

Czy na poziomie 0.05 mozna twierdzi´c, ze wyniki z egzaminu i p÷e´c s ¾a od
siebie niezalezne?

Egzamin poprawkowy

1. Rozpoznaj w÷a´sciwy model zalezno´sci dla prawdopodobie´nstw:

z1

z2

y1

0,04

0,06

y2

0,18

0,12

y1

0,16

0,24

y2

0,12

0,08

x1

x2

Wsk. Wybierz spo´sród modeli: [??][??], [??][?], [X][Y][Z]. Zamiast ? musisz

wstawi´c odpowiednie litery X,Y,Z. Je´sli kilka modeli pasuje, wybierz jeden

z nich.

2. Zbuduj metod ¾

a najmniejszych kwadratów model logitowy dla danych:

W P

L

w

k

1

m 0

n

k

-1

m -1

gdzie L jest logitem prawdopodobie´nstwa dobrego samopoczucia, W wzrostem

(w - wysoki, n- niski), P p÷ci ¾a badanego.
Wsk. Metoda najmniejszych kwadratów dla danych (x

i

; y

i

) i = 1; 2; :::n w

modelu

y = f (x; ®; ¯; :::)

gdzie ®; ¯; ::: s ¾a nieznanymi parametrami modelu, polega na ich wyznacze-
niu takim, ze

n

X

i=1

(f (x

i

; ®; ¯; :::) ¡ y

i

)

2

osi ¾aga minimum wzgl ¾edem ®; ¯; :::

3. Po wykonaniu zad.2 wyznacz iloraz krzyzowy dla tablicy

zadowoleni niezadowoleni

kobiety
m ¾ezczy´zni

74

´Cwiczenia

dla kazdego ustalonego poziomu wzrostu. Która para dominuje

(a) zadowolone kobiety i niezadowoleni m ¾ezczy´zni, czy

(b) niezadowolone kobiety i zadowoleni m ¾ezczy´zni

4. Ala, Basia i Celina rzuca÷y po 100 razy, kazda swoj ¾a monet ¾a. Ala uzyska÷a

40 or÷ów, Basia i Celina po 30 or÷ów. Czy na poziomie 0.05 mozna twierdzi´c,
ze Ala i Basia rzuca÷y tak ¾a sam ¾a monet ¾a a prawdopodobie´nstwo wyrzucenia
or÷a przez Celin ¾e by÷o dwa razy mniejsze od prawdopodobie´nstwa wyrzuce-

nia or÷a przez Al ¾e?

5. Na ponizszym drzewku podane s ¾

a wyniki oblicze´n dla hierarchicznych model

logliniowych trzech zmiennych X; Y; Z. Na kraw ¾edzi, ÷ ¾

acz ¾acej dwa modele

podane s ¾a warto´sci G

2

(M

r

jM

r

¡1

) :

Na przyk÷ad G

2

([X Z][Y Z] j[XY ][Y Z][XZ]) = 8: Pocz ¾atkowa warto´s´c, nie

zaznaczona na drzewku, oznaczaj ¾aca G

2

(M

1

jM

0

) = G

2

([XY ][Y Z][X Z] j[XY Z )

wynosi 10. Liczba róznych warto´sci cechy X jest równa I = 4;cechy Y jest
równa J = 4; cechy Z jest równa K = 2:

[XY][XZ][YZ]

[XZ][YZ]

[XY][XZ]

[XZ][Y]

[XZ][Y]

[X][Y][Z]

[XY][YZ]

[XY][Z]

[X][YZ]

2

4

8

6

10

4

4

9

13

8

12

3

3

Znajd´z wszystkie modele, zaakceptowane na poziomie 0.05.

Indeks

Â

2

, 15

dane, 8

ilo´sciowe, 9
jako´sciowe, 9

G

2

, 15

hipoteza

jednorodno´sci, 18
niezalezno´sci, 21

iloraz krzyzowy, 24

reprezentacja standardowa, 25

kryterium

Akaike, 57
bayesowskie, 57

metoda

IPF, 64

model

hierarchiczny, 47
logarytmiczno-liniowy, 40
nasycony, 41
proporcjonalnych szans, 36
sta÷y, 41

niezalezno´s´c

warunkowa, 43

odchylenie G

2

, 15

odleg÷o´s´c

Â

2

Pearsona, 15

paradoks Simpsona, 40

regresja

logitowa, 32

ze zmiennymi nominalnymi, 34

ze zmiennymi porz ¾adkowymi, 36

probitowa, 33

rozk÷ad

dwumianowy, 13
wielomianowy, 14

produktowy, 14

rozk÷ad

Poissona, 13

skala

ilorazowa, 9
kwantylowa, 60
logitowa, 61
nominalna, 8
podwójnie logarytmiczna, 61
porz ¾adkowa, 8
prawdopodobie´nstw, 60
probitowa, 61
przedzia÷owa, 8

stopnie swobody

dla modeli prostych, 44

stosunek szans, 23

tablica

kontyngencji, 12

zapis bilansowy, 41
zmienna

grupuj ¾aca, 18
wynikowa, 18

zmienne

indykatorowe, 34

75

76

INDEKS

Literatura

[1] Agresti, A., (1990), Categorical Data Analysis, New York: Wiley

[2] Deming, W.E., Stephan F.F., (1940), On a least squares adjustment of a

sampled frequency table when the expected marginal totals are known. Ann.
Math. Statist.

11: 427-444

[3] Friendly,

M.,

Categorical

Data

Analysis

with

Graphics,

http://www.math.yorku.ca/SCS/Courses/grcat/

[4] McPherson, G.,(1990), Statistics in Scienti…c Investigation, New York:

Springer

77