
Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Podsumowanie
Każde bazowe rozwiązanie dopuszczalne jest
punktem wierzchołkowym zbioru X.
Istnieje punkt wierzchołkowy zbioru X w którym
funkcja celu zadania PL przyjmuje maksimum
Każdemu punktowi wierzchołkowemu zbioru X
odpowiada m wektorów liniowo niezależnych z
danego zbioru n wektorów związanych z tym
punktem.

Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Rozwiązania optymalne
Twierdzenie 6.1
Twierdzenie 6.1
Je
Je
ś
ś
li zadanie programowania liniowego PL posiada rozwi
li zadanie programowania liniowego PL posiada rozwi
ą
ą
zanie optymalne i
zanie optymalne i
wszystkie rozwi
wszystkie rozwi
ą
ą
zania bazowe s
zania bazowe s
ą
ą
niezdegenerowane to za pomoc
niezdegenerowane to za pomoc
ą
ą
algorytmu
algorytmu
simpleks uzyskuje si
simpleks uzyskuje si
ę
ę
rozwi
rozwi
ą
ą
zanie optymalne po co najwy
zanie optymalne po co najwy
ż
ż
ej
ej
m
n
iteracjach.
iteracjach.
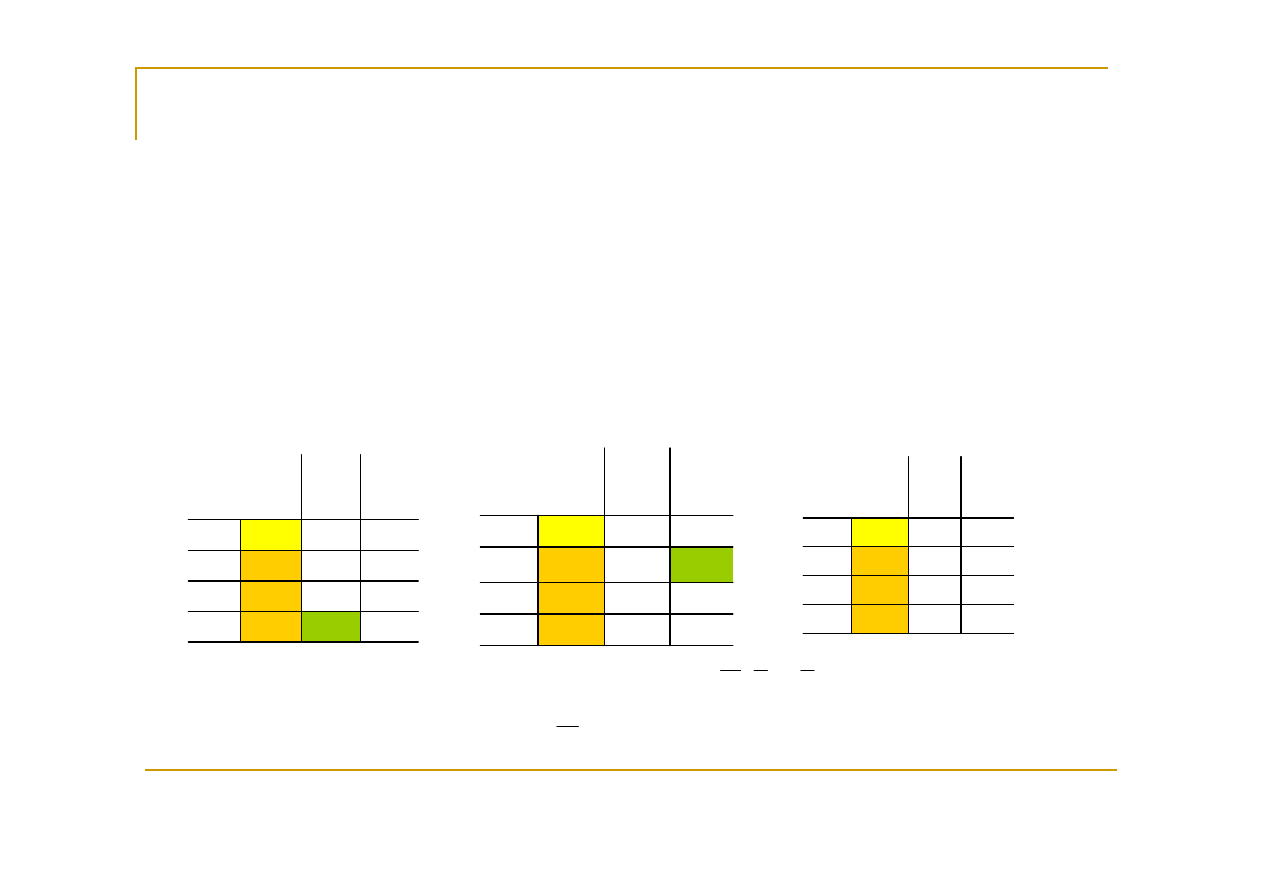
Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Zadanie programowania liniowego PL dla ograniczeń mniejszościowych
2
1
0
1
2
max
x
x
X
x
+
=
∈
x
≥
≤
+
≤
+
−
≤
+
=
0
,
21
2
6
0
5
:
2
1
2
1
2
1
x
x
x
x
x
x
x
x
X
2
6
21
x
5
1
-1
0
x
4
1
1
5
x
3
-1
-2
0
x
0
x
2
x
1
Przykład:
Założenia:
1. Zbiór X rozwiązań dopuszczalnych
2. algorytm simpleks startuje z bazowego dopuszczalnego rozwiązania oraz w
trakcie jego realizacji nie występuje degeneracja
I. Zadanie programowania liniowego PL posiada jedno rozwiązanie
Rozwiązanie bazowe optymalne:
Wartość optymalna funkcji celu:
4
31
]
0
,
4
1
,
0
,
4
9
,
4
11
[
]
.
,
,
,
[
0
5
4
3
2
1
=
=
=
∧
x
x
x
x
x
x
x
T
T
1/3
1/6
7/2
x
1
4/3
1/6
7/2
x
4
2/3
-1/6
3/2
x
3
-1/3
1/3
7
x
0
x
2
x
5
-1/2
1/4
11/4
x
1
-2
1/2
1/2
x
4
3/2
-1/4
9/4
x
2
1/2
1/4
31/4
x
0
x
3
x
5
0
≠
X
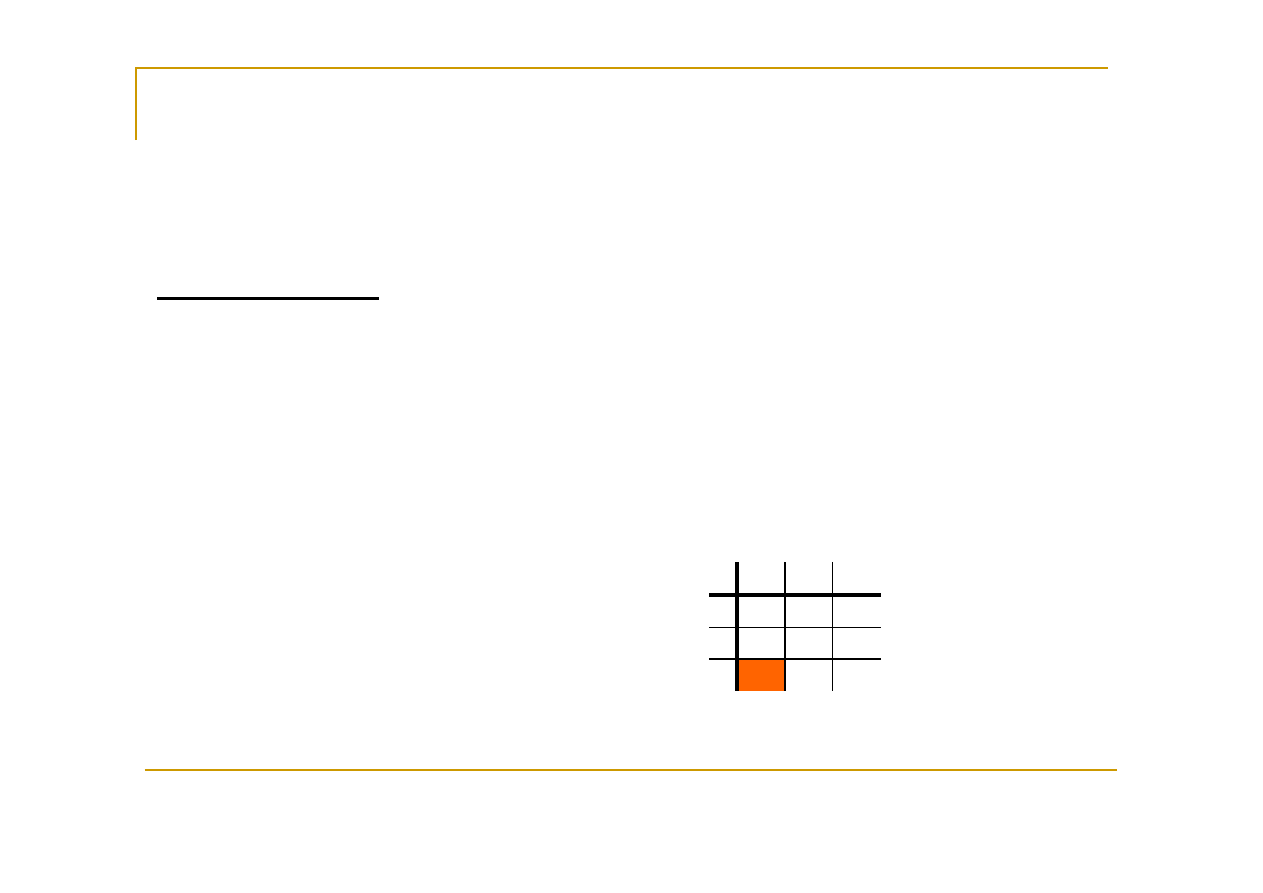
Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Przypadki szczególne cd.
Twierdzenie 6.2
Jeśli zadanie PL jest nieograniczone, to istnieją rozwiązania
bazowe dopuszczalne
oraz wektor
taki, że:
Wówczas zbiór rozwiązań jest pusty.
B
x
K
y
,
min
2
1
0
x
x
x
−
−
=
0
,
1
2
2
1
2
1
2
1
≥
−
≥
−
≤
−
−
x
x
x
x
x
x
m
i
dla
y
i
y
ik
k
,...,
1
0
0
0
=
≤
<
Przykład:
II. Zadanie programowania liniowego - nieograniczone
x
1
x
2
x
0
0
-1
-1
x
3
2
-1
1
x
4
1
-1
1

Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Przypadki szczególne cd.
III. Zadanie programowania liniowego – posiadające nieskończoną ilość
rozwiązań optymalnych na zbiorze ograniczonym
Ten przypadek wystąpi wtedy, gdy można znaleźć tablicę simpleksową, której
odpowiada optymalne rozwiązanie bazowe, takie że:
i istnieje para
dla której:
Dla przestrzeni o wymiarze n rozwiązanie optymalne jest kombinacją wypukłą
wierzchołków należących do zbioru optymalnego.
i
x
[ ]
p
i
gdy
x
x
i
p
i
i
p
i
i
i
,...,
1
,
1
,
0
,
1
1
1
=
∈
=
=
∑
∑
=
∧
=
∧
∧
λ
λ
λ
n
j
dla
y
oraz
m
i
dla
y
j
i
,...,
1
0
,...,
1
0
0
0
=
≥
=
≥
(
)
{
}
{
}
n
j
m
i
j
i
,...,
1
,
,...,
1
,
,
0
0
0
0
∈
∈
0
0
,
0
0
0
0
0
0
0
>
>
=
j
i
i
j
y
i
y
y
!!
Dla rozwiązania zdegenerowanego, przypadek ten może zaistnieć również
pod innymi warunkami.
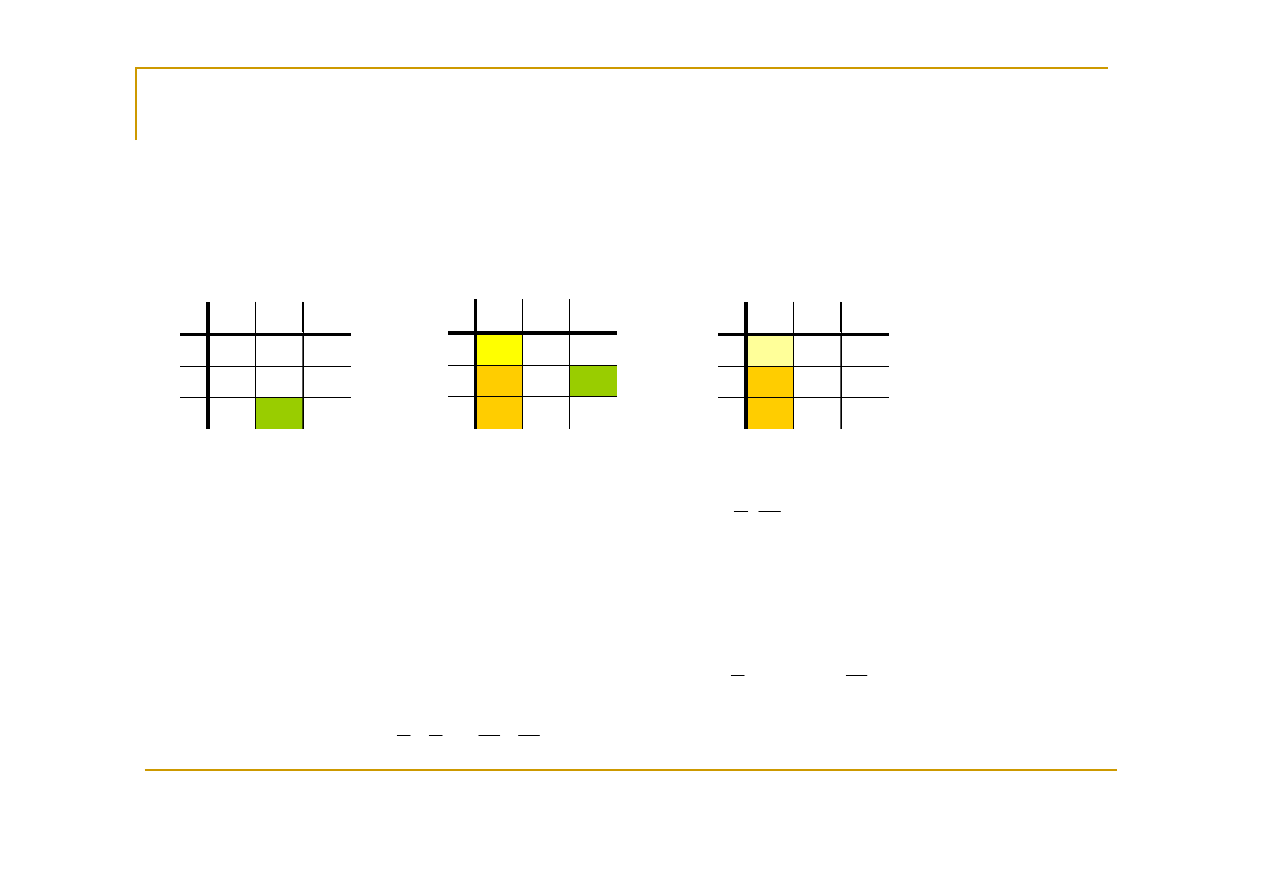
Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Przypadki szczególne cd.
III. Przykład gdy jest wiele rozwiązań optymalnych na zbiorze ograniczonym
x
1
x
2
x
0
0
-4
-2
x
3
4
-1
1
x
4
6
2
1
x
4
x
2
x
0
12
2
0
x
3
7
0.5
1.5
x
1
3
0.5
0.5
x
4
x
3
x
0
12
2
0
x
2
4.66 0.33 0.66
x
1
0.66 0.33
0.5
•1 rozwiązanie bazowe optymalne:
•2 rozwiązanie bazowe optymalne:
T
T
x
x
]
3
14
,
3
2
[
]
0
,
3
[
2
1
=
=
∧
∧
Zadanie posiada dwa dopuszczalne bazowe rozwiązania optymalne. Odpowiadają one dwóm
wierzchołkom w zbiorze rozwiązań optymalnych.
Zbiór rozwiązań optymalnych
[ ]
{
}
[ ]
.
)
3
14
3
14
(
),
3
7
3
2
(
:
1
,
0
)),
1
(
3
14
0
(
)),
1
(
3
2
3
(
:
1
,
0
,
)
1
(
:
2
1
−
+
=
=
∈
−
+
−
+
=
=
∈
−
+
=
=
∧
λ
λ
λ
λ
λ
λ
λ
λ
λ
x
x
x
x
x
x
x
x
X
2
1
0
2
4
max
x
x
X
x
+
=
∈
x
≥
≤
+
≤
+
−
=
0
,
6
2
4
:
2
1
2
1
x
x
x
x
x
x
X

Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Przypadki szczególne cd.
IV. Zadanie programowania liniowego – posiadające nieskończoną ilość
rozwiązań optymalnych na zbiorze nieograniczonym
Ten przypadek wystąpi wtedy, gdy można znaleźć tablicę simpleksową, której odpowiada optymalne
rozwiązanie bazowe, takie że:
dla której, że istnieje j
0
takie, że i dla wszystkich „i” zachodzi
y
i0
=0 (degeneracja) bądź
0
0
0
=
j
y
n
j
dla
y
oraz
m
i
dla
y
j
i
,...,
1
0
,...,
1
0
0
0
=
≥
=
≥
0
0
0
≤
j
y
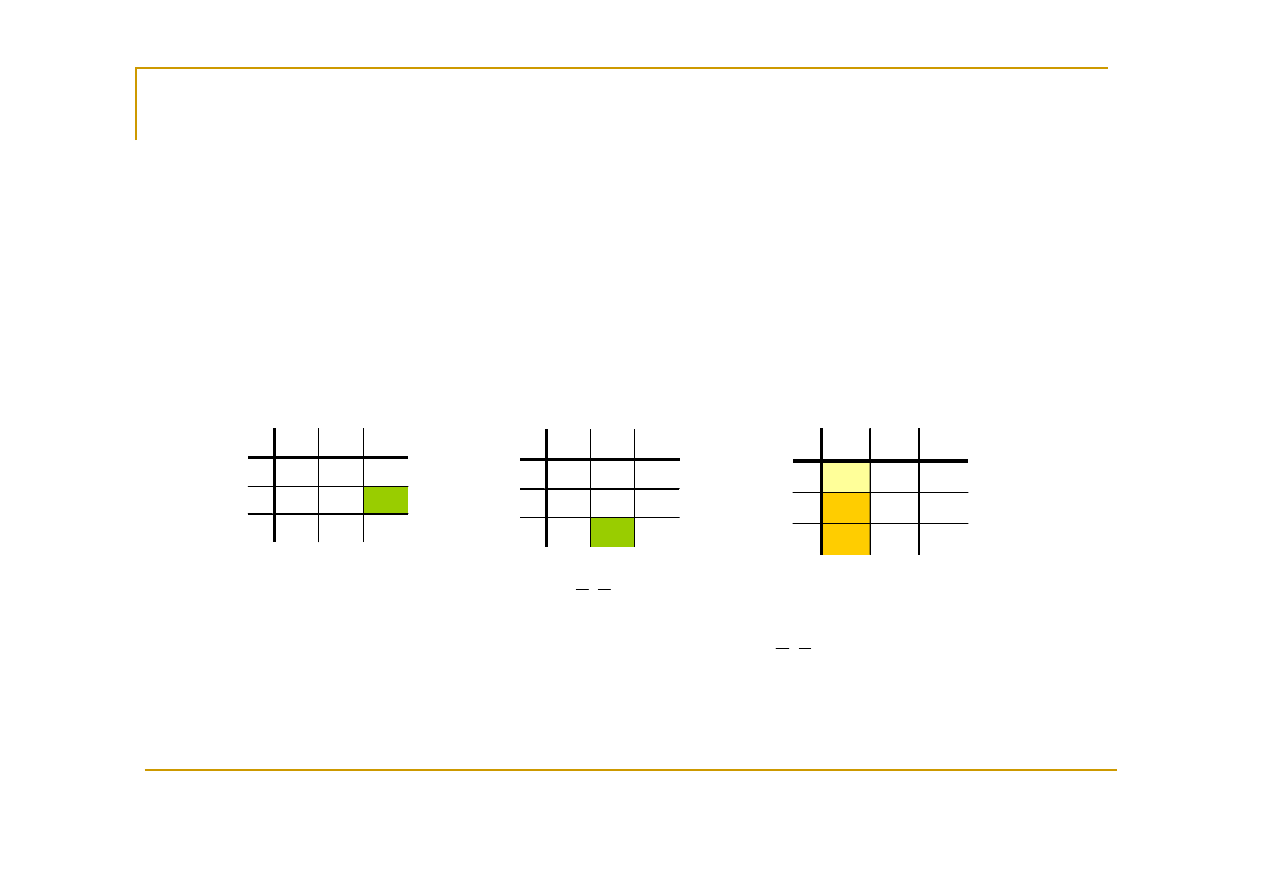
Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
Rozwiązanie optymalne zadania PL przyjmuje postać parametryczną:
Dla n=2 równanie parametryczne prostej,
Dla n=3 równanie parametryczne płaszczyzny itd.
T
x
)
3
7
,
3
2
(
=
∧
Przykład:
Bazowe rozwiązanie optymalne:
Zbiór rozwiązań optymalnych jest półprostą:
≥
+
=
∈
=
∧
∧
0
,
)
3
1
,
3
2
(
:
2
t
t
x
x
R
x
X
T
2
1
0
4
2
max
x
x
X
x
+
−
=
∈
x
≥
≤
+
−
≤
+
−
=
0
,
4
2
1
1
2
:
2
1
2
1
x
x
x
x
x
x
X
x
1
x
2
x
0
0
2
-4
x
3
1
-2
1
x
4
4
-1
2
x
4
x
3
x
0
4
-6
4
x
2
1
-2
1
x
4
2
3
-2
x
4
x
3
x
0
8
2
0
x
2
2.33 0.66 -0,33
x
1
0.66 0.33 -0,66
IV. Zadanie programowania liniowego – posiadające nieskończoną ilość
rozwiązań optymalnych na zbiorze nieograniczonym
cd

Technika optymalizacji
Dr inż. Ewa Szlachcic
Wydzia
Wydzia
ł
ł
Elektroniki
Elektroniki
Kierunek
Kierunek
EiT
EiT
III r Potok: Elektronika
III r Potok: Elektronika
.
.
V. Zadanie programowania liniowego – zbiór rozwiązań dopuszczalnych
jest zbiorem pustym - brak rozwiązania
φ
=
X
2
1
0
4
max
x
x
X
x
+
=
∈
x
≥
−
≤
−
≤
+
=
0
,
2
4
:
2
1
2
1
x
x
x
x
x
x
X
W tej wersji metody prymalnej simpleks algorytm nie potrafi stworzyć pierwszego
rozwiązania bazowego dopuszczalnego z powodu wektora b, który posiada składowe
ujemne.
Przykład:
x
1
x
2
x
0
0
-1
-4
x
3
4
1
1
x
4
-2
1
-1
−
+
=
=
2
4
2
1
b
b
b
m
i
dla
y
i
,...,
1
0
0
=
≥
Nie jest spełniony warunek dopuszczalności pierwszej tablicy simpleks
Krok 1.
(start). Rozpoczynamy algorytm od znalezienia pierwszego rozwiązania bazowego
dopuszczalnego. Należy sprawdzić dopuszczalność
rozwiązania:
Wyszukiwarka
Podobne podstrony:
5w to przypadki 2011
5w to pl przypadki
1w to wprowadzenie 2011
6w to dpl 2011
6 sposobów na to, PITY 2011, Informacje o podatkach, dokumenty
7w to wlasnosci 2011
4w to simpleks 2011
3w to proglin 2011
2w to przyklady 2011
więcej podobnych podstron