F1-37 

Minimalizacja „oparta na kostkach”

 

 

• 

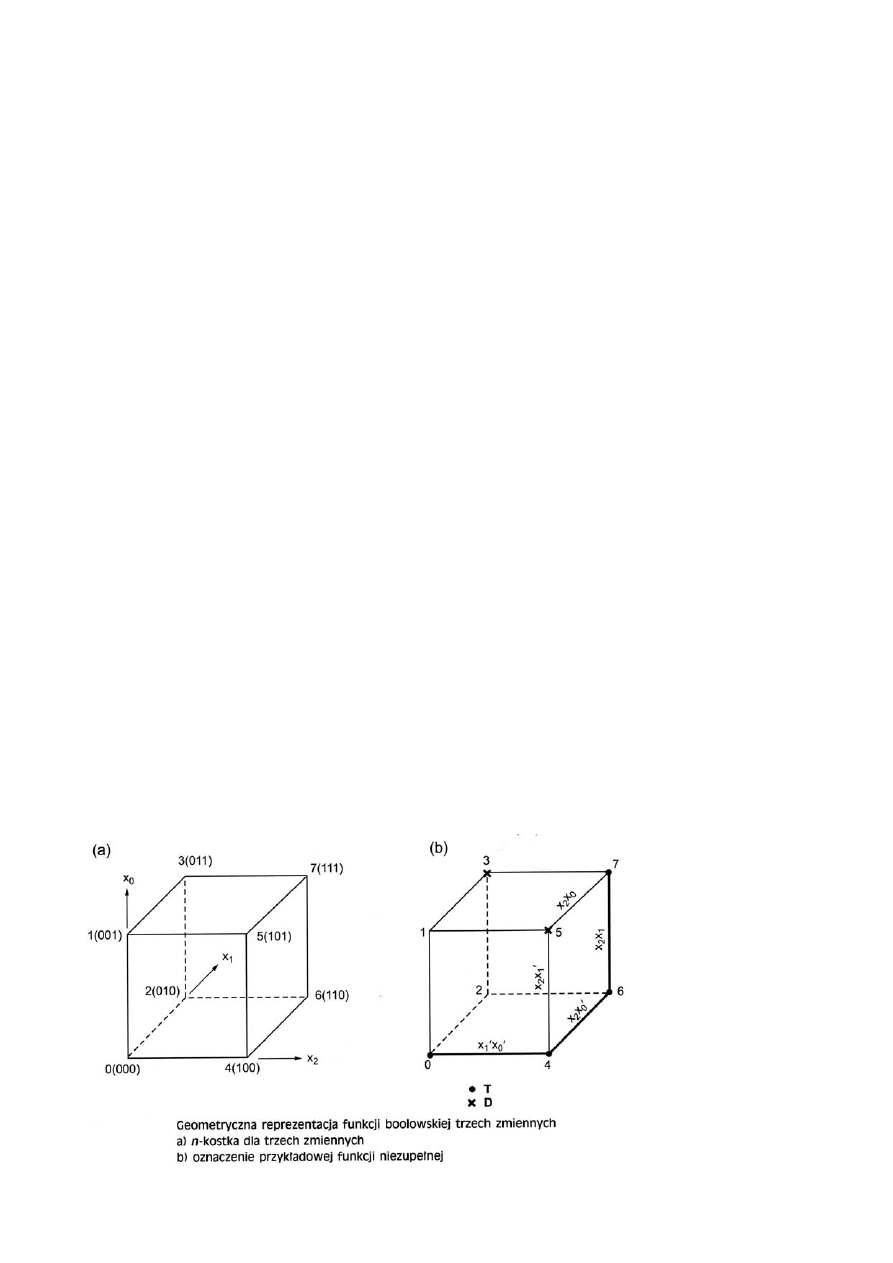
Funkcję boolowską n zmiennych można przedstawić w postaci 
n-wymiarowej kostki (n-kostki)

  

 

•  Każdy wierzchołek (0-kostka) reprezentuje jeden z możliwych 

2

n

 mintermów 

•  Dwa wierzchołki są 

sąsiednimi

, jeżeli opisujące je liczby 

dwójkowe różnią się na jednej pozycji. 
 

•  Wierzchołki oznacza się odpowiednimi liczbami dwójkowymi b

k

 

lub równoważnikami dziesiętnymi k

 

– zaznacza się wierzchołki, 

dla których k 

∈ T lub k ∈ D. 

 

•  Zbiór 2

i

 wierzchołków n-kostki tworzy i-(sub)kostkę opisaną 

przez (n – i) zmiennych. 
 

• 

Krawędź

 łącząca dwa sąsiednie wierzchołki stanowi 

1-kostkę

 

opisaną (n – 1) zmiennymi (1-kostka 

pokrywa

 dwie 0-kostki) 

 

• 

2-kostka 

jest

 kwadratem

, a

 3-kostka 

jest

 sześcianem.

 

 

• 

Przykład:

    T = {0, 4, 6, 7}    i    D = {3, 5} 

 

Dwie 0-kostki 0 i 4 ► 1-kostka 

l

l

x x

1 0

 |  Cztery 0-kostki 4,5,6,7 ► 2-kostka 

x

2

  

0-kostka 5 

wykorzystana

,  0-kostka 3 

niewykorzystana

 

 
 
 

Forma minimalna: 

 

l

l

x x

1 0

 + x

2

 

© J. Kalisz, WAT, 2008