Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych
Nr 59
Politechniki Wrocławskiej
Nr 59
Studia i Materiały Nr
26
2006
__________
dławik, indukcyjność, pomiar indukcyjności
Józef NOWAK
*
, Jerzy BAJOREK
*
, Andrzej KAŁWAK
*
, Józef KOLASA
*
,
Grzegorz KOSOBUDZKI
F
*
WYZNACZANIE INDUKCYJNOŚCI DŁAWIKÓW
W WARUNKACH ICH PRACY
W elektroenergetyce dławiki są stosowane najczęściej do tłumienia pulsacji wyprostowanego
prądu zmiennego głównie dla potrzeb trakcji elektrycznej. Parametrem charakteryzującym dławik
jest jego indukcyjność, którą należy wyznaczyć przy obecności dużej składowej stałej prądu i w za-
leżności od wartości tej składowej.
Jednoznacznie określonej metody wyznaczania indukcyjności dławików nie ma. Normy [1] i [2]
pozostawiają sposób pomiaru do uzgodnienia pomiędzy użytkownikiem a wykonawcą. Postawione są
tylko wymagania: aby badania typu wykonać prądem, którego przebieg odpowiada rodzajowi pracy
dławika, aby metoda pomiaru uwzględniała składową zmienną nałożoną na prąd stały oraz aby wyni-
ki pomiarów indukcyjności podać w funkcji wartości średniej prądu pulsującego w całym zakresie
stosowania dławika.
Do pomiaru indukcyjności dławików opracowywanych i produkowanych dla potrzeb trakcji elek-
trycznej stosuje się specjalnie wykonywaną aparaturę laboratoryjną i trudne do stosowania modele
teoretyczne dla jej wyznaczenia [3]. Z przeprowadzonych przez autorów badań wynika, że są tyko
dwie możliwości wyznaczenia indukcyjności dławika w warunkach jego pracy. Rzeczywistą wartość
indukcyjności dławików o charakterystyce liniowej, nieliniowej symetrycznej, nieliniowej niesyme-
tryczne oraz nieliniowej niejednoznacznej można wyznaczyć tylko dla zerowej składowej zmiennej
prądu; zarówno wtedy, gdy przebieg prądu jest symetryczny jak również wtedy, gdy zawiera składo-
wą stałą. Uśrednioną indukcyjność dławika w warunkach jego pracy można natomiast wyznaczyć
mierząc powierzchnię pętli, jaką tworzy charakterystyka dławika we współrzędnych prąd, napięcie
(moc bierną) i wartość skuteczną pochodnej prądu [4].
Układ dla wyznaczenia indukcyjności dławików w warunkach ich pracy można zestawić stosując
wcześniej opracowany przez nas indukcyjny czujnik prądu oraz synchronicznie działające przetwor-
niki wartości chwilowych liniowo przetworzonych przebiegów wielkości elektrycznych i magne-
tycznych [5, 6].
1. ANALIZA TEORETYCZNA
*
Politechnika Wrocławska, Instytut Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław
ul. Smoluchowskiego 19; jerzy.bajorek@pwr.wroc.pl; andrzej.kalwak@pwr.wroc.pl;
jozef.kolasa@pwr.wroc.pl; grzegorz.kosobudzki@pwr.wroc.pl
1.1. DŁAWIK
Dławik jest obiektem elektromagnetycznym, w którym energia prądu elektrycznego
zamienia się głównie na energię pola magnetycznego. Zasadniczym elementem dławika
jest uzwojenie (cewka). Jeśli wytworzony, na skutek przepływu prądu w uzwojeniu,
strumień magnetyczny zamyka się w powietrzu, to charakterystyka dławika
( )
i
f
=
ψ
(1.1)
jest liniowa, gdzie ψ – strumień magnetyczny skojarzony z uzwojeniem, i – prąd. Dla
wzmocnienia strumienia w dławiku stosuje się obwody ferromagnetyczne całkowicie
zamknięte lub ze szczeliną powietrzną. Charakterystyka dławika (1.1) staje się wtedy
nieliniowa. Dławiki pracują przy zasilaniu symetrycznym napięciem, a także w obecno-
ści składowej stałej w napięciu i pobieranym przez dławik prądzie.
1.2. DEFINICJA INDUKCYJNOŚCI.
Siła elektromotoryczna indukowana w uzwojeniu obejmującym strumień magne-
tyczny w dławiku jest proporcjonalna do pochodnej tego strumienia
dt
d
e
ψ
−
=
. (1.2)
Jeżeli strumień ψ skojarzony z uzwojeniem jest proporcjonalny do prądu w uzwo-
jeniu, to równanie (1.2) zapisuje się w postaci
dt
di
L
e
⋅
−
=
, (1.3)
gdzie
i
L
ψ
=
(1.4)
− indukcyjnością dławika liniowego.
Strumień skojarzony z uzwojeniem dławika o liczbie zwojów N jest równy sumie
strumieni
n
φ
objętych przez poszczególne zwoje uzwojenia dławika
. (1.5)
∑
=
=
N
1
n
n
ψ
φ
Jeżeli każdy zwój obejmuje ten sam strumień, to
φ
ψ
⋅
= N
. (1.6)
Jeżeli w obwodzie magnetycznym dławika występują elementy ferromagnetyczne,
to indukcyjność dławika nie jest stała, lecz zależy od prądu. Zależność jest nie tylko
nieliniowa ale także niejednoznaczna. Indukcyjność definiuje się jednak nadal na pod-
stawie równań (1.2) i (1.3), Z których wynika, że
di
d
L
ψ
=
. (1.7)
1.3. MODELE ZASTĘPCZE DŁAWIKA.
Procesy elektromagnetyczne zachodzące w dławiku można modelować za pomocą
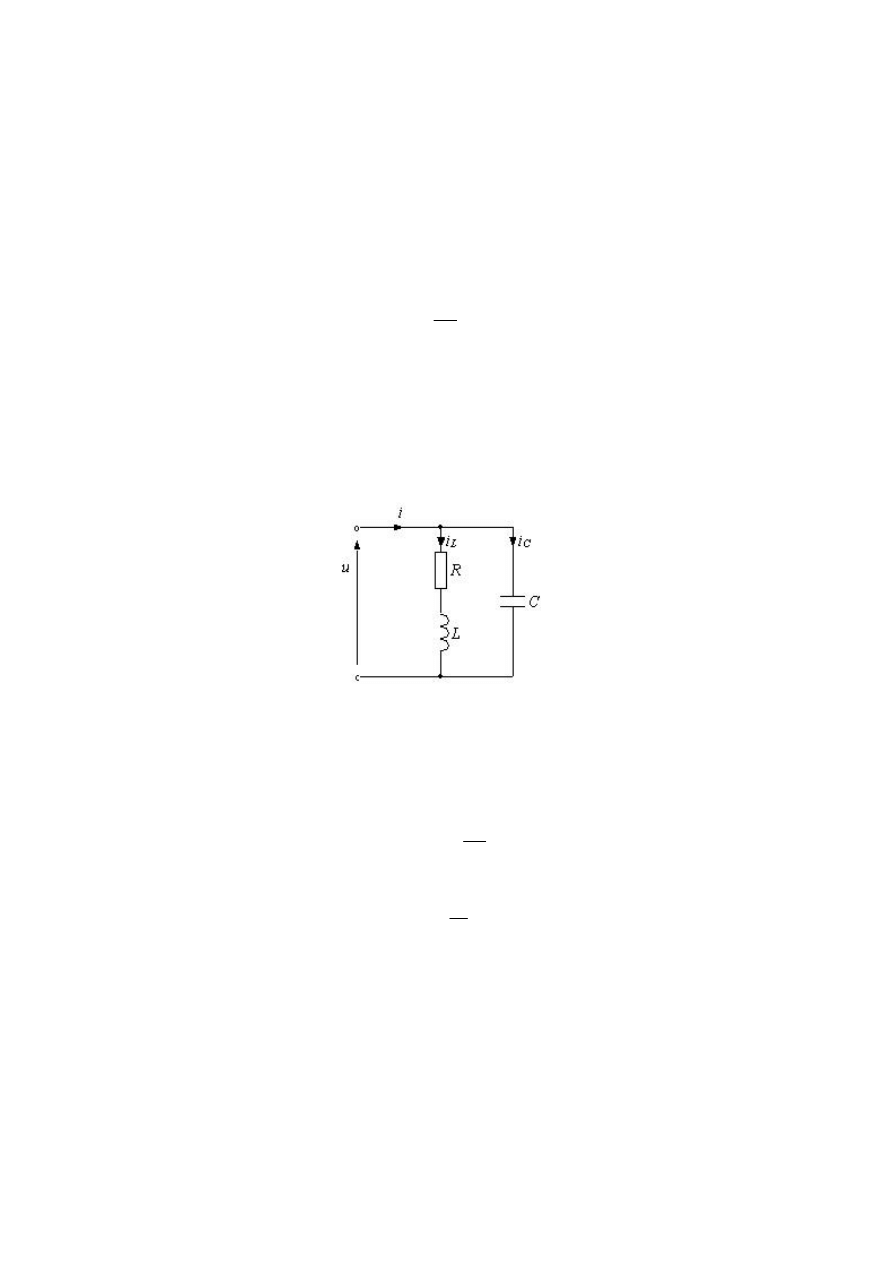
obwodu elektrycznego (rys.1.1). Rezystancja R modeluje rozpraszanie energii elek-
trycznej w uzwojeniu i elementach ferromagnetycznych, C przedstawia zastępczą
pojemność elektryczną między zwojami cewki, natomiast L jest indukcyjnością dła-
wika.
Rys. 1.1. Obwód elektryczny modelujący procesy elektromagnetyczne zachodzące w dławiku
Fig. 1.1. Electric circuit modeling electromagnetic process proceed in reactor
Prąd i pobierany przez obwód zależy od napięcia u według równań
C
L
i
i
i
−
=
, (1.8)
dt
di
L
i
R
u
L
L
⋅
+
⋅
=
, (1.9)
gdzie
dt
du
C
i
C
⋅
=
(1.10)
− prąd płynący przez pojemność C. Z równań (1.8), (1.9) i (1.10) otrzymuje się
jedno równanie
2
2
dt
u
d
C
L
dt
du
C
R
dt
di
L
i
R
u
⋅
⋅
−
⋅
⋅
−
⋅
+
⋅
=
(1.11)
− model matematyczny dławika.
Równanie różniczkowe (1.11) jest równaniem nieliniowym, z którego nie da się
wyznaczyć indukcyjności L w przypadku ogólnym, na podstawie napięcia i pobiera-
nego prądu przez dławik w warunkach jego pracy. Model dławika (rys.1.1) trzeba
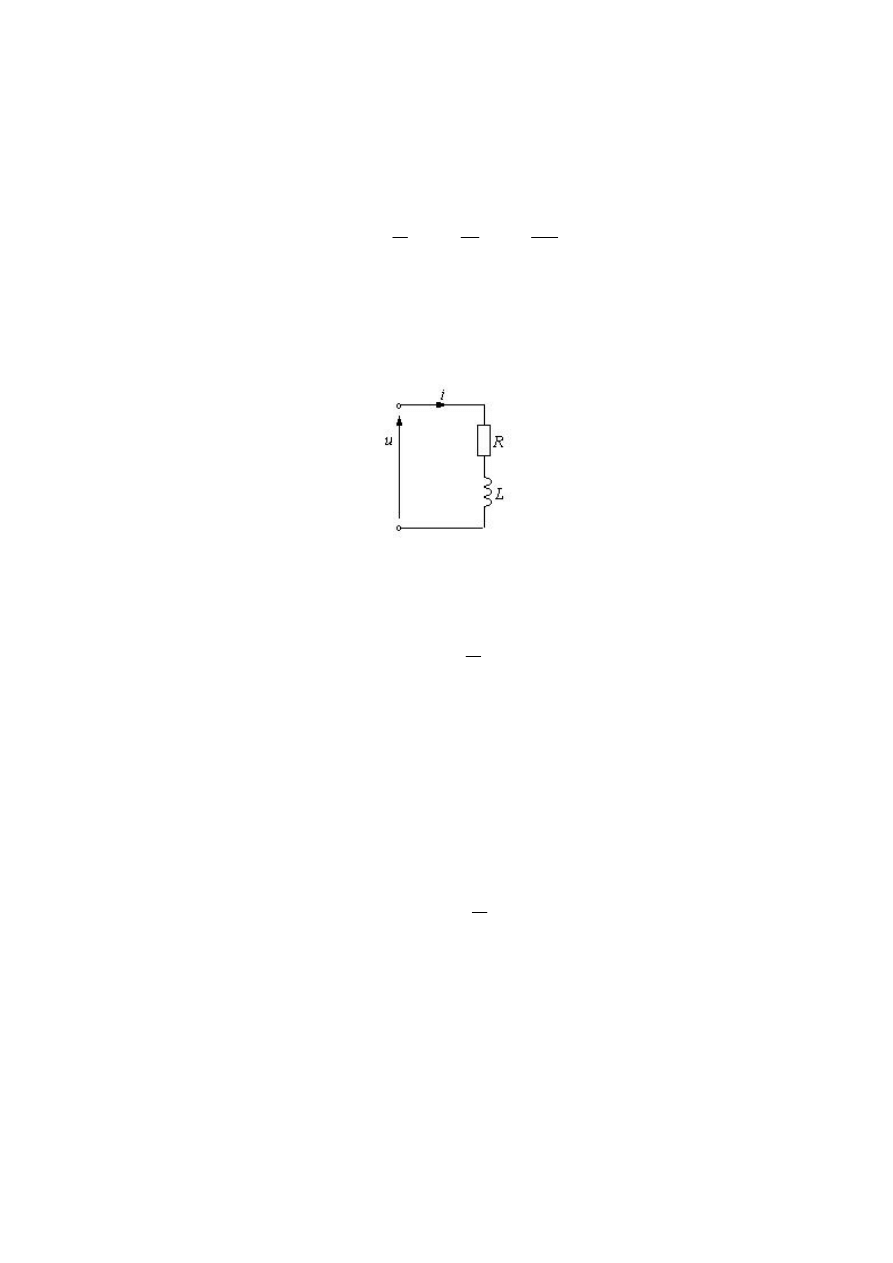
koniecznie uprościć. Należy pominąć pojemność C, pozostawiając szeregowo połą-
czoną rezystancję R i indukcyjność L (rys.1.2).
Rys. 1.2. Uproszczony obwód zastępczy dławika
Fig. 1.2. Simplified equivalent circuit of reactor
Równanie opisujące uproszczony obwód zastępczy dławika jest liniowe
dt
di
L
i
R
u
⋅
+
⋅
=
. (1.12)
Z tego równania da się wyznaczyć indukcyjność L nawet wtedy, gdy nie jest stała
oraz gdy jest wieloznaczna.
Jeśli prąd i pobierany przez dławik zawiera składową zmienną i
~
i składową stałą i
=
=
+
=
i
i
i
~
, (1.13)
to również napięcie przyłożone u do dławika zawiera składową zmienną u
~
i skła-
dową stałą u
=
=
+
=
u
u
u
~
. (1.14)
Podstawiając zależności (1.13) i (1.14) do równania (1.12) otrzymuje się
(
)
(
=
=
=
+
+
+
=
+
i
i
d
)
t
d
L
R
i
i
u
u
~
~
~
. (1.15)
Rezystancja R modeluje proces rozpraszania energii elektrycznej w obwodzie prą-
dowym i w magnetowodzie
m
R
R
R
+
=
1
. (1.16)
Jeśli w równaniu (1.15) uwzględni się zależność (1.16) oraz właściwości:
− pochodna składowej stałej jest równa zeru
0
=
=
dt
di
,
− składowa stała napięcia jest tylko spadkiem napięcia na rezystancji obwodu prą-
dowego spowodowanym przez składową stałą prądu
=
=
= i
R
u
1
,
− składowa stała prądu nie powoduje spadku napięcia na rezystancji dynamicznej
magnetowodu
0
=
=
i
R
m
,
to równanie (1.15) upraszcza się do postaci
dt
di
L
Ri
u
~
~
~
+
=
. (1.17)
Równanie (1.17), dla składowych zmiennej przy obecności składowej stałej w na-
pięciu i w prądzie, ma dokładnie taką samą postać jak równanie (1.12). Wynika stąd,
że cała informacja o parametrach R, L jest zawarta w składowych zmiennych napięcia
i prądu. Dla wyznaczenia parametrów R, L nie jest więc potrzebne uwzględnienia
składowych stałych tych wielkości.
2. BADANIA EKSPERYMENTALNE
2.1. SYSTEM WYZNACZANIA INDUKCYJNOŚCI
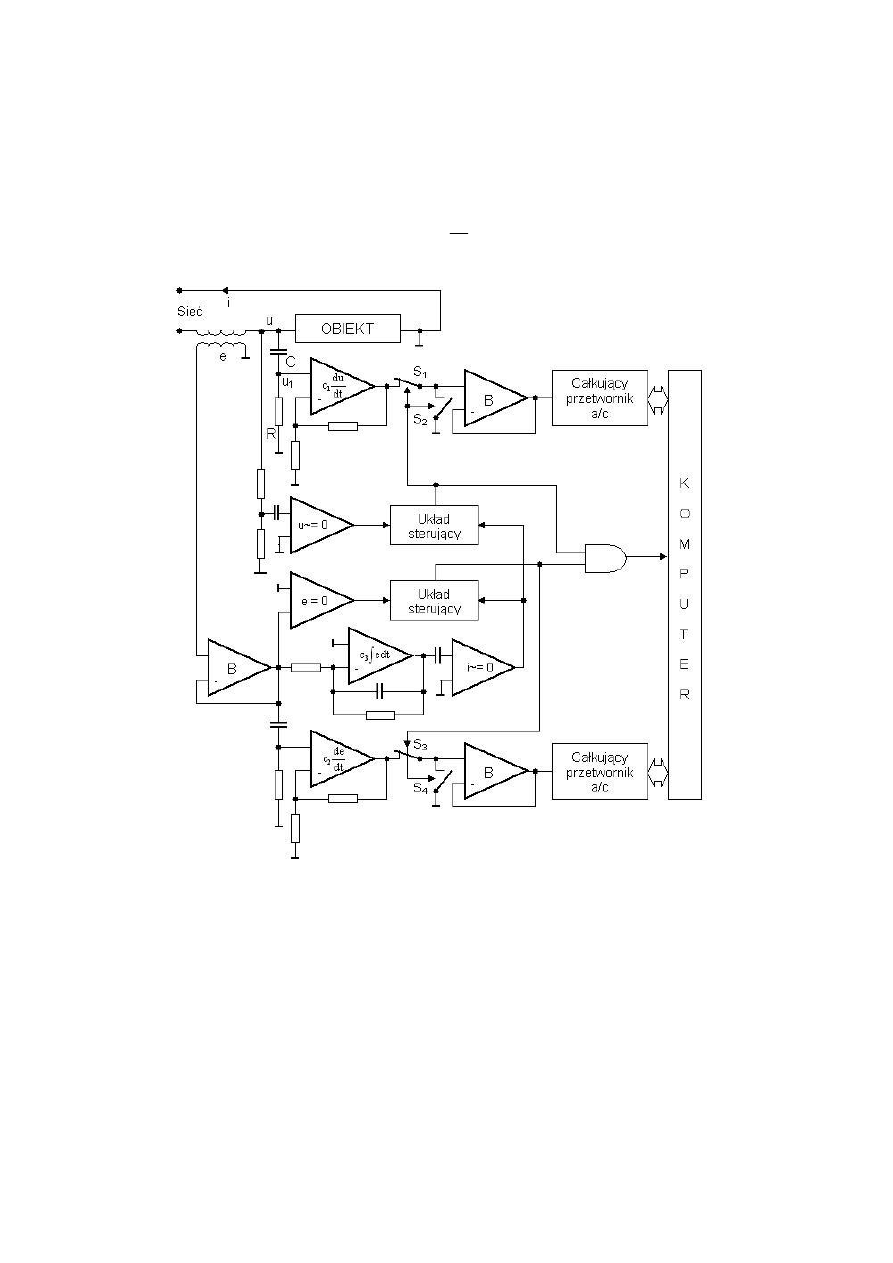
Opracowany układ dla wyznaczania indukcyjności dławika w warunkach jego pra-
cy, realizujący funkcje wynikające z równania (1.17), jest przedstawiony na rysunku
2.1. Sygnał
dt
di
M
e
−
=
, (2.1)
zależny tylko od składowej zmiennej pobieranego przez dławik prądu, otrzymuje
się stosując do przetwarzania prądu czujnik indukcyjny [6]. Sygnał zależny tylko od
składowej zmiennej napięcia otrzymuje się za pomocą dzielnika pojemnościowo-
rezystancyjnego. Jeśli spadek napięcia na rezystancji (sygnał) jest o kilka rzędów
mniejszy od spadku napięcia na pojemności, to
dt
du
RC
u
=
1
. (2.2)
Rys. 2.1.Układ do wyznaczania indukcyjności dławika w warunkach jego pracy
Fig. 2.1. System for determining inductance of reactor under normal operating conditions
Dla dowolnego przebiegu składowej zmiennej napięcia i składowej zmiennej prą-
du, prawidłową wartość indukcyjności otrzymuje się tylko dla zerowej wartości chwi-
lowej prądu (1.17). Jeśli w chwili t
0
i(t
0
) = 0, to
)
(
)
(
0
~
0
~
t
i
t
u
L
′
=
, (2.3)
gdzie i’
~
− pochodna prądu.
Chwila t
0
, w której składowa zmienna prądu przechodzi przez wartość zerową jest
wykrywana (w układzie rysunek 2.1) przez porównanie scałkowanego sygnału (2.1) z
wartością zerową za pomocą komparatora napięcia. Wartość napięcia w chwili t
0
jest
wynikiem operacji całkowania wzmocnionego sygnału (2.2) w przedziale czasu od
chwili t
0
do chwili najbliższego przejścia napięcia przez wartość zerową (próbkowanie
całkowe napięcia). Dla otrzymania wartości pochodnej prądu w chwili t
0
realizowana
jest operacja całkowania zróżniczkowanego sygnału (2.1) w przedziale od chwili t
0
do
chwili najbliższego przejścia pochodnej prądu przez wartość zerową (próbkowanie
całkowe pochodnej prądu). Chwila, w której składowa zmienna napięcia przechodzi
przez wartość zerową jest wykrywana przez porównanie tej składowej z wartością
zerową. Podobnie jest wykrywana chwila przejścia pochodnej prądu przez wartość
zerową – przez porównanie sygnału (2.1) z wartością zerową.
2.2. ZALEŻNOŚĆ INDUKCYJNOŚCI OD PRĄDU
Badania zależności charakterystyk dławików od wartości chwilowych prądu wy-
konano przy symetrycznym przemagnesowywaniu ich obwodów magnetycznych.
Schemat zestawionego do badań układu pomiarowego przedstawia rysunek 2.2.
Układ zawiera trzy tory pozwalające synchronicznie (jednocześnie) mierzyć wartości
chwilowe napięcia, prądu i pochodnej prądu oraz ciągi tych wartości chwilowych
równomiernie wypełniające okres. Tor 1 służący do pomiaru wartości chwilowych
napięcia można łatwo dostosować do pomiaru wartości chwilowych strumienia za-
stępczego; wystarczy tylko pominąć układ różniczkujący napięcie.
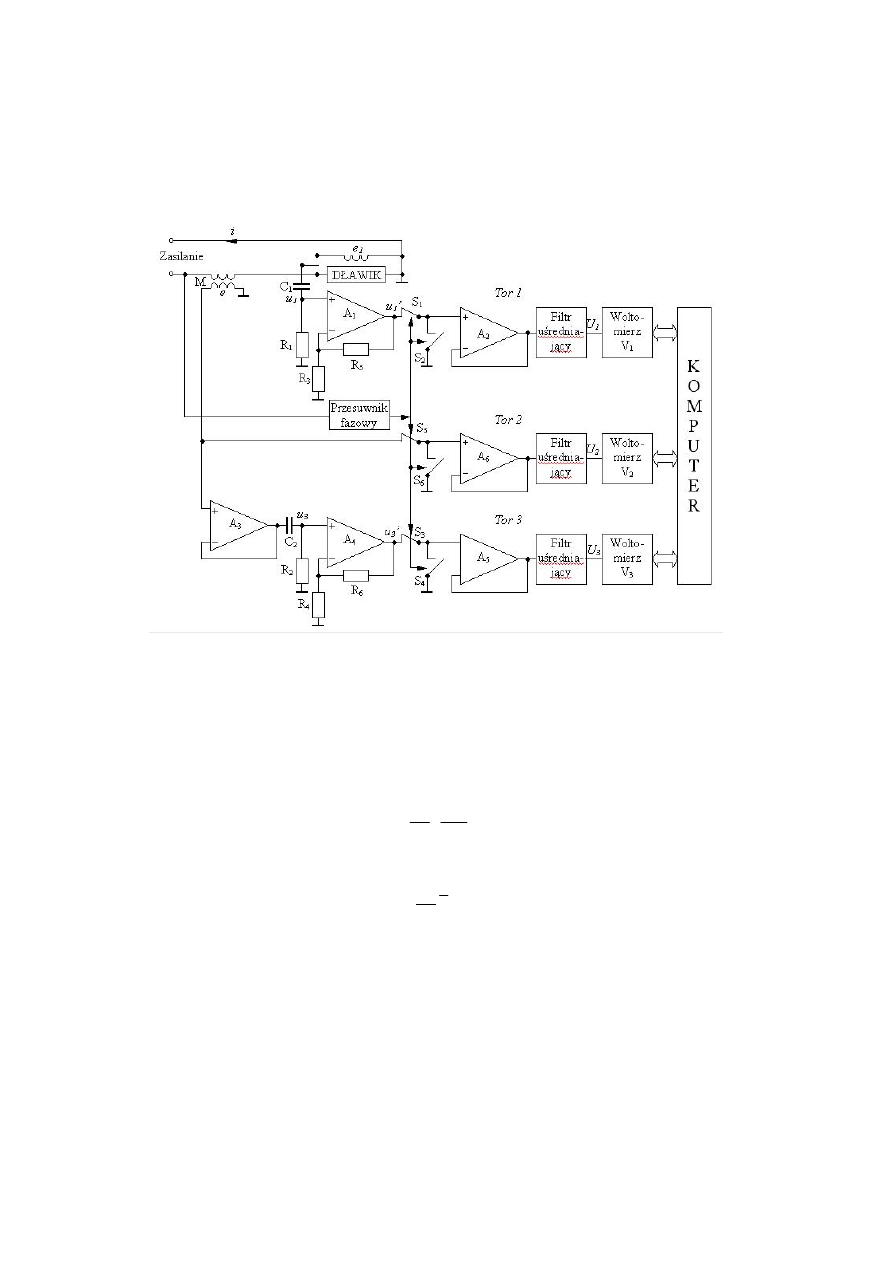
Rys. 2.2. Schemat układu do wyznaczania charakterystyk dławików
Fig. 2.2 System diagram for determining characteristics of reactors
Zawarte w okresie ciągi odpowiadających sobie wartości chwilowych napięcia i
prądu pozwalają także wyznaczyć moc bierną dławika, która dla dowolnych przebie-
gów napięcia i prądu jest proporcjonalna do powierzchni pętli jaką tworzy charaktery-
styka dławika we współrzędnych: prąd, napięcie [4].
t
d
i
dt
du
Q
T
~
0
~
2
1
∫
−
=
π
. (2.4)
Z równania (1.17) i (2.4) wynika, że
( )
2
'
~
2
I
L
T
Q
π
=
, (2.5)
gdzie I
’
~
− wartość skuteczna pochodnej prądu.
⎯
L – indukcyjność uśredniona.
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
0
2
4
6
8
10
+
L [H]
i [A]
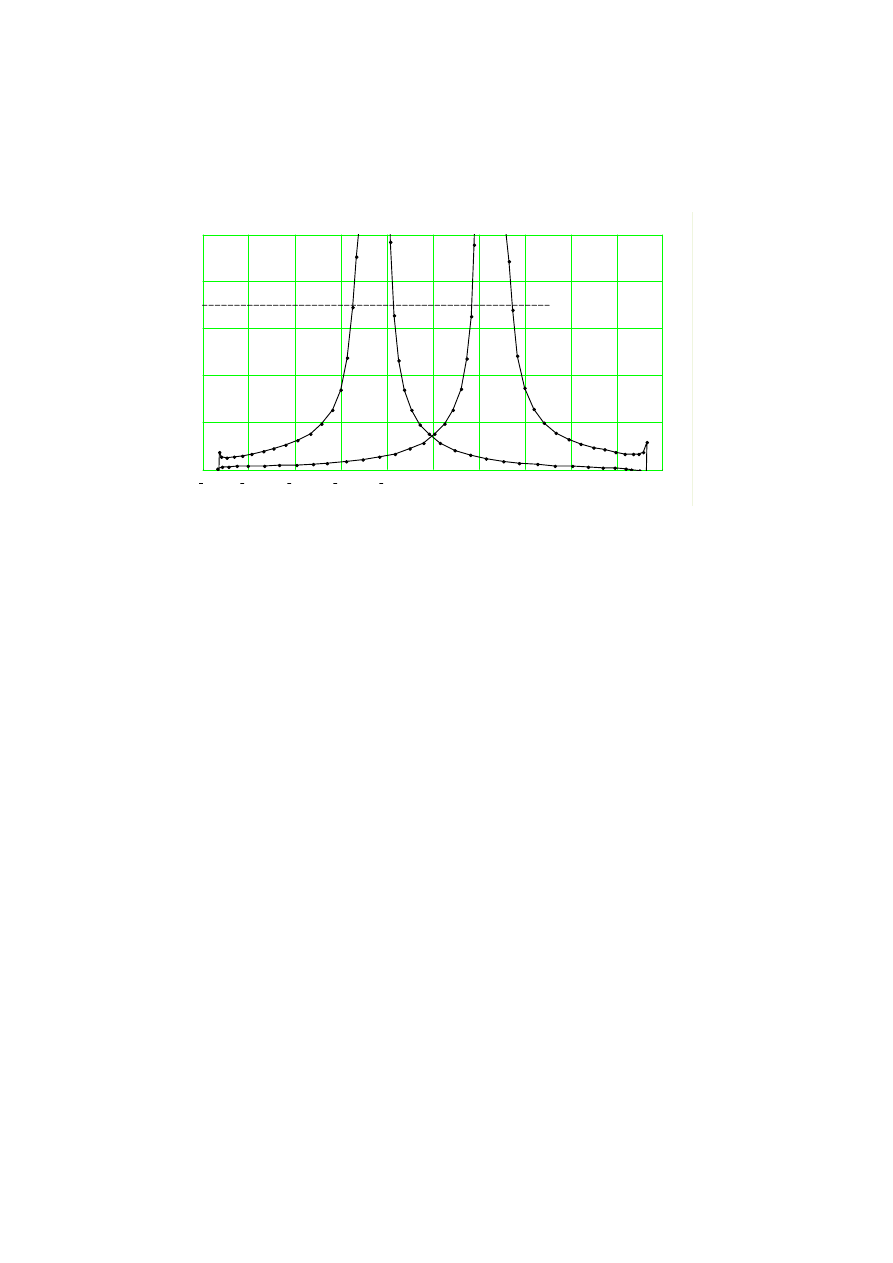
Rys. 2.3. Zależność indukcyjności od wartości chwilowych prądu dławika z zamkniętym magnetowodem
ferromagnetycznym
Fig. 2.3. The dependence of inductance of closed magnetic circuit reactor versus instantaneous current
value
Rysunek 2.3 przedstawia zależność, wyznaczonej według wzoru (1.7) indukcyj-
ność dławika z zamkniętym magnetowodem ferromagnetycznym, od wartości chwi-
lowych prądu. Strumień magnetyczny w magnetowodzie mierzono za pomocą spe-
cjalnie nawiniętych zwojów. Zależność (rys. 3.2) jest silnie nieliniowa
i niejednoznaczna. Na krańcach przedziału zmienności prądu indukcyjność jest nie-
oznaczona (pochodna prądu staje się zerowa). Dla zerowych wartości chwilowych
prądu występuje charakterystyczny punkt (zaznaczony krzyżykiem) – przecięcie gałę-
zi charakterystyki. Wartość indukcyjności w tym punkcie można wyznaczyć mierząc
wartość chwilową napięcia przyłożonego do obiektu i wartość chwilową pochodnej
pobieranego prądu w chwili, gdy prąd przechodzi przez wartość zerową (2.3). Linią
przerywaną zaznaczono wartość uśrednioną indukcyjności wyznaczoną według rów-
nania (2.5) na podstawie zmierzonych ciągów odpowiadających sobie wartości chwi-
lowych napięcia, prądu i pochodnej prądu. Przetwarzając liniowo przyłożone do dła-
wika napięcie i pobierany prąd można wyznaczyć tylko szczególne wartości
indukcyjności. Dla dowolnej wartości chwilowej prądu wyznaczenie rzeczywistej
indukcyjności dławika z magnetowodem ferromagnetycznym w warunkach jego pracy
jest nierealne.
0.8
0.64
0.48
0.32
0.16
0
0.16
0.32
0.48
0.64
0.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
×
u/i
′
i [A]
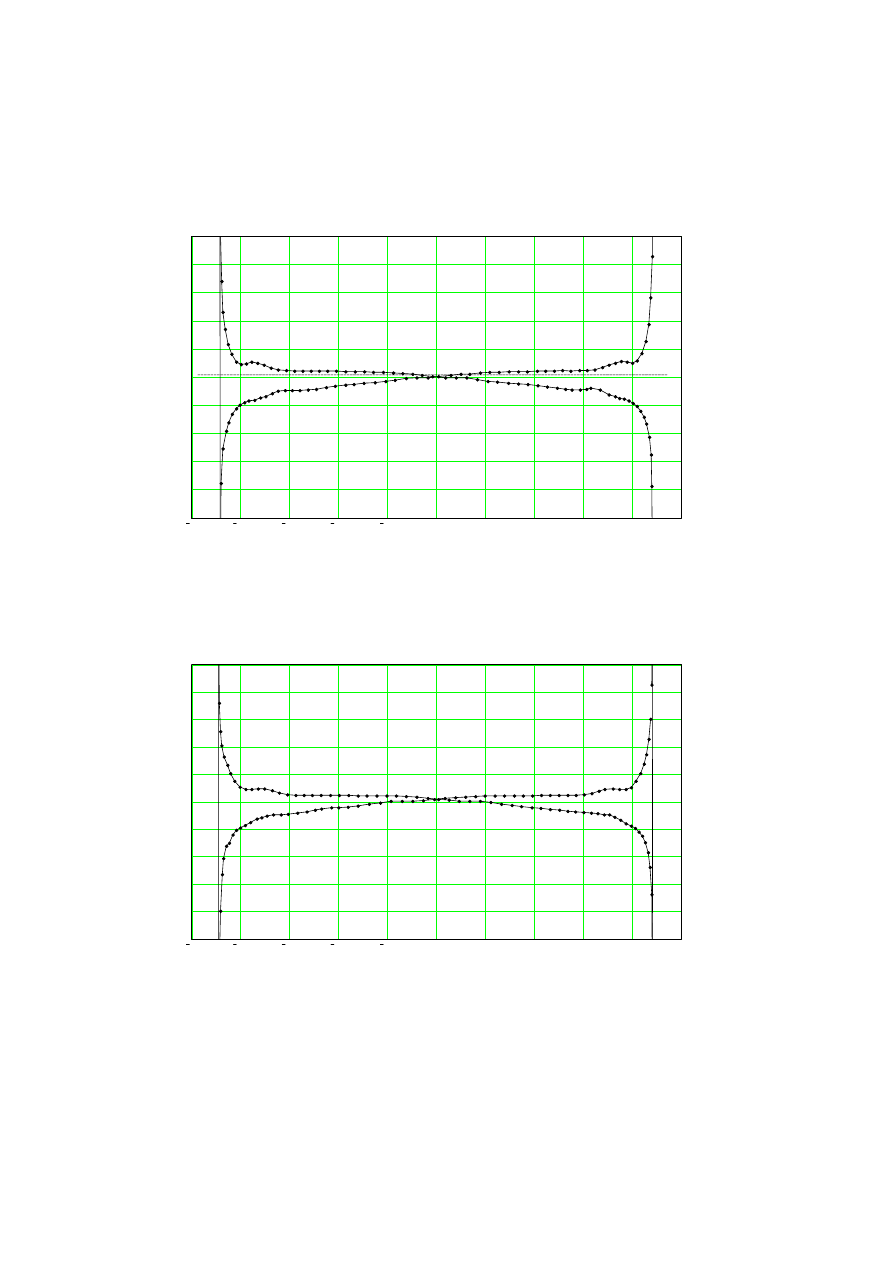
Rys. 2.4. Charakterystyka dławika ze szczeliną, długość szczeliny równa 1% długości magnetowodu,
prąd sinusoidalny o wartości skutecznej 0,5A
Fig. 2.4. Characteristic of reactor, gap length is equal to 1% magnetic core length, rms value of sinusoidal
current 0,5A
1.6
1.28
0.96
0.64
0.32
0
0.32
0.64
0.96
1.28
1.6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
×
u/i
′
i [A]
Rys. 2.5. Charakterystyka dławika ze szczeliną, prąd sinusoidalny o wartości skutecznej 1A
Fig. 2.5. Characteristic of reactor, rms value of sinusoidal current 1A
2.5
2
1.5
1
0.5
0
0.5
1
1.5
2
2.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
×
u/i
′ [H]
i [A]
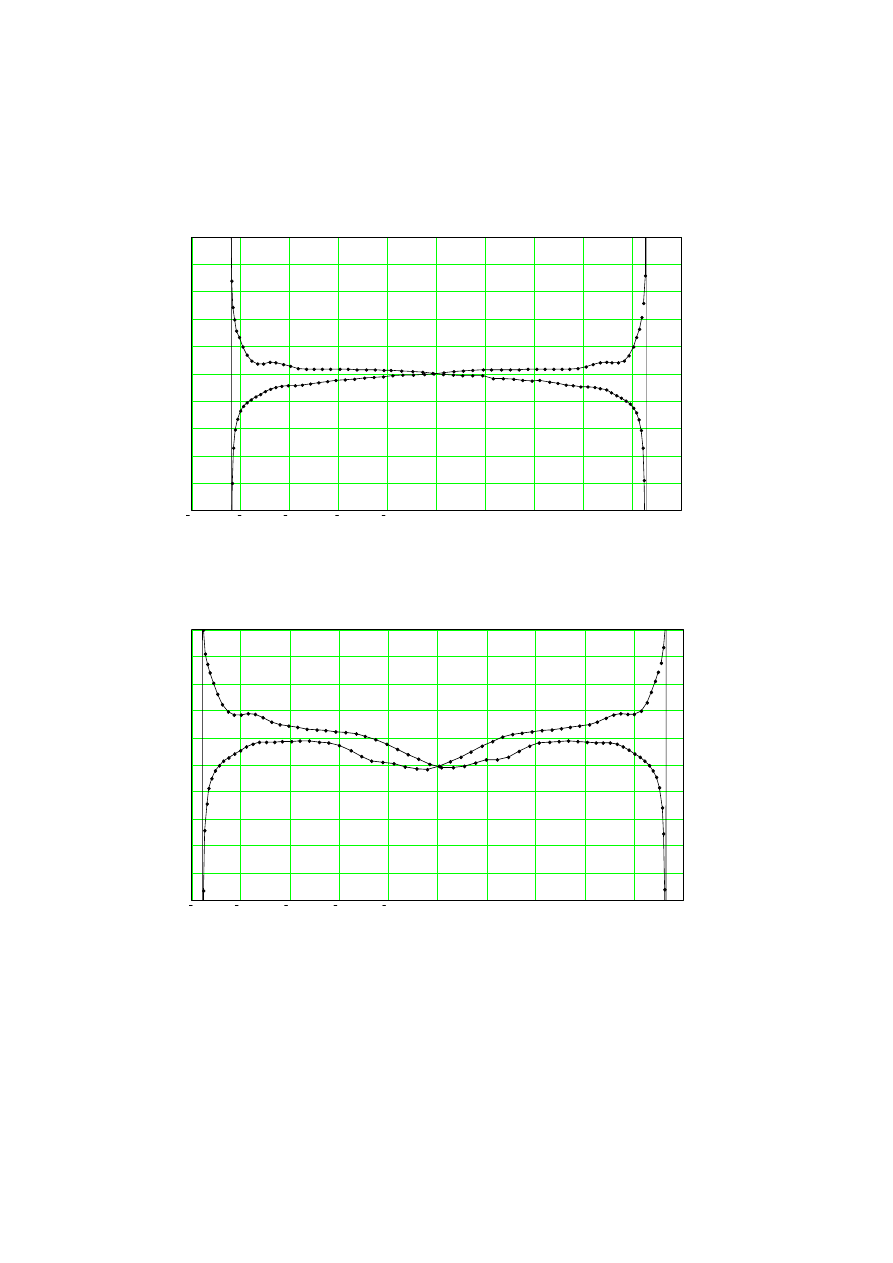
Rys. 2.6. Charakterystyka dławika ze szczeliną, prąd sinusoidalny o wartości skutecznej 1,5A
Fig. 2.6. Characteristic of reactor, rms value of sinusoidal current 1,5A
3
2.4
1.8
1.2
0.6
0
0.6
1.2
1.8
2.4
3
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
×
u/i
′
i [A]
Rys. 2.7. Charakterystyka dławika ze szczeliną, prąd sinusoidalny o wartości skutecznej 2A
Fig. 2.7. Characteristic of reactor, rms value of sinusoidal current 2A
Nawet niewielka szczelina powietrzna stanowiąca na przykład jeden procent śred-
niej długości magnetowodu powoduje znaczne poprawienie liniowości dławika. In-
dukcyjność, którą można zmierzyć w warunkach pracy dławika w punkcie i = 0 jest w
otoczeniu tego punktu praktycznie stała (rys. 2.4) i bliska wartości uśrednionej wy-
znaczonej według równania (2.5) (linia przerywana).
Przedstawione na rysunkach (2.4), (2.5), (2.6) i (2.7) charakterystyki dowodzą, że
rzeczywista indukcyjność dławika, którą można zmierzyć tylko dla chwilowej warto-
ści prądu równej zeru nie zależy od zakresu zmienności prądu. Rzeczywista wartość
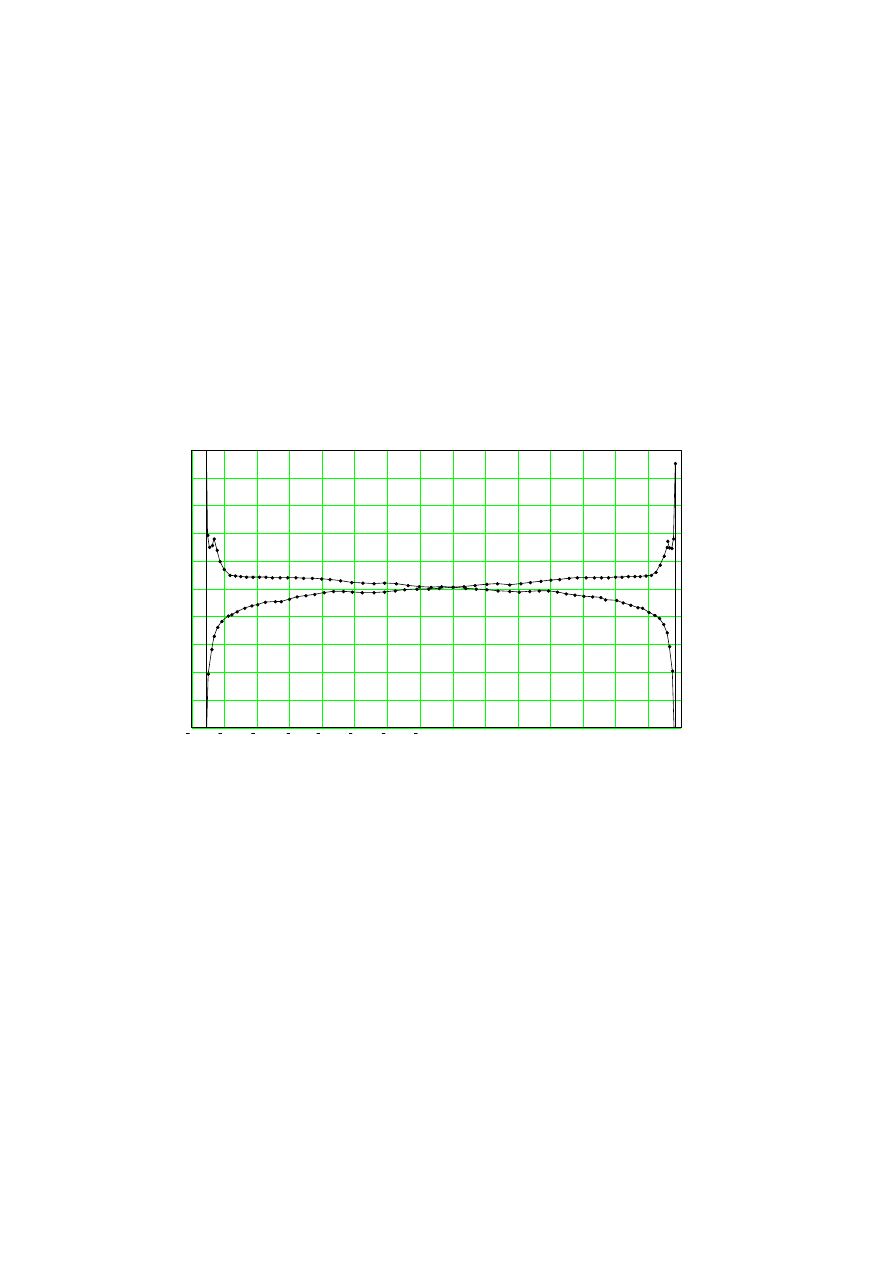
indukcyjności nie zależy także od rezystancji zastępczej dławika. Dowodzi tego cha-
rakterystyka przedstawiona na rysunku 2.8. Charakterystykę tę wyznaczono dla ukła-
du, dławik z dołączonym szeregowo rezystorem.
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
×
i [A]
u/i
′
Rys.2.8. Charakterystyka układu: dławik ze szczelną (długość szczeliny równa 1% długości magnetowo-
du) połączony szeregowo z rezystorem
Fig. 2.8. Characteristic of serial connection reactor (gap length is equal to 1% magnetic core length) and
resistor
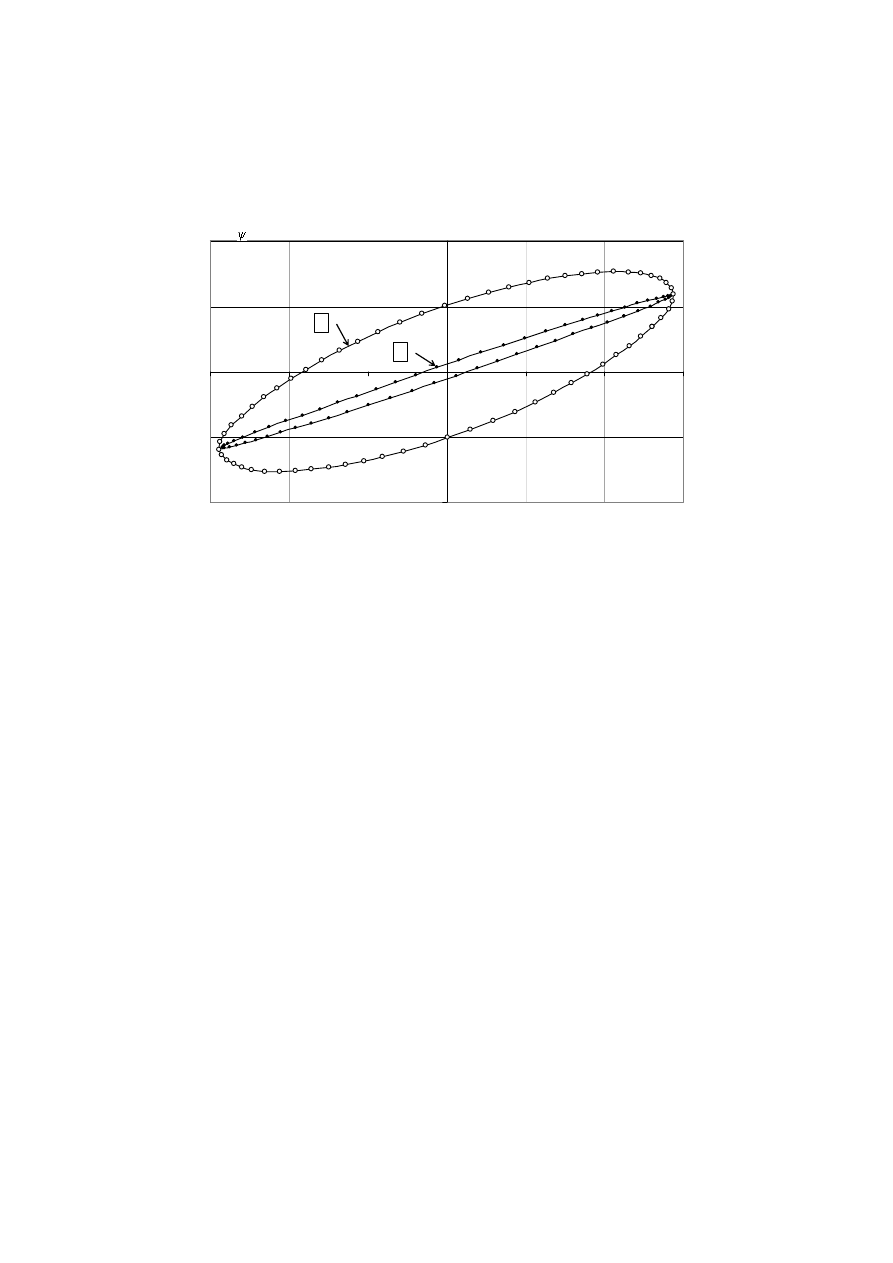
Na rysunku 2.9 są przedstawione charakterystyki we współrzędnych prąd, strumień
zastępczy (pętle histerezy) samego dławika i dławika z dołączonym rezystorem. Pętle
te znacznie się różnią; jednak nachylenie stycznej w punkcie i = 0 jest na obydwu
pętlach jednakowe i równe rzeczywistej indukcyjności dławika. Wynika stąd ogólny
wniosek: indukcyjność zmierzona dla wartości chwilowej prądu równej zeru jest jedy-
ną wartością niezależną od rezystancji zastępczej obiektu elektromagnetycznego.
-0,2
-0,1
0
0,1
0,2
-1,5
-1
-0,5
0
0,5
1
1,5
i [A]
` [Wb]
b
a
Rys 2.9. Pętle histerezy dławika (a) i układu szeregowo połączonego dławika z rezystorem (b)
Fig. 2.9. Hysteresis loops of reactor (a) and serial connection reactor and resistor (b)
3. WNIOSKI
Indukcyjność jest jednoznacznie zdefiniowana dla obiektów liniowych, jako stały
współczynnik proporcjonalności strumienia skojarzonego z obwodem prądowym do
natężenia prądu w tym obwodzie.
Dla obiektów nieliniowych przyjmuje się, że indukcyjność jest równa pochodnej
strumienia względem prądu.
W warunkach pracy dławika informacja o jego indukcyjności jest dostępna tylko w
składowej zmiennej przyłożonego napięcia i składowej zmiennej pobieranego prądu.
Składowa stała napięcia i składowa stała prądu nie zawierają takiej informacji.
Na podstawie informacji zawartej w napięciu i w prądzie można wyznaczyć induk-
cyjność dławika tylko przy założeniu, że można go zastąpić dwójnikiem w postaci
szeregowo połączonej rezystancji i indukcyjności oraz tylko w szczególnych punktach
jego charakterystyki dynamicznej
ψ
= f(i), w takich, w których składowa zmienna
prądu przechodzi przez wartość zerową. Na podstawie informacji zawartej w napięciu
i prądzie można wyznaczyć także indukcyjność uśrednioną dławika mierząc moc bier-
ną i wartość skuteczną pochodnej prądu.
Sygnał zależny od składowej zmiennej prądu przy obecności składowej stałej moż-
na pobrać tylko za pomocą czujnika indukcyjnego, a sygnał zależny tylko od składo-
wej zmiennej napięcia przy obecności składowej stałej –za pomocą dzielnika pojem-
nościowo-rezystancyjnego.
Sygnały pomiarowe dla wyznaczania indukcyjności są proporcjonalne do pochod-
nej prądu i pochodnej napięcia. Do ich przetworzenia najlepiej nadaje się metoda
próbkowania całkowego.
Indukcyjność wyznaczona w punkcie, w który wartość chwilowa składowej
zmiennej prądu jest równa zeru nie zależy od zakresu zmienności prądu i jest jedyną
wartością niezależną od rezystancji zastępczej dławika.
LITERATURA
[1] Transformatory i dławiki trakcyjne, PN-IEC 310:1998
[2] Transformatory trakcyjne i dławiki w taborze kolejowym, PN-EN 60310
[3] Buze A. Pomiar indukcyjności dławika prądu pulsującego przy użyciu przekładnika
prądu stałego, Przegląd Elektrotechniczny, 80 (2004), nr.2, 157-160
[4] Kosobudzki G., Nawrocki Z., Nowak J., Measure of Electric Reactive Power,
Metrology and Measurement Systems, 11 (2005), n.2, 131-149
[5] Kałwak A., Kolasa J., Nowak J., Przetwarzanie wartości chwilowych prądu siecio-
wego, Przegląd Elektrotechniczny, 80 (2004), nr.2, 154-157
[6] Bajorek J., Kosobudzki G., Kałwak A., Kolasa J., Nowak J., Indukcyjne
przetwarzanie prądu sieciowego o dowolnym kształcie, Raport PRE nr 15/2005
DETERMINATION OF REACTOR INDUCTANCE UNDER NORMAL OPERATING
CONDITIONS
Inductance of reactors witch are made for electric traffic purpose are measured by special made
measuring apparatus. Theoretical models of reactors are difficulty to used for inductance measurement.
Determining inductance of reactors under normal operating conditions are possible when use one of two
methods. That come from our research results. Real value of reactor inductance could be determine only
for zero-sequence alternating current. Average value of reactor inductance could be determine by meas-
ure loop surface in u,i coordinates and rms value of current derivative.