Akademia Techniczno Humanistyczna
w Bielsku - Białej
Wydział Nauk o Materiałach i Środowisku
Kierunek: Budownictwo
I rok, II semestr

Ćwiczenia nr 85

„Wyznaczanie górnej granicy energii

promieniowania β-„

Robert Sikorski

Gr. III

Budownictwo

(niestacjonarne)

Część teoretyczna:

Promieniotwórczość naturalna:

Zjawisko promieniotwórczości naturalnej jest konsekwencja występowania
w naturze nietrwałych jader atomowych – jader promieniotwórczych, które rozpadając sie
wysyłają (emitują) promienie



,



lub



. Jadra promieniotwórcze ulegając rozpadowi

przemieniają sie w jadra innego pierwiastka, które mogą być trwałe lub nietrwałe –
promieniotwórcze. Samorzutna przemiana jader atomowych jednego pierwiastka w jadra
innego pierwiastka jest nazywana rozpadem promieniotwórczym. Jest to proces przypadkowy
(stochastyczny), niezależny od czynników zewnętrznych i można przyjąć, _e zachodzi ze
stałym prawdopodobieństwem
Ilość rozpadów promieniotwórczych zachodzących w pewnym przedziale czasu dt jest
proporcjonalna zarówno do długości tego przedziału czasu jak i całkowitej liczby jader
promieniotwórczych N w danej chwili. Zatem zmiana (ubytek) liczby jader dN można
wyrazić zależnością:

dN





Ndt

Po scałkowaniu tej zależności otrzymujemy prawo rozpadu promieniotwórczego, opisującego
zależność liczby jader N(t), które nie uległy rozpadowi

N



t



N0



e



t

gdzie:
N

0

– liczba jader promieniotwórczych w chwili t = 0



- stała rozpadu promieniotwórczego

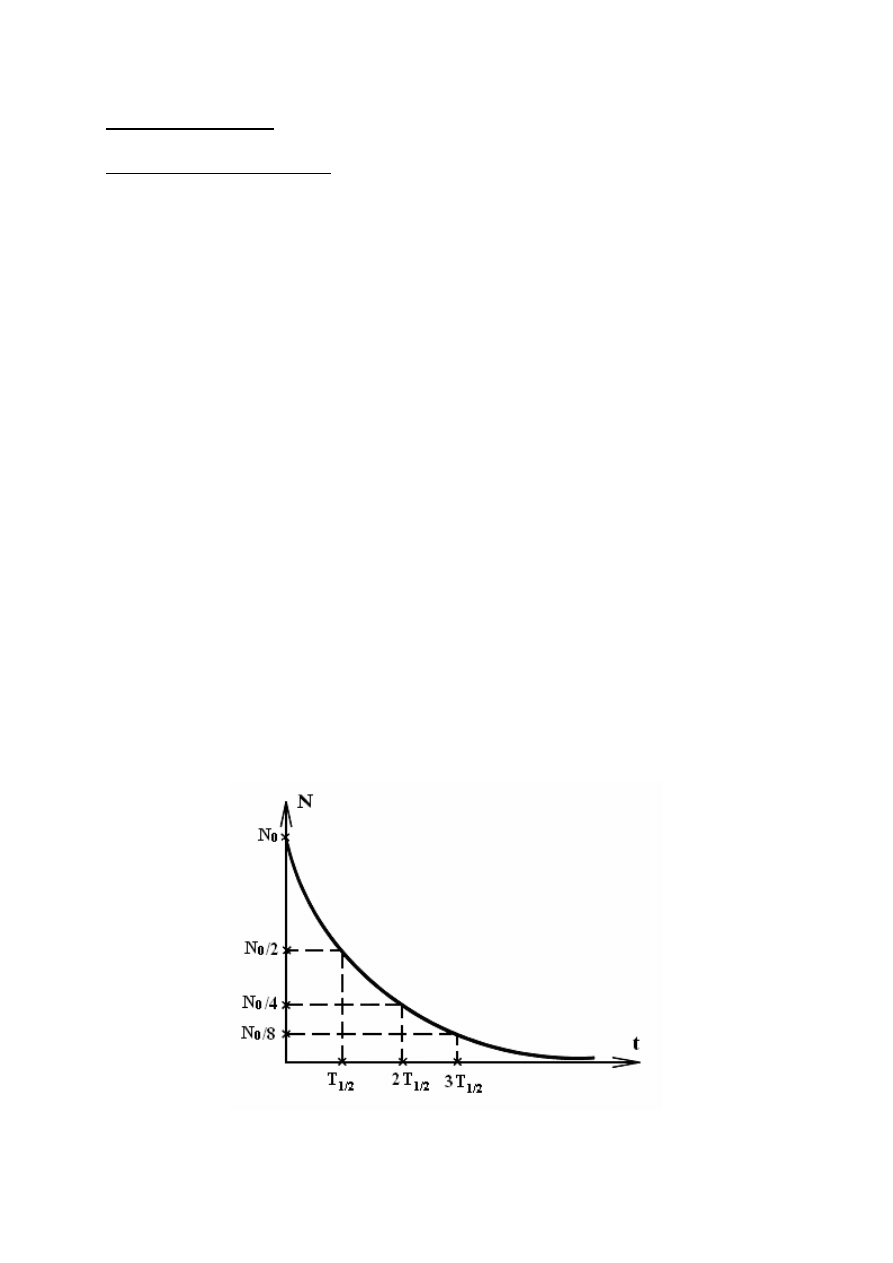
Graficznie prawo rozpadu promieniotwórczego:

Do scharakteryzowania szybkości rozpadu promieniotwórczego używa sie tzw. czasu
połowicznego rozpadu T

1/2

. Jest to czas, po którym liczba jader promieniotwórczych

zmaleje o połowę w stosunku do ilości pierwotnej. Z prawa rozpadu promieniotwórczego
otrzymujemy związek pomiędzy czasem połowicznego rozpadu a stała rozpadu
promieniotwórczego:

Promieniowanie przy kolejnych aktach zderzenia zmienia swój kierunek i dlatego
charakter osłabienia wiązki elektronów w materii jest w dużym zakresie grubości ośrodka, w
którym zachodzi absorpcja podobny do straty energii promieniowania elektromagnetycznego

Podczas przenikania cząstek _

-

przez materie tory ruchu tych cząstek są bardzo złożone,

a rzeczywista droga elektronu w absorbencie jest kilkakrotnie większa od jego grubości.
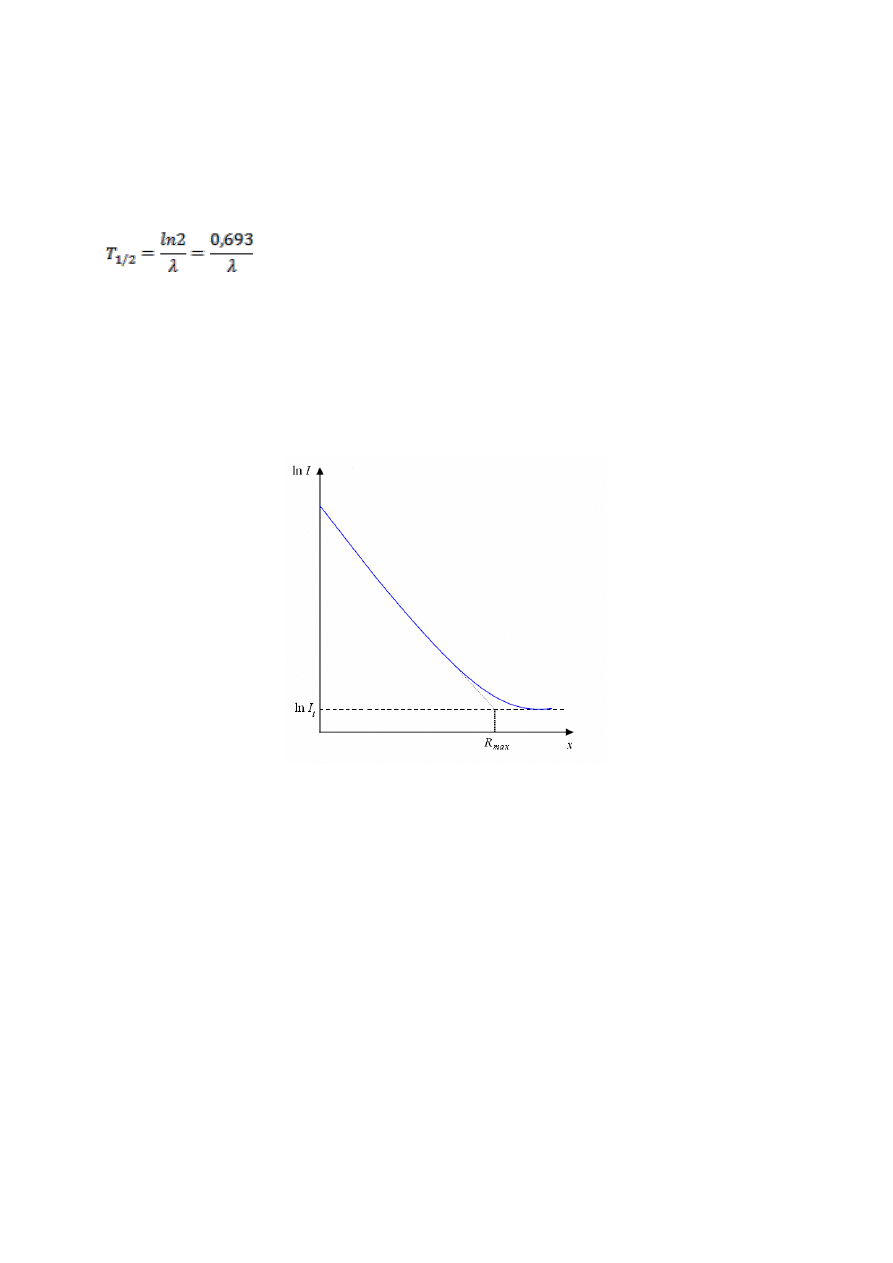
Typowa, eksperymentalna zależność zmiany strumienia cząstek

od grubości absorbentu

Przedstawiony został na wykresie.

Na jego podstawie można wywnioskować, że:
- istnieje pewna charakterystyczna grubość absorbentu, tzw. zasięg maksymalny R

max

,

powyżej której elektrony przez absorbent nie przenikają. Zasięg maksymalny odpowiada
cząstkom o największej energii,

Promieniotwórczość lub radioaktywność pewnych pierwiastków, takich jak np. : uran,

tor, aktyn i innych polega na tym, że wysyłają one samorzutnie z jąder atomowych
charakterystyczne promieniowanie. Promieniowanie to ma skład złożony : wyróżniamy w
nim promieniowanie



(cząsteczki



- które są podwójnie zjonizowanymi atomami He

++

),

promieniowanie



(cząstki



, które są elektronami o bardzo dużej prędkości) i

promieniowanie



, które są falami elektromagnetycznymi, krótszymi od promieni X.

Wykrycie i badanie promieniotwórczości jest możliwe dzięki zjawiskom wywołanym w
materii przenikanej przez to promieniowanie. Do zjawisk tych należą :

1.

jonizacja materii;

2.

pobudzanie do świecenia (fluorescencja);

3.

działanie chemiczne.

Do badania promieniotwórczości najczęściej stosuje się jonizację gazów.

W zależności od tego czy dane jądro w porównaniu z optymalnymi warunkami

trwałości ma nadmiar protonów, czy neutronów, wykazuje ono tendencję do przemiany jednej
postaci nukleonu w drugą :
p.

+

n + e

+

n

p. + e

-

.

W przypadku takich przemian w jądrze mówimy o promieniotwórczości. Rozpadem
promieniotwórczym nazywamy samorzutną przemianę jąder jednego układu nuklidu w jądro
innego nuklidu. Z rozpadającego się jądra atomowego wysyłane są cząsteczki



i



(elektrony) i neutrina oraz kwanty



. W przemianie



emitowany jest elektron zwany

cząsteczką



-

oraz antyneutrino elektronowe o masie spoczynkowej równej zero i nie

posiadające ładunku elektrycznego. W wyniku takiej przemiany liczba atomowa zwiększa się
o jeden:
Z

f

= Z

i

+ 1,

a liczba masowa pozostaje bez zmiany : A

f

= A

i

(co jest zgodne z regułą przesunięć Fajansa -

wynik emisji cząsteczek



-

,



lub



+

powstaje jądro należące do atomu znajdującego się w

układzie okresowym w stosunku do pierwiastka macierzystego odpowiednio



-

o jedno

miejsce w prawo,



+

o jedno miejsce w lewo i dla



-

o dwa miejsca w lewo.

Zapis rozpadu



: AX AY + e +



e

Z

Z+1

Podczas rozpadu promieniotwórczego wydziela się energia. Część energii spoczynkowej
jądra lub energia wzbudzania jądra ulegnie zmianie na energię kinetyczna produktów rozpadu
i energię promieniowania elektromagnetycznego. Wartość energii wydzielającej się w
pojedynczym akcie rozpadu nazywa się energią rozpadu (Q). Bilans energetyczny rozpadu
oparty jest na zasadzie zachowania energii całkowitej. Równanie bilansu energetycznego ma
postać :





MxC

U

My

Z

Z me

me C

U

Q

i

i

f

f

2

2

















gdzie : Mx - masa atomu
My - masa atomu końcowego
Z

i

, Z

f

- energia wzbudzania jądra rozpadającego się i końcowego

me



- suma mas produktu rozpadu

Q - energia rozpadu, na którą składają się energia kinetyczna produktów rozpadu i
energia kwantów



.

Energia rozpadu dla przemiany



-

jest równa :

Q

Mx My C

U

Q

U

f

f

















2

0

Typy rozpadu promieniotwórczego:

- rozpad





-jeden z neutronów jądra zmienia się w proton z jednoczesną emisją e



(negaton) i antyneutrina



_

- rozpad





- jeden z protonów jądra przekształca się w neutron z jednoczesną emisją

e



(pozytonu) i neutrina



- wychwyt K - wychwyt elektronu z powłoki K przez jądro z jednoczesną emisją
neutronu
Prawo rozpadu promieniotwórczego:

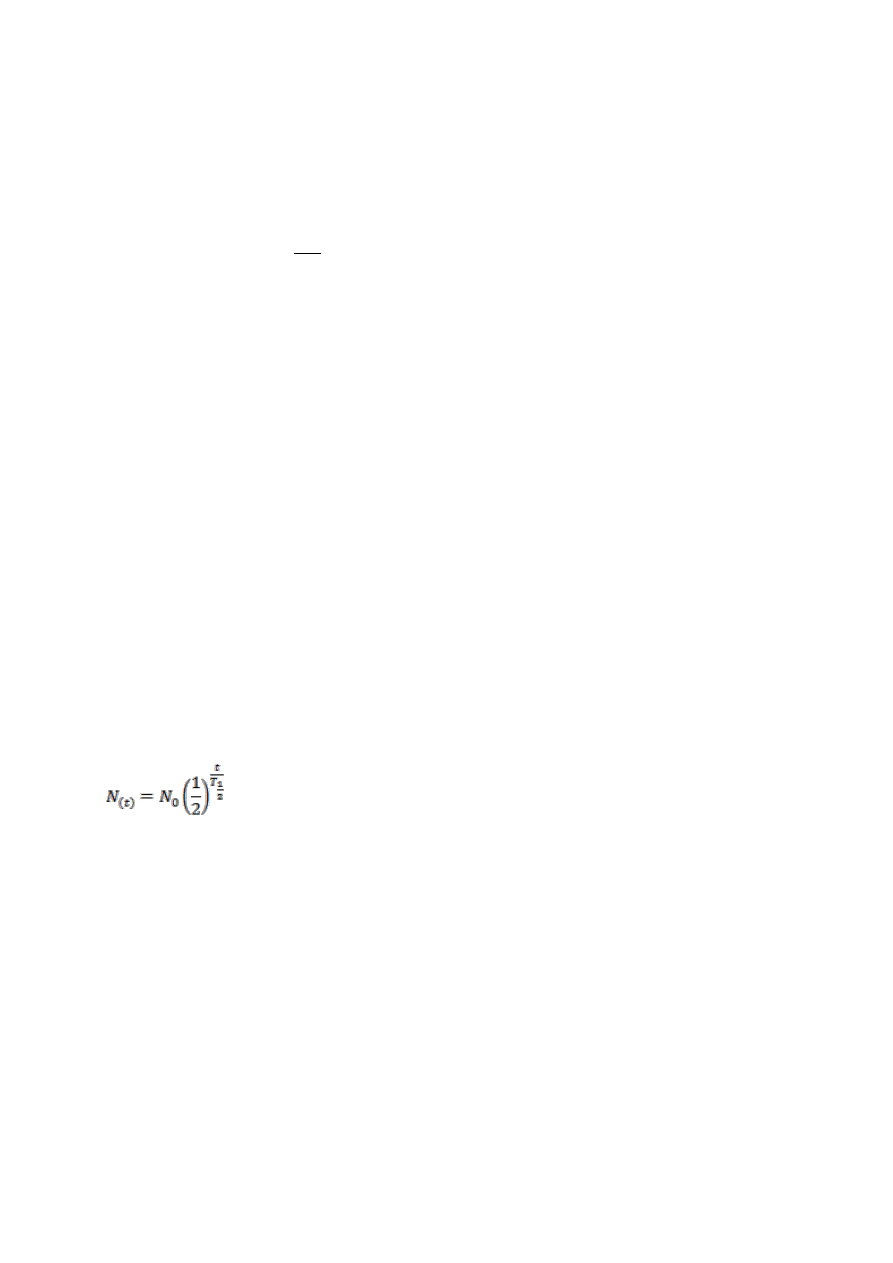
N t

N

e

t

( )

*





0



gdzie:
N(t) - liczba jąder, które uległy rozpadowi po czasie t,

N

0

- początkowa liczba jąder,



- stała rozpadu, określa szybkość rozpadu





ln 2

T

T - czas połowicznego zaniku (

N

N



0 5

0

. *

)

Reguła przesunięć Soddy’ego - Fajansa:
- emitując



pierwiastek przesuwa się w układzie okresowym pierwiastków o dwa miejsca

wstecz (Z-2),

- emitując





przesuwa się o jedno miejsce w przód (Z+1),

- emitując





przesuwa się o jedno miejsce wstecz (Z-1),

- wychwyt K przesuwa się o jedno miejsce wstecz (Z-1).

Prawo rozpadu promieniotwórczego:
Mówi, jak liczba jąder danego pierwiastka promieniotwórczego, które jeszcze nie uległy
rozpadowi, zależy od czasu. Tysiąc czerwonych kółeczek to tysiąc jąder atomowych
pierwiastka, którego czas połowicznego rozpadu wynosi 20 s. Wykres przedstawia zależność
od czasu części jąder, które się jeszcze nie rozpadły (N/N

0

) zgodnie z prawem:

N = N

0

· 2

-t/T

N

0

... początkowa liczba jąder

N .... liczba jąder, które się jeszcze nie rozpadły
t .... czas od chwili rozpoczęcia pomiaru
T .... czas połowicznego rozpadu

Czas połowicznego rozpadu:
Czas, w ciągu którego liczba nietrwałych obiektów lub stanów zmniejsza się o połowę. Czas
ten, oznaczany symbolem T1/2, zgodnie z definicją musi spełniać zależność:

Gdzie:

N(t) – liczba obiektów pozostałych po czasie t,
N0 – początkowa liczba obiektów.

Pierwotnie

czas

ten

dotyczył

nietrwałych

jąder

atomowych

pierwiastków

(promieniotwórczych). W tym przypadku po czasie połowicznego rozpadu aktywność
promieniotwórcza próbki zmniejsza się również o połowę. Okres połowicznego rozpadu
dotyczy również nietrwałych cząstek. Może być wyznaczony z wykładniczego charakteru
rozpadu, który w przypadku izotopów promieniotwórczych nosi nazwę prawa rozpadu
naturalnego.

Aktywność źródła promieniowania:
Liczba spontanicznych przemian jądrowych zachodzących w źródle w jednostce czasu.
Aktywność pewnej ilości nuklidu promieniotwórczego w określonym stanie energetycznym
w danej chwili czasu, zdefiniowana jest jako: iloraz dN i dt, gdzie dN oznacza wartość

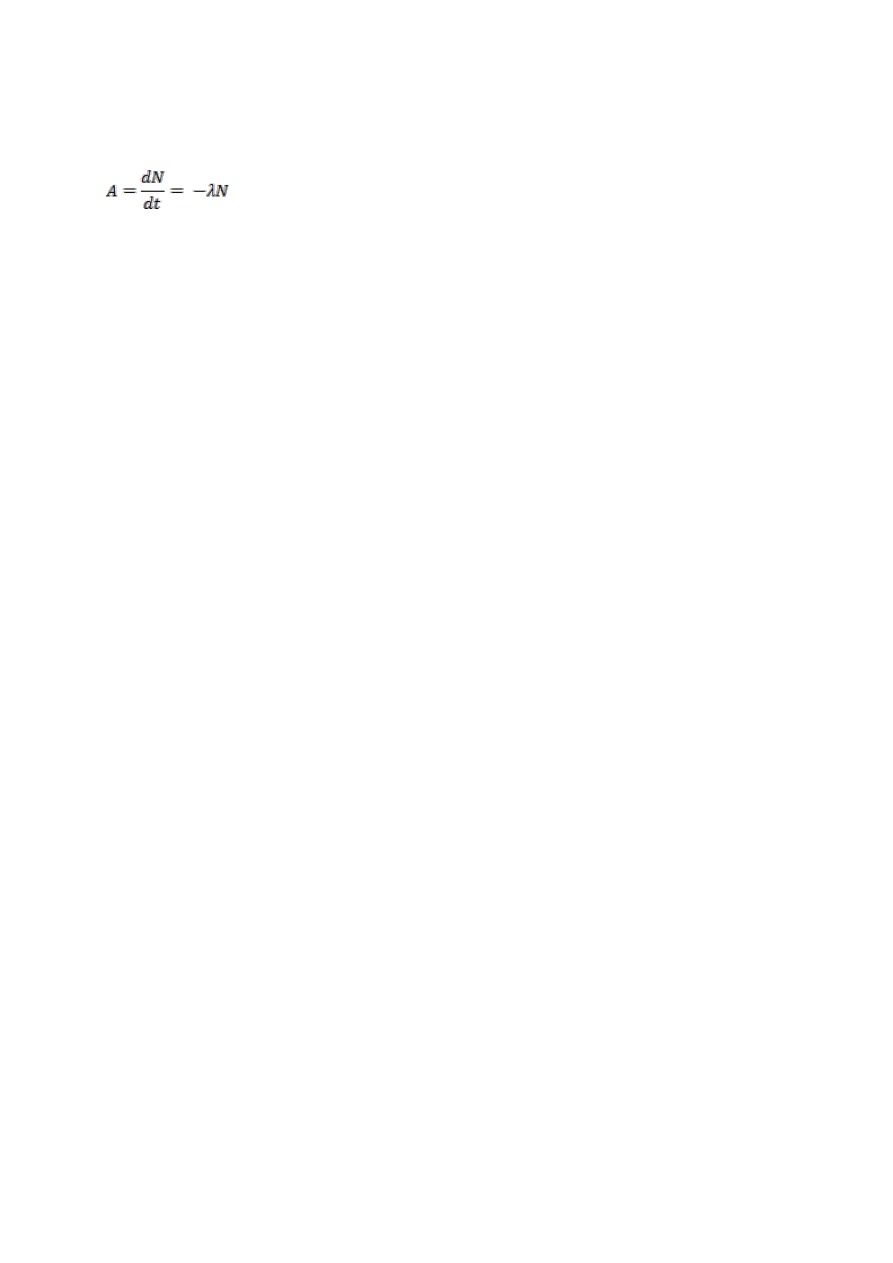
oczekiwaną liczby spontanicznych przemian jądrowych z tego stanu energetycznego,
zachodzącego w ciągu czasu dt:

W układzie SI podstawową jednostką aktywności jest bekerel (Bq). Źródło ma aktywność
jednego bekerela, jeżeli w ciągu jednej sekundy następuje w nim jeden rozpad
promieniotwórczy.

1 Bq = 1 s

-1

Reguła przesunięć Soddy’ego i Fajansa:
Reguła określająca położenie pierwiastka powstałego po emisji cząstki α lub β z jądra
macierzystego

pierwiastka.

Emisja cząstki α powoduje zmniejszenie masy jądra o cztery jednostki masy atomowej, a
ładunku - o dwa ładunki elementarne, wskutek czego powstały pierwiastek znajduje się o dwa
miejsca na lewo w układzie okresowym w stosunku do pierwiastka macierzystego (liczba
masowa maleje o 4, atomowa maleje o 2). Emisja ß

-

powoduje przesunięcie położenia

pierwiastka o jedno miejsce na prawo (liczba atomowa wzrasta o 1, masowa bez zmian).

Obecnie reguła Fajansa i Soddy’ego obejmuje także emisję ß

+

(przesunięcie o jedno miejsce

na lewo w układzie okresowym – liczba atomowa maleje o 1, masowa bez zmian) -
przemiana ta nie była znana, gdy formułowano pierwotną wersję reguły.

Jądro atomowe:
Każdy atom zbudowany jest z jądra oraz z krążących wokół niego elektronów. Jądro
atomowe składa się z dodatnio naładowanych protonów i elektrycznie obojętnych neutronów.
Ponieważ masa elektronu jest ok. 1830 razy mniejsza od masy protonu czy neutronu
(Mp=1,0073 u, Mn=1,00866 u), dlatego też jądro skupia niemal całą masę atomu.
Liczba protonów w jądrze i zarazem liczba elektronów na orbicie nazywana jest liczbą
atomową Z. Decyduje ona jąder własnościach fizycznych i chemicznych pierwiastka.
Suma liczb protonów i neutronów, czyli liczbę nukleonów wyraża liczba masowa jąder.
Atomy tego samego pierwiastka różniące się liczbą masową noszą nazwę izotopów.
Natomiast atomy pierwiastków, których jądra zawierają taką samą liczbę nukleonów, ale
różnią się liczbą atomową nazywa się izobarami.
Trwałość jąder atomowych jest skutkiem działania sił jądrowych. Są to siły przyciągani
między nukleonami. Mają bliski zasięg, rzędu 1.5m
Masa jądra atomowego jest zawsze mniejsza od sumy mas nuklidów wchodzących w jego
skład. Ta różnica nosi nazwę defektu masy i jest ilościowo jest równa energii wiązania
nukleonów w jądrze. Obie te wielkości wiąże wzór Einsteina: , gdzie c - prędkość światła w
próżni.

Liczba masowa:
Wartość opisująca liczbę nukleonów (protonów i neutronów) w jądrze określonego izotopu
atomu danego pierwiastka. Liczby masowej nie należy mylić z masą atomową, która
wyznaczana jest metodami chemicznymi. Nierówność ta spowodowana jest trzema
powodami:

1. izotopów;
2. defektem masy jądra;
3. atom składa się z jądra i elektronów.

Liczbę masową izotopów pisze się tradycyjnie w górnym, lewym indeksie symbolu
pierwiastka. Np. symbol

12

C oznacza izotop węgla posiadający 12 nukleonów w jądrze - 6

neutronów i 6 protonów, zaś izotop

13

C posiada 13 nukleonów - 6 protonów i 7 neutronów.

Izotopy:
Odmiany pierwiastka chemicznego różniące się liczbą neutronów w jądrze atomu (z
definicji atomy tego samego pierwiastka mają tę samą liczbę protonów w jądrze). Izotopy
tego samego pierwiastka różnią się liczbą masową (łączną liczbą neutronów i protonów w
jądrze), ale mają tę samą liczbę atomową (liczbę protonów w jądrze).
Izotopy tego samego pierwiastka na ogół mają zbliżone własności fizyczne i chemiczne.
Jednak im większa jest różnica mas atomowych izotopów, tym większe mogą być różnice ich
własności fizycznych lub chemicznych. Izotopy danego pierwiastka mogą mieć inną gęstość,
temperaturę wrzenia, topnienia i sublimacji. Różnice te występują także w związkach
chemicznych tworzonych przez te izotopy.
Pierwiastki mogą mieć po kilka, a nawet kilkanaście izotopów. Przykładowo wodór ma
trzy naturalne izotopy:

* prot:

1

H – ma jeden proton i nie ma neutronów, jest trwały,

* deuter:

2

H (D) – ma jeden proton i jeden neutron, jest trwały,

* tryt:

3

H (T) – ma jeden proton i dwa neutrony, jest nietrwały.

Izobary :
Są to atomy rożnych pierwiastków mających taką sama liczbę masową (mogą zawierać różne
liczby protonów i neutronów, ale ich suma jest identyczna), np. :

14

C i

14

N

Rozpad β

−

polega na przemianie jądrowej, w wyniku której neutron zostaje zastąpiony

protonem. Oddziaływanie ma miejsce poprzez emisję bozonu pośredniczącego W

−

przez

jeden z kwarków d neutronu. W

−

rozpada się następnie na elektron i antyneutrino

elektronowe według schematu:

W rezultacie w wyniku rozpadu beta minus powstaje elektron i antyneutrino elektronowe.
Rozpad β

−

może zachodzić również dla swobodnego neutronu.

Rozpadem promieniotwórczym nazywamy samorzutną przemianę jąder jednego układu

nuklidu w jądro innego nuklidu. Z rozpadającego się jądra atomowego wysyłane są cząsteczki



i



(elektrony) i neutrina oraz kwanty



. W przemianie



emitowany jest elektron

zwany cząsteczką



-

oraz antyneutrino elektronowe o masie spoczynkowej równej zero i

nieposiadające ładunku elektrycznego. W wyniku takiej przemiany liczba atomowa zwiększa

się o jeden:

Z

f

= Z

i

+ 1,

a liczba masowa pozostaje bez zmiany : A

f

= A

i

(co jest zgodne z regułą przesunięć Fajansa -

wynik emisji cząsteczek



-

,



lub



+

powstaje jądro należące do atomu znajdującego się w

układzie okresowym w stosunku do pierwiastka macierzystego odpowiednio



-

o jedno

miejsce w prawo,



+

o jedno miejsce w lewo i dla



-

o dwa miejsca w lewo.

Zapis rozpadu



:

e

A

1

Z

A

Z

ν

e

Y

X











gdzie:

X

A

Z

– jądro atomu wyjściowego o liczbie atomowej Z i liczbie masowej A

Y

A

1

Z



– jądro atomu końcowego o liczbie atomowej Z+1 i liczbie masowej A

e

-

– elektron

v

e

– antyneutrino elektronowe

Podczas rozpadu promieniotwórczego wydziela się energia. Część energii spoczynkowej

jądra lub energia wzbudzania jądra ulegnie zmianie na energię kinetyczną produktów rozpadu

i energię promieniowania elektromagnetycznego. Wartość energii wydzielającej się w

pojedynczym akcie rozpadu nazywa się energią rozpadu (Q).

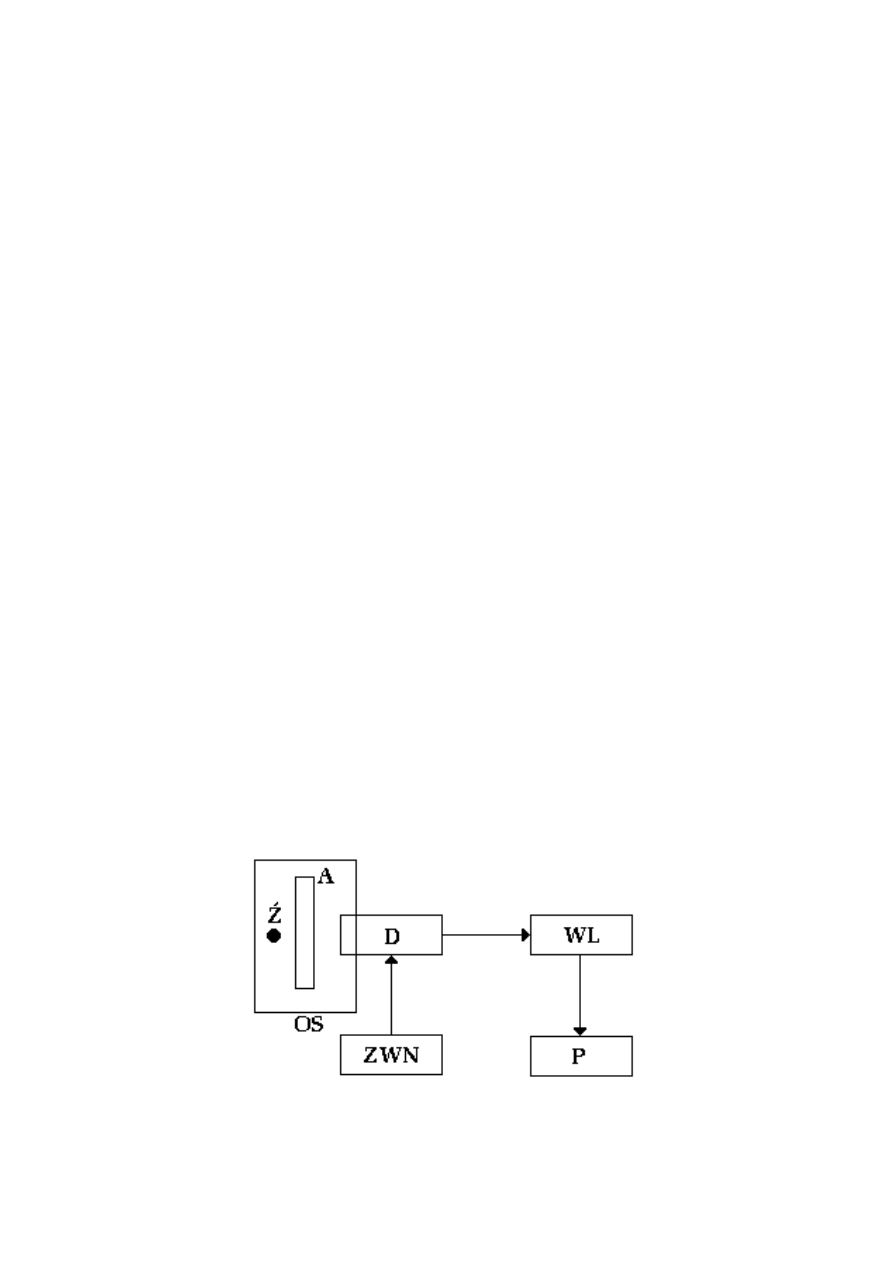
Opis układu pomiarowego:

Układ pomiarowy do wyznaczania absorpcji promieniowania jądrowego składa się z
następujących elementów:



Domku pomiarowego (OS), w którym umieszczone jest źródło promieniotwórcze (Ź),

absorbent (A) oraz detektor promieniowania (D),



Zasilacza wysokiego napięcia (ZWN),



Wzmacniacza liniowego (WL),



Przelicznika (P).

Schemat ideowy układu pomiarowego

Przebieg ćwiczenia:

1. Przygotowujemy aparaturę pomiarową:

Włączamy układ pomiarowy , następnie po 3 minutach ustawiamy napięcie pracy sondy
scyntylacyjnej na wartość U

p

= 900V

2. Pierwszym pomiarem jaki wykonaliśmy jest pomiar tzw. tła N

t1

. Pomiar ten polega na

włączeniu układu bez izotopu promieniotwórczego talu Tl – 204 oraz bez absorbentu
aluminiowego. Czynność tą wykonaliśmy 3 krotnie, a wartości zarejestrowanych
impulsów zanotowaliśmy w tabeli:

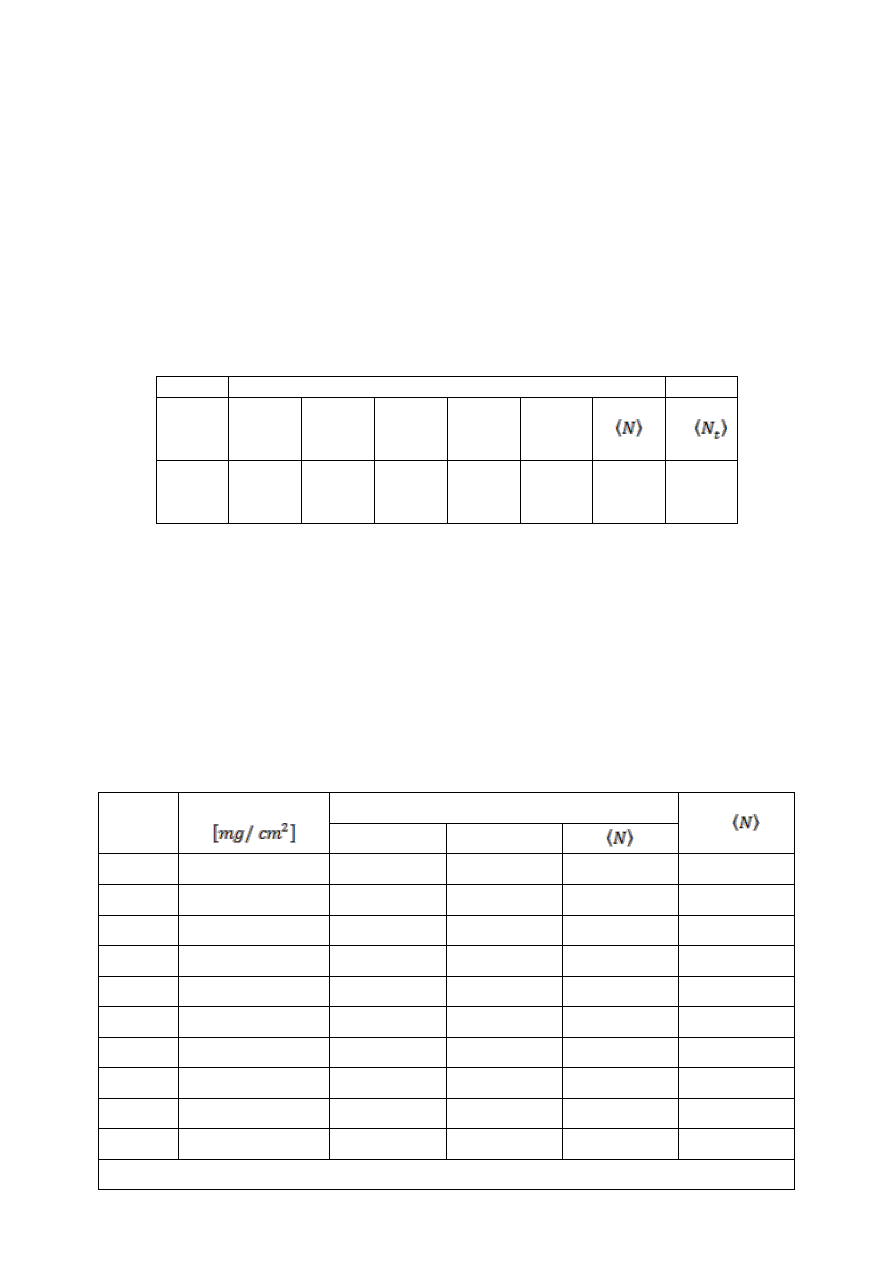
Tabela 1

Liczba zliczeń w czasie 100 s

N

t1

N

t2

N

t3

N

t4

N

t5

N

t6

ln

36

27

26

37

24

26

29,3

3.4

3. Następnie umieszczamy źródło promieniotwórcze w domku pomiarowym OS po czym

wykonujemy trzykrotnie pomiar cząstek promieniowania β

-

zarejestrowany przez

przelicznik bez absorbentu aluminiowego. Otrzymane wartości wpisujemy do tabeli
kolejno jako N

1

, N

2

.

4. Następnie nad źródłem umieściliśmy absorbent w postaci pojedynczej blaszki

aluminiowej. Pomiar wykonujemy dwukrotnie. Następnie zwiększamy liczbę blaszek
dokładając po jednej, aż będzie ich 9. Otrzymane wartości zarejestrowanych impulsów
zapisujemy w tabeli.

Tabela 2

Ilość

płytek

X

Liczba zliczeń w czasie 100s

ln

N

1

N

2

0

55

19330

17336

18333

9,81

1

82.5

10931

11051

10991

9,3

2

110

6162

6306

6234

8,73

3

137.5

3173

3135

3154

8,05

4

165

1376

1432

1404

7,24

5

192.5

536

620

578

6,35

6

220

223

238

230,5

5,44

7

247.5

84

92

88

4,5

8

275

36

46

41

3,71

9

302.5

32

32

32

3,5

a= - 0.028 [cm

2

/mg] Δa = 0.001 [cm

2

/mg] b = 11.62 Δb = 0.18

Po zakończeniu ćwiczenia i zapisaniu otrzymanych wyników, które zapisaliśmy w
odpowiednich tabelach przystępujemy do obliczenia pozostałych wartości zgodnie z
instrukcją ćwiczenia.

Opracowanie pomiarów i wyników:

1. Na podstawie danych z pierwszej tabeli obliczamy średnią wartość z pomiarów

stosując wzór:

Następnie obliczamy ln ze średniej wartości tła

2. Następnie na podstawie danych z tabeli 2 obliczamy:
a) Grubość aluminiowych absorbentów x wykorzystując wzór:

x = x

0

+ p ∙ x’..l\

x

0

= 55 mg/cm2 – stały parametr uwzględniający absorpcje w powietrzu i okienku

sondy,
x'= Nr ∙ d – grubość warstwy absorbentu,
Nr – odpowiada ilości płytek,
d = 0,01 cm – grubość płytki aluminiowej,
p = 2750 mg/cm3 – gęstość aluminium.

Dla 1 płytki aluminiowej

Dla 2 płytek aluminiowych

Dla 3 płytek aluminiowych

Dla 4 płytek aluminiowych

Dla 5 płytek aluminiowych

Dla 6 płytek aluminiowych

Dla 7 płytek aluminiowych

Dla 8 płytek aluminiowych

Dla 9 płytek aluminiowych

b) Następnie obliczamy średnie wartości liczby N cząstek



-

rejestrowanych po przejściu

promieniowania przez absorbenty o odpowiednich grubościach wykorzystując wzór:

Wykorzystując ten wzór liczymy średnie wartości dla wszystkich par pomiarów i oba
wyniki wpisujemy do tabeli 2.

c) Po obliczeniu wartości średnich liczymy ln dla tych właśnie wartości które zapisujemy

w tabeli nr 2 .

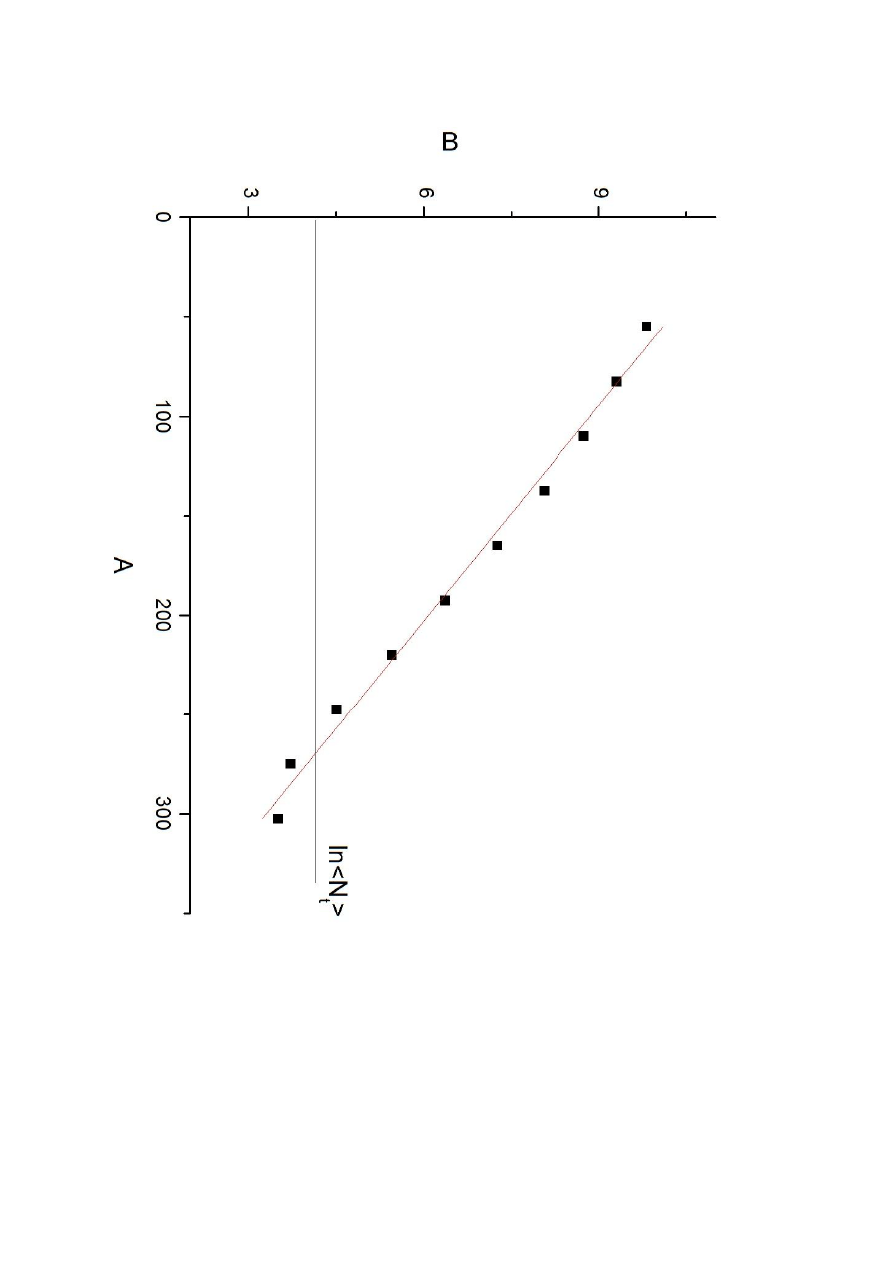
3. Następnym krokiem było wprowadzenie wyników obliczeń zgromadzonych w tabeli 1

i 2 do programu komputerowego. Program ten obliczył parametry a i b prostej regresji
dopasowanej metodą najmniejszych kwadratów do eksperymentalnej zależności:
ln

= f(x). Program wyliczył również błędy Δa i Δb tych parametrów. Otrzymane

wyniki wpisujemy do tabeli 2.

4. Z wartości parametrów a i b prostej korelacji określić wartość masowego współczynnika
absorpcji μ oraz lnN

0

, a następnie obliczyć zasięg R

max

korzystając ze wzoru (14). Wyznaczone

wartości μ i R

max

zanotować w tabeli 3.

4.

Kolejnym krokiem jest obliczenie wartości masowego współczynnika absorpcji μ oraz
lnN

0

na podstawie wartości parametrów a i b.

Współczynnik a = -0,028
Współczynnik b = 11,62

Zgodnie ze wzorem (13) lnN = lnN

0

– μx oraz z zależnością y = ax + b możemy łatwo

Wywnioskować, że a = – μ oraz b = lnN

0

Tak więc

otrzymujemy :

- Masowy współczynnik absorpcji µ = 0,028
- lnN

0

= 11,62

Kiedy znamy wartości obu parametrów możemy zgodnie wzorem

obliczyć zasięg maksymalny:

Otrzymane wartości umieszczamy w tabeli 3

5. Następnie, wykorzystując dotychczasowe wyniki obliczamy:

a) Przekształcając wzór

obliczamy energię maksymalną

promieniowania:

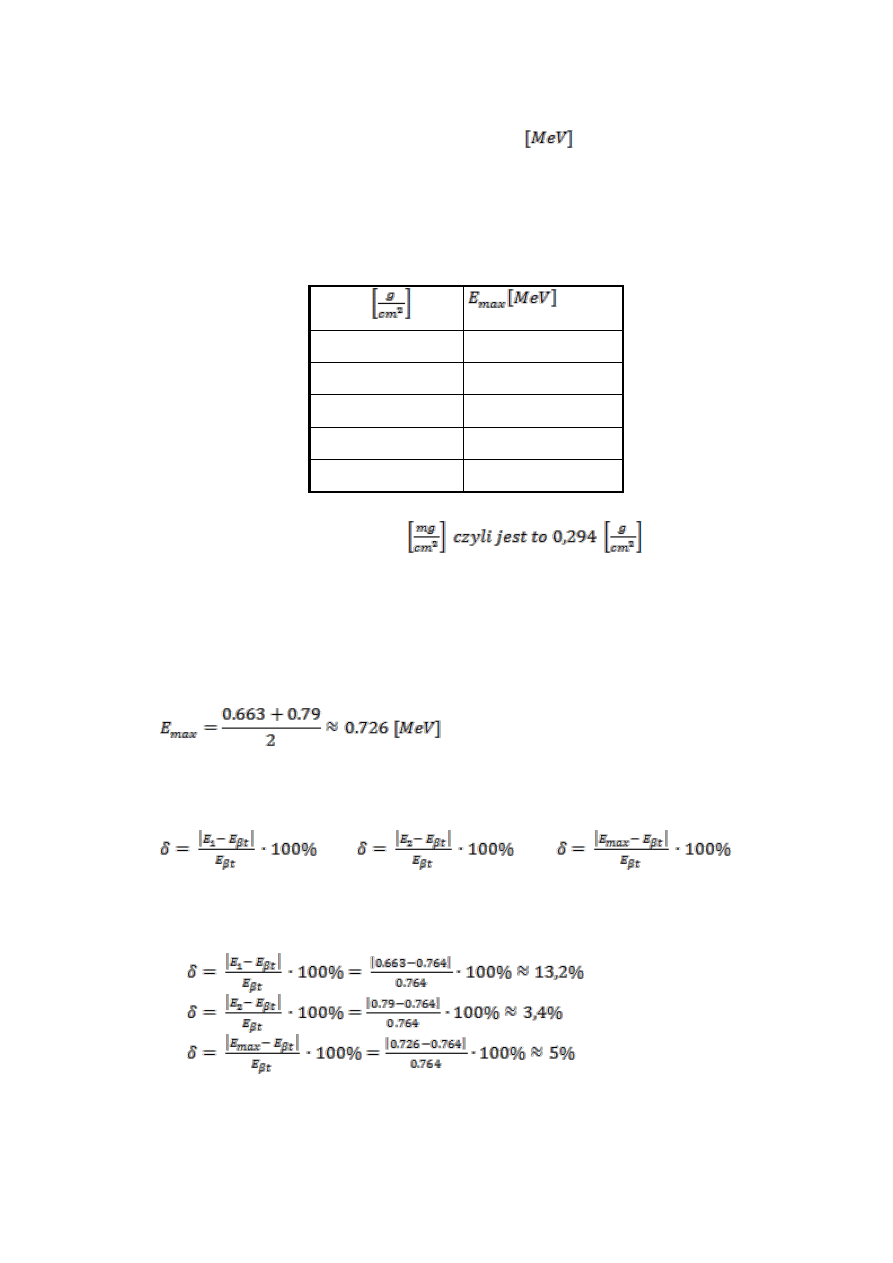
Tabela A

R

max

R < 0.003

E=1.275R

0,6

0.002 < R < 0.02

E=6.67R+0.0186

0.02 < R < 0.3

E=1.92R

0.725

R > 0.3

E=1.85R+0.245

R > 0.4

E=1.75R+0.281

Otrzymany wynik oznaczamy jako E

1

= 0,663

Korzystając z tabeli A energię maksymalną promieniowania w oparciu o uzyskaną
wartość R

max

(Otrzymane wartości umieszczamy w tabeli 3)

\

R

max

= 294

t

E

max

= E

2

= 1.92 ∙ 0.294

0.725

=0,79 [MeV]

6. Kolejnym krokiem jest obliczenie wartości średniej z E

1

i E

2

, oznaczenie jej jako

E

max

.

7. Następnie wykorzystując wzory:

Obliczamy względne różnice (wyrażone w procentach) pomiędzy doświadczalnymi
wartościami energii maksymalnej promieniowania β- a jej wartością teoretyczną.

a)

b)

c)

Otrzymane wartości umieszczamy w tabeli 3.

Tabela 3

µ = 0.026

R

max

= 288,08

0,764

δ [%]

0,663

13,2

0,79

3,4

0,726

5

Wnioski:

1. Na podstawie przeprowadzonego badania, obliczeń i wykresu, można dojść do

wniosku, że aluminium skutecznie zapobiega rozprzestrzenianiu się cząstek
promieniowania



-. Wraz ze wzrostem grubości warstwy chłonnej ( blaszki

aluminiowe ) wyraźnie maleje ilość cząstek jakie docierają do detektora w urządzeniu
badawczym.