Co to jest drzewo algorytmu?

Drzewa to jedne z najważniejszych

struktur danych w informatyce. Można

je wykorzystać do wielu celów, min. do

graficznej reprezentacji hierarchii,

sortowania, itd.

Każde drzewo składa się z wierzchołków (węzłów) ,oraz

łączących je krawędzi.

Każdy wierzchołek może posiadać wielu przodków i

potomków.

Potomkowie „bezpośredni” to dzieci wierzchołka, a

przodek bezpośredni to ojciec (każdy wierzchołek ma

dokładnie jednego ojca).

Drzewo może posiadać wiele dzieci, choć są drzewa o ich

określonej liczbie, np. binarne.

Wierzchołki drzewa reprezentują konkretne dane

(liczby, napisy albo bardziej złożone struktury danych).

Odpowiednie ułożenie danych w drzewie może ułatwić i

przyspieszyć ich wyszukiwanie.

-

Pierwszy obiekt zwany jest korzeniem

- Liście są to węzły nie mające potomstwa

- Droga w drzewie to sekwencja węzłów w drzewie

odpowiadających przejściu od jednego wierzchołka do

drugiego, po krawędziach łączących je

- Długość ścieżki od korzenia do danego węzła nazywamy

głębokością danego węzła w drzewie

- Największa głębokość węzła w drzewie jest wysokością

tego drzewa

Przykładem szczególnym drzewa jest tzw.

jako najpopularniejsza i najczęściej używana w procesie

rozwiązywania problemów algorytmicznych forma

***

posiada ono tę właściwość, że każdy węzeł może mieć

maksymalnie 2 dzieci, (prawe i lewe)

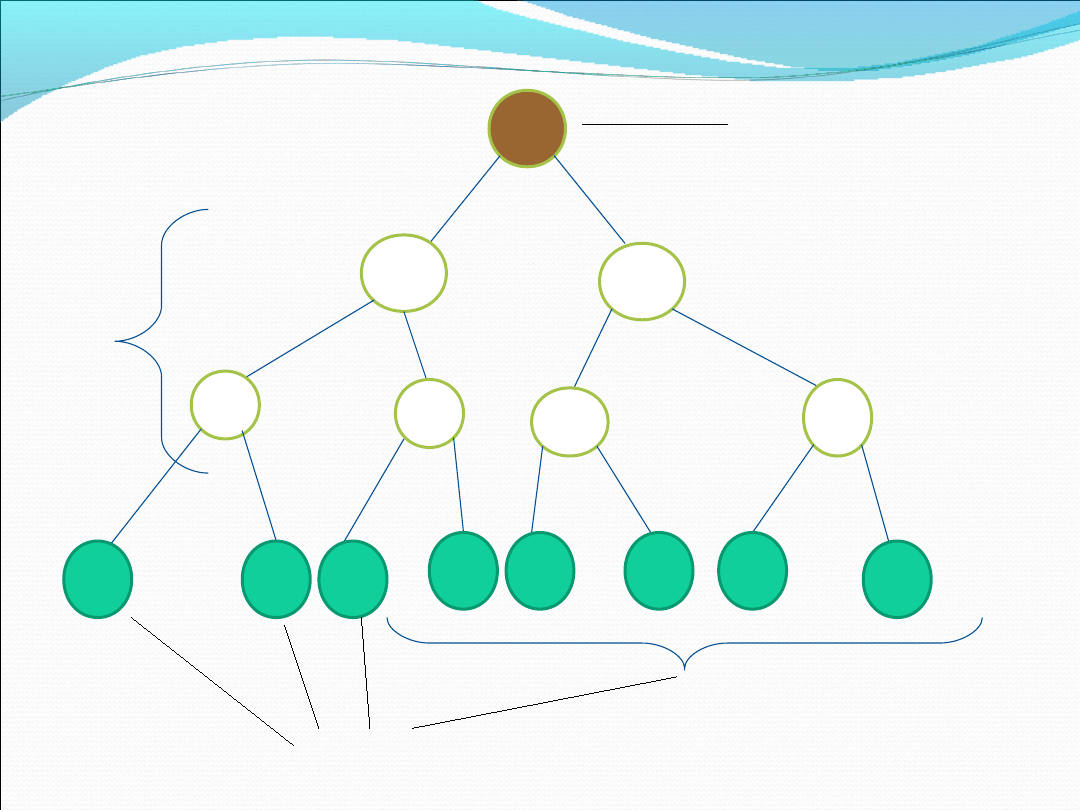
A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

Korzeń

Liście

W

ęz

ły

w

ew

nę

tr

zn

e

Przykład drzewa

binarnego

Struktura drzewa binarnego przypomina w dużym stopniu

strukturę poznanej już listy jednokierunkowej

W przypadku listy operowaliśmy wskaźnikiem

Następny

W przypadku drzew binarnych, zastępujemy ten wskaźnik

dwoma:

Lewy oraz Prawy

będącymi operatorami wskazującymi na odpowiednio lewą i

prawą stronę drzewa binarnego

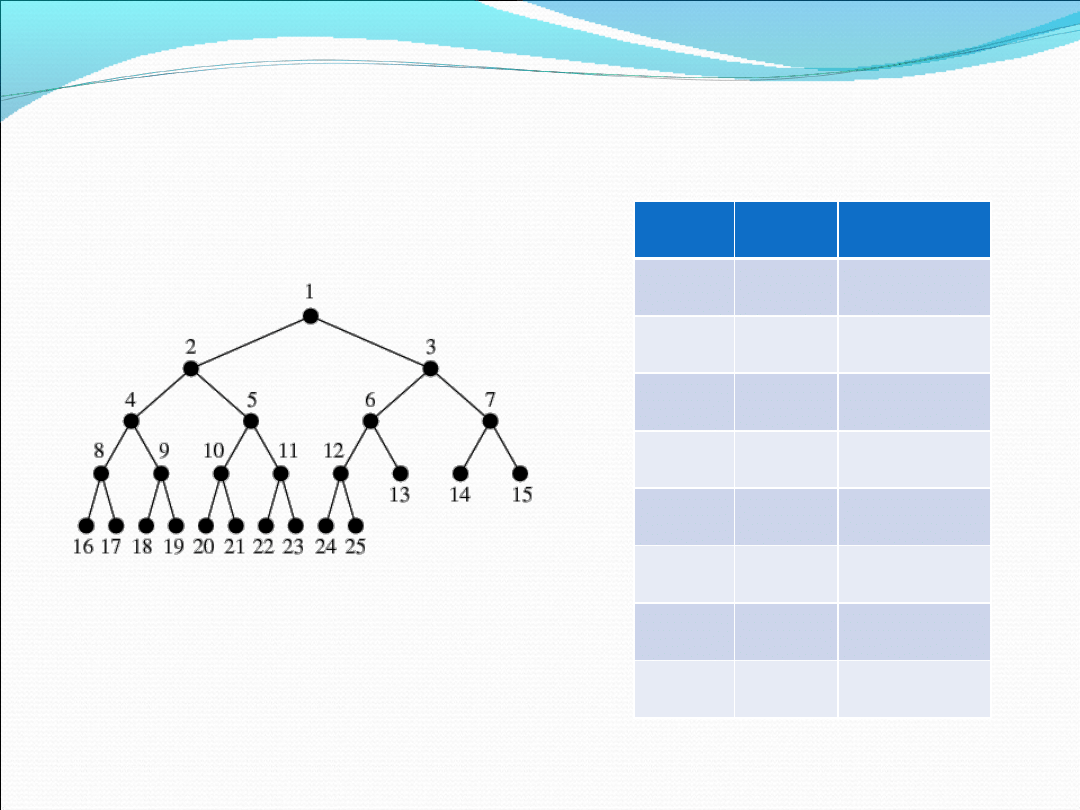
Tablicowa reprezentacja drzewa

binarnego

Węzeł

Syn

Ojciec

1

2;53

1

2

4;5

1

3

6;7

1

4

8;9

2

5

10;11

2

6

12;13

3

7

14;15

3

…

…

…

Przykład zastosowania drzewa binarnego do

reprezentacji wyrażenia arytmetycznego

*

+

12.5

+

*

2

3

7

9

Liście = wartości

Węzły wewnętrzne= operatory

Krok I 2+3=5

Krok II 7*9=63

Krok III 5+63=68

Krok IV 68*12.5=850

W kolejnych krokach dwa liście o najbliższym stopniu pokrewieństwa

rozpatrywane są wraz ich ojcem jako podstawowe wyrażenie do obliczenia.

Takie poddrzewo staje się liściem o obliczonej wcześniej wartości i schemat

powtarza się do momentu zastosowania wszystkich liści.

Typedef struckt
{

double val;
char op;

}

Int main()
{

STOS<wyrazenie*> s; // będzie zapamiętywał wskaźniki do rekordów

// w kolejności FILO co zostało omówione poprzednio

Val t[9]={{2,’0’}, {3,’0’}, {9,’+’}, {7,’0’}, {9,’0’}, {0,’*’},

{0,’+’}, {12.5,’0’}, {0,’*’}};

// tablica zawierająca operatory i operandy (wartości)

wyrazenie *x; // tworzymy wskaźnik x o typie „wyrazenie”

(węzeł)

For(int i=0; i<9; i++) // pętla odczytuje po kolei elementy tablicy

// analizując jej zawartość pod kątem znalezienia

// operatorów bądź wartości

{

x= new wyrazenie;
if ((t[i].op==‘*’ || t[i].op==‘+’ || t[i].op==‘-’ || t[i].op==‘:’

||t[i].op==‘/’))

x->op = t[i].op // jeśli element tablicy zawiera operator to x

// wskazuje operator, a temu operatorowi zostaje

// przypisany znak operatora

else

// w przeciwnym razie x będzie wskazywał na wartość,

{

// a operator jest „zerowany”

x-> val=t[i].val;
x-> op=‘0’;
}

x->lewy =NULL;

// inicjujemy komórki pamięci czyli lewą i

x->prawy=NULL;

// prawą gałąź, które są potomkami

węzła x

if((t[i].op==‘*’|| t[i].op==‘+’||t[i].op==‘-’

|| t[i].op==‘:’ ||t[i].op==‘/’))

{

wyrazenie *l1, *p1; // tworzymy wskaźniki gałęzi
s.pop(l1);

// na stos wrzucamy lewą gałąź

s.pop(p1); // na stos wrzucamy prawą gałąź
x->lewy =l1; // lewej gałęzi węzła x przypisujemy l1
x->prawy =p1; // prawej gałęzi węzła x przypisujemy p1

}

s.push(x); // zdejmujemy ze stosu w wiadomej kolejności

}

//w tym miejscu następuje wypisanie elementów stosu oraz obliczenie wyrażenia
//podanego w Odwrotnej Notacji Polskiej, a mianowicie: *12.5+*97+32=850

}

Wynik : (12.5*((9*7)+(3+2)))=850

Ujmując to „po ludzku”

funkcja wypisująca drzewo pod koniec przytoczonego

przykładu pozwala wyrazić się prostym algorytmem

rekurencyjnym (wywołującym siebie samego):

wypisz(w)
{

jeśli wyrażenie w jest liczbą, to wypisz ją;
jeśli wyrażenie jest operatorem op, to wypisz je
w kolejności:

(wypisz(w->lewy) op wypisz(w->prawy))

}

Grafy

Graf to – w uproszczeniu – zbiór wierzchołków, które
mogą być połączone krawędziami, w taki sposób, że
każda krawędź kończy się i zaczyna w którymś z
wierzchołków. Grafy to podstawowy obiekt rozważań
teorii grafów.

Za pierwszego teoretyka i badacza grafów uważa się

Leonarda Eulera, który rozstrzygnął zagadnienie

mostów królewieckich.

Problem mostów w Królewcu

Euler w 1736 roku

rozwiązał

problem, który

nurtował

mieszkańców

Królewca, a

mianowicie, jak

przejść przez

wszystkie siedem

mostów nie

przechodząc dwa

razy przez ten

sam.

Ostatecznie Euler doszedł do wniosku, iż problem jest nie

do rozwiązania, a przyczyną jest takie, a nie inne

rozmieszczenie mostów.

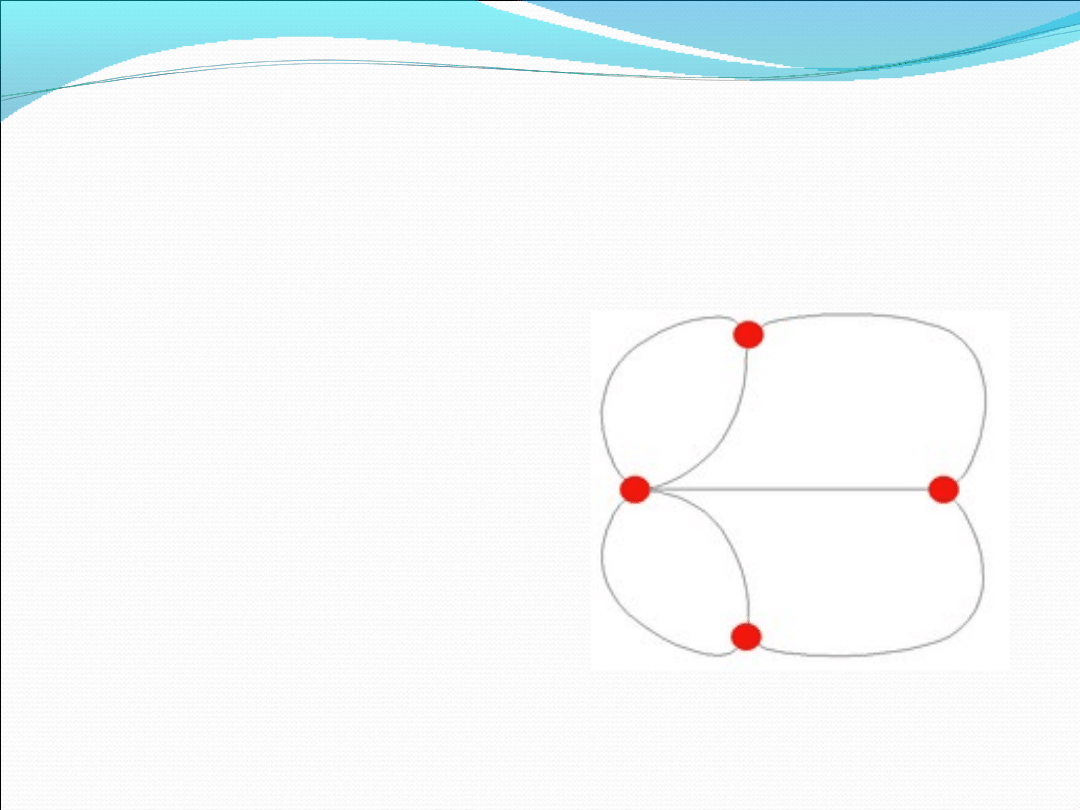
Uproszczony schemat problemu

mostów

(po

prawej)

daje

pierwsze pojęcie o tym jak i co

reprezentują grafy. Czerwone

kropki,

oznaczające

węzły,

reprezentują pewne obiekty (w

tym przypadku ląd), a krawędzie

łączące ze sobą wierzchołki

stanowią reprezentację relacji

zachodzących

pomiędzy

obiektami (w naszym przypadku

są to mosty).

Pojęcia podstawowe



Grafem G nazywamy parę(X,V), gdzie X oznacza zbiór

węzłów (wierzchołków), a V jest zbiorem określonych

krawędzi łączących wierzchołki z X



Graf jest skierowany jeśli jego krawędziom został

zadany kierunek (najczęściej oznaczany na rysunkach

przez strzałkę)



Jeśli rozpatrujemy dany przykład X→Y to węzeł X jest

węzłem początkowym

, a węzeł Y jest

węzłem

końcowym

Pojęcia c.d.



Stopniem wejściowym wierzchołka grafu nazywamy

liczbę krawędzi dochodzących do wierzchołka i

analogicznie…



Graf jest spójny jeśli każde dwa wierzchołki połączone

są drogą



Stopniem wyjściowym wierzchołka grafu nazywamy

liczbę krawędzi wychodzących od danego wierzchołka



Grafem regularnym nazywamy graf, w którym

wszystkie wierzchołki posiadają ten sam stopień

Pojęcia c.d.



Drogą (lub ścieżką) grafu nazywamy ciąg

wierzchołków, w którym każde dwa kolejne

wierzchołki (elementy tego ciągu) połączone są

krawędzią



Grafem zredukowanym G bądź podgrafem grafu G

nazywamy graf, którego elementy stanowią podzbiór

zbioru elementów grafu G (tzn. wierzchołki podgrafu

grafu G stanowią podzbiór zbioru wierzchołków grafu

G i odpowiednio krawędzi grafu zredukowanego G

stanowią podzbiór zbioru krawędzi grafu G)

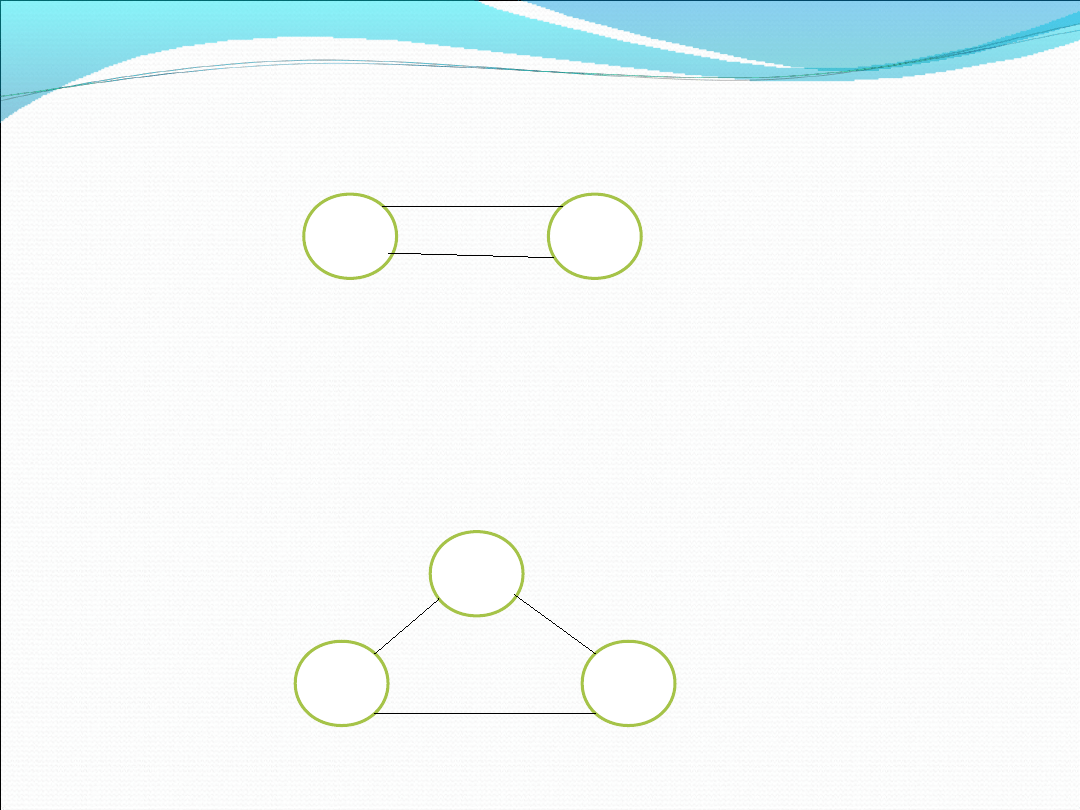
Przykład normalizacji grafu

Rysunek jest niezgodny z definicją (istnieje tylko

jedna możliwa krawędź łącząca dwa wierzchołki w

dany sposób). Problem rozwiązywany jest poprzez

dołączenie dodatkowych wierzchołków:

X

Y

X

Y

Z

Plan skonstruowania

dwóch dróg X→Y

został zrealizowany

Sposoby reprezentacji grafów

-reprezentacja tablicowa

Jest to jedna z dwóch najpopularniejszych metod

reprezentacji grafu. Polega na stworzeniu tablicy

kwadratowej o wymiarach n x n, gdzie n oznacza

liczbę węzłów. Tablica w takiej implementacji

ukazywać będzie związek (krawędź) pomiędzy

poszczególnymi węzłami. W zależności od widzimisię

programisty, kolumna węzłów może reprezentować

ojców, a wiersz synów lub na odwrót lecz musi on

(programista) pozostać konsekwentny.

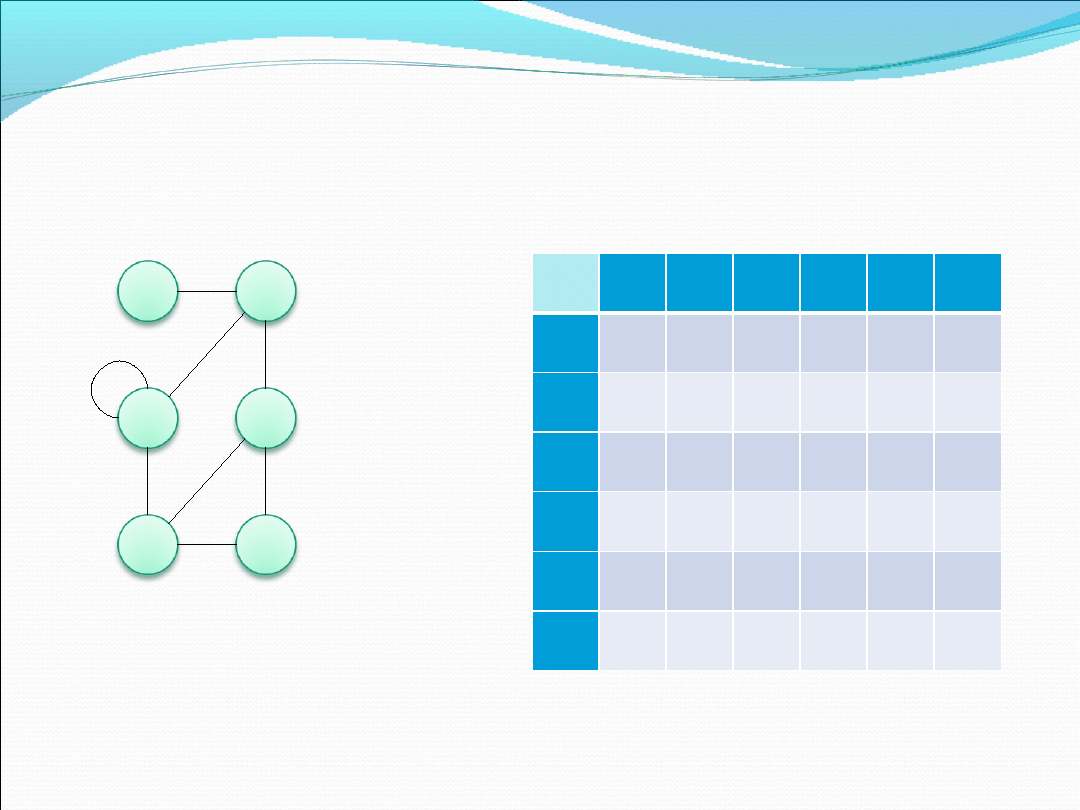
Przykład reprezentacji grafu w formie tablicowej

A

B

C

D

F

E

A

B

C

D

E

F

A

X

B

X

X

C

X

X

D

X

X

E

X

F

Po

pr

ze

dn

ik

i

-

O

jc

ow

ie

Następniki - Synowie

Tablica pokazuje po prostu, że węzeł A ma krawędź skierowaną do B, B

ma krawędzie skierowane do C i do D, zaś C do samego siebie oraz do E

itd.

Sposoby reprezentacji grafów

-słownik węzłów

Jest to druga najpopularniejsza metod reprezentacji

grafu polegająca na stworzeniu listy wskaźników do

list węzłów. Podstawową cechą słownika węzłów jest

opieranie się podczas wyszukiwania połączenia na

węźle wyjściowym, który wskazuje na dane. Lista

może (tak jak w przypadku tablic) działać

dwukierunkowo. Wskaźnik może wskazywać zarówno

na poprzedniki węzła (czyli węzły, od których

krawędzie dochodzą do opisywanego wskaźnika) jak i

następniki (węzły, które połączone są krawędziami

wychodzącymi od wskaźnika)

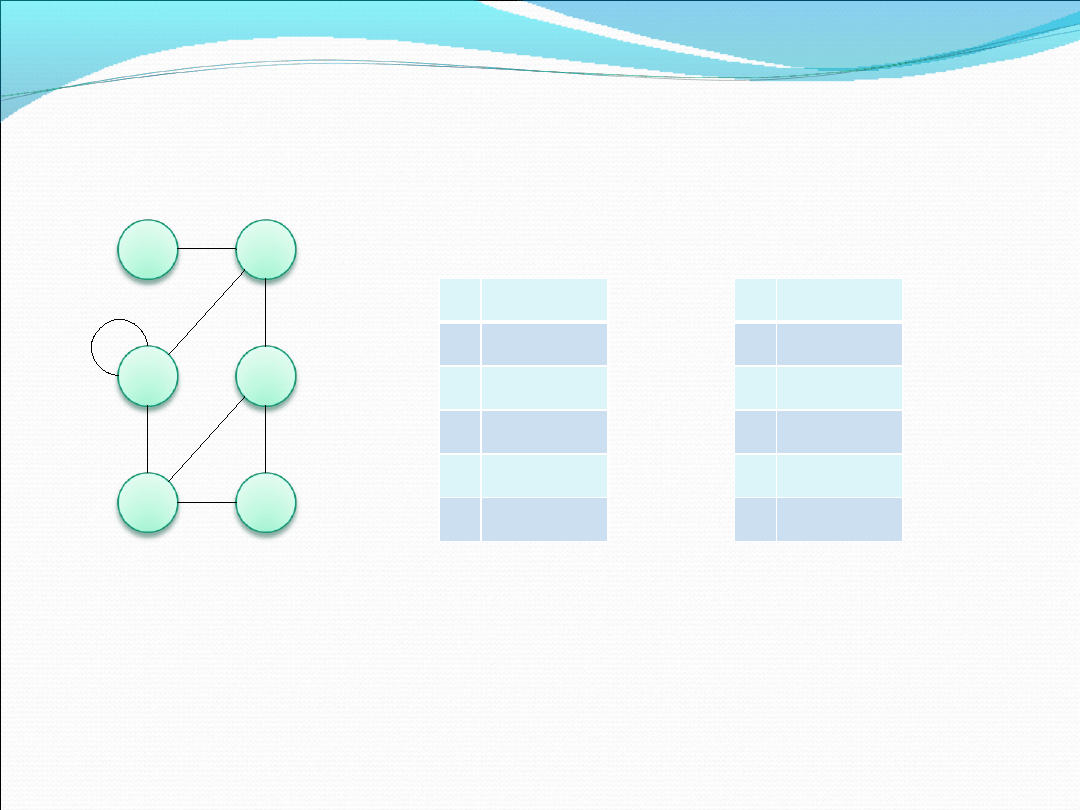
Przykład reprezentacji grafu w formie słownika węzłów

A

B

C

D

F

E

A B
B C, D
C C, E
D E, F
E F
F NULL

A NULL
B A
C B, C
D B
E C, D
F D, E

Lista następników

danego węzła

Lista poprzedników

danego węzła

Użycie słownika węzłów jest korzystniejsze niż tablic ze względu na

możliwość dynamicznej rozbudowy grafu bez obawy przepełnienia stosu z

czym trzeba się liczyć w przypadku dużej dynamicznej tablicy.

Przeszukiwanie grafu „w głąb”

Ten typ przeszukiwania grafu charakteryzuje

przechodzenie się po jego elementach w ramach raz

obranej drogi. Nazywa się to maksymalną eksploatacją

raz obranej drogi przed ewentualnym wybraniem

następnej. Ważne jest zapamiętywanie w programie

wierzchołków już raz odwiedzonych aby nie

wstępować drugi raz do już odwiedzonego węzła.

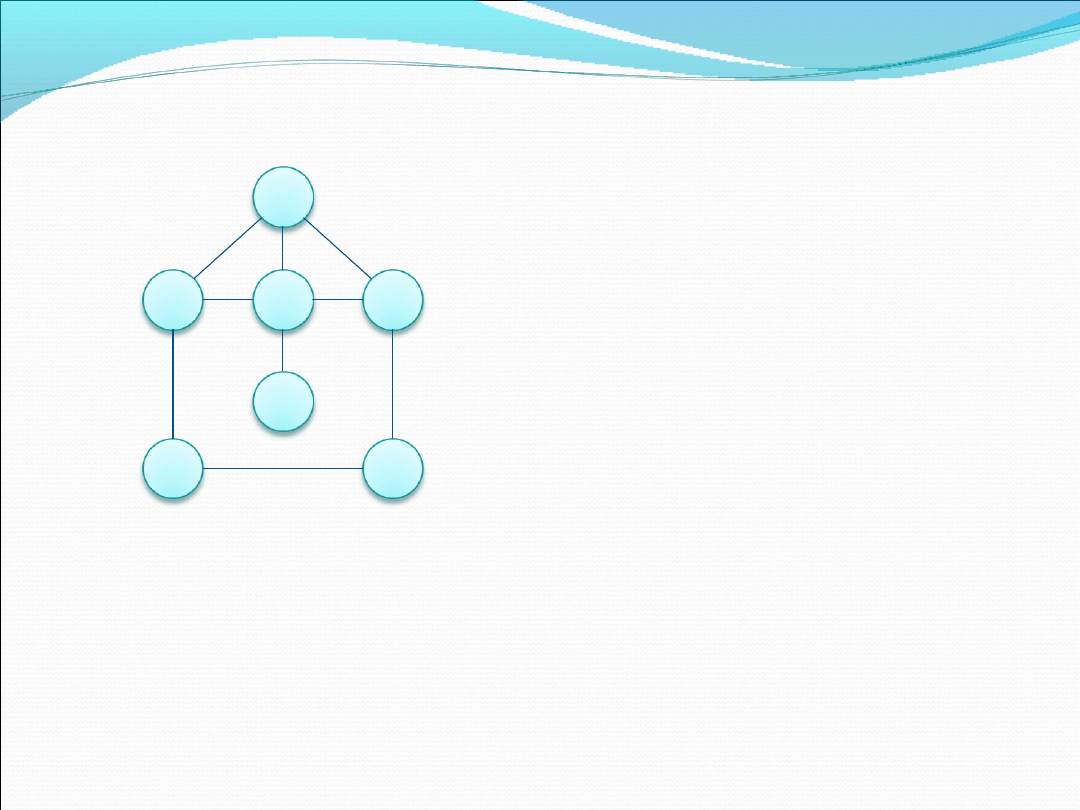
Przykład

A

E

B

D

G

F

C

Lista wierzchołków sąsiadujących

A: B, E, D

B: A, C, E

C: B, G

D: A, E, G

E: A, B, D, F

F: E

G: C, D

Algorytm przeszukiwania „w głąb” rozpocznie się od wierzchołka A. zapamięta go

jako już odwiedzony i rozpatrzy jedną z trzech dróg: B, E lub D. Na początek

wybierze wierzchołek B, zapamięta go jako odwiedzony i rozpatrzy jego węzły

sąsiadujące czyli: A, C, E. Ponieważ A został już odwiedzony, skierujemy się do

wierzchołka C. Stamtąd jedyną drogą jest G. Z G z kolei możemy skierować się

jedynie do D. Ponieważ A i G są już „odwiedzone” jedyną ścieżką pozostaje

krawędź w kierunku węzła E, a potem do F. Droga przebyta przez algorytm

prezentuje się następująco: A →B →C →G →D →E →F.

Przeszukiwanie grafu „wszerz”

A

E

B

D

G

F

C

Przeszukiwanie „wszerz” opiera się na badaniu

grafu na jednej głębokości. Kolokwialnie można

powiedzieć, że algorytm „wszerz” idzie „ławą”.

Dla przykładu posłużymy się takim samym grafem

jak w przypadku przeszukiwania „w głąb”.

W tym przypadku zaczynamy również od wierzchołka A. Badamy jego węzły

sąsiadujące czyli B, D i E. Następnie algorytm przeszukuje nieodwiedzonych

przez nasz algorytm sąsiadów tych węzłów czyli C, G i F. W efekcie droga

przeszukiwania odbyła się następująco: A, B, D, E, C, G, F.

Cykle w grafach

Definicja: Cyklem nazywamy drogę w grafie, która

rozpoczyna się i kończy w tym samym wierzchołku

Cykl skierowany to cykl, w którym wierzchołki są

uporządkowane zgodnie z kierunkiem krawędzi

łączących poszczególne pary

Jeśli graf skierowany nie zawiera ani jednego cyklu

skierowanego nazywamy go acyklicznym grafem

skierowanym

Dlaczego acykliczny graf skierowany dotyczy jedynie

grafów skierowanych?

Odpowiedź jest bardzo prosta. Każdy graf

nieskierowany

możemy zaprezentować jako graf skierowany w

obu kierunkach

co czyni z tego grafu, graf zawierający cykl skierowany

X

Y

X

Y

Cykl Hamiltona

Jeśli droga cyklu, którą obraliśmy, przechodzi przez

każdy z wierzchołków dokładnie raz, to taki cykl

nazywamy cyklem Hamiltona – od nazwiska słynnego

irlandzkiego matematyka, który w ogromnym stopniu

przyczynił się do rozwoju teorii grafów

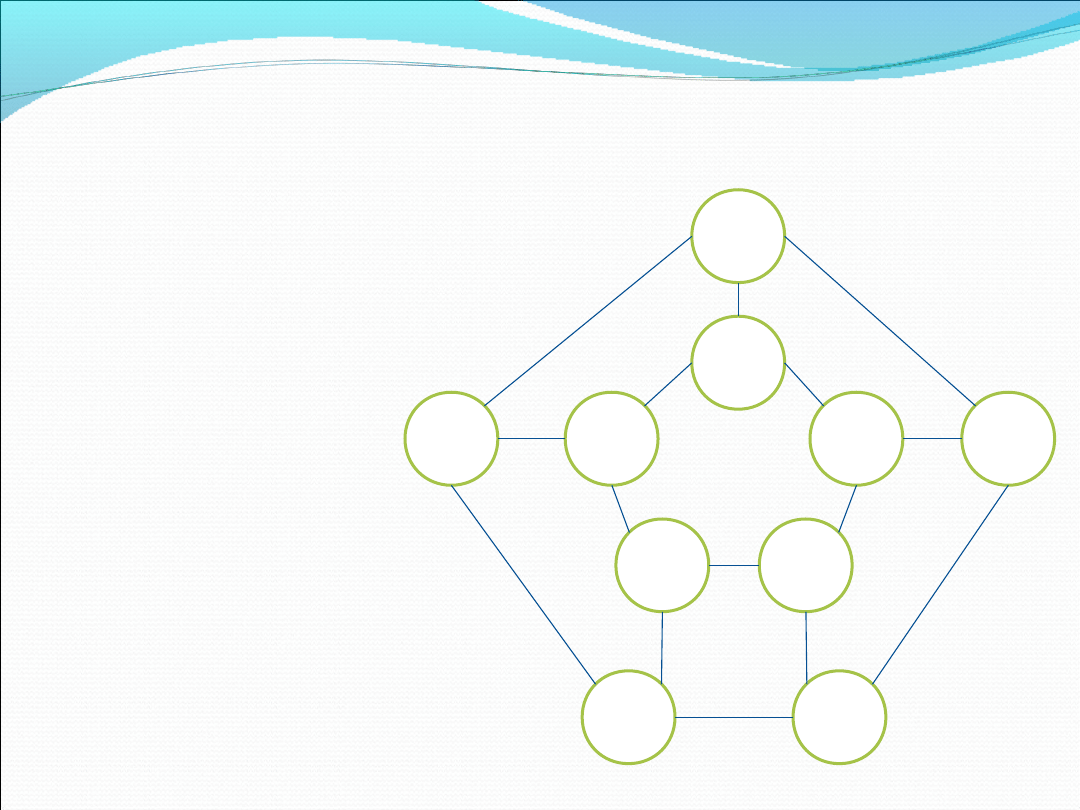
Cykl Hamiltona- przykład

A

E

F

B

C

D

G

H

I

J

Podążając

alfabetycznie, w

grafie

nieskierowanym, od

wierzchołka A do J (i

następnie do A)

przechodzimy przez

wszystkie wierzchołki

dokładnie jeden raz (i

kończąc na

wierzchołku

początkowym)

udowadniając, że

dany graf stanowi

cykl Hamiltona.

A

H

I

J

F

G

B

C

D

E

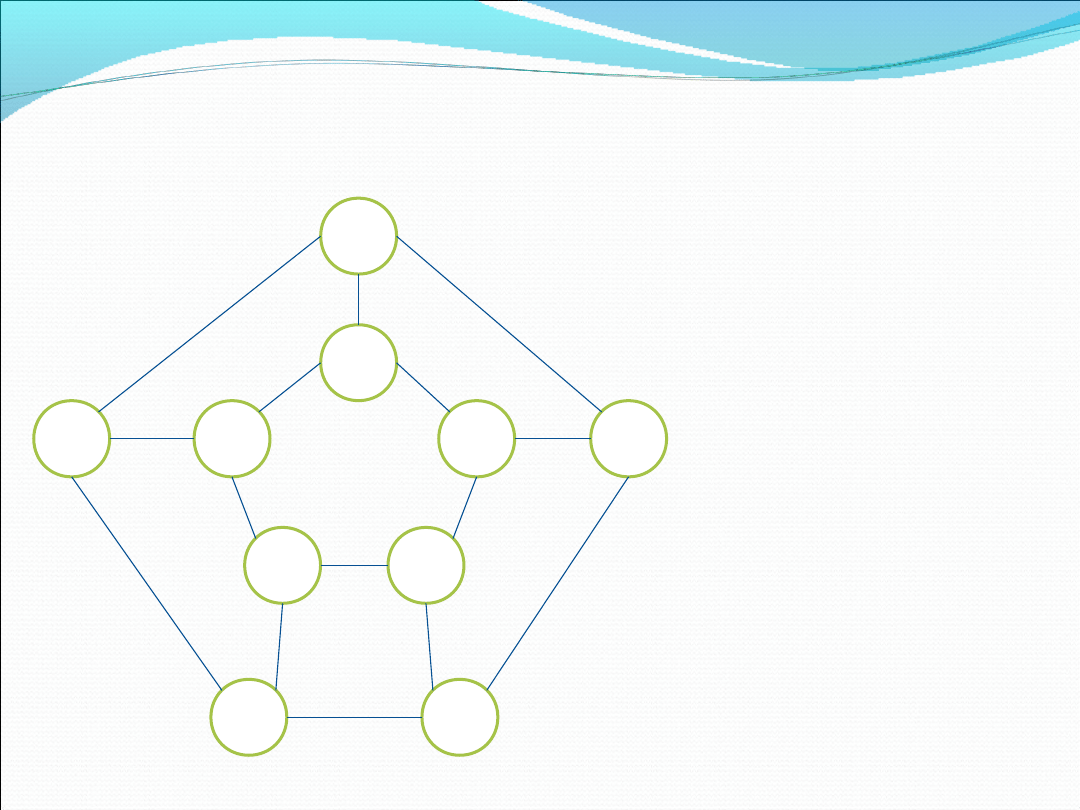
Ten sam graf (o tej

samej strukturze)

możemy „przejść”

również w taki

sposób.

Podążajmy po raz

kolejny

alfabetycznie od A

do J.

A

H

G

F

E

D

J

I

C

B

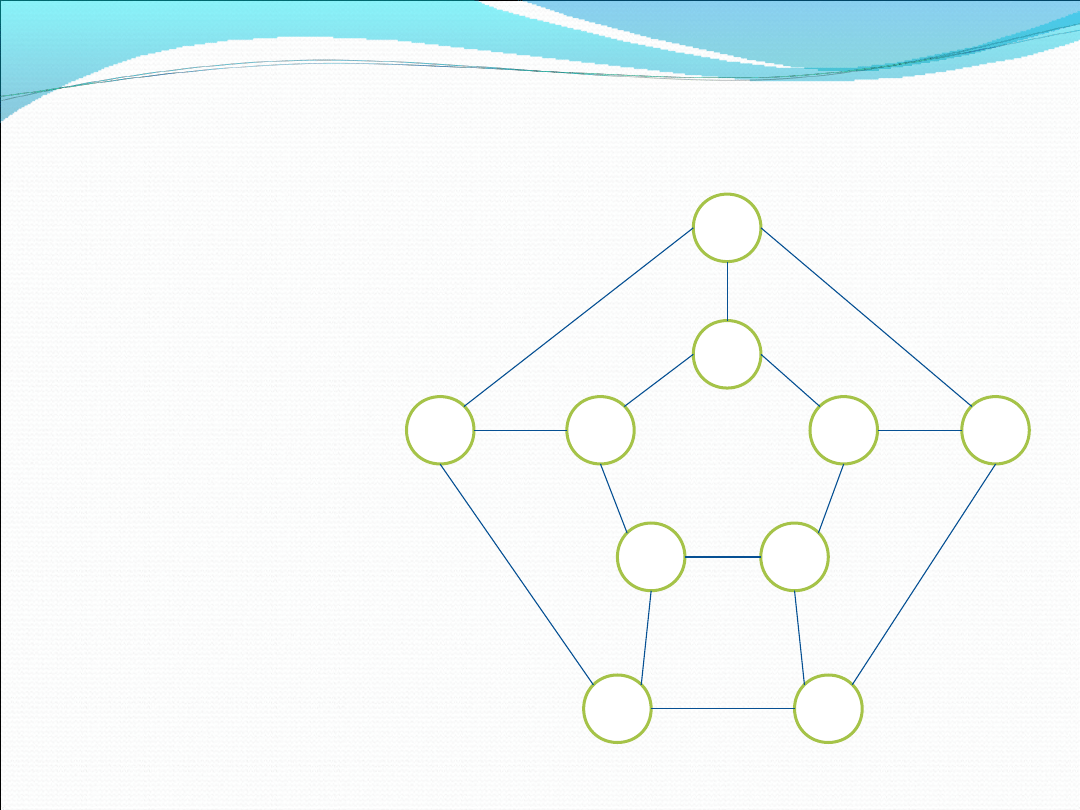
Ale również w ten

sposób, stosując

znaną metodę.

Problem komiwojażera

Z cyklem Hamiltona związany jest słynny problem
optymalizacji drogi zwany problemem komiwojażera.
Zadaniem, jakie stoi przed bohaterem problemu, jest
jednokrotne zawitanie do każdego z miast zaplanowanych
do odwiedzenia przy minimalizacji wysiłku (kosztów,
długości drogi itp.). Możemy przyjąć np., że miasta dzieli
pewna

odległość

lub

koszt

przejazdu

między

poszczególnymi miastami różni się itd. w zależności od
minimalizowanej cechy.

Problem komiwojażera c.d.

Nowy

Jork

Chicago

Los

Angeles Seattle

Nowy

Jork

0

400

750

900

Chicago

400

0

650

350

Los

Angeles

750

650

0

200

Seattle

900

350

200

0

Przykładow

e ceny lotów

pomiędzy

miastami w

USA

NY

C

LA

S

400

750

200

650

900

350

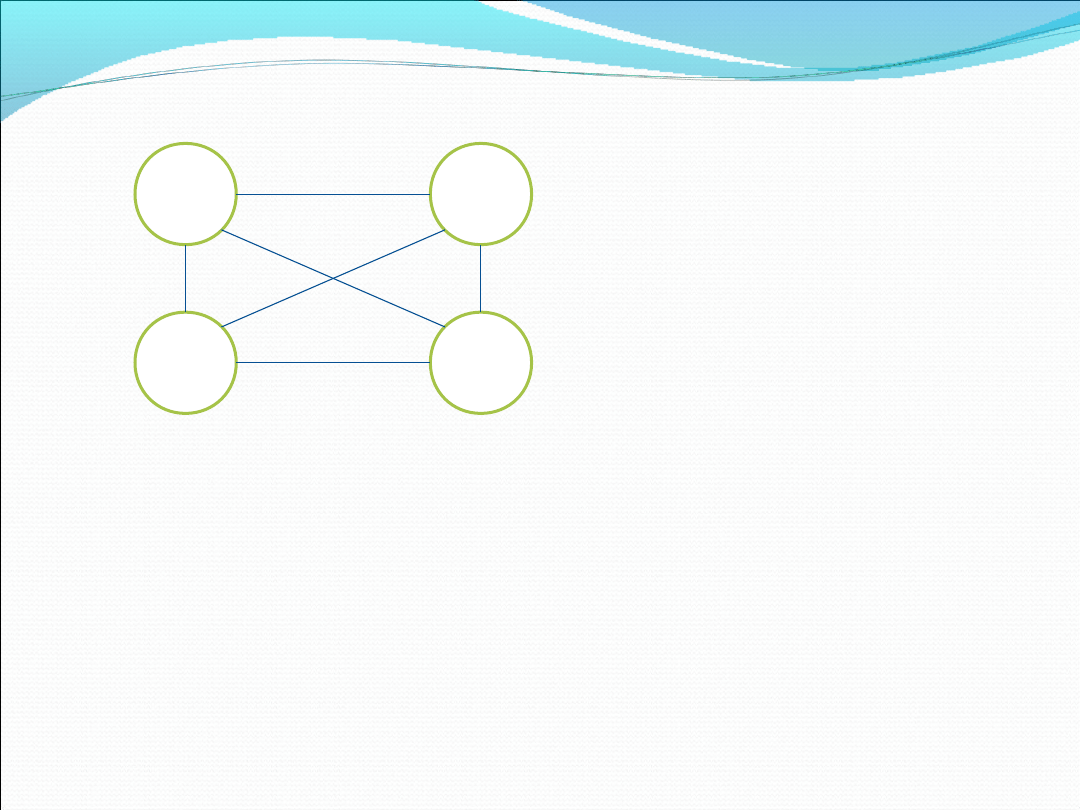
NY→S→C→LA→NY = 900+350+650+750 = 2650
NY→S→LA→C→NY = 900+200+650+400 = 2150

NY→C→S→LA→NY = 400+350+200+750 = 1700

NY→C→LA→S→NY = 400+650+200+900 = 2150
NY→LA→S→C→NY = 750+200+350+400 = 1700

NY→LA→C→S→NY = 750+650+350+900 = 2650

Wyruszamy z Nowego Jorku i

tam też chcemy wrócić po

odwiedzeniu Chicago, Seattle

i Los Angeles (w dowolnej

kolejności. Jak wybrać trasę?

Z obliczeń wynika

jasno, że najtaniej

zrealizujemy naszą

podróż lecąc do LA,

potem do Seattle, a

następnie do Chicago i

z powrotem do NY

(lub na odwrót)

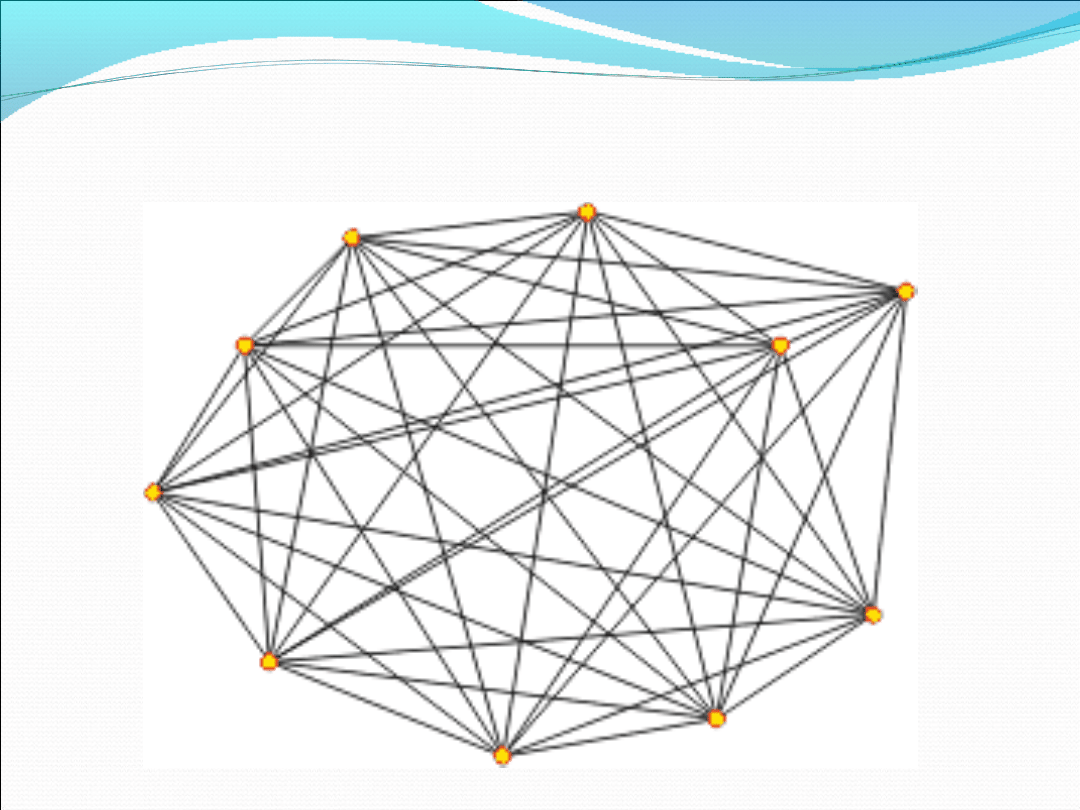
A co jeśli nasz graf ma dziesięć wierzchołków i wygląda tak?

Ile różnych cykli Hamiltona zawiera taki graf?

Otóż pierwszą krawędź cyklu można wybrać na 9 różnych

sposobów, ponieważ każdy wierzchołek grafu jest

połączony krawędzią z pozostałymi dziewięcioma. Po

wyborze pierwszej krawędzi pozostaje nam 8 możliwych

wyborów, później 7, 6 5 ... 1. W efekcie otrzymujemy liczbę

cykli Hamiltona równą:

L

H

= 9 • 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1 = 9! = 362880

Dla n wierzchołków:

L

H

= (n - 1) • (n - 2) • ... • 3 • 2 • 1 = (n - 1)!

Implementacja C++

#include <iostream>

#include <list>

 

using namespace std;

 

const int MAXV = 50; // maksymalna liczba wierzchołków

const int MAXINT = 2147483647; // maksymalna, dodatnia liczba

//całkowita

 

 

// ++++++++ konstruujemy strukturę krawędzi z wagą

 

struct edge

{

int v,d; // v to numer wierzchołka, a d to suma wag

};

// +++++++++++ wprowadzamy zmienne globalne

 

int n,m,d,dh; // n i m to liczba wierzchołków i krawędzi w grafie

// d i dh to odpowiednio suma wag dla cyklu oraz

// bieżąca suma wag

 

list <edge> L[MAXV + 1]; // deklarujemy listę tablic o dwóch zmiennych ze

// struktury edge i maksymalnej długości = 50,

// Każdy element tablicy jest z kolei listą

// wierzchołków oraz wag krawędzi prowadzących do

// tych wierzchołków: {v, d}

 

list <int> q,qh; // tworzymy listę odwiedzonych wierzchołków

// bieżącą i ogólną

bool visited[MAXV + 1]; // oraz warunek logiczny, który zapamięta czy dany

// wierzchołek był odwiedzony



// tworzymy funkcję rekurencyjną (czyli wywołującą samą siebie)



// przeszukiwania w głąb o nazwie TSP



 



void TSP(int v)



{



qh.push_back(v); // dorzucamy do listy odwiedzonych wierzchołków



// numer wierzchołka



 



if(qh.size() == n) // jeśli rozmiar listy równa się zadanej ilości



// wierzchołków, czyli odwiedzone zostały już



// wszystkie to:



{



for(list<edge>::iterator i = L[v].begin(); i != L[v].end(); i++)



 



// wykonujemy pętlę przesuwając iterator (swego rodzaju kursor, wskaźnik)

po



// kolejnych pozycjach listy zawierającej numery wierzchołków oraz wagi



// krawędzi prowadzących wierzchołka v



 



if(i->v == 1) // warunek, istnienia krawędzi od v do

pierwszego



// wierzchołka czyli „czy dla danego v iterator = 1”



// jeśli tak, to…



{



dh += i->d; // do bieżącej sumy wag doda się waga

wskazanej



// przez iterator krawędzi oraz…



 



if(dh < d) // oraz wykona się warunek logiczny



// sprawdzający czy bieżąca suma wag jest



// mniejsza od znanej już sumy wag krawędzi



{



d = dh; // jeśli tak, to bieżąca suma stanie się



// najmniejszą sumą dotychczas poznaną



// na odcinku od początkowego



// wierzchołka do obecnie sprawdzanego



 



q.assign(qh.begin(), qh.end());



// wtedy to zapamiętujemy



// kolejność wierzchołków



// od pierwszego do bieżącego



 



q.push_back(1); // zamykamy cykl dopisując do kolejki

v=1



}



dh -= i->d; // w przeciwnym razie od zwiększonego



// wcześniej dh o daną wagę odejmiemy ją

i



// wrócimy do sumy wag z poprzedniej

pętli



break;



}



}

Jeszcze trochę…



else // jeśli jednak lista kolejnych wierzchołków nie osiągnęła



// rozmiaru zadanej ilości wierzchołków to…



 



{



visited[v] = true; // oznaczamy wierzchołek v jako już

// odwiedzony



 



for(list<edge>::iterator i = L[v].begin(); i != L[v].end(); i++)



 



// wykonujemy pętlę dla każdego sąsiada



// wierzchołka v



 



if(!visited[i->v]) // jeśli “sąsiad” nie był odwiedzony to…



 



{



dh += i->d;

// zwiększamy sumę wag ścieżki



TSP(i->v);

// wywołujemy poszukiwanie cyklu (czyli listy



// kolejnych wierzchołków dla której suma wag



// jest najmniejsza)



 



dh -= i->d; // odejmujemy od sumy wag tę ostatnią wagę



// krawędzi aby w nowej pętli odwoływać się do

// poprzedniej



}



visited[v] = false; // kończymy pracę z tym wierzchołkiem oraz…



}



qh.pop_back(); // usuwamy wierzchołek z listy



}



//wykonujemy główną funkcję poszukującą najkorzystniejszego

cyklu //Hamiltona



 



main()



{



 



// Odczytujemy definicję grafu ze standardowego wejścia



 



cin >> n >> m;



 



for(int i = 1; i <= m; i++)



{



int v,w,dx; cin >> v >> w >> dx;



edge x;



x.v = w; x.d = dx; L[v].push_back(x);



x.v = v; L[w].push_back(x);



}



cout << endl;



// Rozpoczynamy wyszukiwanie cyklu Hamiltona



// o najmniejszej sumie wag krawędzi



 



for(int i = 1; i <= n; i++)



{



visited[i] = false;

// zerujemy odwiedziny



q.clear(); qh.clear();

// zerujemy kolejki



d = MAXINT; dh = 0;

// przypisujemy nieskończoność

// do d, a do sumy wag 0



TSP(i);

// wyszukujemy cykl Hamiltona

}

// zaczynając od wierzchołka 1

do

// n-tego



// Wypisanie wyników



 



if(q.size())

// jeśli cykl został znaleziony wypisujemy:



 



{



cout << "CYKL HAMILTONA : ";



for(list<int>::iterator i = q.begin(); i != q.end(); i++)



cout << (* i) << " ";



cout << "\n SUMA WAG WYNOSI : " << d << endl;



}



// jeśli jednak nie ma cyklu to wypiszemy:



 



else cout << "GRAF NIE POSIADA CYKLU HAMILTONA\n";



 



cout << endl;



system("PAUSE");



}



 



Koniec programu.

Cykl Eulera

Bardzo podobnym do cyklu Hamiltona problemem

(często z resztą mylonym z nim) jest cykl Eulera. W

cyklu Hamiltona dany wierzchołek odwiedzony był

dokładnie raz, natomiast w przypadku Eulera tą

„jednorazowością” charakteryzują się krawędzie.

Innymi słowy: Hamilton pokazuje jak jednorazowo

znaleźć się na każdym z brzegów, a Euler, jak przejść

dokładnie jeden raz przez każdy z mostów.

Oczywiście w przypadku podanego już przykładu

mostów królewieckich nie znajdujemy ani cyklu

Eulera, ani Hamiltona

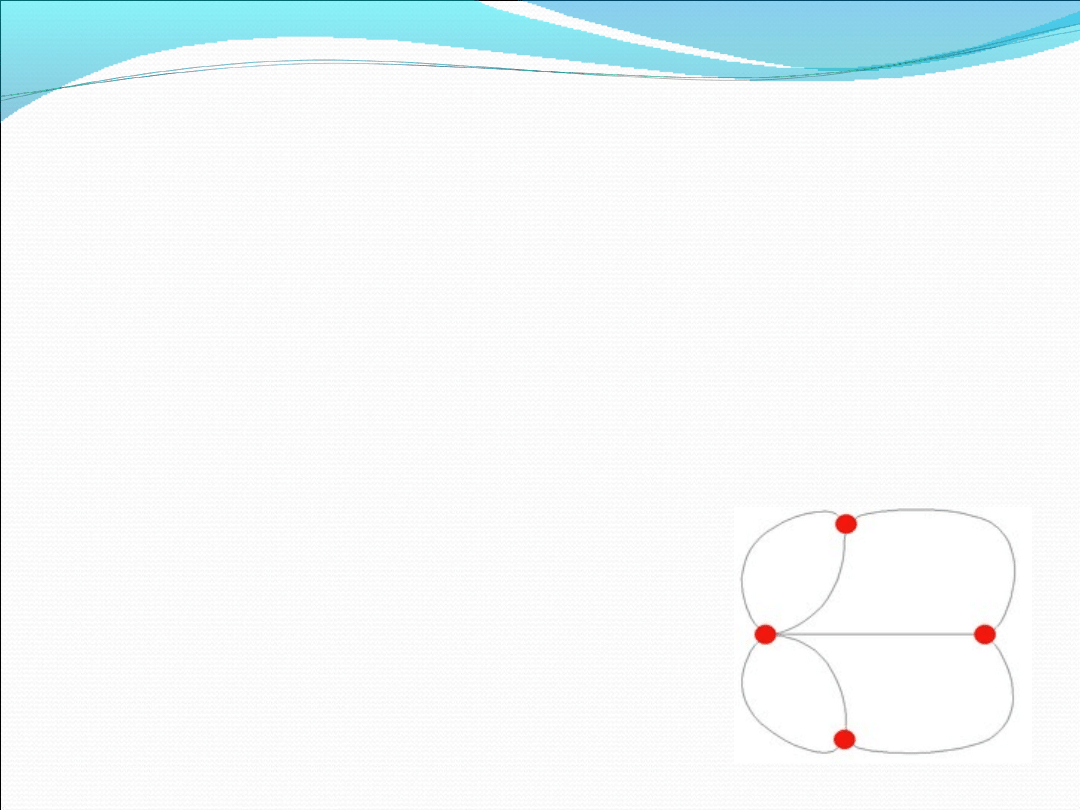
Twierdzenie Eulera

Graf nieskierowany zawiera cykl Eulera, jeśli jest

spójny i jego wierzchołki mają parzysty stopień. W

przypadku grafu skierowanego, zawierającego cykl

Eulera, oprócz spójności musi występować taki sam

stopień wyjściowy i wejściowy dla każdego

wierzchołka.

Dzięki tej definicji jesteśmy w stanie odpowiedzieć

na pytanie dlaczego mostów w Królewcu nie da się

przejść jednocześnie wszystkich jeden raz. Na

rysunku dokładnie widać, że nie jest spełniony

warunek parzystości stopnia wierzchołków.

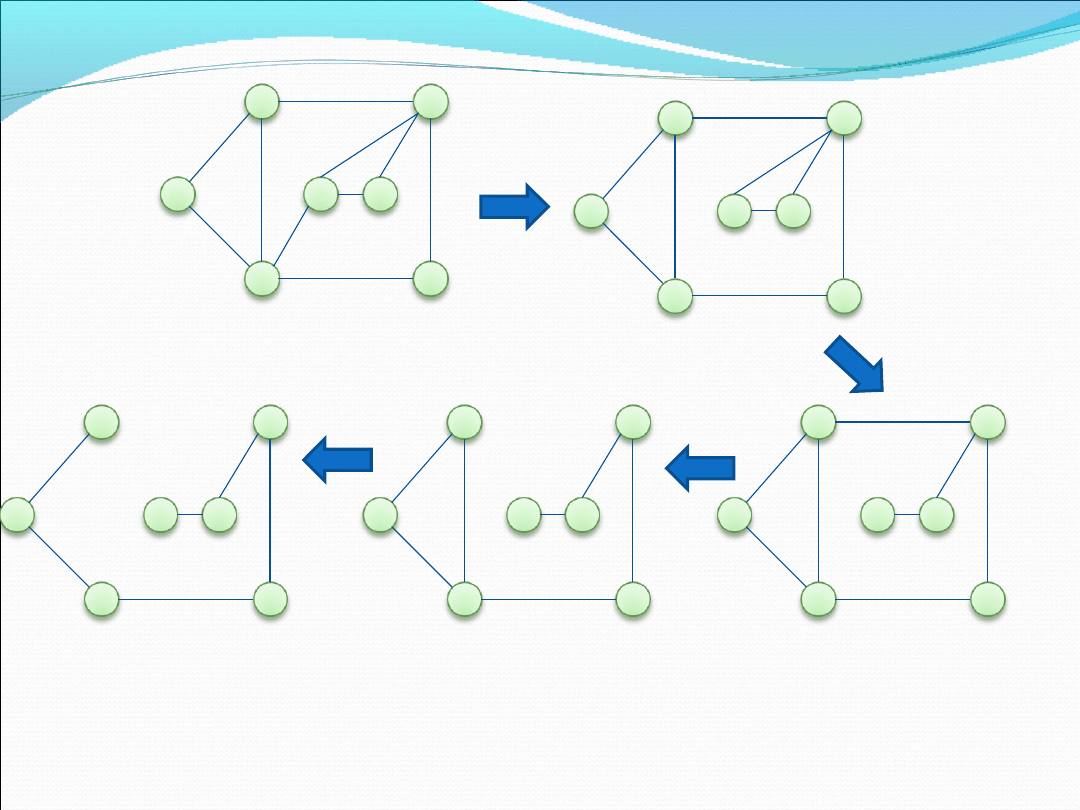
Algorytm Fleury’ego

Ten algorytm jest uzupełnieniem twierdzenia Eulera

ponieważ, pozwala odszukać cykl Eulera w momencie

gdy samo twierdzenie pozwala jedynie stwierdzić jego

istnienie. Jest on opisany w prosty sposób:

1. Wybierz początkowy węzeł

2. Wybierz dowolną , nieprzechodzoną jeszcze krawędź spośród

krawędzi wychodzących z wierzchołka, w którym aktualnie się

znajdujemy. Dodatkowo postaraj się nie wybierać krawędzi

tzw. Cięcia grafu czyli takiej krawędzi, której usunięcie

podzieliłoby graf (chyba że nie ma wyboru)

3. Przejdź przez wybraną krawędź do następnego wierzchołka

4. Zapamiętaj wybraną krawędź i usuń ją z grafu

5. Powtarzaj kroki 2, 3 i 4 aż do momentu przejścia wszystkich

krawędzi i powrotu do wierzchołka początkowego

D

F

C

G

B

A

E

D

F

C

G

B

A

E

D

F

C

G

B

A

E

D

F

C

G

B

A

E

D

F

C

G

B

A

E

Dziękuję za uwagę!

Zachęcam do zgłębiania fascynującego tematu jakim są zagadnienia

algorytmiki, a który w bardzo okrojonym stopniu próbowałem

Państwu przedstawić.

Prezentacja oparta została w dużej mierze na książce Piotra

Wróblewskiego pt.: Algorytmy, struktury danych i techniki

programowania oraz na stronach:

http://edu.i-lo.tarnow.pl/inf/utils/002_roz/ol027.php

http://www.adaptivebox.net/CILib/code/tspcodes_link.html
http://pl.wikipedia.org

Niektóre użyte sformułowania są dosłownymi cytatami lub są

bardzo zbliżone do cytowanych fragmentów ww. źródeł. Brak

oznaczenia w każdym z miejsc powodowany był przejrzystością

prezentacji. Jednocześnie chciałbym zaznaczyć, że użyte cytaty

czy kody źródłowe w najlepszy możliwy sposób opisywały

omawiane zagadnienia, w związku z czym pozwoliłem sobie na

dosłowne ich skopiowanie. Tam gdzie uznałem za zasadne i

możliwe, formułowałem zdania we własnym zakresie.