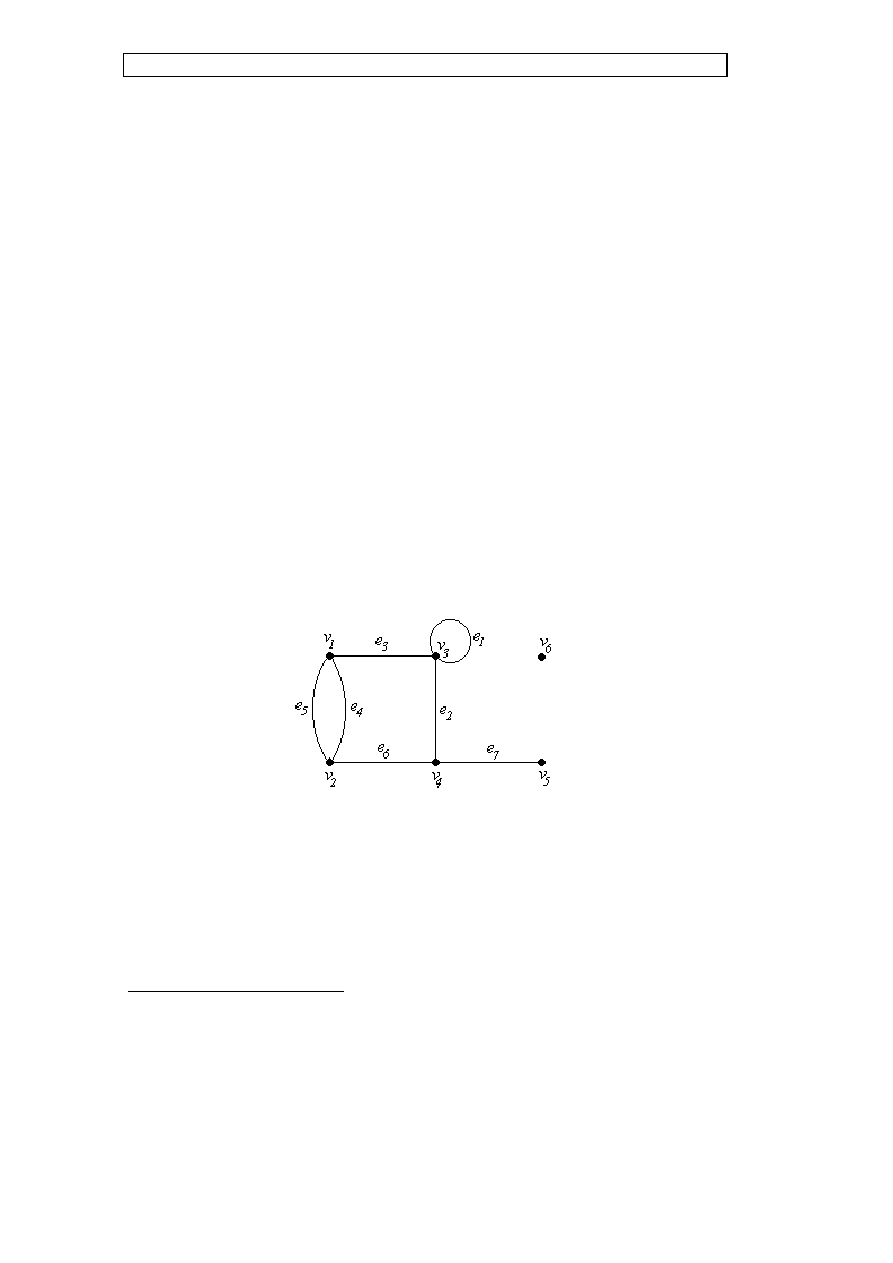
Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
1
G. Wybrane elementy teorii grafów
W matematyce teorię grafów klasyfikuje się jako gałąź topologii. Jest ona
jednak ściśle związana z algebrą i teorią macierzy. Grafy są stosowane
współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
modeluje
się
i
rozwiązuje
szeroki
wachlarz
złożonych
problemów
ekonomicznych, tak w skali mikro- jak i makro zarządzania. Krótki rys
historyczny rozwoju teori grafów wygląda następująco:
•
1736 Leonard Euler (uważany za twórcę teorii grafów)
•
1847 G.R.Kirchhoff (teoria obwodów elektrycznych)
•
1857 A.Cayley (chemia: izomery węglowodorów nasyconych)
•
1859 W.R.Hamilton
•
1945 i dalsze - intensywny rozwój teorii grafów (N.Deo, F.Harary) i jej
zastosowań
G.1. Co to jest graf
Figura przedstawiona na rysunku G.1. nazywa się grafem
1
. Wyróżnione
punkty nazywają się wierzchołkami grafu (ang. vertex), zaś linie noszą nazwę
krawędzi grafu (ang. edge). Wymagane jest, aby każda krawędź i każdy
wierzchołek miały swoją nazwę (etykietę).
Rys. G.1. Przykład grafu liniowego
Wierzchołki grafu oznaczamy
v v
v
m
1
2
,
, ... ,
. Zbiór wierzchołków oznaczymy jako
{
}
V
v v
v
m
=
1
2
,
, ... ,
i musi to być zbór niepusty (
V ≠ ∅
).
Krawędzie grafu oznaczamy
e e
e
n
1
2
, , ... ,
. Zbiór krawędzi oznaczymy jako
{
}
E
e e
e
n
=
1
2
, , ... ,
i może to być zbór pusty.
1
Ściśle graf liniowy, ale ponieważ nie istnieją grafy nieliniowe to mówimy krótko graf.
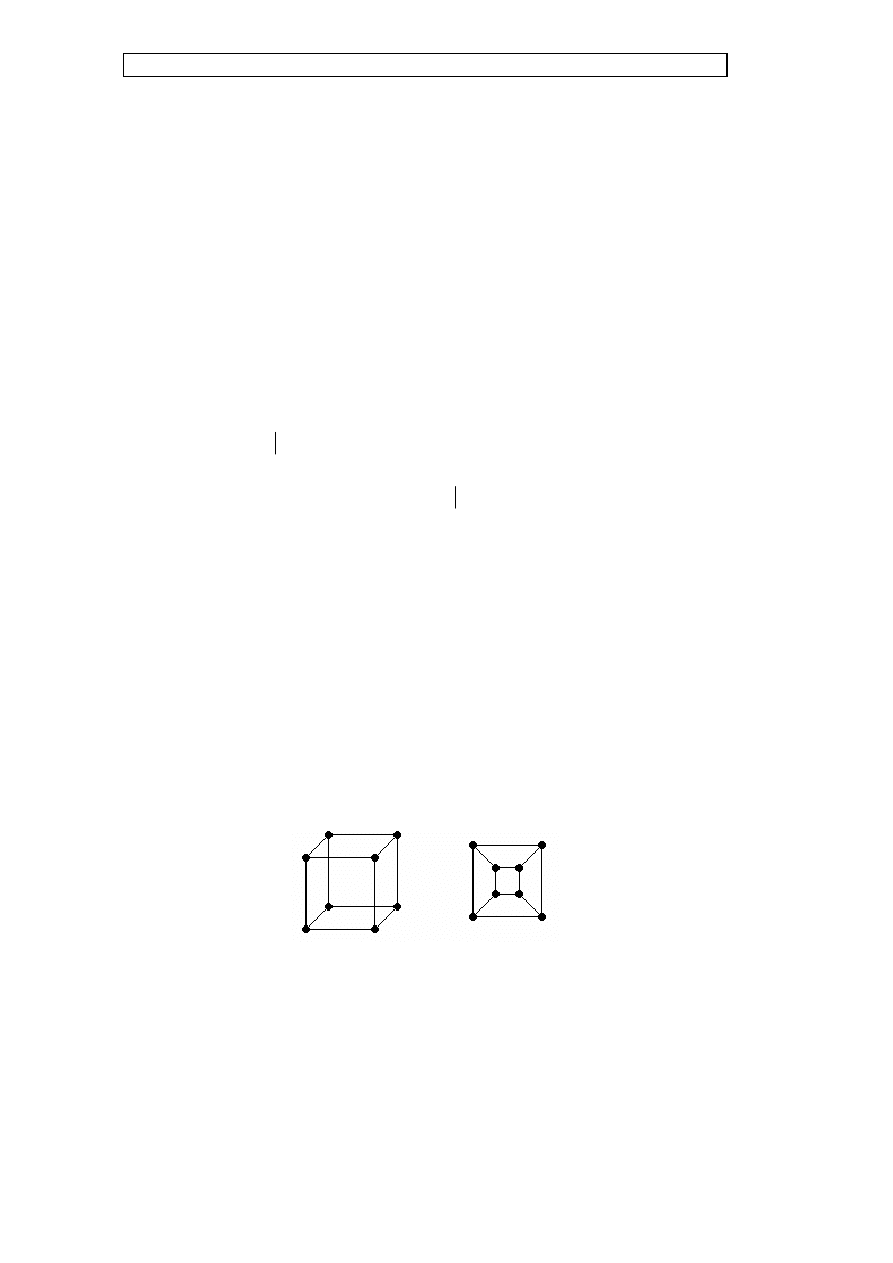
Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
2
Gdy nie zachodzi obawa pomyłki, etykiety wierzchołków i krawędzi mogą być
liczbami naturalnymi, tj.
{
}
V
m
= 1 2
, , ... ,
oraz
{
}
E
n
= 1 2
, , ... ,
.
Dla oznaczenia grafu G możemy zapisać krótko
(
)
G
V E
=
,
, co oznacza, że graf G
składa się ze zbioru wierzchołków V i zbioru krawędzi E.
Dowolna krawędź
e
k
utożsamia się z nieuporządkowaną parą wierzchołków
(
)
v v
i
j
,
. Wierzchołki
v
i
oraz v
j
związane z krawędzią
e
k
nazywa się
wierzchołkami końcowymi krawędzi
e
k
. O krawędzi
e
k
mówimy, że jest ona
incydentna z wierzchołkami
v
i
oraz v
j
.
G.1.1. Definicja grafu
Niech
{
}
V
i i
m
=
=
1 2
, , ... ,
będzie dowolnym zbiorem skończonym i
niech S oznacza zbiór wszystkich (różnych) nieuporządkowanych par (i,j)
elementów zbioru V, to znaczy
( )
{
}
S
i j
i V
j V
=
∈ ∩ ∈
,
. Pary (i,j) oraz (j,i)
oznaczają:
ten sam element - dla grafu nieskierowanego lub
różne elementy - dla grafu skierowanego.
Para
(
)
G
V E
=
,
oraz E
S
⊆ nosi nazwę grafu (nieskierowanego lub
skierowanego w zależności od definicji zbioru S).
G.1.2. Jak rysować grafy
1. kształt linii jest obojętny; graf musi tylko oddawać połączenia (incydencje)
pomiędzy wierzchołkami za pomocą krawędzi
2. przecinanie się krawędzi nie jest wierzchołkiem
Na przykład grafy na rysunku G.2. są identyczne (izomorficzne) choć na pierwszy
rzut oka wydają się różne.
Rys. G.2. Przykład grafu narysowanego na dwa sposoby
Inny przykład to odwzorowanie za pomocą grafu problemu decyzyjnego
postawionego przez L.Eulera tzw. problem mostów królewieckich (rysunek G.3.).

Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
3
"Królewiec położony po obu brzegach rzeki Pregoły i na dwóch wyspach jest
połączony siecią siedmiu mostów. Należy wychodząc z dowolnego brzegu (A lub
B) odwiedzić obie wyspy (C i D), niekoniecznie raz, i powrócić do punktu wyjścia
przechodząc tylko raz przez każdy z 7 mostów." (L.Euler udowodnił, że problem
ten nie ma rozwiązania).
Rys. G.3. "Problem mostów królewieckich"
G.2. Grafy - wybrane pojęcia
G.2.1. Grafy nieskierowane
pętla własna - krawędź grafu, której końce są incydentne (związane) z jednym
wierzchołkiem (rys. G.1. - krawędź e
1
)
krawędzie równoległe - krawędzie incydentne do tej samej pary wierzchołków
(rys. G.1. - krawędzie e
5
i e
6
)
graf prosty - graf bez pętli własnych i krawędzi równoległych.
wierzchołek izolowany - nie posiada żadnej krawędzi incydentnej do niego (rys.
G.1. - wierzchołek v
6
)
stopień wierzchołka (d) - liczba krawędzi incydentnych z nim (rys. G.1. - stopień
wierzchołka v
4
jest równy 3; d=3)
graf zerowy - graf bez krawędzi (
E = ∅
)
grafy izomorficzne - grafy pokrywające się. Warunkiem koniecznym jest:
1. taka sama liczba wierzchołków
2. taka sama liczba krawędzi
3. taka liczba wierzchołków o danym stopniu
Warunku wystarczającego
brak w teorii. Przykład grafów, które nie są
izomorficzne, a warunek konieczny jest spełniony pokazuje rysunek G.4.. Oba
grafy nie są izomorficzne choć mają: po 6 wierzchołków, po 5 krawędzi, po 3

Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
4
wierzchołki o stopniu 1, po 2 wierzchołki o stopniu 2 oraz po 1 wierzchołku o
stopniu 3.
Rys. G.4. Grafy pozornie izomorficzne - grafy spełniające tylko warunek
konieczny izomorfizmu
podgraf - graf
(
)
g
V E
= ' , '
jest podgrafem grafu
(
)
G
V E
=
,
jeżeli V
V
'
⊆ , E
E
'
⊆
oraz każda krawędź grafu g ma te same wierzchołki końcowe jak w grafie G.
droga (łańcuch) - ciąg (skończony) naprzemienny wierzchołków i krawędzi
rozpoczynający się i kończący wierzchołkami, taki że krawędź jest incydentna do
wierzchołków poprzedzających i następujących po niej (rys. G.1. - ciąg {v
3
, e
3
,
v
1
, e
4
, v
2
, e
6
, v
4
, e
6
, v
2
, e
5
, v
1
})
droga otwarta - droga rozpoczynająca się i kończąca różnymi wierzchołkami (rys.
G.1. - ciąg {v
5
, e
7
, v
4
, e
2
, v
3
, e
1
, v
3
, e
2
, v
4
})
droga zamknięta - droga rozpoczynająca się i kończąca tym samym
wierzchołkiem (rys. G.1. - ciąg {v
5
, e
7
, v
4
, e
2
, v
3
, e
1
, v
3
, e
2
, v
4
, e
7
, v
5
})
droga Eulera - droga przechodząca przez każdą krawędź grafu dokładnie jeden
raz (patrz: problem mostów królewieckich)
graf Eulera - graf
(
)
G
V E
=
,
, w którym wszystkie wierzchołki są stopnia
parzystego (graf dla którego istnieje droga Eulera)
ścieżka - (droga ekstremalna) droga otwarta, w której jeden wierzchołek pojawia
się tylko jeden raz; można powiedzieć, że ścieżka "nie przecina" samej siebie (rys.
G.1. - ciąg {v
3
, e
3
, v
1
, e
5
, v
2
, e
6
, v
4
})
obwód - droga zamknięta, w której tylko wierzchołek początkowy może pojawić
się dwa razy (rys. G.1. - ciąg {v
3
, e
3
, v
1
, e
5
, v
2
, e
6
, v
4
, e
2
, v
3
})
obwód Hamiltona - obwód przechodzący przez wszystkie wierzchołki grafu (graf
przykładowy z rys. G.1.. nie ma obwodu ponieważ wierzchołek v
6
jest izolowany)
ścieżka Hamiltona - obwód Hamiltona z usuniętą krawędzią
graf spójny - graf jest spójny jeżeli między każdą parą wierzchołków istnieje
przynajmniej jedna ścieżka
drzewo - graf spójny bez obwodów
przekrój - każdy zbiór krawędzi grafu spójnego, którego usunięcie powoduje, że
graf staje się niespójny. Graf z rys. G.1.. nie jest spójny ze względu na izolowany
wierzchołek v
6
. Usunięcie wierzchołka v
6
prowadzi do grafu spójnego. W takim

Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
5
nowym grafie przekrojem jest np. zbiór krawędzi {e
3
, e
6
}. Usunięcie krawędzi e
3
oraz e
6
powoduje powstanie niespójności. Inne przekroje to: {e
2
, e
6
} oraz {e
2
, e
4
,
e
5
}.
G.2.2. Macierzowy zapis grafu nieskierowanego
macierz incydencji - grafu
(
)
G
V E
=
,
o m wierzchołkach i n krawędziach to
macierz
[ ]
A
mxn
ij
a
=
gdzie
a
ij
= 1 jeżeli krawędź e
j
jest incydentna z wierzchołkiem v
i
a
ij
= 0 w przeciwnym wypadku
Własności macierzy incydencji:
1. liczba jedynek w każdej kolumnie = 2
2. liczba jedynek w wierszu = stopień wierzchołka
3. wiersz z zerami to wiersz wierzchołka izolowanego
4. krawędzie równoległe mają identyczne kolumny
5. jeżeli graf G jest niespójny to można podzielić macierz A na niezależne
bloki diagonalne (po odpowiednim uporządkowaniu wierszy i kolumn)
6. rz A=m-1
macierz przyległości - grafu
(
)
G
V E
=
,
o m wierzchołkach i n krawędziach to
macierz kwadratowa stopnia m
[ ]
A
m
ij
a
=
gdzie
a
ij
= 1 jeżeli wierzchołki v
i
oraz v
j
łączy krawędź
a
ij
= 0 w przeciwnym wypadku
Własności macierzy przyległości:
1. liczba jedynek w wierszu (kolumnie) = stopień wierzchołka
2. wiersz (kolumna) z samymi zerami = wierzchołek izolowany
3. a
ii
≠0 ozacza pętlę własną wierzchołka v
i
Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
6
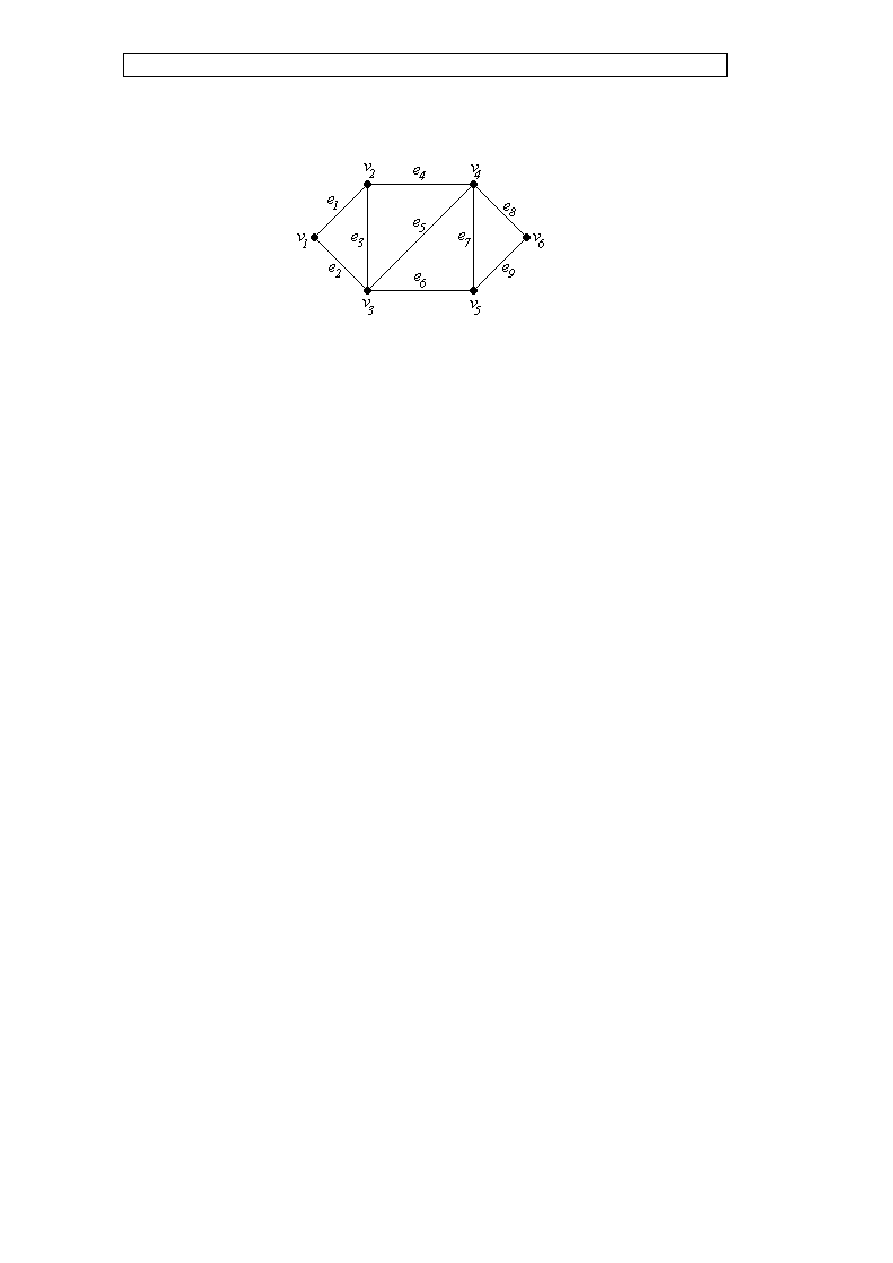
Przykład
Rys. G.5. Graf nieskierowany do ilustracji zapisu macierzowego
Macierze incydencji i przyległości grafu z rysunku G.5. są następujące
A
6 9
x
=
1 1 0 0 0 0
0 0 0
1 0 1 1 0 0
0 0 0
0 1 1 0 1 1
0 0 0
0 0 0 1 1 0
1 1 0
0 0 0 0 0 1
1 0 1
0 0 0 0 0 0
0 1 1
A
6 6
x
=
0
1 1 0 0 0
1 0
1 1 0 0
1 1 0
1
1 0
0
1 1 0
1 1
0 0
1 1 0
1
0 0 0
1
1 0
G.2.3. Grafy skierowane i sieci
graf skierowany (zorientowany) - graf
(
)
G
V E
=
,
, w którym za pomocą
odwzorowania
Ψ przekształcić można każdą krawędź e
k
, związaną z
wierzchołkami v
i
oraz v
j
, w uporządkowaną parę wierzchołków (v
i
,v
j
). O
wierzchołku v
i
mówimy, że krawędź e
k
jest incydentna z wierzchołka v
i
,
natomiast o wierzchołku v
j
mówimy, że krawędź e
k
jest incydentna do
wierzchołka v
j
.
krawędź skierowana (łuk) - krawędź w grafie skierowanym
wierzchołek początkowy krawędzi (źródło krawędzi) - wierzchołek dla którego
krawędź e
k
= (v
i
,v
j
) jest incydentna z wierzchołka (v
i
)
wierzchołek końcowy krawędzi (odpływ krawędzi) - wierzchołek dla którego
krawędź e
k
= (v
i
,v
j
) jest incydentna do wierzchołka (v
j
)
stopień wejściowy wierzchołka ( d
v
j
+
) - liczba krawędzi incydentnych do
wierzchołka v
j
stopień wyjściowy wierzchołka ( d
v
j
−
) - liczba krawędzi incydentnych z
wierzchołka v
j

Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
7
wierzchołek izolowany - wierzchołek, dla którego stopień wejściowy i stopień
wyjściowy są równe zero
łuki równoległe (krawędzie skierowane równoległe) - krawędzie grafu
skierowanego odwzorowane za pomocą tej samej uporządkowanej pary
wierzchołków
sieć - graf skierowany (zorientowany), bez pętli własnych i łuków równoległych
(tj. graf prosty), bez wierzchołków izolowanych oraz obwodów skierowanych, w
którym z każdym łukiem e
k
związana jest pewna nieujemna liczba
zródło sieci - wierzchołek (v
j
) o zerowym stopniu wejściowym ( d
v
j
+
= 0 )
odpływ sieci - wierzchołek (v
j
) o zerowym stopniu wyjściowym ( d
v
j
−
= 0 )
sieć zredukowana - sieć o jednym źródle i jednym odpływie
Pojęcia dróg, ścieżek, itd. są analogiczne jak w grafie nieskierowanym.
Definiując te pojęcia należy pamiętać, że krawędzie grafu są skierowane, tj. para
(v
i
,v
j
) odpowiada zupełnie innej krawędzi niż para (v
j
,v
i
)
G.2.4. Macierzowy zapis grafu skierowanego
macierz incydencji - grafu skierowanego
(
)
G
V E
=
,
o m wierzchołkach i n
krawędziach (łukach) to macierz
[ ]
A
mxn
ij
a
=
gdzie
a
ij
= 1 jeżeli krawędź e
j
jest incydentna z wierzchołka v
i
a
ij
= −1 jeżeli krawędź e
j
jest incydentna do wierzchołka v
i
a
ij
= 0 w pozostałych przypadkach
Własności macierzy incydencji grafu skierowanego:
1. stopień wejściowy wierzchołka jest równy liczbie "-1" w wierszu
2. stopień wyjściowy wierzchołka jest równy liczbie "1" w wierszu
3. liczba jedynek w każdej kolumnie = 2
4. liczba jedynek w wierszu = stopień wierzchołka
5. wiersz z zerami to wiersz wierzchołka izolowanego
6. krawędzie równoległe mają identyczne kolumny
7. jeżeli graf G jest niespójny to można podzielić macierz A na niezależne
bloki diagonalne (po odpowiednim uporządkowaniu wierszy i kolumn)
8. suma elementów w kolumnie jest równa zero
9. rz A=m-1
Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
8
macierz przyległości - grafu
(
)
G
V E
=
,
o m wierzchołkach i n krawędziach to
macierz kwadratowa stopnia m
[ ]
A
m
ij
a
=
gdzie
a
ij
= 1 jeżeli wierzchołki v
i
oraz v
j
łączy łuk (v
i
, v
j
)
a
ij
= 0 w przeciwnym wypadku
Własności macierzy przyległości:
1. liczba "1" w wierszu = stopień wyjściowy wierzchołka
2. liczba "1" w kolumnie = stopień wejściowy wierzchołka
3. wiersz z samymi zerami = wierzchołek typu odpływ
4. kolumna z samymi zerami = wierzchołek typu źródło
5. wiersz (kolumna) z samymi zerami = wierzchołek izolowany
6. a
ii
≠0 ozacza pętlę własną wierzchołka v
i
7. jeżeli numeracja wierzchołków sieci jest taka, że dla każdego łuku (v
i
,v
j
)
numer wierzchołka v
i
<
v
j
i jednocześnie macierz przyległości jest macierzą
trójkątną dolną, to graf skierowany nie posiada obwodów skierowanych
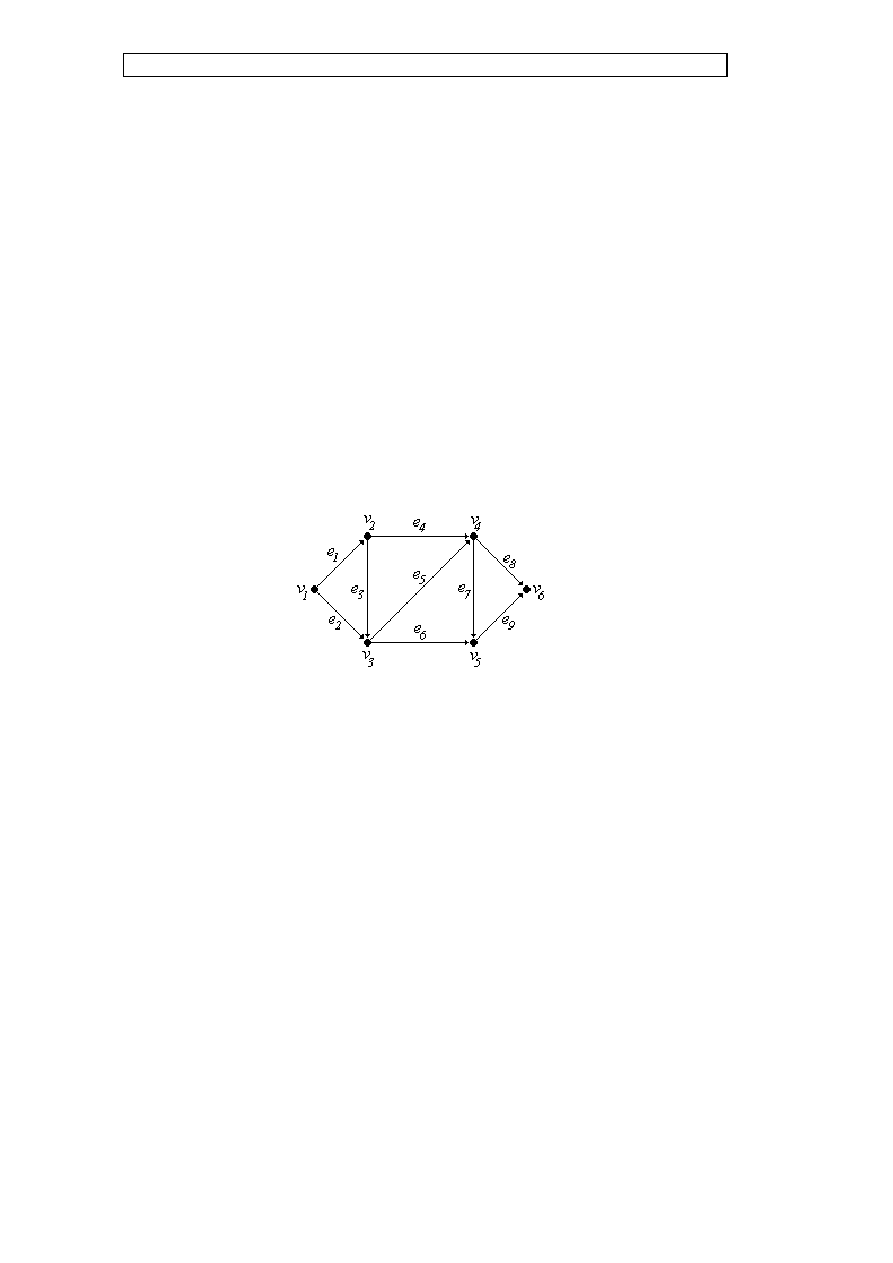
Przykład
Rys. G.6. Graf skierowany do ilustracji zapisu macierzowego
Macierze incydencji i przyległości grafu z rysunku G.6. są następujące
A
6 9
x
=
−
−
−
−
−
−
−
−
−
1
1
0
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
1
1
0
1
1
0
0
0
0
0
0
1
1
0
1
1
0
0
0
0
0
0
1
1
0
1
0
0
0
0
0
0
0
1
1
A
6 6
x
=
0
1 1 0 0 0
0 0
1 1 0 0
0 0 0
1
1 0
0 0 0 0
1 1
0 0 0 0 0
1
0 0 0 0 0 0
G.2.5. Numerowanie wierzchołków grafu skierowanego
Opisane dalej postępowanie realizuje numerację wierzchołków grafu
skierowanego według zasady narastania numerów, tj. dla każdego łuku (v
i
,v
j
)
numer wierzchołka v
i
<
v
j
.Opisane postępowanie wykrywa jednocześnie
ewentualne obwody skierowane w grafie.
Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
9
Krok 1 Przyjmij k=1
Krok 2 Znajdź niezaetykietowany wierzchołek o zerowym stopniu wejściowym i
przypisz mu etykietę k. Jeżeli taki wierzchołek nie istnieje to idź do kroku 4.
Krok 3 Ustaw k=k+1 i przejdź do kroku 2.
Krok 4 Jeżeli wszystkie wierzchołki są zaetykietowane to koniec postępowania;
jeżeli nie to idź do kroku 5.
Krok 5 Jeżeli stopień wyjściowy każdego zaetykietowanego już wierzchołka nie
jest równy zero to usuń wszystkie łuki incydentne z każdego zaetykietowanego
wierzchołka i przejdź do kroku 2. Jeżeli są niezaetykietowane wierzchołki i
jednocześnie stopień wyjściowy każdego zaetykietowanego wierzchołka jest
równy zeru to w sieci istnieje cykl (obwód skierowany) - koniec postępowania.
Przykład
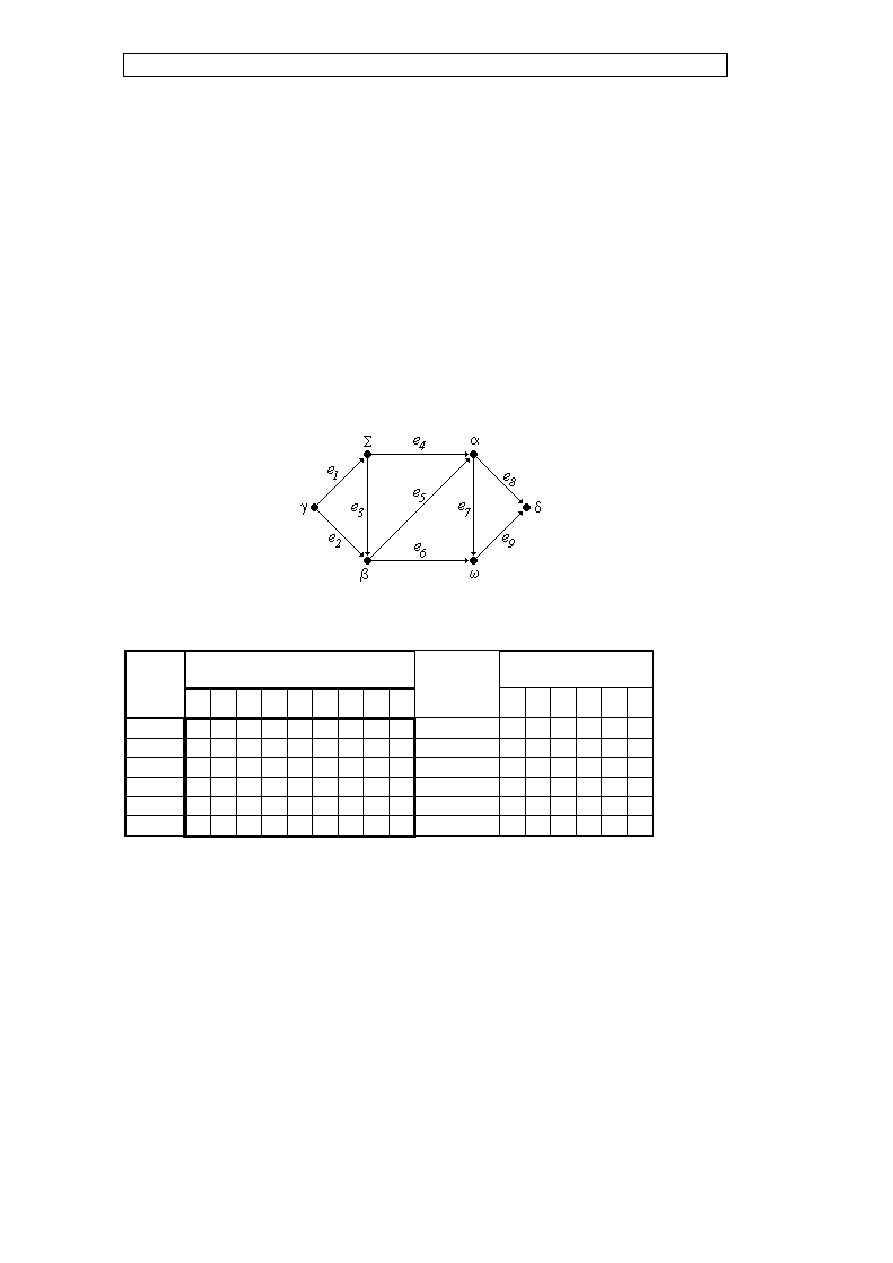
Rys. G.7. Graf do ilustracji algorytmu numerującego wierzchołki
Tabela G.1. Numeracja wierzchołków grafu z rysunku G.7.
nadany
numer
stopień wierzchołka w
kolejnych iteracjach
e
1
e
2
e
3
e
4
e
5
e
6
e
7
e
8
e
9
wierzchołka I
II III IV V VI
α
0
0
0 -1 -1 0
1
1
0
4
2
2
1
0
x
x
β
0 -1 -1 0
1
1
0
0
0
3
2
1
0
x
x
x
γ
1
1
0
0
0
0
0
0
0
1
0
x
x
x
x
x
δ
0
0
0
0
0
0
0 -1 -1
6
2
2
2
2
1
0
Σ
-1 0
1
1
0
0
0
0
0
2
1
0
x
x
x
x
ω
0
0
0
0
0 -1 -1 0
1
3
2
2
2
1
0
x
Kolejne iteracje numerowania wierzchołków grafu z rysunku G.7. były
następujące.
1. W iteracji I zerowy stopień wejściowy miał wierzchołek
γ. Otrzymał on nr 1 i
wykreślono kolumny e
1
i e
2
.
2. W iteracji II zerowy stopień wejściowy miał wierzchołek
Σ. Otrzymał on nr 2 i
wykreślono kolumny e
3
i e
4
.
3. W iteracji III zerowy stopień wejściowy miał wierzchołek
β. Otrzymał on nr 3 i
wykreślono kolumny e
5
i e
6
.

Marek Miszczyński KBO UŁ.
Wybrane elementy teorii grafów
10
4. W iteracji IV zerowy stopień wejściowy miał wierzchołek
α. Otrzymał on nr 4
i wykreślono kolumny e
7
i e
8
.
5. W iteracji V zerowy stopień wejściowy miał wierzchołek
δ. Otrzymał on nr 5 i
wykreślono kolumnę e
9
.
6. Wierzchołek
δ dostał automatycznie nr 6 po wykreśleniu wszystkich kolumn
macierzy incydencji A.
Literatura
[1] Narshing DEO, "Teoria grafów oraz jej zastosowanie w technice i
informatyce", PWN, Warszawa, 1980, Seria: Biblioteka Naukowa Inżyniera
[2] Robert S.GARFINKEL, George L.NEMHAUSER, "Programowanie
całkowitoliczbowe", PWN, Warszawa, 1978, Seria: Biblioteka Naukowa
Inżyniera
Spis treści dodatku G
G. Wybrane elementy teorii grafów .................................................................................................... 1
G.1. Co to jest graf ........................................................................................................................ 1
G.1.1. Definicja grafu .............................................................................................................. 2
G.1.2. Jak rysować grafy ......................................................................................................... 2
G.2. Grafy - wybrane pojęcia................................................................................................... 3
G.2.1. Grafy nieskierowane ..................................................................................................... 3
G.2.2. Macierzowy zapis grafu nieskierowanego .................................................................... 5
G.2.3. Grafy skierowane i sieci................................................................................................ 6
G.2.4. Macierzowy zapis grafu skierowanego ......................................................................... 7
G.2.5. Numerowanie wierzchołków grafu skierowanego.................................................................... 8
Literatura............................................................................................................................................. 10
Spis treści dodatku G .......................................................................................................................... 10
Wyszukiwarka
Podobne podstrony:
Mat dla stud 2
Wyklad 1' stud
Metabolizm kkw tł stud
strukturalnaMinuchina stud
Tętnice szyjne sem dla stud II
ZO NST 14 ĆW1CZ 1, 2 STUD F F3
kosztkapitału4 stud
6 Mielizna stud nowy
CEMENTY stud
Audyt personalny 1a stud
KM W 25 lekkie konst met stud
Piekny umysl po czterdziestce wersja dla IIroku STUD
Obserwacja Stud, Psychologia
więcej podobnych podstron