EKONOMETRIA

CZ. II

W. Borucki

Met. Simplex – rozwiązanie

początkowe

1.

Doprowadzić zadanie do postaci kanonicznej (poprzez wprowadzenie zmiennych

swobodnych - nieujemnych) tak by prawa strona równań była nieujemna (Uwaga:

zmiennym swobodnym przypisujemy zerowe wartości współczynników funkcji celu)

2.

Poszukać macierzy jednostkowej. Tej macierzy odpowiadać będzie rozwiązanie

bazowe, którego odpowiednie zmienne bazowe przyjmą wartości równe wartościom

odpowiednich składowych wektora wyrazów wolnych.

3.

Jeśli nie można wskazać macierzy jednostkowej, to należy wprowadzić zmienne

sztuczne do odpowiednich równań tak by można było wskazać macierz jednostkową
Uwaga:
a) rozwiązanie zawierające zmienne sztuczne nie jest rozwiązaniem dopuszczalnym;

dopiero nieujemne bazowe rozwiązanie nie zawierające zmiennych sztucznych jest

rozwiązaniem bazowym dopuszczalnym
b) trzeba wyeliminować zmienne sztuczne z rozwiązania i w tym celu współczynniki

funkcji celu im odpowiadające przyjmują wartości bardzo duże dla

minimalizowanych funkcji celu i bardzo małe dla maksymalizowanych funkcji celu.

4.

Dopuszczalne (nieujemne) bazowe uznajemy za rozwiązanie początkowe i dla tego

rozwiązania sprawdzamy kryteria optymalności rozwiązania

Metoda simplex – sprawdzenie

optymalności rozwiązania



Zmiennym bazowym (dla bazy B) z otrzymanego, poprzedniego

rozwiązania przyporządkowujemy odpowiednie współczynniki występujące

w funkcji celu (x

i

↔ c

i

; pamiętamy, że zmienne nie bazowe mają wartość 0)



Obliczamy wartość funkcji celu dla otrzymanego rozwiązania (suma

iloczynów c

i

x

i

)



Dla każdej zmiennej wyznaczamy wartość z

j

(suma iloczynów c

i

d

ij

, gdzie d

ij

- współczynniki kombinacji równoważnej zawarte w macierzy B

-1

A)



Obliczamy różnice K

j

= c

j

– z

j

. K

j

wskazują o ile wzrośnie wartość funkcji

celu gdy do rozwiązania wprowadzona zostanie jedna jednostka zmiennej

x

j

, wartości K

j

dla aktualnych zmiennych bazowych zawsze wynoszą zero



Rozwiązanie jest optymalne gdy wszystkie wartości K

j

są niedodatnie

(ujemne i zera) w przypadku zadania, w którym maksymalizujemy funkcję

celu, a nieujemne w przypadku zadania, w którym funkcja celu jest

minimalizowana



Jeżeli powyższy warunek nie jest spełniony, to otrzymane rozwiązanie nie

jest optymalne i trzeba przejść do kroku poszukiwania rozwiązania

lepszego od poprzedniego.



Jeżeli rozwiązanie jest optymalne, to obliczenia można zakończyć.



Warto jednakże na koniec przeprowadzić analizę wrażliwości rozwiązania.

Metoda simplex – poprawa

rozwiązania



Zgodnie z interpretacją wartości K do nowego rozwiązania

bazowego wprowadzamy zmienną o największej efektywności

poprawy wartości funkcji celu (dla zadań z max. – zmienną x

j

,

dla której K

j

= max)



Następnie wskazujemy tę zmienną x

i

(ze starej bazy), dla

której iloraz (x

i

/d

ij

) jest najmniejszy. Ta zmienna zostanie z

bazy usunięta, a na jej miejsce wprowadzona będzie zmienna

x

j

, dla której K

j

było maksymalne.



Ta operacja zapewni nam, że następne rozwiązanie bazowe

będzie nieujemne (trzeba zastosować operacje elementarne

doprowadzające do uzyskanie wektora jednostkowego w j-tej

kolumnie z jedynką w i-tym wierszu - odpowiadającym

zmiennej x

i

).



Po dokonaniu przekształceń należy przejść do procedury

sprawdzenia optymalności rozwiązania.

Metoda simplex - zadanie 1

3x

1

+ 4x

2

+ 8x

3

→max

x

1

+ x

2

+ 5x

3

≤ 1

3x

1

+ x

2

+ x

3

≤ 1

x

1

, x

2

, x

3

≥ 0

Metoda simplex – zadanie 2

3x

1

+ x

2

+ x

3

→ min

x

1

+ 5x

2

+ 2x

3

= 9

2x

2

+ x

3

= 4

x

1

+ x

2

= 1

x

1

, x

2

, x

3

≥ 0

Problem diety 1

–

Dany niech będzie zbiór produktów żywnościowych P

1

, P

2

, …P

n

,

możliwych do wykorzystania w planowanej diecie.

–

Każdy z produktów charakteryzuje się zawartością a

ij

jednostek j-

tego składnika odżywczego (spośród m składników) w i-tym

produkcie.

–

Dla każdego składnika odżywczego znane są dolne (d

j

) i górne kresy

(g

j

), poniżej lub powyżej których ich spożycie jest niewskazane ze

względów zdrowotnych.

–

Znane są też jednostkowe ceny nabycia poszczególnych produktów

żywnościowych – c

i

.

–

Należy zaproponować taki sposób wyżywienia indywiduum (określić

ilości produktów – x

i

// zmienne decyzyjne), ażeby spełniając

warunki zdrowego żywienia koszt jego wyżywienia był minimalny.

Problem diety 2

0

min

1

1

















i

j

n

i

i

ij

j

n

i

i

i

x

g

x

a

d

x

c

Problem wyboru planu

produkcji



W danym zakładzie produkcyjnym produkuje się wyroby w

1

, w

2

, …,

w

n

.



Każdy z wyrobów, do jego wyprodukowania, wymaga

zastosowania określonej ilości zasobów z

1

, z

2

, …, z

m

(np. energii,

pracy, surowców, …), których wielkości są limitowane odpowiednio

l

1

, l

2

, …, l

m

.



Ograniczenia panujące na rynku są takie, że z jednej strony (dla

utrzymania stałych klientów) należy wyprodukować co najmniej d

i

jednostek produktu i, a z drugiej strony, ograniczony rynek nie jest

w stanie wchłonąć więcej niż g

i

jednostek produktu i.



Ceny sprzedaży hurtowej na poszczególne produkty są stałe i

wynoszą c

i

jednostek.



Należy sporządzić taki plan produkcji wyrobów (określić ile

jednostek poszczególnych produktów należy wyprodukować – x

i

//

zmienne decyzyjne), ażeby osiągnąć maksymalny przychód.

Problem wyboru planu prod.

2

)

,...,

1

(

)

,...,

1

(

max

1

1

n

i

dla

g

x

d

m

j

dla

l

x

a

x

c

i

i

i

j

n

i

i

ij

n

i

i

i





















Problem rozkroju

(jednowymiarowego)



Dane są podzbiory elementów o długości w

j

(dla j=1,…n) i

każdy z nich liczebności odpowiednio g

j

.



Elementy tych podzbiorów należy pociąć na wyroby A o

długości l

1

i B o długości l

2



Jeden komplet stanowi r wyrobów A i p wyrobów B.



W wyniku cięcia elementów powstaje odpad (część elementu

do pocięcia, z której nie można uzyskać wyroby o długości l

1

lub l

2

, lub nie ma już takiej potrzeby).



Elementy przeznaczone do pocięcia należy pociąć w taki

sposób, ażeby zminimalizować odpad lub zmaksymalizować

liczbę kompletów



Jaka zmienna decyzyjna?



Jakie zależności – warunki ograniczające?

Problem rozkroju

(jednowymiarowego) 2



Zmienna decyzyjna – ile razy zastosować określony

sposób cięcia (x

j

)



Jak utworzyć tabelę wydajności technologii

-sposobów cięcia (dla elementów o długości w

i

)

x

1

x

2

…

x

m

Liczba

elementów A

a

11

a

12

a

1m

Liczba

elementów B

a

21

a

22

a

2m

Odpad

o

1

o

2

o

m

Problem rozkroju

(jednowymiarowego) 3

max

1

lub

min

0

)

)

,...,

1

(

1

2

1

1

2

1

1

1

































m

i

i

i

m

i

i

i

i

m

i

i

i

m

i

i

i

j

m

i

i

x

a

p

x

o

by

takie

x

oraz

p

r

x

a

x

a

n

j

dla

l

x

j

Dualność w programowaniu

liniowym



Definicja zadań dualnych

–

Dla zadań w postaci standardowej

–

Dla zadań w postaci kanonicznej



Jakie korzyści mamy z zadań dualnych

–

Twierdzenie o równowadze



Jak interpretujemy zmienne dualne

–

Ceny równowagi / jakie ceny równowagi?

Dualność

c

T

x → max

Ax ≤ b
x≥ 0

c

T

x → min

Ax ≥ b
x≥ 0

b

T

y → min

A

T

y ≥ c

y ≥ 0

b

T

y → max

A

T

y ≤ c

y ≥ 0

Prymalne i dualne zadania programowania liniowego

Dualność 2



Twierdzenie o równowadze – wartość funkcji celu dla

rozwiązania optymalnego zadania prymalnego równa jest

wartości funkcji celu dla rozwiązania optymalnego

zadania dualnego.



Warunkom ograniczającym zadania prymalnego

spełnionym z równością dla rozwiązania optymalnego,

odpowiadają zmienne dualne, których wartości są różne

od zera (bazowe) dla rozwiązania optymalnego zadania

dualnego.



Interpretacja zmiennych dualnych dla rozwiązania

optymalnego zadania dualnego: ceny zasobów

wykorzystanych w pełni (zgodnie z limitem) w warunkach

równowagi

Dualność – przykład –

– rozwiązać zadanie

3x

1

+ 4x

2

+ 8x

3

→max

x

1

+ x

2

+ 5x

3

≤ 1

3x

1

+ x

2

+ x

3

≤ 1

x

1

, x

2

, x

3

≥ 0

Analiza wrażliwości



Powody:

–

Uproszczenia modelowania (ograniczenie listy zmiennych decyzyjnych

lub warunków ograniczających),

–

Zmienność otoczenia (np. zmienność wartości parametrów funkcji celu,

lub wartości limitów zasobowych),

–

Zmienność wewnętrzna, np. zastosowanie innowacji (np. konieczność

wprowadzenia nowych zasobów – warunków ograniczających),

–

Niedoskonały pomiar wartości parametru zadania – możliwość zmiany

wartości współczynników technologicznych,



Podstawowe pytania

–

Czy znalezione rozwiązanie pozostanie optymalne pomimo zmiany

wartości parametrów, lub

–

dla jakiego przedziału zmienności parametrów rozwiązanie pozostaje

optymalne?

–

Jak zmieni się rozwiązanie optymalne gdy parametry zadania ulegną

zmianie? (Czy zmieni się lista zmiennych decyzyjnych występujących w

decyzji optymalnej z wartościami niezerowymi – czy zmieni się baza dla

decyzji optymalnej?),

Analiza wrażliwości

(kilka definicji pomocniczych)

–

Krawędzie sąsiednie zbioru rozwiązań dopuszczalnych
dla rozwiązania optymalnego, bazowego – krawędzie
mające wspólny punkt (rozwiązanie bazowe)

–

Gradienty krawędzi – wektory prostopadłe do
płaszczyzn zawierających odpowiednie krawędzie.

–

Warunek wiążący – warunek posiadający ze zbiorem
rozwiązań dopuszczalnych co najmniej jeden punkt
wspólny

–

Warunek istotnie wiążący – warunek wyznaczający
rozwiązanie optymalne

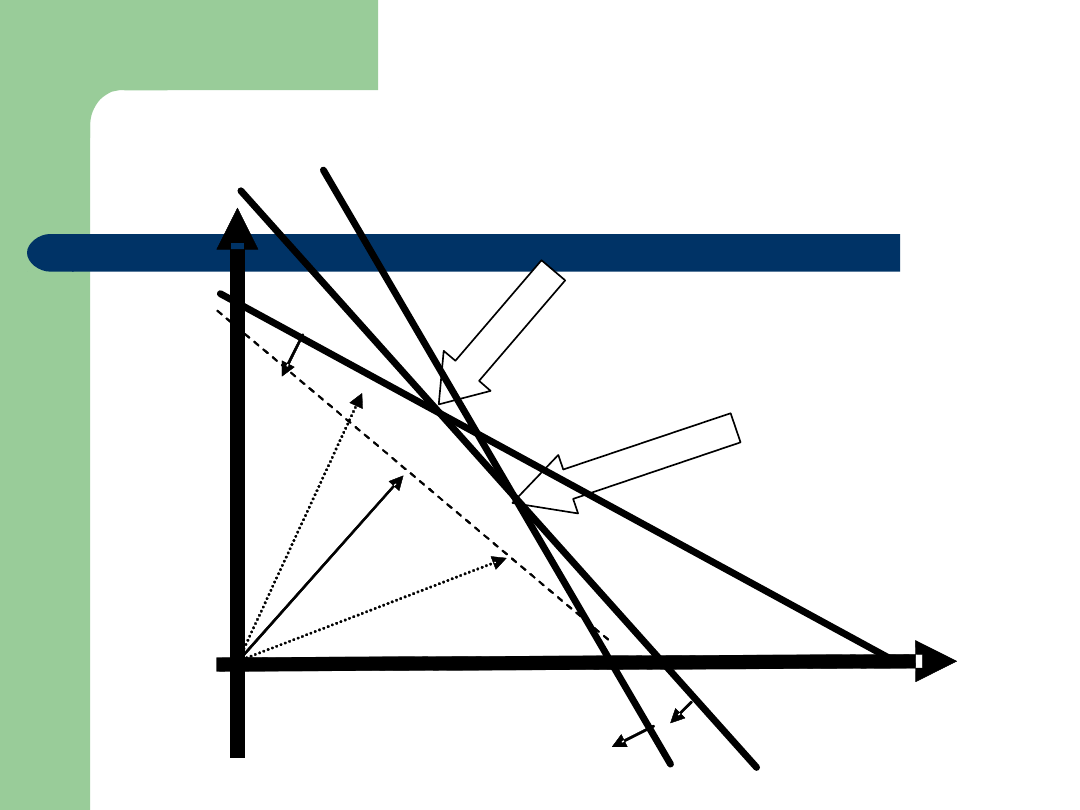
R2. - Analiza wrażliwości 2

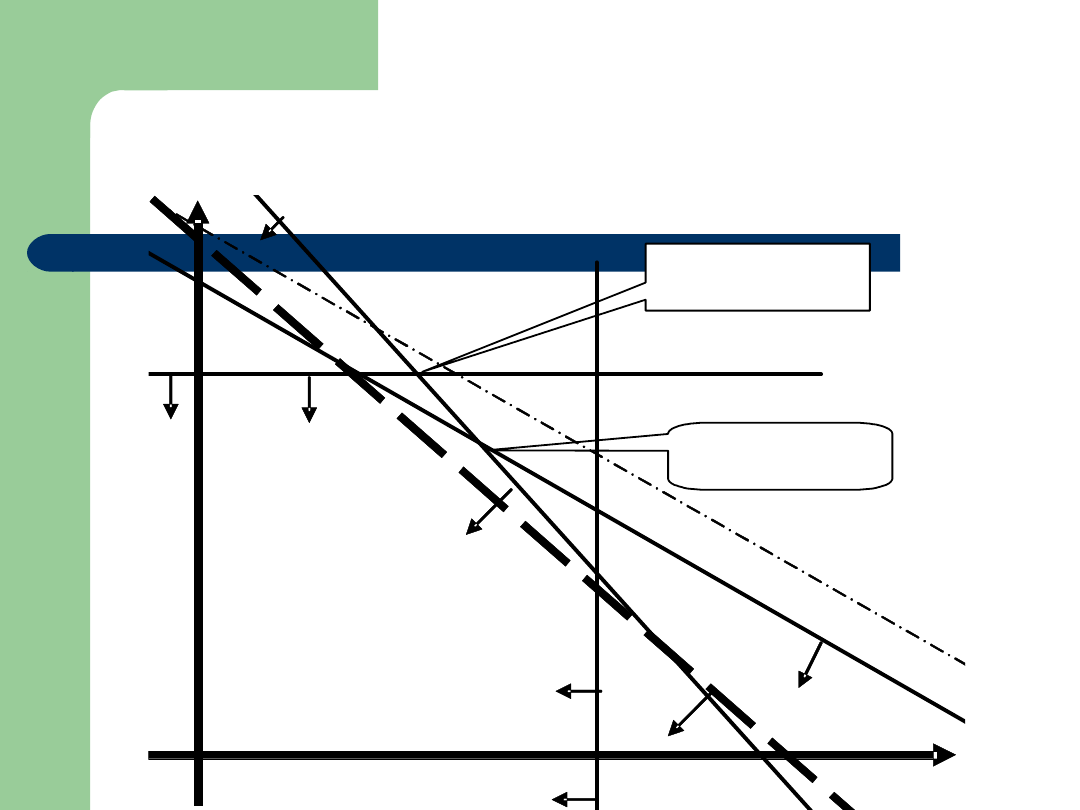
Analiza wrażliwości 3

Rozw. opt. I

Rozw. opt. II

R2.- Analiza wrażliwości 4



Zmiany wartości współczynników funkcji celu w granicach wskazanych

przez „gradienty graniczne” (odpowiadające krawędziom zbioru

rozwiązań dopuszczalnych sąsiednim w stosunku do analizowanego

rozwiązania optymalnego nie pociągają za sobą zmiany rozwiązania

optymalnego zadania.



Jeżeli zmiany wartości ograniczeń (dostępności zasobów) dotyczą

warunków wiążących to modyfikują zbiór rozwiązań dopuszczalnych



Jeżeli zmiany wartości ograniczeń dotyczą warunków istotnie

wiążących, to zawsze skutkują zmianą rozwiązania optymalnego.



Zmiany wartości ograniczeń dla warunków niewiążących mogą

wpłynąć na rozwiązanie, jeżeli prowadzą do ograniczenia zbioru

rozwiązań dopuszczalnych (stają się wiążące lub istotnie wiążące).

2

1

2

2

1

2

1

1

1

2

c

c

c

c

c

c

o

o





R3. Zadanie transportowe

Danych jest n dostawców i m odbiorców pewnego jednorodnego

towaru. Każdy z dostawców posiada a

i

jednostek (i=1,…,n) tego

towaru, a odbiorcy zgłaszają zapotrzebowanie na b

j

jednostek (j=1,

…m) tego towaru. Znane są też jednostkowe koszty transportu c

ij

od i-tego dostawcy do j-tego odbiorcy.

Towar należy przewieźć od dostawców do odbiorców w taki sposób,

ażeby zaspokoić poszczególnych odbiorców towarem pochodzącym

od dowolnego dostawcy i jednocześnie zminimalizować łączne

koszty transportu.

Jest oczywiste, że dowolny dostawca nie może wysłać więcej towaru

aniżeli sam posiada.

Tak sformułowane zadanie ma rozwiązanie gdy

Zadanie, dla którego warunek spełniony jest z równością nazywamy

zamkniętym zadaniem transportowym











m

j

j

n

i

i

b

a

1

1

R4. Zadanie transportowe 2



Model
matematyczny

 

























n

i

m

j

ij

ij

ij

n

i

j

ij

m

j

i

ij

x

c

x

m

j

dla

b

x

n

i

dla

a

x

1

1

1

1

min

0

,...,

1

,...,

1

R3. Zadanie transportowe –

algorytm ogólny



K1. Znaleźć rozwiązanie początkowe



K2. Ocenić czy rozwiązanie jest optymalne

–

a. Jeżeli tak, to zakończyć obliczenia w K4.

–

b. Jeżeli nie, to przejść do K3.



K3. Znaleźć inne rozwiązanie, nie gorsze
od otrzymanego i przejść do K2.



Przyjąć rozwiązanie optymalne i
wyznaczyć wartość funkcji celu

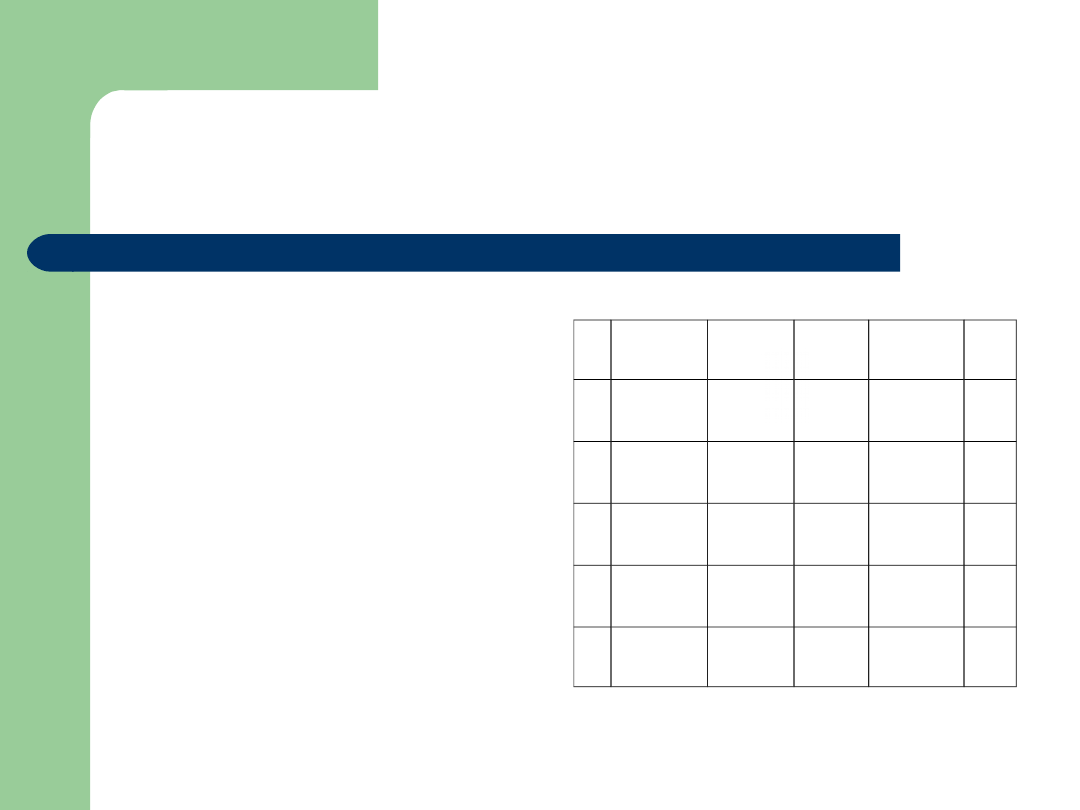
R3. Zadanie transportowe –

rozwiązanie początkowe



Zbilansowanie

macierzy przepływów

–

(uwaga: nie musi to być

rozwiązanie bazowe!)



Metoda kąta północno

zachodniego

–

(uwaga: może to być

bardzo odległe od

rozwiązania dobrego!)



Metoda minimum

kosztu jednostkowego

–

(uwaga: to tylko

optymalizacja lokalna)

1

2

…

m

1

C

11

X

11

C

12

X

12

A1

2

C

22

X

22

A2

C

ij

X

ij

…

n

C

nm

X

nm

An

B

1

B

2

…

B

m

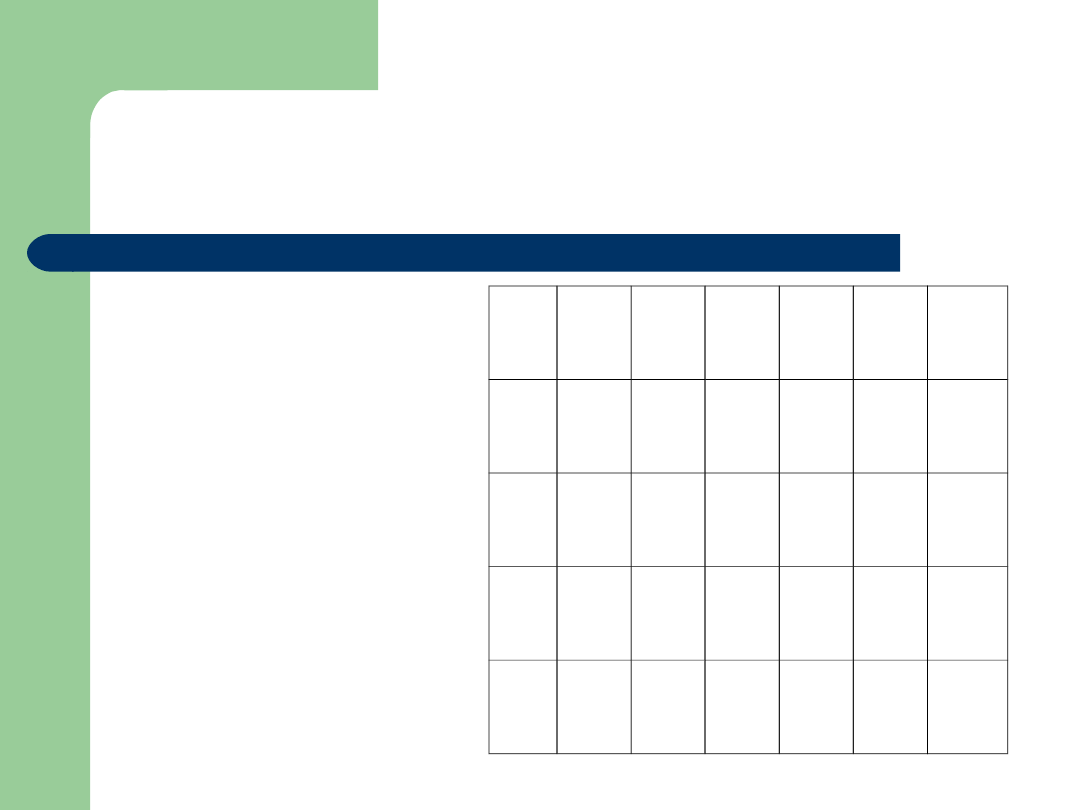
ZZT rozw. pocz. 2

1

2

3

4

5

1

100

130

230

2

20

200

110

330

3

140

300

440

100

150

200

250

300

Przykład Tabela [Xij]

R3. Zadanie transportowe

– ocena dobroci rozwiązania



Oczywiście najlepsze rozwiązanie jest wtedy, gdy wszystkie

niezerowe zmienne decyzyjne związane są tylko z takimi trasami,

dla których koszty jednostkowe transportu są zerowe (wtedy tez

minimalna wartość funkcji celu wynosi zero)



Warto zauważyć, że jeżeli do wiersza lub kolumny macierzy

kosztów jednostkowych dodamy (lub odejmiemy) stałą, to

rozwiązanie optymalne ZZT nie ulegnie zmianie



Jak połączyć oba fakty ?



Należy dodać do wierszy lub kolumn takie wartości (α

i

, β

j

), ażeby

otrzymać w każdym wierszu i kolumnie zera pozwalające na

wpisanie takich wartości zmiennych decyzyjnych, dla których

spełnione są warunki ograniczające.



A jeśli nie wszystkie zmienne dadzą się wpisać na pola o zerowych

wartościach, to należy zastanowić się gdzie w tabeli można

(powinno się) otrzymać zero .

R3. Zadanie transportowe

– ocena dobroci rozwiązania 2



Wyznaczyć koszty zastępcze: α

i

i β

j

–

Rozwiązać układ równań

ĉ

ij

= (α

i

- β

j

), przy czym

ĉ

ij

=c

ij

dla (i,j) € B (aktualna baza)

–

układ m+n-1 równań o m+n

niewiadomych (jeden stopień

swobody – ustalić jedną wartość

np. α

1

= 0).



Wyznaczyć tabele różnic

–

r

ij

= c

ij

–

ĉ

ij

–

Jeśli wszystkie są nieujemne, to

rozwiązanie jest optymalne.

–

Jeżeli istnieje r

ij

<0, to rozwiązanie

nie jest optymalne i należy przejść

do poprawy rozwiązania.

Tabela c

ij

1

2

3

4

5

1 2

5

7

4

1

230

2

4

8

6

5

6

330

3

2

2

8

9

9

440

10

0

15

0

20

0

25

0

30

0

ZZT - Ocena dobroci

rozwiązania 3



Tabela ĉ

ij

1

2

3

4

5

1

2

5

3

2

2 230

2

5

8

6

5

5

330

3

9

12

10

9

9

440

100 150 200 250 300

R3. Zadanie transportowe

– poprawa rozwiązania



Znaleźć najmniejszą (ujemną )

wartość r

ij



Znaleźć cykl zmian wartości x

ij



Wyznaczyć wartość zmiennej

wprowadzanej



Skorygować wartości

zmiennych z cyklu zmian



Usunąć z bazy (jedną)

zmienną, która przyjęła

wartość zero,



Przejść do kroku „Wyznaczyć

wartości kosztów zastępczych”

Tabela r

ij

1

2

3

4

5

1

0

0

4

2

-1

230

2

-1

0

0

0

1

330

3

-7

-10

-2

0

0

440

100

150

200

250

300

Tabela X

2

ij

1

2

3

4

5

1 100

130

0

0

0

23

0

2

0

20-

d

20

0

110+

d

0

33

0

3

0

+d

0

140

-d

30

0

44

0

100

150

20

0

250

30

0

Zadania pokrewne 1

Zadanie transportowo-magazynowe
W n magazynach znajdują się odpowiednio a

i

jednostek

pewnego jednorodnego towaru, który zamawiany jest

przez m odbiorców składających zamówienia w ilości b

j

jednostek (Σa

i

>Σb

j

). Jednostkowe koszty transportu z i-

tego magazynu do j-tego odbiorcy wynoszą c

ij

. Nadwyżki

towarów ponad zapotrzebowanie odbiorców pozostają w

magazynie. Ich składowanie pociąga za sobą koszty

proporcjonalne do ilości magazynowanych jednostek, a

jednostkowe koszty magazynowania wynoszą m

i

. Należy

wyznaczyć taki plan przewozów i magazynowania

nadwyżki towarów ażeby zminimalizować łączne koszty

transportu i magazynowania.

Zadania pokrewne 2

Model zadania transportowo-magazynowego

...

,

0

,...

2

,

1

,...

2

,

1

min

1

1

1

1

j

i

dla

x

n

i

dla

a

y

x

m

j

dla

b

x

y

m

x

c

ij

m

j

i

i

ij

j

n

i

ij

i

i

n

i

ij

ij

m

j























 









Zadania pokrewne 2

Zadanie transportowo-produkcyjne

Danych jest n zakładów produkcyjnych, których zdolności

produkcyjne przewyższają zapotrzebowanie rynku i wynoszą

odpowiednio a

i

jednostek określonego i jednorodnego produktu.

Jednostkowy koszt produkcji zależy od zakładu i wynosi

odpowiednio p

i

jednostek.

Towar po wyprodukowaniu transportowany jest do m odbiorców,

którzy zgłaszają zapotrzebowanie w ilości b

j

jednostek.

Jednostkowe koszty transportu z i-tego zakładu produkcyjnego do

j-tego odbiorcy wynoszą odpowiednio c

ij

jednostek.

Należy tak zaplanować wykorzystanie zdolności produkcyjnych

poszczególnych zakładów i zaproponować taki plan transportu

wyprodukowanych towarów, ażeby zminimalizować łączne

koszty transportu i produkcji towarów.

Zadanie pokrewne 4

Model zadania transportowo-produkcyjnego

...

,

0

,...

2

,

1

,...

2

,

1

min

)

(

1

1

1

1

j

i

dla

x

n

i

dla

a

x

m

j

dla

b

x

x

p

c

ij

m

j

i

ij

j

n

i

ij

n

i

ij

i

ij

m

j





























Zadanie pokrewne 5



Zadanie wieloetapowe

Jednorodny towar znajduje się u n dostawców w ilościach

odpowiednio a

i

(i=1,2,…n) jednostek. Na towar zgłasza

zapotrzebowanie m odbiorców odpowiednio w ilościach b

j

(j=1,2,…m) jednostek. Towar ten może trafić do

odbiorców jedynie za pośrednictwem jednego z k

magazynów, których zdolności magazynowania wynoszą

odpowiednio d

l

(l=1,2,…,k) jednostek tego towaru. Znane

są jednostkowe koszty transportu na etapie od

dostawców do magazynów – c

1il

i na etapie od

magazynów do odbiorców c

2lj

. Należy wyznaczyć taki plan

przewozu na obu etapach, ażeby łączny koszt transportu

towaru na obu etapach był minimalny.

Zadanie pokrewne 6



Model
zadania
dwuetapowe
go

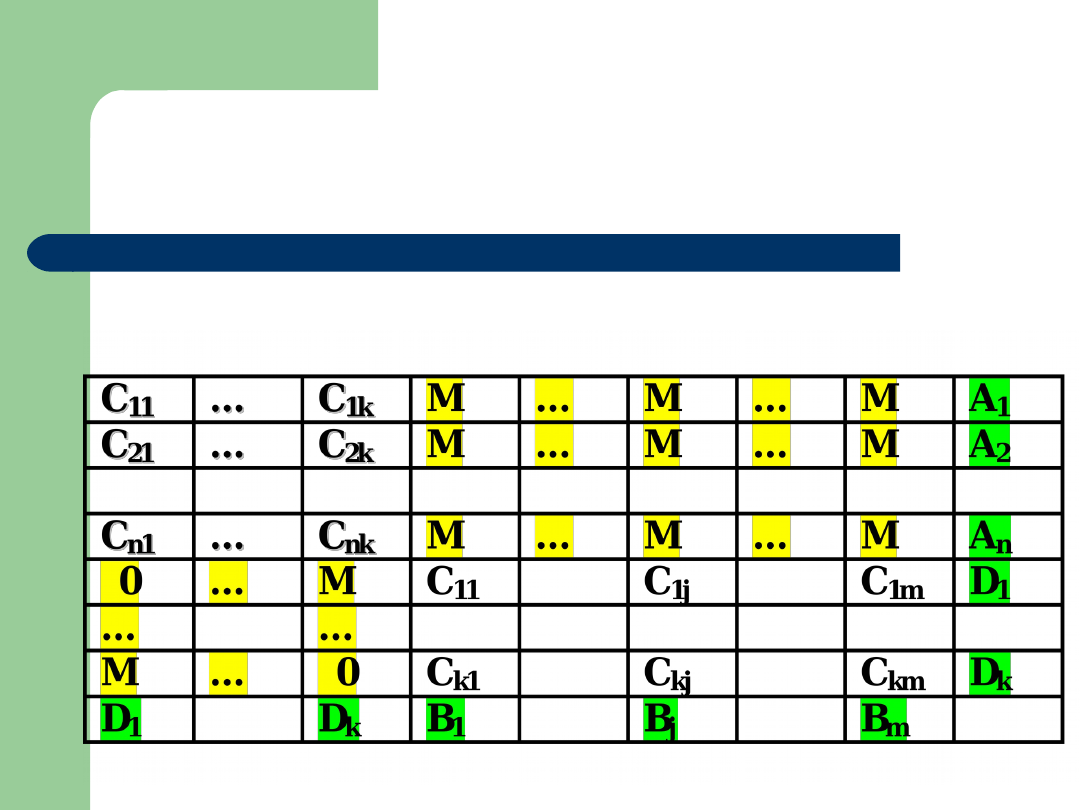
Zadania pokrewne 6

Sprowadzić do ZZT z macierzą kosztów

Zadanie transportowe 1



Trzech dostawców, z których każdy ma po 250 jednostek

pewnego towaru ma dostarczyć ten towar do pięciu

odbiorców zgłaszających zapotrzebowanie w ilości

odpowiednio 40, 55, 125, 140 i 180 jednostek. Nadwyżka

towaru nad zapotrzebowanie powinna pozostać w

magazynach, przy czym odpowiednie jednostkowe koszty

magazynowania wynoszą 4, 6, i 8, a jednostkowe koszty

transportu do poszczególnych odbiorców wynoszą :

od dostawcy pierwszego 3, 5, 7, 4, 5,
od dostawcy drugiego 6, 8, 2, 4, 1,
a od dostawcy trzeciego 3, 3, 2, 2, 3



Wskazać plan przewozów i magazynowania nadwyżki

towarów nad zapotrzebowanie minimalizujący łączne

koszty transportu i magazynowania.

Zadanie transportowe 2

Trzech dostawców posiada odpowiednio 105, 145 i 185 jednostek

pewnego towaru. Na towar ten zgłaszane jest zapotrzebowanie

przez czterech odbiorców w wysokości odpowiednio: 70, 80,

110 i 130 jednostek. Zanim towar trafi do odbiorców musi

przejść przez jeden z dwóch magazynów, których pojemność

wynosi po 300 jednostek każdy. Jednostkowe koszty transportu

od dostawców do magazynów wynoszą odpowiednio: 2, 4, 6 do

pierwszego magazynu i 3, 7, 5 do drugiego magazynu, zaś

jednostkowe koszty transportu z magazynu pierwszego do

kolejnych odbiorców wynoszą: 9, 7, 9, 5, a z magazynu

drugiego odpowiednio: 5, 7, 7, 5. Nadwyżka towarów nad

zapotrzebowania pozostaje w magazynach, w których

jednostkowy koszt magazynowania wynosi 3 i 4.

Wyznaczyć plan przewozów minimalizujący łączne koszty

transportu na obu etapach oraz koszty magazynowania

nadwyżki towarów nad zapotrzebowanie.