3. Podstawowe metody wyceny akcji
Metody wyceny akcji możemy generalnie podzielić na 4 grupy: majątkowe (oparte na wartości majątku firmy), dochodowe (oparte na dochodzie generowanym przez firmę), porównawcze oraz mieszane.
Dochodowe metody wyceny akcji (na podstawie przyszłych dywidend):
a) Model jednofazowy (inaczej model stałego wzrostu albo model Gordona) - właściwy dla dojrzałych spółek:
![]()
gdzie:
P0 - bieżąca wartość akcji (w momencie „0”)
D0 - dywidenda na 1 akcję w roku bieżącym („0”)
D1 - dywidenda na 1 akcję w roku przyszłym
k - oczekiwana giełdowa stopa zwrotu (lub dostosowany do ryzyka koszt kapitału)
g - przewidywana roczna stopa wzrostu dywidendy
Spółka Permedia S.A. wypłaciła w ostatnim roku dywidendę wysokości 1zł na akcję. Zarząd spółki obiecał, że w przyszłych latach dywidenda będzie taka sama. Przewidywana (roczna) stopa zwrotu dla akcji tej spółki wynosi 5%. Wyceń akcje spółki metodą zdyskontowanych dywidend.
W spółce Krehbiel dostosowany do ryzyka koszt kapitału (lub oczekiwana stopa zwrotu) wynosi 10%. Bieżąca dywidenda na 1 akcję wynosi 2,50USD i rosła w stałym tempie 3% rocznie. Oczekuje się, że w wyniku wprowadzenia w spółce nowej technologii produkcji, tempo wzrostu dywidend zwiększy się do 6% w skali roku.
Wyceń, ile warte były akcje spółki przed i po ogłoszeniu wprowadzenia nowej technologii produkcji (odp:36,79 i 66,25).
Czy zmiana wyceny zasugerowana w rozwiązaniu podpunktu a) wydaje się racjonalna, uwzględniając fakt, że spółka będzie miała ten sam zarząd, te same aktywa rzeczowe i ten sam produkt co przed ogłoszeniem nowej technologii?
Wistil S.A. wypłacił w ostatnim roku dywidendę w wysokości 10zł. Spółka obiecała inwestorom, że dywidendy będą rosły w tempie 10% rocznie. Oczekiwana stopa zwrotu z akcji tej spółki wynosi 15%. Dokonaj wyceny akcji.
Orbis S.A. wypłacił w ostatnim roku dywidendę w wysokości 0,50zł. Wysokość dywidendy spadała w ostatnich latach o 10% rocznie. Oczekiwana stopa zwrotu z akcji tej spółki wynosi 8%. Dokonaj wyceny akcji.
Spółka Edwards wypłaciła ostatnio dywidendę w wysokości 4USD na 1 akcję. Dywidendy rosły w stałym tempie 8% rocznie i oczekuje się, że w najbliższej przyszłości to tempo się utrzyma. Jeżeli oczekiwana stopa zwrotu dla akcji spółki Edwards wynosi 14%, to jaka jest wartość tych akcji (odp:72USD)?
*b) Model dwufazowy dywidendy gotówkowej (dla spółek wzrostowych)
Równanie poprzednie nie może być stosowane do wyceny akcji spółek wzrostowych, gdyż w ich przypadku g jest większe od k. W modelu dwufazowym zakłada się, że dywidendy przez kilka lat szybko rosną, a następnie powracają do normalnego tempa (niższego).
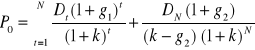
gdzie:
DN - dywidenda na akcję w okresie N (ostatnim roku wolniejszego wzrostu dywidendy)
g1 - początkowa stopa wzrostu dywidend
g2 - długoterminowa stopa wzrostu dywidend
N - liczba lat, w której występuje wzrost g1
t - numer okresu (roku)
Dywidendy z akcji Babet Computer w ciągu ostatnich 6 lat rosły w ponadprzeciętnym tempie 20% rocznie. Oczekuje się dalszego ponadnormalnego wzrostu przez następne 5 lat, a potem zwolnienia tempa do 6% rocznie. Ostatnia dywidenda Babet wyniosła 0,50USD na akcję. Oblicz wartość akcji spółki, jeśli ich oczekiwana stopa zwrotu wynosi 15% (odp: 10,14USD).
*Dywidendy z akcji BioTechnology w ciągu ostatnich 4 lat rosły w ponadprzeciętnym tempie 25% rocznie. Oczekuje się dalszego ponadnormalnego wzrostu przez następne 3 lata, a potem zwolnienia tempa do 5% rocznie. Ostatnia dywidenda wyniosła 10USD na akcję. Oblicz wartość akcji spółki, jeśli ich oczekiwana stopa zwrotu wynosi 12%.
c) Wykorzystanie zysków zamiast dywidend w modelu:
![]()
gdzie:
EPS1 - zysk na 1 akcję (w okresie 1 - czyli przyszłym)
b - współczynnik zatrzymania zysku [(1-b) to wskaźnik wypłaty dywidendy]
Aktualna wartość zysku na 1 akcję spółki Logan (EPS0) wynosi 4USD. W ostatnich latach zyski rosły w tempie 7,5% w skali roku i oczekuje się, że takie tempo wzrostu zysków utrzyma się w przyszłości. Jeżeli wskaźnik zysków zatrzymanych dla spółki Logan wynosi 40%, a oczekiwana stopa zwrotu 14%, to jaka jest bieżąca wartość jej akcji (odp:39,69)?
*Aktualna wartość zysku na 1 akcję spółki Logan wynosi 4USD. W ostatnich latach zyski rosły w tempie 7,5% w skali roku i oczekuje się, że takie tempo wzrostu zysków utrzyma się w przyszłości. Jeżeli wskaźnik zysków zatrzymanych dla spółki Logan wynosi 40%, a oczekiwana stopa zwrotu 14%, to jaka będzie wartość jej akcji za 4 lata?
*d) Model ograniczonego wzrostu zysków (znany okres inwestycji):
![]()
gdzie:
(1-b) - wskaźnik wypłaty dywidendy
N - okres inwestycji (tu: w latach)
(C/Z)N - wskaźnik C/Z w okresie N (tj. na koniec okresu inwestycji)
Carl próbuje ocenić wartość akcji spółki Franklin. Oczekiwana stopa wzrostu zysków spółki wynosi 10%, wskaźnik wypłaty dywidendy = 60%. Planowany wskaźnik C/Z na koniec okresu inwestycji wynosi 20, a aktualna wartość zysku na akcję (EPS0) = 4USD. Jeżeli oczekiwana stopa zwrotu dla tych akcji wynosi 15%, to na ile można wycenić akcje spółki Franklin? Carl planuje trzymać akcje przez 6 lat. (odp.: 73,62USD)
*e) Metoda DCF
Jedną z bardziej rozpowszechnionych metod dochodowych jest metoda zdyskontowanych przepływów pieniężnych, czyli DCF (Discounted Cash Flow). Istnieje kilka odmian wyceny wartości przedsiębiorstwa metodą DCF różniących się między sobą zarówno poziomem szczegółowości, jak i konstrukcją (sposobem obliczania) prognozowanych przepływów pieniężnych oraz określaniem stopy dyskontowej.
Podejście DCF jest najbardziej wyrafinowanym, najtrudniejszym, ale też najwięcej wnoszącym podejściem do wyceny firm. Jego główna trudność polega na konieczności sporządzenia wieloletnich prognoz finansowych dla wycenianej firmy, natomiast jego największa zaleta - na umożliwieniu zrozumienia i ilościowej ocenie wpływu rozmaitych czynników na wartość firmy.
Według tej metody wartość przedsiębiorstwa wynika z przyszłych zdyskontowanych przepływów pienieżnych oczekiwanych do wygenerowania przez te przedsiębiorstwo. Prognozując przyszłe wyniki przedsiębiorstwa przyszłość dzieli się na dwa okresy. Dla pierwszych n lat szczegółowo prognozuje się poszczególne pozycje z bilansu i rachunku zysków i strat decydujące o wielkości przepływów pieniężnych. Ponieważ 1mln otrzymany za kilka lat jest mniej warty niż 1mln otrzymany za rok, FCF dla kolejnych lat w przyszłości dyskontowany jest na wartość teraźniejszą przy użyciu WACC (Weighted Average Cost of Capital) obliczonego z formuły:
WACC = D/(E+D) * kd * (1-t) + E/(E+D) * ke
gdzie:
E - wielkość kapitału własnego
D - wielkość długu
t - stopa opodatkowania
kd - koszt kapitału obcego
ke - koszt kapitału własnego obliczony z modelu CAPM według wzoru:
ke = Rf + Rr * beta
gdzie:
Rf - stopa wolna od ryzyka
Rr - premia za ryzyko rynkowe
beta - współczynnik ryzyka specyficznego
Oszacowane i zdyskontowane przy użyciu WACC FCF sumuje się:
Wartość spółki (V1) = ![]()
Przepływy pieniężne do firmy (FCF - Free Cash Flow) na podstawie, których dokonujemy wyceny obliczamy z formuły:
FCF = NOPAT + amortyzacja - inwestycje w majatek trwały - inwestycje w majatek obrotowy
gdzie:
NOPAT (Net Operation Profit Less Adjusted Taxes) = zysk operacyjny EBIT * (1-stopa podatkowa)
Natomiast po tych n latach zakłada się, iż firma osiągnie stabilizację i jej przepływy w dalszej przyszłości będą wzrastać w stałym tempie g. Wartość spółki w okresie stałego wzrostu nazywamy wartością końcową i obliczamy wg wzoru:
Wartość końcowa = V2 = ![]()
Następnie otrzymaną wartość końcową dyskontujemy za pomocą WACC przez taką ilość okresów ile wynosi n. Dalej, sumujemy otrzymaną wartość końcową i wartość spółki z okresu zmiennego wzrostu (V1+V2). Otrzymujemy w ten sposób wartość całkowitą firmy (TV), od której jeszcze należy odjąć wartość rynkową długu i akcji uprzywilejowanych i podzielić tę kwotę przez liczbę akcji spółki znajdującą się w obrocie.
Przykład - zad.8.7. (s.412 Brigham i Houston - Podstawy Zarządzania Finansami)
Ze względu na wysoki poziom specjalizacji przemysłu elektronicznego Barrett Industries inwestują znaczne środki w badania i rozwój potencjalnych produktów. Konsekwentnie więc firma zatrzymuje całość zysków i reinwestuje je wewnątrz spółki (innymi słowy nie płaci dywidendy). Barrett nie planuje wypłacania dywidendy w bliskiej przyszłości. Jeden z większych funduszy emerytalnych jest zainteresowany nabyciem akcji firmy Barrett, które są notowane na nowojorskiej giełdzie. Dyrektor finansowy funduszu zbadał dokładnie firmę Barrett i zdaje sobie sprawę, że jej wycena musi być oparta na modelu całkowitej wartości spółki. Według jego szacunków wolne środki pieniężne spółki w następnych 4 latach będą równe odpowiednio: 3 mln, 6 mln, 10 mln, 15 mln dol. W następnych latach prognozowane wolne środki pieniężne będą rosły w stałym tempie 7%. WACC firmy Barrett wynosi 12%, spółka ma 60 mln dol. długu i akcji uprzywilejowanych oraz 10 mln akcji zwykłych.
Jaka jest wartość obecna wolnych środków pieniężnych firmy w ciągu najbliższych 4 lat?
Jaka jest wartość końcowa firmy?
Jaka jest dzisiejsza całkowita wartość firmy?
Jaka jest cena jednej akcji firmy Barrett?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
*f) Modele empiryczno - indukcyjne - SERM (single equation regression models — SERM)
Budowanie modelu następuje na podstawie analizy regresji, w trakcie której wartość akcji (Y) uzależnia się, od wpływających na nią czynników ekonomicznych (X1, X2, ..., Xk), co formalnie można zapisać jako:
Y = f(X1, X2, …,Xn)
Podstawowym zadaniem osoby konstruującej taki model jest prawidłowa specyfikacja czynników determinujących zmienną objaśnianą i oszacowanie na podstawie danych historycznych wielkości (wag) ich wpływu. Rozwój tych modeli dokonał się w szczególności w Stanach Zjednoczonych po 1960 r.
Podstawowymi determinantami określającymi wartość akcji mogą być takie zmienne jak: zysk, dywidenda, tempo wzrostu zysku przypadającego na jedną akcję, wskaźnik ogólnego zadłużenia firmy, wskaźnik ryzyka oczekiwanych w przyszłości zysków itp. (czynnik ryzyka może być również określony
przez stopień zadłużenia przedsiębiorstwa). Zmienne te w modelu pełnią rolę zmiennych objaśniających. Powinny one być tak dobrane, aby stopień objaśnienia zmiennej Y był jak najwyższy. Z kolei znaki współczynników mierzących wpływ poszczególnych zmiennych objaśniających na zmienną objaśnianą powinny być prawidłowe z merytorycznego punktu widzenia, czyli wynikać z naszej wiedzy o kierunku oddziaływania danego czynnika na wartość akcji. Teoretycznie, liczba zmiennych w modelu mogłaby być dowolnie duża, jednak w praktyce korzysta się najczęściej z 3-4 zmiennych, gdyż większa ich liczba powoduje jedynie marginalne zmiany w wartości zmiennej objaśnianej. Model może mieć np. następującą postać:
![]()
Gdzie wartości b są współczynnikami regresji pokazującymi oddziaływanie każdej zmiennej na zmienną objaśnianą Y.
Wycena akcji na podstawie modelu empiryczno-indukcyjnego sprowadza się do obliczenia teoretycznej wartości zmiennej objaśnianej (Yp) dla prognozowanych wartości zmiennych objaśniających, czyli:
![]()
Praktyczne wykorzystanie modeli SERM do szacowania wartości akcji nastręcza jednak szereg problemów:
niestabilność współczynników b w dłuższych okresach,
nieprecyzyjność szacunku danych wymaganych w modelu.
Testowanie modeli SERM [J. Cragg, B.G. Malkiel, 1970] doprowadziło do tego, że dla dwóch kolejnych okresów model o takiej samej strukturze wykazywał zasadniczo różne współczynniki regresji. Ponadto okazało się, że w zależności od fazy rozwoju gospodarczego zmienia się znaczenie poszczególnych zmiennych objaśniających.
Modele empiryczno-indukcyjne mogą więc być modelami efektywnymi ale raczej dla transakcji krótkookresowych. Stosowanie ich w dłuższych okresach, szczególnie w nieustabilizowanych warunkach gospodarczych wymagałoby międzyokresowych korekt współczynników regresji w celu zapewnienia lepszej zdolności objaśniającej modelu.
g) Metoda porównawcza (mnożnikowa)
Metoda porównawcza opiera się na porównaniu wskaźników spółki (najczęściej kilku jednocześnie) do grupy przedsiębiorstw stanowiących punkt odniesienia wyceny. Najczęściej wykorzystuje się tu spółki z tej samej branży. Wskaźniki jakie najczęściej się wykorzystuje w porównaniach to: P/E (C/Z) i P/BV (C/WK).
Ponieważ P/E jest równy:
Po odpowiednim przekształceniu tego równania otrzymujemy wzór na wyznaczanie kursu akcji:
P/E jest tutaj mnożnikiem (multiplikatorem), stąd nazwa metody.
Przykład:
Przeciętny wskaźnik PIE w danym sektorze wynosi 10, a zysk na 1 akcję danego przedsiębiorstwa 15 zł. Jaki będzie kurs akcji danego przedsiębiorstwa?
Kurs akcji, czyli jej wartość rynkową, obliczamy na podstawie wzoru i mamy:
15 zł x 10 =150 zł
Tak samo można wykorzystać wskaźnik C/WK.
< przykład z analizy fundamentalnej DM BOŚ - spółka Netmedia - s.6.>
h) Wycena akcji uprzywilejowanych
Wycena akcji uprzywilejowanych opiera się na równaniu:
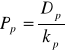
Gdzie D oznacza wysokość dywidendy wypłacanej rocznie, a kp to wymagana stopa zwrotu (równa kosztowi kapitału uprzywilejowanego patrząc od strony przedsiębiorstwa). Jak widać, obliczenia są tu dość proste. Wycena komplikuje się jeśli mamy do czynienia z akcjami wygasającymi po określonym czasie lub zamieniającymi się po pewnym czasie na akcje zwykłe.
4. Nasza wycena a rynkowa cena akcji.
Jeśli nasza wycena akcji jest wyższa niż obecna cena akcji na giełdzie, oznacza to że akcje są niedowartościowane i należy je kupić. W przeciwnym wypadku (wycena niższa niż obecna cena rynkowa) akcje są przewartościowane i należy je sprzedać. Jeśli natomiast te 2 ceny są podobne - akcja jest wyceniona poprawnie (oczywiście według przyjętej przez nas metody wyceny i przyjętych założeń np. co do wzrostu dywidendy).
5. Portfel papierów wartościowych - dywersyfikacja
Analiza portfelowa opiera się na stopach zwrotu i ryzyku mierzonym najczęściej odchyleniem standardowym. W przypadku pojedynczej akcji łatwo jest policzyć te 2 wartości. Sprawa się komplikuje gdy mamy portfel papierów wartościowych. Stopa zwrotu z portfela to po prostu średnia ważona stóp zwrotu (ważona udziałem w portfelu poszczególnych aktywów). W przeciwieństwie do stopy zwrotu, ryzyko portfela nie jest średnią ważoną odchylenia standardowego poszczególnych aktywów, ponieważ mamy do czynienia z korelacją dochodów z aktywów. Tzn. jeśli mamy portfel złożony z 2 akcji to teoretycznie możliwe jest znalezienie nawet takich 2 spółek, które same oddzielenie są bardzo ryzykowne (mają duże odchylenia standardowe), ale w jednym portfelu całkowicie pozbawione ryzyka (![]()
). Byłoby tak, jeśli te 2 akcje byłyby ściśle ujemnie skorelowane, czyli ich wskaźnik korelacji =-1.
W praktyce, znalezienie takich akcji (o ściśle ujemnej korelacji) jest raczej niemożliwe. Mało tego, nawet znalezienie akcji o ujemnej korelacji jest bardzo trudne. Większość akcji tendencję do zachowań pozytywnych, gdy gospodarka jest silna, i do zachowań negatywnych, kiedy jest słaba. Tak więc, nawet bardzo duże portfele są obarczone istotnym ryzykiem, ale oczywiście nie tak dużym, jak wtedy, gdy wszystkie pieniądze są zainwestowane tylko w jeden rodzaj akcji.
Aby przekonać się, w jaki sposób wielkość portfela wpływa na jego ryzyko zanalizujemy rysunek, na którym pokazano, w jaki sposób, tworząc coraz większe portfele losowo wybranych akcji z giełdy nowojorskiej (NYSE), wpływamy na ryzyko portfela:
Na wykresie przedstawiono odchylenia standardowe dla przeciętnego portfela zawierającego kolejno — jeden pakiet akcji, dwa pakiety akcji itd., aż do portfela składającego się z ponad 2 tys. pakietów akcji zwykłych notowanych na giełdzie w czasie, gdy sporządzano ten wykres. Jak widać, w ogólnym przypadku ryzyko portfela składającego się z akcji zwykłych ma tendencję do zmniejszania się i do asymptotycznego zbliżania do pewnej linii granicznej wraz ze wzrostem liczby pakietów akcji w portfelu. Według danych zebranych w ostatnich latach, odchylenie standardowe portfela „jednopakietowego" (albo inaczej, przeciętnego pakietu akcji) wynosi około 35%. Odchylenie standardowe portfela składającego się, ze wszystkich rodzajów akcji, zwanego portfelem rynkowym, wynosiłoby około 20,4%, co na wykresie pokazano jako poziomą linie, przerywaną.
Tak więc, można wyeliminować prawie połowę ryzyka związanego z posiadaniem tylko jednego rodzaju akcji, jeżeli pakiet takich akcji jest częścią dobrze zróżnicowanego portfela, tzn. takiego, który zawiera przynajmniej 40 różnych pakietów akcji. Jakieś ryzyko zawsze jednak pozostaje, jest więc praktycznie niemożliwe, aby przez dywersyfikacje, wyeliminować efekty głębokich nieraz ruchów rynków papierów wartościowych, które mają wpływ na prawie wszystkie akcje.
Ta część ryzyka, która może być wyeliminowana, jest nazywana ryzykiem dywersyfikowalnym (niesystematycznym), a część, której wyeliminować się nie da — ryzykiem rynkowym (niedywersyfikowalnym, systematycznym lub beta - bo jest mierzone współczynnikiem beta). Fakt, że duża część ryzyka związanego z pojedynczymi akcjami może być wyeliminowana, jest niezmiernie istotny, ponieważ racjonalni inwestorzy mogą je wyeliminować lub zminimalizować.
Ryzyko dywersyfikowalne jest spowodowane takimi wydarzeniami losowymi, jak procesy sądowe, strajki, udane i nieudane programy marketingowe, powodzenie lub niepowodzenie w otrzymaniu dużych kontraktów lub innymi zdarzeniami, które dotyczą tylko danej firmy. Ponieważ zdarzenia takie są w istocie losowe, ich wpływ na portfel może być wyeliminowany dzięki odpowiedniej dywersyfikacji — złe wydarzenia w jednej firmie mogą być kompensowane dobrymi wydarzeniami w innej. Z drugiej strony, ryzyko rynkowe wywodzi się z czynników, które systematycznie dotykają większość firm: fazy cyklu koninkturalnego (recesja, ożywienie), wojny, wysoka inflacja. Ponieważ czynniki te wywierają negatywny wpływ na większość akcji, ryzyka rynkowego nie można wyeliminować przez dywersyfikację.
Zaliczamy tu m.in. metody oparte na dywidendzie i zyskach opisane poniżej oraz b. popularną metodę DCF.
J.C. Francis, R.W. Taylor, Podstawy inwestowania - wycena papierów wartościowych i konstrukcja portfela, Dom wydawniczy ABC, Kraków 2001, s. 302.
Ibidem.
Ibidem, s. 305.
J.C. Francis, R.W. Taylor, Podstawy inwestowania..., op. cit., s. 307.
Ibidem.
Ibidem, s.308.
Brigham, Houston, Podstawy zarządzania Finansami, T1, s. 388-393.
Formalnie zalicza się je do metod dochodowych, gdyż zmiennymi objaśniającymi są czynniki determinujące dochodowość akcji.
Wykorzystuje się również np. wskaźniki: MC/S (market capitailzation/sales - stosunek kapitalizacji do przychodów), P/OP (price/operating profit - cena do zysku operacyjnego na 1 akcję).
Ujemne zwroty z akcji 1 byłyby rekompensowane dodatnimi z akcji 2.
Nietrudno jest znaleźć kilka rodzajów akcji, którym w przeszłości zdarzyło się, szczególnemu zbiegowi okoliczności, pójść w górę, gdy wartość większości akcji malała. Dużo trudniej jest znaleźć akcje, które według praw logiki powinny w przyszłości pójść w górę, gdy inne będą spadać.
2
bo: D1 = EPS1 (1-b)
Wyszukiwarka
Podobne podstrony:
konspekt6 v2 mat dla stud[1], EKONOMIA
Mat dla stud 2
chlorowcop mat dla stud
zw metalorgan mat dla stud
PR w wersji skróconej dla kulturo, mat. dla stud. sponsoring
Zarządzanie Cwiczenie 1 mat dla stud, Geodezja, 01-2sem, management
Bialka i kw nukle mat dla stud w 09
mat dla stud Zachowania nabywców a merchandising
mat dla stud
PR w wersji skróconej dla kulturo, mat. dla stud.-PR wewn.
mat dla stud wykII chem org
mat dla stud uzup cukry i białka
alkohole mat dla stud
PR w wersji skróconej dla kulturo, mat. dla stud.-kontakty z med.+kamp.
mat dla stud 1
Mat dla stud 2
chlorowcop mat dla stud
więcej podobnych podstron