Drzewa binarne

Przyjmując następującą definicję węzła drzewa binarnego rozwiąż podane zadania.

struct node

{

int dane;

node *left;

node *right;

};

Zad 1 Napisz funkcję sprawdzającą, czy dany element x znajduje się w drzewie.

bool search(node *&korzen, int x)
Zad 2 Napisz funkcje wyznaczające: liczbę węzłów drzewa binarnego, liczbę liści, liczbę prawych

potomków w całym drzewie, wysokość drzewa.
Zad 3 Napisz funkcję sprawdzającą, czy drzewo binarne jest zbalansowane (zrównoważone)

(różnica wysokości lewego i prawego poddrzewa każdego węzła wynosi zero lub jeden).
Zad 4 Napisz funkcję sprawdzającą, czy drzewo binarne jest drzewem BST (ng. binary search

tree), czyli czy zachodzi następująca własność. Niech x będzie węzłem drzewa. Jeśli y jest

węzłem znajdującym się w lewym poddrzewie węzła x, to dana(x) > dana(y). Jeśli y jest węzłem

znajdującym się w prawym poddrzewie węzła x, to dana(x) < dana(y).
Zad 5 Napisz procedurę usuwającą wszystkie liście danego drzewa binarnego.
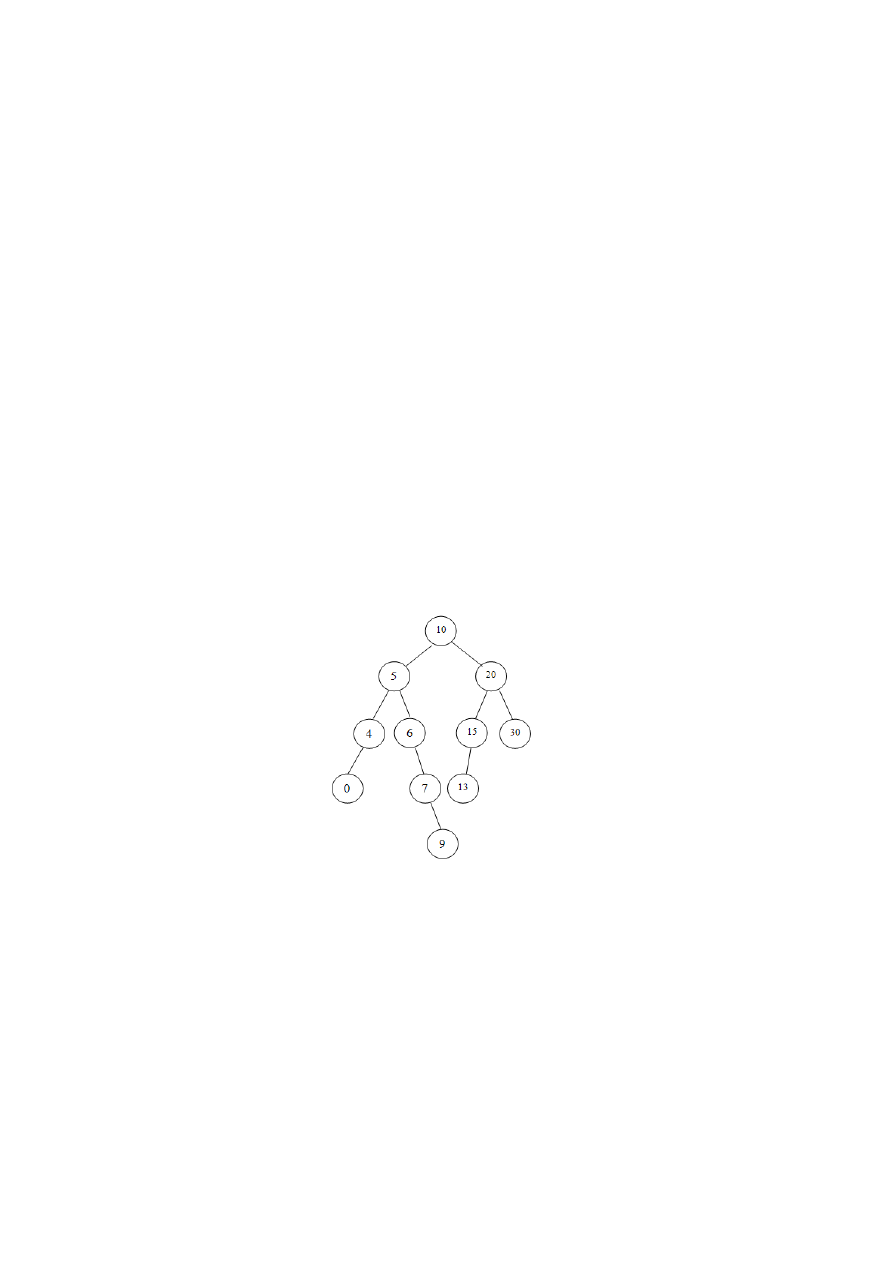
Zad 6 Zastosuj procedury preorder(), inorder(), postorder() do poniższego drzewa,

zakładając, że odwiedzenie węzła p wiąże się z następującym działaniem:

• if(p->left!=NULL && p->dana - p->left->dana < 2)

p->left->dana+=2;

• if(p->left==NULL)

p->right=0;

Zad 7 Pokaż drzewo dla którego metody preorder i inorder generują ten sam ciąg.
Zad 8 Napisz funkcję tworzącą „odbicie lustrzane” podanego drzewa binarnego.
Zad 9 Napisz funkcję, która drukuje drzewo jak pokazano poniżej.

1

A

B

D

E

C

F

H

I

G

Zad 10 Dana jest tablica a = [a

1

, a

2

, . . . , a

n

] o długości n = 2

k

− 1, dla całkowitych k > 0.

Napisz funkcję tworzącą drzewo jak pokazano w poniższych przykładach.

• a

1

⇒ {a

1

},

• a

1

, a

2

, a

3

⇒ {a

2

, {a

1

}, {a

3

}},

• a

1

, a

2

, a

3

, a

4

, a

5

, a

6

, a

7

⇒ {a

4

, {a

2

, {{a

1

}, {a

3

}}}, {a

6

, {{a

5

}, {a

7

}}}}.

Zad 11 Strukturę drzewiastą zdefiniowano następująco:

struct node{

char op; //*, +, -

int num;

node *left, *right;

};

Drzewa zdefiniowane w ten sposób mogą reprezentować wyrażenia arytmetyczne (węzły

wewnętrzne to operatory, a zewnętrzne to liczby). Na przykład wyrażenie (7+8)*(3-2) można

przedstawić jako następujące drzewo:

Napisz funkcję, która oblicza wartość takich drzew (dla drzewa z rysunku funkcja powinna

zwrócić wartość 15).

2