Binarne drzewo poszukiwań(BST)

Binarne drzewo poszukiwań (BST)

1. Drzewo binarne:

Drzewa binarne są to drzewa, które posiada węzeł główny (drzewo), który posiada co
najwyżej dwójkę potomków - lewy i prawy (poddrzewa). Każdy z potomków może posiadać
również najwyżej dwójkę dzieci (lewe dziecko i prawe dziecko).
Drzewa ułatwiają i przyspieszają wyszukiwanie, a także pozwalają w łatwy sposób operować
na posortowanych danych. Znaczenie tych struktur jest bardzo duże i ze względu na swoje
własności drzewa są stosowane praktycznie w każdej dziedzinie informatyki (np. bazy
danych, grafika komputerowa, przetwarzanie tekstu, telekomunikacja).

2. Drzewo BST:

Drzewo BST (binary search tree) jest drzewem binarnym. Oprócz pola wartości drzewo BST
posiada jeszcze dwa pola: L i P, wskazujące odpowiednio na lewy i prawy następnik. Drzewo
BST ma szczególną własność:

Ø jeżeli element drzewa znajduje się w lewej gałęzi to jest mniejszy od swego

poprzednika

Ø jeżeli element drzewa znajduje się w prawej gałęzi to jest większy od swego

poprzednika

type ref=^wezel;
wezel=record
klucz :integer;
licznik :integer;
lewe, prawe :ref;
end;

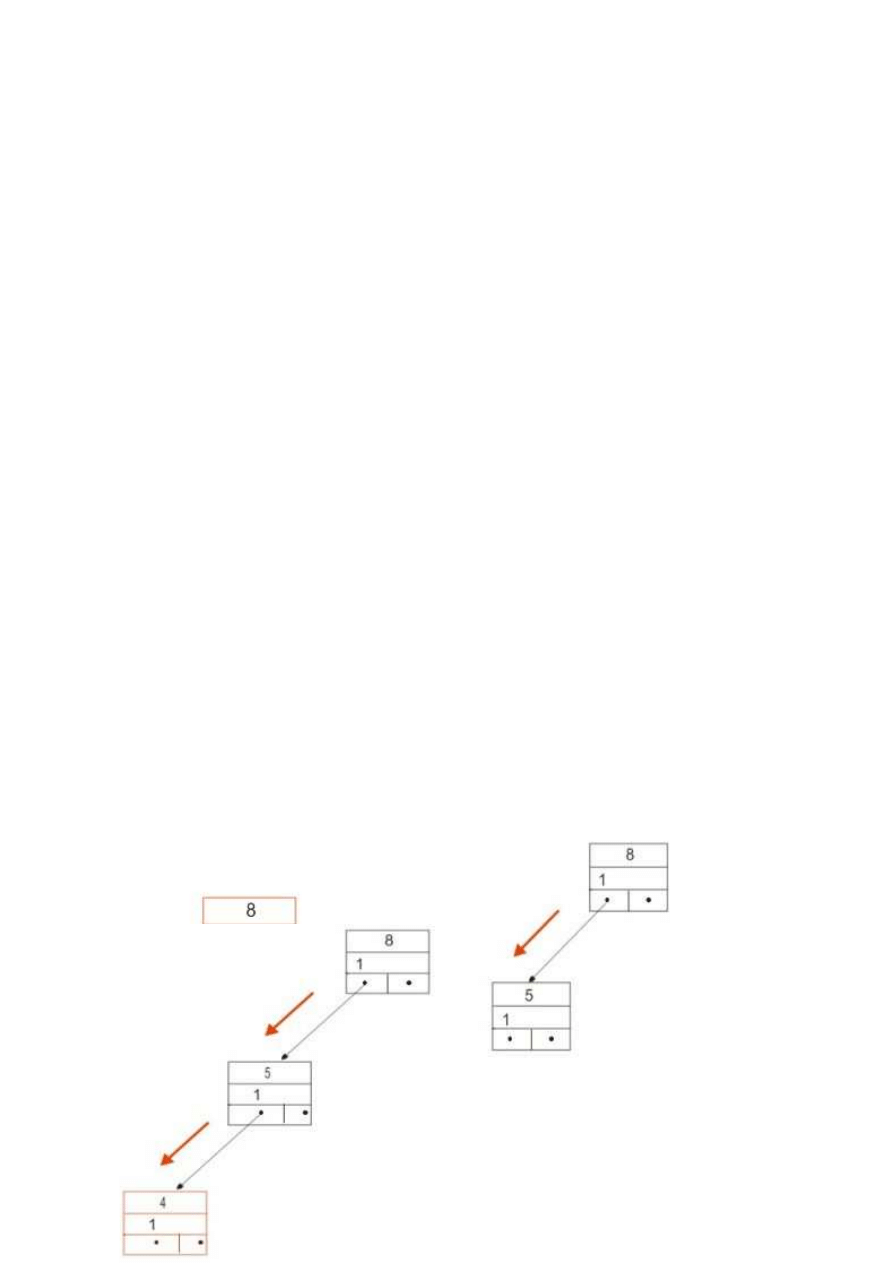
Dodawanie elementów:
Jeśli drzewo BST jest puste (korzeń=nil) należy wstawić element (nie porównujemy go z
innymi), w przeciwnym wypadku porównujemy wartość elementu z następnikami każdego
węzła (zaczynając od korzenia). Jeżeli wartość elementu jest niewiększa od wartości
porównywanego wierzchołka to przechodzimy do lewego następnika, w przeciwnym razie
przechodzimy do prawego następnika. Krok ten powtarzamy aż znajdziemy dla naszego
elementu odpowiednie miejsce, tzn. gdy następnik, do którego powinniśmy iść jest pusty
(nil). Następnie wstawiamy element jako odpowiedni następnik (prawy, jeśli element jest
większy od węzła, lewy jeśli niewiększy).

{-----------------------------tworzenie drzewa--------------------------}
procedure szukaj (x :integer; var p:ref);

begin
if p=nil then
begin
new(p);
with p^ do
begin
klucz:=x;
licznik:=1;
lewe:=nil;
prawe:=nil;
end
end else
if x < p^.klucz then szukaj (x, p^.lewe) else
if x > p^.klucz then szukaj (x, p^.prawe) else
p^.licznik:=p^.licznik+1;
end;

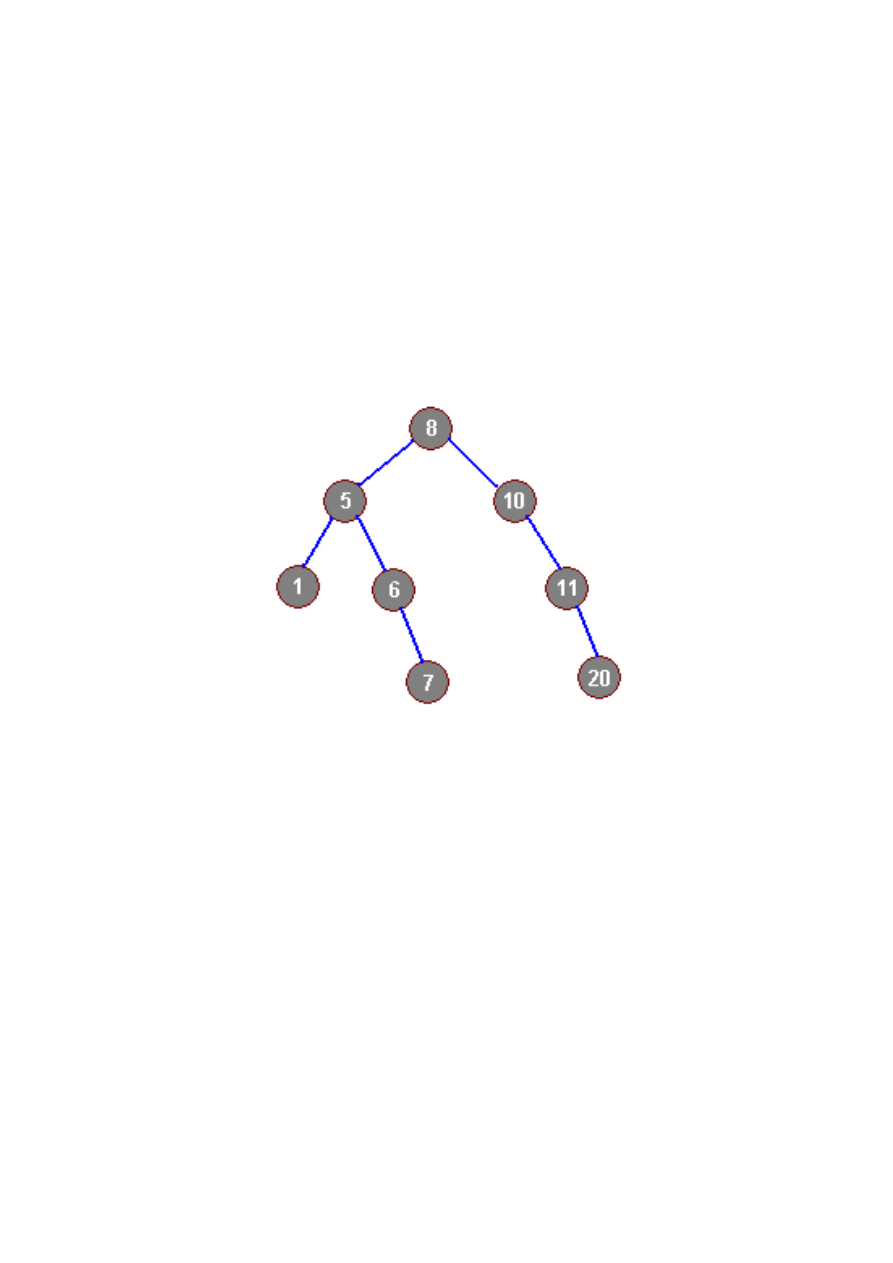
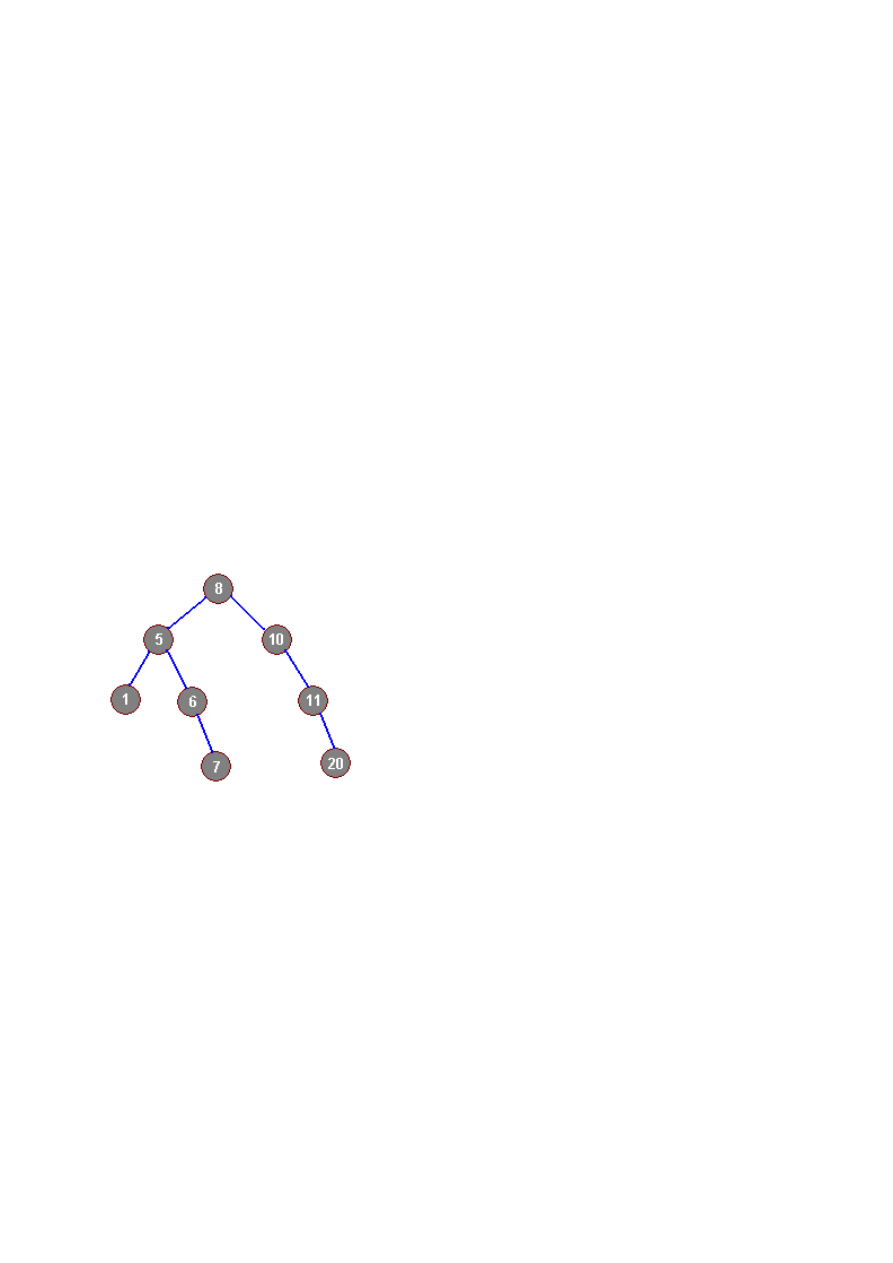
A oto przykład tworzenia drzewa dla liczb: 8,5,4,6,4,9,10,1


rys.1

rys.2

rys.3

rys.4

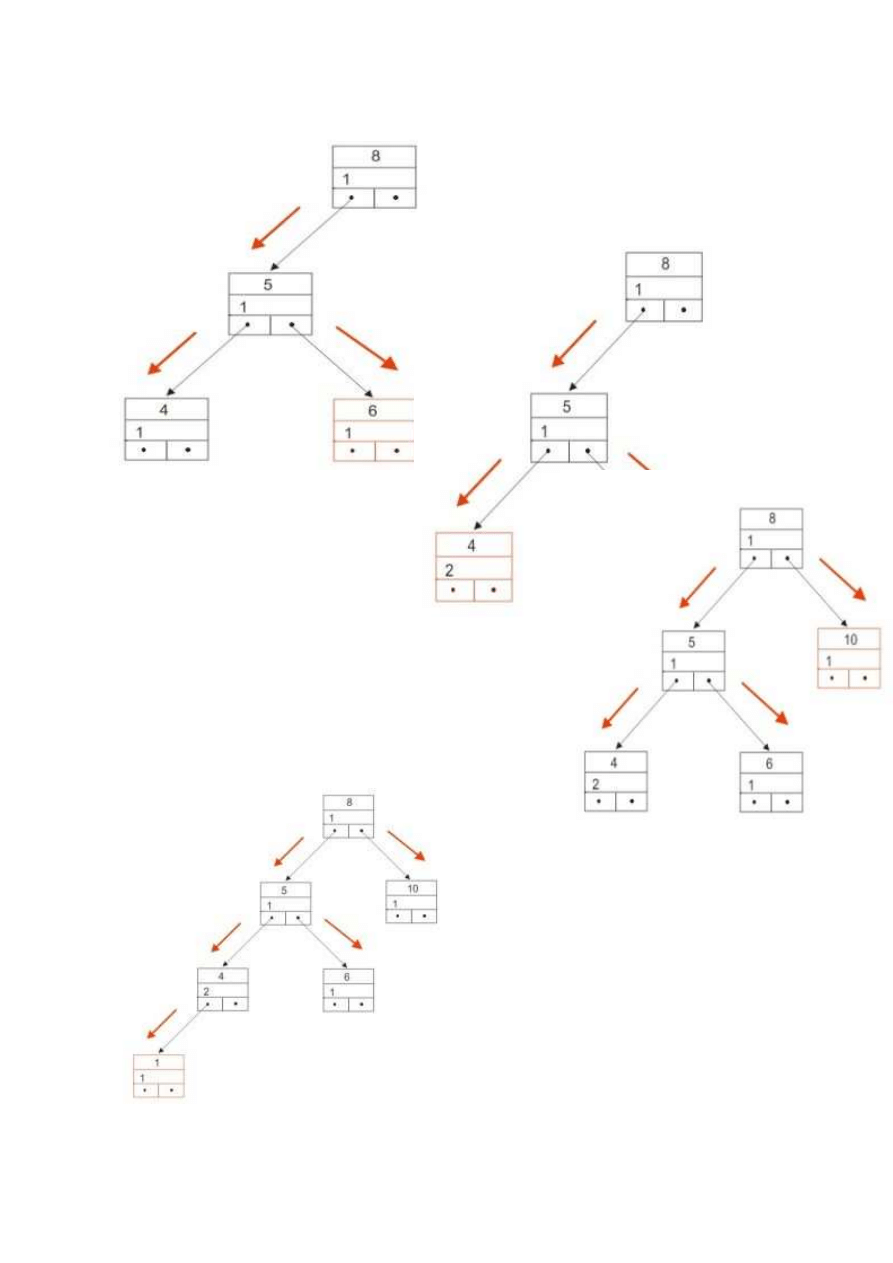
Rys.6

Rys.5

Rys.7

Usuwanie elementów z drzewa:

Przy usuwaniu węzła należy rozważyć trzy przypadki:

· Jeżeli element x jest liściem (nie ma synów) – można go po prostu usnąć.

· Jeżeli element x ma co najwyżej jednego syna – należy element x zastąpić jego synem.

· Jeżeli element x ma dwóch potomków:

1.

Szukamy jego następnika y (najbardziej lewy element w prawym poddrzewie x
– element o najmniejszej wartości z prawego poddrzewa usuwanego
elementu).

v

zamiast następnika można również wykorzystać poprzednik (czyli
najbardziej prawego elementu w lewym poddrzewie x – element o
największej wartości z lewego poddrzewa usuwanego elementu).
Obydwa sposoby są dobre. Ważne jest jednak, aby stosować jeden
sposób w danym programie.

2.

Zastępujemy wartość węzła x przez wartość węzła y.

3.

Wycinamy węzeł y który może posiadać najwyżej jednego syna (jeżeli element
y posiada syna, to stanie się on synem swojego dziadka).

{--------------------------usuwanie węzła z drzewa---------------------------}
procedure usun (x :integer; var p:ref);

var q:ref;

procedure us (var r:ref); {kiedy węzeł ma 2 potomków}
begin
if r^.prawe<>nil then us (r^.prawe) else
begin
q^.klucz:=r^.klucz;
q^.licznik:=r^.licznik;
q:=r;
r:=r^.lewe
end;
end;

begin
if p = nil then
writeln ('Brak słowa w drzewie')
else if x < p^.klucz then usun (x, p^.lewe)
else if x > p^.klucz then usun (x, p^.prawe)
else
begin
q:=p;
if q^.prawe = nil then p:=q^.lewe else
if q^.lewe = nil then p:=q^.prawe else
us (q^.lewe);
end
end;

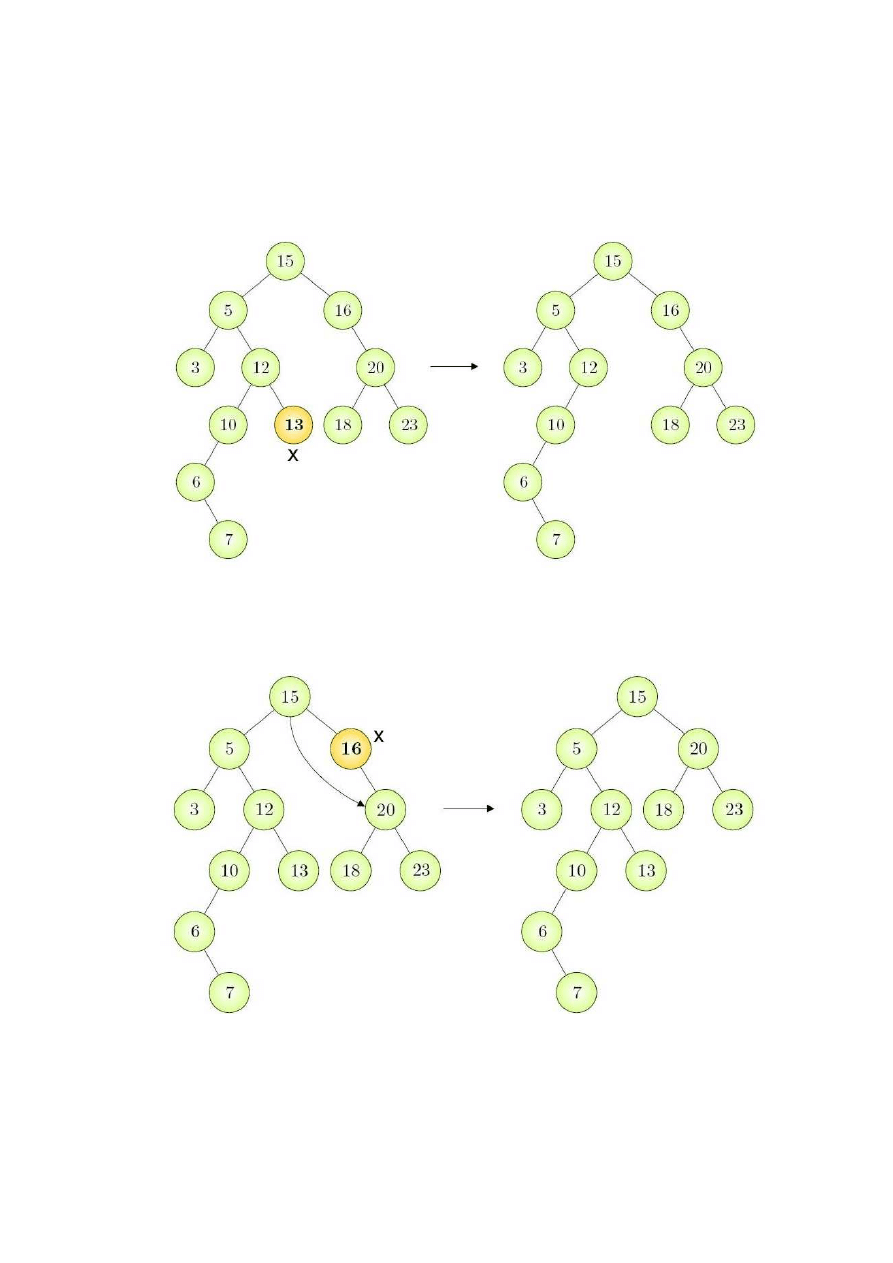
Oto przykłady usuwania elementów dla poszczególnych przypadków:

1. Element usuwany x nie ma ani jednego syna:

2. Element usuwany x ma tylko jednego syna:

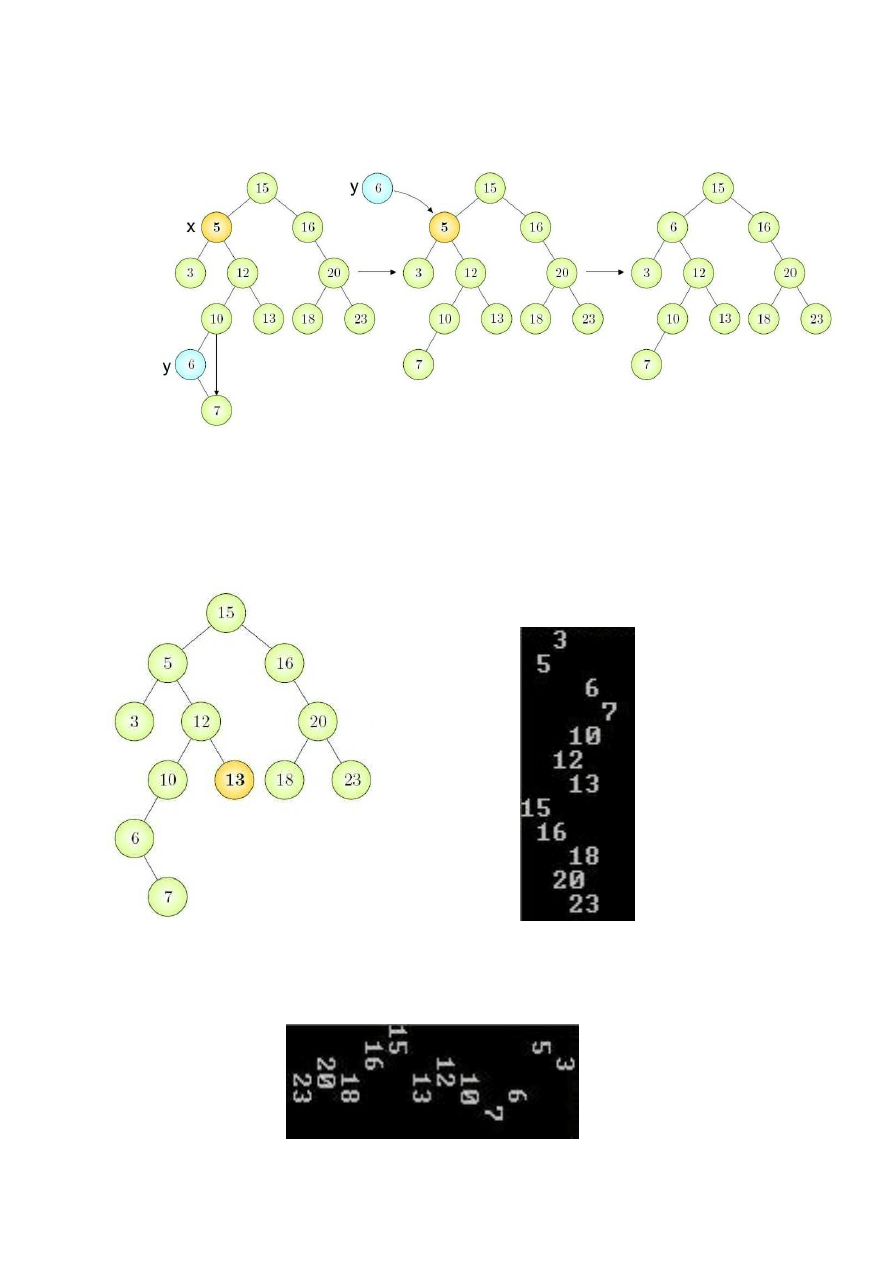
3. Element usuwany x ma dwóch synów:

Drukowanie drzewa:
Elementy drzewa drukowane są w kolejności rosnącej z góry na dół. Odległość elementu od
lewej krawędzi ekranu pokazuje jego pozycję w drzewie. W ten sposób drzewo które
utworzyliśmy dla elementów: 15, 5, 16, 3, 12, 20, 10, 13, 18, 23, 6, 7 (rys.1) po
wydrukowaniu na ekran (rys.2) będzie miało następująco formę:

Rys.1 Rys.2

Ponadto, gdy obrócimy rys.2 o 90° w prawo, łatwo można zauważyć, ze wydruk jest taki sam
jak zdjęcie elementów drzewa podczas ich wprowadzania: