(c) T. Pankowski, Drzewa

decyzyjne

1

Tadeusz Pankowski

www.put.poznan.pl/~tadeusz.pankowski

Klasyfikacja obiekt

Klasyfikacja obiekt

ó

ó

w

w

–

–

Drzewa decyzyjne

Drzewa decyzyjne

(c) T. Pankowski, Drzewa

decyzyjne

2

Klasyfikacja i predykcja

Klasyfikacja i predykcja

1. Odkrywaniem

reguł klasyfikacji

nazywamy proces

znajdowania modeli (lub funkcji) klasyfikacji

umożliwiających określenie klasy, do której powinien

należeć wskazany obiekt.

2. Model klasyfikacji budowany jest w wyniku analizy zbioru

danych treningowych

, tj. zbioru obiektów o znanej

przynależności klasowej.

3. Model klasyfikacji może być reprezentowany za pomocą:

• reguł o postaci IF_THEN,
• drzew decyzyjnych,
• sieci neuronowych,
• innych ...

(c) T. Pankowski, Drzewa

decyzyjne

3

Klasyfikacja i predykcja

Klasyfikacja i predykcja

1. Klasyfikacja danych jest procesem dwuetapowym.

2. W pierwszym kroku budowany jest model (np. relacyjny)

opisujący zadany zbiór danych (treningowy zbiór

danych) składający się ze zbioru obiektów (krotek)

opisanych za pomocą atrybutów.

3. Jeden z atrybutów jest

atrybutem klasyfikującym

(predykcyjnym)

i jego wartości określają

etykiety klas

,

do których należą obiekty.

4. Obiekty tworzące zbiór treningowy wybierane są losowo

z pewnej populacji.

5. Ten etap klasyfikacji nazywany jest też

uczeniem z

nadzorem

, gdyż podana jest klasyfikacja każdego

obiektu (przykładem nauczania bez nadzoru jest

tworzenie skupień,

clustering

)

(c) T. Pankowski, Drzewa

decyzyjne

4

Klasyfikacja i predykcja (c.d.)

Klasyfikacja i predykcja (c.d.)

1.

Utworzony model klasyfikacji reprezentowany jest w postaci:

reguł klasyfikacji,
drzew decyzyjnych,
formuł matematycznych.

2.

Przykład: mając bazę danych z informacjami o osobach (wiek,

wykształcenie, dochód, pochodzenie społeczne) można utworzyć

reguły klasyfikacyjne istotne dla biur turystycznych (tzn. reguły

określające, w jakiego rodzaju wycieczkach osoby te byłyby skłonne

uczestniczyć).

3.

Podstawą utworzenia tych reguł jest analiza dotychczas znanych

przypadków opisujących zachowanie się klientów. Przypadki te

tworzą zbiór treningowy (uczący).

4.

Reguły mogą być wykorzystane do klasyfikacji przyszłych

przypadków, jak również do lepszego zrozumienia zawartości bazy

danych.

(c) T. Pankowski, Drzewa

decyzyjne

5

Klasyfikacja i predykcja (c.d.)

Klasyfikacja i predykcja (c.d.)

1.

Utworzony model jest następnie używany do klasyfikacji.

2.

Najpierw oceniana jest dokładność modelu (klasyfikatora). W tym

celu posługujemy się zbiorem testowym, który wybrany jest

losowo i jest niezależny od zbioru treningowego.

3.

D

okładność

modelu na zadanym zbiorze testowym określona jest

przez procentową liczbę trafnych klasyfikacji, tzn. jaki procent

przypadków testowych został prawidłowo zaklasyfikowany za

pomocą modelu. Dla każdego przypadku możemy porównać znaną

etykietę klasy z etykietą przypisaną przez model.

4.

Jeśli dokładność modelu została oceniona jako wystarczająca,

model można użyć do klasyfikacji przyszłych przypadków

(obiektów) o nieznanej etykiecie klasy.

(c) T. Pankowski, Drzewa

decyzyjne

6

Klasyfikacja i predykcja (c.d.)

Klasyfikacja i predykcja (c.d.)

1.

W czym

predykcja

różni się od

klasyfikacji

?

2.

P

redykcja

(

przewidywanie

) może być rozumiana jako

wykorzystanie modelu do oszacowania (obliczenia) wartości

(lub przedziału wartości), jaką z dużym prawdopodobieństwem

może mieć atrybut analizowanego obiektu. Wartością tego

atrybutu może być w szczególności etykieta klasy.

3.

Z tego punktu widzenia

klasyfikacja

i

regresja

są dwoma

głównymi rodzajami problemów predykcyjnych; przy czym

klasyfikacja jest używana do przewidzenia wartości

dyskretnych lub nominalnych, a

regresja

do oszacowania

wartości ciągłych lub uporządkowanych.

4.

Umowa:

przewidywanie etykiet klas –

klasyfikacja

,

przewidywanie wartości ciągłych (technikami regresji) –

predykacja

.

(c) T. Pankowski, Drzewa

decyzyjne

7

Klasyfikacja i predykcja

Klasyfikacja i predykcja

–

–

zastosowania

zastosowania

¾ Klasyfikacja i predykcja mają wiele zastosowań,

na przykład:

akceptacja udzielenia kredytu,
diagnostyka medyczna,
przewidywanie wydajności,
selektywny marketing,
inne

(c) T. Pankowski, Drzewa

decyzyjne

8

Klasyfikacja za pomoc

Klasyfikacja za pomoc

ą

ą

drzew

drzew

decyzyjnych

decyzyjnych

1. Drzewo decyzyjne jest diagramem przepływu o

strukturze drzewa, gdzie każdy wierzchołek wewnętrzny

oznacza

testowanie

atrybutu, każda krawędź

reprezentuje

wyjście

z testu (wartość lub zbiór wartości

atrybutu), a każdy liść reprezentuje

klasę

.

2. W celu sklasyfikowania nieznanego obiektu wartości jego

atrybutów testowane są zgodnie z informacją zawartą w

drzewie decyzyjnym.

3. W procesie testowania przechodzimy ścieżkę w drzewie

od korzenia do jednego z liści – w ten sposób określana

jest klasa, do której zostanie zaklasyfikowany obiekt.

4. Drzewa decyzyjne mogą być łatwo przekształcone w

reguły klasyfikacyjne.

(c) T. Pankowski, Drzewa

decyzyjne

9

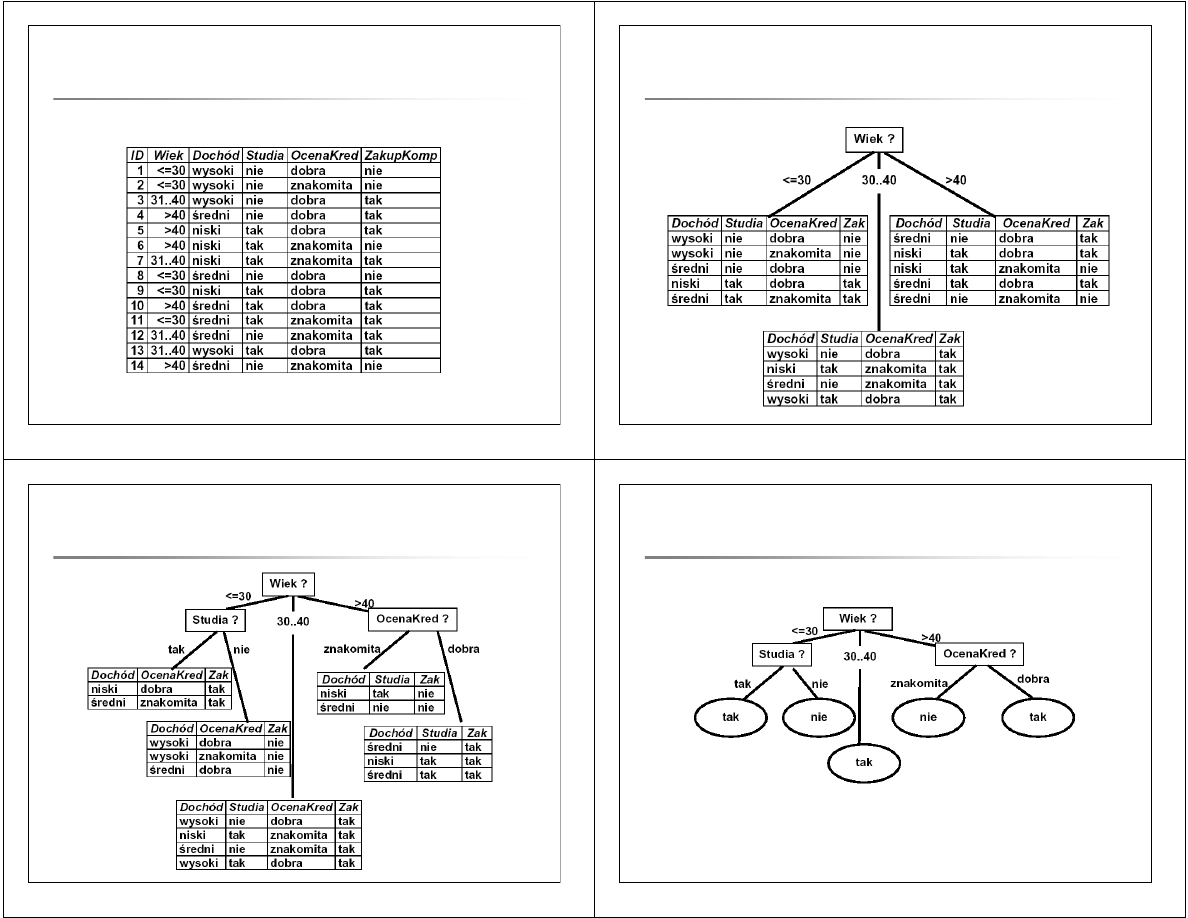
Zbi

Zbi

ó

ó

r treningowy danych o klientach

r treningowy danych o klientach

(c) T. Pankowski, Drzewa

decyzyjne

10

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

pierwszy poziom: atrybut Wiek

pierwszy poziom: atrybut Wiek

(c) T. Pankowski, Drzewa

decyzyjne

11

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

drugi

drugi

poziom: atrybuty Studia i

poziom: atrybuty Studia i

OcenaKred

OcenaKred

(c) T. Pankowski, Drzewa

decyzyjne

12

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

ostateczna

ostateczna

posta

posta

ć

ć

(c) T. Pankowski, Drzewa

decyzyjne

13

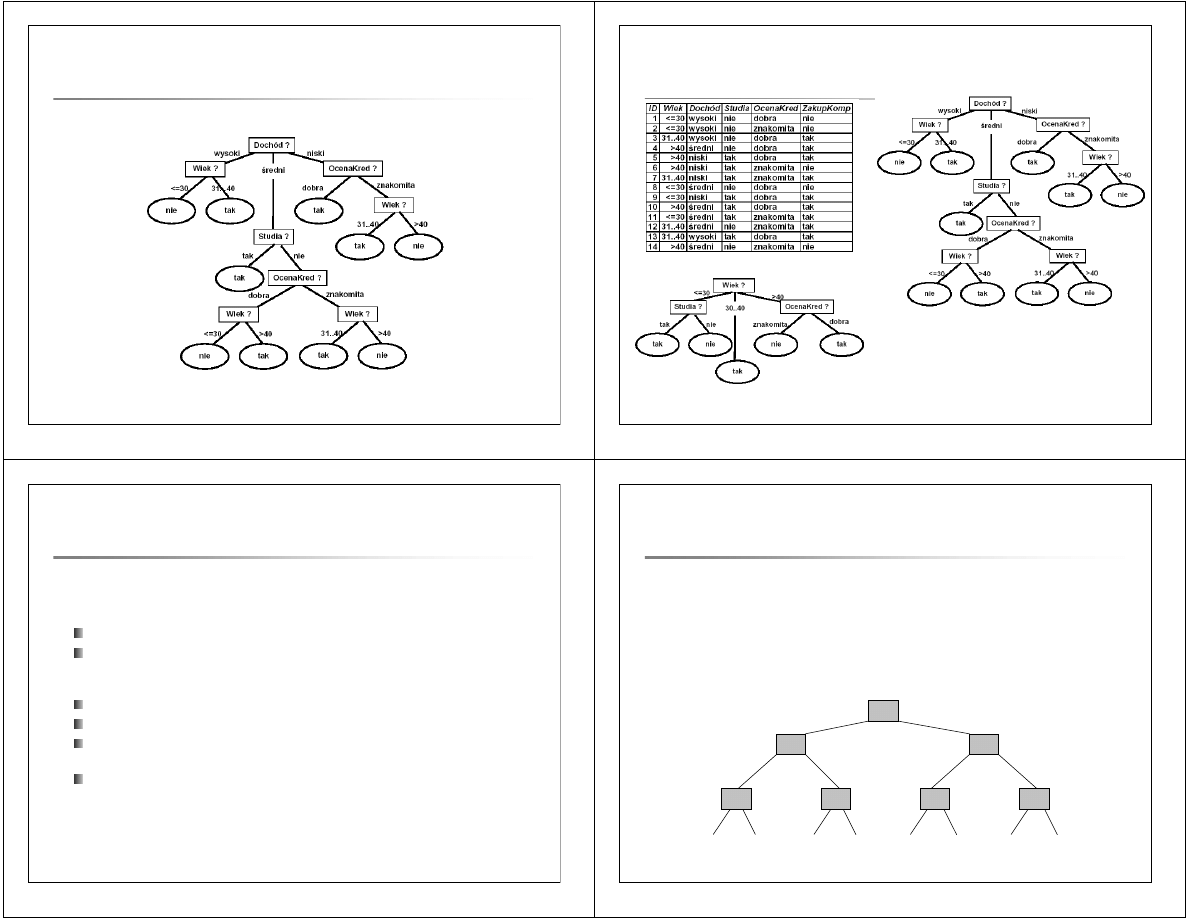
Drzewo decyzyjne

Drzewo decyzyjne

–

–

inna kolejno

inna kolejno

ść

ść

testowania atrybut

testowania atrybut

ó

ó

w

w

(c) T. Pankowski, Drzewa

decyzyjne

14

Drzewa decyzyjne klasyfikuj

Drzewa decyzyjne klasyfikuj

ą

ą

ce dane

ce dane

treningowe

treningowe

–

–

dwa warianty

dwa warianty

(c) T. Pankowski, Drzewa

decyzyjne

15

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

podstawy teorii informacji

podstawy teorii informacji

Charakterystyka zbioru treningowego

S - zbiór złożony z s obiektów (zbiór treningowy), s = 14
m – liczba klas, do których klasyfikowane są obiekty; etykiety klas

określone są przez atrybut "ZakupKomp", który przyjmuje dwie

wartości: TAK, NIE; m = 2
C

1

- klasa TAK, C

2

- klasa NIE

s

1

- liczba obiektów w C

1

, s

2

- liczba obiektów w C

2

, s

1

= 9, s

2

= 5

p

i

- prawdopodobieństwo, że losowo wybrany obiekt należy do

klasy C

i

, 0 < p

i

< 1, p

1

+ p

2

=1

E(p

1

, p

2

) - oczekiwana informacja potrzebna do klasyfikacji

danego obiektu (

entropia układu

):

E(p

1

,... ,p

n

) = – p

1

*log

2

(p

1

) – p

2

log

2

(p

2

), I(9/14, 5/14) = 0.9403

16

Entropia uk

Entropia uk

ł

ł

adu

adu

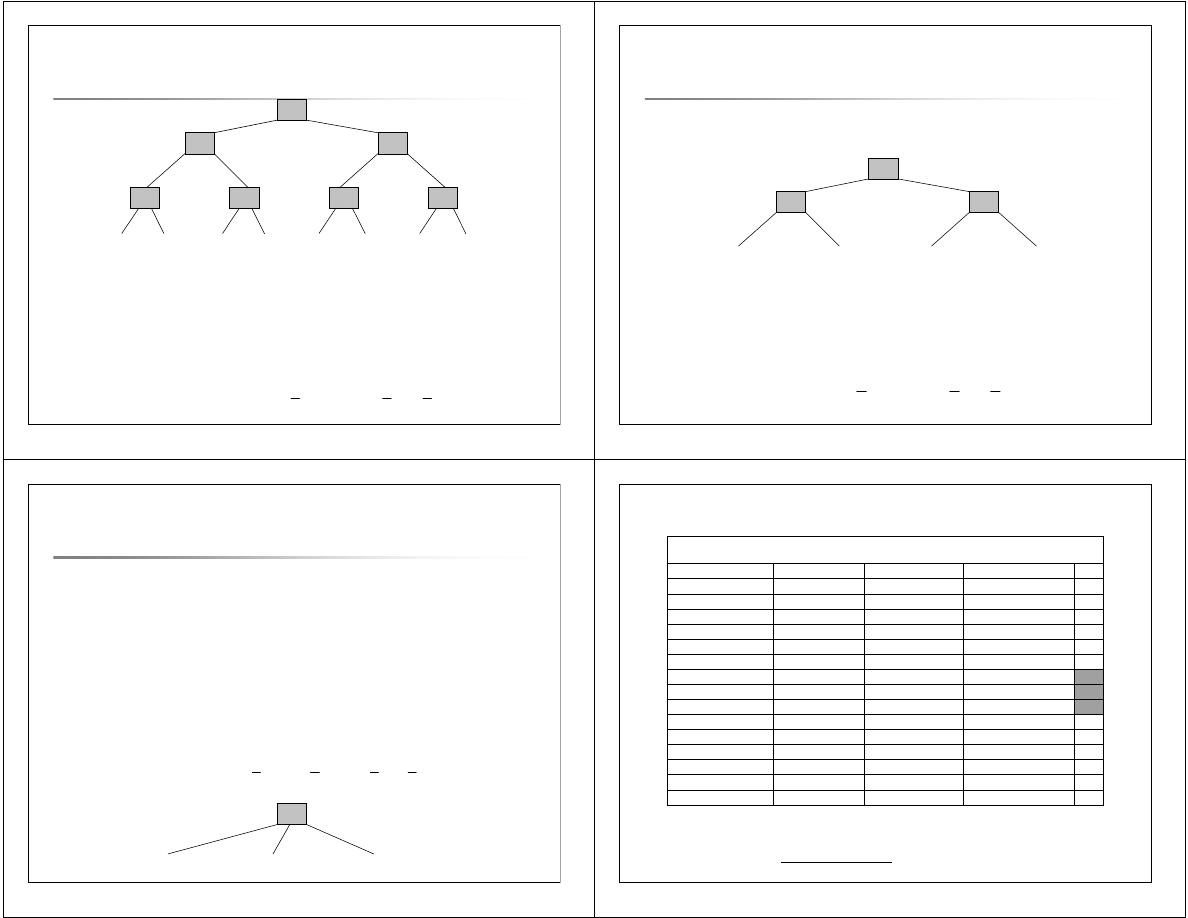
Niech danych będzie układ złożony z 8 jednoelementowych klas.

Entropia

tego układu wyraża się wzorem:

Entr(1,1,1,1,1,1,1,1) = log

2

8 = 3

i oznacza średnią

ilość informacji

(

bitów informacji

), jaka jest potrzebna,

aby zadany element zaklasyfikować do jednej z tych klas. (Argumenty

funkcji Entr oznaczają liczbę elementów w zbiorach tworzących układ).

{0} {1} {2} {3} {4} {5} {6} {7}

>0

>5

>2

>1

>4

>6

>3

1

0

0

0

1

1

0

0

0

0

1

1

1

1

17

Entropia uk

Entropia uk

ł

ł

adu

adu

{0} {1} {2} {3} {4} {5} {6} {7}

>0

>5

>2

>1

>4

>6

>3

1

0

0

0

1

1

0

0

0

0

1

1

1

1

•

Komunikat, że obiekt należy do klasy {i}

niesie w sobie

(

zawiera, przekazuje

) 3 bity

informacji.

•

Prawdopodobieństwo wyboru klasy {i} wynosi 1/8.

•

Zatem średnia ważona (entropia) całego układu, a więc średnia ilość informacji

(bitów informacji) przekazywana w komunikacie, że obiekt należy do klasy {i}

jest równa ilości informacji potrzebnej do zaklasyfikowania obiektu do klasy {i}

wyraża się wzorem:

3

8

1

8

1

8

8

1

1

1

1

1

1

1

1

1

2

8

1

2

8

1

=

−

=

=

∑

∑

=

=

log

log

)

,

,

,

,

,

,

,

(

Entr

i

i

18

Entropia uk

Entropia uk

ł

ł

adu

adu

{0,1} {2,3} {4,5} {6,7}

>5

>1

>3

1

0

0

0

1

1

2

4

1

4

1

4

4

1

2

2

2

2

2

4

1

2

4

1

=

−

=

=

∑

∑

=

=

log

log

)

,

,

,

(

Entr

i

i

Dla rozważanego przykładu utwórzmy klasy 2-elementowe.

Wówczas:

•

Komunikat, że obiekt należy do określonej klasy

niesie:

log

2

8/2 = 2 bity informacji.

•

Prawdopodobieństwo wyboru każdej klasy wynosi 2/8.

•

Zatem entropia układu, a więc średnia ilość informacji (bitów informacji)

potrzebnej do zaklasyfikowania obiektu do klasy wyraża się wzorem:

19

Entropia uk

Entropia uk

ł

ł

adu

adu

Utwórzmy teraz 3 klasy, które zawierają odpowiednio: 1, 2 i 5 elementów.
Zauważmy, że wówczas:
•

ilość informacji potrzebnej do zaklasyfikowania obiektu do każdej z

tych klas wynosi odpowiednio:

log

2

8 = 3, log

2

4 = 2, log

2

8/5 = 0,678

•

prawdopodobieństwo, że obiekt zaklasyfikowany zostanie do każdej z

grup wynosi odpowiednio:

1/8, 1/4, 5/8

•

entropia tego układu (średnia ilość informacji potrzebna do

zaklasyfikowania obiektu do klasy) jest więc równa:

{0} {1, 2} {3, 4, 5, 6, 7}

30

1

5

8

8

5

4

4

1

8

8

1

5

2

1

2

2

2

,

log

log

log

)

,

,

(

Entr

=

+

+

=

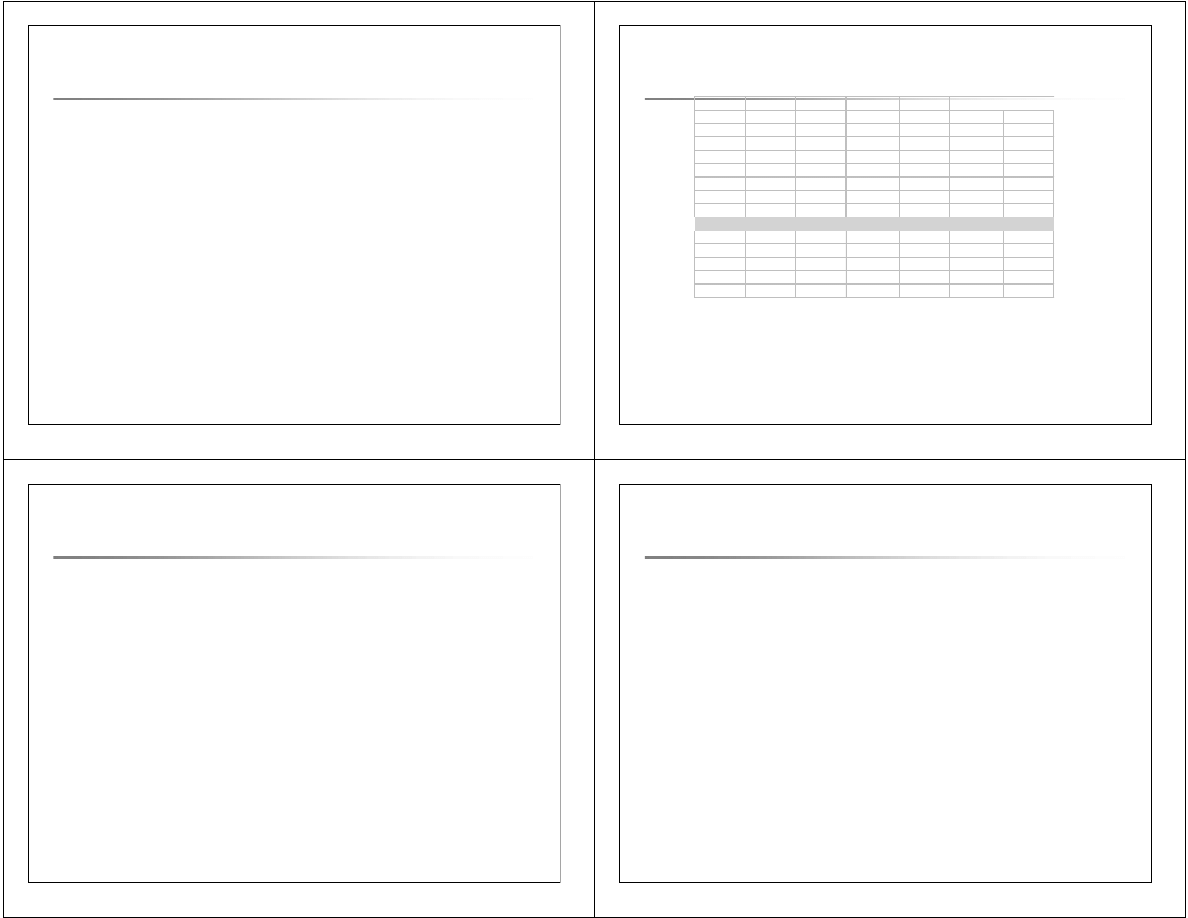
Entropia dla przyk

Entropia dla przyk

ł

ł

adowych uk

adowych uk

ł

ł

ad

ad

ó

ó

w

w

14

1,585

4

4

4

13

1,555

5

4

3

12

1,500

6

3

3

11

1,483

5

5

2

10

1,459

6

4

2

9

1,384

7

3

2

6

1,252

8

2

2

8

1,325

6

5

1

7

1,281

7

4

1

5

1,189

8

3

1

4

1,041

9

2

1

3

0,817

10

1

1

2

0,414

11

1

0

1

0,000

12

0

0

Entropia

Klasa3

Klasa2

Klasa1

Entropia dla trzech klas zawierających 12 elementów

i

i

i

p

log

p

)

p

,

p

,

p

(

E

2

3

1

3

2

1

∑

=

−

=

(Argumentami funkcji E są prawdopodobieństwa przynależności elementów do
poszczególnych zbiorów tworzących układ.)

21

Entropia

Entropia

–

–

podsumowanie

podsumowanie

1.

Entropia układu jednostkowego złożonego ze zbioru A o
prawdopodobieństwie p:

E(p) = – log

2

(p)

2.

Entropia układu jednostkowego złożonego ze zbioru o
prawdopodobieństwie 1 jest równa 0

E(1) = 0

3.

Entropia układu jednostkowego złożonego ze zbioru będącego
sumą zbiorów rozłącznych o prawdopodobieństwach odpowiednio
p

A

i p

B

, jest równa entropii układu jednostkowego złożonego ze

zbioru o prawdopodobieństwie p

A

+ p

B

:

E(p

A

∪ B

) = E(p

A

+ p

B

)

4.

Entropia układu złożonego z n zbiorów o prawdopodobieństwach
odpowiednio p

1

, …, p

n

, jest średnią ważoną entropii n układów

jednostkowych złożonych z każdego z tych zbiorów:

E(p

1

,…,p

n

) = – (p

1

E(p

1

) + … + p

n

E(p

n

))

22

Analiza informacyjna

Analiza informacyjna

–

–

miara ilo

miara ilo

ś

ś

ci informacji

ci informacji

s1

s2

p1

p2

I(s1,s2)

h=log(N/s;2)

1,0000

13,0000

0,0714

0,9286

0,3712

3,8074

2,0000

12,0000

0,1429

0,8571

0,5917

2,8074

3,0000

11,0000

0,2143

0,7857

0,7496

2,2224

4,0000

10,0000

0,2857

0,7143

0,8631

1,8074

5,0000

9,0000

0,3571

0,6429

0,9403

1,4854

6,0000

8,0000

0,4286

0,5714

0,9852

1,2224

7,0000

7,0000

0,5000

0,5000

1,0000

1,0000

8,0000

6,0000

0,5714

0,4286

0,9852

0,8074

9,0000

5,0000

0,6429

0,3571

0,9403

0,6374

10,0000

4,0000

0,7143

0,2857

0,8631

0,4854

11,0000

3,0000

0,7857

0,2143

0,7496

0,3479

12,0000

2,0000

0,8571

0,1429

0,5917

0,2224

13,0000

1,0000

0,9286

0,0714

0,3712

0,1069

14,0000

0,0000

1,0000

0,0000

0,0000

0,0000

h = log

2

(N/s) = log

2

(1/p) = -log

2

(p) – wysokość binarnego drzewa poszukiwań obiektu,

= ilość bitów informacji potrzebna do klasyfikacji obiektu do klasy o prawdopodob.

p

,

= ilość informacji, jaką posiadamy wiedząc, że obiekt należy do klasy o prawdop.

p

,

I(s

1

, s

2

) = średnia ważona klasyfikacji obiektu do jednej z dwóch klas (entropia układu!)

(c) T. Pankowski, Drzewa

decyzyjne

23

Entropia

Entropia

–

–

miara ilo

miara ilo

ś

ś

ci informacji

ci informacji

1. Powyższy wzór wyraża entropię układu składającego się z

m

rozłącznych klas (podzbiorów):

C

1

,

C

2

, ...,

C

m

o liczebnościach,

odpowiednio s

1

,…, s

m

; s

1

+…+ s

m

= s.

2. Prawdopodobieństwo zaklasyfikowania obiektu do klasy

C

i

wynosi

p

i

,

p

i

= s

i

/s, 0 <

p

i

< 1,

i

= 1,2, ...,

m

.

3. Wzór wyraża oczekiwaną ilość informacji potrzebną do

zaklasyfikowania podanego obiektu do jednej z klas.

4. Entropia osiąga wartość maksymalną przy jednakowym rozkładzie, tj.

gdy klasy są jednakowo prawdopodobne, tej samej wielkości.

5. Im większe zróżnicowanie układy tym mniejsza entropia.

Entropia:

i

m

i

i

m

p

log

p

)

p

,...,

p

(

E

2

1

1

∑

=

−

=

(c) T. Pankowski, Drzewa

decyzyjne

24

Ocena informacyjna wa

Ocena informacyjna wa

ż

ż

no

no

ś

ś

ci atrybut

ci atrybut

ó

ó

w

w

1. W zadaniach eksploracji danych, a przede wszystkim w

problemach klasyfikacji istotna jest analiza istotności

atrybutów (

attribute relevance analysis

).

2. W wyniku tej analiza uzyskujemy uporządkowanie zbioru

atrybutów od najbardziej do najmniej istotnych z punktu

widzenia klasyfikacji obiektów do zadanych klas.

3. Atrybut jest tym bardziej istotny (z punktu widzenia

klasyfikacji obiektów) im mniejsza jest jego entropia.

4. Wyniki analizy istotności atrybutów mają zastosowanie

do charakterystyki opisowej i dyskryminacyjnej klas

obiektów, a także podczas budowy drzew decyzyjnych.

25

Analiza istotno

Analiza istotno

ś

ś

ci atrybut

ci atrybut

ó

ó

w w zadaniach

w w zadaniach

klasyfikacji

klasyfikacji

• S – zbiór obiektów podzielony na m klas C

1

,...,C

m

, gdzie s

i

oznacza liczbę

obiektów w klasie C

i

, i = 1,...,m, a s liczbę wszystkich obiektów.

•

Niech A będzie atrybutem opisującym obiekty ze zbioru S i niech

{a

1

, ..., a

n

) będzie zbiorem wartości atrybutu A.

• Niech

s

i,k

– liczba obiektów klasy i, dla których atrybut A ma wartość a

k

.

Wówczas wartość a

k

atrybutu A wyznacza układ m klas określony za

pomocą wektora liczebności tych klas:

(s

1,k

,… ,s

m,k

)

• Entropię tego układu nazywamy

entropią wartości a

k

atrybutu A

,

p

log

p

)

p

,...,

p

(

E

)

a

,

A

(

r

EntrWartAt

k

,

i

m

i

k

,

i

k

,

m

k

,

k

2

1

1

∑

=

−

=

=

gdzie p

i,k

oznacza prawdopodobieństwo przynależności obiektu do klasy

C

i

, gdy wartość atrybutu A tego obiektu jest równa a

k

,

k

,

m

k

,

k

,

i

k

,

i

s

...

s

s

p

+

+

=

1

26

Analiza istotno

Analiza istotno

ś

ś

ci atrybut

ci atrybut

ó

ó

w w zadaniach

w w zadaniach

klasyfikacji

klasyfikacji

•

Entropią atrybutu A

nazywamy średnią ważoną entropii wszystkich

wartości tego atrybutu

),

a

,

A

(

r

EntrWartAt

)

A

(

w

)

A

(

EntrAtr

k

n

k

a

k

∑

=

=

1

gdzie waga entropii wartości a

k

atrybutu A, w

ak

(A), jest równa

prawdopodobieństwu tego, że wartość atrybutu A dla rozważanego
zbioru obiektów jest równa a

k

.

,

s

s

...

s

)

A

(

w

k

,

m

k

,

a

k

+

+

=

1

27

Analiza istotno

Analiza istotno

ś

ś

ci atrybut

ci atrybut

ó

ó

w w zadaniach

w w zadaniach

klasyfikacji

klasyfikacji

1.

Za najbardziej istotny uważany jest ten atrybut, którego wartość

entropii

EntrAtr

(

A

) względem podziału {

C

1

,...,

C

m

} jest

najmniejsza

.

2.

Najistotniejszy atrybut maksymalizuje funkcję

zysk informacji

(

information gain

):

Gain

(

A

) = E(

p

1

, ...,

p

m

) –

EntrAtr

(

A

).

3.

W analizie istotności atrybutów obliczamy zysk informacji każdego

atrybutu opisującego obiekty w zbiorze treningowym.

4.

Atrybut o największej wartości zysku informacji jest atrybutem

najbardziej dyskryminującym (rozróżniającym).

5. Gain

(

A

) opisuje różnicę między ilością informacji potrzebnej do

klasyfikacji obiektu ze zbioru S, a klasyfikacją tego obiektu, gdy

wartość atrybutu

A

ma ustaloną wartość.

6. Gain

(

A

) określa więc

zysk informacji

przy wyborze atrybutu

A

. Im jest

on większy, tym mniejsze będzie „zaszumienie” w zbiorach powstałych

w wyniku podziału S względem wartości atrybutu

A

.

28

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

wyb

wyb

ó

ó

r atrybutu

r atrybutu

pierwszego poziomu

pierwszego poziomu

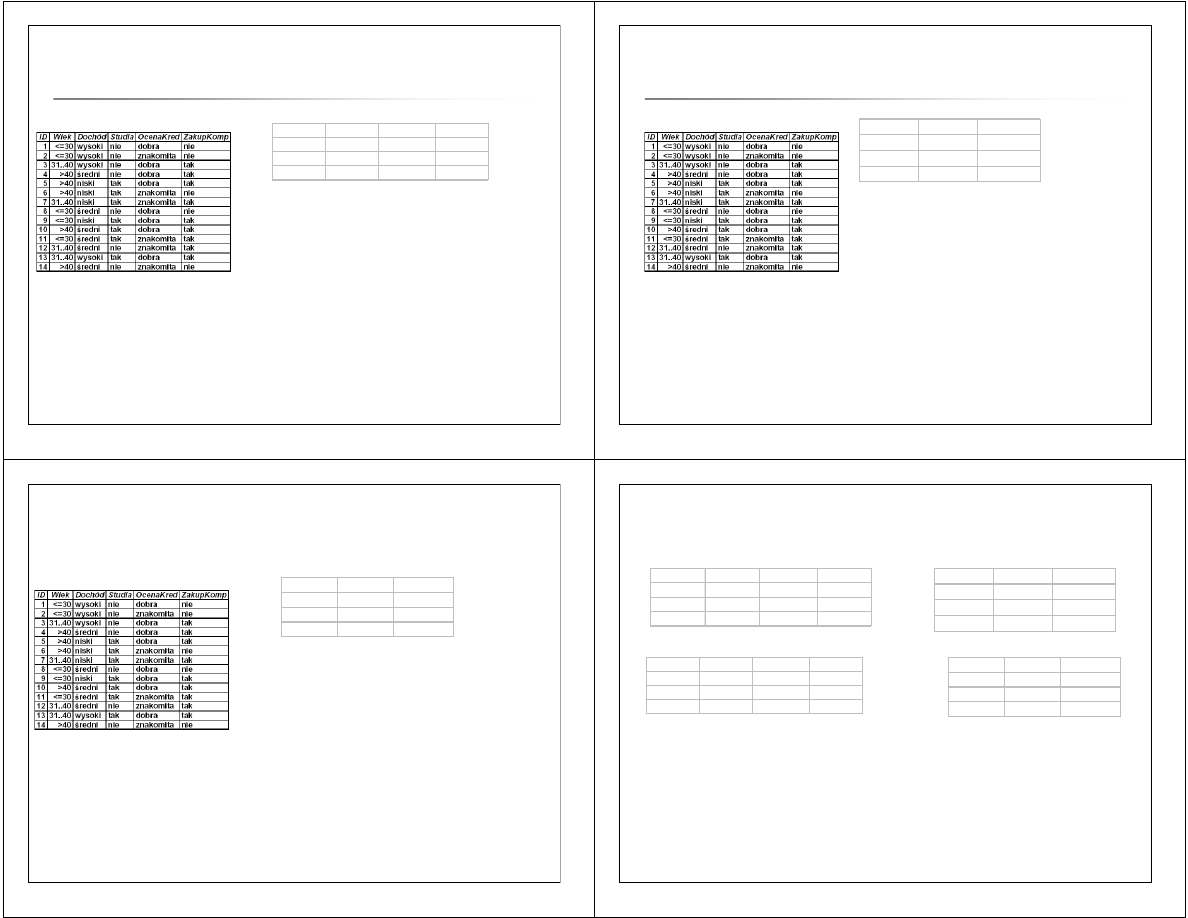
Zbiór treningowy:

Ocena atrybutu Wiek:

C

1

= nie,

C

2

= tak

E(5/14, 9/14) = – (5/14*log

2

(5/14) +

9/14*log

2

(9/14)) = 0.9403

EntrWartAtr(Wiek,<=30) =
= E(3/5, 2/5) = – (3/5*log

2

(3/5) + 2/5*log

2

(2/5)) = 0.9710

EntrWartAtr(Wiek,31..40) = E(0/4, 4/4) = = 0.0
EntrWartAtr(Wiek,>40) = E(2/5, 3/5) = 0.9710

w

<=30

(Wiek) = 5/14,

w

31..40

(Wiek) = 4/14,

w

>40

(Wiek) = 5/14,

EntrAtr(Wiek) =

w

<=30

(Wiek) * EntrWartAtr (Wiek,<=30) +

+ w

31..40

(Wiek) * EntrWartAtr(Wiek,31..40) +

+ w

>40

(Wiek) * EntrWartAtr(Wiek,>40) = 0,6935

Gain(Wiek) = E(5/14,9/14) – EntrAtr(Wiek) = 0.2467

k =

<=30

31..40

>40

s1k =

3,0000

0,0000

2,0000

s2k =

2,0000

4,0000

3,0000

5,0000

4,0000

5,0000

29

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

wyb

wyb

ó

ó

r atrybutu

r atrybutu

pierwszego poziomu

pierwszego poziomu

Zbiór treningowy:

Ocena atrybutu Dochód:

C

1

= nie,

C

2

= tak

E(5/14, 9/14) = – (5/14*log

2

(5/14) +

9/14*log

2

(9/14)) = 0.9403

EntWartAtr(Dochód, niski) = E(1/4,3/4) = 0.8113
EntWartAtr(Dochód, średni) = E(2/6,4/6) = 0.9183
EntWartAtr(Dochód, wysoki) = E(2/4,2/4) = 1.0000

w

niski

= 4/14,

w

ś

redni

= 6/14,

w

wysoki

= 4/14,

EntrAtr(Dochód) =
=

w

niski

* EntWartAtr(Dochód, niski) +

w

ś

redni

* EntWartAtr(Dochód, średni) +

w

wysoki

* EntWartAtr(Dochód, wysoki) = 0.9111

Gain(Dochód) = E(5/14,9/14) – EntrAtr(Dochód) = 0.0292

k =

niski

ś

redni

wysoki

s1k =

1,0000

2,0000

2,0000

s2k =

3,0000

4,0000

2,0000

4,0000

6,0000

4,0000

(c) T. Pankowski, Drzewa

decyzyjne

30

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

wyb

wyb

ó

ó

r atrybutu

r atrybutu

pierwszego poziomu

pierwszego poziomu

Zbiór treningowy:

Ocena atrybutu Studia:

C

1

= nie,

C

2

= tak

E(5/14, 9/14) = – (5/14*log

2

(5/14) +

9/14*log

2

(9/14)) = 0.9403

EntWartAtr(Studia, tak) = E(1/7,6/7) = 0.5917
EntWartAtr(Studia, nie) = E(4/7,3/7) = 0.9852

w

tak

= 7/14,

w

nie

= 7/14,

EntrAtr(Studia) =
=

w

tak

* EntWartAtr(Studia, tak) +

w

nie

* EntWartAtr(Studia, nie) = 0.7885

Gain(Studia) = E(5/14,9/14) – EntrAtr(Studia) = 0.1518

k =

tak

nie

s1k =

1,0000

4,0000

s2k =

6,0000

3,0000

7,0000

7,0000

Budowa drzewa decyzyjnego

Budowa drzewa decyzyjnego

–

–

wyb

wyb

ó

ó

r atrybutu

r atrybutu

pierwszego poziomu

pierwszego poziomu

Zbiór treningowy:

Ocena atrybutu OcenaKred:

C

1

= nie,

C

2

= tak

E(5/14, 9/14) =
– (5/14*log

2

(5/14) + 9/14*log

2

(9/14))

= 0.9403

EntrWartAtr(OcenaKred,dobra) = 0.8113
EntrWartAtr(OcenaKred,znakomita) = 1.0000

w

dobra

= 8/14,

w

znakomita

= 6/14,

EntrAtr(OcenaKred) =
=

w

dobra

* E(2/8, 6/8) +

w

znakomita

* E(3/6, 3/6) = 0.8922

Gain(Studia) = E(5/14,9/14) – EntrAtr(OcenaKred) = 0.0481

k =

dobra

znakomita

s1k =

2,0000

3,0000

s2k =

6,0000

3,0000

8,0000

6,0000

Analiza istotno

Analiza istotno

ś

ś

ci atrybut

ci atrybut

ó

ó

w

w

–

–

podsumowanie

podsumowanie

OcenaKred: Gain(OcenaKred) = 0.0481

k =

dobra

znakomita

s1k =

2,0000

3,0000

s2k =

6,0000

3,0000

8,0000

6,0000

Studia: Gain(Studia) = 0.1518

k =

tak

nie

s1k =

1,0000

4,0000

s2k =

6,0000

3,0000

7,0000

7,0000

Dochód: Gain(Dochód) = 0.0292

k =

niski

ś

redni

wysoki

s1k =

1,0000

2,0000

2,0000

s2k =

3,0000

4,0000

2,0000

4,0000

6,0000

4,0000

Wiek: Gain(Wiek) = 0.2467

k =

<=30

31..40

>40

s1k =

3,0000

0,0000

2,0000

s2k =

2,0000

4,0000

3,0000

5,0000

4,0000

5,0000

¾

Analiza istotności atrybutów wykazała, że z punktu widzenia klasyfikacji
związanej z rozważanym zbiorem treningowym, najbardziej istotny jest
atrybut Wiek. Atrybut ten powinien więc być jako pierwszy brany pod uwagę
przy budowie drzewa decyzyjnego.

¾

Wiedza o wartości atrybutu Wiek najbardziej pomaga w procesie klasyfikacji.
Ma on właściwość największego różnicowania obiektów z punktu widzenia
rozważanego zadania klasyfikacji.

Algorytm ID3: Decision_tree

(

S

,

U

).

Wej

ś

cie:

S – zbiór treningowy obiektów;

U

– zbiór atrybutów o dyskretnych wartościach opisujących obiekty z

S

.

Wyj

ś

cie:

Drzewo decyzyjne.

Kroki:

1. Utwórz wierzchołek N;
2.

if

wszystkie obiekty z

S

należą tej samej klasy

C then

return

liść N z etykietą

C

;

stop

;

3.

if U

jest pusty

then

return

liść etykietowany najczęstszą klasą w

S

;

stop

;

4.

A

– atrybut z

U

o najmniejszej entropii (największym zysku informacji);

wierzchołkowi

N

przypisz etykietę

A

;

5.

for each

wartości

a

atrybutu

A

begin

a) utwórz krawędź wychodzącą z

N

dla warunku

A

=

a;

b) niech

S’

będzie zbiorem obiektów w zbiorze

S

, dla których

A

=

a;

c) końcem krawędzi jest wierzchołek zwrócony przez

Decision_tree

(

S’

,

U

– {

A

})

end;