{Energo_05_06_E_VI_W6.doc}

Kierunek E (Elektrotechnika)
r.a. 2005/2006, sem. VI
hasło: EVI

W

W

W

Wyk

yk

yk

yk

ład

ład

ład

ład

6

6

6

6

30 marca 2006

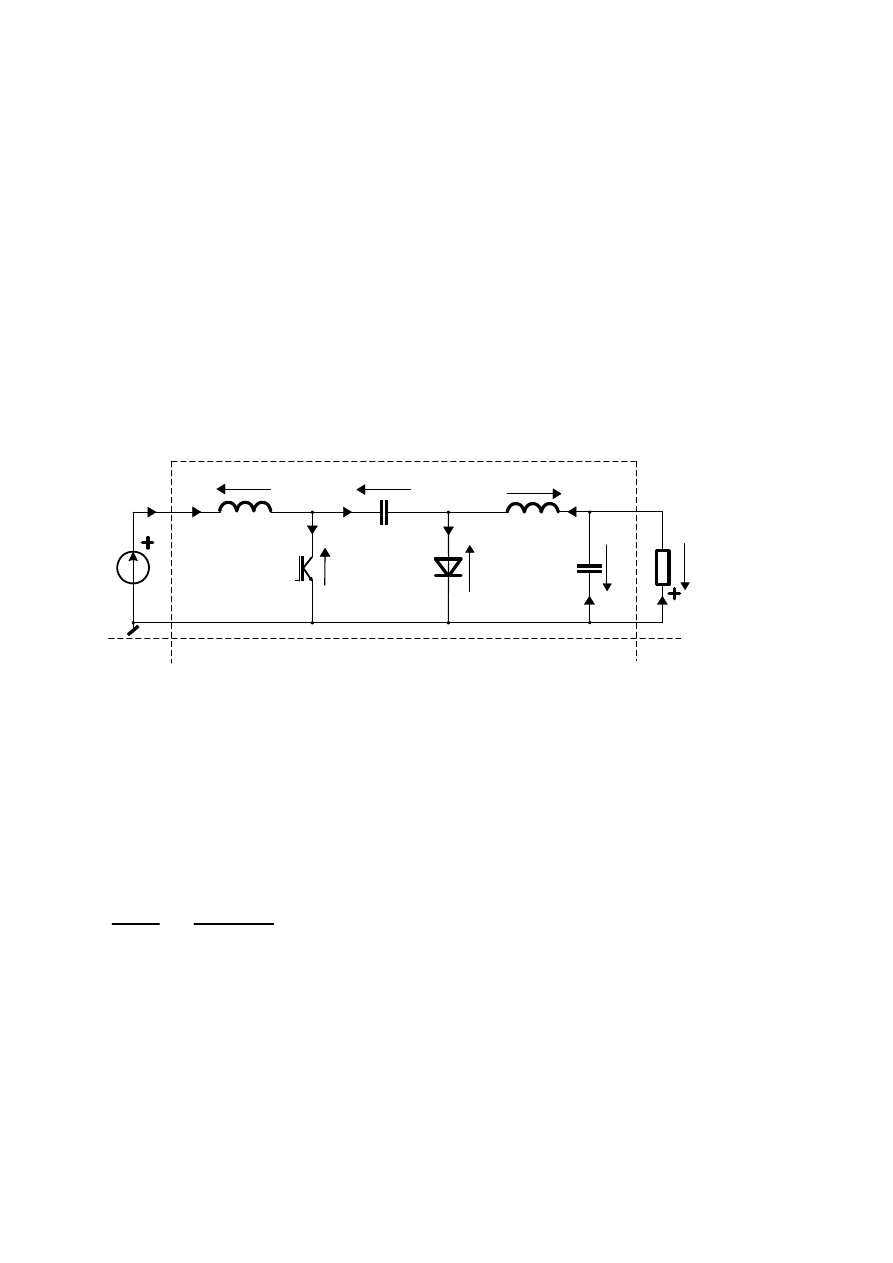
Przekształtnik DC-DC Cúk

Schemat przekształtnika Cúk zamieszczono na Rys. W6.1. Jest to
przekształtnik DC-DC obni

ż

aj

ą

co-podwy

ż

szaj

ą

cy napi

ę

cie. Zmienia on

biegunowo

ść

napi

ę

cia wyj

ś

ciowego u

O

wzgl

ę

dem napi

ę

cia wej

ś

ciowego

E.

E

i

E

Q

T,D

i

Di

Di

u

Di

u

C1

R

u

C

i

L2

L1

u

L1

u

CE

PRZEKSZTAŁTNIK

SIE

Ć

DC

ODBIORNIK

i

L1

i

C1

C1

i

CE

u

O

i

O

u

L2

L2

i

C

C

Rys. W6.1 Przekształtnik Cúk


Charakterystyka sterowania przekształtnika jest okre

ś

lona zale

ż

no

ś

ci

ą

(W6.1). Tak wi

ę

c charakterystyka sterowania tego przekształtnika jest

taka

sama

jak

charakterystyka

przekształtnika

obni

ż

aj

ą

co-

podwy

ż

szaj

ą

cego – Rys. W6.2.

D

D

E

U

−

=

1

o

(W6.1)

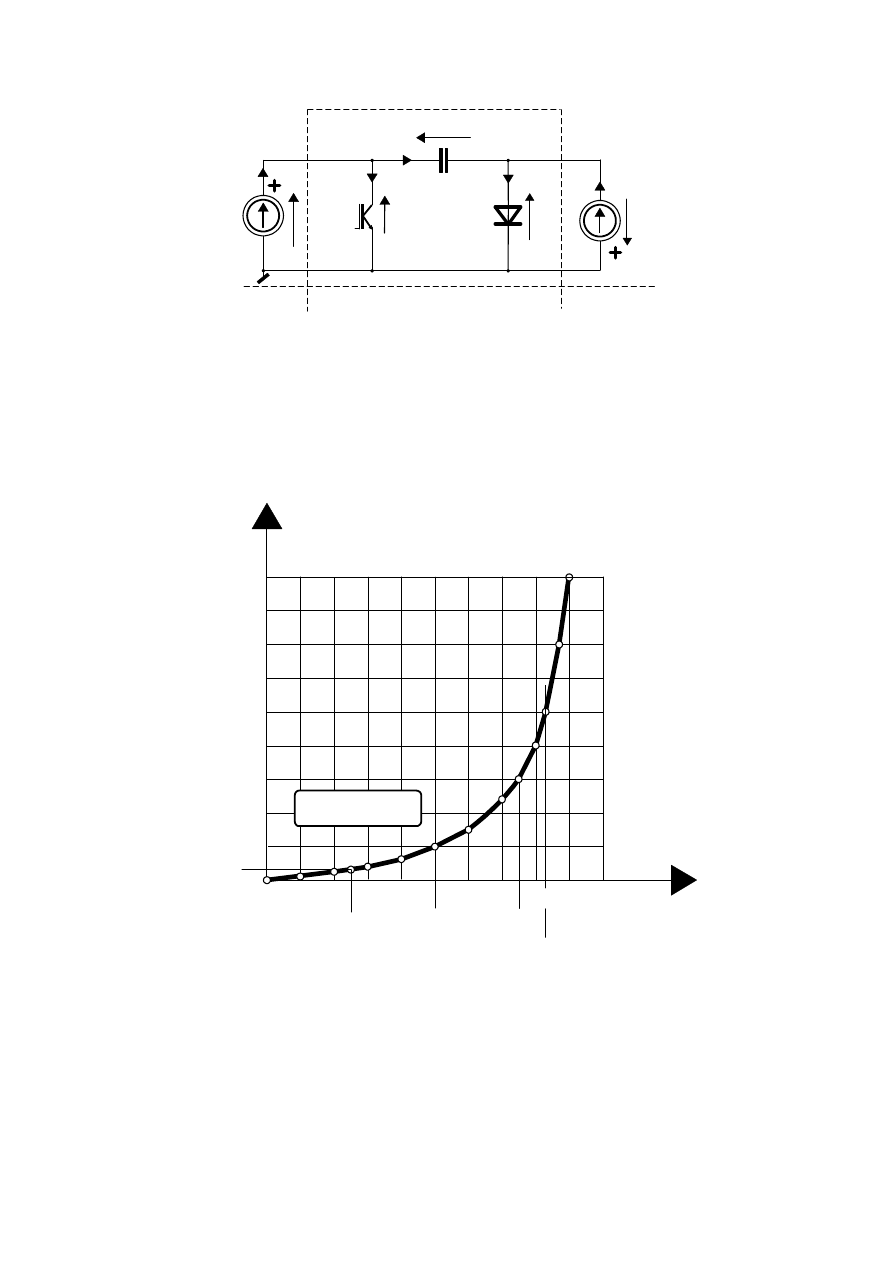
Przy

J

E

Q

T,D

i

Di

Di

u

Di

u

C1

u

CE

PRZEKSZTAŁTNIK

SIE

Ć

DC

ODBIORNIK

i

C1

C1

i

CE

u

JE

J

O

u

JO

i

JE

i

JO

Rys. W6.2 Przekształtnik Cúk – schemat uproszczony

0.4

0.2

D

0

U

O

/E

1

8

2

3

4

7

i

L

i

L

: ci

ą

gły

9

0.6

0.8

1.0

0.5

0.33

0.25

0.75

6

0.83

5

Rys. W6.3 Charakterystyka sterowania przekształtnika Cúk

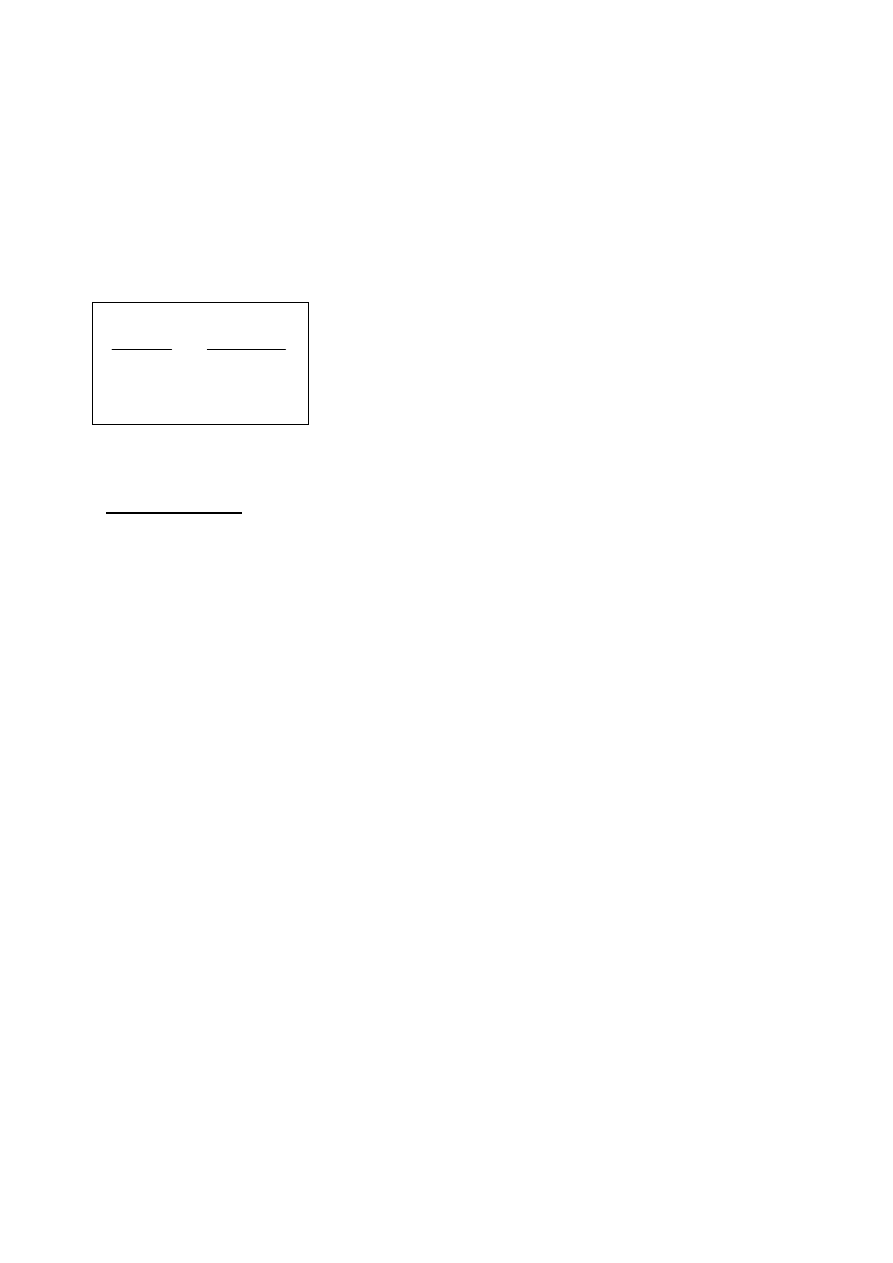
Do uproszczonej analizy zakłada si

ę

:

i

L1

=I

L1

⇒

⇒

⇒

⇒

U

L1

=0

i

L2

=I

L2

⇒

⇒

⇒

⇒

U

L2

=0

u

C1

=U

C1

U

C1

=E-U

O

Napi

ę

cie na kondensatorze C1 mo

ż

na obliczy

ć

z całki napi

ę

cia na

ka

ż

dym dławiku, co daje:

D

E

U

C

−

=

1

1

1

(W6.2)

Przykład W6.1

W celu zilustrowania procesu przekształcania maj

ą

cego miejsce w

przekształtniku Cúk przeprowadzono symulacj

ę

TCAC przy parametrach

zapisanych w listingu:

;topologia utworzona przez TCadSchem 1.0

[OBWÓD GŁÓWNY]
!/8/5/
/E{E1}/1/0/1/0.01/10/
/L{L2}/2/1/2/1E-3/0/
/C{C4}/3/2/3/10E-6/20/
/D{D5}/4/3/0/100E3/1E-3/BLOKUJE/Irm=0/Trr=0/0/0/Uf0=0.6/
/L{L6}/5/4/3/1E-3/0/
/R{R8}/6/0/4/5/
/C{C7}/7/0/4/1000E-6/10/
/TM{T3}/8/2/0/100E3/1E-3/NIE/0/5E-6/10E-
6/BLOKUJE/Irm=0/Trr=0/0/0/>>
Uf0=1/
$
[UKŁAD POMOCNICZY]

[PARAMETRY SYMULACJI]
/CP/0/
/CK/50E-3/
/KROK/1E-7/

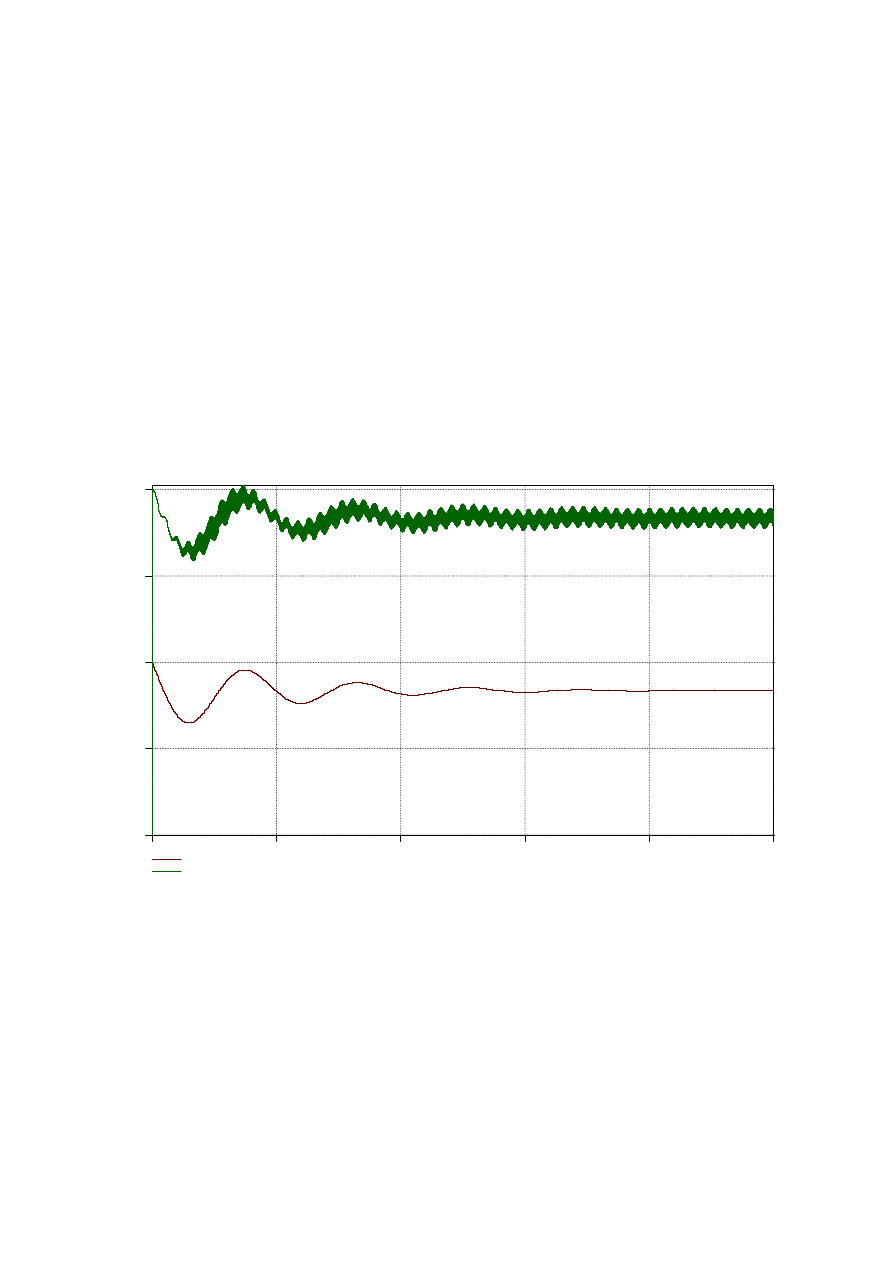
/ROZDZIELCZOSC/1E-7/

[MONITORING]

[REJESTRACJE]
/REJ.U/0/4/-- uC2/
/REJ.U/2/3/-- uC1/
!

Uwaga: cz

ę

stotliwo

ść

f=50 kHz, wypełnienie D=0.5

Teoretyczne warto

ś

ci dla powy

ż

szego przykładu wynosz

ą

U

O

=E=10V

I

O

=E/R=10/5=2A=I

E

0

10

20

30

40

50

0

5

10

15

20

uC2 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK
uC1 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK

czas w [ms]

Rys. W6.4 Przekształtnik Cúk – Przykład W6.1; t=0..50 ms

40

42

44

46

48

50

0

5

10

15

20

uC2 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK
uC1 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK

czas w [ms]

Rys. W6.5 Przekształtnik Cúk – Przykład W6.1; t=40..50 ms

49.5

49.6

49.7

49.8

49.9

50

5

10

15

20

uC2 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK
uC1 z pliku C:\ TCAD\ TCAD62~1\ EXAMPLES\ CUK01.WNK

czas w [ms]

Rys. W6.6 Przekształtnik Cúk – Przykład W6.1; t=49,5..50 ms

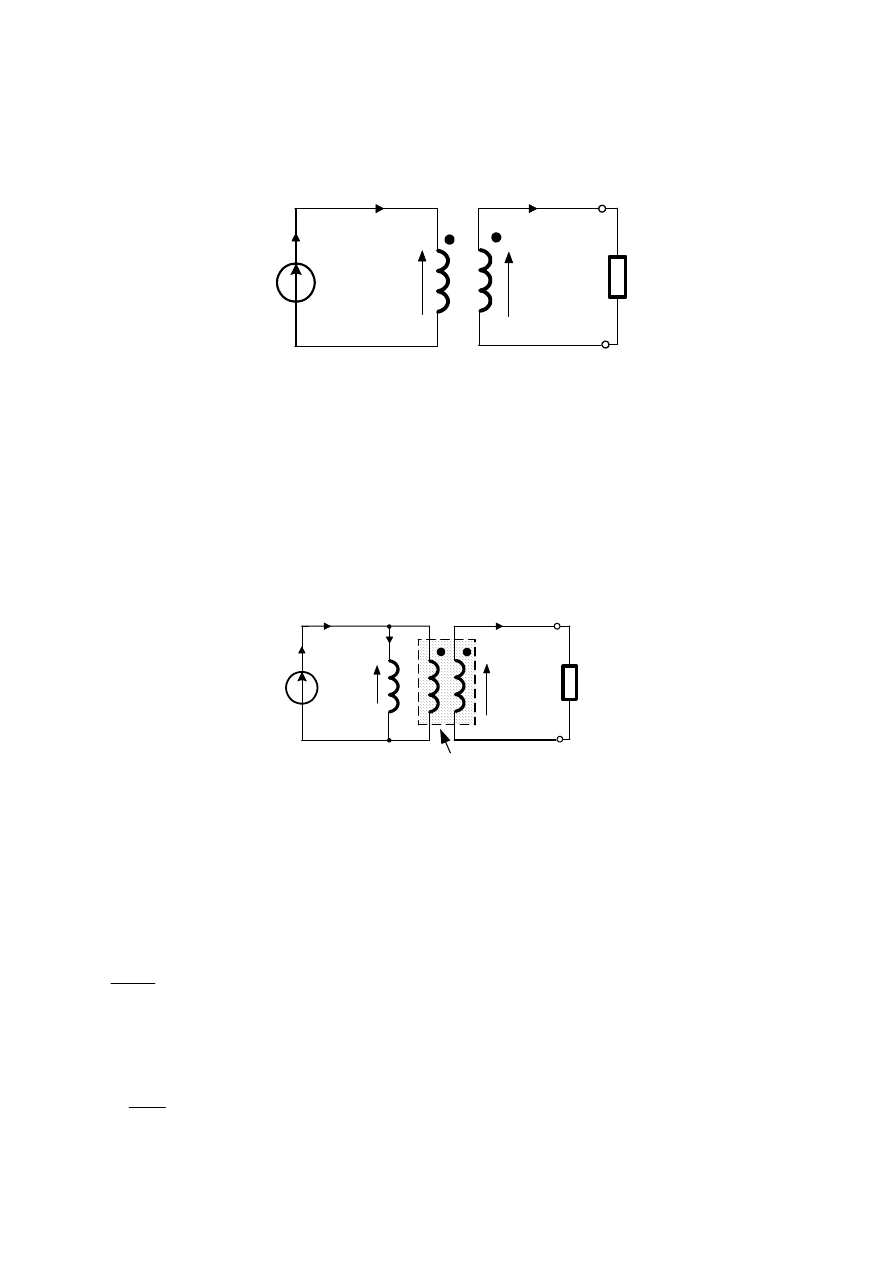
Transformator w przekształtnikach energoelektronicznych

i

e

u

1

u

2

i

2

z

2

i

1

z

1

e

Rys. W6.7 Schemat transformatora

Pomijaj

ą

c indukcyjno

ś

ci rozproszenia, rezystancje szeregowe oraz

rezystancj

ę

poprzeczn

ą

transformator z Rys. 6.7 mo

ż

na przedstawi

ć

za

pomoc

ą

indukcyjno

ś

ci poprzecznej L

m

oraz transformatora idealnego, tak

jak to ma miejsce na schemacie z Rys. W6.8. Indukcyjno

ść

poprzeczna

L

m

jest najistotniejszym elementem takiego modelu transformatora.

Strumie

ń

skojarzony

Ψ

opisany jest zale

ż

no

ś

ci

ą

(W6.3).

i

e

u

1

u

2

i

2

z

2

i

1

z

1

e

L

m

transformator

idealny

i

m

R

odbiornik

Rys. W6.8 Uproszczony schemat transformatora (z transformatorem

idealnym i indukcyjno

ś

ci

ą

magnesowania

L

m

)

1

u

dt

d

=

ψ

(W6.3)

Na podstawie (W6.3) uzyskuje si

ę

zale

ż

no

ść

na strumie

ń

Φ

- (W6.4)

1

u

dt

d

z

=

φ

(W6.4)

Z kolei (W6.4) pozwala okre

ś

li

ć

równanie na indukcj

ę

B oraz pr

ą

d im –

odpowiednio: (W6.5) oraz (W6.6)

1

u

dt

dB

zS

=

(W6.5)

zakładaj

ą

c stał

ą

warto

ść

przenikalno

ś

ci magnetycznej

µ

z zale

ż

no

ś

ci

(W6.5) uzyskuje si

ę

wzór (W6.6)

1

2

u

dt

di

S

z

m

=

µ

(W6.6)

Dla zilustrowania procesu zachodz

ą

cego w modelu z Rys. 6.7, opisanym

zale

ż

no

ś

ciami (W6.3) – (W6.6) zakłada si

ę

,

ż

e napi

ę

cie

e jest okre

ś

lone

zale

ż

no

ś

ci

ą

(W6.6)

))

2

sgn(sin(

t

T

E

e

π

=

(W6.7)

Przy takim napi

ę

ciu zasilaj

ą

cym

e oraz R=

∞

∞

∞

∞

przebiegi indukcji B oraz

pr

ą

du

i

m

s

ą

takie jak na Rys. W6.9 (zało

ż

ono,

ż

e

z

1

=

z

2

). Na Rys. W6.9

zaznaczono przebieg napi

ę

cia zasilaj

ą

cego (W6.7). Przy transformatorze

nieobci

ąż

onym pr

ą

d pobierany ze

ź

ródła e ma przebieg taki jak na Rys.

W6.9a; jest to

i

1

=

i

m

. Przy obci

ąż

eniu do pr

ą

du im dodaje si

ę

pr

ą

d i2 –

pokazano to na Rys. W6.9b,c.

W wielu przekształtnikach transformator pracuje ze składow

ą

stał

ą

strumienia i w takich przypadkach przebiegi strumienia s

ą

odpowiednio

zmodyfikowane. Przykładem mo

ż

e by

ć

przekształtnik DC-DC

dwutaktowy (flyback) – Rys. W6.10.

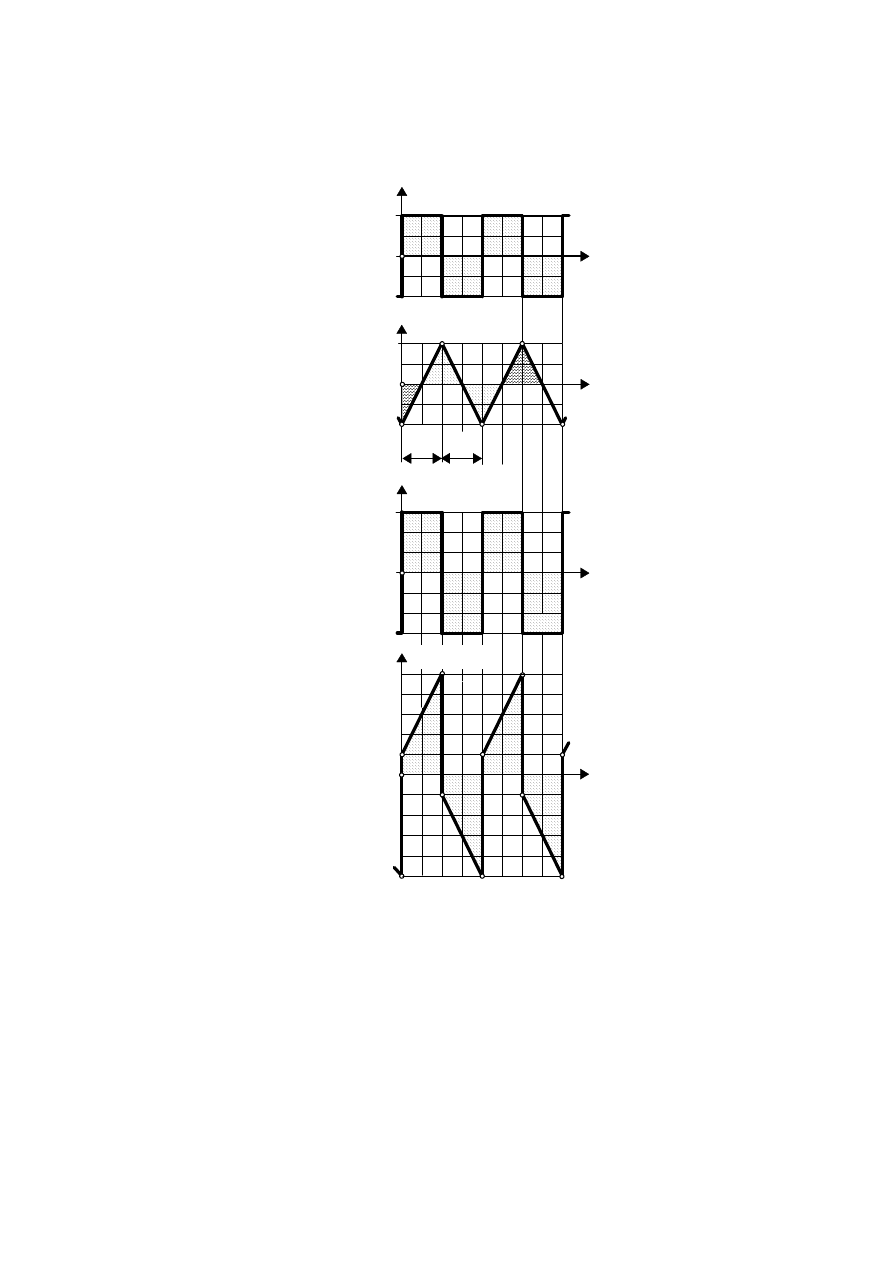
t

B, i

L

0

B

m

T/2 T/2

t

0

e

E

-E

t

0

i

2

I

2

-I

2

i

1

=i

2

+i

m

=I

Lm

= -I

m

-B

m

0

t

a)

b)

c)

Rys. W6.9 Przebiegi napi

ę

cia e, pr

ą

du i

m

, pr

ą

du i

2

, pr

ą

du i

1

przy biegu

jałowym (a), oraz przy obci

ąż

eniu (b. c)

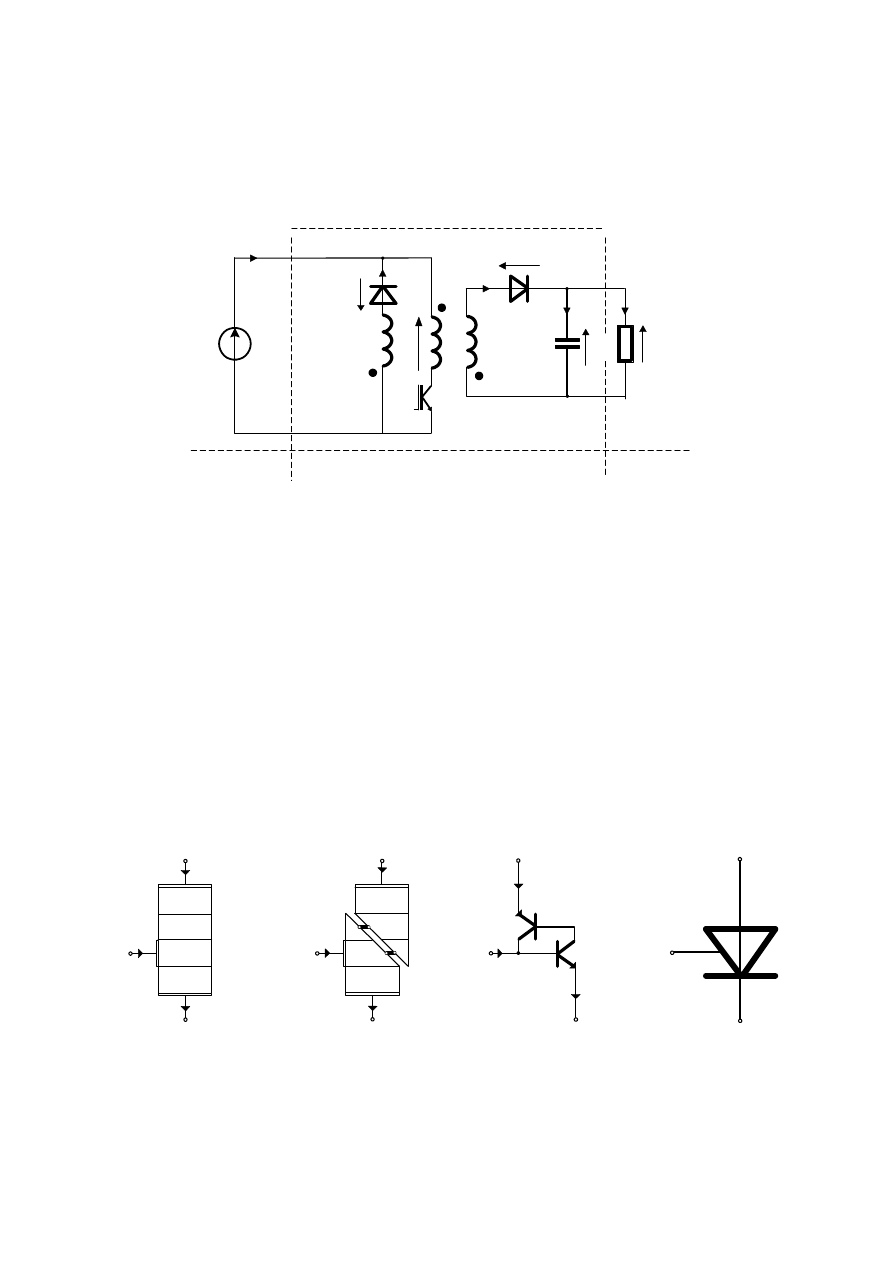
Przekształtnik DC-DC dwutaktowy z transformatorem
(flyback)

E

i

E

Q

T,D

i

Di

Di

u

Di

u

C

R

u

o

i

O

PRZEKSZTAŁTNIK

ZASILANIE DC

(

ź

ródło napi

ę

cia)

ODBIORNIK

i

Di0

i

C

C

u

Di0

z

1

z

0

z

2

u

1

Rys. W6.10 Przekształ™nik DC-DC dwutaktowy z transformatorem

(flyback)

Tyrystor

Tyrystor jest ł

ą

cznikiem energoelektronicznym, który mo

ż

na zał

ą

cza

ć

za

pomoc

ą

pr

ą

du bramki i

G

ale nie jest mo

ż

liwe jego wył

ą

czenie za pomoc

ą

pr

ą

du bramki (je

ż

eli i

A

>I

H

). I

H

jest pr

ą

dem podtrzymania. Mo

ż

liwo

ść

zał

ą

czania tyrystora za pomoc

ą

pr

ą

du bramki jest zaznaczona na

charakterystyce głównej i

A

=f(u

AK

) za pomoc

ą

strzałki i

G

.

A

K

G

i

A

i

K

i

G

p

1

n

1

n

2

p

2

A

K

G

i

A

i

K

i

G

p

2

n

2

p

1

n

1

n

1

n

1

p

2

A

G

K

A

K

G

i

A

i

K

i

G

αααα

1111

αααα

2222

a)

c)

b)

d)

Rys. W6.11 Tyrystor; a), b) – symbol pnpn; c) – model

dwutranzystorowy; d) – symbol graficzny

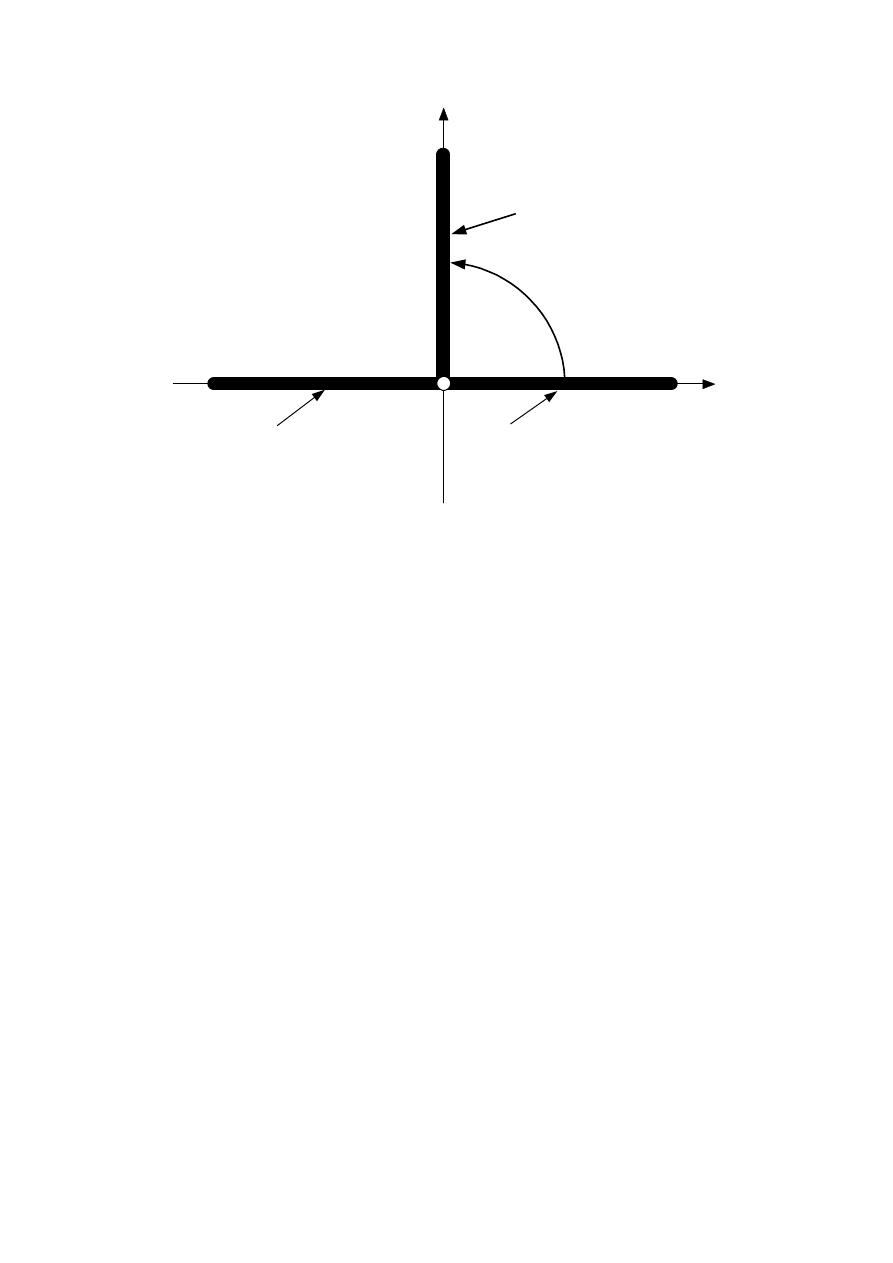
i

A

u

AK

(F) - stan

przewodzenia

(D) - stan

blokowania

(R) - stan

zaworowy

i

G

Rys. 6.11 Tyrystor – model idalny; charakterystyka główna a), b) –

symbol pnpn; c) – model dwutranzystorowy; d) – symbol graficzny

Warunek zał

ą

czania tyrystora.

Zał

ą

czanie tyrystora mo

ż

e mie

ć

miejsce je

ż

eli:

- napi

ę

cie u

AK

jest dodatnie,

- przez obwód bramka G – katoda K przełynie impuls pr

ą

du bramkowego

(steruj

ą

cego) przez czas tak długi,

ż

e pr

ą

d i

A

osi

ą

gnie warto

ść

wi

ę

ksz

ą

od pr

ą

du podtrzymania I

H

.

Warunek wył

ą

czania tyrystora.

Wył

ą

czenie tyrystora mo

ż

e nast

ą

pi

ć

, je

ż

eli pr

ą

d i

A

zostanie obni

ż

ony

poni

ż

ej pr

ą

du podtrzymania I

H

i porzez czas dłu

ż

szy od czasu

wył

ą

czania t

off

b

ę

dzie on spolaryzowany napi

ę

ciem ujemnym (u

A

<0).

Zał

ą

czanie i wył

ą

czanie tyrystora mo

ż

na prze

ś

ledzi

ć

analizuj

ą

c prac

ę

tyrystorowego ł

ą

cznika pr

ą

du stałego z Rys. W6.12.

Nale

ż

y zauwa

ż

y

ć

,

ż

e tyrystor po zał

ą

czeniu podtrzymuje si

ę

w stanie

przewodzenia pomimo,

ż

e pr

ą

d bramki i

G

zanikn

ą

ł.

Jako

ś

ciowo zał

ą

czanie tyrystora mo

ż

na wyja

ś

ni

ć

nast

ę

puj

ą

co za

pomoc

ą

modelu dwutranzystorowego (Rys. W6.11c):

i

G

↑

⇒

i

B(pnp)

↑

⇒

i

C(npn)

↑

⇒

i

B(pnp)

↑

⇒

i

C(pnp)

↑

⇒

i

B(npn)

↑

⇒

i

C(npn)

↑

itd.

W pewnej mierze ilo

ś

ciowo zał

ą

czanie tyrystora mo

ż

ana wyja

ś

ni

ć

posługuj

ą

c

si

ę

modelem

dwutranzystorowym

tyrystora.

Aby

przeprowadzi

ć

wyja

ś

nienie,

nale

ż

y

zauwa

ż

y

ć

,

ż

e

ka

ż

dy

ze

współczynników wzmocnienia

α

1N

,

α

2N

ro

ś

nie wraz ze wzrostem pr

ą

du

i

A

przy czym

α

1N

,>

α

2N

.

Z równa

ń

pr

ą

dowych opisuj

ą

cych model

dwutranzystorowy tyrystora (W6.11c) wynika zale

ż

no

ść

(W6.8).

)

(

1

2

1

2

α

α

α

+

−

=

G

A

i

i

(W6.8)

Analizuj

ą

c wzór (W6.8) mo

ż

na zauwa

ż

y

ć

,

ż

e zał

ą

czenie nast

ę

puje gdy

spełniony jest warunek (W6.9).

∞

→

⇒

→

+

A

i

1

)

(

2

1

α

α

(W6.9)

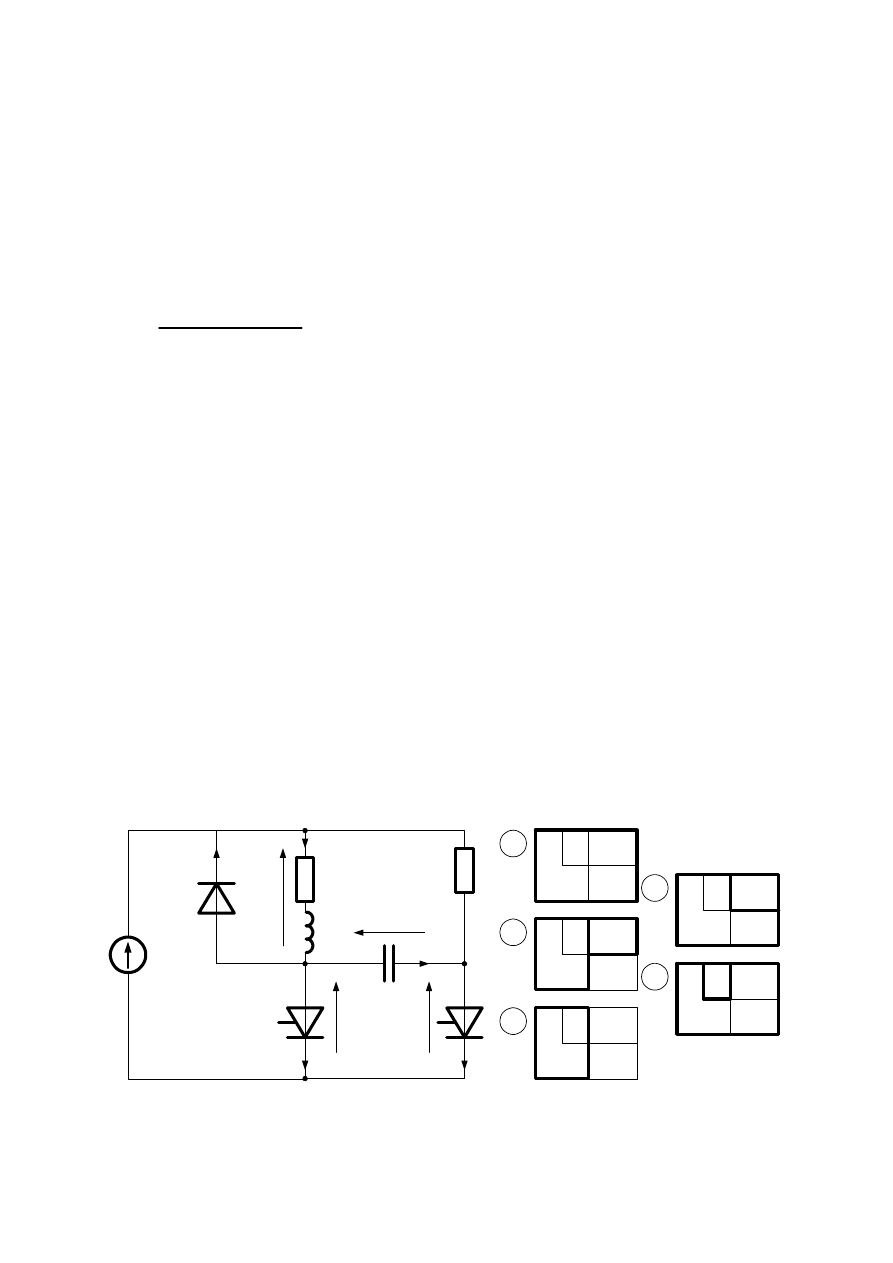
Tyrystorowy ł

ą

cznik pr

ą

du stałego

Tyrystorowy ł

ą

cznik pr

ą

du stałego, o schemacie z Rys. W6.12 słu

ż

y do

zaprezentowania zał

ą

czania i wył

ą

czania tyrystora. Jest on opisany

szczegółowo

w

podr

ę

czniku

„Energoelektronika

–

Ć

wiczenia

laboratoryjne”. Grzesik B. (red), Wydawnictwo Politechniki

Ś

l

ą

skiej,

Gliwice 2001 –

Ć

wiczenie 11, str. 130

E

R

o

T

2

C

k

T

1

i

T1

u

T2

u

T1

i

T2

i

Ck

u

Ck

L

o

R

p

u

o

i

o

i

Do

D

o

1

2

3

4

5

Rys. W6.12 Tyrystorowy ł

ą

cznik pr

ą

du stałego