Binarne drzewo poszukiwań

Przegląd zagadnień

Jedną z podstawowych wad list jest mało efektywny proces wyszukiwania
elementu. Posortowanie listy jednokierunkowej nie wpływa na szybkość
przeszukiwania. W zależności od położenia elementu w liście, może być
potrzebne od jednego do n porównań, gdzie n jest liczbą węzłów listy, w celu
sprawdzenia czy lista zawiera dany element. Proces wyszukania lub
sprawdzenia, czy w dany zbiór zawiera żądany element, można znacznie
przyśpieszyć stosując struktury zwane drzewami.

Po zakończeniu tego rozdziału student powinien wiedzieć i potrafić:



Jaką strukturę danych nazywamy drzewem.



Dodawać elementy do drzewa.



Przeglądać drzewo.



Usuwać węzły drzewa.

Definicja binarnego drzewa poszukiwań

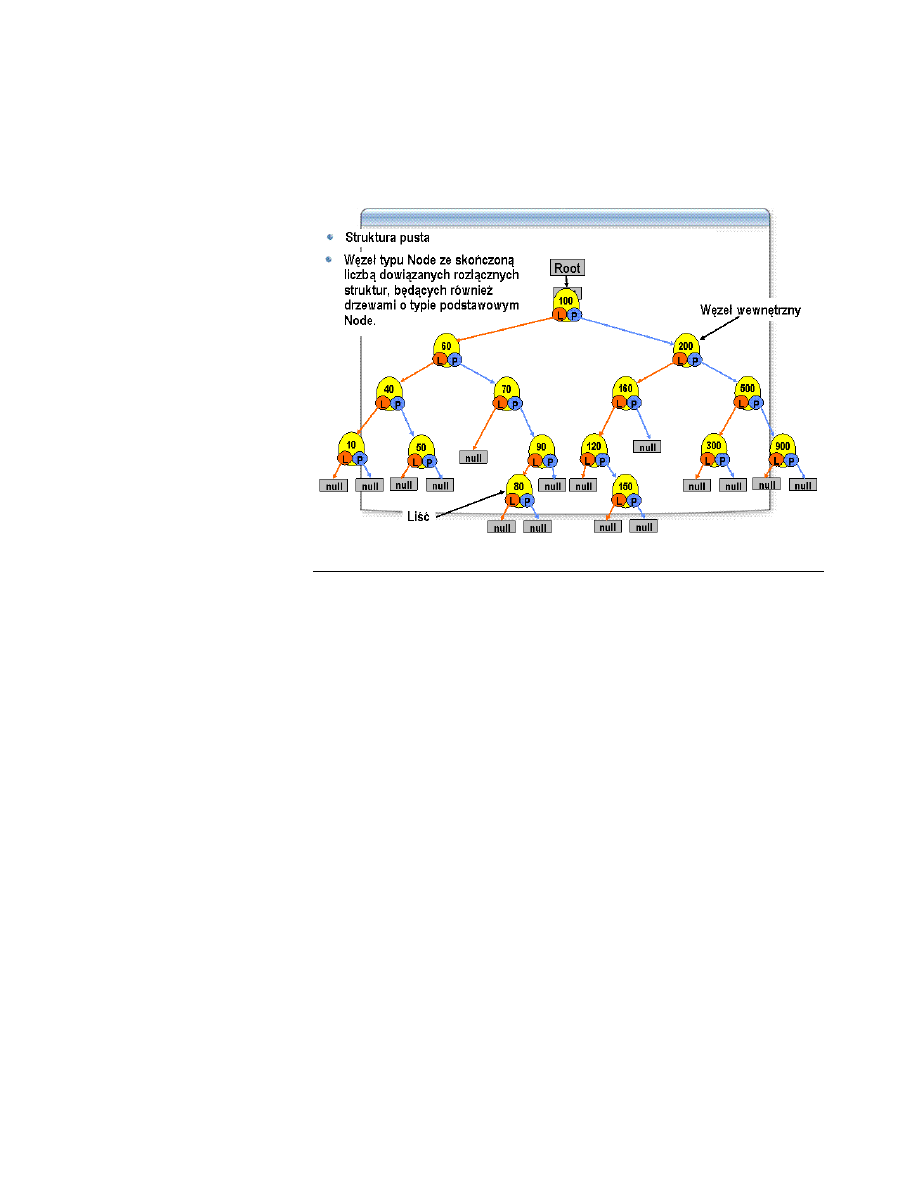
Drzewem nazywamy strukturę danych, która zbudowana jest z zera lub więcej
elementów zwanych węzłami, które charakteryzują się następującymi
właściwościami:



Każdy węzeł, z wyjątkiem pierwszego, ma dokładnie jeden węzeł
bezpośrednio go poprzedzający, zwany bezpośrednim przodkiem
(rodzicem).



Każdy węzeł posiada co najwyżej n, gdzie n jest większe lub równe
dwa, węzłów bezpośrednio po nim występujących, zwanych
bezpośrednimi potomkami - dziećmi.



Węzeł pierwszy, nieposiadający rodzica, nazywamy korzeniem (root).



Węzły, które nie posiadają żadnych potomków, nazywamy liśćmi.

Przyjmując typ węzła jako Node, drzewo możemy zdefiniować rekurencyjnie
w następujący sposób. Drzewem o typie podstawowym Node jest albo:

1. Struktura pusta, albo

2. Węzeł typu Node ze skończoną liczbą dowiązanych rozłącznych

struktur, będących również drzewami o typie podstawowym Node.
Dowiązane struktury nazywamy również poddrzewami.

Każdy węzeł drzewa jest osiągalny z korzenia przez jednoznacznie określony
ciąg węzłów i połączeń między węzłami, czyli krawędzi. Ciąg ten nazywamy
ścieżką. Poziomem węzła będziemy określać liczbę węzłów należących do
ścieżki do tego węzła. Wysokość drzewa to maksymalny poziom węzła

należącego do danego drzewa. I tak drzewo puste ma wysokość równą zero, zaś
drzewo zawierające pojedynczy element ma wysokość jeden.

Drzewo, w którym każdy z węzłów może mieć maksymalnie dwóch potomków
bezpośrednich, nazywamy drzewem binarnym. Jeden z potomków nazywamy
lewym dzieckiem, drugi prawym dzieckiem. Poddrzewo danego węzła, którego
korzeniem jest lewe dziecko, nazywamy lewym poddrzewem, poddrzewo
którego korzeniem jest prawe dziecko, nazywamy prawym poddrzewem danego
węzła.
W tym rozdziale zajmiemy się tylko binarnymi drzewami poszukiwań lub
inaczej uporządkowanymi drzewami binarnymi. Drzewa te charakteryzują się
następującymi właściwościami:



Wszystkie wartości przechowywane w lewym poddrzewie danego
węzła są mniejsze od wartości przechowywanej w danym węźle.



Wszystkie wartości z prawego poddrzewa są większe od wartości
zawartej w węźle.

Znaczenie określeń "większe" oraz "mniejsze" zależy od typu elementu
przechowywanego w drzewie.

W dalszej części rozdziału używając słowa drzewo, będziemy mieli na myśli
binarne drzewo poszukiwań.

Dodawanie elementów do drzewa

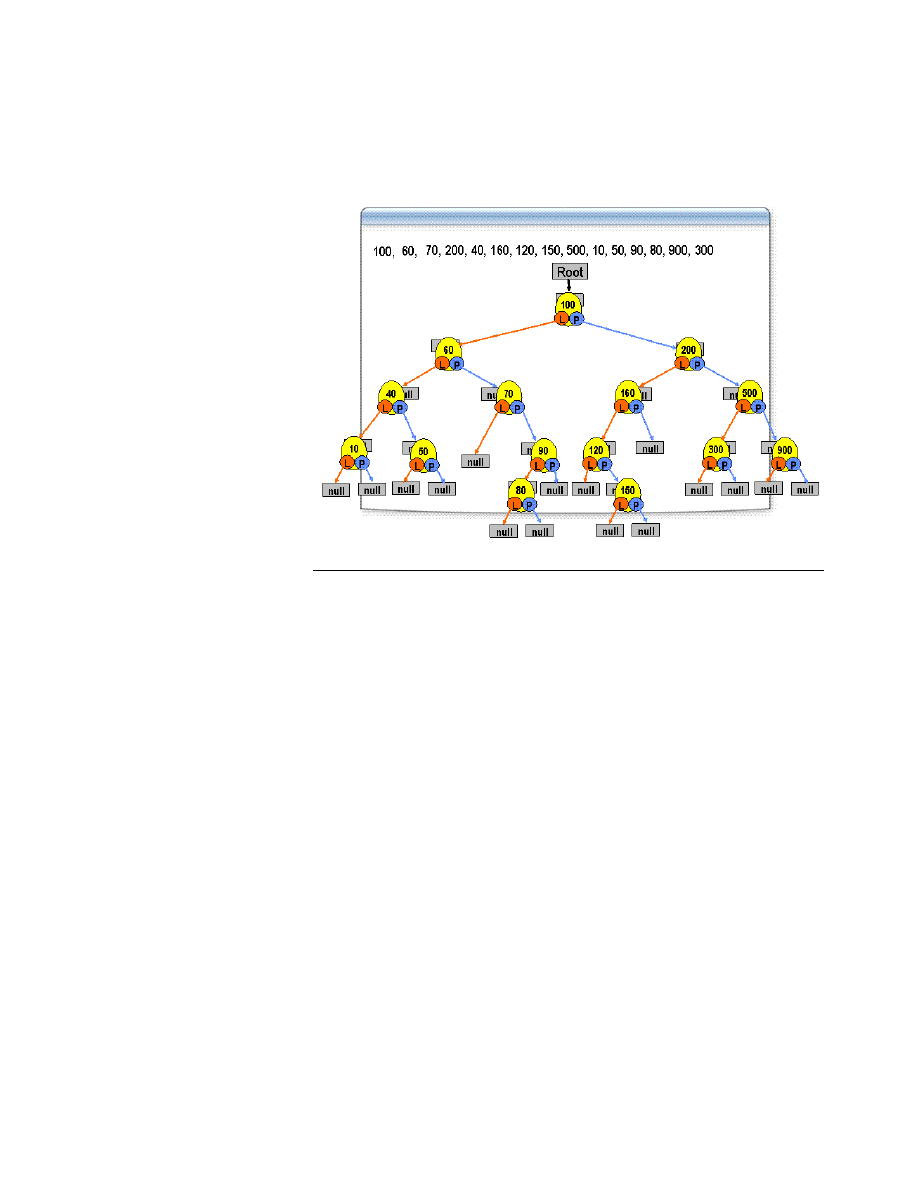
Tworzenie drzewa w sposób schematyczny zostało przedstawione na slajdzie.

Metodę dodającą nowy element do drzewa można zapisać w sposób
rekurencyjny. Metoda przyjmuję jako parametry referencję do korzenia drzewa,
do którego chcemy dodać nowy element oraz wartość którą chcemy umieścić w
drzewie. W metodzie sprawdzamy, czy korzeń jest pusty. Jeżeli korzeń
wskazuje na wartość null, ustawiamy go na nowo utworzony węzeł. W
przeciwnym przypadku sprawdzamy, czy wartość dodawana do drzewa jest
mniejsza od wartości przechowywanej w korzeniu. W przypadku gdy wartość
jest mniejsza to ją dodajemy do lewego poddrzewa, a w przeciwny wypadku
dodajemy ją do prawego poddrzewa.

W wersji iteracyjnej również na początku sprawdzamy, czy korzeń nie jest
pusty. Jeżeli korzeń jest pusty to tworzymy nowy węzeł, który będzie
przechowywał dodawaną wartość i odwołujemy się do niego zmienna
reprezentującą korzeń. Gdy korzeń istnieje, sprawdzamy czy dodawana wartość
jest mniejsza od wartości przechowywanej w korzeniu. Jeżeli jest mniejsza to
sprawdzamy, czy istnieje lewe dziecko, w przeciwnym wypadku sprawdzamy,
czy istnieje prawe dziecko. Gdy odpowiednie dziecko nie istnieje to nowy
węzeł podłączamy odpowiednio jako prawe lub lewe dziecko korzenia. W
przeciwny razie przechodzimy do prawego lub lewego dziecka korzenia,
porównujemy wartość przechowywaną w węźle z wartością dodaną i w
zależności która wartość jest mniejsza znowu sprawdzamy lewe albo prawe
dziecko. Jeżeli odpowiednie dziecko jest ustawione na null to wskazujemy im
na nowy węzeł. Jeżeli dziecko istnieje to znowu sprawdzamy element w nim
zawarty i w zależności od jego wartości przechodzimy do jego odpowiedniego
potomka. Czynność powtarzamy, aż umieścimy węzeł w drzewie.

Istnieje pewne niebezpieczeństwo, gdy kolejne elementy dodawane do drzewa
tworzą ciąg posortowany. W wyniku działania powyższego algorytmu
powstanie drzewo przypominające listę. Drzewo, którego każdy węzeł ma co
najwyżej jedno dziecko, nazywamy drzewem zdegenerowanym. W celu
uniknięcia tworzenia drzew zdegenerowanych stosuje się algorytmy zwane
równoważeniem drzewa. Algorytmy równoważenia drzewa jak i drzewa
zrównoważone są niestety poza zakresem tego kursu.

Wyszukiwanie w drzewie binarnym

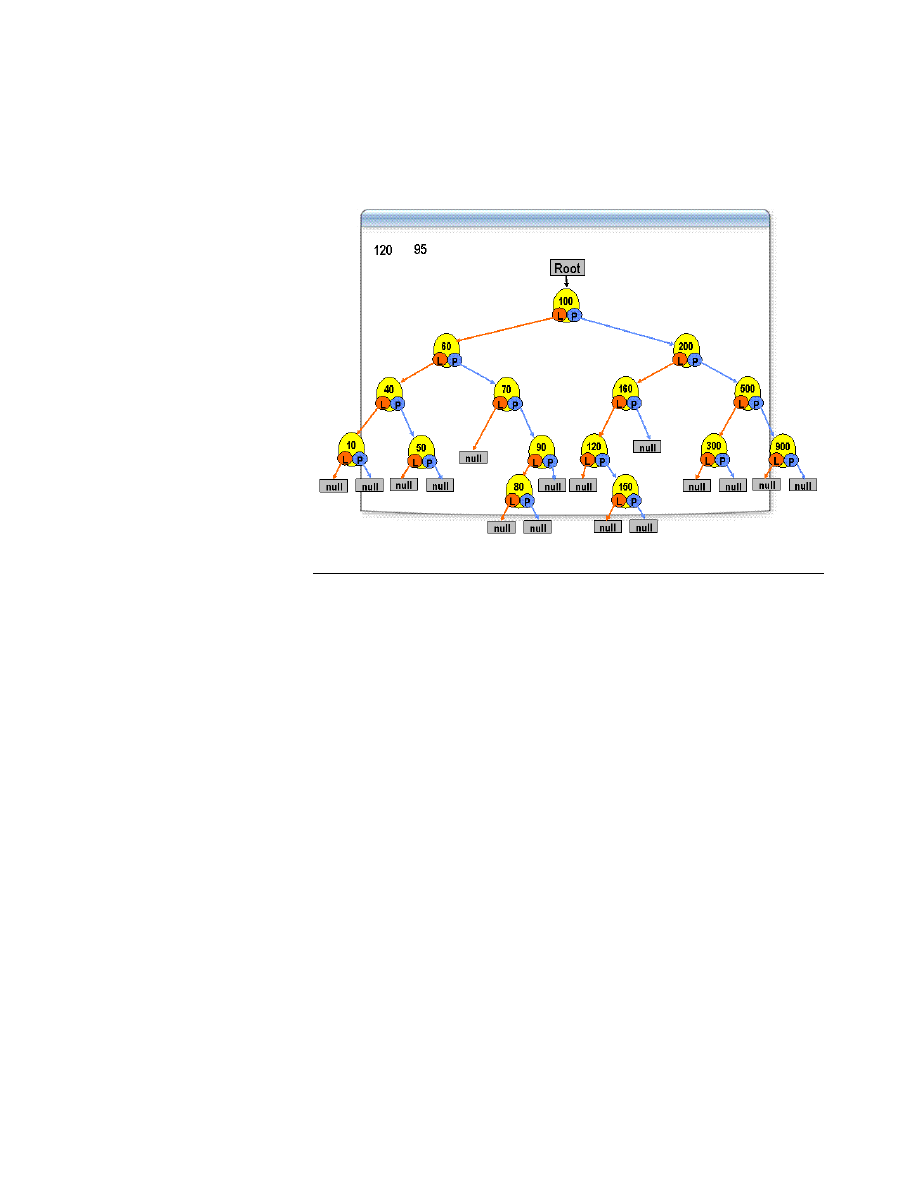
Algorytm pozwalający znaleźć żądany element w drzewie jest przedstawiony w
uproszczony sposób na rysunku na slajdzie.

Dla każdego węzła porównujemy wartość szukanego elementu z wartością
elementu danego węzła. Jeżeli wartość szukanego elementu jest mniejsza od
wartości elementu w aktualnym węźle, to analogicznie sprawdza się lewe
poddrzewo, w przeciwnym wypadku przechodzimy do prawego poddrzewa.
Jeżeli badany węzeł ma wartość równą szukanemu elementowi, szukanie
przerywamy. Szukanie również przerywamy, gdy nie ma możliwości przejścia
do odpowiedniego poddrzewa, odpowiednie dziecko ma wartość null.
Oznacza to, że w badanym drzewie nie ma żądanego elementu.

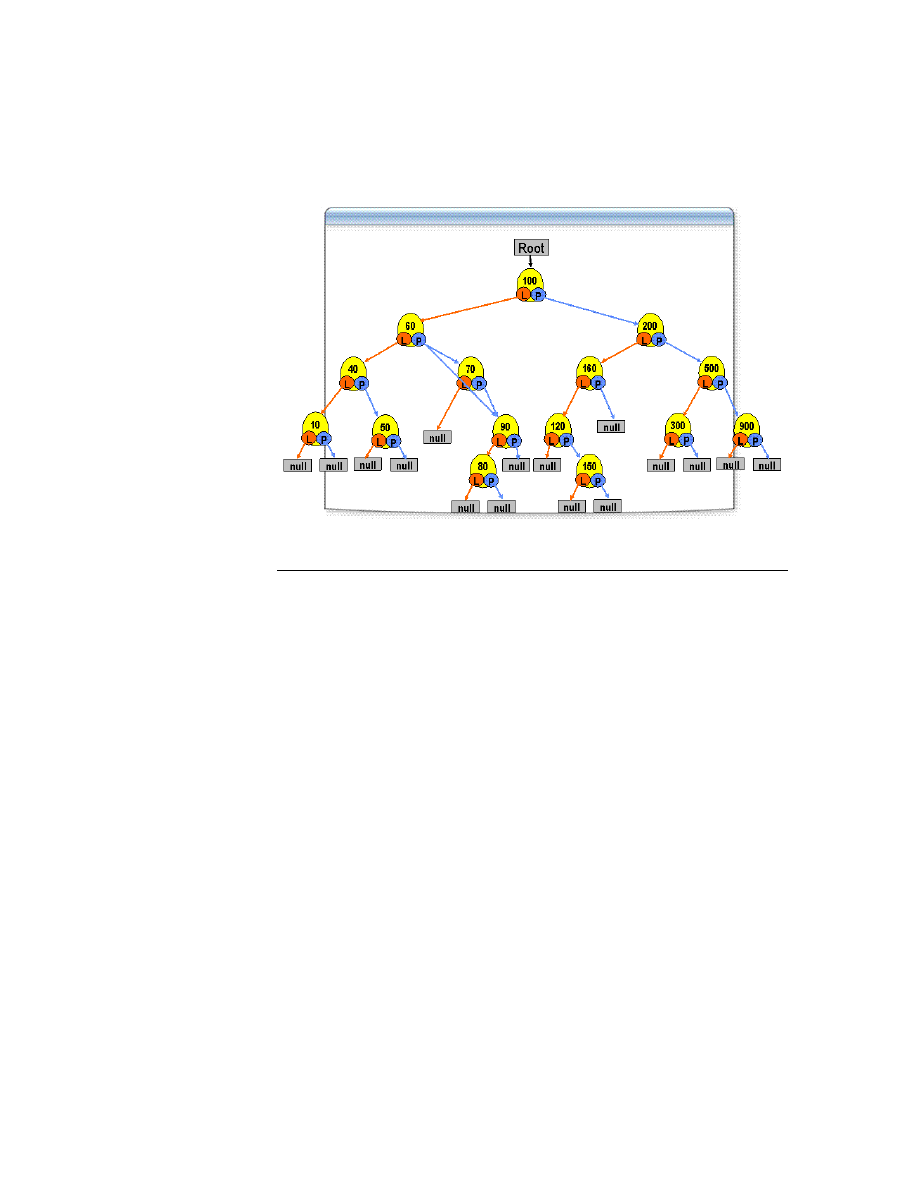
Przeglądanie drzewa (tree traversal

Przeglądanie drzewa lub przechodzenie po drzewie jest to proces polegający na
wywołaniu pewnej operacji na elemencie przechowywanym w węźle, na
przykład wypisanie wartości elementu, dla każdego węzła należącego do
drzewa dokładnie raz. Definicja przechodzenia po drzewie nie precyzuje, w
jakiej kolejności węzły mają być odwiedzane. Wśród wielu sposobów możemy
wyróżnić dwa rodzaje metod przechodzenia:



przechodzenie wszerz



przechodzenie wprzód

Przechodzenie wszerz polega na odwiedzeniu węzłów poziomami. Zaczynamy
od poziomu najwyższego lub najniższego i przechodzimy kolejno po tych
poziomach. W przechodzeniu po poziomie możemy obrać kierunek albo od
prawej do lewej albo od lewej do prawej. Uproszczony kod implementujący
przechodzenie wszerz z góry na dół i od lewej do prawej, korzystający z kolejki
FIFO umieszczono poniżej:

static void Wypisz(Drzewo tree)
{

KolejkaFIFO kolejka = new KolejkaFIFO();

Node node = tree.Root;

if(node != null)

{

KolejkaFIFO.Enqueue(kolejka, node);

while(! KolejkaFIFO.IsEmpty(kolejka)

{

node = KolejkaFIFO.Dequeue(kolejka);

WypiszElement(node);

if(node.Left != null)

KolejkaFIFO.Enqueue(kolejka,

node.Left);

if(node.Right != null)

KolejkaFIFO.Enqueue(kolejka,

node.Right);

}

}

}

Przeszukiwanie w głąb, jak sam nazwa wskazuje polega na sięganiu "głębiej" w
drzewo. Najprostszą implementacją jest metoda rekurencyjna, którą można
przedstawić w następujących krokach

1. Sprawdź czy węzeł nie jest pusty. Jeżeli węzeł jest pusty zakończ

metodę. W przeciwnym wypadku przejdź do kroku dwa.

2. Wywołaj metodę dla lewego dziecka bieżącego węzła.

3. Wypisz element znajdujący się w aktualnym węźle.

4. Wywołaj metodę dla prawego dziecka bieżącego węzła.

Kroki od dwa do trzy mogą być wykonane w dowolnej kolejności. Algorytm
wypisujący najpierw element bieżącego węzła (krok 3), a następnie
"odwiedzający" poddrzewa nazywamy przechodzeniem z wyprzedzeniem
(preorder). Algorytm "odwiedzający" najpierw poddrzewa, a następnie dopiero
wypisujący element bieżącego węzła nosi nazwę przechodzenia z opóźnieniem
(postorder). Algorytm "odwiedzający" najpierw lewe poddrzewo, następnie
wypisujący element bieżącego węzła i na koniec "odwiedzający prawe
poddrzewo, nazwy się przechodzeniem bezpośrednim (inorder).

W celu wypisanie elementów w kolejności rosnącej należy zastosować
przechodzenie bezpośrednie.

Usuwanie węzła - węzeł ma najwyżej jedno dziecko

Algorytm usuwający węzeł z jednym dzieckiem, jest przedstawiony w
uproszczony sposób na rysunku na slajdzie.

Najprostszy przypadek usuwania węzła mamy wtedy, gdy węzeł jest liściem,
czyli nie ma potomków. Odwołanie do danego węzła z węzła rodzica
ustawiamy na null.

W przypadku, gdy usuwany węzeł ma tylko jedno dziecko, algorytm również
nie jest skomplikowany. Odwołanie do danego węzła z węzła rodzica
ustawiamy na jedyne dziecko węzła do usunięcia.

W przypadku, gdy usuwany węzeł ma dwoje dzieci, możemy wyróżnić dwa
algorytmy, które zostaną przedstawione w dalszej części tego rozdziału.

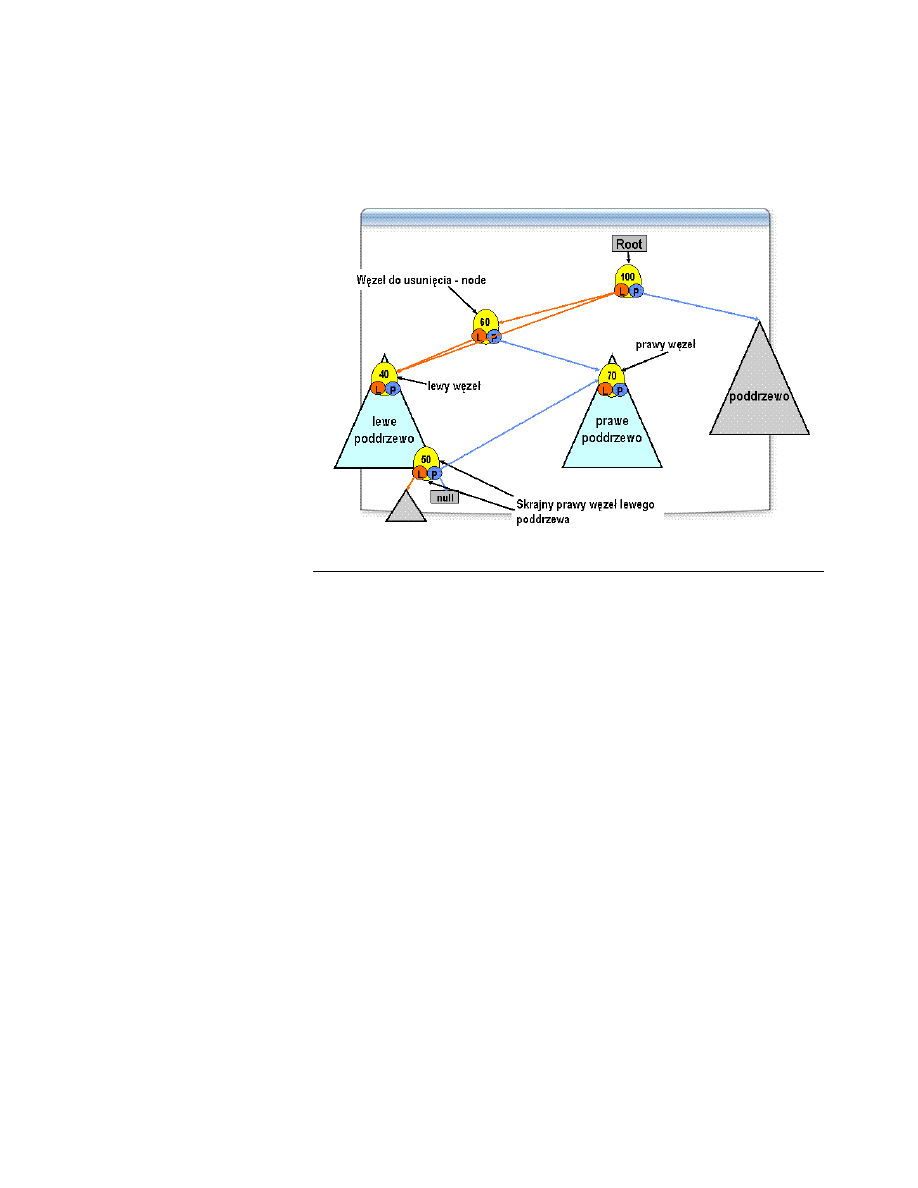
Usuwanie przez złączanie

Algorytm usuwający węzeł metodą przez złączanie, jest przedstawiony w
uproszczony sposób na rysunku na slajdzie.

Algorytm usuwanie przez złączanie polega na tym, że z dwóch poddrzew
usuwanego węzła tworzymy jedno drzewo, które dołączamy do węzła rodzica
w miejsce usuniętego węzła.
Na korzeń tworzonego drzewa wybieramy skrajny prawy węzeł lewego
poddrzewa. Z własności binarnych drzew poszukiwań wynika, że element tego
węzła jest "mniejszy" od elementów w prawym poddrzewie węzła do usunięcia.
Znalezienie tego węzła polega na przejściu z węzła do usunięcia do lewego jego
dziecka, a następnie przesuwaniu się po tym poddrzewie, wybierając za każdym
razem prawe dziecko, aż do znalezienia odwołania pustego. Po znalezieniu
skrajnego prawego węzła lewego poddrzew, ustawiamy jego odwołanie do
prawego dziecka na prawe poddrzewo węzła do usunięcia. Następnie odwołanie
do usuwanego węzła ustawiamy na lewe dziecko węzła do usunięcia.

Uwaga:
Stosowanie algorytmu usuwania przez złączanie może powodować wydłużanie
się drzewa..

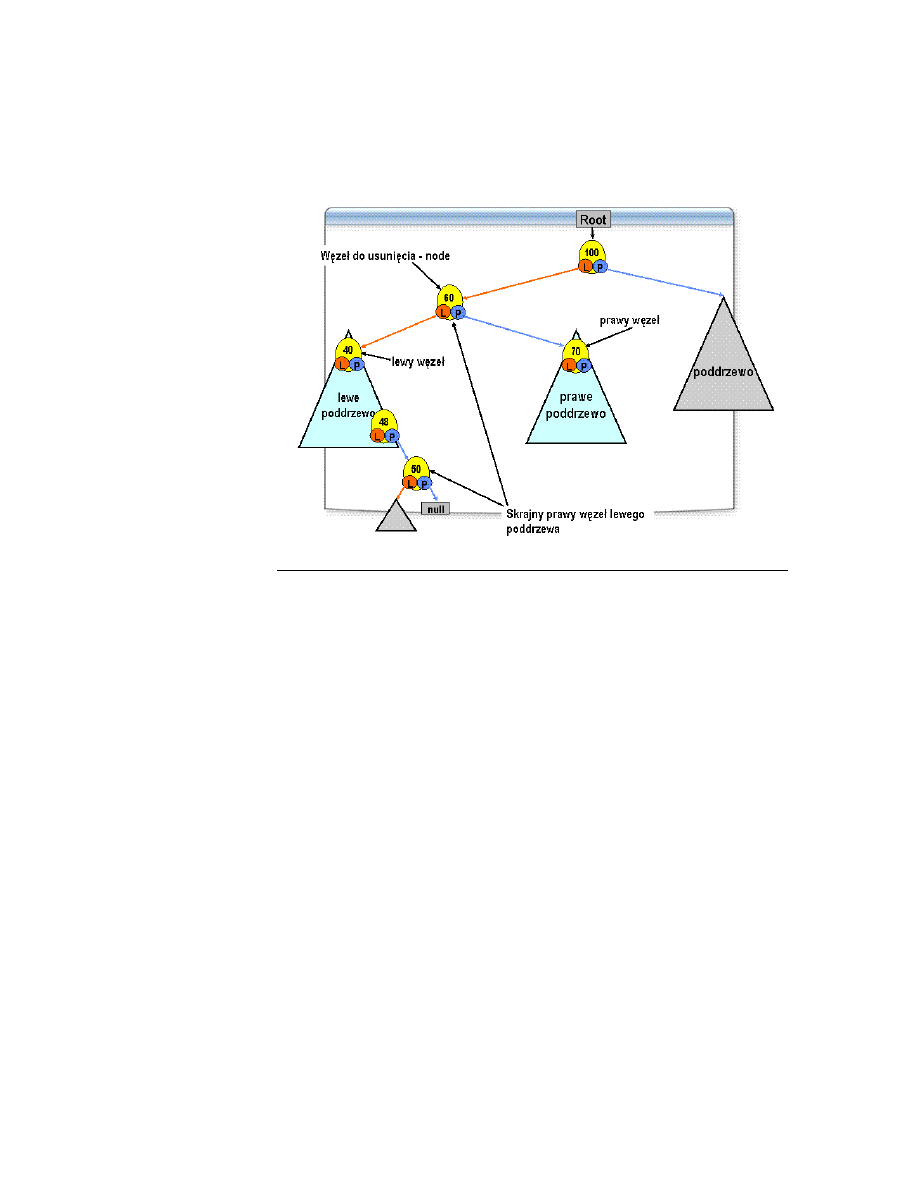
Usuwanie przez kopiowanie

Algorytm usuwający węzeł metodą przez kopiowanie, jest przedstawiony w
uproszczony sposób na rysunku na slajdzie.

Wartość elementu skrajnego prawego węzła lewego poddrzewa jest mniejsza od
wartości elementów prawego poddrzewa węzła do usunięcia i większa od
wartości pozostałych elementów lewego poddrzewa węzła do usunięcia, co
wynika bezpośrednio z właściwości binarnych drzew poszukiwań.
Element ten możemy skopiować do węzła, które ma być usunięty, nie niszcząc
binarnego drzewa poszukiwań. Po skopiowaniu elementu, węzłem do usunięcia
zostaje skrajny prawy węzeł lewego poddrzewa. Węzeł ten ma najwyżej jedno
dziecko, dlatego możemy zastosować algorytm usuwania węzła, który ma
najwyżej jedno dziecko. Algorytm ten był juz omawiany wcześniej w tym
rozdziale.

Pytania sprawdzające

1. Co to jest drzewo?

Odp.
Drzewem o typie podstawowym Node jest albo:



Struktura pusta, albo



Węzeł typu Node ze skończoną liczbą dowiązanych rozłącznych
struktur, będących również drzewami o typie podstawowym Node.

2. Co to jest drzewo binarne?

Odp.
Drzewo, w którym każdy z węzłów może mieć maksymalnie dwóch
potomków bezpośrednich, nazywamy drzewem binarnym.

3. Co to jest binarne drzewo poszukiwań?

Odp.
Drzewo binarne charakteryzują się następującymi właściwościami:



Wszystkie wartości przechowywane w lewym poddrzewie danego
węzła są mniejsze od wartości przechowywanej w danym węźle.



Wszystkie wartości z prawego poddrzewa są większe od wartości
zawartej w węźle.

nazywamy binarnymi drzewami poszukiwań.

4. Jakie znasz metody usuwania węzła z drzewa?

Odp.
Usuwanie przez łączenie i usuwanie przez kopiowanie.

Laboratorium

Ćwiczenie 1:
Napisz program, który będzie zawierał implementację binarnego drzewa
poszukiwań. Do drzewa będą dodawane obiekty klasy Osoba. Klasa Osoba
jest zaimplementowana w projekcie Biblioteka. Projekt Biblioteka jest częścią
rozwiązania Kurs\Modul13\Start\Start.sln, gdzie Kurs jest
katalogiem, gdzie skopiowano pliki kursu. Program będzie składał się z dwóch
podzespołów:



Biblioteki dll, o nazwie Drzewo, która będzie zawierała implementację
binarnego drzewa poszukiwań. W klasie Drzewo będą zaimplementowane
następujące metody:

o IsEmpty - sprawdzenie czy drzewo jest puste

o AddElement - dodanie elementu do drzewa

o DeleteElement - usunięcie osoby z drzewa o podanym imieniu i

nazwisku

o PrintAll - wypisanie na ekranie danych wszystkich osób dodanych do

drzewa w kolejności alfabetycznej

o FindElemnt - metoda zwraca dany obiekt Osoba w przypadku, gdy w

drzewie znajduje się osoba o podanym imieniu i nazwisku albo wartość
null, gdy drzewo nie zawiera osoby o podanym imieniu i nazwisku.



Programu głównego, w którym przetestujemy drzewo.

Do porównania osób użyj metody :

public static int CompareTo(Osoba os1, Osoba os2,

która znajduje się w klasie Osoba. Metoda ta najpierw porównuje nazwiska
osób. Jeżeli nazwisko osoby os1 jest wcześniej w kolejności alfabetycznej, niż
nazwisko osoby os2 metoda zwraca wartość mniejszą od zera. Jeżeli nazwisko
osoby os1 jest dalej w kolejności alfabetycznej, niż nazwisko osoby os2 metoda
zwraca wartość większą od zera. Jeżeli nazwiska są jednakowe metoda w
analogiczny sposób sprawdza imiona osób. Jeżeli również imiona są jednakowe
metoda zwraca wartość zero.

1. Skopiuj rozwiązanie Kurs\Lab\Modul13\Start\Start.sln, gdzie

Kurs jest katalogiem, gdzie skopiowano pliki kursu.

2. Otwórz skopiowane rozwiązanie Start.sln

3. Dodaj do bieżącego rozwiązania nowy projekt

a. Z menu File wybierz Add/New Project...

b. W oknie dialogowym Add New Project określ następujące

właściwości:

c. typu projektu: Visual C#/Windows

i. szablon: Class Library

ii. lokalizacja: Moje Dokumenty\Visual Studio 2005\Projects\

iii. nazwa projektu: Drzewa.

4. Podłącz do programu Drzewa, podzespół Biblioteka.

a. W okienku Solution Explorer, z menu kontekstowego związanego z

elementem reprezentującym projekt Drzewa wybierz Add Reference...

b. W okienku Add Reference przejdź do zakładki Projects, zaznacz

projekt Biblioteka i naciśnij OK.

5. Zaznacz, że będziemy korzystać z przestrzeni nazw Biblioteka.

using Biblioteka;

6. Zmień nazwę pliku Class1.cs na Tree.cs.

7. Zmień nazwę klasy z Class1 na Tree. Wewnątrz klasy Tree (drzewo)

zdefiniuj klasę Node (Węzeł). .Do klasy Node dodaj następujące pola:
pole Data (Dane) typu Osoba, pole Left(lewy) i Right(prawy) typu
Node. Do klasy Tree dodaj pole Root (korzeń) typu Node.

public class Tree
{
public class Node
{
public Osoba Data;
public Node Left,Right;
}
public Node Root;
}

8. Do klasy Tree dodaj metodę IsEmpty::

public static bool IsEmpty (Tree drzewo)
{

return drzewo.Root == null;
}

9. Do klasy Tree dodaj metodę AddElement::

public static void AddElement(Tree drzewo,

Osoba os)

{
if(drzewo.Root == null)
{
drzewo.Root = new Node();
drzewo.Root.Data = os;
return ;
}
Node p = drzewo.Root, prev;
do
{
prev = p;
if(Osoba.CompareTo(os,p.Data )<0)
p = p.Left;
else
p = p.Right;
}
while(p != null);
if (Osoba.CompareTo(os, prev.Data) < 0)
{
prev.Left = new Node();
prev.Left.Data = os;
}
else
{
prev.Right = new Node();
prev.Right.Data = os;
}
}

10. Do klasy Tree dodaj metodę DeleteElement::

public static Osoba DeleteElement(Tree drzewo,

string nazwisko, string imie)

{
Osoba os = new Osoba();
os.Imie = imie;
os.Nazwisko = nazwisko;
Node p = drzewo.Root, parent = drzewo.Root;
while (p != null)
{
if (Osoba.CompareTo(os, p.Data) == 0)
break;
else
{
parent = p;
if (Osoba.CompareTo(os, p.Data)<0)
p = p.Left;
else
p = p.Right;

}
}

if (p == null)
return null;
os = p.Data;
if (p == drzewo.Root)
DeleteWezel(ref drzewo.Root);
else
if (p == parent.Right)
DeleteWezel(ref parent.Right);
else
DeleteWezel(ref parent.Left);
return os;
}

public static void DeleteWezel(ref Node wezel)
{
if (wezel.Right == null)
wezel = wezel.Left;
else
if (wezel.Left == null)
wezel = wezel.Right;
else
{
Node tmp = wezel.Left;
Node prev = wezel;
while (tmp.Right != null)
{
prev = tmp;
tmp = tmp.Right;
}
wezel.Data = tmp.Data;
if (prev == wezel)
prev.Left = tmp.Left;
else
prev.Right = tmp.Left;
}
}

11. Do klasy Tree dodaj metodę PrintAll::

public static void PrintAll(Tree drzewo)
{
PrintWezel(drzewo.Root);
}

public static void PrintWezel(Node wezel)
{
if (wezel != null)
{
PrintWezel(wezel.Left);
Osoba.WypiszOsobe(wezel.Data);
Console.WriteLine();
PrintWezel(wezel.Right);

}
}

12. Do klasy Tree dodaj metodę FindElemnt::

public static Osoba FindElemnt(Tree drzewo,

string nazwisko,string imie)

{
Osoba os = new Osoba();
os.Imie = imie;
os.Nazwisko = nazwisko;
Node p = drzewo.Root;
while (p != null)
{
if (Osoba.CompareTo(os,p.Data)==0)
return p.Data;
else
if (Osoba.CompareTo(os, p.Data)<0)
p = p.Left;
else
p = p.Right;
}
return null;
}

13. Do rozwiązania dodaj nowy projekt, w którym będziemy testowali listę.

a. Z menu File wybierz Add/New Project...

b. W oknie dialogowym Add New Project określ następujące

właściwości:

i. typu projektu: Visual C#/Windows

ii. szablon: Console Application

iii. nazwa projektu: TestDrzewa.

c. Uczyń nowo utworzony projekt projektem startowym

d.

Podłącz do programu TestDrzewa, podzespoły Biblioteka oraz
Drzewa.

e.

Zaznacz, że będziemy korzystać z przestrzeni nazw Biblioteka
oraz Drzewa.

using Biblioteka;
using Drzewa;

14. Napisz kod testujący listę

static char Menu()
{
Console.Clear();
Console.WriteLine("\n\t\tA - Dodaj osobę do

¬rzewa");

Console.WriteLine("\n\t\tB - Usuń osobę z

¬drzewa");

Console.WriteLine("\n\t\tC - Zanjdź osobę w

¬drzewie");

Console.WriteLine("\n\t\tD - Wypisz osoby z

¬drzewa");

Console.WriteLine("\n\t\tK - Koniec");
return Console.ReadKey(true).KeyChar;
}

static void Main(string[] args)
{
Tree mojeDrzewo = new Tree();
Osoba tmp;
string imie, nazwisko;
char c;
do
{
c = Menu();
switch (c)
{
case 'a':
case 'A':
Osoba.WprowadzOsobe(out tmp);
Tree.AddElement(mojeDrzewo, tmp);
break;
case 'b':
case 'B':
Console.Write("Podaj nazwisko osoby do

¬usunięcia: ");

nazwisko = Console.ReadLine();
Console.Write("Podaj imie osoby do

¬usunięcia: ");

imie = Console.ReadLine();
tmp = Tree.DeleteElement(mojeDrzewo,

nazwisko, imie);

if (tmp == null)
Console.WriteLine("Nie ma takiej

¬osoby");

else
Osoba.WypiszOsobe(tmp);
Console.ReadKey();
break;
case 'c':
case 'C':
Console.Write("Podaj nazwisko osoby do

¬znalezienia: ");

nazwisko = Console.ReadLine();
Console.Write("Podaj imie osoby do

¬znalezienia: ");

imie = Console.ReadLine();
tmp = Tree.FindElemnt(mojeDrzewo,

nazwisko, imie);

if (tmp == null)
Console.WriteLine("Nie ma takiej

¬osoby");

else
Osoba.WypiszOsobe(tmp);
Console.ReadKey();

break;
case 'd':
case 'D':
Tree.PrintAll(mojeDrzewo);
Console.ReadKey();
break;
}
}
while (!(c == 'k' || c == 'K'));
}

15. Skompiluj i uruchom program.