Reprezentacja liczb w
systemie binarnym
ułamki i liczby ujemne
M@rek Pudełko
Urządzenia Techniki
Komputerowej
Reprezentacja liczb w
systemie binarnym
ułamki i liczby ujemne
M@rek Pudełko
Urządzenia Techniki
Komputerowej
Spis treści
• System zapisu znak – moduł
• System zapisu U1
• System zapisu U2
• Ułamki w systemie binarnym
2
System zapisu znak-moduł
• W tym systemie najstarszy bit (z lewej
strony) informuje o znaku liczby.
• 0
liczba dodatnia
• 1
liczba ujemna
• Pozostałe bity mają takie samo
znaczenie i reprezentują wartość liczby.
3
System zapisu znak-moduł
• 1011
2
= 11
10
• -11
10
11011
zm
• +11
10
01011
zm
• Liczbę w tym systemie oznaczamy
sygnaturką zm (znak-moduł) lub sm
(sign – magnitude)
• Spotyka się jeszcze inny sposób zapisu
przez oddzielenie znaku od modułu
wykrzyknikiem
• -11
10
1!1011
zm
• +11
10
0!1011
zm
4
Przykład zapisu systemu
znak-moduł
5
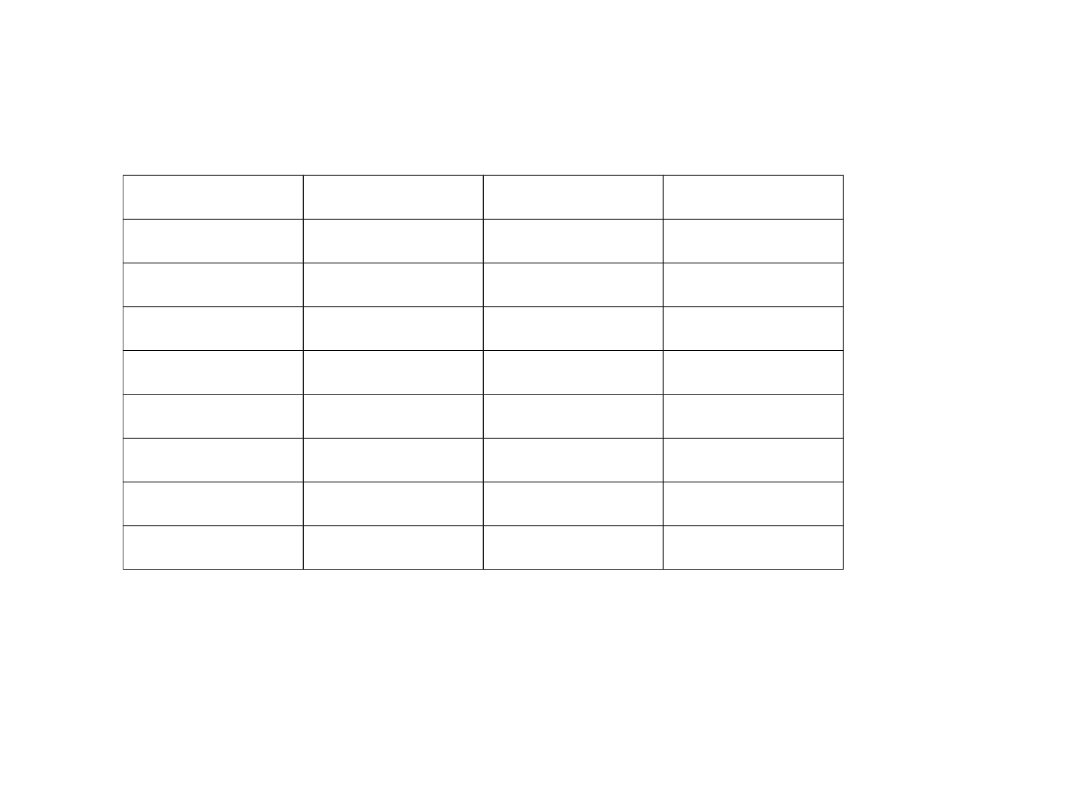
Liczba ZM
wartość
Liczba ZM
wartość
0000
0
1000
-0
0001
1
1001
-1
0010
2
1010
-2
0011
3
1011
-3
0100
4
1100
-4
0101
5
1101
-5
0110
6
1110
-6
0111
7
1111
-7
• Dla 4 bitów najwyższy bit informuje o znaku, a pozostałe 3 to
wartość liczby.
• Zwraca uwagę podwójna reprezentacja zera jako 0000 i 1000.
System zapisu U1
(uzupełnienie do 1)
• W tym systemie najstarszy bit (z lewej
strony) informuje o znaku liczby.
• 0
liczba dodatnia
• 1
liczba ujemna
• Liczby ujemne tworzy się negując
odpowiadającą jej liczbę dodatnią.
6
System zapisu U1
• 1011
2
= 11
10
• +11
10
01011
u1
• Wartość liczby dodatniej jest
analogiczna jak dla naturalnego kodu
binarnego.
• -11
10
10100
u1
• Liczbę ujemna uzyskujemy negując (0
→ 1 i 1→0) poszczególne cyfry liczby
dodatniej.
• Liczbę w tym systemie oznaczamy
sygnaturką U1
7
Liczba ujemna w systemie
zapisu U1
8
• Chcąc uzyskać liczbę ujemną, należy
najpierw utworzyć odpowiadającą jej
liczbę dodatnią.
• +19
10
010011
U1
• Następnie negujemy ją zmieniając 0 w
1, a 1 w 0.
• -19
10
101100
U1
Przykład zapisu systemu U1
9
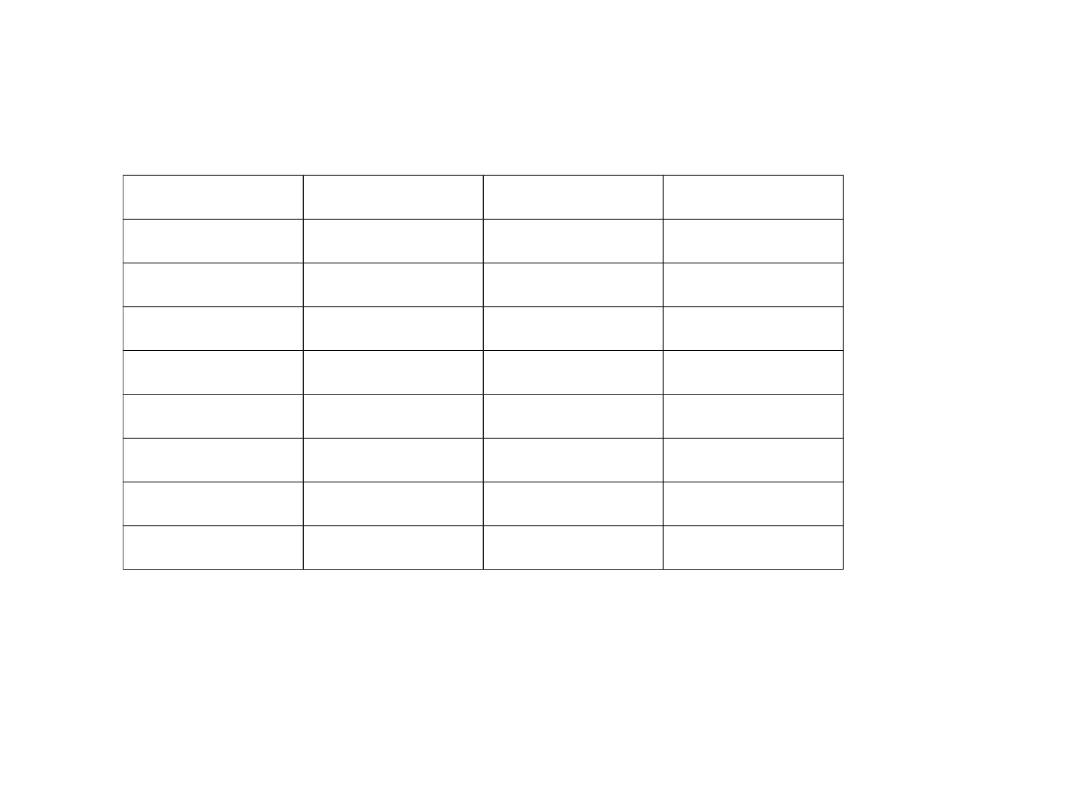
Liczba U1
wartość
Liczba U1
wartość
0000
0
1000
-7
0001
1
1001
-6
0010
2
1010
-5
0011
3
1011
-4
0100
4
1100
-3
0101
5
1101
-2
0110
6
1110
-1
0111
7
1111
-0
• Dla 4 bitów najwyższy bit informuje o znaku, a pozostałe 3 to
wartość liczby.
• Zwraca uwagę podwójna reprezentacja zera jako ciąg samych
zer lub samych jedynek.
System zapisu U2
(uzupełnienie do 2)
• W tym systemie najstarszy bit (z lewej
strony) informuje o znaku liczby.
• 0
liczba dodatnia
• 1
liczba ujemna
• Liczby ujemne tworzy się negując
odpowiadającą jej liczbę dodatnią i
zwiększając ją o 1.
10
System zapisu U2
• 1011
2
= 11
10
• +11
10
01011
U2
• Wartość liczby dodatniej jest
analogiczna jak dla naturalnego kodu
binarnego.
• -11
10
10101
U2
• Liczbę ujemną uzyskujemy negując (0
→ 1 i 1→0) cyfry liczby dodatniej i
zwiększając ją o 1.
• Liczbę w tym systemie oznaczamy
sygnaturką U2
11
Liczba ujemna w systemie
zapisu U2
12
• Chcąc uzyskać liczbę ujemną, należy
najpierw utworzyć jej dopowiadającą
liczbę dodatnią.
• +19
10
010011
2
• Następnie negujemy ją zmieniając 0 w
1, a 1 w 0.
• -19
10
101100
U1
• Na końcu dodajemy do wyniku 1.
• -19
10
101101
U2
Obliczanie liczby ujemnej w
systemie zapisu U2
13
• Najwyższa cyfra w liczbie z systemu U2 ma
znak -, a pozostałe plus. Zamiana na system
dziesiętny polega na dodaniu pozostałych
pozycji i odjęciu ich od największej wagi
.
• 101101
U2
= -19
Waga
5
4
3
2
1
0
Cyfra
1
0
1
1
0
1
Znak
cyfry
-
+
-1*2
5
0*2
4
1*2
3
1*2
2
0*2
1
1*2
0
-1 * 32
0 * 16
1*8
1*4
0*2
1*1
-32 +
0 +
8 +
4+
0 +
1
-32 +
13 =
= -19
Przykład zapisu systemu U2
14
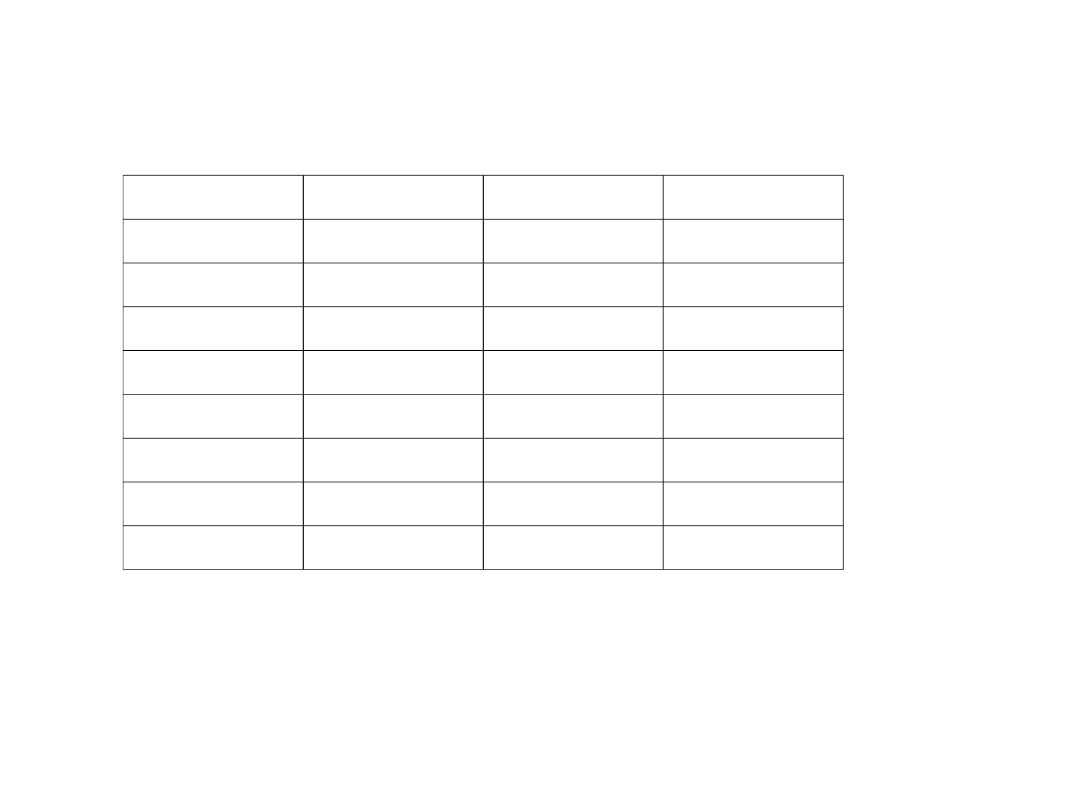
Liczba U2
wartość
Liczba U2
wartość
0000
0
1000
-8
0001
1
1001
-7
0010
2
1010
-6
0011
3
1011
-5
0100
4
1100
-4
0101
5
1101
-3
0110
6
1110
-2
0111
7
1111
-1
• Dla 4 bitów najwyższy bit informuje o znaku, a pozostałe 3 to
wartość liczby.
• Zwraca uwagę pojedyncza reprezentacja zera.
Zero w systemach zapisu
15
Liczba ZM
Zero dodatnie
Zero ujemne
Znak-moduł
0000
1000
U1
0000
1111
U2
0000
• Kody Z-M i U1 są kodami symetrycznymi. Stąd
pojawiają się dwie postacie zera. Stanowi to kłopot
przy reprezentacji liczb w informatyce.
• Zero nie jest ani dodatnie, ani ujemne. W
powyższych systemach ma ono albo obie postacie
(Z-M, U1) albo jest traktowane jako liczba dodatnia
(U2).
• Kod U2 jest kodem niesymetrycznym.
Porównanie zapisu w
systemach
Z-M, U1, U2
16
Liczba
System Znak-
Moduł
System U1
System U2
Liczba parzysta
+22 010110
ZM
010110
U
1
010110
U2
-22 110110
ZM
101001
U
1
101010
U2
Liczba nieparzysta
+25 011001
ZM
011001
U
1
011001
U2
-25 111001
ZM
100110
U
1
100111
U2
Ćwiczenia
17
• Przelicz następujące liczby dziesiętne na
system zapisu Znak-Moduł, U1, U2.
1. -17
2. -22
3. -32
4. -11
5. -59
6. -43
7. -94
8. -19
9. -25
10.-74
11.-73
12.-62
13.-38
14.-91
15.-66
16.-77
17.-42
18.-39
19.-15
20.-14
21.-31
22.-21
23.-79
24.-23
25.-14
26.-89
27.-35
28.-27
29.-36
30.-55
Zadania
1. Jaka to liczba w systemie U-1?
a) 1111
u1
b) 111111
u1
c) 11111111
u1
2. Porównaj sposób liczby zapisane w systemie
U-2?
a) -16 i +16
b) -32 i +32
c) -64 i +64
d) -128 i +128
3. s
18
Ułamki w systemie binarnym
• W systemie binarnym ułamki
zapisujemy analogicznie jak liczby
rzeczywiste.
• Do przedstawienia liczb po przecinku
używamy potęg ujemnych.
19
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
20
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
21
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
1
0,25
*2
22
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
1
0,25
*2
0,5
0
0,5
23
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
1
0,25
*2
0,5
0
0,5
*2
1
1
0
24
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
1
0,25
*2
0,5
0
0,5
*2
1
1
0
25
0,625
10
=0,101
2
Przeliczanie z dziesiętnego na
binarny
• Ułamek dziesiętny obliczamy wg
schematu:
0,625
10
=
Mnoż
na
Mnożn
ik
Wynik
Część
całkowita
0,625
*2
1,25
1
0,25
*2
0,5
0
0,5
*2
1
1
0
26
0,625
10
=0,101
2
Przeliczanie z binarnego na
dziesiętny
• Każdy ułamek dziesiętny możemy
przedstawić jako sumę liczb binarnych
o ujemnych potęgach.
• Ułamek dziesiętny z binarnego
obliczamy ze wzoru:
• n= c
0
*2
0
+c
1
*2
-1
+ c
2
*2
-2
+ ... +
c
i
*2
-i
n=
c
i
*
2
i
Wartość
pozycji
Waga
pozycji
27
Przeliczanie z binarnego na
dziesiętny
• Jakim ułamkiem dziesiętnym jest 0,101
binarne?
0,
1
0
1
0
-1
-2
-3
Wag
a
28
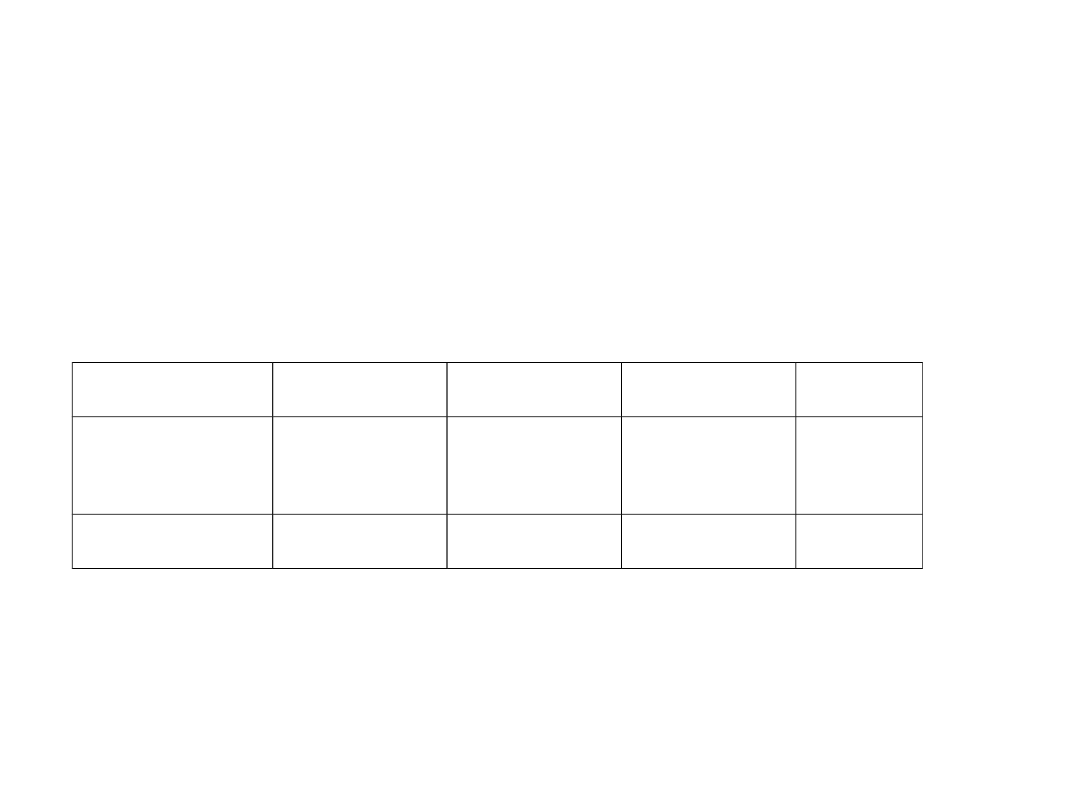
Przeliczanie z binarnego na
dziesiętny
• Jakim ułamkiem dziesiętnym jest 0,101
binarne?
0,
1
0
1
0
-1
-2
-3
Wag
a
0 *
2
0
+ 1 *
2
-1
+ 0 *
2
-2
+ 1 *
2
-3
+
=
29
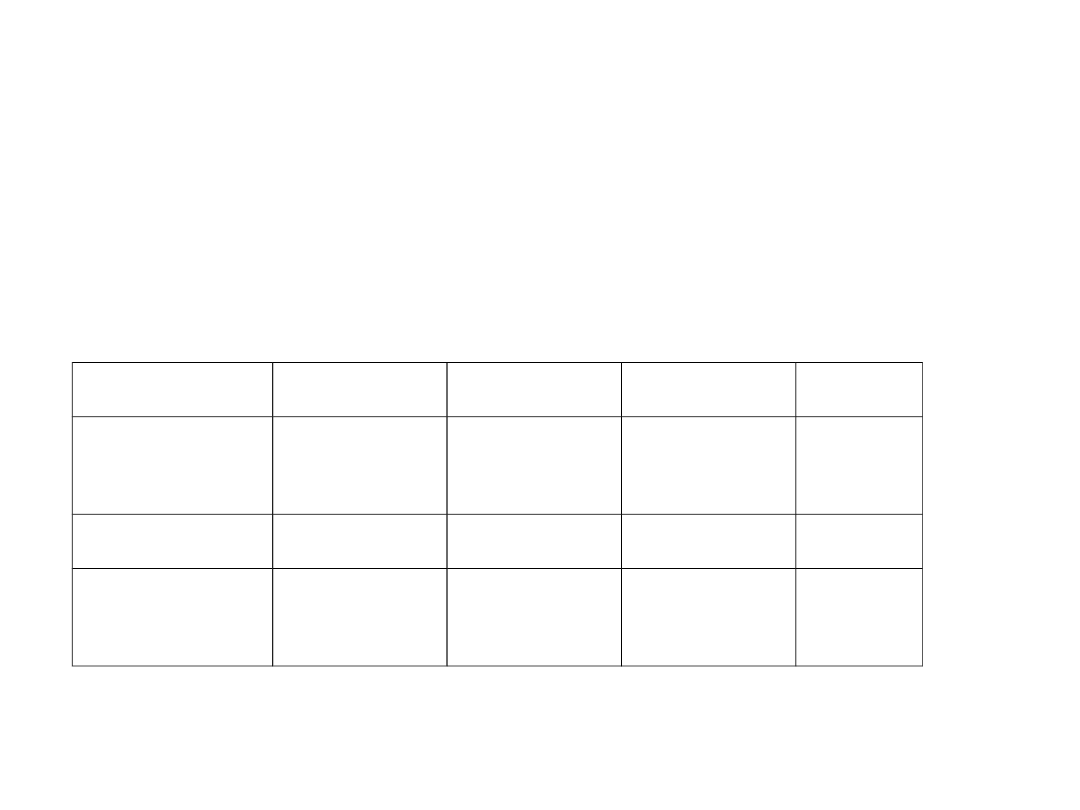
Przeliczanie z binarnego na
dziesiętny
• Zamieniamy ujemne potęgi na ułamek zwykły
0,
1
0
1
0
-1
-2
-3
Wag
a
0 *
2
0
+ 1 *
2
-1
+ 0 *
2
-2
+ 1 *
2
-3
+
=
0 *
0
+
1 *
1/2
1
+
0 *
1/2
2
+
1 *
1/2
3
+
=
30
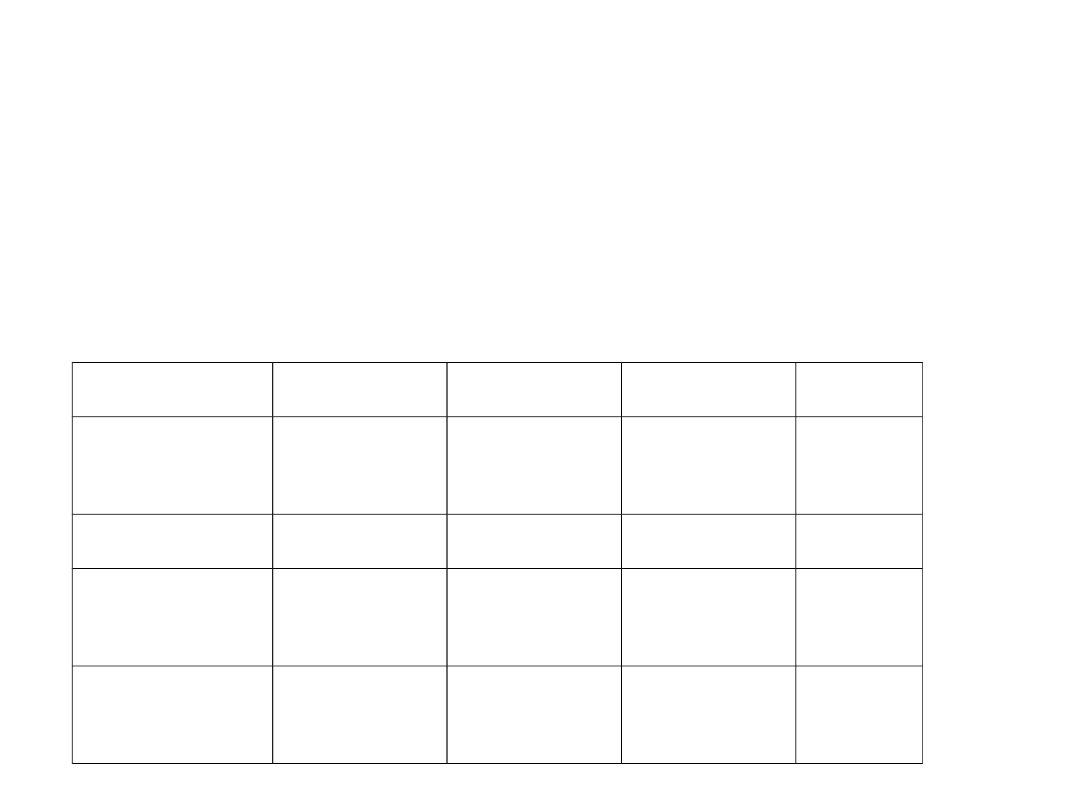
Przeliczanie z binarnego na
dziesiętny
• Wyliczamy ułamki
0,
1
0
1
0
-1
-2
-3
Wag
a
0 *
2
0
+ 1 *
2
-1
+ 0 *
2
-2
+ 1 *
2
-3
+
=
0 *
0
+
1 *
1/2
1
+
0 *
1/2
2
+
1 *
1/2
3
+
=
0 *
0
+
1 *
1/2
+
0 *
1/4
+
1 *
1/8
+
=
31
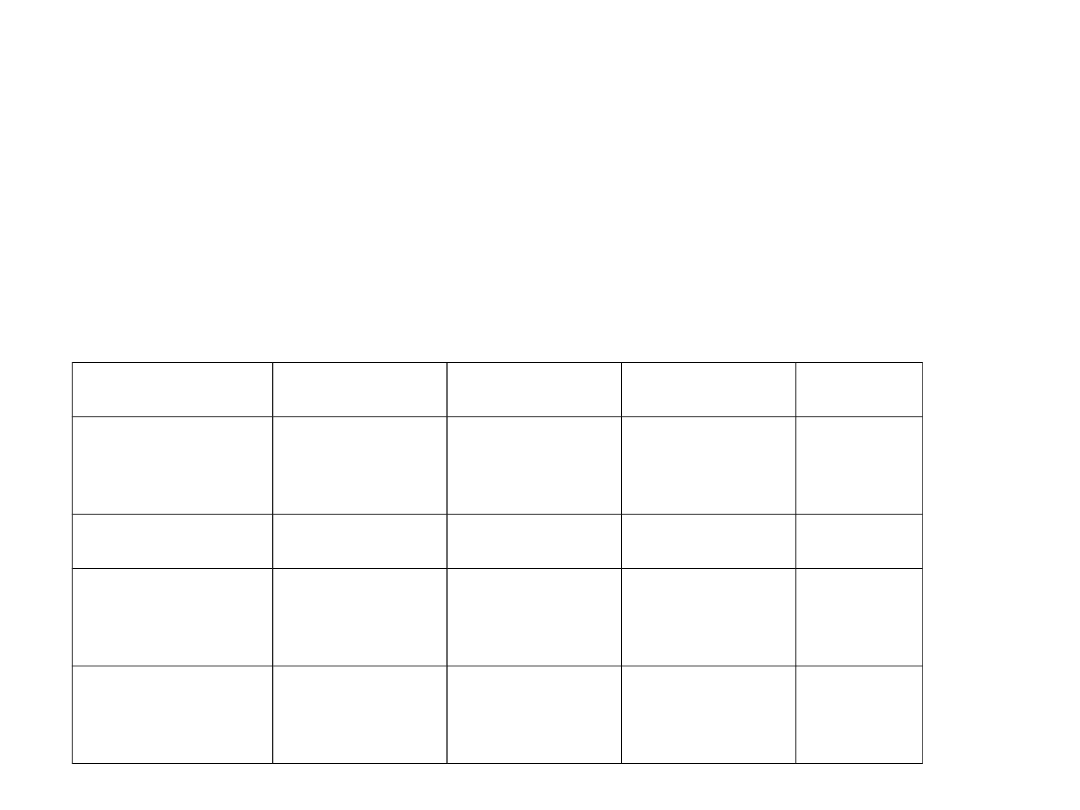
Przeliczanie z binarnego na
dziesiętny
• Zamieniamy ułamki zwykłe na
dziesiętne
0,
1
0
1
0
-1
-2
-3
Wag
a
0 *
2
0
+ 1 *
2
-1
+ 0 *
2
-2
+ 1 *
2
-3
+
=
0 *
0
+
1 *
1/2
1
+
0 *
1/2
2
+
1 *
1/2
3
+
=
0 *
0
+
1 *
0,5
+
0 *
0,25
+
1 *
0,125
+
=
32
Przeliczanie z binarnego na
dziesiętny
• Zamieniamy ułamki zwykłe na
dziesiętne
0,
1
0
1
0
-1
-2
-3
Wag
a
0 *
2
0
+ 1 *
2
-1
+ 0 *
2
-2
+ 1 *
2
-3
+ =
0 *
0
+
1 *
1/2
1
+
0 *
1/2
2
+
1 *
1/2
3
+
=
0 +
0,5+
0 +
0,125 =0,6
25
33
0,101
2
=0,625
10
Co to za ułamek dziesiętny?
• 0,1101
2
• 0,10011
2
34
Co to za ułamek dziesiętny?
• 0,1101
2
= 0,8125
• 0,10011
2
= 0,59375
35
Zamień na ułamek binarny
• 0,375
• 0,5125
• 0,6
• 0,15
36
Zamień na ułamek binarny
• 0,375 = 0,011
2
• 0,5125 = 0, 1000 (0011)
2
• 0,6 = 0, (1001)
2
• 0,15 = 0, 00 (1001)
2
37