System binarny

M@rek Pudełko

Urządzenia Techniki

Komputerowej

1

• Co to jest pozycyjny system zapisu?

2

Pozycyjny system zapisu

• Pozycyjny system zapisu

charakteryzuje się tym, że wielkość
liczby zależy od wartości cyfr i od
tego gdzie one się znajdują (na jakiej
pozycji).

3

Pozycyjny system zapisu

• Która liczba jest większa?

• 12900 czy 90012
• 10000 czy 00001
• 12345 czy 12345

4

Niepozycyjny system zapisu

• MCMLXXIV

5

Niepozycyjny system zapisu

• Rzymski sposób zapisu liczb

• MMXI
• MCMXMIII

I

1

V

5

X

10

L

50

C

100

D

500

M

1000

6

Dziesiętny system zapisu

• Ile cyfr potrzeba do zapisu w

systemie dziesiętnym?

• Skąd się wziął system dziesiętny?

7

Dziesiętny system zapisu

• Dziesiętny system zapisu posiada 10

cyfr do zapisu liczb:

• 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

• Kiedy cyfra ma być większa niż 9

zmieniamy wartość tej i następnej
pozycji.

9

+

1

1

0

8

Binarny system zapisu

• Binarny (dwójkowy) system zapisu

posiada 2 cyfry do zapisu liczb:

• 0, 1

• Liczba w systemie dwójkowym ma

postać:
c

i

... c

1

c

0

gdzie c

i

= 1 lub 0

• 10101001010101001

9

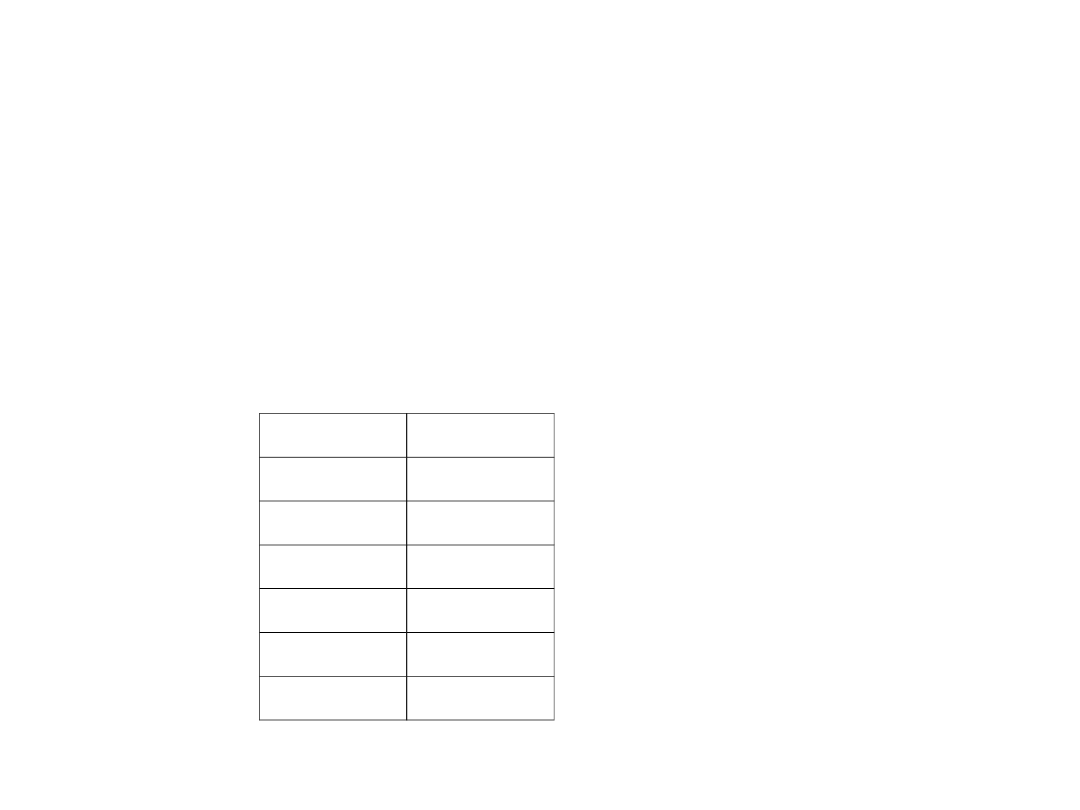
Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

10

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

11

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

:2

0

5

12

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

:2

0

5

:2

1

2

13

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

:2

0

5

:2

1

2

:2

0

1

14

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

:2

0

5

:2

1

2

:2

0

1

:2

1

0

STOP

15

Przeliczanie z dziesiętnego na

binarny

• Liczbę binarną z dziesiętnej obliczamy wg

schematu:

Dziel
na

Dzieln
ik

Reszta z
dzielenia

43

:2

1

21

:2

1

10

:2

0

5

:2

1

2

:2

0

1

:2

1

0

43

10

=101011

2

16

Przeliczanie - ćwiczenia

1) 45
2) 72
3) 81
4) 77
5) 19
6) 86
7) 26
8) 37
9) 88
10)54

11)59
12)28
13)65
14)93
15)91
16)41
17)97
18)68
19)39
20)24

21)29
22)58
23)85
24)73
25)69
26)46
27)72
28)71
29)64
30)32

17

Przeliczanie z binarnego na

dziesiętny

• Każdą liczbę dziesiętną możemy

przedstawić jako sumę liczb binarnych.

• Liczbę dziesiętną z binarnej obliczamy

ze wzoru:

• n= c

i

*2

i

+ ... + c

1

*2

1

+ c

0

*2

0

n=

c

i

*

2

i

+ ... +

c

1

*2

1

+ c

0

*2

0

Wartość

pozycji

Waga

pozycji

18

Przeliczanie z binarnego na

dziesiętny

• Jaka liczbą dziesiętną jest 101011

binarne?

1

0

1

0

1

1

5

4

3

2

1

0

wa

ga

19

Przeliczanie z binarnego na

dziesiętny

• Jaka liczbą dziesiętną jest 101011

binarne?

1

0

1

0

1

1

5

4

3

2

1

0

wa

ga

1 *

2

5

+

0 *

2

4

+

1*

2

3

+

0*

2

2

+

1*

2

1

+

1*

2

0

20

Przeliczanie z binarnego na

dziesiętny

• Jaka liczbą dziesiętną jest 101011

binarne?

1

0

1

0

1

1

5

4

3

2

1

0

wa

ga

1 *

2

5

+

0 *

2

4

+

1*

2

3

+

0*

2

2

+

1*

2

1

+

1*

2

0

1*

32

+

0

*

16

+

1 *

8

+

0 *

4

+

1 *

2

+

1 *

1

21

Przeliczanie z binarnego na

dziesiętny

• Jaka liczbą dziesiętną jest 101011

binarne?

1

0

1

0

1

1

5

4

3

2

1

0

wa

ga

1 *

2

5

+

0 *

2

4

+

1*

2

3

+

0*

2

2

+

1*

2

1

+

1*

2

0

1*

32

+

0

*

16

+

1 *

8

+

0 *

4

+

1 *

2

+

1 *

1

32+

0 +

8 +

0 +

2 +

1

=

43

22

101011

2

=43

10

Przeliczanie - ćwiczenia

1)

10101010

2)

10010101

3)

10101110

4)

11010100

5)

10000111

6)

10001111

7)

10111100

8)

10011101

9)

10011100

10)

10011001

11)1011101

0

12)1111111

0

13)1000000

1

14)1100110

0

15)1010111

1

16)1011111

1

17)1100000

0

18)1111000

0

19)1000111

0

20)1001010

0

21)11111111
22)11010101
23)10001100
24)10100000
25)10001000
26)10010001
27)10100010
28)11100011
29)10011001
30)11111100

23

Powtórzenie

24