W

ykresy s³u¿¹ do obrazowego przedstawiania da-
nych. Maj¹ pomóc nam wyobraziæ sobie opisy-
wane zale¿noœci. Przemawiaj¹ one bowiem do

wyobraŸni lepiej ni¿ go³e liczby.
Wykresy s¹ wszechobecne w ¿yciu wielu ludzi. Polity-
cy z wykresów odczytuj¹ jak wysokie poparcie ma ich
partia i na tej podstawie podejmuj¹ decyzje. Gracze
gie³dowi na podstawie wykresów podejmujê decyzje
o sprzeda¿y lub zakupie akcji co pozwala im zdobyæ
fortunê a uczniowie musz¹ siê z nimi zmagaæ w szkole.
Do tych ostatnich adresowany jest ten artyku³. Na lek-
cjach matematyki uczeñ najczêœciej ma do czynienia
z wykresami s³upkowymi

i wykresami ko³owymi

.

Na lekcjach fizyki z kolei najczêœciej mamy do czynie-
nia z wykresami liniowymi g³ównie drogi w funkcji cza-
su lub prêdkoœci w funkcji czasu.

Zajmiemy siê w pierwszej kolejnoœci matematyk¹.
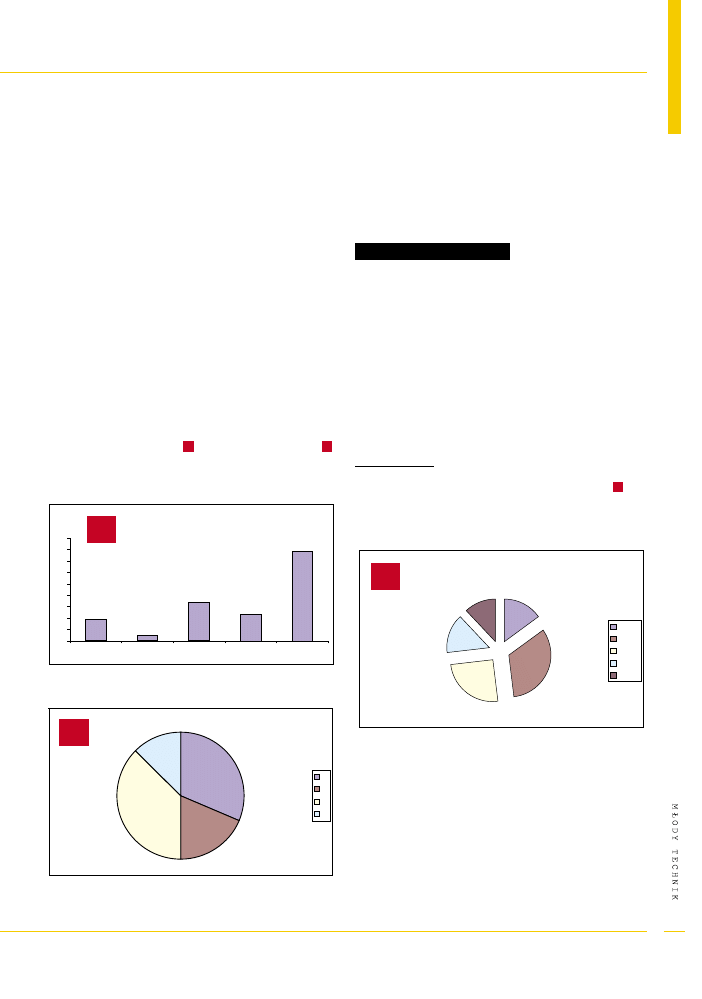
Wykres s³upkowy s³u¿y do obrazowania jak du¿a w po-
równaniu z innymi jest dana wielkoœæ w porównaniu
z innymi. Patrz¹c na rysunek 1 od razu widaæ jakim gi-
gantem jest obiekt 5 a jaki ma³y w porównaniu z pozos-
ta³ymi jest obiekt 2. Wykresy ko³owe z kolei s³u¿¹ g³ów-
nie do obrazowania udzia³u w ca³oœci. Ca³e ko³o to
100% danej wartoœci po³owa 50% æwiartka 25% itd. Za-
dania przed jakimi stoi uczeñ w czasie lekcji lub na eg-
zaminie mo¿na zasadniczo podzieliæ na dwie grupy.
Pierwsza grupa polega na czytaniu wykresów druga na
ich tworzeniu. Oto przyk³ad zadania z grupy pierwszej.

Zadanie 1

Zbadano wiek ludzi ogl¹daj¹cych film „Czterej pancer-
ni i kangur”. Wyniki przedstawiono na wykresie

.

Oblicz ile osób doros³ych powy¿ej 18 roku ¿ycia obej-
rza³o ten film jeœli wiadomo, ¿e ³¹czna liczba widzów
wynios³a 2500000.

Jak rozwi¹zujemy taki problem?
Oczywiœcie ka¿dy przedzia³ wiekowy ma swój kolor.
Tak jak to pokazano w legendzie wykresu np widzom
w wieku od 15–18 lat odpowiada kolor ¿ó³ty i jak widaæ
stanowi¹ oni 25 % wszystkich widzów ogl¹daj¹cych
ten film. Nas jednak interesuj¹ widzowie doroœli. Tym
widzom odpowiadaj¹ dwie barwy i co za tym idzie
dwie kategorie wiekowe. Widzowie z grupy 19–30
i 31–50. Procent widzów doros³ych bêdzie sum¹ pro-
centów odpowiadaj¹cym obu grupom z osobna. Nieste-
ty w przypadku grupy 19-30 nie mamy takiej informac-
ji. Jak j¹ zdobyæ? Mimo i¿ wiemy, ¿e procent jest pro-

3

2

1

1

1

ZADANIA Z WYKRESAMI

w fizyce i matematyce

Z b i g n i e w W i œ n i e w s k i

Rys. 1

0

10

20

30

40

50

60

70

80

90

123

45

Rys. 3

15%

33%

25%

12%

510
10 15
15 18
19 30
30 50

y

1
2
3
4

1

2

3

Typowy wykres słupkowy. Wysokość słupka jest
uzależniona od liczebności danego obiektu.

Wykres do zadania 1.

Typowy wykres kołowy. Przypomina tort pokrojony
na nierówne kawałki. Służy głównie do obrazowania
udziału obiektów pewnego rodzaju w całości populacji.

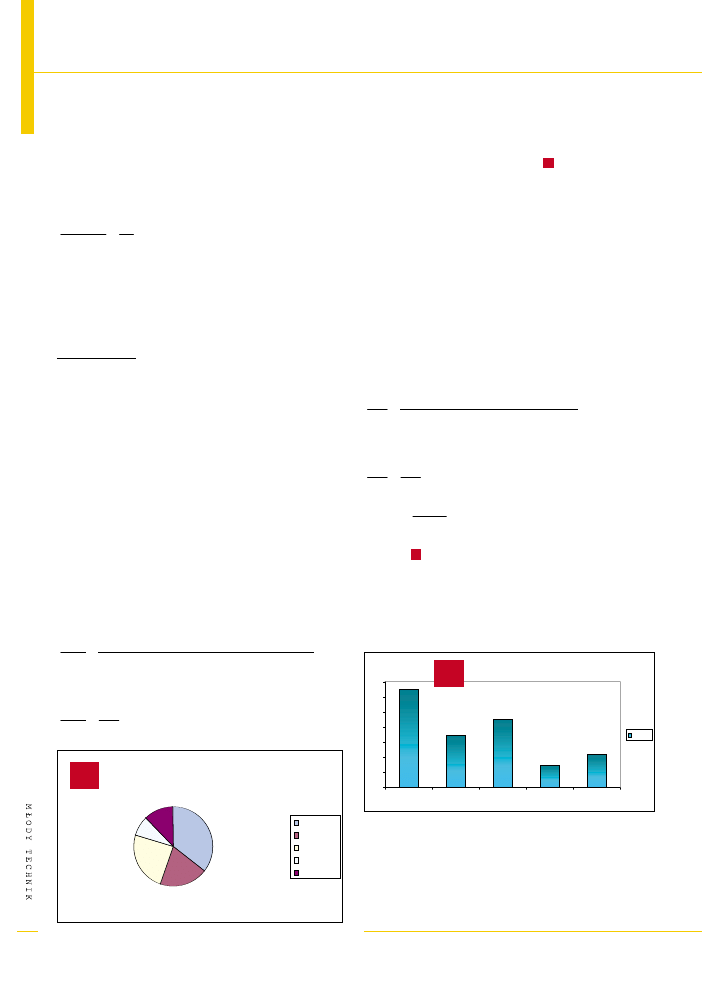
porcjonalny do k¹ta nie nale¿y pos³ugiwaæ siê k¹tomie-
rzem. Tutaj nale¿y po prostu dodaæ wszystkie pozos-
ta³e procenty. Daje to 85%. Jeœli teraz odejmiemy to od
100% co odpowiada pe³nemu ko³u to otrzymamy 100%–
85% = 15%. Teraz ju¿ wiemy ile procent widzów przy-
pada na ka¿d¹ z grup wiekowych widzowie w wieku
19–30 stanowili 15% a widzowie w wieku 31–50 – 12%
co razem daje 27% .
Liczbê widzów doros³ych mo¿emy wiêc obliczyæ pos³u-
guj¹c siê proporcj¹

teraz mno¿¹c „na krzy¿” otrzymujemy
27 · 2500000 = 100x czyli
x = 675000
I zadanie rozwi¹zane.
Trochê trudniejsze s¹ zadania, w których uczeñ musi
przedstawiæ coœ na wykresie. Oto przyk³ad.

Zadanie 2

Wypo¿yczalnia filmów „¯ó³ty Tygrys” Ma filmy pogru-
powane w nastêpuj¹cych dzia³ach.
Krymina³y – 650 filmów, sensacja – 350 filmów, komedie
– 450 filmów, romanse – 150 filmów, filmy dla dzieci
220.
Przedstaw powy¿sze dane za pomoc¹ wykresu
a)

ko³owego

b)

s³upkowego

Rozwi¹zanie punktu a)
Jak wynika z tego co zosta³o uprzednio powiedziane
wielkoœæ wycinka ko³a przypadaj¹ca na dany film jest
wprost proporcjonalna do udzia³u filmów danego ga-
tunku w ca³oœci zbiorów wypo¿yczalni. Aby sporz¹dziæ
wykres ko³owy nale¿y najpierw obliczyæ ile jest ³¹cznie
filmów. Czyli najpierw dodajemy filmy z ka¿dej grupy.
£¹cznie wypo¿yczalnia ma 1820 filmów. Na tej podsta-
wie wiemy, ¿e liczbie 1820 odpowiada ca³e ko³o czyli
360 stopni. Wartoœæ poszczególnych udzia³ów oblicza-
my z prostej proporcji

Na przyk³ad dla filmów sensacyjnych

Wielkoœæ szukanego k¹ta wynosi

.

W ten sam sposób znajdujemy pozosta³e k¹ty. Maj¹c
obliczone k¹ty odpowiadaj¹ce poszczególnym typom
filmów bez trudu konstruujemy odpowiedni wykres.
Powinien on wygl¹daæ jak na rys.

.

PrzejdŸmy teraz do punktu b) czyli do konstrukcji wyk-
resu s³upkowego.
Podstawowa zasad¹, o której powinno siê pamiêtaæ ro-
bi¹c wykres s³upkowy jest, ¿e wykres nie mo¿e byæ za
ma³y oraz to ¿e ¿aden s³upek nie mo¿e byæ wy¿szy ni¿
wysokoœæ obszaru na którym mamy rysowaæ s³upki
(czyli s³upki musz¹ siê zmieœciæ na wykresie). Aby to
osi¹gn¹æ znajdujemy najpierw najwiêksz¹ liczbê fil-
mów. W wypo¿yczalni z naszego zadania najwiêcej by-
³o krymina³ów – 650. Za³ó¿my, ¿e obszar nad osi¹ na
którym mo¿emy rysowaæ wynosi 12,5 cm (mniej wiêcej
po³owa d³u¿szego boku kartki A4). Rozs¹dnie bêdzie
wtedy przyj¹æ ¿e s³upek odpowiadaj¹cy krymina³om
powinien mieæ wysokoœæ 12 cm. Wysokoœæ pozosta³ych
s³upków liczymy z proporcji.

Na przyk³ad dla filmów sensacyjnych obliczenia wygl¹-
daj¹ nastêpuj¹co

St¹d

.

Wykres zrobiony wed³ug tych regu³ pokazany jest na
rysunku

. Wygl¹da ca³kiem ³adnie.

Myœlê ¿e przedstawione tu zasady i przyk³ady pozwol¹
wam lepiej rozwi¹zywaæ podobne problemy na lek-
cjach matematyki.
Niestety zadania, w których wa¿n¹ rolê odgrywaj¹
wykresy wystêpuj¹ równie¿ w fizyce. Postaramy siê te-
raz wyjaœniæ jak sobie radziæ z takimi zadaniami.

5

mm

x

5

,

6

650

12

·

350

≈

=

350

650

12

x

=

film w

liczba

slupka

wysoko y

szukana

_

_

_

650

12 =

4

°

≈ 69

α

α

350

360

1820 =

k„

szukany

gatunku

danego

film w

liczba

_

_

_

_

360

1820 =

x

27

2500000

100

=

t

Rys. 4

Krymina³y; 650

Sensacyjne; 350

Komedie; 450

Romanse; 150

Dla dzieci; 220

Krymina³y

Sensacyjne

Komedie

Romanse

Dla dzieci

Rys. 5

0

100

200

300

400

500

600

700

Kry mina³y

Sensacy jne

Komedie

Romanse

Dla dzieci

Serie1

s‡

Rozwiązanie zadania 2 punkt a).

Rozwiązanie zadania 2 punkt b).

4

5

2

2

liczba_ filmów_ danego_ gatunku

szukany_k¹t

szukana_ wysokoœæ_ s³upka

liczba_ filmów

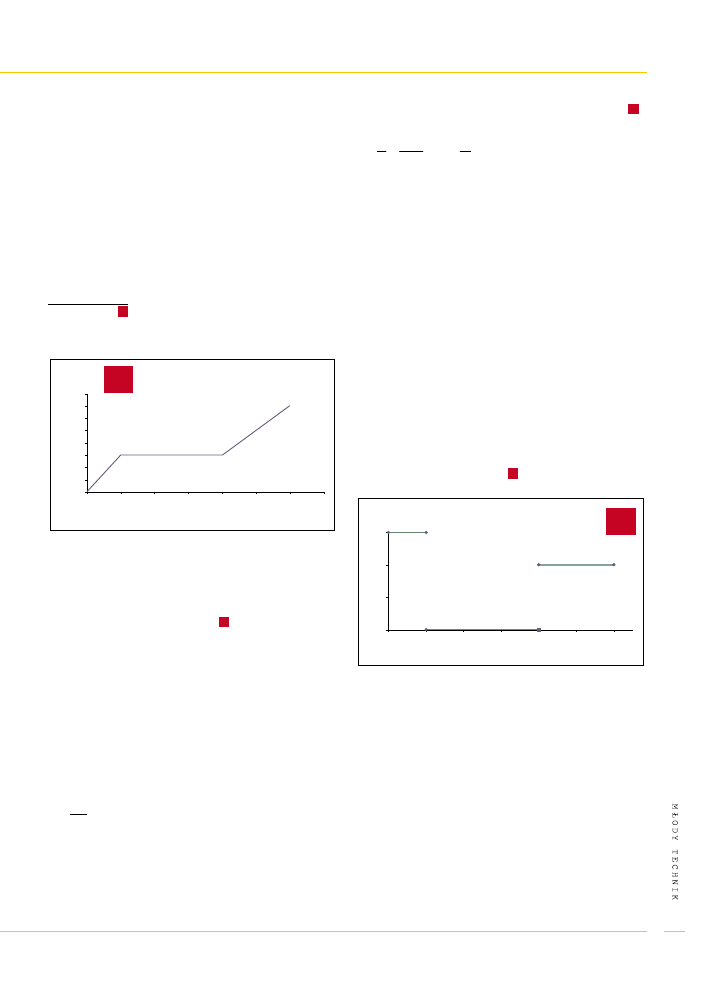
Wykresy w zadaniach z fizyki
Na lekcjach fizyki wykresy miêdzy innymi pojawiaj¹ siê
w trakcie omawiania ró¿nego rodzaju ruchów. Najczêœ-
ciej s¹ to wtedy wykresy prêdkoœci w funkcji czasu lub
drogi w funkcji czasu. Na pocz¹tek krótkie przypomnie-
nie. W ruchu jednostajnym po linii prostej wykres prêd-
koœci w funkcji czasu ma postaæ prostej równoleg³ej do
osi czasu. Wykres drogi w funkcji czasu jest prost¹ na-
chylon¹ do osi t pod pewnym k¹tem. W ruchu jednos-
tajnie przyœpieszonym wykres prêdkoœci od czasu ma
postaæ prostej nachylonej do osi czasu. Zaœ wykres dro-
gi w funkcji czasu ma kszta³t paraboli. Czêsto jednak
spotyka siê zadania na których wykres np. drogi od
czasu ma bardziej skomplikowany kszta³t Oto przyk³ad
takiego zadania

Zadanie 3

Na wykresie

pokazano zale¿noœæ drogi przebytej

przez pewne cia³o od czasu. Skonstruuj wykres prêd-
koœci od czasu.

Na pierwszy, rzut oka zadanie wydaje siê niezwykle
trudne. Przecie¿ na prezentowanym wykresie nie ma
s³owa o prêdkoœci. Ale za chwile poka¿emy, ¿e jednak
to siê da zrobiæ. £amana na rys.

sk³ada siê z trzech

odcinków, ka¿dy o ró¿nym k¹cie nachylenia do pozio-
mu. Oznacza to ¿e ruch odbywa³ siê w trzech etapach.
Pierwszy etap zakoñczy³ siê w 2 sekundzie ruchu, dru-
gi obejmowa³ okres od drugiej do 8 sekundy ruchu. os-
tatni okres od 8 do 12 sekundy. W ka¿dym z tych eta-
pów ruch mo¿na uwa¿aæ za ruch jednostajny po linii
prostej, chocia¿ ruch rozpatrywany w ca³ym okresie
czasu od zerowej do dwunastej sekundy nie by³ ru-
chem jednostajnym. W ka¿dym przedziale czasowym
prêdkoœæ by³a sta³a ale inna ni¿ w pozosta³ych. Prêd-
koœæ t¹ mo¿emy policzyæ pos³uguj¹c siê znanym wzo-
rem:

gdzie

S oznacza drogê, t – czas, zaœ v – szukan¹ przez

nas prêdkoœæ. Symbol

∆ oznacza ró¿nicê tak wiêc wyra-

¿enie

∆S nale¿y rozumieæ jako ró¿nica pomiêdzy koñco-

wym a pocz¹tkowym po³o¿eniem.

∆t z kolei nale¿y ro-

zumieæ jako czas trwania danego etapu ruchu.
Jednym z czêstszych b³êdów przy wyznaczaniu prêd-
koœci na podstawie takiej analizy jest bezpoœrednie

„sczytywanie” wartoœci bez uwzglêdnienia ró¿nic po-
miêdzy etapami. Uczniowie czêsto przeprowadzaj¹ na-
stêpuj¹ce rozumowanie

t = 12s, droga s = 14 m (rys.

,

linia przerywana) w zwi¹zku z tym prêdkoœæ wynosi

Nic bardziej b³êdnego.

Prawid³owe rozumowanie jest

nastêpuj¹ce. Ostatni trzeci etap ruchu trwa³ od 8 do 12
sekundy ruchu czyli

∆t = 12 – 8 = 4 [s]. W tym czasie

cia³o przeby³o drogê od 6 do 14 metra czyli

∆S = 8 [m].

Tak wiêc prêdkoœæ wynosi

2 m/s. (Otrzymany wynik jest

teraz ³adniejszy ni¿ ten poprzednio co mo¿e stanowiæ
dodatkow¹ przes³ankê co do poprawnoœci wykonanych
obliczeñ, autorzy zadañ staraj¹ siê je zazwyczaj tak uk-
³adaæ aby wyniki by³y liczbami ca³kowitymi.). W ten
sam sposób znajdujemy prêdkoœæ w pierwszym etapie
ruchu obejmuj¹cym okres od pocz¹tku ruchu do 2 s.
Tym razem

v = 3 m/s. Drugi 6-sekundowy okres ruchu

charakteryzowany jest odcinkiem równoleg³ym do osi
czasu co od razu informuje nas, ¿e prêdkoœæ w tym
przedziale czasowym wynosi 0.
Maj¹c wszystkie te dane mo¿emy przyst¹piæ do two-
rzenia wykresu. Wykres ten bêdzie mia³ postaæ odcin-
ków równoleg³ych do osi czasu (osi poziomej). Robi¹c
wykresy z fizyki nie wolno zapomnieæ o opisaniu osi
tzn. nale¿y podaæ po zewnêtrznej stronie osi symbol
wielkoœci bêd¹cej na osi i jej jednostkê. Pamiêtaj¹c
o tym mo¿emy skonstruowaæ wykres, który bêdzie
wygl¹da³ tak jak na rysunku

.

Na tym zakoñczê na razie moje rozwa¿ania na temat
wykresów i ich zastosowañ w matematyce i fizyce. Mo-
¿e oka¿¹ siê one dla was pewn¹ pomoc¹ w waszej ka-
rierze szkolnej. ¯yczê wielu zaliczonych klasówek
i zdanych egzaminów.

7









≈

=

=

s

m

s

m

t

S

v

16

,

1

12

14

6

t

S

v

∆

∆

=

6

6

3

3

Rys. 6

0

2

4

6

8

10

12

14

16

0246

8

10

12

14

t[s]

s[

m

]

Rys. 7

0

1

2

3

02

46

8

10

12

t[s]

v[

m

/s

]

Wykres do zadania 3. Zależność drogi od czasu.

6

7

Rozwiązanie zadania 3. Wykres przedstawiający
zależność prędkości od czasu.