Wyznaczanie reakcji w ramie statycznie wyznaczalnej przy
użyciu zasady prac wirtualnych
Zadanie
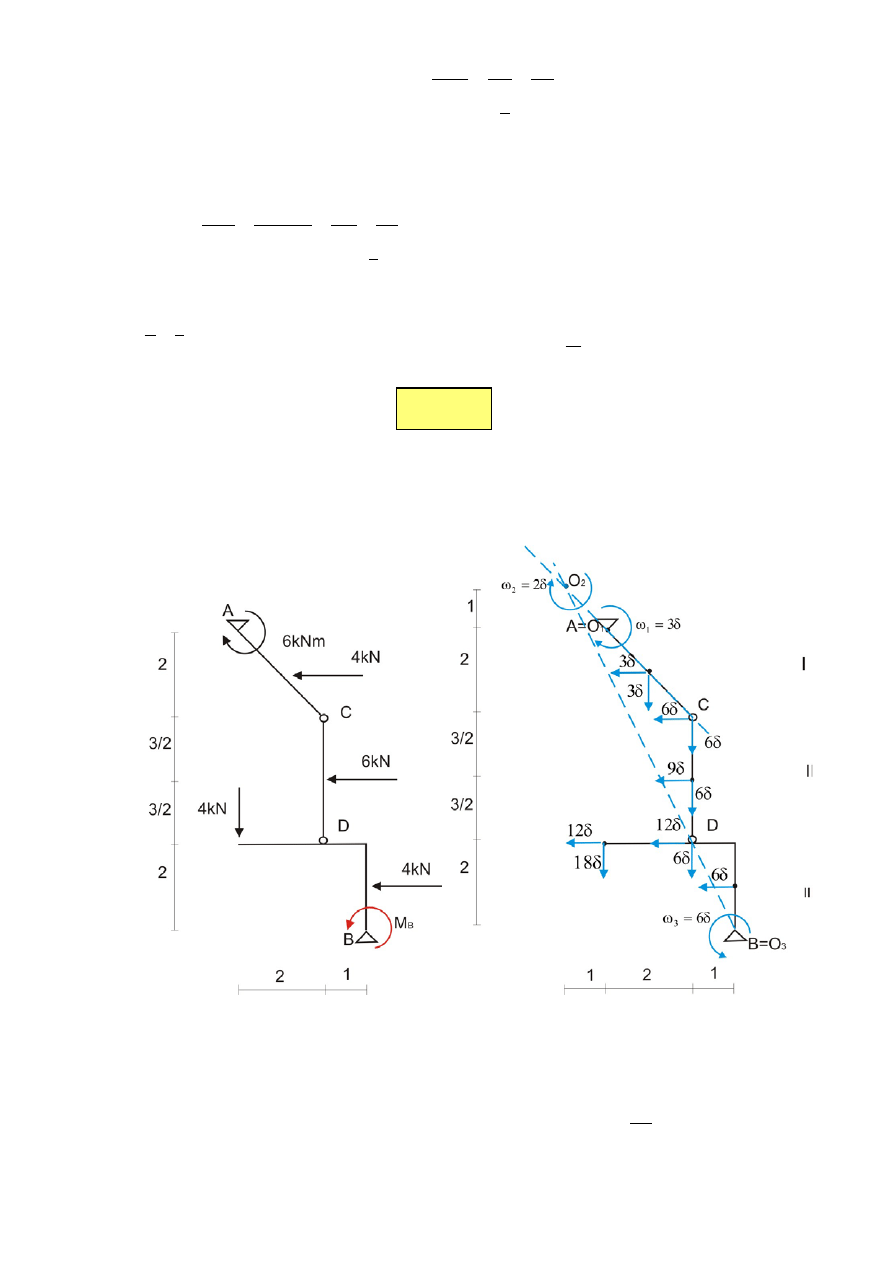
Korzystając z zasady prac wirtualnych wyznacz reakcje w ramie podanej na rysunku 1.
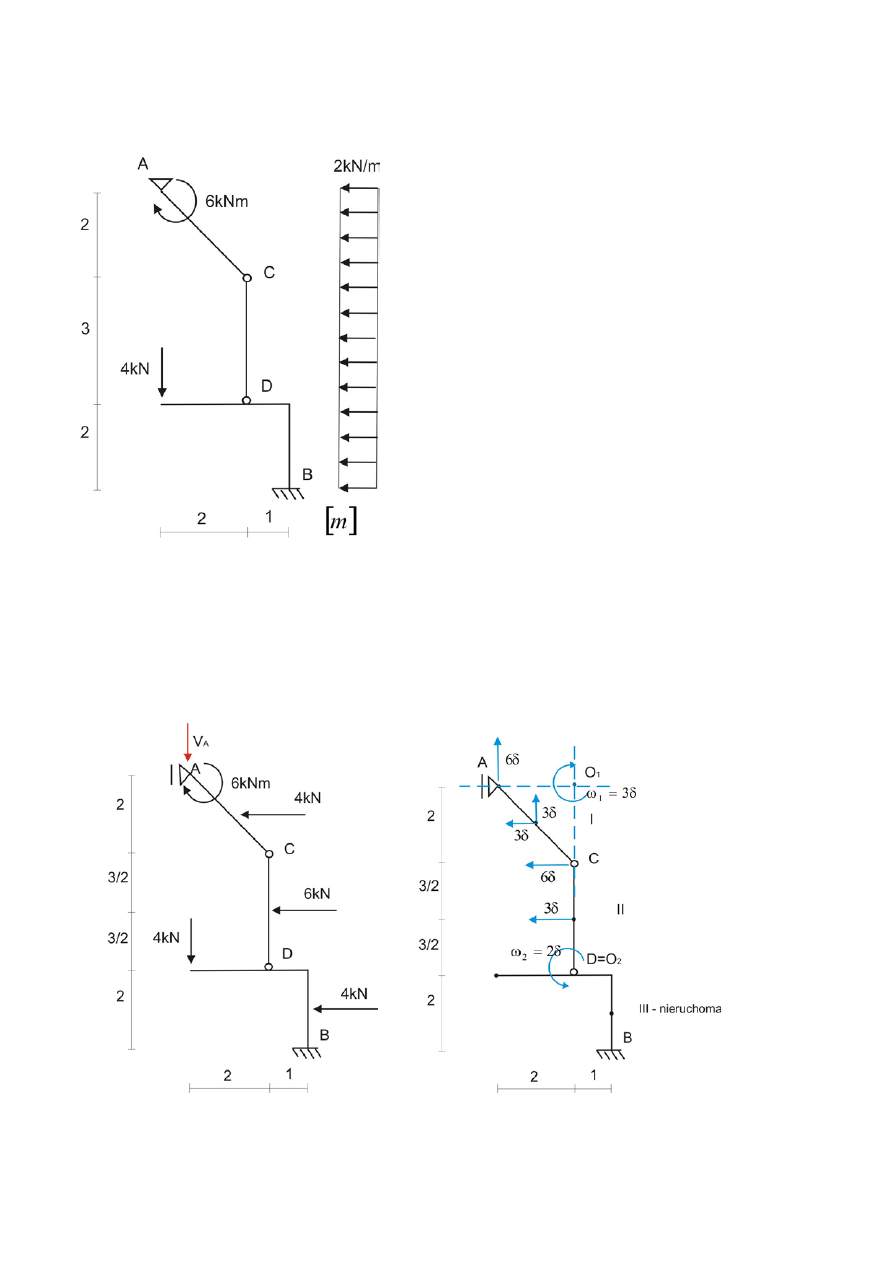
Rys.1
Rama jest złożona z trzech tarcz połączonych przegubami D i C.
Wyznaczenie każdej reakcji oznacza rozwiązanie osobnego zadania.
1. Wyznaczanie reakcji V
A
Podporę przegubową w punkcie A zastępujemy podporą przegubowo przesuwną z przesuwem
pionowym. Do układu sił czynnych dodajemy reakcję V
A
(rys. 2)
Rys.2 Rys.3
Wyznaczanie przemieszczeń wirtualnych (prędkości możliwych) układu (rys.3).
•
Analizę możliwych prędkości układu zaczynamy od tarczy III (najbardziej podpartej)
która jest nieruchoma.
• Nieruchomy przegub D jest
środkiem chwilowego obrotu tarczy II.
•
Przyjmujemy prędkość kątową tego obrotu jako
δ
ω
2
2
=
(jednostka
m
δ
- na rysunku
zaznaczona bez jednostek).
• Przy pomocy
2
ω
wyznaczamy przemieszczenia
wirtualne punktów bryły II (także
przegubu C).
•
Znając kierunek prędkości przegubu C oraz podpory A wyznaczamy środek chwilowego
obrotu tarczy I.
•
Wyznaczamy prędkość kątową
m
m
C
O
C
δ
δ
ω
3
2
6
v
1
1
=
=
=
zwrot przyjmujemy tak aby przy
obrocie wokół O
1
zgadzał się zwrot prędkości
C
v .
•
Prędkość kątowa
1
ω
pozwala wyznaczyć przemieszczenia wirtualne punktów tarczy I.
Zapisujemy zasadę prac wirtualnych dla układu:
(
)
δ
δ
δ
δ
δ
δ
δ
δ
∀
=
+
+
+
−
=
⋅
+
⋅
+
⋅
+
⋅
−
=
=
∑
0
18
18
12
6
3
6
3
6
3
4
6
kN
kN
kN
V
kN
m
kNm
kN
V
F
L
A
A
i
i
kN
V
kN
kN
kN
V
A
A
8
0
18
18
12
6
=
→
=
+
+
+
−
2. Wyznaczanie reakcji H
A
Podporę przegubową w punkcie A zastępujemy podporą przegubowo przesuwną z przesuwem
poziomym. Do układu sił czynnych dodajemy reakcję H
A
(rys. 4).
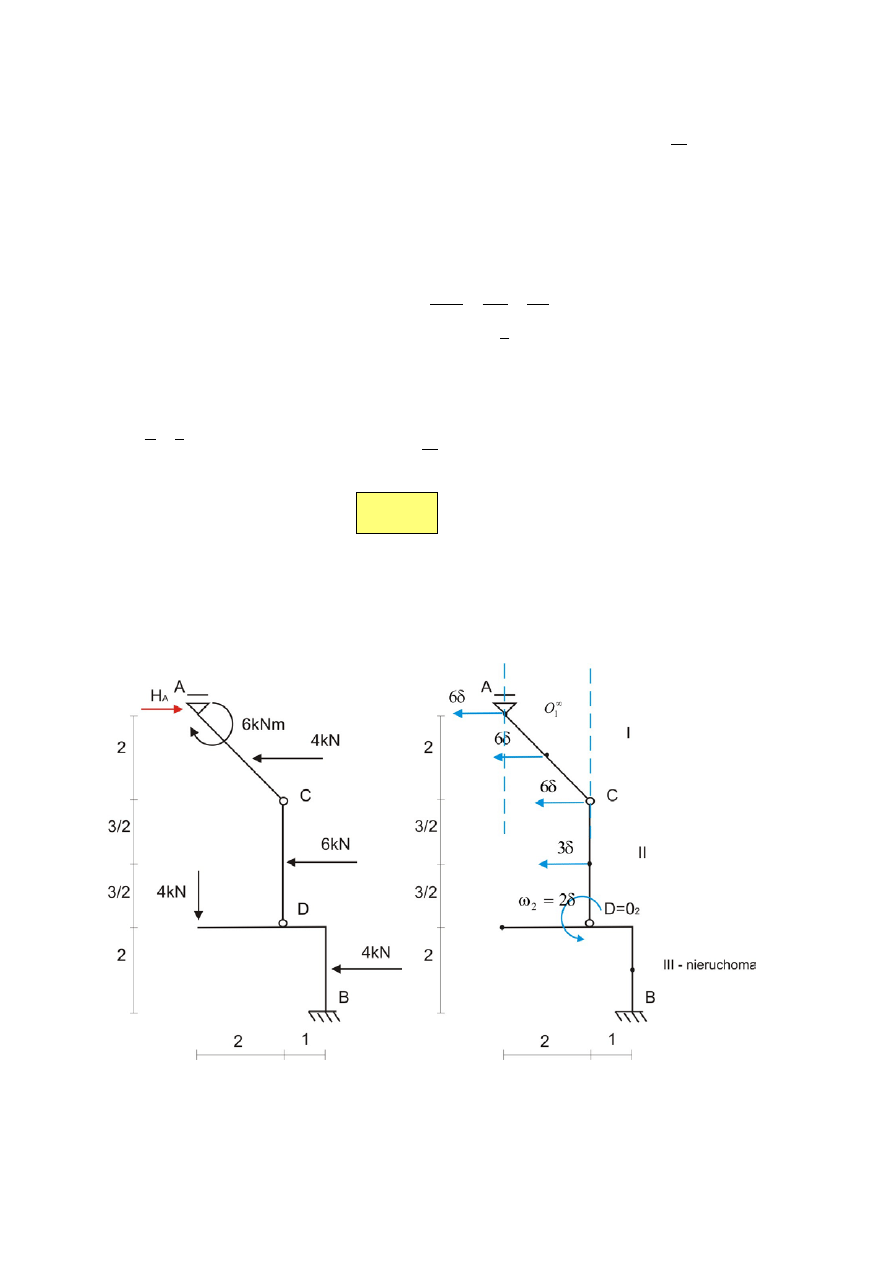
Rys. 4 Rys.5
Wyznaczanie przemieszczeń wirtualnych (prędkości możliwych) układu (rys.5).
•
Analizę możliwych prędkości układu zaczynamy od tarczy III która jest nieruchoma.
•
Nieruchomy przegub D jest środkiem chwilowego obrotu tarczy II.
•
Przyjmujemy prędkość kątową tego obrotu jako
m
δ
ω
2
2
=
• Przy pomocy
2
ω
wyznaczamy przemieszczenia wirtualne punktów bryły II (także
przegubu C).
•
Znając kierunek prędkości przegubu C oraz podpory A wyznaczamy środek chwilowego
obrotu tarczy I ( leży on w nieskończoności – bryła I porusza się poprzez poziomą
translację).
•
Wszystkie punkty bryły I mają takie same przemieszczenia wirtualne jak punkt C.
Zapisujemy zasadę prac wirtualnych dla układu:
(
)
δ
δ
δ
δ
δ
δ
δ
δ
∀
=
+
+
−
=
⋅
+
⋅
+
⋅
+
⋅
−
=
=
∑
0
18
24
6
3
6
0
6
6
4
6
kN
kN
H
kN
m
kNm
kN
H
F
L
A
A
i
i
kN
H
kN
kN
H
A
A
7
0
18
24
6
=
→
=
+
+
−
3. Wyznaczanie reakcji H
B
Utwierdzenie w punkcie B zastępujemy utwierdzeniem z przesuwem poziomym. Do układu sił
czynnych dodajem
y reakcję H
B
(rys. 6).
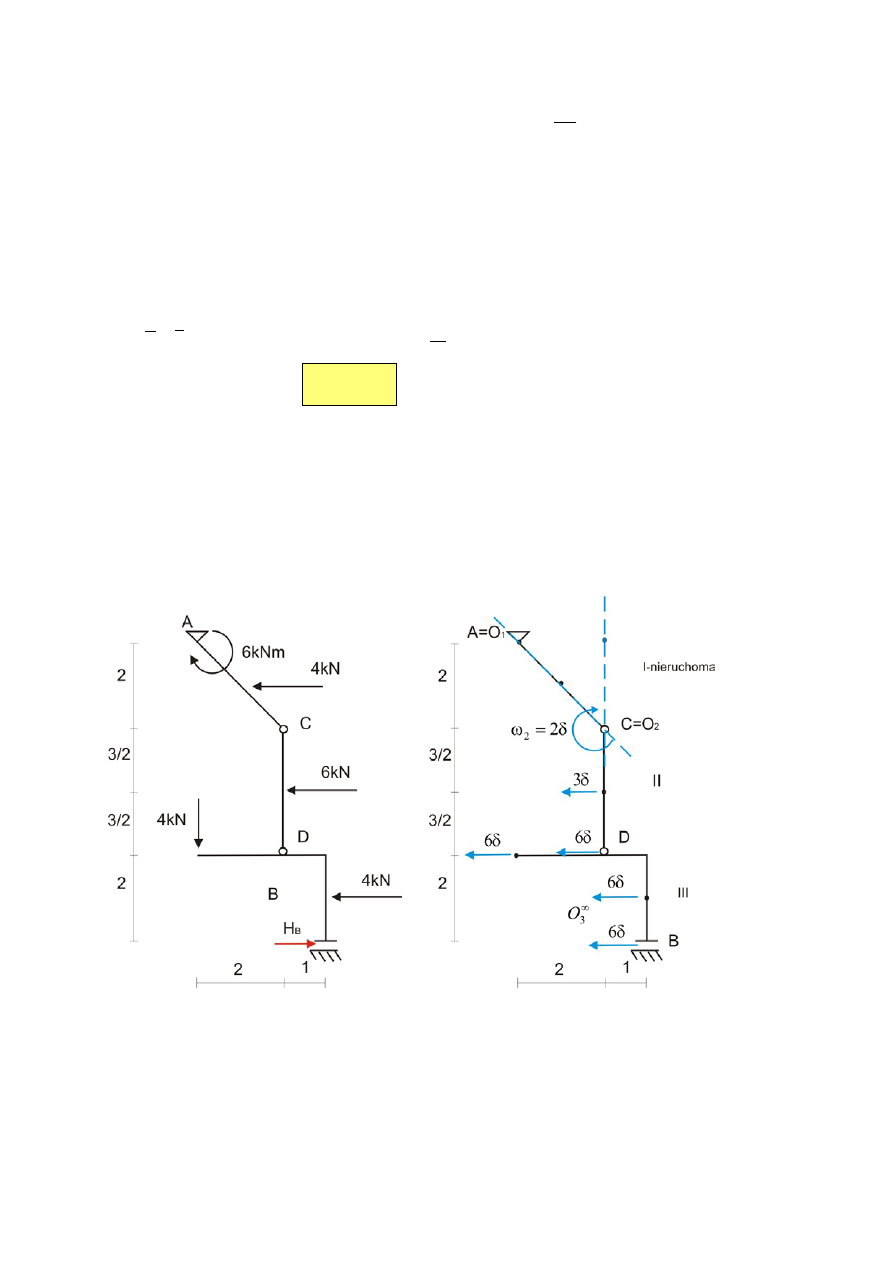
Rys. 6 Rys.7
Wyznaczanie przemieszczeń wirtualnych (prędkości możliwych) układu (rys.7).
•
Analizę możliwych prędkości układu zaczynamy od tarczy III która porusza się przez
poziomą translację. Przyjmujemy przemieszczenia wirtualne wszystkich punktów tej tarczy
jako
δ
6
.
•
Środek chwilowego obrotu tarczy II musi leżeć na prostej pionowej przechodzącej przez
punkt D. Jedn
ocześnie, (ponieważ środek obrotu tarczy I leży w podporze A) środek
obrotu tarczy II musi
leżeć na prostej AC. Te dwie proste przecinają się w punkcie C który
jest środkiem chwilowego obrotu tarczy II.
•
Wyznaczamy prędkość kątową
m
m
D
O
D
δ
δ
ω
2
3
6
v
2
2
=
=
=
, zwrot przyjmujemy tak aby przy
obrocie wokół O
2
zgadzał się zwrot prędkości
D
v .
•
Prędkość kątowa
2
ω
pozwala wyznaczyć przemieszczenia wirtualne punktów tarczy II.
• Tarcza I jest nieruchoma pon
ieważ ma dwa nieruchome punkty A i C.
Zapisujemy zasadę prac wirtualnych dla układu:
(
)
δ
δ
δ
δ
δ
δ
δ
∀
=
+
+
−
=
⋅
+
⋅
+
⋅
−
=
=
∑
0
18
24
6
3
6
6
4
6
kN
kN
H
kN
kN
H
F
L
B
B
i
i
kN
H
kN
kN
H
B
B
7
0
18
24
6
=
→
=
+
+
−
4. Wyznaczanie reakcji V
B
Utwierdzenie w punkcie B zastępujemy utwierdzeniem z przesuwem pionowym. Do układu sił
czynnych dodajemy reakcję V
B
(rys. 8).
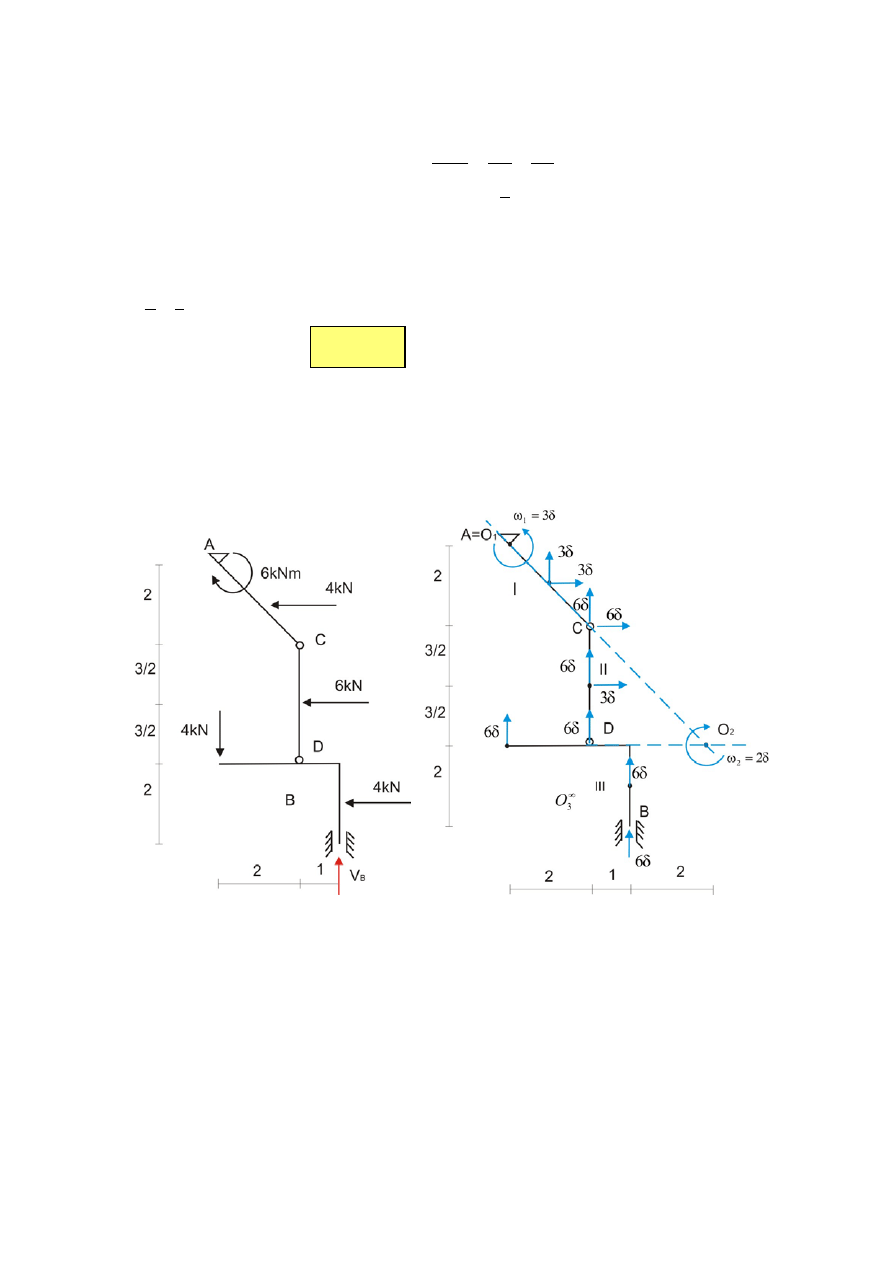
Rys. 8 Rys.9
Wyznaczanie przemieszczeń wirtualnych (prędkości możliwych) układu (rys.9).
•
Analizę możliwych prędkości układu zaczynamy od tarczy III która porusza się przez
pionową translację. Przyjmujemy przemieszczenia wirtualne wszystkich punktów tej tarczy
jako
δ
6
.
•
Środek chwilowego obrotu tarczy II musi leżeć na prostej poziomej przechodzącej przez
punkt D. Jednocześnie, (ponieważ środek obrotu tarczy I leży w podporze A) środek
obrotu tarczy II musi
leżeć na prostej AC. Te dwie proste przecinają się w punkcie O
2
który
jest środkiem chwilowego obrotu tarczy II.
•
Wyznaczamy prędkość kątową
m
m
D
O
D
δ
δ
ω
2
3
6
v
2
2
=
=
=
, zwrot przyjmujemy tak aby przy
obrocie wokół O
2
zgadzał się zwrot prędkości
D
v .
•
Prędkość kątowa
2
ω
pozwala wyznaczyć przemieszczenia wirtualne punktów tarczy II ( w
tym przegubu C).
•
Tarcza I obraca się wokół punktu A. Wyznaczamy jej prędkość kątową
m
m
C
O
C
O
X
CY
C
δ
δ
ω
3
2
6
)
(
v
v
1
1
1
=
=
=
=
, zwrot przyjmujemy tak aby przy obrocie wokół O
1
zgadzał się zwrot prędkości
C
v .
Zapisujemy zasadę prac wirtualnych dla układu:
(
)
δ
δ
δ
δ
δ
δ
δ
δ
δ
∀
=
−
−
−
−
=
=
⋅
−
⋅
−
⋅
−
⋅
−
⋅
=
=
∑
0
18
12
18
24
6
3
6
3
4
3
6
6
4
6
kN
kN
kN
kN
V
m
kNm
kN
kN
kN
V
F
L
B
B
i
i
kN
V
kN
kN
kN
kN
V
B
B
12
0
18
12
18
24
6
=
→
=
−
−
−
−
5. Wyznaczanie momentu M
B
Utwierdzenie w pun
kcie B zastępujemy podporą przegubową. Do układu sił czynnych dodajemy
moment utwierdzenia M
B
(rys. 10).
Rys. 10 Rys.11
Wyznaczanie przemieszczeń wirtualnych (prędkości możliwych) układu (rys.11).
•
Analizę możliwych prędkości układu zaczynamy od tarczy III która obraca się wokół
przegubu B. Przyjmujemy
prędkość kątową tej tarczy jako
m
δ
ω
6
3
=
.
•
Środek chwilowego obrotu tarczy II musi leżeć na prostej BD. Jednocześnie, (ponieważ
środek obrotu tarczy I leży w podporze A) środek obrotu tarczy II musi leżeć na prostej
AC. Te dwie proste przecina
ją się w punkcie O
2
który jest środkiem chwilowego obrotu
tarczy II.
•
Wyznaczamy prędkość kątową
m
m
D
O
D
O
Y
DX
D
δ
δ
ω
2
6
12
)
(
v
v
2
2
2
=
=
=
=
, zwrot przyjmujemy tak
aby przy obrocie wokół O
2
zgadzał się zwrot prędkości
D
v .
•
Prędkość kątowa
2
ω
pozwala wyznaczyć przemieszczenia wirtualne punktów tarczy II ( w
tym przegubu C).
•
Tarcza I obraca się wokół punktu A. Wyznaczamy jej prędkość kątową
m
m
C
O
C
O
Y
CX
C
δ
δ
ω
3
2
6
)
(
v
v
1
1
1
=
=
=
=
, zwrot przyjmujemy tak aby przy obrocie wokół O
1
zgadzał się zwrot prędkości
C
v .
Zapisujemy zasadę prac wirtualnych dla układu:
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
∀
=
+
+
+
+
+
=
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
=
∑
0
18
12
54
72
24
6
3
6
3
4
9
6
18
4
6
4
6
kN
kN
kN
kN
kN
m
M
m
kNm
kN
kN
kN
kN
m
M
F
L
B
B
i
i
kNm
M
kN
kN
kN
kN
kN
m
M
B
B
30
0
18
12
54
72
24
6
−
=
→
=
+
+
+
+
+
Zadania do samodzielnego rozwiązania:
Korzystając z zasady prac wirtualnych wyznacz reakcje podpór w zadaniach:
Zadanie 1 z pliku ‘zadania z reakcji 1.pdf’,
Zadania 1 i 2 z pliku ‘zadania z reakcji 2.pdf’.