Drying is a separation process that converts a wet solid,
semisolid, or liquid feedstock into a solid product by
evaporation of the liquid into a vapor phase with the
application of heat. Essential features of the drying
process are phase change and production of a solid.

Thermal drying is one of the most important unit

operations in most industrial sectors. Indeed, it is
hard to find a product in daily use that has not
undergone drying as a stage of its manufacture.

Drying is an essential operation in the chemical,

agricultural, biotechnology, food, polymer, ceramic,
pharmaceutical, pulp and paper, and wood process-
ing industries. Drying is extremely energy-intensive
and in many cases has important implications as
the thermal energy needed for drying is obtained by
combustion of fossil fuels, leading to emission of
carbon dioxide. Well-designed modern drying eq-
uipment with high thermal efficiencies is becoming
increasingly important.

One of the most widely used drying systems is

flash drying and is also known as pneumatic drying.
Flash dryers are most commonly direct drying units

and are also known as convective dryers. Pneumatic
or flash dryers may be classified as gas–solid transport
systems that are characterized by continuous convect-
ive heat and mass transfer processes. Hot air pro-
duced by indirect heating or direct firing is the most
common drying medium in these systems. In direct
flash dryers, the gas stream transports the solid par-
ticles through the system, and makes direct contact
with the material to be dried. This gas stream (drying
medium) also supplies the heat required for drying
and carries away the evaporated moisture. Super-
heated steam can also be used as drying medium
yielding sometimes to higher efficiencies and often to
higher product quality.

The large surface area for heat and mass transfer

and the high convective heat and mass transfer coef-
ficients, which take place at these units, result in high
drying rates and as a result, high drying capacity. The
size of particulates to be dried is usually in the range
of 10–500 mm. One of the features of these types of
dryers is the relatively short contact time between
the hot air and the particulate materials (0.5–10 s)
at the drying section. Because of this the material
temperature stays always low in the drying process.

2006 by Taylor & Francis Group, LLC.

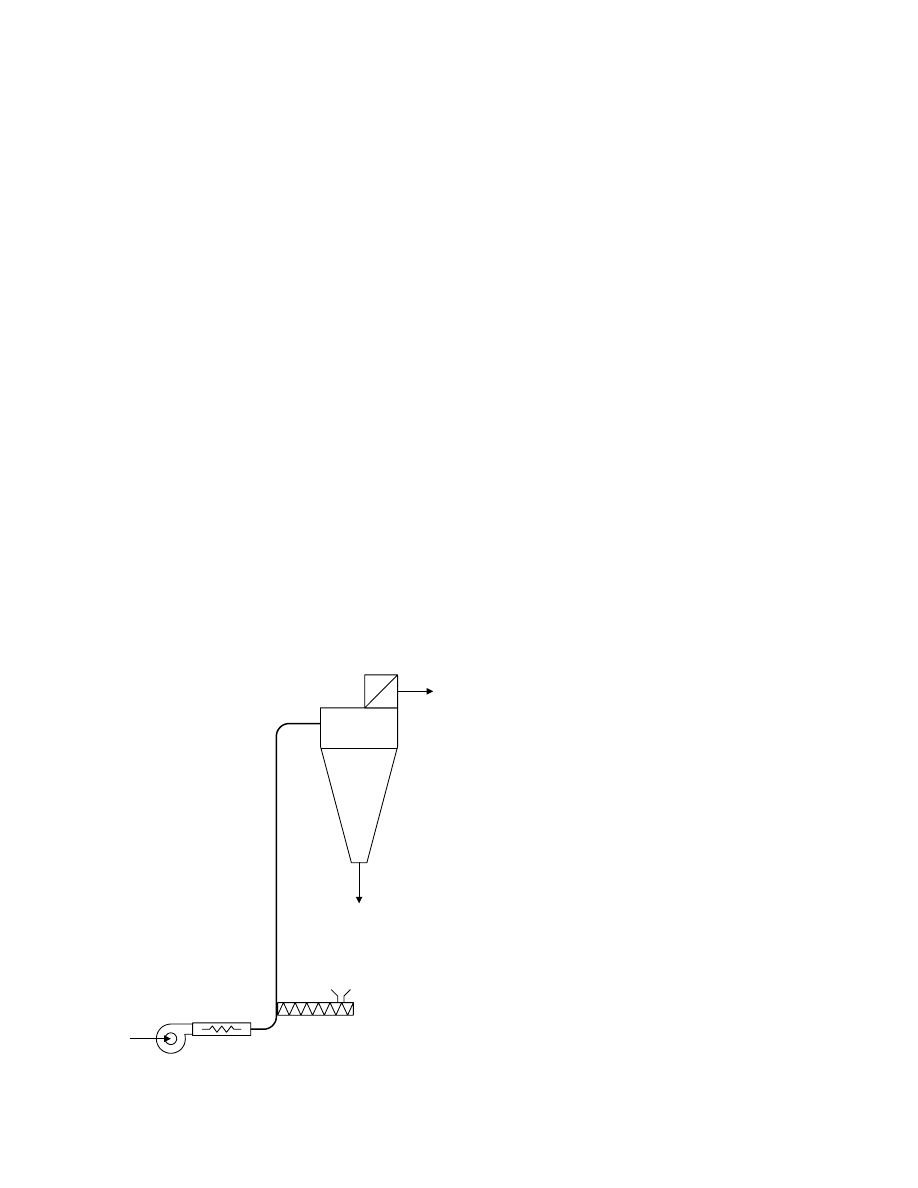
16.2 BASIC OPERATION PRINCIPLE AND

APPLICATIONS OF FLASH DRYERS

Figure 16.1 shows a simple pneumatic flash drying
system in which particulate solids are dried during
transport in a hot gas stream (usually air or combus-
tion gases). The simple flash drying system includes
six basic components: the gas heater, the wet material
feeder, the drying duct, the separator, exhaust fan,
and a dried product collector. The wet particles are
fed into the hot gas stream sometimes with special
mixing devices. The stream flows up the drying tube.
The gas velocity must be greater than the free fall
velocity of the largest particle to be dried. The gas
velocity in relation to the particle velocity is high.
Thermal contact between the conveying air and the
solids as mentioned above is usually very short and
therefore flash dryers are most suitable for removal of
external moisture (surface moisture) and are less suit-
able for removal of internal moisture. At the end of
the drying process a dust separation arrangement is
installed. It must comply with the regulations for
pollution control. For this purpose cyclone dust sep-
arators, fabric filters, electrostatic precipitators, wet
scrubbers, and fabric filters are used.

High rates of evaporation in flash dryers are lead-

ing to low temperatures of the dried material and
indicate that flash dryers are particularly useful for
drying granular, crystalline, pasty, and powdery prod-
ucts, etc. Flash dryers are used in various branches

of the chemical, pharmaceutical, ceramic, gypsum,
wood, and mining industries. Flash dryers are simple
in construction and have low capital cost and they are
almost trouble free.

Vertical type of construction, which facilitates in-

stallation in existing buildings, is advantageous for the
flash drying systems. The tube of most flash dryers is of
circular and uniform cross section. In some cases, the
tube may diverge and converge and may have sudden
expansions and contractions. The tube may be heated
through the wall to keep up the temperature of the gas.

In order to shorten the drying time, recirculation

of the material is used. In this case the number of
cycles of different particles may be different and as a
result the residence time of the particles will not be the
same. In conclusion the advantages of flash dryers are
the following:

Short contact time and parallel flow make
possible to dry thermolabile materials.

The dryer needs only a very small area and can
be installed outside a building. However, the gas
cleaning system should be located inside the
building in order to avoid moisture and dust
deposition.

The dryer is easy to control. The low mate-
rial content in the dryer enables equilibrium
conditions to be reached very quickly.

Due to small number of moving parts the main-
tenance cost is low.

The capital costs are low in comparison with
other types of dryers.

Simultaneous drying and transportation is useful
for materials handling process.

The disadvantages of flash dryers are as follows:

High efficiency of gas cleaning system is required.

Because of powder emission, the dryer cannot
be used for toxic materials.

In some cases this disadvantage can be avoided
using superheated steam as a drying agent.

For lumped materials difficult to disperse, drying
is impossible to carry out in this apparatus.

There is a risk of fire and explosion, so care
must be taken to avoid flammability limits in
the dryer.

In general, especially when recirculation is ap-
plied, not all material particles have the same
residence time in the dryer [1].

In order to achieve efficient pneumatic drying pro-
cess, the air velocity should be as low as possible to
achieve materials transport, the mass flow rate of the
gas should be the minimum necessary to achieve the

Air outlet

Heater

Air inlet

Wet material inlet

Feeder

Dry

product

Bag filter

FIGURE 16.1 Simple flash drying system.

2006 by Taylor & Francis Group, LLC.

specified drying rate, the temperature of the hot gas
should be as high as possible without exceeding limits
imposed by the thermal sensitivity of the solids or
safety considerations, and the construction of the
dryer should allow to achieve thermal equilibrium
between the gas and the solid [2].

16.3 DESIGN OF FLASH DRYERS

The materials dried in flash dryers have different
properties and each product requires specific design
solutions. It depends on the initial and final re-
quired moisture, temperature sensitivity, size and
shape of the particles, etc. Finally, each product to
be dried requires an optimum solution of the problems
involved (efficiency and product quality).

Design procedure of dryers has to find:

Dimensions of flash dryer

Choose the type and amount of drying agent

Requirement of energy supply

Inlet and outlet parameters for the drying agent
and material to be dried (temperature, moisture
content, velocity, etc.)

Basically, the design consists of execution of the fol-
lowing steps:

Heat balance

Mass balance

Momentum balance

Determination of heat and mass transfer co-
efficients

By design of the whole drying system, care must be
taken of the gas-heating unit, the material feed sec-
tion, the particle separation section, and the product
collection system.

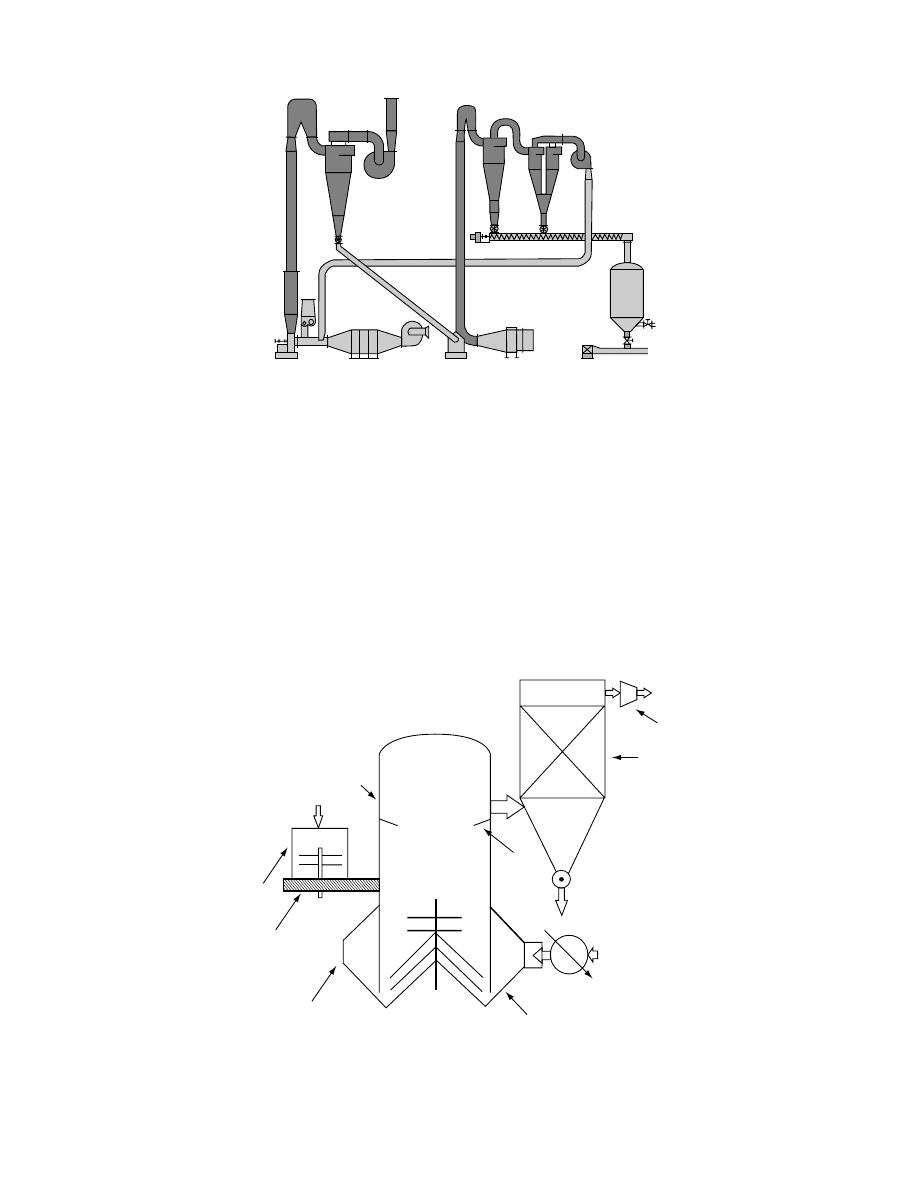
The feed system has to be carefully chosen and

designed in order to supply the wet material into the
dryer at the required rate. Typical feed systems are
shown in Figure 16.2 [3]. Metering and feed elements,
sometimes with mixing devices arranged upstream
lead the wet product into the flash dryer. For free-
flowing powdery solids, a screw feeder or a rotary
valve may be used effectively. Pasty or sticky mater-
ials need to be preconditioned by blending them with
dried product using single- or twin-shaft paddle
blender and then dispersed mechanically using a
kicker mill or one of the several other designs of
rotating disperser [4].

The selection of gas–solid separators is based

mainly on the material characteristics, required de-
gree of separation, concentration of solids, moisture
content of solids, environmental regulations, and cost.
In utilization are mainly: gravity separators; different
types of cyclones with different efficiencies; fabric fil-
ters, and wet scrubbers. Usually a combination of
separation units is applied.

There are different possibilities of modifications of

simple flash dryers. For instance in a simple flash
dryer a rapid decrease of drying force along the tube
takes place. The design of a dryer with internal pipe
through which hot drying agent is flowing leads to an
increase of the driving force. Another possibility to
increase the drying force is to heat up the tube of the
dryer through the wall.

In order to decrease the dryer height and increase

the drying tim e, the material is recircu lated. In

Fig-

ure 16.3

a two-st age syst em is present ed [3]. The solid

particles, after passing through the first stage, which
has the form of a vertical tube, are separated in the
upper part of the dryer, fall down, and are directed to
the second stage. Wet material is supplied to the first
stage by a special feeding system. Each drying stage in
the system is equipped with its own heat generator.
The drying agent from the second drying stage is fed

(a)

(b)

(c)

FIGURE 16.2 Typical feed systems for pneumatic flash dryers. 1, Wet product bin; 2, metering; 3, recirculated product; 4,
mixer; 5, sling; 6, flash dryer tube; 7, disc feeder. (From Flash Dryer, Deutsche Babcock, Babcock-BSH GMBH, 1998. With
permission.)

2006 by Taylor & Francis Group, LLC.

back to the first drying stage. This system is particu-
larly efficient if the drying agent is superheated steam.
Separation is by means of cyclone separators.

A second drying stage can also be used as a cool-

ing stage. Two-stage flash dryers can be used for
products difficult to dry, e.g., for methylcellulose.
The number of cycles of different particles in two-
stage systems may be different and as a result the
resistance time of the particles will not be the same.

For longer resistance times the duct can be formed

into a continuous loop (ring dryers). In these systems

the material is recirculated until it is dried to the
required humidity. For instance high-temperature
short-time ring dryers are used in the food industry
to expand the starch cell structure in potatoes or
carrots to give a rigid porous structure, which enhances
conventional drying rates [5].

Figure 16.4 presents a spin-flash dryer that can be

utilized for some special applications. As described in
Ref. [4] the spin-flash dryer is basically a mechanically
agitated fluidized bed device for very short resi-
dence times. Hence it is targeted for surface moisture

FIGURE 16.3 Two-stage pneumatic dryer with vapor utilization. 1, Wet product; 2, primary air inlet; 3, heat generator;
4, fan; 5, dryer tube; 6, cyclones; 7, cyclone separator; 8, predried product discharge; 9, dried product discharge; 10, vapor
return line; 11, waste gas stack. (From Flash Dryer, Deutsche Babcock, Babcock-BSH GMBH, 1998. With permission.)

Exhaust air

Fan

Bag filter

Orifice

Dried solids

Inlet air

Air heater

Annular air inlet

Rotor

Hot air plenum

Solids feeder

Feed hopper

and agitator

Wet feed

Drying chamber

FIGURE 16.4 Spin-flash dryer. (From Devahastin, S. (Ed.), Mujumdar’s Practical Guide To Industrial Drying—Principles,
Equipment And New Developments, Exergex Corporation, Montreal, Canada, 2000. With permission.)

2006 by Taylor & Francis Group, LLC.

remova l. As can be seen in

Figure 16.4

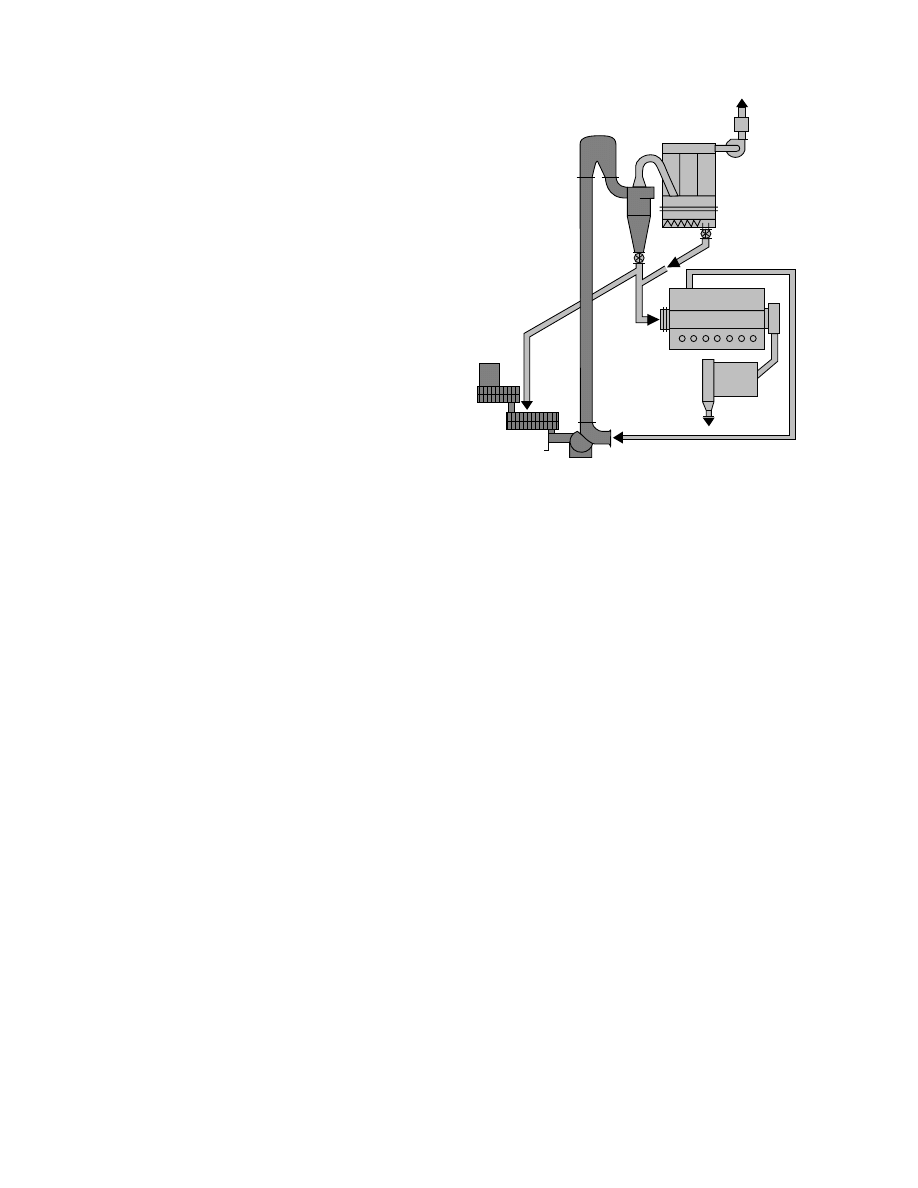
, a rotor,

placed at the bottom of the chamber, is used to dis-
perse the feed, which falls into the agitated fluidized
bed by gravity. Hot drying air enters the chamber
tangentially and spirals upward, carrying and drying
the dispersed particles. The exhaust air containing the
dried powder is entering into a separation device,
which separates the powder from the exhaust air.
Heavier wet particles remain within the drying cham-
ber for a longer time and are broken up by the rotor.
Thus only dried fine powder can escape to the gas
separation system. This type of dryer can be a re-
placement for the more expensive spray dryer (which
needs more thermal energy because the feed is wetter
due to the pumpability requirements and also expen-
sive because of the need for an atomizer). It is suited
for drying sludge, pulps, pastes, filter cakes, high
viscosity liquids, without the use of an atomizer. Nu-
merous materials have been dried successfully in such
units at capacities up to 10 tons/h. The spin-flash
dryer units are more expensive than the conventional
flash or fluidized bed dryers. Care must be taken to
ensure that there is no danger of product accumulation
on the walls due to stickiness.

Flash dryers using superheated steam as drying

medium instead of air have some advantages such as
no fire or explosion risk and higher efficiency (if
exhaust steam is utilized elsewhere in the process). It
is well known that in air-drying units the latent heat
in exhaust gases is difficult to recover. Sometimes the
quality of the dried product in superheated steam
dryers is superior in comparison to air-drying units.
The limitations of using superheated steam as drying
medium are that the system itself and the operation
of the system are more complex. Leaks are pro-
hibited as noncondensables cause problems with
energy recovery by condensation or compression of
the exhaust steam. The feeding and discharge pro-
cess must not allow infiltration of air and start-up
and shutdown processes are more complex than for
air dryers.

As mentioned by Devahastin [4] more recently

flash dryers consisting of inert media have been
employed at pilot scales to dry slurries and suspen-
sions, which are sprayed onto them. The particles are
coated thinly by the slurry and dried rapidly as a thin
film. Due to particle–particle interactions, particle
collisions, and shrinkage of the film in the drying
process, the powder from the slurry is produced.

Flash dryers can be used as a drying stage in more

complex systems for instance as a predrying stage to a
fluidized bed dryer (batch or continuous) or fluidized
bed cooler, spray dryer, drum dryer, etc. In the food
industry flash dryers are often used after spray drying
to produce foods that have a lower moisture content

than normal like special milk or egg powders and
potato granules [5].

In Figure 16.5 a flash dryer is used as a drying

stage in a complex system with a rotary calcining
unit [3]. The drying agent in the flash dryer is indir-
ectly heated in the calcining unit. Such arrangement
provides sufficient heat utilization and is used by
Babcock BSH for instance, for catalyst compounds
and other products.

16.4 MATERIALS DRIED IN FLASH DRYERS

Flash dryers are suitable for drying granular, pow-
dery, pasty, and crystalline products. As mentioned
above the residence time of the particles in the dryer is
very short that leads to the fact that only products
containing surface moisture can be dried in flash
dryers. Drying of heat-sensitive products in this type
of dryers is very useful. Flash dryers are successfully
used in the chemical, food, pharmaceutical, mining,
ceramic, and wood industries. Some of the materials
dried in flash dryers as described by Kisaku¨rek [6] are:

Magnesium sulfate, magnesium carbonate, copper

sulfate, dicalcium phosphate, ammonium sulfate and
phosphate, calcium carbonate and phosphate, and
boric and adipic acids are common examples of chem-
icals and by-products. Antibiotics, salt, blood clot,

FIGURE 16.5 Flash dryer as a drying stage. 1, Wet product
feed; 2, flash dryer; 3, cyclones; 4, fabric filter; 5, indirectly
heated rotary calciner; 6, cooler, final product discharge.
(From Flash Dryer, Deutsche Babcock, Babcock-BSH
GMBH, 1998. With permission.)

2006 by Taylor & Francis Group, LLC.

bonemeal, bread crumbs, cornstarch, corn gluten,
casein, gravy powder, soup powder, vegetable pro-
tein, spent tea, wheat starch, soybean protein, meat
residue, and flour are examples of food products.
Cement, aniline dyes, blowing agents, chlorinated
rubber, coal dust, copper oxide, gypsum, iron oxide,
and silica gel catalyst are typical by-products and
minerals that can be dried in a very efficient way
in flash dryers. Flash dryers are widely used in the
plastic and polymer industries.

16.5 MODELING AND SIMULATIONS OF

PNEUMATIC AND FLASH DRYERS

Mathematical modeling is a very important aspect in
drying technology, allowing the engineer to choose
suitable operating conditions for the chosen method
of drying and if necessary apply scale-up procedures
[7]. It should be kept in mind that the developed
mathematical model should be experimentally valid-
ated in order to use it as a design tool. Reliable
mathematical modeling for conveying of various
powders in a dilute phase pneumatic conveying sys-
tems was developed and validated during the last
three decades [8–11]. In a dilute phase flow, com-
monly referred as a suspension flow, the transport
velocity is sufficient to ensure that the majority of
the particles are suspended in the conveying gas.
Since the particles in pneumatic and flash dryers are
conveying in a suspension mode of flow, the various
models, which were developed for pneumatic trans-
port systems, were extended to model the flow in pneu-
matic and flash dryers by including heat and mass
transfer between the particles and the conveying gas.

In general, two approaches can be used for mod-

eling the flow through pneumatic and flash dryers.
The first approach is based on empirical correla-
tions for specific dryer and dried products. In this
approach, a variety of semiempirical correlations
[12–14] for estimating the pressure drop have been
proposed for gas–solids flow in pipes. Frequently
these models consider the total pressure drop as the
sum of gas and solids pressure drop components:

¼ Dp

þ Dp

(16:1)

This type of relationship is usually employed in the
analysis of experimental data, where the total pres-
sure drop is measured and the gas pressure drop
component is evaluated by assuming that only gas is
flowing in the pipe. A correlation may then be derived
for the solids pressure drop component. Examples of
this type of approach are the work of Muschelknautz
and Wojahn [9], Pan and Wypych [12], and Mason

et al. [13]. Pan and Wypych [12] employed a modified
version of Equation 16.1 by expressing the solids
pressure drop as a function of the gas pressure drop
multiplied by the solid loading ratio and a corrected
friction factor as follows:

¼ (1 þ a)Dp

(16:2)

¼ 4f

1
2

(16:3)

(16:4)

A similar approach was adopted by Mason et al. [13]
and Bradley et al. [15] for estimating the pressure
drop caused by bends in the pneumatic transport
system.

In order to estimate the moisture content of the

particle at the dryer outlet, two additional common
assumptions are needed, namely isothermal flow and
particle’s exit temperature similar to the gas tempera-
ture. Based on these assumptions, various macro-
scopic mass and energy balance equations can be
solved [16,17].

The second approach is based on theoretical and

mathematical modeling for gas–particle flows. Three
types of theoretical approaches can be used for mod-
eling the gas–particle flows in the pneumatic dryer,
namely two-fluid theory [18], Eulerian granular [19],
and discrete element method [20,21]. Both the two-
fluid theory and the Eulerian granular theory are
based on macroscopic balance equations of mass,
momentum, and energy for both the gas and the
solid phases. It is assumed that both phases are
occupying any point (x, y, z) of the computational
domain with its own volume fraction. The solid phase
is considered as a pseudofluid. The main difference
between these theories is that the Eulerian granular
method employs the kinetic theory of rarify gases to
model the granular phase properties, such as pressure,
temperature, viscosity, etc., whereas the two-fluid the-
ory uses macroscopic correlations to model similar
properties for the solid phase. It should be noted
that traditionally, the two-fluid theory was widely
used to model dilute phase flow whereas the Eulerian
granular was used to simulate both dense and dilute
phase flows. Unlike these theories, the discrete elem-
ent method is an Eulerian–Lagrangian approach, in
which the gas phase is assumed as the continuous
phase, which occupies every point in the computa-
tional domain, and the solid particles are occupying
discrete points in the computational domain. As a

2006 by Taylor & Francis Group, LLC.

consequence, mass, momentum, and energy balance
equation should be solved for each particle within the
computational domain. This method is able to take
into account various types of particle–particle and
wall–particle interactions from the basic dynamic ap-
proach and gas–particle interactions from the basic
hydrodynamic models for the flow of a single particle
through a conveying phase. Hence, there is no need to
develop or to use macroscopic modeling for the trans-
port of heat and mass from the solid phase to the
conveying gas. This modeling needs large amount of
memory and CPU time in order to solve real prob-
lems, which include millions of particles. As a result,
no full-scale three-dimensional problem has been
solved yet by using the discrete element method.

16.5.1 H

YDRODYNAMIC

ODELS

Many researches adopted one of the above-mentioned
approaches and modified it to include various aspects
of the pneumatic drying process. Andrieu and Bressat
[16] presented a simple model for pneumatic drying of
PVC particles. Their model was based on elementary
momentum, heat, and mass transfer between the fluid
and the particles. In order to simplify their model,
they assumed that the flow is unidirectional, the rela-
tive velocity is a function of the buoyancy and drag
forces, solid temperature is uniform and equal to the
evaporation temperature and that evaporation of free
water occurs in a constant rate period. Based on their
simplifying assumptions, six balance equations were
written for six unknowns, namely relative velocity, air
humidity, solid moisture content, equilibrium humid-
ity, and both solid and fluid temperatures. The model
was then solved numerically and satisfactory agree-
ment with their experimental results was obtained.
Similar model was presented by Tanthapanichakoon
and Srivotanai [22]. Their model was solved numeric-
ally and compared to their experimental data. Their
comparison between the experimental data and their
model predictions showed large scattering for the gas
temperature and absolute humidity. However, their
comparisons for the solid temperature and the water
content were failed.

Mindziul and Kmiec [23–25] investigated the aero-

dynamics of the gas–solid flow in a pneumatic flash
dryer. Their mathematical model was based on the
continuity equation for both the gas and the solid
phase and momentum equations for the solid phase
and the solid–gas mixture. Heat and mass transfer
were neglected. Although the drying apparatus was
composed of three elements with varying cross-
sectional area, one-dimensional model was solved.
The effect of various empirical correlations for solid-
wall friction factor has been investigated. The results

of the numerical calculations were partially compared
with experimental data and the influence of the fric-
tion factor on the pressure, gas and particle velocities,
voidage and residence time of particle along the axis
of the apparatus have been presented.

Blasco and Alvarez [26] and Alvarez and Blasco

[27] considered the application of flash drying to
moisture removal of fish and soya meals. Heat, mo-
mentum, and mass balance equations were formu-
lated. The model was solved numerically with
appropriate coefficients of convective heat and mass
transfer. Dilute phase transport of homogeneous ra-
dial monosize particle distribution was considered.
The conveying superheated steam was assumed to
be an ideal gas. The initial period for heating the
particles, during which condensation takes place,
was neglected. Using the film theory [28], the effect
of the mass transfer on the heat transfer coefficient
was considered. A variable diffusivity model was util-
ized for the prediction of the drying rate during the
postcritical drying period. Using a pulse technique
under isothermal conditions, the empirical param-
eters of the variable diffusivity model were experi-
mentally determined. The predictions of the model
were then compared with their experimental data
and good agreement was presented.

Kemp et al. [29] presented a theoretical model for

particle motion, heat and mass transfer, and drying
rates in vertical tubular pneumatic conveying dryers.
The model was one dimensional and it took into
account particle–wall interaction, feed agglomeration
effects, and the effect of particle shape on the drag
factor. The flow pattern at the inlet, near the feed point,
was neglected, i.e., fully developed flow. Kemp and
Oakley [17] extended this model and employed it for
simulating co- and countercurrent dispersion-type
dryers. Equations for particle motion, heat and mass
transfer, heat and mass balance, and local gas condi-
tions were solved simultaneously over a small one-
dimensional increment along the dryer. Using the
Ranz–Marshal and modified Weber heat transfer cor-
relations, the moisture content of the particles was
underestimated. Similar observations were obtained
by Baeyens et al. [30] and Levy and Borde [31]. Since
the heat transfer correlations were obtained for a
single particle, it is not therefore surprising that the
proximity of other particles in the conveying system
reduces the heat and mass transfer rates. In order to
overcome this problem, Kemp and Oakley [17] ap-
plied a fitting mode procedure to achieve good agree-
ments between their numerical simulations and the
experimental data.

Silva and Correa [32] used DryPak for simulating

the drying of sand in a pneumatic dryer. Their pre-
dictions were compared with the experimental results

2006 by Taylor & Francis Group, LLC.

and the two models of Rocha [33]. The main differ-
ences between the DryPak and Rocha mathematical
models and their assumptions are given below.

16.5.1.1 Rocha [33] Models

The basic difference between both models is related to
conservation equation of momentum. In the first
model (Model a), the momentum conservation equa-
tion for the fluid as a mixture of fluid and particles
was solved, whereas in the second model (Model b),
conservation of momentum for each phase was
solved. For both models, the following assumptions
were considered: steady-state one-dimensional flow;
nonhygroscopic spherical particles; no shrinkage dur-
ing drying; plug flow for both phases; uniform prop-
erties and geometry at a pipe cross section; work done
between the phases was neglected. Based on the
above-mentioned assumptions, mass, momentum,
and energy balance equations were formulated for
the mixture and the solid phase. The correlation of
Ranz and Marshall was used for calculating the heat
and the mass transfer coefficients. Although Rocha
[33] introduced a heat transfer term from the fluid
phase to the ambient, no specific model was presented.

16.5.1.2 DryPak Model [34]

All the assumptions, which were considered by Rocha
[33], were also considered in DryPak balance equa-
tions, with the exception that in DryPak adiabatic
flow conditions were assumed. Other differences
were in the way of calculating the area for heat and
mass transfer and modification of the heat and mass
transfer coefficients. DryPak used the Frossling equa-
tion for calculating the Nusselt number. Different
types of heat and mass transfer analogies were pre-
sented and Ackermann correction was used to include
the influence of mass transfer on the heat transfer
coefficient. It should be noted that unlike Rocha [33]
models, DryPak can take into account particles
shrinkage; internal resistance to heat and mass trans-
fer; and moisture content profile inside the particle
could be obtained, although it was not used in the
study of Silva and Correa [32]. Silva and Correa [32]
concluded that predictions of DryPak produced
better agreements with experimental data than the
numerical results of Rocha [33].

Levy and Borde [35] adopted the two-fluid theory

for modeling the flow of particulate materials through
pneumatic dryer. The model was solved for a one-
dimensional steady-state condition and was applied
to the drying process of wet PVC particles in a large-
scale pneumatic dryer and to the drying process of
wet sand in a laboratory-scale pneumatic dryer.

A two-stage drying process was implemented. In the
first drying stage, heat transfer controls evaporation
from the saturated outer surface of the particle to the
surrounding gas. At the second stage, the particles
were assumed to have a wet core and a dry outer
crust; the evaporation process of the liquid from a
particle assumed to be governed by diffusion through
the particle crust and by convection into the gas
medium. As evaporation proceeds, the wet core
shrinks whereas the particle dries. The drying process
is assumed to stop when the moisture content of a
particle falls to a predefined value or when the particle
reaches the exit of the pneumatic dryer. The devel-
oped model was solved numerically and two operat-
ing conditions, adiabatic and given pneumatic dryer
wall temperature, were simulated. Comparison be-
tween the prediction of the numerical models of
Rocha and DryPak [34], which were presented by
Silva and Correa [32], with the prediction of our
numerical simulation revealed better agreements
with DryPak than with the models of Rocha. The
results of the developed model were also compared
with experimental results of Baeyens et al. [30] and
Rocha [33].

Rocha and Paixa˜o [36] presented a pseudo two-

dimensional mathematical model for a vertical pneu-
matic dryer. Their model was based on the two-fluid
approach. Axial and radial profiles were considered
for gas and solid velocity, water content, porosity,
temperatures, and pressure. The balance equations
were solved numerically using a finite difference
method and the distributions of the flow field charac-
teristics were presented. This model was not validated
with experimental results.

Silva and Nerba [37] also used the two-fluid ap-

proach and presented a mathematical model of drying
in cyclone. Slip condition of particles on the wall,
particle–wall heat transfer, and particles shrinkage
were considered. The mathematical model considered
a steady state, incompressible, two-dimensional, axi-
symmetric, turbulent gas–solids flow. The gravity
force effect on the particles was neglected. The par-
ticles were assumed to be spherical and distributed in
a layer of uniform concentration on the cyclone wall
and a very small concentration in the central flow.
The discretized balance equations were solved by the
SIMPLE algorithm [38]. Silva and Nerba [37] com-
pared the predictions of their numerical simulations
with experimental results and claimed that the most
influencing parameters on the predictions are the par-
ticle slip conditions and the material shrinkage during
the drying process.

Unlike the above-mentioned models, Fyhr and

Rasmuson [39,40] and Cartaxo and Rocha [41] used
an Eulerian–Lagrangian approach, in which the gas

2006 by Taylor & Francis Group, LLC.

phase is assumed as the continuous phase and the
solid particles are occupying discrete points in the
computational domain. As a consequence, mass, mo-
mentum, and energy balance equations were solved
for each particle within the computational domain.

Fyhr and Rasmuson [39,40] presented a two-

dimensional model for superheated steam drying of
wood chips in a pneumatic conveying dryer. One-
dimensional plug flow was assumed. Steady-state sin-
gle particle flow and drying models were solved inter-
actively. Particle–particle interactions were neglected.
The irregular movement and the nonsphericity shape
of the wood chips were accounted by measuring
drag and heat transfer coefficients. The predictions
of the temperature and the pressure profiles as well as
the final moisture content of bark chips agreed well
with experimental results. Based on the model valid-
ation, a parametric study was conducted. The calcu-
lation showed that the drying rate varies in a very
complex manner through the dryer. The internal re-
sistance to mass transfer becomes a dominant factor
in the drying of less permeable wood chips. As the
particle size was increased, the heat transfer rate de-
creases and the residence time increases. Hence, they
concluded that less permeable wood species or larger
chips size leads to longer dryer in order to obtain the
desired final moisture content.

Another two-dimensional, discrete element model

was presented by Cartaxo and Rocha [41]. In this
work, only the dynamic phenomenon was investi-
gated (i.e., heat and mass transfer between the phases
were not considered). Thus the influence of the mo-
mentum coupling between the discrete particles and
the conveying air on the air radial velocity and the
mass concentration profiles were presented. An ob-
ject-oriented numerical model was developed to simu-
late the conveying of large spherical particles (3 mm)
through 9.14 m vertical tube with 7.62 cm bore size.

16.5.2 T

-F

LUID

ODEL

ALANCE

QUATIONS

In the following, the Eulerian governing equations for
the pneumatic drying process are presented in their
three-dimensional form. These equations are based
on the two-fluid approach [18].

16.5.2.1 The Continuity Equations

The continuity equation for the k-phase is given by

(«

)

þ r («

)

¼ S

(16:5)

where k-phase can be the gas or the solid phase, «

, r

and V

are the volume fraction, the density, and the

velocity vector of the k-phase. The mass source term
of the k-phase is S

and to maintain the conservation

of mass S

¼ S

16.5.2.2 The Momentum Equations

The momentum equation for the k-phase is given by

(«

)

þ r [«

]

¼ r [«

]

r(«

)

þ «

þ M

þ S

(16:6)

Generally, the variation of the solid’s density, which
composes the wet particle, is less than few percent. As
a consequence, constant solid density may be as-
sumed to simplify the model. Thus by using the mix-
ture theory the density of the dispersed phase can be
expressed as

(16:7)

where j is the liquid mass ratio in the particle and r

and r

are the densities of the liquid and the solid,

which compose the particle. Another common as-
sumption is that the conveying air behaves as an
ideal gas. Thus the gas pressure–density relation is
described by

¼ r

R T

(16:8)

The effective normal stress of the solids phase may be
written as a sum of the sheared gas pressure and the
solids contact stress. Thus the effective normal stress
of the solid phase is described by

¼ r

R T

þ s

(«

=«

)

1=b

(16:9)

where s

is a particular value of the solids contact

stress for solid volume fraction «

and b is a constant

coefficient over a given range of contact pressure
[42,43].

The interphase momentum transfer is represented

¼ K(V

)

þ P

r«

(16:10)

The interphase momentum transfer term can be de-
rived from correlation developed to model fluidi-
zation

processes,

since

the

range

solids

concentrations experienced in pneumatic transport
systems is similar. This form has been employed by
Patel and Cross [44] for modeling gas–solid fluidized

2006 by Taylor & Francis Group, LLC.

beds. For solids co ncentra tions greater than 0.2, the
interph ase frictio n coeffici ent, K , may be computed
by using the Ergu n [45] equati on

¼ 150

þ 1: 75 «

j V

j (16 : 11)

For soli ds con centrations less than 0.2, the inter -

phase frictio n co efficient is usually based upon the
aerodynam ic force on pa rticle as follows :

¼ ( C

2 :65
g

)

3«

1
2

j V

j (16 : 12)

where the singl e particle drag coeffici ent, C

, is g iven

by [46]

¼ max

þ 0: 15 Re

0: 687

), 0: 44

(16 : 13)

and is modified to take acco unt of multipart icle ef-
fects using the method of Ric hardson and Zaki [47] .
The parti cle Reynol ds number is given by

( «

j V

(16 : 14)

The turbul ent stresses , t

, in the moment um eq ua-

tions for the k-phase might be calcul ated by using
the Bous sinesq turbul ent-viscos ity model [8] for both
phases or by ap plying a model of a Newtonia n fluid
for the gas phase and a granula r shear stress for the
solid pha se [19] .

The fricti on forces betw een each pha se and the

pipe wall can be mod eled by add ing a source term
to the pha se moment um equati on for those control
volume s ad jacent to the pipe wall [11,23,39 ].

16.5.2 .3 The Energy Equation s

The conserva tion of energy in multiphase applic ation
can be wri tten as an enthal py equati on for each
phase:

@ t

( «

)

þ r [ «

]

¼ «

@ p

@ t

r V

r q

þ Q

þ S

(16 : 15)

In this equati on, h

is the specific enthalp y of the k -

phase, q

is the heat flux, Q

is a heat source term (due

to chemi cal reaction or radiation) , Q

is the inter -

phase heat exchange between the phases, and h

is the

interph ase enthal py (i. e., the enthal py of the vapor at
the tempe ratur e of the solid parti cles).

16.5.2 .4 Heat an d Mass Transfer

The rate of en ergy trans fer be tween the phases is
usually exp ressed as a functi on of the tempe rature
difference betw een that of the conveying gas and
that of the parti cle surface (i.e., T

– T

). Hence, the

interph ase heat exchange between the phases can be
calculated by

6«

)

(16:16)

The convective heat transfer coefficient, h

, is calcu-

lated from the Nusselt number, Nu, which is defined as

¼ F (Re, Pr)

(16:17)

and is often expressed as a function of the Reynolds
number (Re) and Prandtl number (Pr), which are
defined as follows:

; Pr

(16:18)

Note that k

, m

, and c

are the thermal conductivity,

the viscosity, and heat capacity of the gas phase,
respectivel y.

Tabl e 16.1

presen ts common empir ical

correlations that have been used in the literature to
calculate the heat transfer coefficient in gas–particle
flows.

The mass transfer source term per unit volume can

be obtained by multiplying the evaporation rate from
a single particle, _

, by the total number of particles

in the control volume:

6«

(16:19)

The drying model for a single wet particle and slurry
droplet is based upon a two-stage drying process
[48,49]. In the first drying period, the gas phase resist-
ance controls the evaporation rate. Similar to heat
transfer, this resistance is between the gas and the
wet envelope of the particle. This may be expressed by

¼ h

R T

(16:20)

where h

is the convective mass transfer coefficient,

is the molecular weight of the water, R is the

2006 by Taylor & Francis Group, LLC.

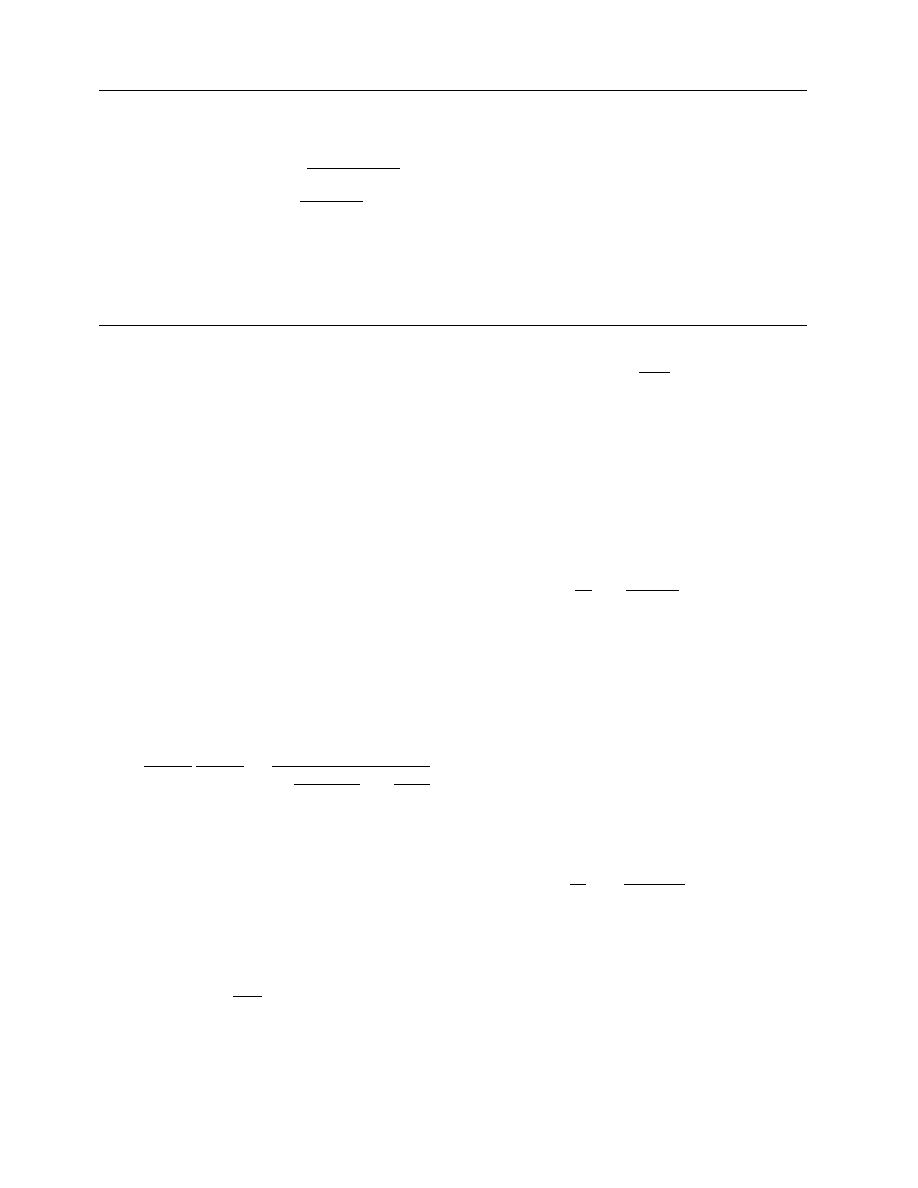
univers al gas con stant, and p

and p

are the pa rtial

pressur es of the water vapor at the parti cle crust and
the ga s pha se, respect ively.

The second drying period starts at a critical soli d-

to-liqui d mass ratio, j

, which is obtaine d from a

minimum vo id fraction, i.e., the porosity of the par-
ticles, « (typica lly varie d be tween 0 .05 and 0.25) . Dur-
ing the secon d period of the drying process , a dry
crust star ts to form , which causes a second resi stance
to mass an d hea t transfer. Thus , the wet parti cle
consis ts of a dry crust surroundi ng a wet core. Thi s
resistance is governed by a diff usion pr ocess, which
occurs between the outsi de diame ter of the particle,
d

, an d the diame ter of the wet c ore, d

. Assu ming

that the pa rticle is not shrinki ng during the second
drying period, the outside diame ter of the partic le
remain s con stant and the diame ter of the wet co re
decreas es. The equ ation for the evaporat ion rate
from a singl e pa rticle is express ed as a Steph an-type
diffusion rule [50]

2p«D

R T

ave

‘n

sat

p d

0
B

1
C

(16 :21)

where D

is the diffusion coeffici ent, p

sat

is the satur -

ation pre ssure insi de the wet co re, and T

ave

is the

average temperatur e of the parti cle.

In analogy to the heat trans fer coeffici ent, the mass

transfer coefficien t h

is calcul ated from the She r-

wood number, Sh , whi ch is equival ent to Nusse lt
number, Nu

¼ F (Re , Sc) (16 : 22)

and is often express ed as a function of the Reyno lds
number, Re , and the Sc hmidt num ber, Sc, which is
equival ent to Prand tl number, Pr , and is defined by

(16 : 23)

The correl ations for the Nusselt number (

see Table

16.1

) can be used to calculate the Sherwo od num ber,

Sh, and the mass trans fer co efficien t h

by replacing

the Prand tl numb er, Pr , with the Schmidt numb er, Sc .

Duri ng the first dr ying stage the diame ter of the

particle, d

, shrinks due to evap oration from the out er

surface to the su rrounding gas. Thus the diame ter of
the wet pa rticle can be calcul ated by

(16 : 24)

At the seco nd drying stage , the evaporat ion pro cess
of liqui d from a parti cle is assum ed to be governed by
diffusion through the particle crust and con vection
into the gas medium . As evapo ration pro ceeds, the
wet core shrinks as the particle dries. In general , both
the particle outer diame ter and the wet core diame ter
can be shrinke d, whi ch may deform the pa rticle’s
shape and size. In order to simplify the model, it
was assumed that the particle’s outer diameter re-
mains constant during the second drying period.
Thus, only the change of the wet core diameter, d

was considered:

«r

(16:25)

16.5.3 C

ASE

TUDY

The two-fluid model has been used for modeling the
flow of particulate materials through pneumatic
dryer. The model was solved numerically for a one-
dimensional steady-state condition and was applied
to the drying process of wet sand in a pneumatic
dryer. A two-stage drying process was implemented.

TABLE 16.1
Empirical Correlations for Heat Transfer Coefficient in Gas–Particle Flows

Modified Ranz–Marshall

correlation [48]

þ 0:6Re

0:5

0:333

þ B)

0:7

)

Developed for a single wet particle, taking into account

the resistance of the liquid vapors around the particle
to the heat transfer by Spalding number, B. c

denotes

the heat capacity of the liquid vapors in the gas phase
and H

is the latent heat of evaporation for the fluid

Modified Ranz–Marshall

correlation [29]

¼ 2 þ (0.5 Re

0.5

þ 0.06 Re

0.8

)Pr

0.333

Takes into account turbulent boundary layer around

the particle

Gamson correlation [30]

¼ 1.06Re

0.59

0.33

Developed for a fluidized bed dryer

De Brandt correlation [30]

¼ 0.16Re

1.3

0.67

Developed for a pneumatic dryer

Baeyens et al. [30] correlation

¼ 0.15Re

Developed for a large-scale pneumatic dryer

2006 by Taylor & Francis Group, LLC.

The predictions of the numerical simulations were
compared with the experimental results of Rocha
[33] (presented by Silva and Correa [32]) that were
obtained in a 4-m high pneumatic dryer with diameter
of 5.25 cm. In this study, 380-mm sand particles hav-
ing density of 2622 kg/m

and mass flow rate of

4.74

kg/s were dried with 3.947

kg/s air

mass flow rate. The comparison between the predic-
tions of the numerical simulations and the experi-
mental data for changes of gas temperature, solid
temperature, gas humidity, and particle’s moisture
content with length under adiabatic and known wall
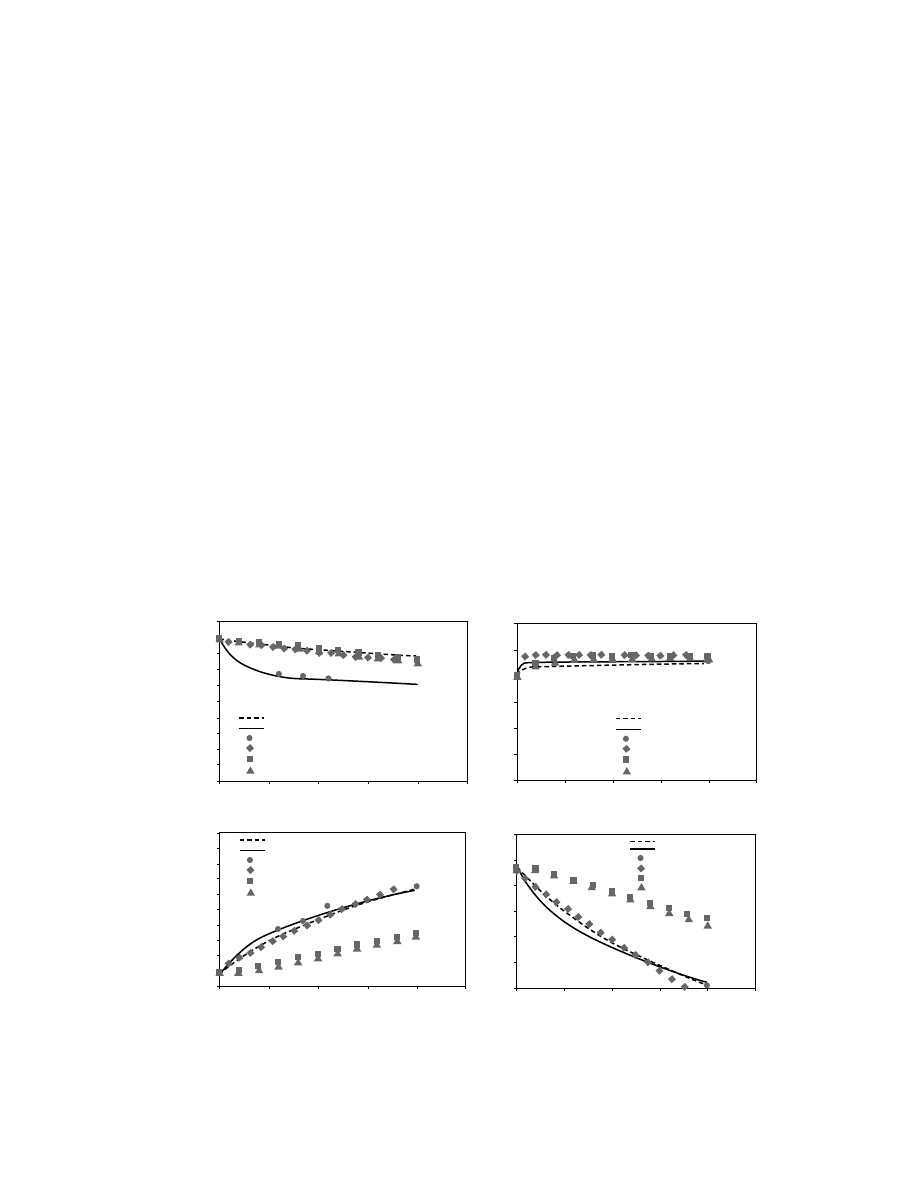
temperature operating conditions is presented in Fig-
ure 16.6a–d, respectively. When known wall tempera-
ture operating conditions were simulated, it was
assumed that in average the pipe wall temperature is
just about the outlet air temperature, and it is falling
linearly from 360 K at the inlet to 354 K at the outlet.
In these figures the circle symbols represent the ex-
perimental data that were published by Silva and
Correa [32] and the two solid lines represent the pre-
dictions of the numerical simulations for the adiabatic
and known wall temperature operating conditions.

It is clearly seen that the numerical model pre-

dicted the gas and the solid temperature profiles (Figure
16.6a and b) very well when known wall temperature
operating conditions were simulated. The maximum

relative error was 0.35 and 0.03%, respectively. When
adiabatic flow condition was simulated, the gas tem-
perature was overestimated and the maximum rela-
tive error was 5%. The predictions of the numerical
simulations for the gas humidity (Figure 16.6c) were
very good for both simulation conditions, i.e., adia-
batic and known wall temperature. The maximum
relative errors were 1.2 and 0.70%, respectively. The
predictions of the numerical simulations for the par-
ticle moisture content (Figure 16.6d) were also very
good for both simulation conditions, i.e., adiabatic
and known wall temperature, although only two ex-
perimental data were given. The maximum relative
errors were about 20% at the pipe outlet (i.e., when
the particles moisture contents were approxima-
tely zero). A comparison between the prediction of
the numerical models of Rocha and DryPak [34],
which were presented by Silva and Correa [32], with
the prediction of the numerical simulation revealed
better agreements with DryPak than with the models
of Rocha.

It should be pointed out that the two-fluid ap-

proach, as described and demonstrated in the previ-
ous sections, was widely used and validated for
various types of pneumatic conveying systems and
pneumatic flash dryers. Nevertheless, it is only one
of various approaches that can be adopted. Section

120
110
100

90
80
70

Abiabatic flow model
Conducting wall model
Rocha (1988) exp. data
DryPak
Rocha (1988) a
Rocha (1988) b

Gas temperature (

⬚C)

60
50
40
30
20

5.6

Gas humidity % (kg/kg)

5.5
5.4
5.3
5.2
5.1

4.9
4.8
4.7

4.6

Dryer length (m)

(a)

(c)

(b)

Dryer length [m]

Solid temperature (

8C)

Moisture content % (kg/kg)

(d)

Dryer length (m)

Abiabatic flow model
Conducting wall model

Rocha (1988) exp. data
DryPak
Rocha (1988) a
Rocha (1988) b

Abiabatic flow model

Conducting wall model

Rocha (1988) exp. data
DryPak
Rocha (1988) a
Rocha (1988) b

Abiabatic flow model

Conducting wall model

Rocha (1988) exp. data
DryPak
Rocha (1988) a
Rocha (1988) b

FIGURE 16.6 Comparison between the predictions of the pneumatic drying model, DryPak model [35], Rocha [33] models
and the experimental data for changes of (a) gas temperature, (b) solid temperature, (c) gas humidity, and (d) particle’s
moisture content with length under adiabatic and known wall temperature operating conditions.

2006 by Taylor & Francis Group, LLC.

16.5.1 presents a summary of the various studies that
were conducted on pneumatic flash dryers and the
various mathematical models that have been adopted
by them.

16.6 EXPECTED NEW DEVELOPMENTS

IN FLASH DRYERS

These developments are expected in the fields of:

Enhancement of product quality

Increased efficiency by heat recovery

Applications of heat pumps in drying systems

Efficient combined processes

Development of models for overall systems that
would include mechanical dewatering, drying,
heat recovery, powder collection, cooling stages,
etc. in order to study interactions between vari-
ous parts of the system and develop improved
design procedures

REFERENCES

1. Strumiłło, C. and Kudra, T., Drying: Principles, Appli-

cations and Design, Gordon & Breach Science Pub-
lishers, London, UK, 1986.

2. Thorpe, G.R., Pneumatic Conveying Driers, Chemical

Industry Development, Incorporating CP&E, 1975,
pp. 13–19.

3. Flash

Dryer,

Deutsche

Babcock,

Babcock-BSH

GMBH, 1998.

4. Devahastin, S. (Ed.), Mujumdar’s Practical Guide To

Industrial Drying—Principles, Equipment And New De-
velopments, Exergex Corporation, Montreal, Canada,
2000.

5. Fellows, P.J., Food Processing Technology—Principles

and Practice, Woodhead Publishing, Cambridge, UK,
1997.

6. Kisaku¨rek, B., Flash drying, in Handbook of Industrial

Drying, 2nd ed. (Mujumdar, A.S. Ed.), Marcel Dekker,
New York, 1995.

7. Kemp, I.C., Scale-up of pneumatic dryers, Drying Tech-

nology, 12(1–2), 279–297, 1994.

8. Boothroyd, R.G., Flowing Gas–Solids Suspensions,

Chapman & Hall, London, 1971.

9. Muschelknautz, E. and Wojahn, H., Auslegung pneu-

matischer fo¨rderanlagen, Chemie-Ing.-Techn., 223–235,
46(6), 1974.

10. Molerus, O., Overview—pneumatic transport of solids,

Powder Technology, 88, 309–321, 1996.

11. Levy, A., Mooney, T., Marjanovic, P., and Mason,

D.J., A comparison of analytical and numerical models
for gas–solid flow through straight pipe of different
inclinations with experimental data, Powder Technol-
ogy, 93, 253–260, 1997.

12. Pan, R. and Wypych, P., Bend pressure drop in pneu-

matic conveying of fly ash, in Proceedings of the Powder
and Bulk Solids Conference, Chicago, USA, 1992,
pp. 349–360.

13. Mason, D.J., Marjanovic, P., and Levy, A., The influence

of bends on the performance of pneumatic conveying
systems, Advanced Powder Technology, 95, 7–14, 1998.

14. Hyder, L.M., Bradley, M.S.A., Reed, A.R., and Het-

tiaratchi, K., An investigation into the effect of particle
size on straight pipe pressure gradients in lean phase
pneumatic conveying, Powder Technology, 112(3), 235–
243, 2000.

15. Bradley, M.S.A., Farnish, R.J., Hyder, L.M., and

Reed, A.R., A novel analytical model for the acceler-
ation of particles following bends in pneumatic convey-
ing systems, in Handbook of Conveying and Handling of
Particulate Solids (Levy, A. and Kalman, H. Eds.), Else-
vier, Amsterdam, 2001.

16. Andrieu, J. and Bressat, R., Experimental and theoret-

ical study of a pneumatic dryer, in Proceedings of the
Third International Drying Symposium, Vol. 2, 1982,
pp. 10–19.

17. Kemp, I.C. and Oakley, D.E., Simulation and scale-up

of pneumatic conveying and cascading rotary dryers,
Drying Technology, 15(6–8), 1699–1710, 1997.

18. Bowen, R.M., Theory of mixtures, in Continuum Phys-

ics (Eringen A.C. Ed.), Academic Press, New York,
1976, pp. 1–127.

19. Gidaspow, D., Multiphase Flow and Fluidization, Aca-

demic Press, New York, 1997.

20. Cundall, P.A. and Strack, O.D., A discrete numerical

model for granular assemblies, Geotechnique, 29, 47–65,
1979.

21. Tsuji, Y., Tanaka, T., and Ishida, T., Lagrangian nu-

merical simulation of plug flow of cohesionless particle
in a horizontal pipe, Powder Technology, 71, 239, 1992.

22. Tanthapanichakoon, W. and Srivotanai, C., Analysis

and simulation of an industrial flash dryer in a Thai
Manioc starch plant, in Drying’96 Proceedings of the
10th International Drying Symposium, Vol. A, 1996,
pp. 373–380.

23. Mindziul, Z. and Kmiec, A., Modelling gas–solid flow

in a pneumatic-flash dryer, in Drying’96 Proceedings of
the 10th International Drying Symposium, Vol. A, 1996,
pp. 275–282.

24. Mindziul, Z. and Kmiec, A., Modelling gas–solid flow

in a pneumatic-flash dryer, Drying Technology, 15(6–8),
1711–1720, 1997.

25. Kmiec, A., Analysis of the gas–solid flow in a riser

reactor, Applied Mechanics and Engineering, 2(1), 133–
152, 1997.

26. Blasco, R. and Alvarez, P.I., Flash drying of fish meals

with superheated steam: isothermal process, Drying
Technology, 17(4–5), 775–790, 1999.

27. Alvarez, P.I. and Blasco, R., Pneumatic drying of

meals: application of the variable diffusivity model,
Drying Technology, 17(4–5), 791–808, 1999.

28. Bird, R., Stewart, E., and Lightfoot, N., Transport

Phenomena, John Wiley & Sons, New York, 1960.

2006 by Taylor & Francis Group, LLC.

29. Kemp, I.C., Bahu, R.E., and Pasley, H.S., Model de-

velopment and experimental studies of vertical pneu-
matic conveying dryers, Drying Technology, 12(6),
1323–1340, 1994.

30. Baeyens, J., van Gauwbergen, D., and Vinckier, I.,

Pneumatic drying: the use of large-scale experimental
data in a design procedure, Powder Technology, 83,
139–148, 1995.

31. Levy, A. and Borde, I., Steady-state one-dimensional

flow for a pneumatic dryer, Chemical Engineering and
Proceedings, 38, 121–130, 1999.

32. Silva, M.A. and Correa, J.L.G., Using DryPak to simu-

late drying process, in Drying’98 Proceedings of the 11th
International Drying Symposium, Vol. A, 1998, pp. 303–
310.

33. Rocha, S.C.S., Contribution to the Study of Pneumatic

Drying: Simulation and Influence of Gas–Particle Heat
Transfer Coefficient, Ph.D. thesis, Sao Paulo Univer-
sity, Sao Paulo, 1988.

34. Pakowski, Z., DryPak v.3. Program for Psychometric

and Drying Computation, 1996.

35. Levy, A. and Borde, I., Two-fluids model for pneumatic

drying of particulate materials, in 12th International
Drying

Symposium,

Nordwijkerhout,

Netherlands,

2000.

36. Rocha, S.C.S. and Paixa˜o, A.E.A., Pseudo two-dimen-

sional model for a pneumatic dryer, in Drying’96 Pro-
ceedings of the 10th International Drying Symposium,
Vol. A, 1996, pp. 340–348.

37. Silva, M.A. and Nerba, S.A., Numerical simulation of

drying in a cyclone, Drying Technology, 15(6–8), 1731–
1741, 1997.

38. Patankar, S.V., Numerical Heat Transfer and Fluid

Flow, Hemisphere Publishing, New York, 1980.

39. Fyhr, C. and Rasmuson, A., Mathematical model of a

pneumatic conveying dryer, fluid mechanics and trans-

port phenomena, AIChE Journal, 43(11), 2889–2902,
1997a.

40. Fyhr, C. and Rasmuson, A., Steam drying of wood

chips in pneumatic conveying dryers, Drying Technol-
ogy, 15(6–8), 1775–1785, 1997b.

41. Cartaxo, S.J.M. and Rocha, S.C.S., Object-oriented

simulation of pneumatic conveying—application to a
turbulent flow, Brazilian Journal of Chemical Engineer-
ing, 16(4), 329–337, 1999.

42. Johanson, J.R., Two-phase-flow effects in solids pro-

cessing and handling, Chemical Engineering, January !,
77–86, 1979.

43. Johanson, J.R. and Cox, B.D., Practical solutions to

fine powder handling, Powder Handling and Processing,
1(1), 83–87, 1989.

44. Patel, M.K. and Cross, M., The modelling of fluidised

beds for ore reduction, in Numerical Methods in Lam-
inar and Turbulent Flow, Pineridge Press, Swansea, UK,
1989, p. 2051.

45. Ergun, S., Fluid flow through packed columns, Chem-

ical Engineering Progress, 48(2), 89–94, 1952.

46. Clift, R., Grace, J., and Weber, M.E., Bubbles, Drops

and Particles, Academic Press, New York, 1987.

47. Richardson, J.F. and Zaki, W.N., Sedimentation and

fluidization: Part I, Transactions of the Institute of
Chemical Engineering, 32, 35–53, 1954.

48. Levi-Hevroni, D., Levy, A., and Borde, I., Mathemat-

ical modelling of drying of liquid/solid slurries in steady
state one dimensional flow, Drying Technology, 13(5–7),
1187–1201, 1995.

49. Levy, A., Mason, D.J., Borde, I., and Levi-Hevroni, D.,

Drying of wet solids particles in a steady-state one-
dimensional flow, Powder Technology, 85, 15–23, 1998.

50. Abuaf, N. and Staub, F.W., Drying of liquid–solid slurry

droplets, in Drying’86 Proceedings of the Fifth Inter-
national Drying Symposium, Vol. 1, 1987, pp. 227–248.

2006 by Taylor & Francis Group, LLC.

Document Outline

Table of Contents
Chapter 016: Pneumatic and Flash Drying

Wyszukiwarka

Podobne podstrony:
Drying, shrinkage and rehydration characteristics of kiwifruits during hot air and microwave drying
Far infrared and microwave drying of peach (Jun Wang, Kuichuan Sheng)
Modeling and minimizing process time of combined convective and vacuum drying of mushrooms and parsl
Preparation of garlic powder with high allicin content by using combined microwave–vacuum and vacuum
Improving nutritional value of dried blueberries combining microwave vacuum, hot air drying and free
Energy Consumption and Colour Characteristics of Nettle Leaves during Microwave, Vacuum and Convecti
A comparative study on heat pump, microwave and freeze drying of fresh fruits
Far infrared and microwave drying of peach (Jun Wang, Kuichuan Sheng)
012 Microwave and Dielectric Drying
Drying kinetics and drying shrinkage of garlic subjected to vacuum microwave dehydration (Figiel)
Flash on English for Mechanics, Electronics and Technical Assistance
New hybrid drying technologies for heat sensitive foodstuff (S K Chou and K J Chua)
Combined Radiant and Conductive Vacuum Drying in a Vibrated Bed (Shek Atiqure Rahman, Arun Mujumdar)
Flash on English for Cooking, Catering and Reception keys
226 General tips for Flash and SSD recovering)
collimated flash test and in sun measurements of high concentration photovoltaic modules
11 4 2 7 Lab Managing?vice Configuration Files Using TFTP, Flash, and USB
Drying kinetics and drying shrinkage of garlic subjected to vacuum microwave dehydration (Figiel)

więcej podobnych podstron

016 Pneumatic and Flash Drying

Document Outline