
Khoa công nghệ thông tin - Đại học Thái Nguyên
Bộ môn công nghệ phần mềm
GIÁO TRÌNH MÔN CHƯƠNG TRÌNH DỊCH
(Compiler Construction)
Thái nguyên, 2007


LỜI NÓI ĐẦU
Môn học chương trình dịch là môn học của ngành khoa học máy tính. Trong
suốt thập niên 50, trình biên dịch được xem là cực kỳ khó viết. Ngày nay, việc viết
một chương trình dịch trở nên đơn giản hơn cùng với sự hỗ trợ của các công cụ
khác. Cùng với sự phát triển của các chuyên ngành lý thuyết ngôn ngữ hình thức và
automat, lý thuyết thiết kế một trình biên dịch ngày một hoàn thiện hơn.
Có rất nhiều các trình biên dịch hiện đại, có hỗ trợ nhiều tính năng tiện ích
khác nữa. Ví dụ: bộ visual Basic, bộ studio của Microsoft, bộ Jbuilder, netbean,
Delphi …
Tại sao ta không đứng trên vai những người khổng lồ đó mà lại đi nghiên
cứu cách xây dựng một chương trình dịch nguyên thuỷ. Với vai trò là sinh viên
công nghệ thông tin ta phải tìm hiểu nghiên cứu xem một chương trình dịch thực sự
thực hiện như thế nào?
Mục đích của môn học này là sinh viên sẽ học các thuật toán phân tích ngữ
pháp và các kỹ thuật dịch, hiểu được các thuật toán xử lý ngữ nghĩa và tối ưu hóa
quá trình dịch.
Yêu cầu người học nắm được các thuật toán trong kỹ thuật dịch.
Nội dung môn học : Môn học Chương trình dịch nghiên cứu 2 vấn đề:
- Lý thuyết thiết kế ngôn ngữ lập trình ( cách tạo ra một ngôn ngữ giúp người
lập trình có thể đối thoại với máy và có thể tự động dịch được).
- Cách viết chương trình chuyển đổi từ ngôn ngữ lập trình này sang ngôn ngữ
lập trình khác.
Học môn chương trình dịch giúp ta:
- Nắm vững nguyên lý lập trình: Hiểu từng ngôn ngữ, điểm mạnh điểm yếu
của nó => chọn ngôn ngữ thích hợp cho dự án của mình. Biết chọn chương trình
dịch thích hợp (VD với pascal dưới Dos: chương trình dịch là turbo pascal. Đối với
ngôn ngữ C: chọn turbo C hay bolean C? Bolean C tiện lợi, dễ dùng, turbo C sinh
mã gọn, không phải lo vè vấn đề tương thích với hệ điều hành nhưng khoá dùng
hơn). Phân biệt được công việc nào do chương trình dịch thực hiện và do chương
trình ứng dụng thực hiện.
- Vận dụng: thực hiện các dự án xây dựng chương trình dịch. Áp dụng vào
các ngành khác như xử lý ngôn ngữ tự nhiên…

Để viết được trình biên dịch ta cần có kiến thức về ngôn ngữ lập trình, cấu
trúc máy tính, lý thuyết ngôn ngữ, cấu trúc dữ liệu, phân tích thiết kế giải thuật và
công nghệ phần mềm.
Những kiến thức của môn học cũng có thể được sử dụng trong các lĩnh vực
khác như xử lý ngôn ngữ tự nhiên.
Tài liệu tham khảo:
1. Giáo trình sử dụng: Dick Grune, Ceriel Jacobs, Parsing Techniques: A
Practical Guide, 1998
2. Một số tài nguyên trực tuyến có thể được tìm thấy bằng việc sử dụng máy
tìm kiếm, chẳng hạn như
và
3. Bài giảng Lý thuyết và Thực hành Chương Trình Dịch của Lê Anh Cường,
khoa Công Nghệ, ĐHQG Hà nội, 2004.
4. Giáo trình lý thuyết, thực hành môn học Chương trình dịch của Phạm
Hồng Nguyên, Khoa Công Nghệ, ĐHQG Hà nội, 1998.
5. Ngôn ngữ hình thức của Nguyễn Văn Ba, ĐHBK Hà nội, 1994
6. Thực hành kỹ thuật biên dịch của Nguyễn Văn Ba, ĐHBK Hà nội, 1993
7. Compiler: principles techniques and tools của A.V. Aho, Ravi Sethi, D.
Ulman, 1986
8. Bản dịch của tài liệu: Trình biên dịch: Nguyên lý, kỹ thuật và công cụ của
Trần Đức Quang, 2000.
Chương 1: Tổng quan về ngôn ngữ lập trình và chương trình dịch
1. Ngôn ngữ lập trình và chương trình dịch.
Con người muốn máy tính thực hiện công việc thì con người phải viết yêu cầu
đưa cho máy tính bằng ngôn ngữ máy hiểu được. Việc viết yêu cầu gọi là lập
trình. Ngôn ngữ dùng để lập trình gọi là ngôn ngữ lập trình. Có nhiều ngôn
ngữ lập trình khác nhau.
Dựa trên cơ sở của tính không phụ thuộc vào máy
tính ngày càng cao người ta phân cấp các ngôn ngữ lập trình như sau:
- Ngôn ngữ máy (machine languge)
- Hợp ngữ (acsembly langguge)
- Ngôn ngữ cấp cao (high level langguage)
Ngôn ngữ máy chỉ gồm các số 0 và 1, khó hiểu đối với người sử dụng. Mà
ngôn ngữ tự nhiên của con người lại dài dòng nhiều chi tiết mập mờ, không rõ ràng
đối với máy.
Để con người giao tiếp được với máy dễ dàng cần một ngôn ngữ trung
gian gần với ngôn ngữ tự nhiên. Vì vậy ta cần có một chương trình để dịch các
chương trình trên ngôn ngữ này sang mã máy để có thể chạy được. Những chương
trình làm nhiệm vụ như vậy gọi là các chương trình dịch. Ngoài ra, một chương
trình dịch còn chuyển một chương trình từ ngôn ngữ nay sang ngôn ngữ khác tương
đương. Thông thường ngôn ngưc nguồn là ngôn ngữ bậc cao và ngôn ngữ đích là
ngôn ngữ bậc thấp, ví dụ như ngôn ngữ Pascal hay ngôn ngữ C sang ngôn ngữ
Acsembly.
* Định nghĩa chương trình dịch:
Chương trình dịch
là một chương trình
thực hiện việc chuyển
đổi một chương trình
hay đoạn chương trình
từ ngôn ngữ này (gọi là
ngôn ngữ nguồn) sang
ngôn ngữ khác (gọi là
ngôn ngữ đích) tương
đương.
Để xây dựng được chương trình dịch cho một ngôn ngữ nào đó, ta cần biết về
đặc tả của ngôn ngữ lập trình, cú pháp và ngữ nghĩa của ngôn ngữ lập trình đó…
Để đặc tả ngôn ngữ lập trình, ta cần định nghĩa:
- Tập các kí hiệu cần dùng trong các chương trình hợp lệ.
- Tập các chương trình hợp lệ.
chương trình
nguồn (ngôn
ngữ bậc cao)
chương trình
dịch
chương trình
đích (ngôn
ngữ máy)
Lỗi
Hình 1.1: Sơ đồ một chương trình dịch

- Nghĩa của từng chương trình hợp lệ.
Việc định nghĩa tập các kí hiệu cần dùng của ngôn ngữ là dế dàng, ta chỉ cần
liệt kê là đủ. Việc xác định các chương trình hợp lệ thì khó khăn hơn. Thông
thường ta dùng các luật của văn phạm để đặc tả. Việc thứ 3, định nghĩa ý nghĩa của
chương trình hợp lệ là khó khăn nhất. Có 3 phương pháp để xác định nghĩa của
chương trình hợp lệ.
+ Phương pháp 1: định nghã bằng phép ánh xạ. ánh xạ mỗi chương trình vào
một câu trong ngôn ngữ mà ta có thể hiểu được.
+ Phương pháp 2: Xác định ý nghĩa của chương trình bằng một máy lý tưởng.
Ý nghĩa của chương rình được đăc tả trong ngôn từ của máy lý tưởng. Máy lý
tưởng là bộ thông dịch của ngôn ngữ.
+ Phương pháp 3: ý nghĩa cảu chương trình nguồn là sản phẩm xuất ra của
trình biên dịch, khi nó dịch chương trình nguồn.
2. Phân loại chương trình dịch.
Có thể phân thành nhiều loại tuỳ theo các tiêu chí
khác nhau.
- Theo số lần duyệt: Duyệt đơn, duyệt nhiều lần.
- Theo mục đích: Tải và chạy, gỡ rối, tối ưu, chuyển đổi ngôn ngữ, chuyển đôỉ
định dạng…
- Theo độ phức tạp của chương trình nguồn và đích:
+ Asembler (chương trình hợp dịch):
Dịch từ ngôn ngữ asembly ra ngôn ngữ
máy.
+ Preproccessor: (tiền xử lý) :
Dịch từ ngôn ngữ cấp cao sang ngôn ngữ cấp
cao khác (thực chất là dịch một số cấu trúc mới sang cấu trúc cũ).
+ Compiler: (biên dịch)
dịch từ ngôn ngữ cấp cao sang ngôn ngữ cấp thấp.
- Theo phương pháp dịch chạy:
+ Thông dịch: (diễn giải - interpreter) chương trình thông dịch đọc chương
trình nguồn theo từng lệnh và phân tích rồi thực hiện nó
. (Ví dụ hệ điều hành thực
hiện các câu lệnh DOS, hay hệ quản trị cơ sở dữ liệu Foxpro)
.
Hoặc ngôn ngữ
nguồn không được chuyển sang ngôn ngữ máy mà chuyển sang một ngôn ngữ
trung gian. Một chương trình sẽ có nhiệm vụ đọc chương trình ở ngôn ngữ trung
gian này và thực hiện từng câu lệnh. Ngôn ngữ trung gian được gọi là ngôn ngữ của
một máy ảo, chương trình thông dịch thực hiện ngôn ngữ này gọi là máy ảo.
Chương
trình
nguồn
Compiler
CT ở NN
trung gian
Interpreter
Kết
quả
Hình 1.2 Hệ thống thông dịch
Ví dụ hệ thông dịch Java. Mã nguồn Java được dịch ra dạng Bytecode. File
đích này được một trình thông dịch gọi là máy ảo Java thực hiện. Chính vì vậy mà
người ta nói Java có thể chạy trên mọi hệ điều hành có cài máy ảo Java.
+ Biên dịch: toàn bộ chương trình nguồn được trình biên dịch chuyển sang
chương trình đích ở dạng mã máy
. Chương trình đích này có thể chạy độc lập trên
máy mà không cần hệ thống biên dịch nữa.
- Theo lớp văn phạm: LL (1) (LL – Left to right, leftmost) LR(1) (LR – letf to
right, right most)
1.3. Cấu trúc của chương trình dịch.
1.3.1. cấu trúc tĩnh (cấu trúc logic)
1) Phân tích từ vựng: đọc luồng kí tự tạo thành chương trình nguồn từ trái
sang phải, tách ra thành các từ tố (token).
- Từ vựng:
Cũng như ngôn ngữ tự nhiên, ngôn ngữ lập trình cũng được xây
dựng dựa trên
bộ từ vựng
. Từ vựng trong ngôn ngữ lập
trình thường được xây dựng
dựa trên bộ chữ gồm có:
+ chữ cái: A .. Z, a . . z
+ chữ số: 0..9
+ các ký hiệu toán học: +, - , *, /, (, ), =, <, >, !, %, /
+ các ký hiệu khác: [, ], . . .
Các từ vựng được ngôn ngữ hiểu bao gồm các từ khóa, các tên hàm, tên hằng, tên
biến, các phép toán, . . .
Các từ vựng có những qui định nhất định ví dụ: tên viết bởi chữ cái đầu tiên sau đó
là không hoặc nhiều chữ cái hoặc chữ số, phép gán trong C là =, trong Pascal là
:=,v. . .
Để xây dựng một chương trình dịch, hệ thống phải tìm hiểu tập từ vựng của
ngôn ngữ nguồn và phân tích để biết được từng loại từ vựng và các thuộc tính của
nó
,
Ví dụ:
Câu lệnh trong chương trình nguồn
viết bằng ngôn ngữ pascal:
“a := b + c * 60”
Chương trình phân tích từ vựng sẽ trả về:
a là tên (tên (định danh ))
:= là toán tử gán
b là tên (định danh)
+ là toán tử cộng
c là định danh
* là toán tử nhân
60 là một số
Kết quả phân tích từ vựng sẽ là: (tên, a), phép gán, (tên, b) phép cộng (tên, c)
phép nhân, (số, 60)
2). Phân tích cú pháp: Phân tích cấu
trúc ngữ pháp của chương trình. Các từ tố
được nhóm lại theo cấu trúc phân cấp.
- Cú pháp:
Cú pháp là thành phần
quan trọng nhất trong một ngôn ngữ. Như
chúng ta đã biết trong ngôn ngữ hình thức
thì ngôn ngữ là tập các câu thỏa mãn văn
phạm của ngôn ngữ đó. Ví dụ như
câu = chủ ngữ + vị ngữ
vị ngữ = động từ + bổ ngữ
v.v. . .
Trong ngôn ngữ lập trình, cú pháp của nó
được thể hiện bởi một bộ luật cú pháp. Bộ
luật này dùng để mô tả cấu trúc của
chương trình, các câu lệnh.
Chúng ta quan
tâm đến các cấu trúc này bao gồm:
1) các khai báo
2) biểu thức số học, biểu thức logic
3) các lệnh: lệnh gán, lệnh gọi hàm,
lệnh vào ra, . . .
4) câu lệnh điều kiện if
5) câu lệnh lặp: for, while
6) chương trình con (hàm và thủ tục)
Nhiệm vụ trước tiên là phải biết được bộ luật cú pháp của ngôn ngữ mà mình định
xây dựng chương trình cho nó.
Với một chuỗi từ tố và tập luật cú pháp của ngôn ngữ, bộ phân tích cú pháp tự
động đưa ra cây cú pháp cho chuỗi nhập.
Khi cây cú pháp xây dựng xong thì quá
trình phân tích cú pháp của chuỗi nhập kết thúc thành công. Ngược lại nếu bộ phân
tích cú pháp áp dụng tất cả các luật hiện có nhưng không thể xây dựng được cây cú
pháp của chuỗi nhập thì thông báo rằng chuỗi nhập không viết đúng cú pháp.
Chương trình phải phân tích chương trình nguồn thành các cấu trúc cú pháp
của ngôn ngữ, từ đó để kiểm tra tính đúng đắn về mặt ngữ pháp của chương trình
nguồn.
3
). Phân tích ngữ nghĩa
: Phân tích các đặc tính khác của chương trình mà
không phải đặc tính cú pháp. Kiểm tra chương trình nguồn để tìm lỗi cú pháp và sự
hợp kiểu.
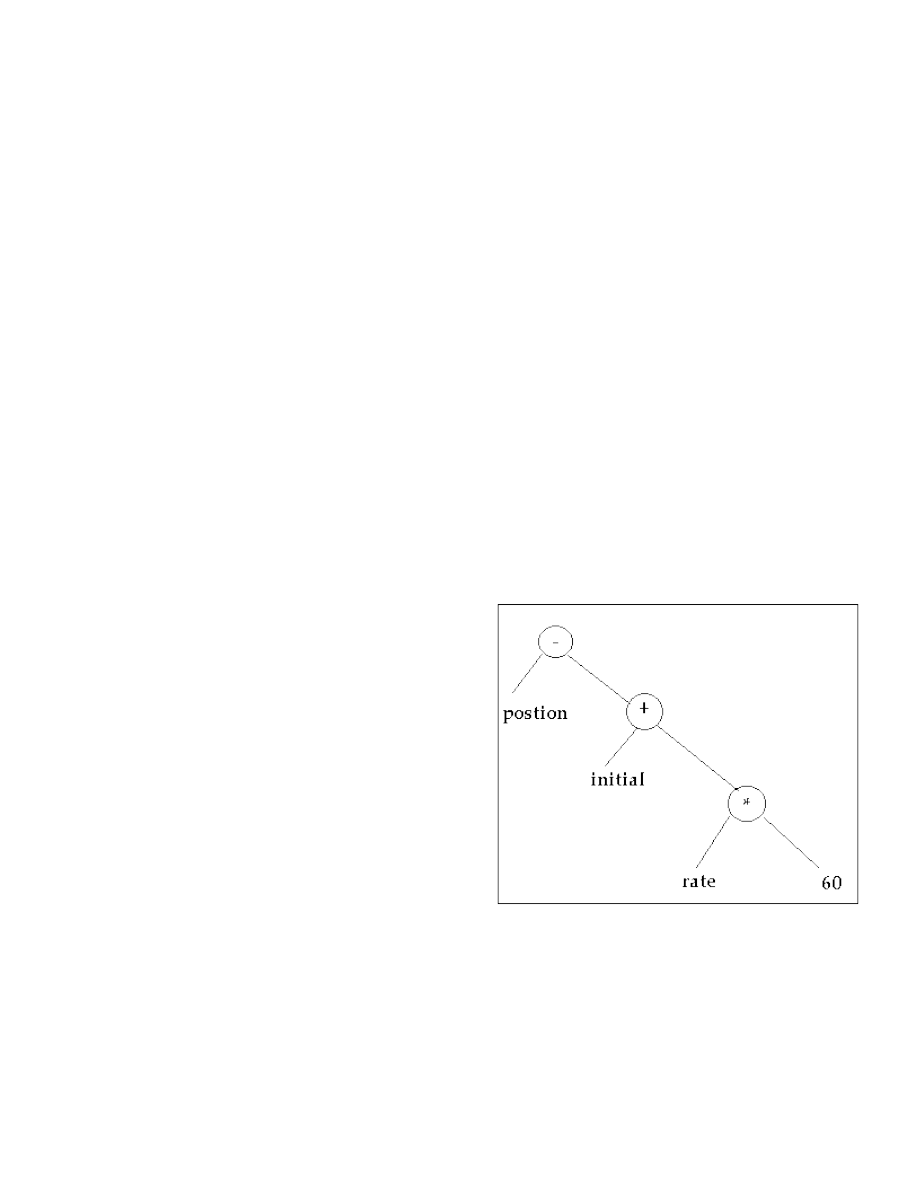
Dựa trên cây cú pháp bộ phân tích ngữ nghĩa xử lý từng phép toán. Mỗi phép
toán nó kiểm tra các toán hạng và loại dữ liệu của chúng có phù hợp với phép toán
không.

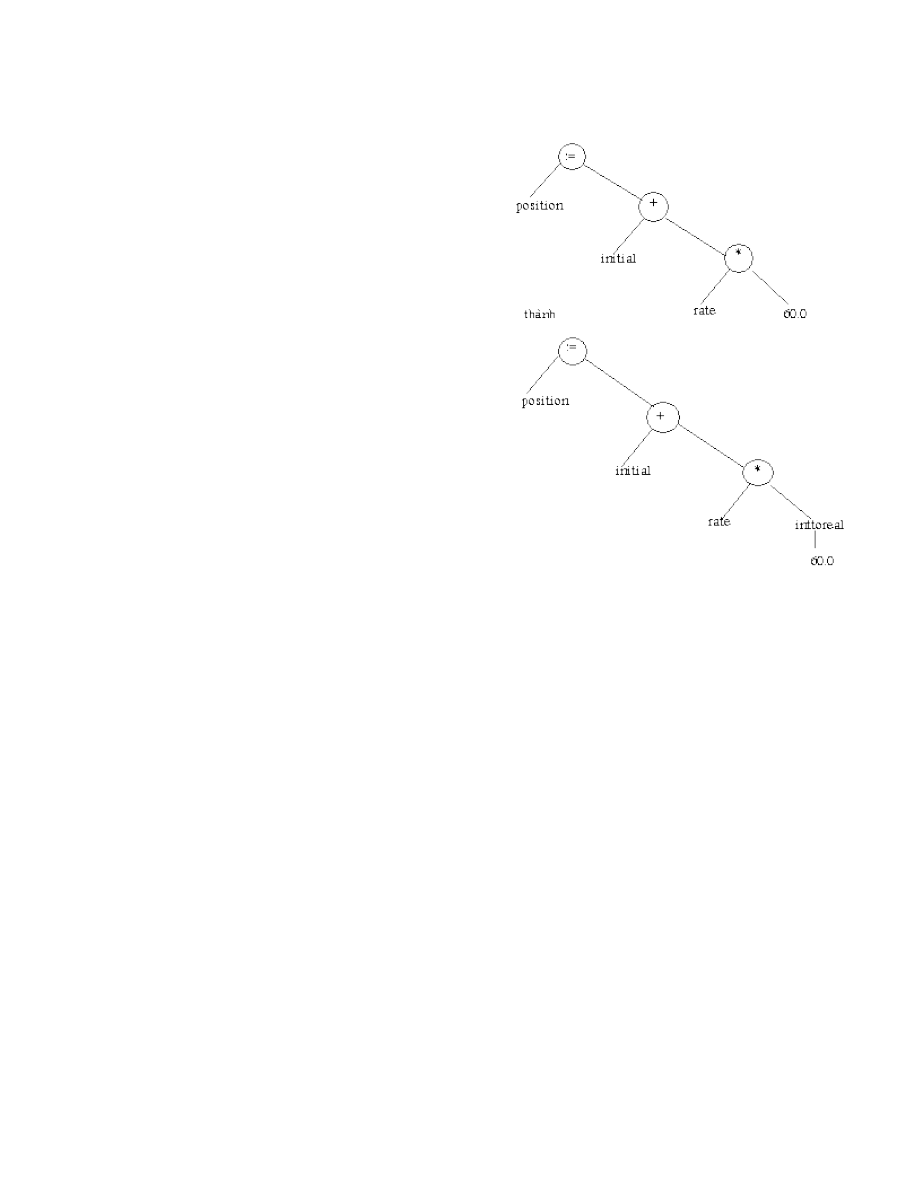
VD: tên (biến) được khai báo kiểu real, 60 là số kiểu interge vì vậy trình biên
dịch đổi thành số thực 60.0.
-
Ngữ nghĩa: của một ngôn ngữ lập trình liên quan đến:
+ Kiểu, phạm vi của hằng và biến
+ Phân biệt và sử dụng đúng tên hằng, tên biến, tên hàm
Chương trình dịch phải kiểm tra được tính đúng đắn trong sử dụng các đại lượng
này.
Ví dụ kiểm tra không cho gán giá trị cho hằng, kiểm tra tính đúng đắn trong
gán kiểu, kiểm tra phạm vi, kiểm tra sử dụng tên như tên không được khai báo
trùng, dùng cho gọi hàm phải là tên có thuộc tính hàm, . . .
4)
Sinh mã trung gian: Sinh chương trình rong ngôn ngữ trung gian nhằm: dễ
sinh và tối ưu mã hơn dễ chuyển đổi về mã máy hơn.
sau giai đoạn phân tích thì mã trung gian sinh ra như sau:
temp1 := 60
temp2 := id3 * temp1
temp3 := id2 + temp 2
id1 := temp3
(1.2)
(trong đó id1 là position; id2 là initial và id3 là rate)
5).
Tối ưu mã: Sửa đổi chương trình trong ngôn ngữ trung gian hằm cải tién
chương trình đích về hiệu năng.
Ví dụ như với mã trung gian ở (1.2), chúng ta có thể làm tốt hơn đoạn mã để
tạo ra được các mã máy chạy nhanh hơn như sau:
temp1 := id3 * 60
id1 := id2 + temp1 (1.3)
6).
Sinh mã: tạo ra chương trình đích từ chương trình trong ngôn ngữ trung
gian đẫ tối ưu.
Thông thường là sinh ra mã máy hay mã hợp ngữ. Vấn đề quyết định là việc
gán các biến cho các thanh ghi.
Chẳng hạn sử dụng các thanh ghi R1 và R2, các chỉ thị lệnh MOVF, MULF,
ADDF, chúng ta sinh mã cho (1.3) như sau:
MOVF id3, R2
MULF #60, R2
MOVF id2, R1
ADDF R2, R1
MOVF R1, id1
(1.4)
Ngoài ra, chương trình dịch còn phải thực hiện nhiệm vụ:
*
Quản lý bảng ký hiệu: Để ghi lại các kí hiệu, tên … đã sử dụng trong
chương trình nguồn cùng các thuộc tính kèm theo như kiểu, phạm vi, giá trị ... để
dùng cho các bước cần đến.

Tõ tè(token) + Thuéc tÝnh (kiÓu, ®Þa chØ lu tr÷) = B¶ng ký
hiÖu (Symbol table).
T
rong quá trình phân tích từ vựng, các tên sẽ được lưu vào bảng ký hiệu, sau
đó từ giai đoạn phân tích ngữ nghĩa các thông tin khác như thuộc tính về tên (tên
hằng, tên biến, tên hàm) sẽ được bổ sung trong các giai đoạn sau.
- Giai đoạn phân tích từ vựng: lưu trữ trị từ vựng vào bảng kí hiệu nếu nó
chưa có.
- Giai đoạn còn lại: lưu trữ thuộc tính của từ vựng hoặc truy xuất các thông
tin thuộc tính cho từng giai đoạn.
Bảng kí hiệu được tổ chức như cấu trúc dữ liệu với mỗi phần tử là một mẩu
tin dùng để lưu trữ trị từ vựng và các thuộc tính của nó.
- Trị từ vựng: tên từ tố.
- Các thuộc tính: kiểu, tầm hoạt động, số đối số, kiểu của đối số ...
VÝ dô: var position, initial, rate : real th× thuéc tÝnh kiÓu
real cha thÓ x¸c ®Þnh. C¸c giai ®o¹n sau ®ã nh ph©n tÝch
ng÷ nghÜa vµ sinh m· trung gian míi ®a thªm c¸c th«ng tin
nµy vµo vµ sö dông chóng. Nãi chung giai ®o¹n sinh m· sÏ sö
dông b¶ng ký hiÖu ®Ó gi÷ c¸c th«ng tin chi tiÕt vÒ danh
biÓu.
* Xử lý lỗi: Khi phát hiện ra lỗi trong quá trình dịch thì nó ghi lại vị trí gặp
lỗi, loại lỗi, những lỗi khác có liên quan đến lỗi này để thông báo cho người lập
trình.
Mçi giai ®o¹n cã thÓ cã nhiÒu lçi, tïy thuéc vµo tr×nh biªn
dÞch
mµ
cã
thÓ
lµ:
- Dõng vµ th«ng b¸o lçi khi gÆp lçi dÇu tiªn (Pascal).
- Ghi nhËn lçi vµ tiÕp tôc qu¸ tr×nh dÞch (C).
+ Giai ®o¹n ph©n tÝch tõ vùng: cã lçi khi c¸c ký tù kh«ng thÓ
ghÐp thµnh mét token (vÝ dô: 15a, a@b,...)
+ Giai ®o¹n ph©n tÝch có ph¸p: Cã lçi khi c¸c token kh«ng
thÓ kÕt hîp víi nhau theo cÊu tróc ng«n ng÷ (vÝ dô: if stmt then
expr).
+ Giai ®o¹n ph©n tÝch ng÷ nghÜa b¸o lçi khi c¸c to¸n h¹ng cã
kiÓu kh«ng ®óng yªu cÇu cña phÐp to¸n.
* Giai đoạn phân tích có đầu vào là ngôn ngữ nguồn, đầu ra là ngôn ngữ trung
gian gọi là kỳ trước (fron end). Giai đoạn tổng hợp có đầu vào là ngôn ngữ trung
gian và đầu ra là ngô ngữ đích gọi là kỳ sau (back end).
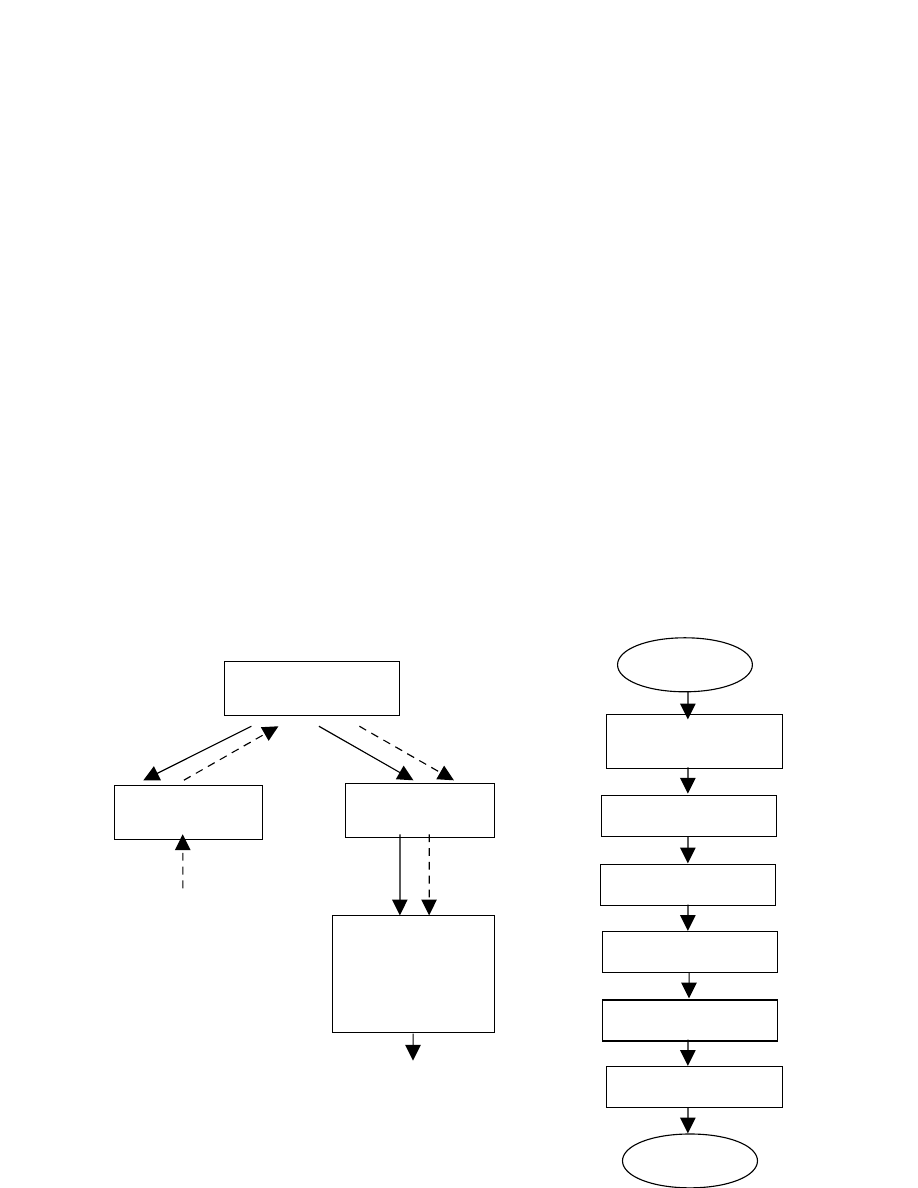
Đối với các ngôn ngữ nguồn, ta chỉ cần quan tâm đến việc sinh ra mã trung
gian mà không cần biết mã máy đích của nó. Điều này làm cho công việc đơn giản,
không phụ thuộc vào máy đích. Còn giai đoạn sau trở nên đơn giản hơn vì ngôn
ngữ trung gian thường thì gần với mã máy. Và nó còn thể hiện ưu điểm khi chúng
ta xây dựng nhiều cặp ngôn ngữ. Ví dụ có n ngôn ngữ nguồn, muốn xây dựng
chương trình dịch cho n ngôn ngữ này sang m ngôn ngữ đích thì chúng ta cần n*m
chương trình dịch; còn nếu chúng ta xây dựng theo kiến trúc front end và back end
thì chúng ta chỉ cần n+m chương trình dịch.
1.3.2. Cấu trúc động.
Cấu trúc động (cấu trúc theo thời gian) cho biết quan hệ giữa các phần khi
hoạt động.
Các thành phần độc lập của chương trình có thể hoạt động theo 2 cách: lần
lượt hay đồng thời. mỗi khi một phần nào đó của chương trình dịch xong toàn bộ
chương trình nguồn hoặc chương trình trung gian thì ta gọi đó là một lần duyệt.
*
Duyệt đơn (duyệt một lần): một số thành phần của chương trình được thực
hiện đồng thời
. Bộ phân tích cú pháp đóng vai trò trung tâm, điều khiển cả chương
trình. Nó gọi bộ phân tích từ vựng khi cần một từ tố tiếp theo và gọi bộ phân tích
ngữ nghĩa khi muốn chuyển cho một cấu trúc cú pháp đã được phân tích. Bộ phân
tích ngữ nghĩa lại đưa cấu trúc sang phần sinh mã trung gian để sinh ra các mã
trong một
ngôn
ngữ trung
gian
rồi đưa
vào
bộ tối ưu
và
sinh mã.
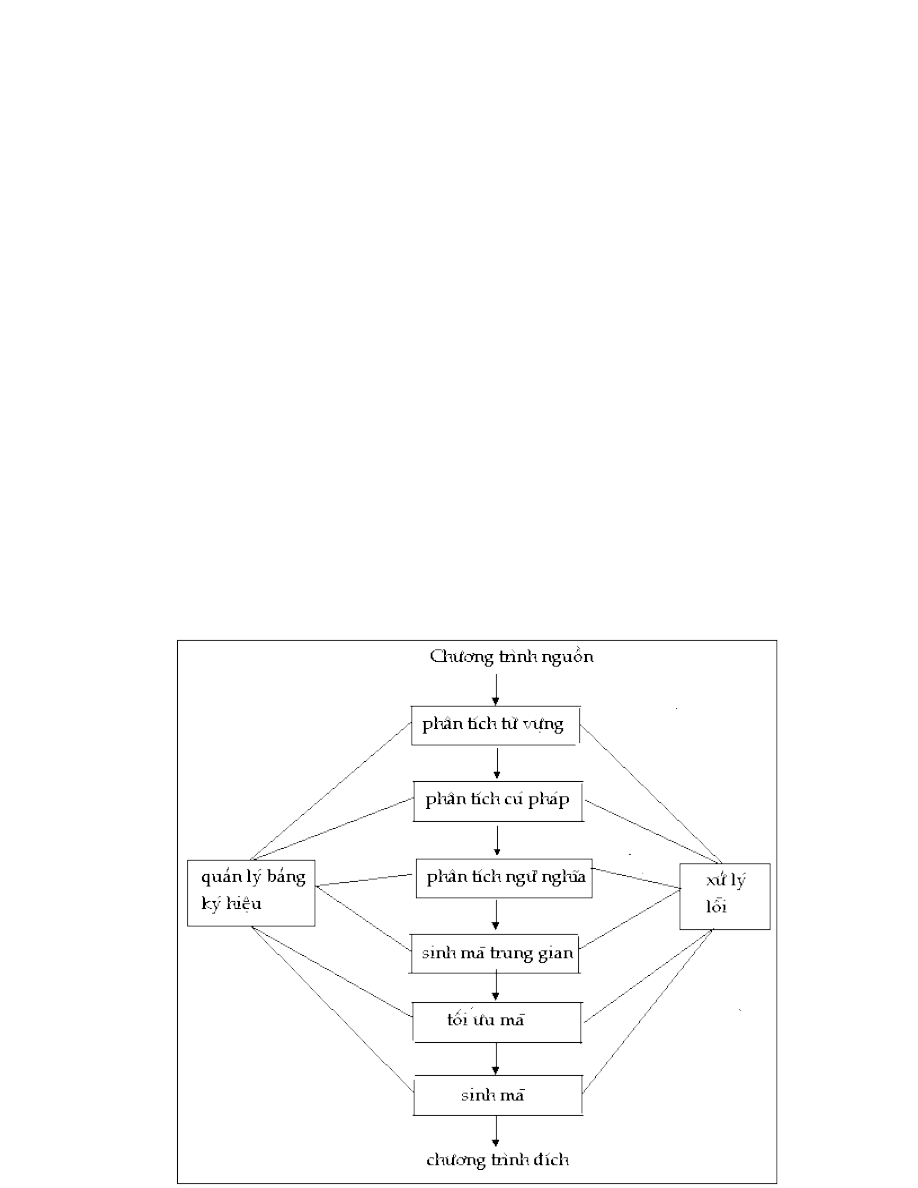
Phân tích
từ vựng
Chương trình nguồn
Phân tích
cú pháp
Phân tích
ngữ nghĩa
Sinh mã trung gian
Tối ưu mã
Sinh mã
Chương trình đích
Phân tích từ vựng
Phân tích cú pháp
Phân tích ngữ nghĩa
Sinh mã trung gian
Tối ưu mã
Sinh mã đích
mã đích
Mã nguồn
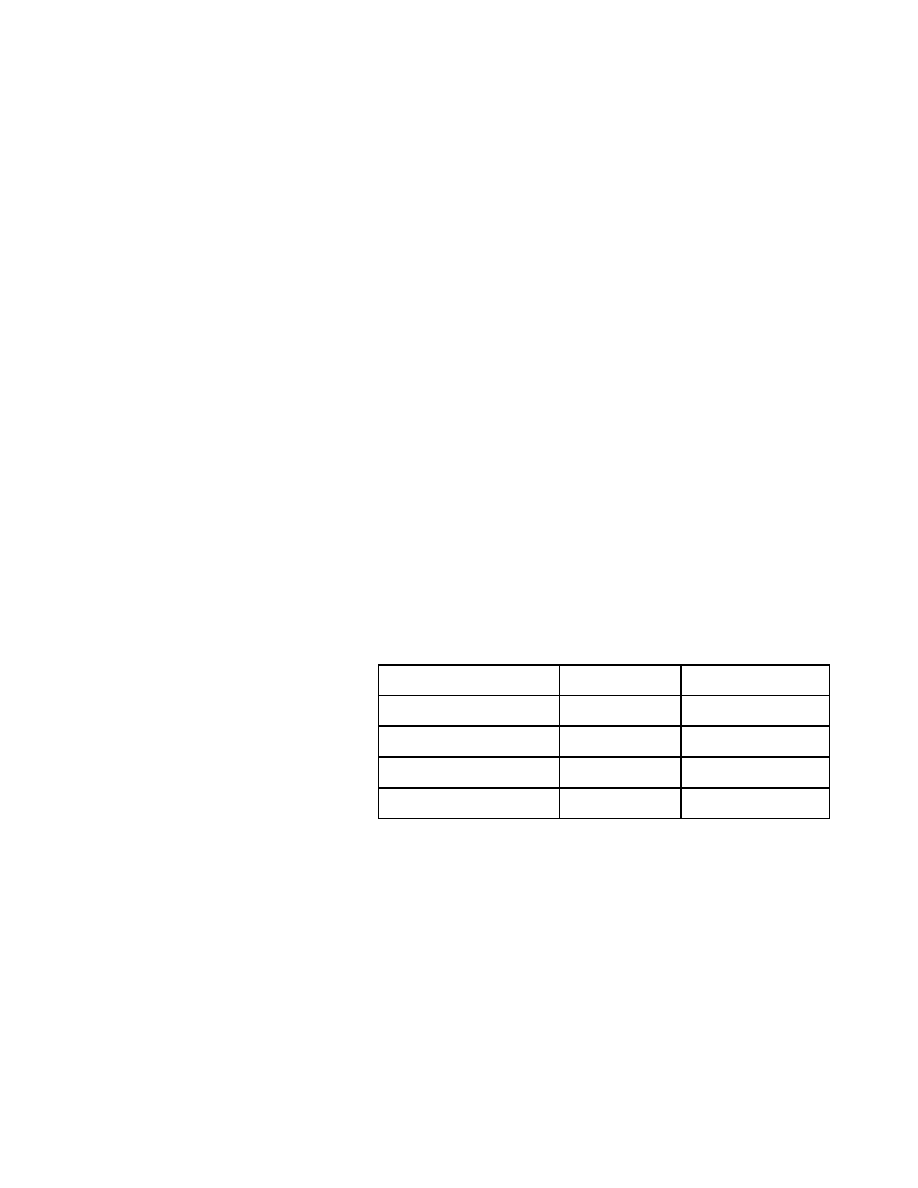
Chương trình dịch duyệt đơn
Chương trình dịch duyệt nhiều lần
* Duyệt nhiều lần: các thành phần trong chương trình được thực hiện lần lượt
và độc lập với nhau. Qua mỗi một phần, kết quả sẽ được lưu vào thiết bị lưu trữ
ngaòi để lại được đọc vào cho bước tiếp theo.
Người ta chỉ muốn có một số ít lượt bởi vì mỗi lượt đều mất thời gian đọc và
ghi ra tập tin trung gian. Ngược lại nếu gom quá nhiều giai đoạn vào trong một lượt
thì phải duy trì toàn bộ chương trình trong bộ nhớ, vì 1 giai đoạn cần thông tin
theo thứ tự khác với thứ tự nó được tạo ra. Dạng biểu diễn trung gian của chương
trình lớn hơn nhiều so với ct nguồn hoặc ct đích, nên sẽ gặp vấn đề về bộ nhớ.
Ưu và nhược điểm của các loại:
Trong giáo trình này
chúng ta nghiên cứu các
giai đoạn của một
chương trình dịch một
cách riêng rẽ nhưng theo
thiết kế duyệt một lượt.
1.4. Môi trường biên dịch
Chương trình dịch là 1 chương trình trong hệ thống liên hoàn giúp cho người
lập trình có được một môi trường hoàn chỉnh để phát triển các ứng dụng của họ.
Chương trình dịch trong hệ thống đó thể hiện trong sơ đồ sau:
So sánh
duyệt đơn
duyệt nhiều lần
tốc độ
tốt
Kém
bộ nhớ
kém
tốt
độ phức tạp
kém
tốt
Các ứng dụng lớn
Kém
tốt
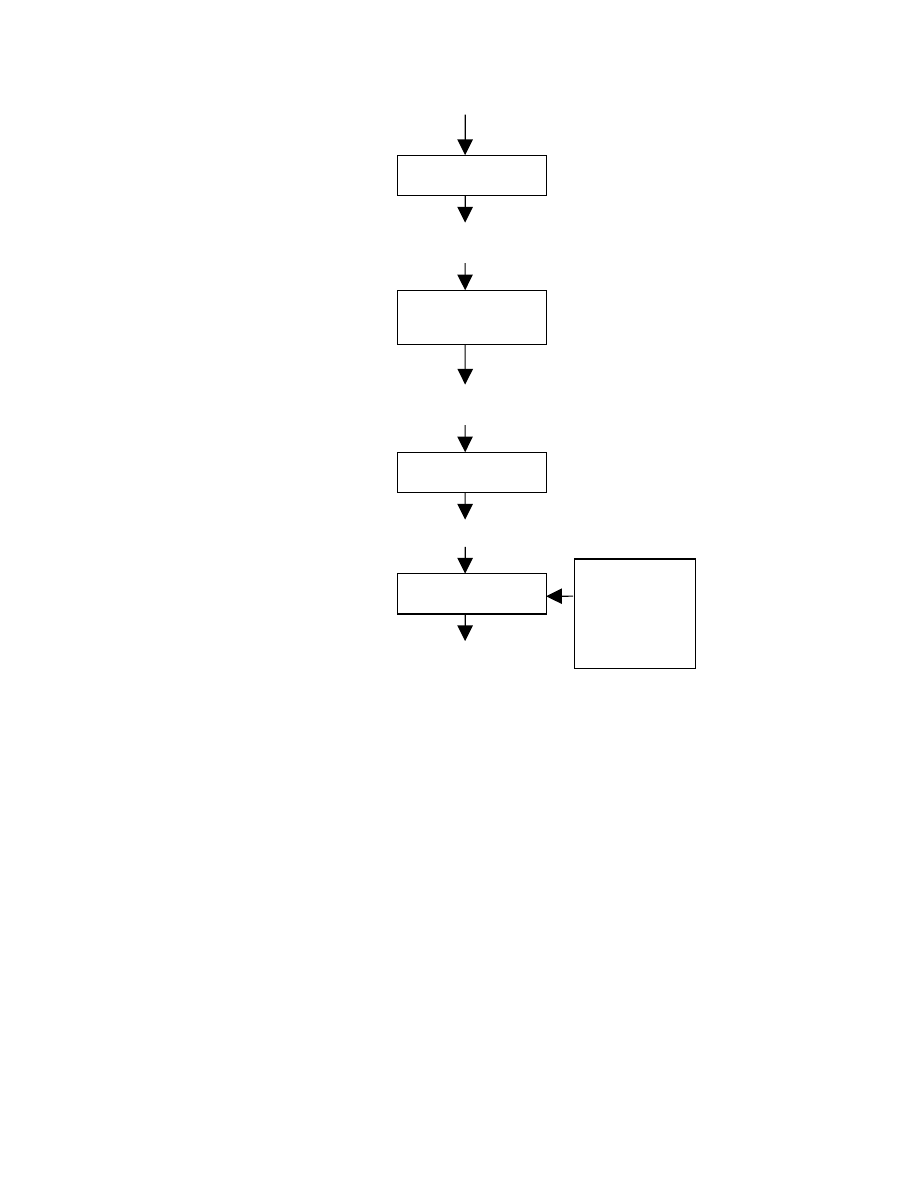
Hình 1.3: Hệ thống xử lý ngôn ngữ
* Bộ tiền xử lý:
Chuỗi kí tự nhập vào chương trình dịch là các kí tự của chương trình nguồn
nhưng trong thực tế, trước khi là đầu vào của một chương trình dịch, toàn bộ file
nguồn sẽ được qua một thậm chí một vài bọo tiền xử lý
. Sản phẩm của các bộ tiền
xử lý này mới là chương trình nguồn thực sự của chương trình dịch
. Bộ tiền xử lý
sẽ thực hiện các công việc sau:
- Xử lý Macro: Cho phep người dùng định nghĩa các macro là cách viết tắt của
các cấu trúc dài hơn.
- Chèn tệp tin: Bổ sung nội dung của các tệp tin cần dùng trong chương trình.
Ví dụ : Trong ngôn ngữ Pascal có khai báo thư viện
Tiền xử lý
Chương trình
dịch
Chương trình nguồn
Chương trình nguồn nguyên thủy
Assembler
Chương trình đích hợp ngữ
Mã máy định vị lại được
Tải / Liên kết
Thư viện và
các file đối
tượng định vị
lại được
Mã máy thật sự

“Uses crt;”
bộ tiền xử lý sẽ chền tệp tin crt vào thay cho lời khai báo.
- Bộ xử lý hoà hợp: hỗ trợ những ngôn ngữ xưa hơn bằng các cấu trúc dữ liệu
hoặc dòng điều khiển hiện đại hơn.
- Mở rộng ngôn ngữ: gia tăng khả năng của ngôn ngữ bằng các macro có sẵn.
* Trình biên dịch hợp ngữ: Dịch các mã lệnh hợp ngữ thành mã máy.
* Trình tải/ liên kết:
Trình tải nhận các max máy khả tải định vị, thay đổi các địa chỉ khả tải định
vị, đặt các chỉ thị và dữ liệu trong bộ nhớ đã được sửa đổi vào các vik trí phù hợp.
Trình liên kết cho phép tạo ra một hcương rình từ các tệp tin thư viện hoặc
nhiều tệp tin mã máy khả tải định vị mà chúng là kết quả của những biên dịch khác
nhau.
CHƯƠNG 2
PHÂN TÍCH TỪ VỰNG
1. Vai trò của bộ phân tích từ vựng.
1.1. Nhiệm vụ.
Bộ phân tích từ vựng có nhiệm vụ là đọc các kí tự vào từ văn bản chương
trình nguồn và phân tích đưa ra danh sách các từ tố (từ vựng và phân loại cú pháp
của nó) cùng một số thông tin thuộc tính.
Đầu ra của bộ phân tích từ vựng là danh sách các từ tố và là đầu vào cho phân
tích cú pháp. Thực tế thì phân tích cú pháp sẽ gọi lần lượt mỗi từ tố từ bộ phân tích
để xử lý, chứ không gọi một lúc toàn bộ danh sách từ tố của cả chương trình nguồn
.
Khi nhận được yêu cầu lấy một từ tố tiếp theo từ bộ phân tích cú pháp, bộ
phân tích từ vựng sẽ đọc kí tự vào cho dến khi đưa ra được một từ tố.
1.2. Quá trình phân tích từ vựng
1). Xóa bỏ kí tự không có nghĩa
(các chú thích, dòng trống, kí hiệu xuống dòng,
kí tự trống không cần thiết)
Quá trình dịch sẽ xem xét tất cả các ký tự trong dòng nhập nên những ký tự
không có nghĩa (khoảng trắng (blanks, tabs, newlines) hoặc lời chú thích phải bị bỏ
qua. Khi bộ phân tích từ vựng bỏ qua các khoảng trắng này thì bộ phân tích cú
pháp không bao giờ quan tâm đến nó nữa.
2). Nhận dạng các kí hiệu: nhận dạng các từ tố.
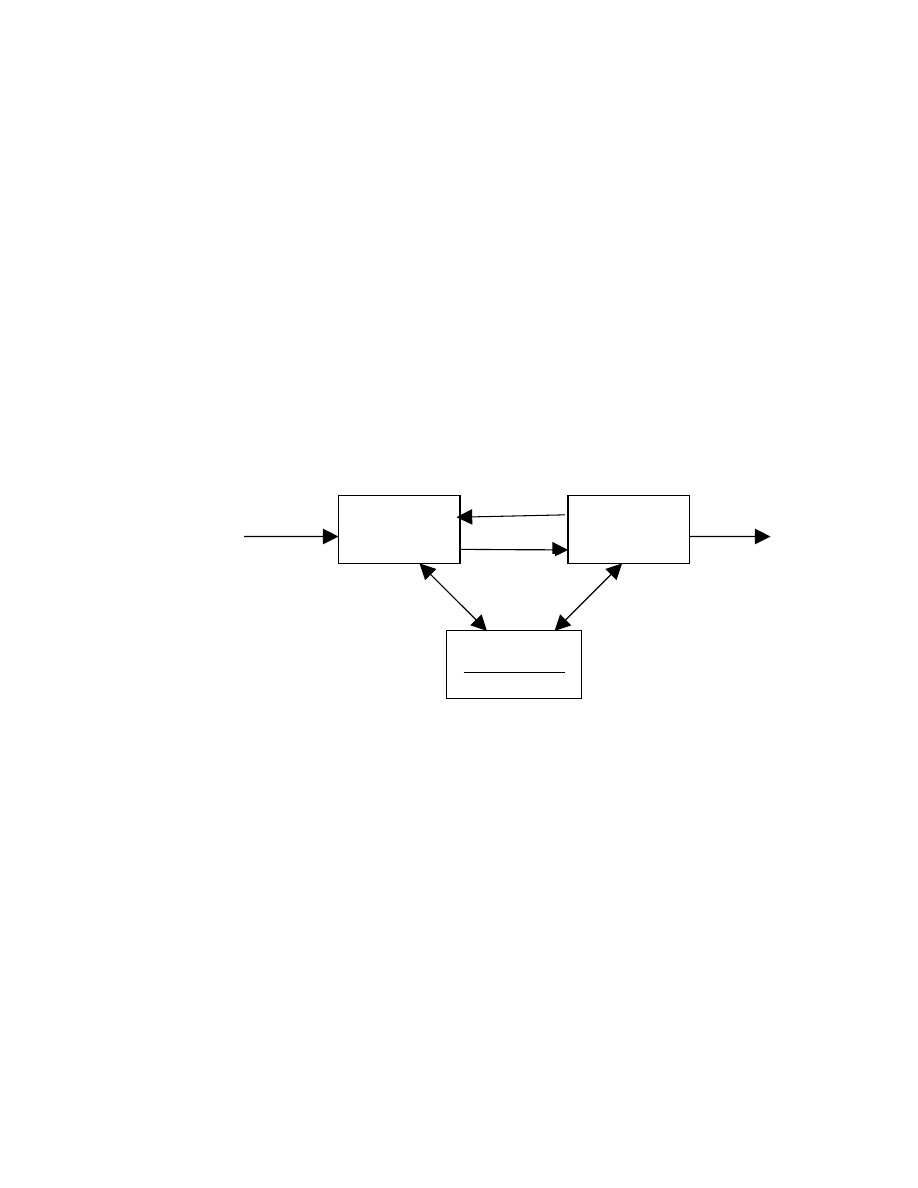
Phân tích
từ vựng
Phân tích
cú pháp
yêu cầu lấy từ tố
tiếp theo
từ tố
chương trình
nguồn
Bảng ký hiệu
Hinh 2.4: Sơ đồ phân tích từ tố

Ví dụ ghép các chữ số để được một số và sử dụng nó như một đơn vị trong
suốt quá trình dịch. Đặt num là một token biểu diễn cho một số nguyên. Khi một
chuỗi các chữ số xuất hiện trong dòng nhập thì bộ phân tích sẽ gửi cho bộ phân tích
cú pháp num. Giá trị của số nguyên đã được chuyển cho bộ phân tích cú pháp như
là một thuộc tính của token num.
3). Số hoá các kí hiệu: Do con số xử lý dễ dàng hơn các xâu, từ khoá, tên, nên
xâu thay bằng số, các chữ số được đổi thành số thực sự biểu diễn trong máy. Các
tên được cất trong danh sách tên, các xâu cất trong danh sách xâu, các chuỗi số trong
danh sách hằng số.
1.2. Từ vị (lexeme), từ tố (token), mẫu (patter).
* Từ vị: là một nhóm các kí tự kề nhau có thể tuân theo một quy ước (mẫu hay
luật) nào đó.
* Từ tố: là một thuật ngữ chỉ các từ vựng có cùng ý nghĩa cú pháp (cùng một
luật mô tả).
- Đối với ngôn ngữ lập trình thì từ tố có thể được phân vào các loại sau:
+ từ khoá
+ tên của hằng, hàm, biến
+ số
+ xâu ký tự
+ các toán tử
+ các ký hiệu.
Ví dụ: position := initial + 10 * rate ;
ta có các từ vựng
position, :=, initial, +, 10, *, rate, ;
trong đó position, initial, rate là các từ vựng có cùng ý nghĩa cú pháp là các tên.
:=
là phép gán
+
là phép cộng
*
là phép nhân
10
là một con số
;
là dấu chấm phẩy
Như vậy trong câu lệnh trên có 8 từ vựng thuộc 6 từ tố.
Phân tích cú pháp sẽ làm việc trên các từ tố chứ không phải từ vựng, ví dụ như
là làm việc trên khái niệm một số chứ không phải trên 5 hay 2; làm việc trên khái
niệm tên chứ không phải là a, b hay c.
* Thuộc tính của từ tố:
Một từ tố có thể ứng với một tập các từ vị khác nhau, ta buộc phải thêm một số thông tin
nữa để khi cần có thể biết cụ thể đó là từ vị nào. Ví dụ: 15 và 267 đều là một chuỗi số có từ tố là
num nhưng đến bộ sinh mã phải biết cụ thể đó là số 15 và số 267.

Thuộc tính của từ tố là những thông tin kết hợp với từ tố đó. Trong thực tế,
một từ tố sẽ chứa một con trỏ trỏ đến một vị trí trên bảng kí hiệu có chứấcc thông
tin về nó.
Ví dụ: position := initial + 10 * rate ; ta nhận được dãy từ tố:
<
tên, con trỏ trỏ đến position trên bảng kí hiệu>
<phép gán, >
<tên, con trỏ trỏ đến initial trên bảng kí hiệu>
<phép cộng, >
<tên, con trỏ trỏ đến rate trên bảng kí hiệu>
<phép nhân>
<số nguyên, giá trị số nguyên 60>
* Mẫu (luật mô tả - patter): Để cho bộ phân tích từ vựng nhận dạng được các
từ tố, thì đối với mỗi từ tố chúng ta phải mô tả đặc điểm để xác định một từ vựng
có thuộc từ tố đó không, mô tả đó được gọi là mẫu từ tố hay luật mô tả.
Token
Trị từ vựng
MÉu (luËt m« t¶)
const
if
quan hÖ
(relation)
tªn (id)
Sè (num)
X©u (literal)
const
if
<,<=,=,<>,>,>
=
pi, count, d2
3.1416, 0, 5
"hello"
const
if
< hoÆc <= hoÆc =hoÆc <> hoÆc
<> hoÆc > hoÆc >=
më ®Çu lµ ch÷ c¸i theo sau lµ ch÷
c¸i, ch÷ sè
bÊt kú h»ng sè nµo
bÊt kú c¸c character n»m gi÷a " vµ "
ngo¹i trõ "
Ta có thể coi: từ vị giống các từ cụ thể trong từ điển như nhà, cửa… từ tố gần giống khái
niệm từ loại như danh từ động từ… Các mẫu (luật mô tả) dùng để nhận dạng loại từ tố, giống
như những quy định để nhận dạng một từ là danh từ hay động từ…
Trị từ vựng được so cùng với mẫu của từ tố là chuỗi kí tự và là đơn vị của từ
vựng. Khi đọc chuỗi kí tự của chương trình nguồn bộ phân tích từ vựng sẽ so sánh
chuỗi kí tự đó với mẫu của từ tố nếu phù hợp nó sẽ đoán nhận được từ tố đó và đưa
từ tố vào bảng kí hiệu cùng với trị từ vưng của nó.
1.4. Cách lưu trữ tạm thời chương trình nguồn.
Việc đọc từng kí tự trong chương trình nguồn tốn một thời gian đáng kể nên nó ảnh hưởng
tới tốc độ chương trình dịch. Để giải quyết vấn đề này,
thiết kế đọc vào một lúc một chuỗi
kí tự lưu trữ vào vùng nhớ tạm buffer
. Nhưng việc đọc như vậy gặp khó khăn do không thể
xác định được một chuỗi như thế nào thì chứa chọn vẹn 1 từ tố.
Và phải phân biệt được một
chuỗi như thế nào thì chứa chọn vẹn một từ tố.
Có 2 phương pháp giải quyết như sau:
1. Cặp bộ đệm (buffer pairs)

* Cấu tạo:
- Chia buffer thành 2 nửa, một nửa chứa n kí tự ( n = 1024, 4096, …).
- Sử dụng 2 con trỏ dò tìm trong buffer:
p1: (lexeme_ beginning) Đặt tại vị trí đầu của một từ vị.
p2: (forwar):di chuyển trên từng kí tự trong buffer để xác định từ tố.
E =
M *
C
* * 2
EOF
* Hoạt động:
- Đọc n kí tự vào nửa đầu của buffer, 2 con trỏ trùng nhau tại vị trí bắt đầu.
- Con trỏ p2 tiến sang phải cho tới khi xác định được một từ tố có từ vị là
chuỗi kí tự nằm giữa 2 con trỏ. Dời p1 lên trùng với p2, tiếp tục dò tìm từ tố mới.
- khi p2 ở cuối nửa đầu của buffer thì đọc tiếp n kí tự vào nửa đầu thứ 2. Khi
p2 nằm ở nửa cuối của buffer thì đọc tiếp n kí tự vào nửa đầu của buffer và p2 được
dời về đầu của bộ đệm.
- Nếu số kí tự trong chương trình nguồn còn lại ít hơn n thì một kí tự đặc biệt
được đưa vào buffer sau các kí tự vừa đọc để báo hiệu chương trình nguồn đã được
đọc hết.
* Giải thuật hình thức
if p2 ở cuối nửa đầu then
begin
Đọc vào nửa cuối. p2 := p2 + 1;
end
else if p2 ở cuối của nửa thứ hai then
begin
Đọc vào nửa đầu. p2 := p2 + 1;
end
else p2 := p2 + 2
2. Phương pháp cầm canh.
Phương pháp trên mỗi lần di chuyển p2 phải kiểm tra xem có phải đã hết một
nửa buffer chưa nên kém hiệu quả vì phải 2 lần test. Khắc phục:
- Mỗi lần chí đọc n-1 kí tự vào mỗi nửa buffer còn kí tự thứ n là kí tự đặc
biệt (thường là EOF). Như vậy ta chỉ cần một lần test.
E = M * EOF
C * * 2 EOF
EOF
Giải thuật:
p2 := p2 + 1;
if p2( = eof then
begin
if p2 ở cuối của nửa đầu then
begin Đọc vào nửa cuối; p2 := p2 + 1 end
else if p2 ở cuối của nửa cuối then
begin Đọc vào nửa đầu; Dời p2 vào đầu của nửa đầu end
else /* eof ở giữa chỉ hết chơng trình nguồn */
kết thúc phân tích từ vựng
end

2. XÁC ĐỊNH TỪ TỐ.
2.1. Biểu diễn từ tố
Cách biểu diễn các luật đơn giản nhất là biểu diễn bằng lời. Tuy nhiên cách này thường
gặp hiện tượng nhập nhằng ( cùng một lời nói có thể hiểu theo nhiều nghĩa khác nhau), phát biểu
theo nhièu cách khác nhau khó đưa vào máy tính. Các từ tố khác nhau có các mẫu hay luật mô tả
khác nhau. Các mẫu này là cơ sở để nhận dạng các từ tố. Ta cần thiết phải hình thức hoá các
mẫu này để làm sao có thể lập trình được. Việc này có thể thực hiện được nhờ biểu thức chính
qui và ôtômát hữu hạn. Ngoài ra ta có thể dùng cách biểu diễn trực quan của văn phạm phi ngữ
cảnh là đồ thị chuyển để mô tả các loại từ tố.
2.1.1. Một số khái niệm về ngôn ngữ hình thức.
2.1.1.1. Kí hiệu, Xâu, ngôn ngữ.
* Bảng chữ cái: là một tập
Σ
≠
∅
hữu hạn hoặc vô hạn các đối tượng. Mỗi
phần tử a
∈Σ
gọi là kí hiệu hoặc chữ cái (thuộc bảng chữ cái
Σ
).
* Xâu: Là một dãy liên tiếp các kí hiệu thuộc cùng một bảng chữ cái.
- Độ dài xâu: là tổng vị trí của tất cả các kí hiệu có mặt trong xâu, kí hiệu là |
w|.
- Xâu rỗng: là từ có độ dài = 0 kí hiệu là
ε
hoặc
∧
. Độ dài của từ rỗng = 0.
- Xâu v là Xâu con của w nếu v được tạo bởi các ký hiệu liền kề nhau trong w.
* Tập tất cả các từ trên bảng chữ cái
Σ
kí hiệu là
Σ
*
. Tập tất cả các từ khác
rỗng trên bảng chữ cái
Σ
kí hiệu là
Σ
+
.
Σ
*
=
Σ
+
∪
{
ε
}
* Tiền tố: của một xâu là một xâu con bất kỳ nằm ở đầu xâu. Hậu tố của một
xâu là xâu con nằm ở cuối xâu.
(Tiền tố và hậu tố của một xâu khác hơn chính xâu đó
ta gọi là tiền tố và hậu tố thực sự
)
* Ngôn ngữ: Một ngôn ngữ L là một tập các chuỗi của các ký hiệu từ một bộ
chữ cái
Σ
nào đó.
(Một tập con A
⊆
Σ
*
được gọi là một ngôn ngữ trên bảng chữ cái
Σ
).
- Tập rỗng được gọi là ngôn ngữ trống (hay ngôn ngữ rỗng). Ngôn ngữ rỗng là
ngôn ngữ trên bất kỳ bảng chữ cái nào.
(Ngôn ngữ rỗng khác ngôn ngữ chỉ gồm từ rỗng:
ngôn ngữ
∅
không có phần tử nào trong khi ngôn ngữ {
ε
} có một phần tử là chuỗi rỗng
ε
)
* Các phép toán trên ngôn ngữ.
+ Phép giao: L = L
1
∩
L
2
= {x
∈Σ
*
| x
∈
L
1
hoặc x
∈
L
2
}
+ Phép hợp: L = L
1
∪
L
2
= {x
∈Σ
*
| x
∈
L
1
và x
∈
L
2
}
+ Phép lấy phần bù của ngôn ngữ L là tập CL = { x
∈Σ
*
| x
∉
L}
+
Phép nối kết (concatenation) của hai ngôn ngữ L
1
/
Σ
1
và L
2
/
Σ
2
là :
L
1
L
2
= {w
1
w
2
|
w
1
∈
L
1
và w
2
∈
L
2
}/
Σ
1
∪
Σ
2
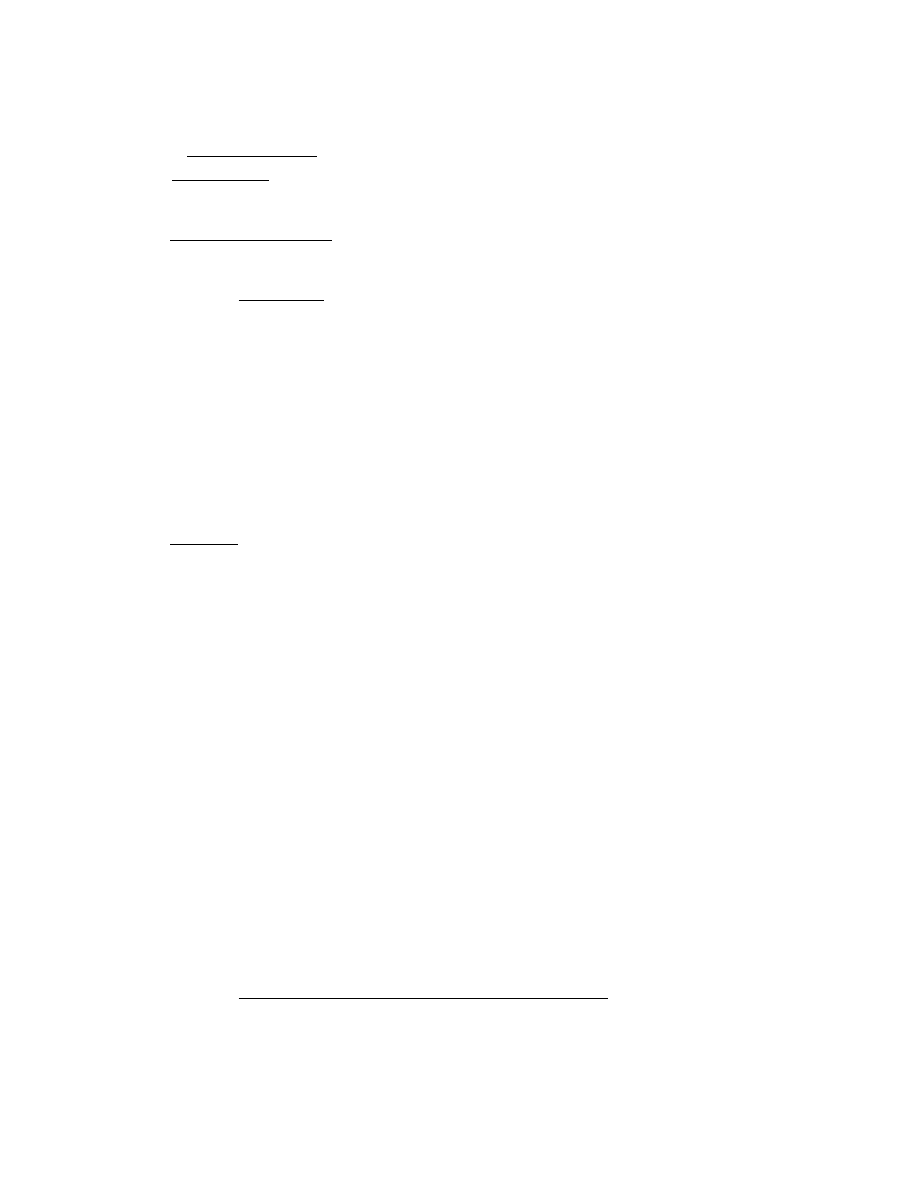
Ký hiệu L
n
= L.L.L…L (n lần). L
i
= LL
i - 1
.
- Trường hợp đặc biệt : L
0
= {
ε
}, với mọi ngôn ngữ L.
+ Phép bao đóng (closure) :
+ Bao đóng (Kleene) của ngôn ngữ L, ký hiệu L
*
là hợp của mọi tập tích trên L:
L* =
∞
∪
Ii= 0
Li
+ Bao đóng dương (positive) của ngôn ngữ L, ký hiệu L
+
được định nghĩa là
hợp của mọi tích dương trên L :
L: L
+
=
∞∪
i = 1
L
I
2.1.1.2. Văn phạm.
* Định nghĩa văn phạm. (văn phạm sinh hay văn phạm ngữ cấu)
- Là một hệ thống gồm bốn thành phần xác định G = (
Σ
,
∆
, P, S), trong đó:
Σ
: tập hợp các ký hiệu kết thúc (terminal).
∆
: tập hợp các biến hay ký hiệu chưa kết thúc (non terminal) (với
Σ
∩
∆
=
∅
)
P : tập hữu hạn các quy tắc ngữ pháp được gọi là các sản xuất (production),
mỗi sản xuất biểu diễn dưới dạng
α
→
β
, với
α
,
β
là các chuỗi
∈
(
Σ
∪
∆
)
*
.
S
⊂
∆
: ký hiệu chưa kết thúc dùng làm ký hiệu bắt đầu (start)
Quy ước:
- Dùng các chữ cái Latinh viết hoa (A, B, C, ...) để chỉ các ký hiệu trong tập biến
∆
.
- Các chữ cái Latinh đầu bảng viết thường (a, b, c, ...) chỉ ký hiệu kết thúc thuộc tập
Σ
- Xâu thường được biểu diễn bằng các chữ cái Latinh cuối bảng viết thường (x, y, z, ...).
* Phân loại Chosmky.
- Lớp 0: là văn phạm ngữ cấu (Phrase Structure) với các luật sản xuất có dạng:
α -> β với α
∈
V
+
, β
∈
V
*
- Lớp 1: là văn phạm cảm ngữ cảnh (Context Sensitive) với các luật sản xuất
có dạng:
α -> β với α
∈
V
+
, β
∈
V
*
, |α| < |β|
- Lớp 2: là văn phạm phi ngữ cảnh (Context Free Grammar - CFG ) với các
luật sản xuất có dạng: A -> α với A
∈
N, α
∈
V
*
- Lớp 3: là văn phạm chính qui (Regular Grammar) với luật sản xuất có dạng:
A -> a, A -> Ba hoặc A-> a, A-> aB với A, B
∈
N và a
∈
T
Các lớp văn phạm được phân loại theo thứ tự phạm vi biểu diễn ngôn ngữ giảm dần, lớp
văn phạm sau nằm trong phạm vi của lớp văn phạm trước:
Lớp 0
∈
Lớp 1
∈
Lớp 2
∈
Lớp 3
2.1.1.3. Văn phạm chính quy và biểu thức chính quy.
* Văn phạm chính quy:
Ví dụ 1: Tên trong ngôn ngữ Pascal là một từ đứng đầu là chữ cái, sau đó có thể là không
hoặc nhiều chữ cái hoặc chữ số.
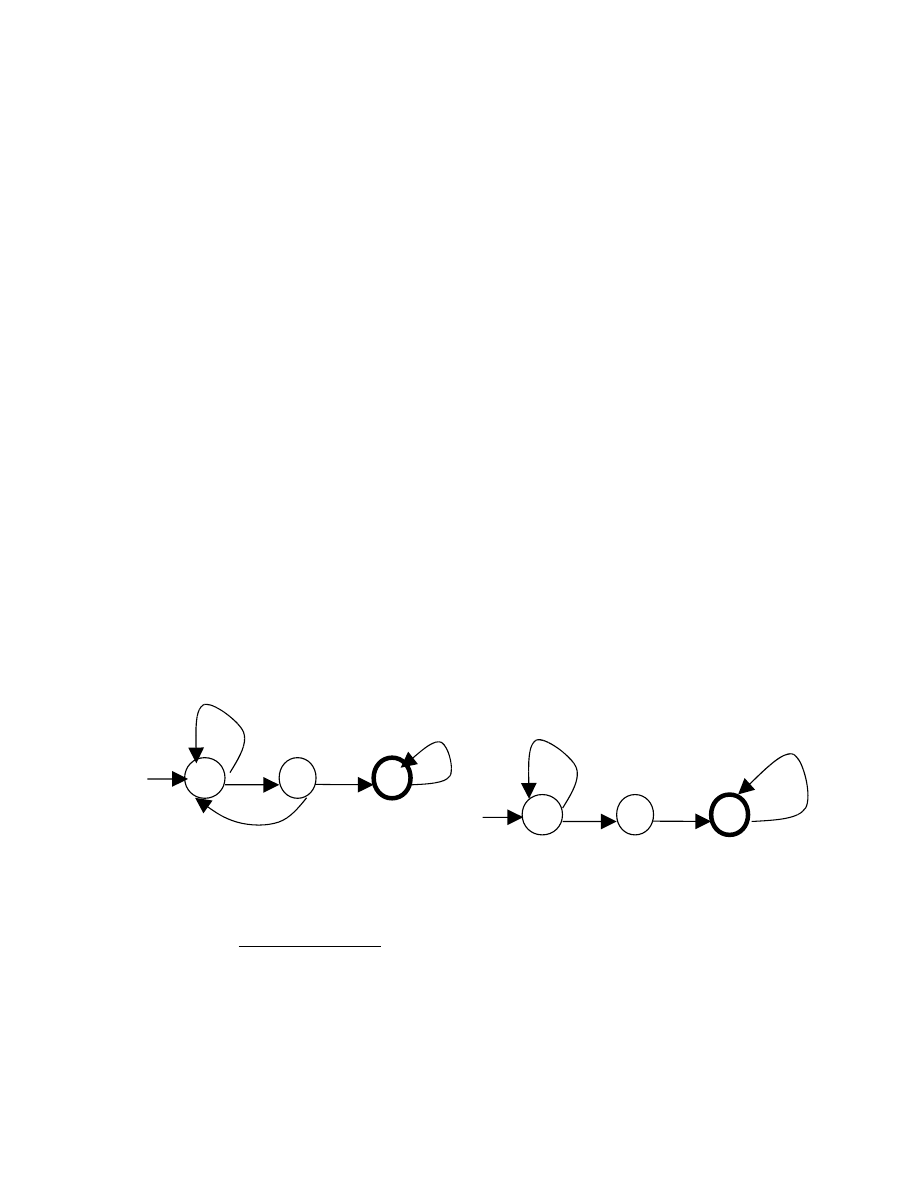
Biểu diễn bằng BTCQ:
tên -> chữ_cái (chữ_cái | chữ_số)
*
Biểu diễn bằng văn phạm chính qui:
Tên -> chữ_cái A;
A -> chữ_cái A | chữ_số A | ε
* Biểu thức chính qui được định nghĩa trên bộ chữ cái
∑
như sau:
-
ε
là biểu thức chính quy, biểu thị cho tập {
ε
}
- a
∈
∑
, a là biểu thức chính quy, biểu thị cho tập {a}
- Giả sử r là biểu thức chính quy biểu thị cho ngôn ngữ L(r), s là biểu thức
chính quy, biểu thị cho ngôn ngữ L(s) thì:
+ (r)|(s) là biểu thứcchính quy biểu thị cho tập ngôn ngữ L(r)
∪
L(s)
+ (r)(s) là biểu thức chính quy biểu thị cho tập ngôn ngữ L(r)L((s)
+ (r)* là biểu thức chính quy biểu thị cho tập ngôn ngữ L(r)*
Biểu thức chính quy sử dụng các ký hiệu sau:
| là ký hiệu hoặc (hợp)
( )
là ký hiệu dùng để nhóm các ký hiệu
*
là lặp lại không hoặc nhiều lần
+
là lặp lại một hoặc nhiều lần
!
là lặp lại không hoặc một lần
Ví dụ 2: Viết biểu thức chính qui và đồ thị chuyển để biểu diễn các xâu gồm các chữ số 0
và 1, trong đó tồn tại ít nhất một xâu con “11”
Biểu thức chính qui:
(0|1)*11(0|1)*
Biểu diễn biểu thức chính quy dưới dạng đồ thị chuyển:
2.1.1.3. Ôtômát hữu hạn.
* Định nghĩa: Một Otomat hữu hạn đơn định là một hệ thống M = (∑, Q,
δ
,
q
0
, F), trong đó:
•
∑ là một bộ chữ hữu hạn, gọi là bộ chữ vào
•
Q là một tập hữu hạn các trạng thái
•
q
0
∈
Q là trạng thái đầu
Đồ thị chuyển đơn định
0
0|1
1
2
1
1
2
start
0
0
0
0|1
1
2
1
1
2
0|1
start
Đồ thị chuyển không đơn định
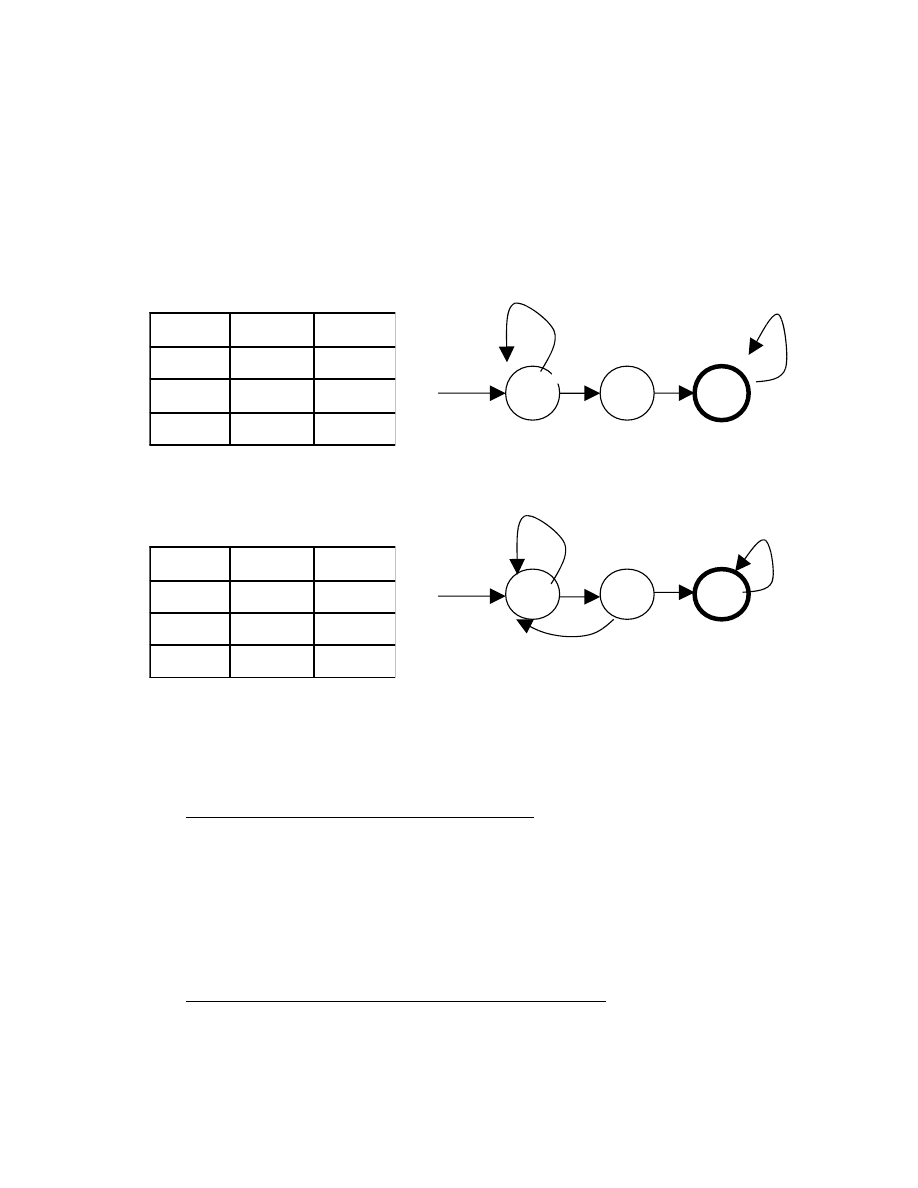
•
F
∈
Q là tập các trạng thái cuối
δ
là hàm chuyển trạng thái
δ
có dạng:
•
δ
: Q x ∑ -> Q thì M gọi là ôtômát mát đơn định (kí hiệu ÔHĐ).
•
δ
: Q x ∑ -> 2
Q
thì M gọi là ôtômát không đơn định (kí hiệu ÔHK).
* Hình trạng: của một OHĐ là một xâu có dạng qx với q
∈
Q là trạng thái
hiện thời và x
∈
∑
*
là phần xâu vào chưa được đoán nhận.
Ví dụ: ∑ = {0, 1}; Q = {q
0
, q
1
, q
2
}; q
0
là trạng thái ban đầu; F={q
2
}.
Hàm chuyển trạng thái được mô tả như bảng sau:(ÔHK)
Hàm chuyển trạng thái ÔHĐ
2.1.1. Biểu diễn từ tố bằng biểu thức chính quy.
* Một số từ tố được mô tả bằng lời như sau:
- Tên là một xâu bắt đầu bởi một chữ cái và theo sau là không hoặc nhiều
chữ cái hoặc chữ số
- Số nguyên bao gồm các chữ số
- Số thực có hai phần: phần nguyên và phần thực là xâu các chữ số và hai
phần này cách nhau bởi dấu chấm
- Các toán tử quan hệ <, <=, >, >=, <>, =
* Mô tả các mẫu từ tố trên bằng biểu thức chính qui:
Tên từ tố
→
biểu thức chính quy biểu diễn từ tố đó.
- chữ_cái
→
A|B|C|…|Z|a|b|c|…|z
- chữ_số
→
0|1||2|3|4|5|6|7|8|9
δ
0
1
Q
0
q
0
q
0
, q
1
Q
1
∅
q
2
Q
2
q
2
q
2
δ
0
1
Q
0
q
0
q
1
Q
1
q
0
q
2
Q
2
q
2
q
2
q
0
0|1
q
1
1
1
q
2
0|1
start
Đồ thị chuyển không đơn định
Đồ thị chuyển đơn định
q
0
0|1
q
1
1
1
q
2
start
0
0
- Tên
→
chữ_cái (chữ_cái | chữ_số)
*
- Số nguyên
→
(chữ_số)
+
- Số thực
→
(chữ_số)
+
.(chữ_số)
- Toán tử quan hệ:
+ Toán tử bé hơn (LT):
<
+ Toán tử bé hơn hoặc bằng (LE):
<=
+ Toán tử lớn hơn (GT):
>
+ Toán tử lớn hơn hoặc bằng (GE):
>=
+ Toán tử bằng (EQ):
=
+ Toán tử khác (NE):
<>
2.1.2. Biểu diẽn từ tố bằng đồ thị chuyển.
Toán tử quan hệ:
0
1
2
<
=
3
4
*
>
≠
5
=
LE
NE
LT
EQ
>
GE
GT
6
7
=
8
*
≠
0
chữ_số
1
3
*
chữ_số
≠
.
2
chữ_số
0
chữ_sô
1
2
*
chữ số
≠
0
chữ_cái
1
2
*
chữ_cái
≠
chữ_số
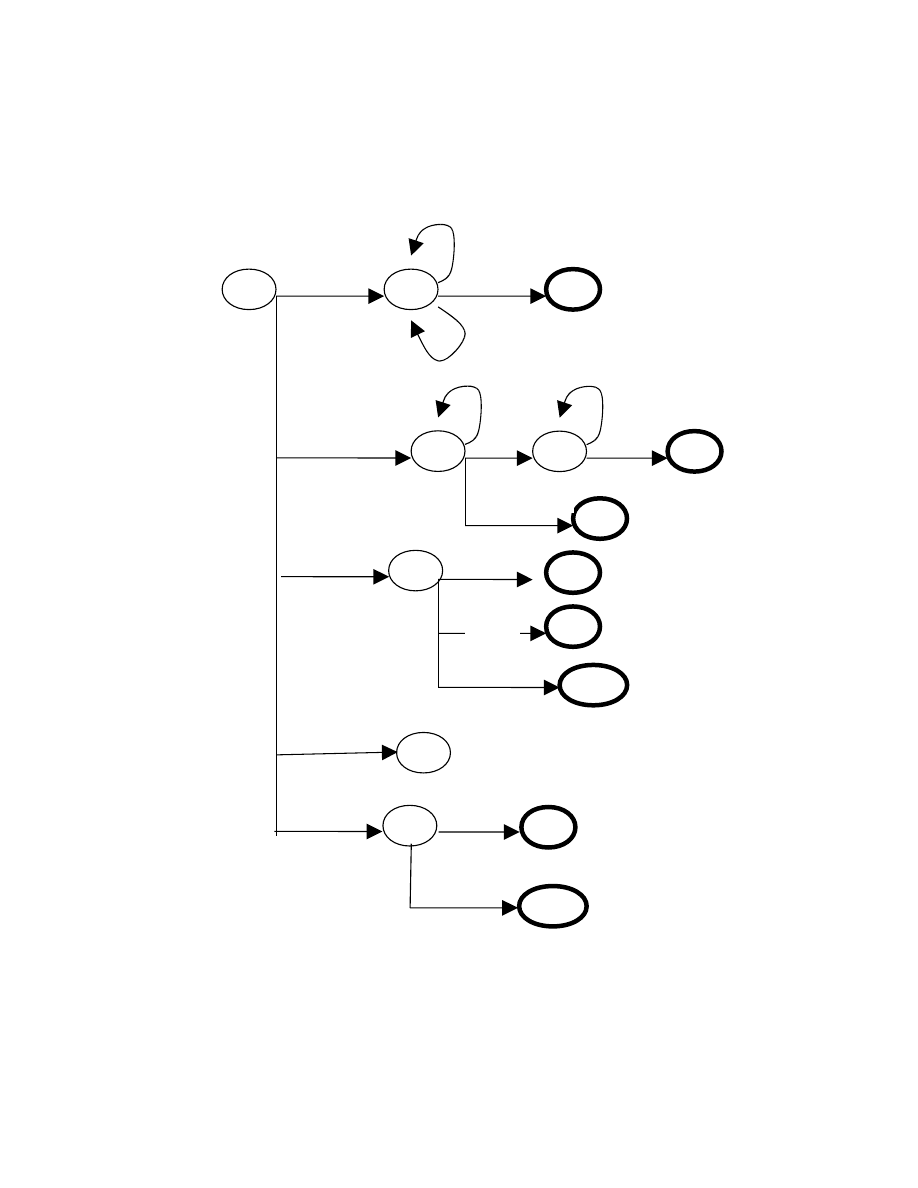
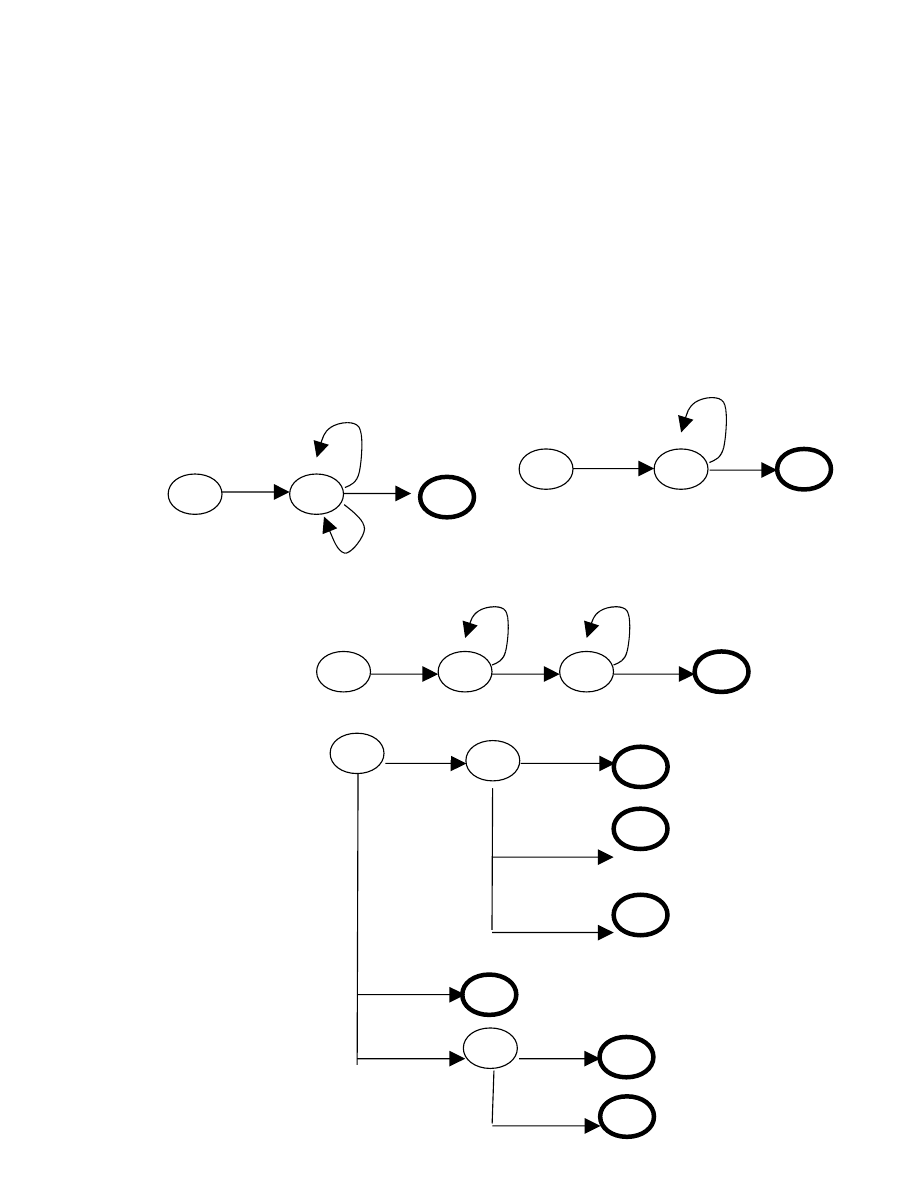
Để xây dựng một chương trình nhận dạng tất cả các loại từ tố này, chúng ta
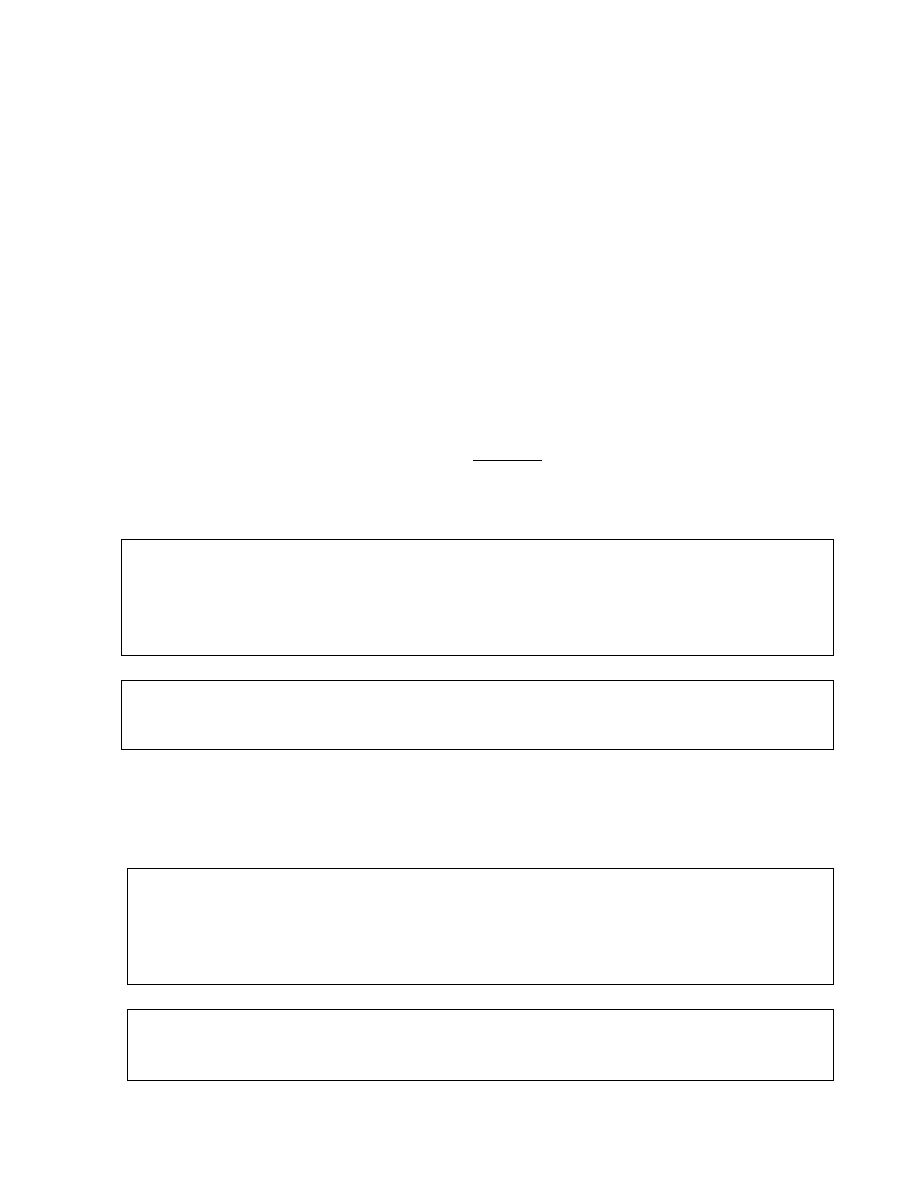
phải kết hợp các đồ thị này thành một đồ thị duy nhất:
2.1.3. Biểu diễn bởi OHĐ
Với ví dụ trên chúng ta xây dựng ôtômát với các thông số như sau:
Q = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}
F = {2,4,6,10,14}
q
0
= 0
0
chữ_cái
1
2
*
chữ_số
chữ_cái
tên
chữ_số
3
4
*
chữ_số
khác
số nguyên
6
*
≠
5
chữ_số
.
số thực
7
8
<
=
9
>
≠
LE
NE
LT
10
*
1
1
=
EQ
1
2
1
3
14
*
=
≠
>
GE
GT

hàm chuyển trạng thái được mô tả bởi bảng sau:
∂
chữ_cái
chữ_số
.
<
=
>
khác
0
1
3
lỗi
7
11
12
lỗi
1
1
1
2
2
2
2
2
3
4
3
5
4
4
4
4
5
6
5
6
6
6
6
6
7
10
10
10
10
8
9
10
12
14
14
14
14
13
14
14
Các trạng thái
∈
F là trạng thái kết thúc
Các trạng thái có dấu * là kết thúc trả về ký hiệu cuối cho từ tố tiếp theo
2.2. Viết chương trình cho đồ thị chuyển.
2.2.1. Lập bộ phân tích từ vựng bằng phương pháp diễn giải đồ thị chuyển.
Đoạn chương trình mô tả việc nhận dạng từ tố bằng cách diễn giải đồ thị
chuyển.
Chúng sẽ sử dụng các hàm sau:.
int IsDigit ( int c); // hàm kiểm tra một ký hiệu là chữ số
int IsLetter ( int c); // hàm kiểm tra một ký hiệu là chữ cái
int GetNextChar(); // hàm lấy ký tự tiếp theo
enum Token {IDENT, INTEGER, REAL, LT, LE, GT, GE, NE, EQ, ERROR};
// hàm này trả về loại từ tố
// từ vị nằm trong s
Token GetNextToken(char *s)
{ int state=0;
int i=0;
while(1)
{
int c=GetNextChar();
switch(state)
{
case 0:
if(IsLetter(c)) state=1;

else if(IsDigit(c)) state=3;
else if(c==‘<’) state=7;
else if(c==‘=’) state=11;
else if(c==‘>’) state=12;
else return ERROR;
s[i++]=c;
break;
case 1:
if(IsLetter(c)||IsDigit(c)) state=1;
else return ERROR;
break;
case 2:
s[i]=0; GetBackChar();
return IDENT;
case 3:
if(IsLetter(c)) state=4;
else if(IsDigit(c)) state=3;
else if(c==‘.’) state=5;
else return 4;
s[i++]=c;
break;
case 4:
s[i]=0; GetBackChar();
return INTEGER;
case 5:
if(IsDigit(c)) state=5;
else state=6;
s[i++]=0;
break;
case 6:
s[i]=0; GetBackChar();
return REAL;
case 7:
if(c==‘=’) state=8;
else if(c==‘>’) state=9;
else state=10;
s[i++]=c;
break;
case 8:
s[i]=0;
return LE;
case 9:
s[i]=0;
return NE;

case 10:
s[i]=0; GetBackChar();
return LE;
case 11:
s[i]=0;
return EQ;
case 12:
if(c==‘=’) state=13;
else state=14;
s[i++]=c;
break;
case 13:
s[i]=0;
return GE;
case 14:
s[i]=0;
return GT;
}
if(c==0) break;
}// end while
}// end function
Nhận xét:
Ưu điểm: chương trình dễ viết và trực quan đối với số lượng các loại từ tố là
bé.
Nhược điểm: gặp nhiều khó khăn nếu số lượng loại từ tố là lớn, và khi cần bổ
sung loại từ tố hoặc sửa đổi mẫu từ tố thì chúng ta lại phải viết lại chương trình.
Chú ý: Trong thực tế khi xây dựng bộ phân tích từ vựng, chúng ta phải nhận dạng các tên
trong chương trình trình nguồn, sau đó dựa vào bảng lưu trữ để phân biệt cụ thể các từ khoá đối
với các tên.
2.2.2. Lập bộ phân tích từ vựng bằng bảng.
Để xây dựng chương trình bằng phương pháp này, điều cơ bản nhất là chúng ta phải xây
dựng bảng chuyển trạng thái. Để tổng quát,
thông tin của bảng chuyển trạng thái nên
được lưu ở một file dữ liệu bên ngoài, như vậy sẽ thuận tiện cho việc chúng ta thay
đổi dữ liệu chuyển trạng thái của ôtômát mà không cần quan tâm đến chương trình.
Đối với các trạng thái không phải là trạng thái kết thúc thì chúng ta chỉ cần tra
bảng một cách tổng quát sẽ biết được trạng thái tiếp theo, và do đó chúng ta chỉ cần
thực hiện các trường hợp cụ thể đối với các trạng thái kết thúc để biết từ tố cần trả
về là gì.
Giả sử ta có hàm khởi tạo bảng trạng thái là: int InitStateTable();
Hàm phân loại ký hiệu đầu vào (ký hiệu kết thúc): int GetCharType();
Khi đó đoạn chương trình sẽ được mô tả như dưới đây:
#define STATE_NUM 100

#define TERMINAL _NUM 100
#define STATE_ERROR –1 // trạng thái lỗi
int table[STATE_NUM][TERMINAL_NUM]
// ban đầu gọi hàm khởi tạo bảng chuyển trạng thái.
InitStateTable();
int GetNextChar(); // hàm lấy ký tự tiếp theo
enum Token {IDENT, INTEGER, REAL, LT, LE, GT, GE, NE, EQ, ERROR};
// hàm này trả về loại từ tố
// từ vị nằm trong s
Token GetNextToken(char *s)
{
int state=0;
int i=0;
while(1)
{
int c=GetNextChar();
int type=GetCharType(c);
switch(state)
{
case 2:
s[i]=0; GetBackChar();
return IDENT;
case 4:
s[i]=0; GetBackChar();
return INTEGER;
case 6:
s[i]=0; GetBackChar();
return REAL;
case 8:
s[i]=0;
return LE;
case 9:
s[i]=0;
return NE;
case 10:
s[i]=0; GetBackChar();
return LE;
case 11:
s[i]=0;
return EQ;
case 13:
s[i]=0;
return GE;
case 14:
s[i]=0;
return GT;
case STATE_ERROR: return ERROR;
defaulf:
state=table[state][type];
s[i++]=c;
}
if(c==0) break;
}// end while
}// end function

Nhận xét:
Ưu điểm:
+ Thích hợp với bộ phân tích từ vựng có nhiều trạng thái, khi đó chương trình
sẽ gọn hơn.
+ Khi cần cập nhật từ tố mới hoặc sửa đổi mẫu từ tố thì chúng ta chỉ cần thay
đổi trên dữ liệu bên ngoài cho bảng chuyển trạng thái mà không cần phải sửa
chương trình nguồn hoặc có sửa thì sẽ rất ít đối với các trạng thái kết thúc.
Nhược điểm: khó khăn cho việc lập bảng, kích thước bảng nhiều khi là quá
lớn, và không trực quan.
3. XÁC ĐỊNH LỖI TRONG PHÂN TÍCH TỪ VỰNG.
Chỉ có rất ít lỗi được phát hiện trong lúc phân tích từ vựng, vì bộ phân tích từ
vựng chỉ quan sát chương trình nguồn một cách cục bộ, không xét quan hệ cấu trúc
của các từ với nhau.
Ví dụ: khi bộ phân tích từ vựng gặp xâu fi trong biểu thức
fi a= b then . . .
thì bộ phân tích từ vựng không thể cho biết rằng fi là từ viết sai của từ khoá if hoặc là một
tên không khai báo. Nó sẽ nghiễm nhiên coi rằng fi là một tên đúng và trả về một từ tố tên. Chú ý
lỗi này chỉ được phát hiện bởi bộ phân tích cú pháp.
Các lỗi mà bộ phân tích từ vựng phát hiện được là các lỗi về một từ vị không
thuộc một loại từ tố nào,
ví dụ như gặp từ vị 12xyz.
Bé xö lý lçi ph¶i ®¹t môc ®Ých sau:
- Th«ng b¸o lçi mét c¸ch râ rµng vµ chÝnh x¸c.
- Phôc håi lçi mét c¸ch nhanh chãng ®Ó x¸c ®Þnh lçi
tiÕp theo.
- Kh«ng lµm chËm tiÕn tr×nh cña mét ch¬ng tr×nh
®óng.
Khi gặp những lỗi có 2 cách xử lý:
+ Hệ thống sẽ ngừng hoạt động và báo lỗi cho người sử dụng.
+ Bộ phân tích từ vựng ghi lại các lỗi và cố gắng bỏ qua chúng để hệ
thống tiếp tục làm việc, nhằm phát hiện đồng thời thêm nhiều lỗi khác. Mặt khác,
nó còn có thể tự sửa (hoặc cho những gợi ý cho những từ đúng đối với từ bị lỗi).
Cách khắc phục là:
- Xoá hoặc nhảy qua kí tự mà bộ phân tích từ vựng không tìm thấy từ tố (panic
mode).
- Thêm kí tự bị thiếu.
- Thay một kí tự sai thành kí tự đúng.
- Tráo 2 kí tự đứng cạnh nhau.
4. CÁC BƯỚC ĐỂ XÂY DỰNG BỘ PHÂN TÍCH TỪ VỰNG.
Các bước tuần tự nên tiến hành để xây dựng được một bộ phân tích từ vựng
tốt, hoạt động chính xác và dễ cải tiến, bảo hành, bảo trì.
1) Xác định các luật từ tố, các luật này được mô tả bằng lời.
2) Vẽ đồ thị chuyển cho từng mẫu một, trước đó có thể mô tả bằng biểu
thức chính qui để tiện theo dõi và chỉnh sửa, và dễ dàng cho việc dựng đồ thị
chuyển.
3) Kết hợp các luật này thành một đồ thị chuyển duy nhất.
4) Chuyển đồ thị chuyển thành bảng.
5) Xây dựng chương trình.
6) Bổ sung thêm phần báo lỗi để thành bộ phân tích từ vựng hoàn chỉnh.
Bài tập
1. Phân tích các chương trình pascal và C sau thành các từ tố và thuộc
tính tương ứng.
a) pascal:
Function max(i,j:integer): Integer
; {Trả lại số lon nhất trong 2 số nguyên i, j }
Begin
If i>j then max:=i;
Else max:=j;
End;
B) C:
Int max(int i, int j)
/* Trả lại số lon nhất trong 2 số nguyên i, j*/
{return i>j?i:j;}
Hãy cho biết có bao nhiêu từ tố được đưa ra và chia thành bao nhiêu loại?
2. Phân tích các chương trình pascal và c sau thành các từ tố và thuộc
tính tương ứng.
a) pascal
var i,j;
begin
for i= 0 to 100 do j=i;
write(‘i=’, ‘j:=’,j);
end;
B) C:
Int i,j:
Main(void
{

for (i=0; i=100;i++)
printf(“i=%d;”,i,”j=%d”,j= =i);
}
3. Mô tả các ngôn ngữ chỉ định bởi các biểu thức chính quy sau:
a. 0(0|1)*0 b.((
ε
|0)1*)*
4. Viết biểu thức chính quy cho: tên, số nguyên, số thực, char, string… trong
pascal. Xây dựng đồ thị chuyển cho chúng. Sau đó, kết hợp chúng thành đồ thị
chuyển duy nhất.
5. Dựng đồ thị chuyển cho các mô tả dưới đây.
a. Tất cả các xâu chữ cái có 6 nguyên âm a, e, i, o, u, y theo thứ tự. Ví dụ:
“abeiptowwrungfhy”
b. tất cả các xâu số không có một số nào bị lặp.
c. tất cả các xâu số có ít nhất một số nào bị lặp.
d. tất cả các xâu gồm 0,1, không chứa xâu con 011.
Bài tập thực hành
Bài 1: Xây dựng bộ phân tích từ vựng cho ngôn ngữ pascal chuẩn.
Bài 2: Xây dựng bộ phân tích từ vựng cho ngôn ngữ C chuẩn.
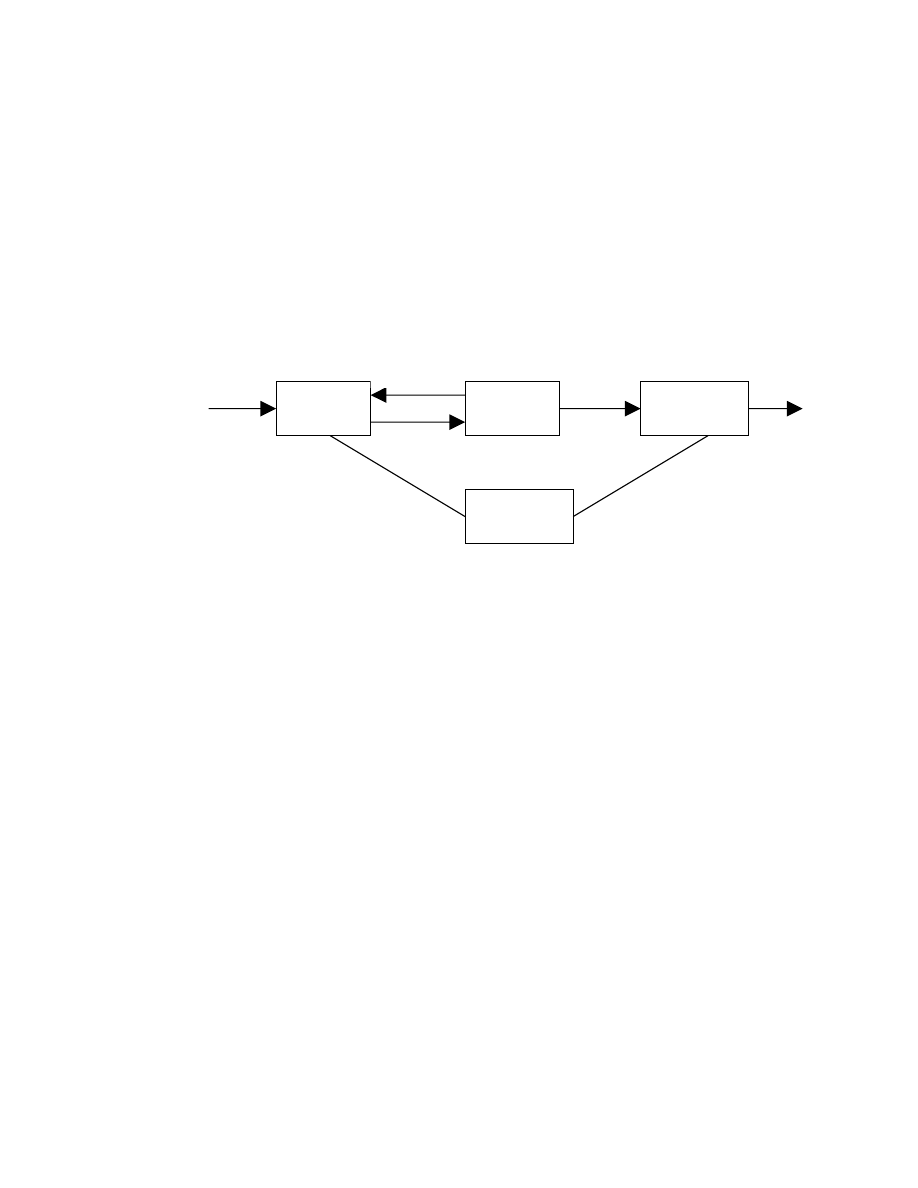
CHƯƠNG 3
PHÂN TÍCH CÚ PHÁP VÀ CÁC PHƯƠNG PHÁP
PHÂN TÍCH CƠ BẢN.
1. MỤC ĐÍCH.
Phân tích cú pháp nhận đầu vào là danh sách các từ tố của chương trình nguồn
thành các thành phần theo văn phạm và biểu diễn cấu trúc này bằng cây phân tích
hoặc theo một cấu trúc nào đó tương đương với cây.
Bộ phân tích cú pháp nhận chuỗi các token từ bộ phân tích từ vựng và tạo
ra cây phân tích cú pháp. Trong thực tế còn một số nhiệm vụ thu nhập thông tin
về token vào bảng ký hiệu, thực hiện kiểm tra kiểu về phân tích ngữ nghĩa cũng
như sinh mã trung gian. Các phần này sẽ được trình bày trong các chương kế.
2. HOẠT ĐỘNG CỦA BỘ PHÂN TÍCH.
2.1.Văn phạm phi ngữ cảnh.
2.1.1. Định nghĩa.
* Định nghĩa: Văn phạm PNC (như trên).
* Dạng BNF (Backus – Naur Form) của văn phạm phi ngữ cảnh
+ Các ký tự viết hoa: biểu diễn ký hiệu không kết thúc, (có thể thay bằng một
xâu đặt trong dấu ngoặc < > hoặc một từ in nghiêng).
+ Các ký tự viết chữ nhỏ và dấu toán học: biểu diễn các ký hiệu kết thúc (có
thể thay bằng một xâu đặt trong cặp dấu nháy kép “ ” hoặc một từ in đậm).
+ ký hiệu -> hoặc = là: ký hiệu chỉ phạm trù cú pháp ở vế trái được giải thích
bởi vế phải.
+ ký hiệu | chỉ sự lựa chọn.
Ví dụ:
<Toán hạng> = <Tên> | <Số> | “(” <Biểu thức> “)”
hoặc
ToánHạng -> Tên | Số | ( BiểuThức
Phân tích
từ vựng
Phân tích
cú pháp
Phân tích
ngữ nghĩa
Chương
trình nguồn
Bảng ký
hiệu
từ tố
yêu cầu
từ tố
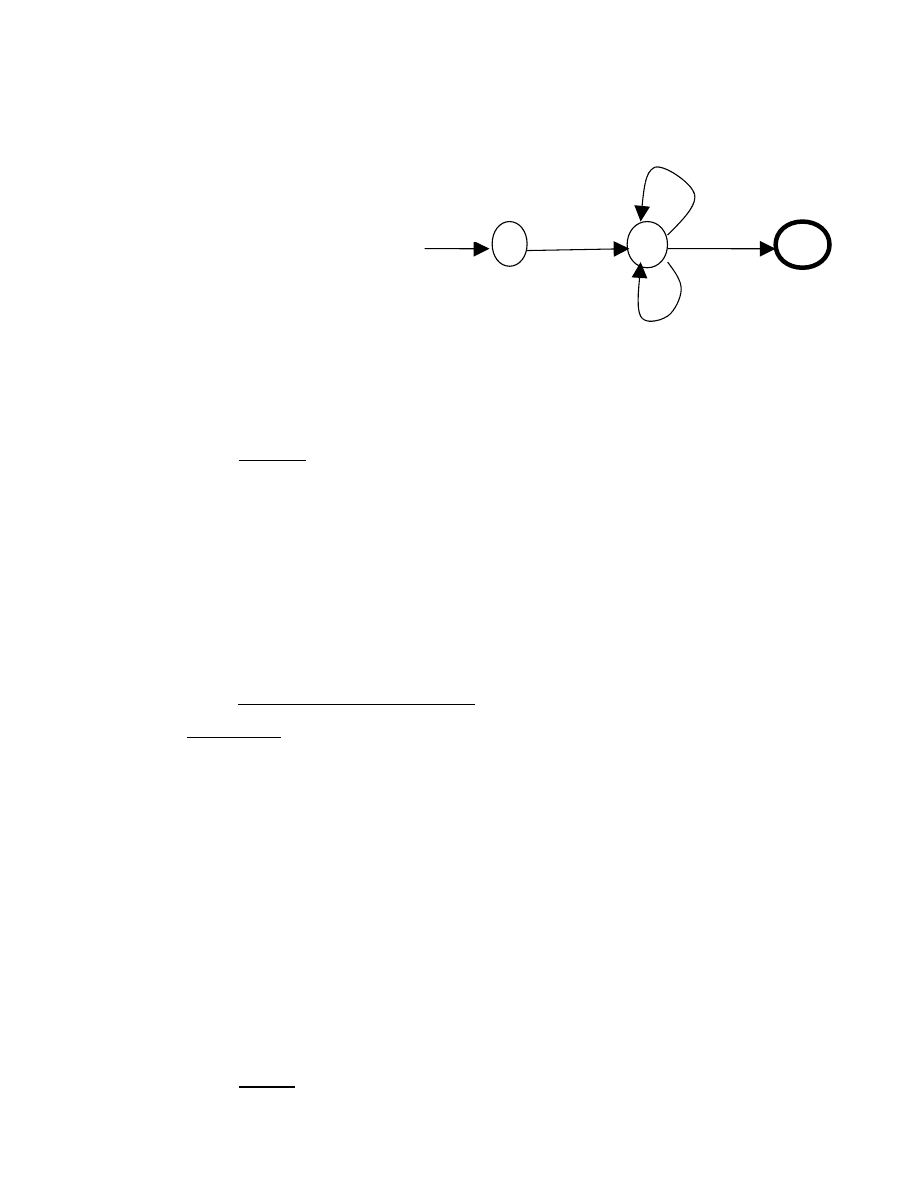
2.1.2. Đồ thị chuyển biểu diễn văn phạm phi ngữ cảnh:
- Các vòng tròn với ký hiệu
bên trong biểu thị cho trạng thái.
Các chữ trên các cung biểu thị
cho ký hiệu vào tiếp theo. Trạng
thái vẽ bằng một vòng tròn kép là
trạng thái kết thúc.
Nếu trạng thái kết thúc có dấu *
nghĩa là ký hiệu cuối không
thuộc xâu đoán nhận.
2.1.3. Cây suy dẫn.
2.1.3.1. Suy dẫn.
Cho văn phạm G=(T,N,P,S).
- Suy dẫn trực tiếp là một quan hệ hai ngôi ký hiệu => trên tập V* nếu αβγ là
một xâu thuộc V* và β->δ là một sản xuất trong P, thì αβγ => αδγ.
- Suy dẫn k bước, ký hiệu là
k
=>
hay
k
β
α
=>
nếu tồn tại dãy α
0
, α
1
, . . . , α
k
sao
cho: α = α
0
=> α
1
=> . . . => α
k
= β
- Xâu α suy dẫn xâu nếu k>=0 và ký hiệu là
*
β
α
=>
- Xâu α suy dẫn không tầm thường xâu β nếu k>0 và ký hiệu là
+
=>
β
α
2.1.3.2. C
â y ph
â n t í ch
(
c â y suy
dẫn
)
* Định nghĩa: Cây phân tích trong một văn phạm phi ngữ cảnh G = (T,N,P,S)
là một cây thỏa mãn các điều kiện sau:
1.
Mọi nút có một nhãn, là một ký hiệu trong (T
∪
N
∪
{ε})
2.
Nhãn của gốc là S
3.
Nếu một nút có nhãn X là một nút trong thì X
∈
N
4.
Nếu nút n có nhãn X và các nút con của nó theo thứ tự trái qua phải có
nhãn Y
1
, Y
2
, . . ., Y
k
thì X->Y
1
Y
2
. . . Y
k
sẽ là một sản xuất
∈
P
5.
Nút lá có nhãn thuộc T hoặc là ε
* Suy dẫn trái nhất (nói gọn là suy dẫn trái), nếu ở mỗi bước suy dẫn, biến
được thay thế là biến nằm bên trái nhất trong dạng câu.
* Suy dẫn phải nhất: (nói gọn là suy dẫn phải), nếu ở mỗi bước suy dẫn, biến
được thay thế là biến nằm bên phải nhất trong dạng câu.
2.1.3.3. Đệ qui
0
1
2
*
Start
chu cai
khac
chu
cai
chu
cai
Hình 2.1: Đồ thị chuyển cho từ tố Tên
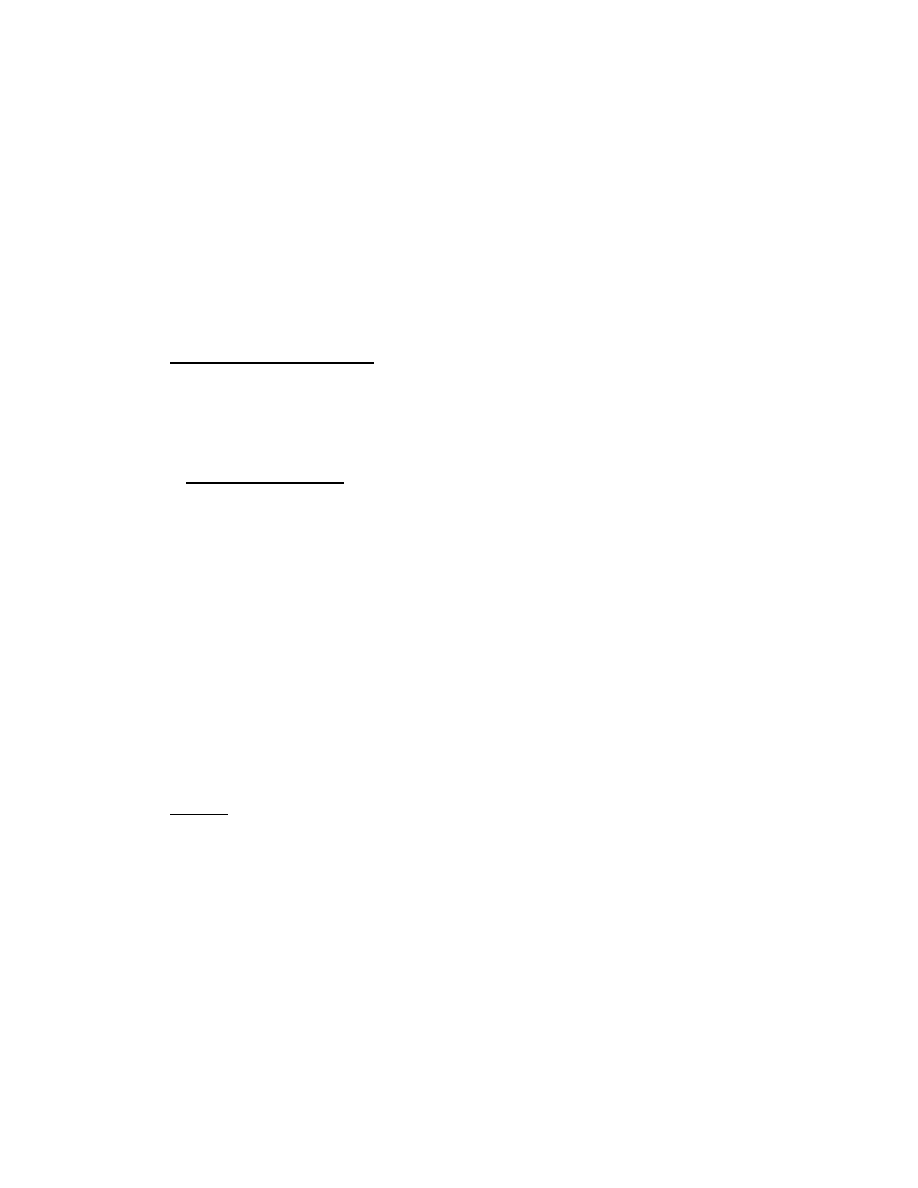
* Định nghĩa: Ký hiệu không kết thúc A của văn phạm gọi là đệ qui nếu tồn
tại:
+
=>
β
α
A
A
với α, β
∈
V
+
Nếu α = ε thì A gọi là đệ qui
trái.
Nếu β = ε thì A gọi là đệ qui
phải.
Nếu α,β
∉
ε thì A gọi là đệ qui
trong.
* Có 2 loại dệ quy trái :
Loại ttrực tiếp: có dạng A
→
A
α
( A
⇒
+
A
α
)
Loại gián tiếp: Gây ra do nhiều bước suy dẫn.
(
VÝ dô: S
→
Aa | b; A
→
Ac | Sd; S lµ ®Ö qui tr¸i v× S
⇒
Aa
⇒
Sda)
* Loại bỏ đệ qui trái: (loại bỏ suy dẫn A =>
+
A
α
)
- Giả sử có luật đệ qui trái A->A
α
|
β
chúng ta thay các luật này bằng các
luật: A ->
β
A’
A’ ->
α
A’ |
ε
- Tổng quát hoá lên ta có:
Nếu có các luật đệ qui trái: A -> A
α
1
| A
α
2
| . . .| A
α
m
|
β
1
|
β
2
| . . .|
β
n
trong đó không
β
i
nào bắt đầu bằng một A . Thay các sản xuất này bởi các
sản xuất:
A ->
β
1
A’ |
β
2
A’ | . . . |
β
n
A’
A’ ->
α
1
A’ |
α
2
A’ | . . . |
α
m
A’ |
ε
Ví dụ2: Xét văn phạm biểu thức số học sau:
E -> E + T | T ;
T -> T * F | F;
F -> ( E ) | id
Loại bỏ đệ qui trái trực tiếp cho các sản xuất của E rồi của T, ta được văn phạm
mới không còn sản xuất có đệ qui trái như sau:
E -> TE’;
E’-> +TE’ |
ε
;
T -> FT’;
T’ -> *FT’ |
ε
;

F -> (E) | id
Qui tắc này loại bỏ được đệ qui trái trực tiếp nằm trong các sản xuất nhưng không loại bỏ
được đệ qui trái nằm trong các dẫn xuất có hai hoặc nhiều bước. Qui tắc này cũng không loại bỏ
được đệ qui trái ra khỏi sản xuất A->A.
Víi ®Ö qui tr¸i gi¸n tiÕp vµ nãi chung lµ ®Ö qui tr¸i, ta sö
dông gi¶i thuËt sau:
VÝ dô : Víi S
→
Aa | b; A
→
Ac | Sd.
Sắp xếp các ký hiệu cha kết thúc theo thứ tự S,A..
Với i=1, không có đệ qui trái trực tiếp nên không có điều gì xảy ra.
với i=2 , thay luật sinh AđSd được AđAc | Aad | bd.
Loại bỏ đệ qui trái trực tiếp cho A, ta được: SđAa |b; AđbdA'; A'đ cA' | adA' | e
* Phép thừa số hoá trái
Thừa số hoá trái (left factoring) là một phép biến đổi văn phạm nhằm sinh ra
một văn phạm thích hợp cho việc phân tích cú pháp không quay lui. Ý tưởng cơ
bản là khi không rõ sản xuất nào trong trong hai sản xuất có cùng vế trái là A được
dùng để khai triển A thì ta có thể viết lại các sản xuất này nhằm “hoãn lại quyết
định”, cho đến khi có đủ thông tin để đưa ra được quyết định lựa chọn sản xuất
nào.
- Nếu có hai sản xuất A ->
α β
1
|
α β
2
thì ta không biết phải khai triển A
theo
α β
1
hay
α β
2
. Khi đó, thay hai sản xuất này bằng:
Input: Văn phạm không tuần hoàn hoặc e_sx (không có dạng Aị
+
A hoặc Ađe)
Output: Văn phạm tương đương không đệ qui trái
Phương pháp:
1. Sắp xếp các ký hiệu không kết thúc theo thứ tự A
1
, A
2
.. .. A
n
2. For i:=1 to n do
Begin
for j:=1 to i-1 do
Begin
Thay luật sinh dạng Aiđ Aj bởi luật sinh Ajđ d
1g
| d
2g
|.. .. |d
kg
Trong đó Aj đd
1g
| d
2g
|.. .. |d
ky
là các luật sinh hiện tại
End
Loại bỏ đệ qui trái trực tiếp trong số các Ai loại
End;
A ->
α
A’;
A’ ->
β
1
|
β
2
Ví dụ: S -> iEtS | iEtSeS | a;
E -> b
Khi được thừa số hoá trái, văn phạm này trở thành:
S -> iEtSS’ | a; S’ -> eS |
ε
; E -> b
vì thế khi cần khai triển S với ký hiệu xâu vào hiện tại là i, chúng ta có thể lựa chọn iEtSS’
mà không phải băn khoăn giữa iEtS và iEtSeS của văn phạm cũ.
Gi¶i thuËt t¹o thõa sè ho¸ tr¸i (yÕu tè tr¸i) cho mét v¨n ph¹m:
Input: Văn phạm G
Output: Văn phạm tương đương với nhân tố trái.
Ph
ơng pháp:
Với mỗi ký hiệu chưa kết thúc A, có các ký hiệu dẫn đầu các vế phải giống nhau, ta
tìm một chuỗi a là chuỗi có độ dài lớn nhất chung cho tất cả các vế phải (a là nhân
tố trái)
Giả sử A
→
ab
1
| ab
2
|.. .. | ab
n
| g
Trong đó g không có chuỗi dẫn đầu chung với các vế phải khác. Biến đổi luật sinh
thành
A
→
a A
'
| g
A'
→
b
1
| b
2
| .. .. | b
n
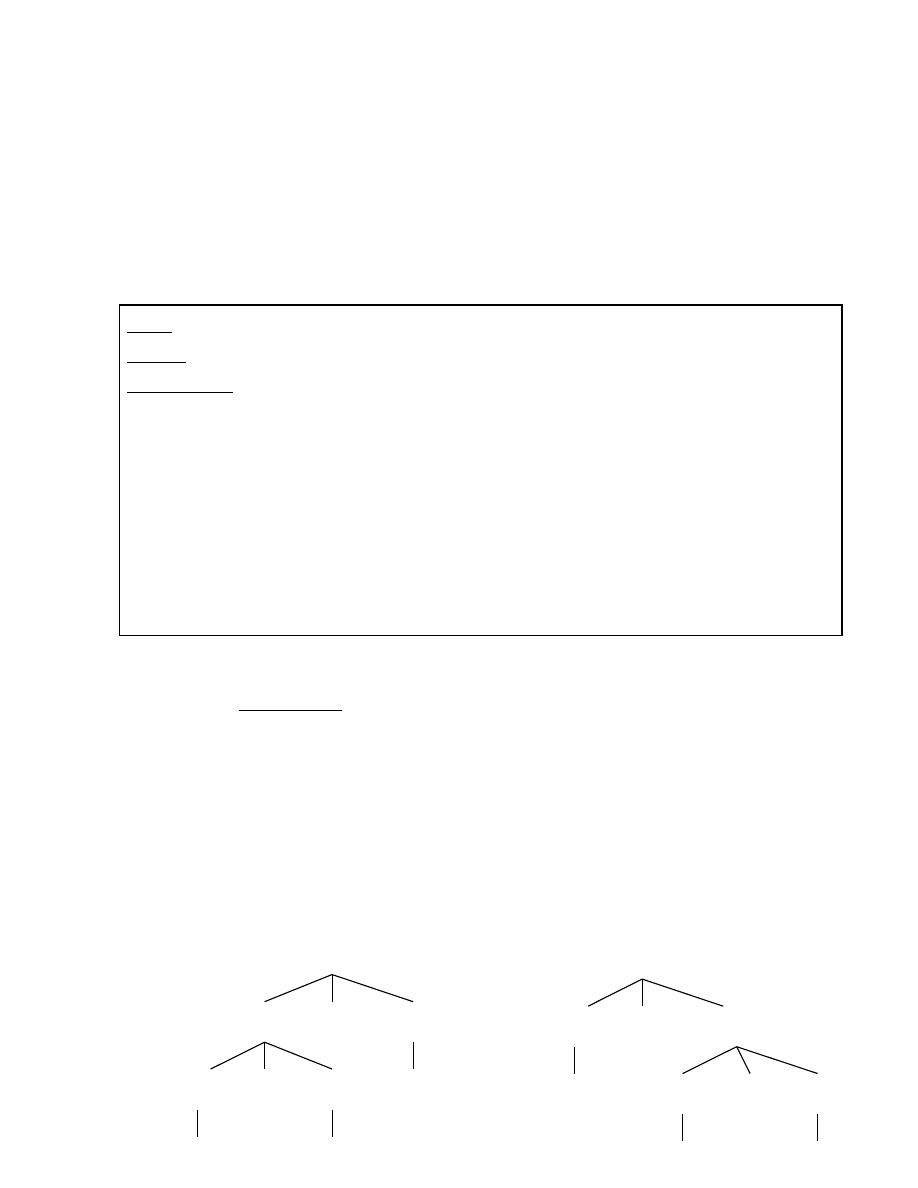
2.1.3.4. Nhập nhằng
Một văn phạm G được gọi là văn phạm nhập nhằng nếu có một xâu α là kết
quả của hai cây suy dẫn khác nhau trong G. Ngôn ngữ do văn phạm này sinh ra gọi
là ngôn ngữ nhập nhằng.
Ví dụ:
Xét văn phạm G cho bởi các sản xuất sau: S -> S + S | S * S | ( S ) | a
Với xâu vào là w = “a+a*a” ta có:
Văn phạm này là nhập nhằng vì có hai cây đối với câu vào w như sau:
S
S
*
S
S
+
S
a
a
a
S
S
+
S
S
*
a
a
a
S

Chúng ta có ví dụ đối suy dẫn trái (đối với cây đầu tiên) là:
S => S * S => S + S => S + S * S => a + S * S => a + a * S => a + a * a
suy dẫn phải (đối với cây đầu tiên ) là:
S => S * S => S * a => S + S * a => S + a * a => a + a * a.
2.2. các phương pháp phân tích.
- Mọi ngôn ngữ lập trình đều có các luật mô tả các cấu trúc cú pháp. Một chương trình viết
đúng phải tuân theo các luật mô tả này. Phân tích cú pháp là để tìm ra cấu trúc dựa trên văn
phạm của một chương trình nguồn.
- Thông thường
có hai chiến lược phân tích
:
+ Phân tích trên xuống (topdown): Cho một văn phạm PNC G = (
Σ
,
∆
, P, S)
và một câu cần phân tích w. Xuất phát từ S áp dụng các suy dẫn trái, tiến từ trái qua
phải thử tạo ra câu w.
+ Phân tích dưới lên (bottom-up): Cho một văn phạm PNC G = (
Σ
,
∆
, P, S)
và một câu cần phân tích w. Xuất phát từ câu w áp dụng thu gọn các suy dẫn phải,
tiến hành từ trái qua phải để đi tới kí hiệu đầu S.
Theo cách này thì phân tích Topdown và LL(k) là phân tích trên xuống, phân tích Bottom-
up và phân tích LR(k) là phân tích dưới lên.
* Điều kiện để thuật toán dừng:
+ Phân tích trên xuống dừng khi và chỉ khi G kông có đệ quy trái.
+ Phân tích dưới lên dừng khi G không chứa suy dẫn A
⇒
+
A và sản xuất
A
→ε
.
* Có các phương pháp phân tích.
1) Phương pháp phân tích topdown.
2) Phương pháp phân tích bottom up.
3) Phương pháp phân tích bảng CYK.
4) Phương pháp phân tích LL.
5) Phương pháp phân tích LR.
Phương pháp 1 và 2: là các phương pháp cơ bản, kém hiệu quả. Phương pháp 5,6 là
phương pháp phân tích hiệu quả
.
2.3.1. phân tích topdown.
Phương pháp phân tích Top-down xây dựng cây phân tích cho một xâu vào bằng cách xuất
phát từ ký hiệu bắt đầu làm gốc và sử dụng các luật sản xuất để đi từ gốc đến lá.
- Đánh dấu thứ tự các lựa chọn của các sản xuất có cùng vế trái.
Ví dụ nếu các sản xuất có dạng S -> aSbS | aS | c thì aSbS là lựa chọn thứ nhất, aS là lựa
chọn thứ hai và c là lựa chọn thứ ba trong việc khai triển S.
- Tại mỗi bước suy diễn, ta cần triển khai một ký hiệu không kết thúc A và văn phạm có
các sản xuất có vế trái là A là A->
α
1
|
α
2
| . . .|
α
k
Khi đó ta có k thứ tự lựa chọn, đánh dấu thứ
tự lựa chọn các sản xuất sau đó khai triển A theo một lựa chọn, nếu quá trình phân tích là không
thành công thì quay lui tại vị trí này và khai triển A theo lựa chọn tiếp theo.
Phân tích Top-down là phương pháp phân tích có quay lui và tạo ra suy dẫn trái nhất.
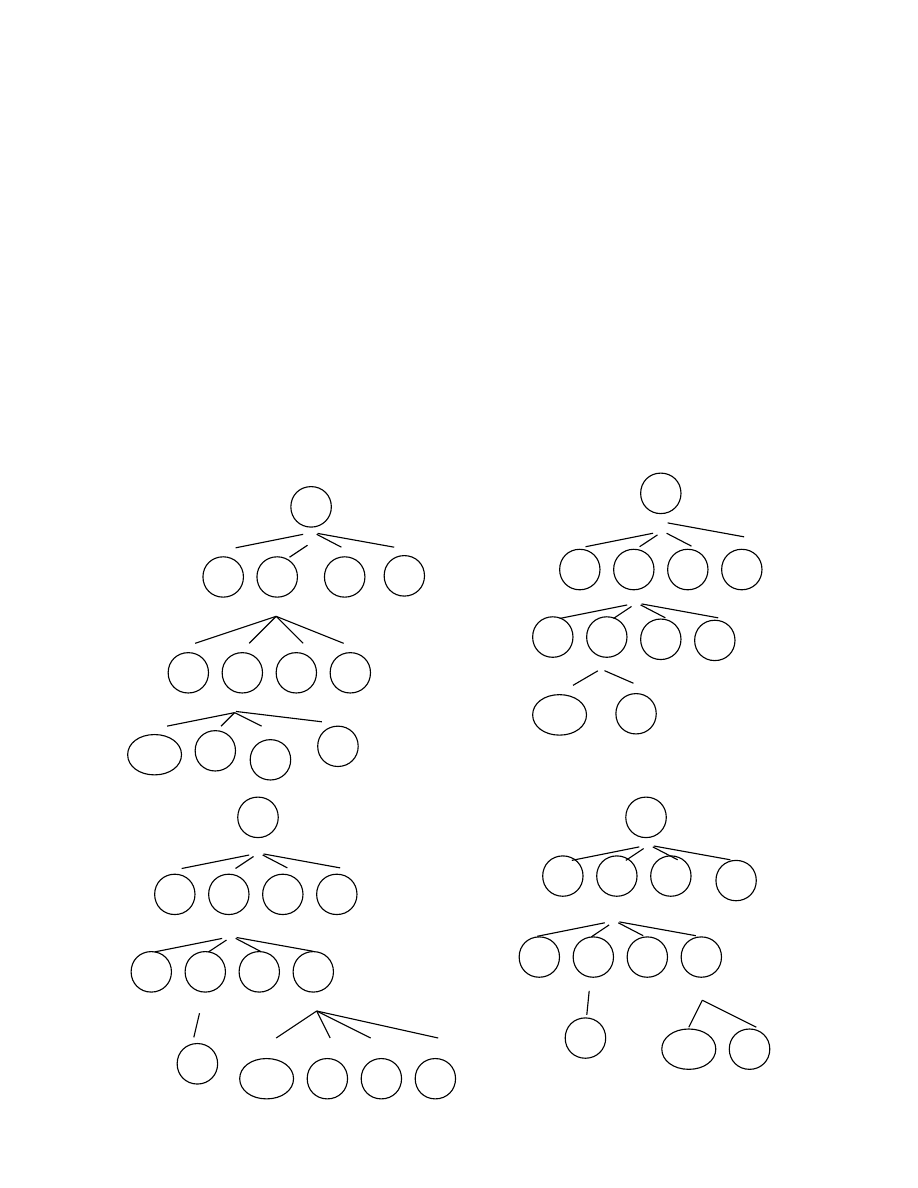
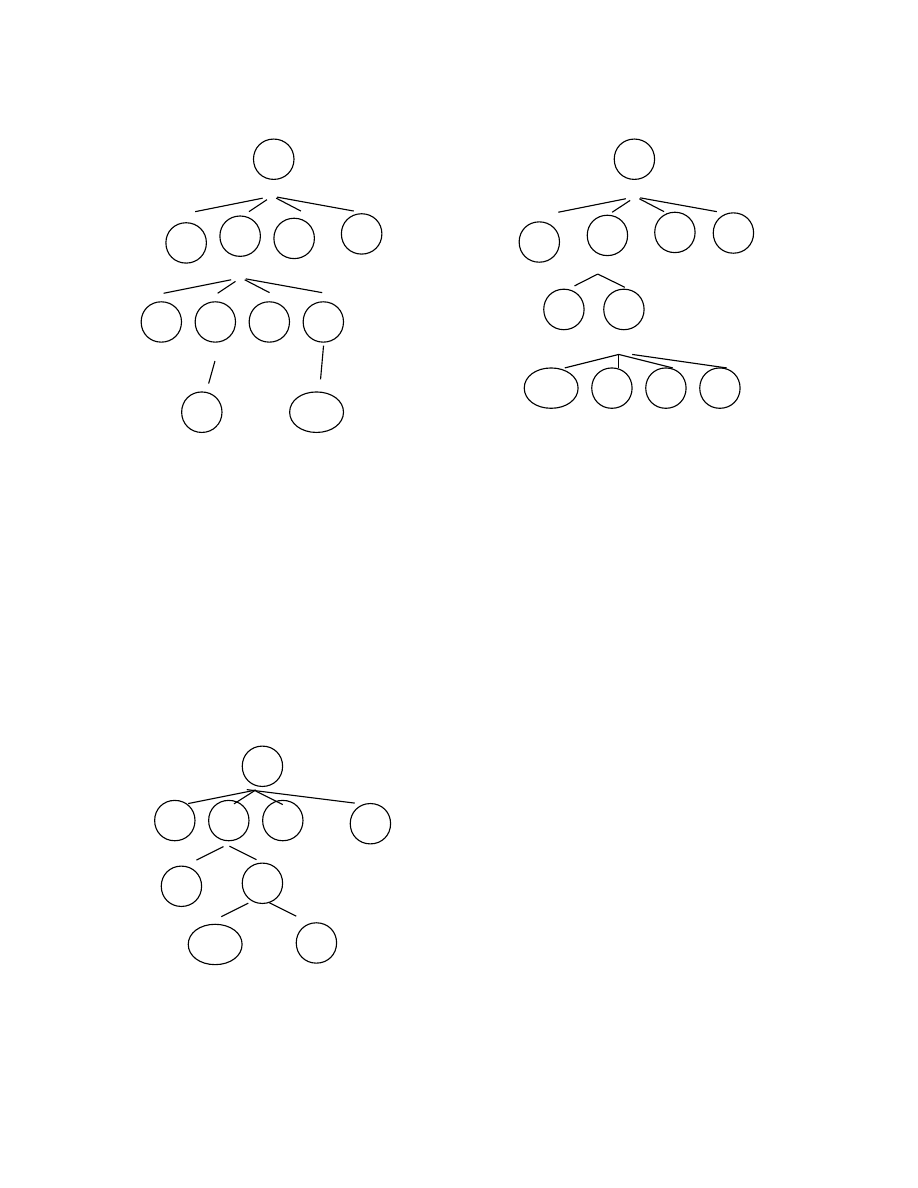
Ví dụ: Cho văn phạm S -> aSbS | aS | c
Hãy phân tích xâu vào “aacbc” bằng thuật toán Top-down, vẽ cây phân tích
trong quá trình phân tích quay lui.
S
a
S
b
S
a
b
S
S
a
*
S
b
S
(1)
S
a
S
b
S
a
S
b
S
a
*
S
(2)
S
a
S
b
S
a
S
b
S
c
a
*
S
b
S
(3)
S
a
S
b
S
a
S
b
S
c
a
*
S
(4)
S
a
S
b
S
a
S
b
S
c
c
*
(5)
S
a
S
b
S
a
S
a
*
S
b
S
(6)
S
a
S
b
S
a
S
a
*
S
(7)
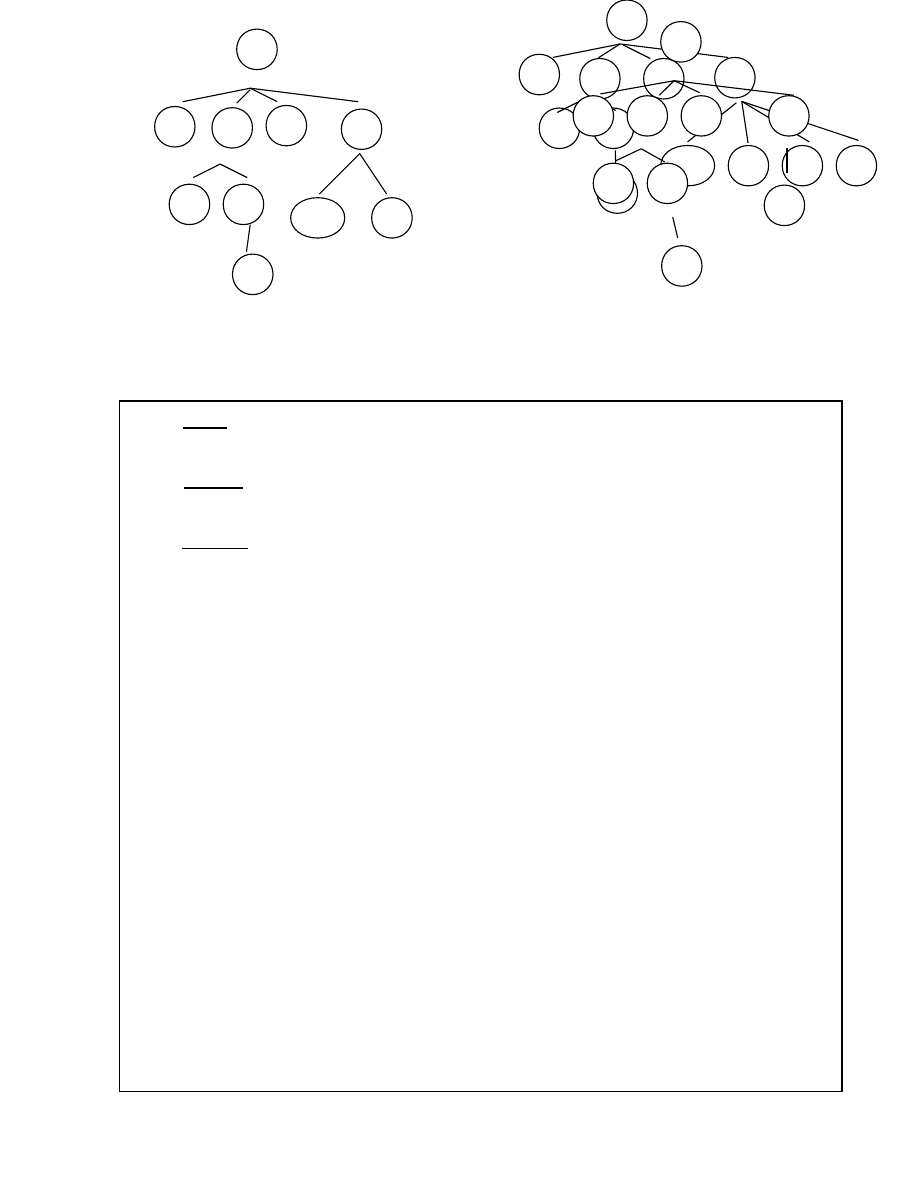
2.3.1.1. Mô tả thuật toán phân tích Top-down
- Input: Văn phạm PNC G = (
Σ
,
∆
, P, S) không đệ quy trái, xâu w = a
1
, a
2
, …
a
n
- Output: Cây phân tích từ trên xuống của xâu w (w
∈
L(G)), báo lỗi (w
∉
L(G)).
- Method:
Dùng một con trỏ chỉ đến xâu vào w. Ký hiệu trên xâu vào do con trỏ chỉ đến
gọi là ký hiệu vào hiện tại.
1)
Khởi tạo cây với gốc là S, con trỏ trỏ đến kí hiệu đầu tiên của xâu w là a
1
.
2)
Nếu nút đang xét
∈
∆
(là ký hiệu không kết thúc) A thì chọn sản xuất
có vế trái là A trong P, giả sử sản xuất A
→
X
1
...X
k
.
+ Nếu k > 0: lấy nút X
1
làm nút đang xét.
+ Nếu k=0 (sản xuất rỗng) thì lấy nút ngay bên phải A làm nút đang xét.
3)
Nếu nút đang xét
∈
Σ
(là ký hiệu kết thúc) a thì đối sánh a với ký hiệu
vào hiện tại.
+ Nếu trùng nhau: thì lấy nút ngay bên phải a làm nút đang xét, con trỏ
dịch sang bên phải một ký hiệu trên xâu w.
+ Nếu không: quay lại nút trước đó và lặp lại b2 với thử lựa chọn tiếp
theo.
Thủ tục trên lặp lại sau hữu hạn bước và có 2 khả năng xảy ra:
- Nếu gặp trường hợp đối sánh hết xâu vào và cây không còn nút nào
chưa xét nữa thì ta được một cây phân tích.
- Nếu đã quay lui hết tất cả các trường hợp mà không sinh được cây phân tích thì
kết luận xâu vào không phân tích được bởi văn phạm đã cho.
S
a
S
b
S
a
S
c
a
*
S
b
S
(8)
S
a
S
b
S
a
S
c
a
*
S
(9)
S
a
S
b
S
a
S
c
c
10
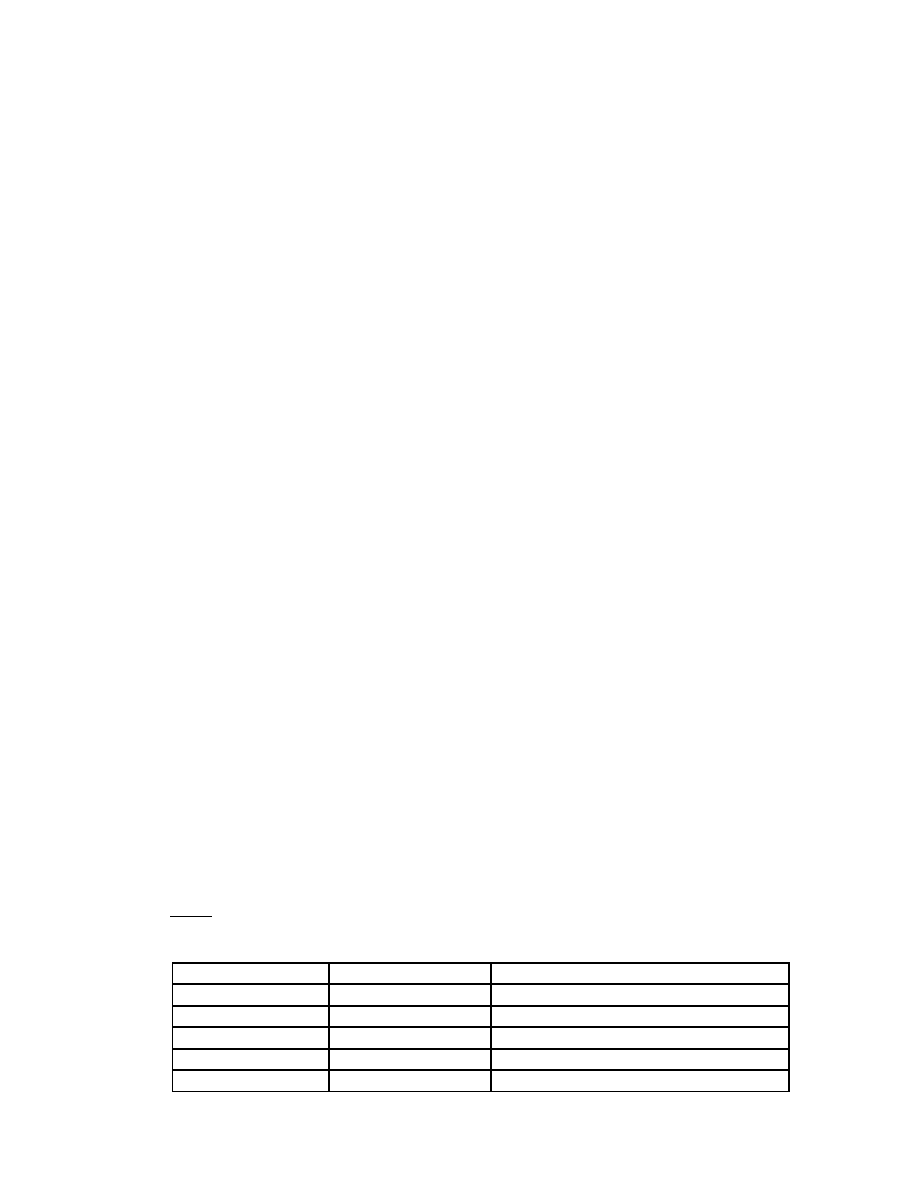
* Điều kiện để một văn phạm phi ngữ cảnh phân tích được bởi thuật toán Top-
down là văn phạm không có đệ qui trái.
(Vì vậy ta phải thực hiện loại bỏ đệ quy trái trước
khi phân tích văn phạm theo phương pháp topdown)
* Độ phức tạp thuật toán là hàm số mũ n với n là độ dài xâu vào.
2.3.2. phân ttích bottom - up.
Phương pháp phân tích Bottom-up về tư tưởng là ngược lại với phương pháp Top-down.
- Xây dựng cú pháp cho xâu nhập bắt đầu từ lá lên tới gốc. Đây là quá trình rút
gọn một xâu thành một kí hiệu mở đầu của văn phạm. Tại mỗi bước rút gọn, một
xâu con bằng một xâu phải của một sản xuất nào đó thì xâu con này được thay thế
bởi vế trái của sản xuất đó. (còn gọi là phương pháp gạt thu gọn - shift reduce
parsing).
Cã 2 vÊn ®Ò: x¸c ®Þnh handle vµ chän luËt sinh.
* CÊu t¹o:
- 1 STACK ®Ó lu c¸c ký hiÖu v¨n ph¹m.
- 1 BUFFER INPUT ®Ó gi÷ chuçi cÇn ph©n tÝch w.
- Dïng $ ®Ó ®¸nh dÊu ®¸y stack vµ cuèi chuçi nhËp.
* Ho¹t ®éng:
- Khëi ®Çu th× stack rçng vµ w n»m trong input buffer. Bé
ph©n tÝch
gạt lần lượt các ký hiệu đầu vào từ trái sang phải vào ngăn xếp đến khi nào
đạt được một thu gọn thì thu gọn (thay thế vế phải xuất hiện trên đỉnh ngăn xếp bởi vế trái
của sản xuất đó).
Nếu có nhiều cách thu gọn tại một trạng thái thì lưu lại cho quá
trình quay lui. Quá trình cứ tiếp tục, nếu dừng lại mà chưa đạt đến trạng thái kết
thúc thì quay lại tại bước quay lui gần nhất.
- Nếu quá trình đạt đến trạng thái ngăn xếp là $S và xâu vào là $ thì quá trình
kết thúc và phân tích thành công.
- Nếu đã xét hết tất cả các trường hợp, tức là không quay lui được nữa mà
chưa đạt đến trạng thái kết thúc thì dừng lại và thông báo xâu vào không phân tích
được bởi văn phạm đã cho.
Ví dụ: S -> aABe; A -> Abc | b; B -> d; Phân tích câu vào “abbcde”
quá trình phân tích Bottom-up như sau:
Ngăn xếp
Đầu vào
Hành động
$
abbcde$
gạt
$a
bbcde$
gạt
$ab
bcde$
thu gọn A -> b
$aA
bcde$
gạt
$aAb
cde$
thu gọn A -> b (2)
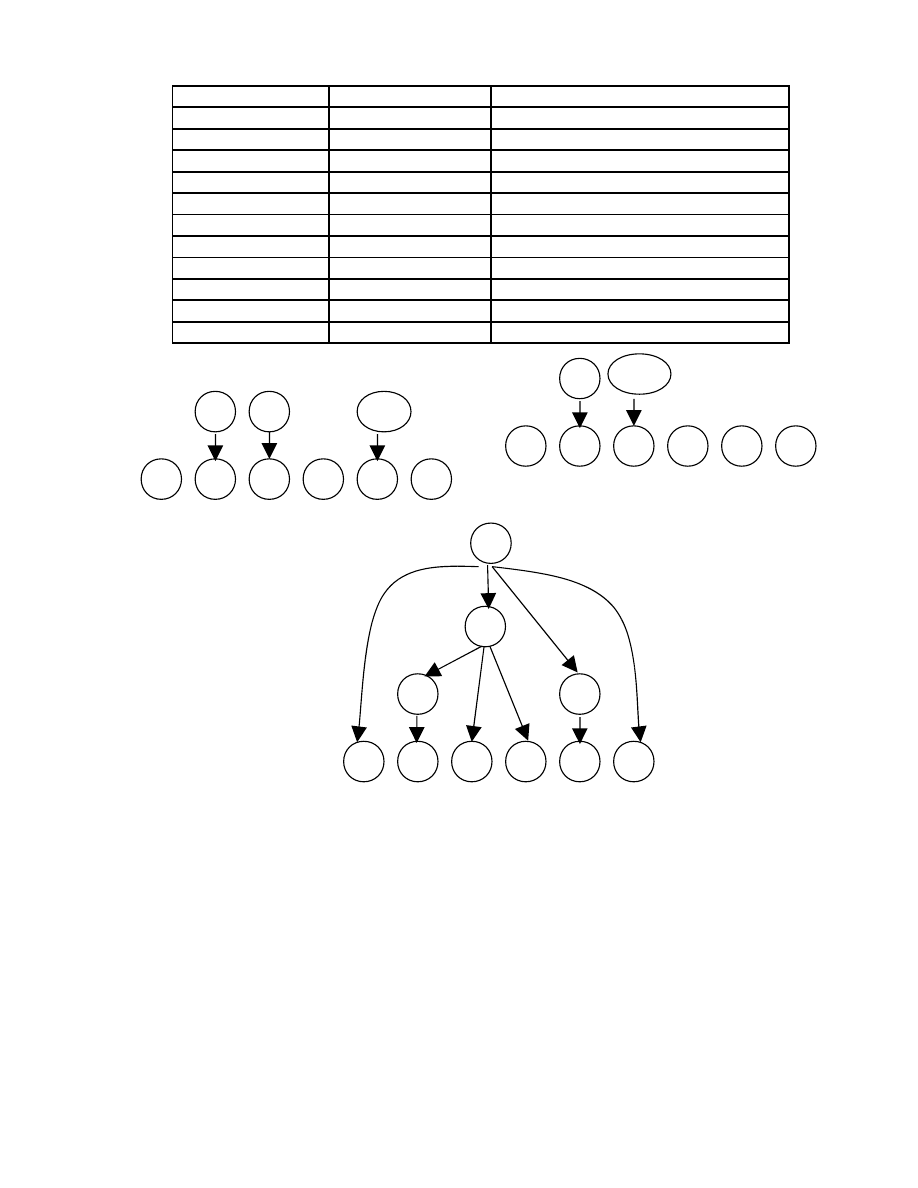
$aAA
cde$
gạt
$aAAc
de$
gạt
$aAAcd
e$
thu gọn B -> d (1)
$aAAcB
e$
gạt
$aAAcBe
$
dừng, quay lui 1 (gạt)
$aAAcde
$
dừng, quay lui 2 (gạt)
$aAbc
de$
thu gọn A -> Abc
$aA
de$
gạt
$aAd
e$
thu gọn B -> d
$aAB
e$
gạt
$aABe
$
thu gọn S -> aABe
$S
$
chấp nhận
Vẽ cây cho quá trình phân tích và quay lui trên, chúng ta có kết quả như sau:
Quá trình 1 Quá trình 2
Quá trình suy dẫn cũng có thể được viết lại như sau:
Abbcde => aAbcde (A -> b) => aAde (A -> Abc) => aABe (B -> d) => S (S -> aABe)
Nếu viết ngược lại chúng ta sẽ được dẫn xuất phải nhất:
S =>rm aABe =>rm aAde =>rm aAbcde =>rm abbcde
- Quá trình phân tích Bottom-up là quá trình sinh dẫn suất phải nhất
a
b
b
c
d
e
A
A
B
*
a
b
b
c
d
e
A
A*
a
b
b
c
d
e
A
B
A
S
(2c) Quá trình 3

- Phân tích Bottom-up không phân tích được văn phạm có các sản xuất B->
ε
hoặc có suy dẫnA =>+ A
*
Handle của một chuỗi
Handle của một chuỗi là một chuỗi con của nó và là vế phải của một sản xuất
trong phép thu gọn nó thành ký hiệu vế trái của 1 sản xuất.
Ví dụ: Trong ví dụ trên.
Ngăn
xếp
Đầu vào
Hành động
Handle
Suy dẫn
phải
Tiền tố khả
tồn
$
abbcde$
gạt
$a
bbcde$
gạt
abbcde
a
$ab
bcde$
thu gọn A -> b
b
abbcde
ab
$aA
bcde$
gạt
aAbcde
aA
$aAb
cde$
thu gọn A -> b (2)
b
aAbcde
aAb
$aAA
cde$
gạt
$aAAc
de$
gạt
$aAAcd
e$
thu gọn B -> d (1)
d không phải là handle do áp dụng thu
gọn này là không thành công
$aAAcB
e$
gạt
$aAAcBe $
dừng, quay lui 1 (gạt)
$aAAcde $
dừng, quay lui 2 (gạt)
$aAbc
de$
thu gọn A -> Abc
Abc
AAbcde
$aA
de$
gạt
$aAd
e$
thu gọn B -> d
d
AAde
$aAB
e$
gạt
$aABe
$
thu gọn S -> aABe
$S
$
chấp nhận
Chú ý Handle là chuỗi mà chuỗi đó phải là một kết quả của suy dẫn phải từ S
và phép thu gọn xảy ra trong suy dẫn đó.
W = a
1
a
2...
a
n
Stack
β
α
a
i
a
i+1 ...
a
n
$
Sản xuất A
->
β
Trên ngăn xếp chứa xâu y =
α β
,
β
là vế phải của một sản xuất
được bộ phân tích áp dụng để thu gọn và bước thu gọn này phải
dẫn đến quá trình phân tích thành công thì
β
là handle của chuỗi
α β
v (v là phần chuỗi còn lại trên input buffer).
Vậy nếu S =>
*rm
α
Aw =>
rm
α β
w thì
β
là handle của
suy dẫn phải
α β
w

Trong việc sử dụng ngăn xếp để phân tích cú pháp gạt thu gọn, handle luôn
luôn xuất hiện trên đỉnh của ngăn xếp.
* Tiền tố khả tồn (viable prefixes)
Xâu ký hiệu trong ngăn xếp tại mỗi thời điểm của một quá trình phân tích gạt -
thu gọn là một tiền tố khả tồn.
Ví dụ: tại một thời điểm trong ngăn xếp có dữ liệu là
α β
và xâu vào còn lại là w thì
α β
w là một dạng câu dẫn phải và
α β
là một tiền tố khả tồn.
2.3.2.Phân tích LL.
Tử tưởng của phương pháp phân tích LL là khi ta triển khai một ký hiệu
không kết thúc, lựa chọn cẩn thận các sản xuất như thế nào đó để tránh việc quay
lui mất thời gian
.Tức là phải có một cách nào đó xác định dực ngay lựa chọn đúng mà không
phải thử các lựa chọn khác. Thông tin để xác định lựa chọn dựa vào những gì đã biết trạng thái và
kí hiệu kết thúc hiện tại.
LL: là một trong các phương pháp phân tích hiệu quả, nó cũng thuộc chiến lược
phân tích topdown nhưng nó hiệu quả ở chỗ nó là phương pháp phân tích không
quay lui.
- Bộ phân tích tất định: Các thuật toán phân tích có đặc điểm chung là xâu vào
được quét từ trái sang phải và quá trình phân tích là hoàn toàn xác định, do đó ta
gọi là bộ phân tích tất định. (Phân tích topdown và bottom – up có phải là phân tích
tất định không? – không do quá trình phân tích là không xác định).
L
: left – to – right ( quét từ phải qua trái ) L : leftmosst – derivation (suy dẫn trái nhất)
;
k là số ký hiệu nhìn trước để đưa ra quyết định phân tích.
Giả sử ký hiệu không kết thúc A có các sản xuất: A ->
α
1
|
α
2
| . . . |
α
n
thoả mãn tính
chấ:t các xâu
α
1
,
α
2
, . . .,
α
n
suy dẫn ra các xâu với ký hiệu tại vị trí đầu tiên là các ký hiệu kết
thúc khác nhau, khi đó chúng ta chỉ cần nhìn vào ký hiệu đầu vào tiếp theo sẽ xác định được cần
khai triển A theo
α
i
nào
.
Nếu cần tới k ký hiệu đầu tiên thì mới phân biệt được các xâu
α
1
,
α
2
,
. . .,
α
n
thì khi đó để chọn luật sản xuất nào cho khai triển A chúng ta cần nhìn k ký hiệu đầu vào
tiếp theo
.
Văn phạm LL(k) là văn phạm cho phép xây dựng bộ phân tích làm việc tất định
nếu bộ phân tích này được phép nhìn k kí hiệu vào nằm ngay bên phải của vị trí vào
hiện tại.
Ngôn ngữ sinh ra bởi văn phạm LL(k) là ngôn ngữ LL(k).
Thông thường chúng
ta xét với k=1.
2.3.2.1. First và follow.
* First của một xâu:
First(
α
) cho chúng ta biết xâu
α
có thể suy dẫn đến tận cùng thành một xâu bắt đầu bằng
ký hiệu kết thúc nào.
Định nghĩa First(
α
)
First(
α
) là tập chứa tất cả các ký hiệu kết thúc a mà a có thể là bắt đầu của
một xâu được suy dẫn từ
α
+ First(
α
) = {a
∈
T |
α
=>* a
β
}
+
ε
∈
First(
α
) nếu
α
=>*
ε
Thuật toán tính First(X) với X là một ký hiệu văn phạm:
1. nếu X là ký hiệu kết thúc thì First(X) = {X}
2.
nếu X ->
ε
là một sản xuất thì thêm
ε
vào First(X)
3.
nếu X -> Y
1
...Y
k
là một sản xuất thì thêm First(Y
1
) vào First(X) trừ
ε
nếu First(Y
t
) chứa
ε
với mọi t=1,...,i với i<k thì thêm First(Y
i+1
) vào
First(X) trừ
ε
. Nếu trường hợp i=k thì thêm
ε
vào First(X)
Cách tính First(
α
) với
α
là một xâu.
Giả sử
α
= X
1
X
2
. . . X
k
. Ta tính như bước 3 của thuật toán trên:
1.
thêm First(X
1
) vào First(
α
) trừ
ε
2.
nếu First(X
t
) chứa
ε
với mọi t=1,...,i với i<k thì thêm First(X
i+1
) vào
First(
α
) trừ
ε
. Nếu trường hợp i=k thì thêm
ε
vào First(
α
)
- Tính First của các ký hiệu không kết thúc: lần lượt xét tất cả các sản
xuất.Tại mỗi sản xuất, áp dụng các qui tắc trong thuật toán tính First để thêm các
ký hiệu vào các tập First. Lặp lại và dừng khi nào gặp một lượt duyệt mà không bổ
sung thêm được bất kỳ ký hiệu nào vào tập First và ta đã tính xong các tập First cho
các ký hiệu
.
Ví dụ 1:
Cho văn phạm sau: S -> AB; A -> aA |
ε
; B -> bB |
ε
Hãy tính First của các ký hiệu S, A, B
Kết quả: Fisrt(A) = {a,
ε
}; First(B) = {b,
ε
}; First(S) = {a,b,
ε
}
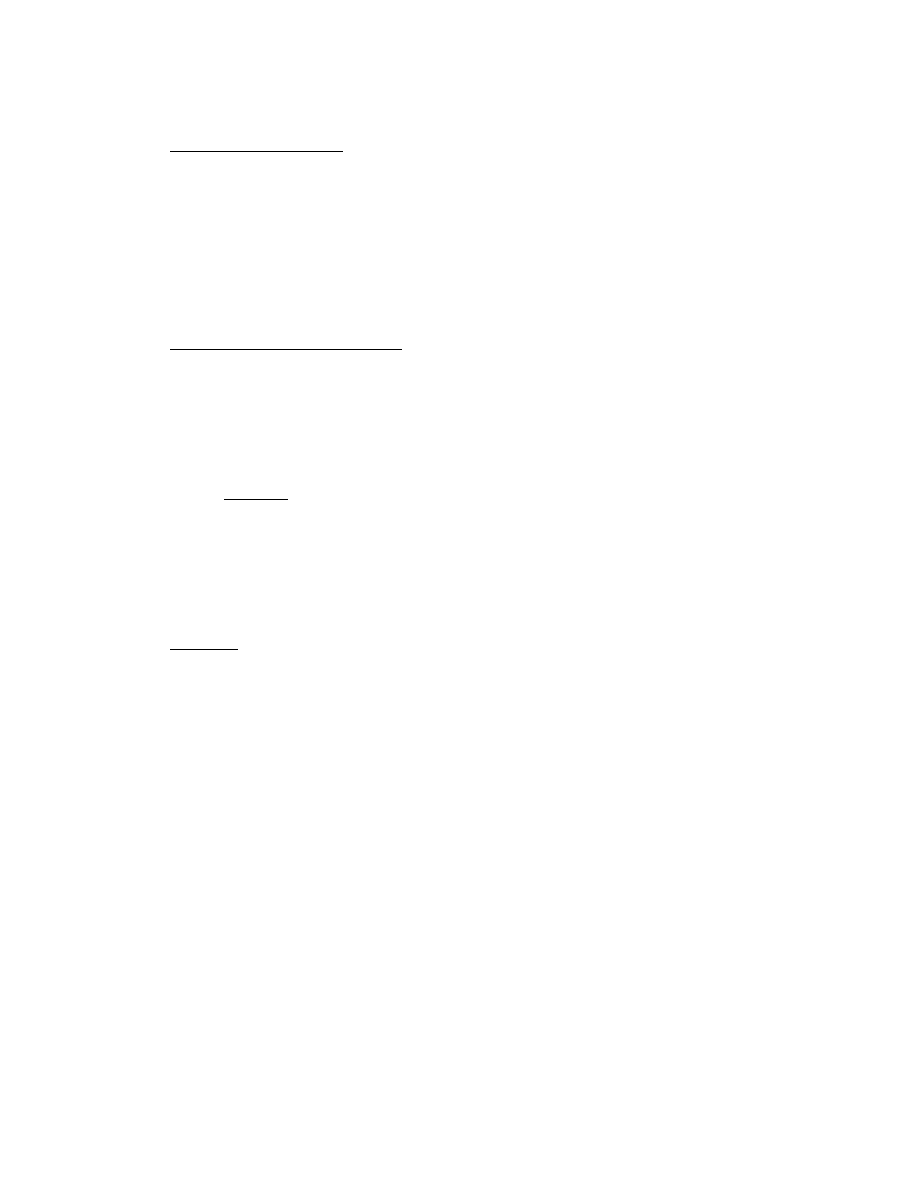
* Follow của một ký hiệu không kết thúc:
Định nghĩa follow(A) A là kí hiệu không kết thúc.
Follow(A) với A là ký hiệu không kết thúc là tập các ký hiệu kết thúc a mà
chúng có thể xuất hiện ngay bên phải của A trong một số dạng câu. Nếu A là ký
hiệu bên phải nhất trong một số dạng câu thì thêm $ vào Follow(A).
+ Follow(A) = {a
∈
T |
∃
S =>*
α
Aa
β
}
+ $
∈
Follow(A) khi và chỉ khi tồn tại suy dẫn S =>*
α
A
Thuật toán tính Follow(A) với A là một ký hiệu không kết thúc
1.
thêm $ vào Follow(S) với S là ký hiệu bắt đầu (
chú ý là nếu ta xét một tập
con với một ký hiệu E nào đó làm ký hiệu bắt đầu thì cũng thêm $ vào Follow(E)).
2.
nếu có một sản xuất dạng B->
α
A
β
và
β ≠ ε
thì thêm các phần tử
trong First(
β
) trừ
ε
vào Follow(A).
thật vậy: nếu a
∈
First(
β
) thì tồn tại
β
=>*a
γ
, khi đó, do có luật B->
α
A
β
nên
tồn tại S =>*
α
1
B
β
1
=>
α
1
α
A
β β
1
=>
α
1
α
Aa
γ β
1
Theo định nghĩa của Follow
thì ta có a
∈
Follow(A)
3.
nếu có một sản xuất dạng B->
α
A hoặc B->
α
A
β
với
ε ∈
First(B) thì
mọi phần tử thuộc Follow(B) cũng thuộc Follow(A)
thật vậy: nếu a
∈
Follow(B) thì theo định nghĩa Follow ta có S =>*
α
1
Ba
β
1
=>*
α
1
α
Aa
β
1
, suy ra a
∈
Follow(A)
- Để tính Follow của các ký hiệu không kết thúc: lần lượt xét tất cả các sản
xuất. Tại mỗi sản xuất, áp dụng các qui tắc trong thuật toán tính Follow để thêm
các ký hiệu vào các tập Follow . Lặp lại và dừng khi nào gặp một lượt duyệt mà
không bổ sung được ký hiệu nào vào các tập Follow.
Ví dụ ở trên, ta tính được tập Follow cho các ký hiệu S, A, B như sau:
Follow(S) = {$} Follow(A) = {b,$} Follow(B) = {}
VÝ dô2: Víi v¨n ph¹m
E
→
T E'; E'
→
+ T E' |
∈;
T
→
F T'; T'
→
* F T' |
∈;
F
→
(E) | id
Theo ®Þnh nghÜa FIRST
V× F
→
E) FIRST(F) = {(, id} F
→
(id)
Tõ T
→
F T' v× ( ( FIRST(F) ( FIRST(T)= FIRST(F)
Tõ E
→
T E' v× ( ( FIRST(T) ( FIRST(E)= FIRST(T)
V× E'
→ε
⇒ε
∈
FIRST(E')

MÆt kh¸c do E' ( +T E' mµ FIRST(+)={ +} ( FIRST(E')= {+, (}
T¬ng tù FIRST(T')= { *, (}
VËy ta cã FIRST(E)= FIRST(T)= FIRST(F)= { (, id}
FIRST(E')= {+,
ε
}
FIRST(T')= { *,
ε
}
Tính follow : Đ
Æt $ vµo trong FOLLOW(E).
Áp dông luËt 2 cho luËt sinh F
→
(E)
⇒ε
∈
FOLLOW(E)
⇒
FOLLOW(E)={$,
ε
}
Áp dông luËt 3 cho E
→
TE
'
⇒ε
,$
∈
FOLLOW(E
'
)
⇒
FOLLOW(E
'
)={$,
ε
}.
Áp dông luËt 2 cho E
→
TE'
⇒
mäi phÇn tö #
ε
cña FIRST(E') tøc +
(FOLLOW(T).
Áp dông luËt 3 cho E' E
'
→
+TE
'
, E
'
→
ε
⇒
FOLLOW(E
'
)
⊂
FOLLOW(T)
⇒
⇒
FOLLOW(T) = { +,
ε
, $ }.
Ap dụng
luËt 3 cho T
→
FT' th× FOLLOW(T') =FOLLOW(T)={+, $,
ε
}.
Ap dông luËt 2 cho T
→
FT'
⇒
*
∈
FOLLOW(F)
Ap dông luËt 3 cho T
'
→
* F T
'
;T
→
ε
'
th× FOLLOW(T') ( FOLLOW(F)th×
FOLLOW(F)= { *, +, $, )}
VËy ta cã FOLLOW(E)= FOLLOW(E') = { $, )}
FOLLOW(T)= FOLLOW(T') = { +,$, )}
FOLLOW(F)= {*,+, $, )}
2.3.2.2. lập bảng phân tích LL(1).
Bảng phân tích LL(1) là một mảng hai chiều: Một chiều chứa các ký hiệu
không kết thúc, chiều còn lại chứa các ký hiệu kết thúc và $.
Vị trí M(A,a) chứa sản xuất A->
α
trong bảng chỉ dẫn cho ta biết rằng khi cần
khai triển ký hiệu không kết thúc A với ký hiệu đầu vào hiện tại là a thì áp dụng sản
xuất A->
α
.
Thuật toán xây dựng bảng LL(1):
Input: Văn phạm G.
Output: Bảng phân tích M.
Phương pháp:
1.
với mỗi sản xuất A->
α
, thực hiện bước 2 và bước 3
2.
với mỗi ký hiệu kết thúc a
∈
First(
α
), định nghĩa mục M(A,a) là A-
>
α
3.
nếu
ε
∈
First(
α
) và với mỗi b
∈
Follow(A) thì định nghĩa mục
M(A,b) là A->
α
(nếu
ε
∈
First(
α
) và $
∈
Follow(A) thì thêm A->
α
vào
M[A,$])
Đặt tất cả các vị trí chưa được định nghĩa trong bảng là “lỗi”.
VÝ dô: E
→
T E'; E'
→
+ T E' |
ε ;
T
→
F T'; T'
→
* F T' |
ε ;
F
→
(E) |
id
TÝnh FIRST(TE') = FIRST(T) = {(,id
}
( M[E,id] vµ M[E,( ]
Kí tự chưa kết
thúc
Kí tự kết thúc
Id
+
*
(
)
$
E
E
→
TE
'
E
→
TE
'
E
'
E
→
+TE
'
E
→
ε
E'
→
ε
T
T
→
FT
'
T
→
FT
'
T
'
T'
→
ε
T'
→
+FT
'
T
'
→
ε
T'
→
ε
F
F
→
id
F
→
(E)
XÐt luËt sinh E
→
TE'
chøa luËt sinh E
→
TE'
XÐt luËt sinh E'
→
+ TE'
TÝnh FIRST(+TE') = FIRST(+) = {+} ( M[E',+] chøa E'
→
+TE'
LuËt sinh E'
→ ε
v×
ε ∈
FIRST(() = FIRST(() FOLLOW(E') = { ), $}
( E
→ ε
n»m trong M[E',)] vµ M[E',$]
LuËt sinh T
→
FT' : FIRST(FT') = {*}
LuËt sinh T'
→ ε:
ε ∈
FIRST(
α
) vµ FOLLOW(T')= {+, ), $}
LuËt sinh F
→
(E) ; FIRST(((E)) = {(}
LuËt sinh F
→
id ; FIRST(id)={id}
2.3.2.3. văn phạm LL (k) và LL (1)
Giải thuật trên có thể áp dụng bất kỳ văn phạm G nào để sinh ra bảng phân
tích M. Tuy nhiên có những văn phạm ( đệ quy trái và nhập nhằng) thì trong bảng
phân tích M có những ô chứa nhiềuhơn một luật sinh.
Ví dụ: Văn phạm S
→
iEtSS’ | aS’
→
eS |
ε Ε →
b
Ký tù cha kÕt
thóc
Ký tù kÕt thóc
A
B
e
i
t
$
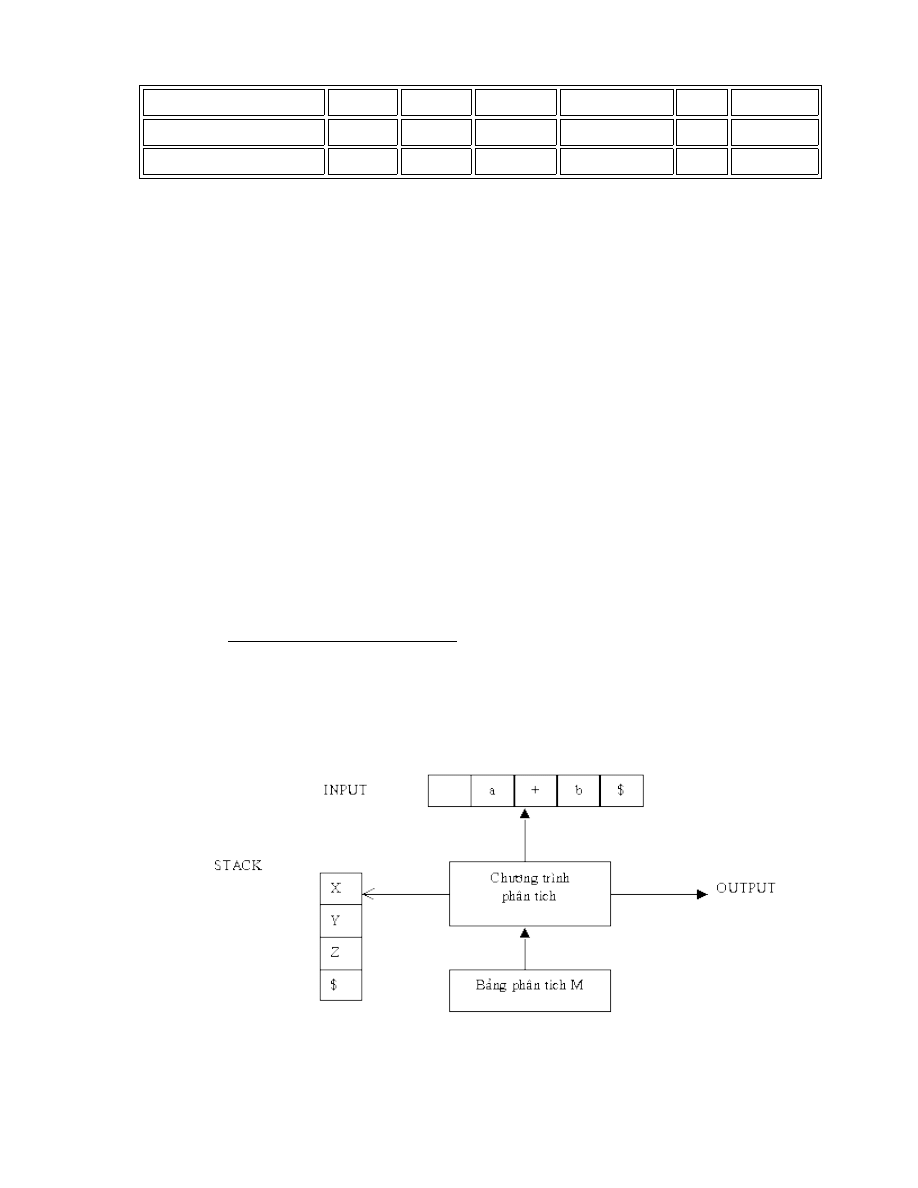
S
S
→
a
S
→
iEtSS
'
S
'
S
→
ε
S
'
→
ε
E
E
→
b
* Định nghĩa: Văn phạm LL(1) là văn phạm xây dựng được bảng phân tích M
có các ô chỉ được định nghĩa nhiều nhất là một lần
.
* Điều kiện để một văn phạm là LL(1)
- Để kiểm tra văn phạm có phải là văn phạm LL(1) hay không ta lập bảng
phân tích LL(1) cho văn phạm đó. Nếu có mục nào đó trong bảng được định nghĩa
nhiều hơn một lần thì văn phạm đó không phải là LL(1), nếu trái lại thì văn phạm là
LL(1).
- Cách khác là dựa vào định nghĩa, một văn phạm là LL(1) phải thoả mãn điều
kiện sau:
nếu A ->
α
|
β
là hai sản xuất của văn phạm đó thì phải thoả mãn:
a)
không tồn tại một ký hiệu kết thúc a mà a
∈
First(
α
) và a
∈
First(
β
)
b)
không thể đồng thời
ε
thuộc First(
α
) và First(
β
).
c)
Nếu
ε
∈
First(
α
) thì Follow(A) và First(
β
) không có phần tử nào
trùng nhau.
2.3.2.4. Thuật toán phân tích LL(1)
* Mô tả: Cơ sở của phân tích LL là dựa trên phương pháp phân tích topdown
và máy ôtômát đẩy xuống.
- Vùng đệm chứa xâu vào với cuối xâu là ký hiệu kết thúc xâu $.

- Ngăn xếp chứa các ký hiệu văn phạm thể hiện quá trình phân tích. Đáy ngăn
xếp kí hiệu $.
- Bảng phân tích M
lµ mét m¶ng hai chiÒu M[A,a], trong ®ã A lµ
ký hiÖu chøa kÕt thóc, a lµ ký hiÖu kÕt thóc hoÆc $.
- Thành phần chính điều khiển phân tích.
Mô hình của phân tích cú pháp LL
Tại thời điểm hiện tại, giả sử X là ký hiệu trên đỉnh ngăn xếp và a là ký hiệu
đầu vào. Các hành động điều khiển được thực hiện như sau:
1.
nếu X = a = $, quá trình phân tích thành công
2.
nếu X = a
≠
$, lấy X ra khỏi ngăn xếp và dịch con trỏ đầu vào đến ký
hiệu tiếp theo
3.
nếu X là một ký hiệu không kết thúc, xét mục M(X,a) trong bảng phân
tích. Có hai trường hợp xảy ra:
a)
nếu M(A,a) = X -> Y
1
. . .Y
k
thì lấy X ra khỏi ngăn xếp và đẩy vào
ngăn xếp Y
1
, . . ., Y
k
theo thứ tự ngược lại (để ký hiệu được phân tích tiếp theo trên
đỉnh ngăn xếp phải là Y
1
, tạo ra dẫn xuất trái).
b)
nếu M(A,a) là lỗi thì quá trình phân tích gặp lỗi và gọi bộ khôi phục
lỗi.
* Thuật toán :
- Input: Một xâu w và một bảng phân tích M của văn phạm G.
- Output: Đưa ra suy dẫn trái nhất của w nếu w
∈
L(G), báo lỗi nếu w
∉
L(G).
- Method:
Ở trạng thái khỉ đầu ngăn xép được đặt các kí hiệu $S (S là đỉnh của cây phân tích
còn xâu vào là w$ )
Đặt con trỏ ip trỏ đến kí tự đầu tiên của xâu w$
Repeat
{Giả sử X là kí hiệu đỉnh của ngăn xếp, a là kí hiệu vào tiếp theo}
If (X
∈Σ
) or (X = $) then
If x=a then
Pop X từ đỉnh ngăn xếp và loại bỏ a khỏi xâu vào
Else error ();
Else
{X không phải là kí tự kết thúc}
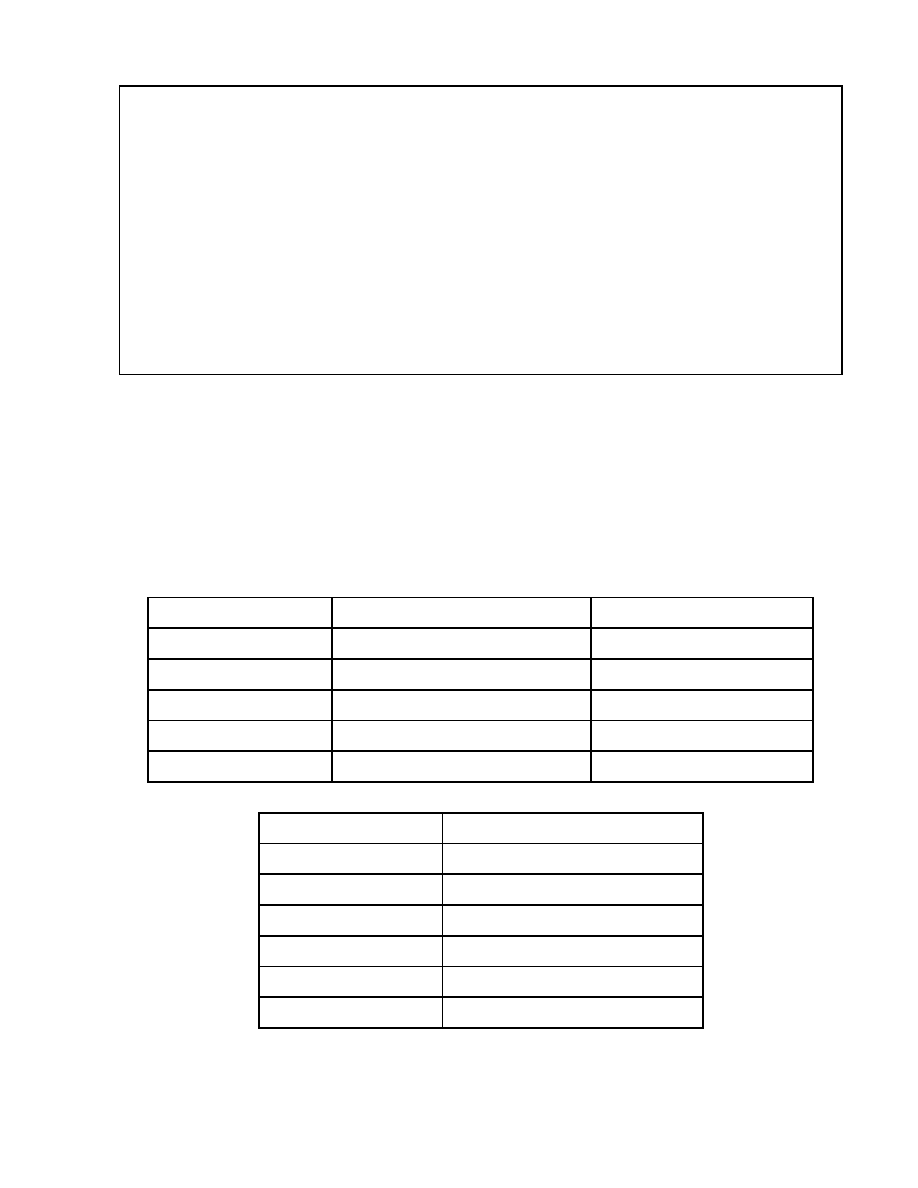
If M[X,a] = X
→
Y
1
, Y
2
, … Y
k
then
Begin
Pop X từ ngăn xếp;
Push Y
k
, Y
k-1
, … Y
1
vào ngăn xếp, với Y
1
ở đỉnh;
Đưa ra sản xuất X
→
Y
1
, Y
2
, … Y
k
;
End;
Else Error();
Until X = $
{ngăn xếp rỗng}
Ví dụ 2: Cho văn phạm: E->TE’; E’->+TE’ |
ε
; T->FT’; T’->*FT’ |
ε
; F-
>(E) | id
a)
tính First và Follow cho các ký hiệu không kết thúc.
b)
tính First cho vế phải của các sản xuất.
c)
xây dựng bảng phân tích LL(1) cho văn phạm trên
d)
phân tích LL đối với xâu vào “id+id*id”
Ký hiệu văn phạm
First
Follow
E
(, id
), $
E’
+,
ε
), $
T
(, id
+, ), $
T’
*,
ε
+, ), $
F
(, id
+, *, ), $
Sản xuất
First của vế phải
E->TE’
(, id
E’->+TE’
+
T->FT’
(, id
T’->*FT’
*
F->(E)
(
F->id
Id
Bảng phân tích LL(1)
Ký hiệu
Vế trái
Ký hiệu đầu vào
Id
+
*
(
)
$
E
E->TE’
E->TE’
E’
E’->+TE’
E’->
ε
E’->
ε
T
T->FT’
T->FT’
T’
T’->
ε
T’->*FT’
T’->
ε
T’->
ε
F
F->id
F->(E)
Phân tích LL(1) cho xâu vào “id+id*id”:
Ngăn xếp
Xâu vào
Đầu ra
$E
id+id*id$
E->TE’
$E’T
id+id*id$
T->FT’
$E’T’F
id+id*id$
F->id
$E’T’id
id+id*id$
rút gọn id
$E’T’
+id*id$
T’->
ε
$E’
+id*id$
E’->+TE’
$E’T+
+id*id$
rút gọn +
$E’T
id*id$
T->FT’
$E’T’F
id*id$
F->id
$E’T’id
id*id$
rút gọn id
$E’T’
*id$
T’->*FT’
$E’T’F*
*id$
rút gọn *
$E’T’F
id$
F->id
$E’T’id
id$
rút gọn id
$E’T’
$
T’->
ε
$E’
$
E’->
ε
$
$
Từ bảng phân tích, chúng ta có suy dẫn trái như sau:
E=>TE’=>FT’E’=>idT’E’=>idE’=>id+TE’=>id+FT’E’=>id+idT’E’=>id+id
*FT’E’=> id+id*idT’E’=>id+id*idE’=>id=id*id .

2.3.4. Phân tích LR.
LR là kỹ thuật phân tích cú pháp từ dưới lên khá hiệu quả, có thể được sử dụng để phân
tích một lớp khá lớn các văn phạm phi ngữ cảnh. Kỹ thuật này gọi là phân tích cú pháp LR(k),
trong đó:
- L là Left to right chỉ việc quét xâu vào từ trái quá phải.
- R là Right most parsing chỉ việc suy dẫn sinh ra là suy dẫn phải.
- k là số ký hiệu nhìn trước để đưa ra quyết định phân tích.
* Phân tích LR có nhiều ưu điểm:
- Nhận biết được tất cả các cấu trúc của ngôn ngữ lập trình được tạo ra dựa theo các văn
phạm phi ngữ cảnh.
- LR là phương pháp phân tích cú pháp gạt - thu gọn không quay lui tổng quát nhất đã
được biết đến nhưng lại có thể được cài đặt hiệu quả như những phương pháp gạt - thu gọn
khác.
- lớp văn phạm phân tích được nhờ phương pháp LR là một tập bao hàm thực sự của lớp
văn phạm phân tích được bằng cách phân tích cú pháp dự đoán.
- Phát hiện được lỗi cú pháp ngay khi có thể trong quá trình quét đầu vào từ trái sang.
* Nhược điểm chủ yếu: ta phải thực hiện quá nhiều công việc để xây dựng được bộ phân
tích LR cho một ngôn ngữ lập trình.
2.3.4.1. Thuật toán phân tích LR.
Phân tích LR là một thể phân tích cú pháp gạt - thu gọn, nhưng điểm khác biệt so với phân
tích Bottom-up là nó không quay lui. Tại mỗi thời điểm nó xác định được duy nhất hành động gạt
hay thu gọn.
* Mô hình: gồm các thành phần sau:
- Stack lưu một chuỗi s
0
X
1
s
1
X
2
s
2
... X
m
s
m
trong đó s
m
nằm trên đỉnh Stack. X
i
là
một ký hiệu văn phạm, si là một trạng thái tóm tắt thông tin chứa trong Stack bên
dưới nó.
- Bảng phân tích bao gồm 2 phần : hàm action và hàm goto.
action[s
m
, a
i
] có thể có một trong 4 giá trị :
1. shift s : đẩy s, trong đó s là một trạng thái.
2. reduce (A
→
β
) :thu gọn bằng luật sinh A
→
β
.
3. accept : Chấp nhận
4. error : Báo lỗi
Goto lấy 2 tham số là một trạng thái và một ký hiệu văn phạm, nó sinh ra
một trạng thái.

*
Cấu hình (configuration) của một bộ phân tích cú pháp LR là một cặp thành
phần, trong đó, thành phần đầu là nội dung của Stack, phần sau là chuỗi nhập chưa
phân tích: (s
0
X
1
s
1
X
2
s
2
... X
m
s
m
, a
i
a
i+1
...
a
n
$)
* Hoạt động:
Với s
m
là ký hiệu trên đỉnh Stack, ai là ký hiệu nhập hiện tại, cấu hình có được
sau mỗi dạng bước đẩy sẽ như sau :
1. Nếu action [s
m
, a
i
] = Shift s : Thực hiện phép đẩy để được cấu hình mới :
(s
0
X
1
s
1
X
2
s
2
... X
m
s
m
a
i
s, a
i +1
...
a
n
$)
Phép đẩy làm cho s nằm trên đỉnh Stack, a
i+1
trở thành ký hiệu hiện hành.
2. Nếu action [s
m
, a
i
] = Reduce(A
→
β
) thì thực hiện phép thu gọn để được cấu
hình : (s
0
X
1
s
1
X
2
s
2
... X
m - i
s
m - i
As, a
i
a
i +1
....
a
n
$)
Trong đó, s = goto[s
m - i
, A] và r là chiều dài số lượng các ký hiệu của
β
. Ở đây,
trước hết 2r phần tử của Stack sẽ bị lấy ra, sau đó đẩy vào A và s.
3. Nếu action[s
m
, a
i
] = accept : quá trình phân tích kết thúc.
4. Nếu action[s
m
, a
i
] = error : gọi thủ tục phục hồi lỗi.
Giải thuật phân tích cú pháp LR
Input: Một chuỗi nhập w, một bảng phân tích LR với hàm action và goto cho văn
phạm G.
Output: Nếu w
∈
L(G), đưa ra một sự phân tích dưới lên cho w . Ngược lại, thông
báo lỗi.
Phương pháp:
Khởi tạo s
0
là trạng thái khởi tạo nằm trong Stack và w$ nằm trong bộ đệm nhập.
Ðặt ip vào ký hiệu đầu tiên của w$;
Repeat forever begin
Gọi s là trạng thái trên đỉnh Stack và a là ký hiệu được trỏ bởi ip;
If action[s, a] = Shift s' then begin
Ðẩy a và sau đó là s' vào Stack;
Chuyển ip tới ký hiệu kế tiếp;
end
else if action[s, a] = Reduce (A
→
β
) then begin
Lấy 2 * |
β
| ký hiệu ra khỏi Stack;
Gọi s' là trạng thái trên đỉnh Stack;
Ðẩy A, sau đó đẩy goto[s', A] vào Stack;
Xuất ra luật sinh A
→
β
;
end
else if action[s, a] = accept then
return
else error ( )
end
Ví dụ:
Cho văn phạm:
(1) E -> E + T (2) E -> T
(3) T -> T * F (4) T -> F
(5) F -> ( E ) (6) F -> a
Giả sử chúng ta đã xây dựng được bảng phân tích action và goto như sau:
chú ý:
các giá trị trong action được ký hiệu như sau:
a)
si có nghĩa là shift i
b)
rj có nghĩa là reduce theo luật (j)
c)
acc có nghĩa là accept
d)
khoảng trống biểu thị lỗi
trạng
thái
Action
goto
a
+
*
(
)
$
E
T
F
0
s5
S4
1
2
3
1
s6
acc
2
r2
s7
r2
r2
3
r4
r4
r4
r4
4
s5
S4
8
2
3
5
r6
r6
r6
r6
6
s5
S4
9
3
7
s5
S4
10
8
s6
s11
9
r1
s7
r1
r1
10
r3
r3
r3
r3
11
r5
r5
r5
r5
Bảng phân tích cú pháp
Chúng ta sử dụng thuật toán LR để phân tích xâu vào “a*a+a” đối với dữ liệu trên
như sau:
Ngăn xếp
Đầu vào
Hành động
0
id * id + id $
gạt
0 id 5
* id + id $
thu gọn F->id
0 F 3
* id + id $
thu gọn T->F
0 T 2
* id + id $
gạt
0 T 2 * 7
id + id $
gạt
0 T 2 * 7 id 5
+ id $
thu gọn F->id
0 T 2 * 7 F 10
+ id $
thu gọn T->T*F
0 T 2
+ id $
thu gọn E->T
0 E 1
+ id $
gạt
0 E 1 + 6
id $
gạt
0 E 1 + 6 id 5
$
thu gọn F->id
0 E 1 + 6 F 3
$
thu gọn T->F

0 E 1 + 6 T 9
$
thu gọn E->E+T
0 E 1
$
chấp nhận (accepted)
Quá trình phân tích LR
Một số đặc điểm của phân tích LR:
- Một tính chất cơ bản đối với bộ phân tích cú phát LR là xác định được khi nào handle xuất hiện
trên đỉnh ngăn xếp.
- Ký hiệu trạng thái trên đỉnh ngăn xếp đã xác định mọi thông tin của quá trình phân tích vì nó
chỉ đến tập mục có nghĩa của tiền tố khả tồn trong ngăn xếp. Dựa vào các mục này, chúng ta có
thể xác định khi nào thì gặp một handle trên đỉnh ngăn xếp và thực hiện hành động thu gọn.
- Một nguồn thông tin khác để xác định hành động gạt-thu gọn là k ký hiệu đầu vào tiếp theo.
Thông thườn chúng ta xét k=0 hoặc 1.
- Điểm khác biệt giữa phương pháp phân tích LR với phương pháp phân tích LL là: Để cho một
văn phạm là LR(k), chúng ta phải có khả năng xác định được sự xuất hiện của vế phải của một
sản xuất khi đã thấy tất cả quá trình dẫn xuất từ vế phải đó với thông tin thêm là k ký hiệu đầu
vào tiếp theo. Điều kiện này rõ ràng là chính xác hơn so với điều kiện của văn phạm LL(k) là
việc sử dụng một sản xuất chỉ dựa vào k ký hiệu đầu vào tiếp theo. Chính vì vậy mà quá trình
phân tích LR ít có xung đột hơn, hay nói cách khác là văn phạm của nó rộng hơn LL rất nhiều.
2.3.4.2. Một số khái niệm.
1) Tiền tố khả tồn (viable prefixes)
Xâu ký hiệu trong ngăn xếp tại mỗi thời điểm của một quá trình phân tích gạt -
thu gọn là một tiền tố khả tồn.
Ví dụ: tại một thời điểm trong ngăn xếp có dữ liệu là
α β
và xâu vào còn lại là w thì
α β
w là một dạng câu dẫn phải và
α β
là một tiền tố khả tồn.
2) Mục (Item) : Cho một văn phạm G.
Với mỗi sản xuất A->xy, ta chèn dấu chấm vào tạo thành A->x .y và gọi kết
quả này là một mục.
Mục A->x.y cho biết qúa trình suy dẫn sử dụng sản xuất A->xy và đã suy dẫn
đến hết phần x trong sản xuất, quá trình suy dẫn tiếp theo đối với phần xâu vào còn
lại sẽ bắt đầu từ y.
Ví dụ: Luật sinh A ( XYZ có 4 mục như sau :
A
→
•
XYZ A
→
X
•
YZ
A
→
XY
•
Z A
→
XYZ
•
Luật sinh A
→
ε
chỉ tạo ra một mục A
→
•
3) Mục có nghĩa (valid item)
Một mục A->
β
1
.
β
2
gọi là mục có nghĩa(valid item) đối với tiền tố khả tồn
α β
1
nếu tồn tại một dẫn xuất: S =>*rm
α
Aw =>rm
α β
1
β
2
w
Tập tất cả các mục có nghĩa đối với tiền tố khả tồn gọi là tập I.
Một tập mục có nghĩa đối với một tiền tố khả tồn nói lên rất nhiều điều trong quá trình suy
dẫn gạt - thu gọn: Giả sử quá trình gạt thu gọn đang ở trạng thái với ngăn xếp là x và phần ký
hiệu đầu vào là v
(*)
ngăn xếp
đầu vào
$x
v$
thế thì, quá trình phân tích tiếp theo sẽ phụ thuộc vào tập mục có nghĩa I của tiền tố khả
tồn thuộc x. Với một mục [A->
β
1
.
β
2
]
∈
I, cho chúng ta biết x có dạng
α β
1
, và quá trình phân
tích phần còn lại w của xâu đầu vào nếu theo sản xuất A->
β
1
β
2
sẽ được tiếp tục từ
β
2
của mục
đó. Hành động gạt hay thu gọn sẽ phụ thuộc vào
β
2
là rỗng hay không. Nếu
β
2
=
ε
thì phải thu gọn
β
1
thành A, còn nếu
β
2
≠
ε
thì việc phân tích theo sản xuất
A->
β
1
β
2
đòi hỏi phải sử dụng hành động gạt.
Nhận xét:
- Mọi quá trình phân tích tiếp theo của trạng thái (*) đều phụ thuộc vào
các mục có nghĩa trong tập các mục có nghĩa I của tiền tố khả tồn x.
- Có thể có nhiều mục có nghĩa đối với một tiền tố x. Các mục này có
thể có các hành động xung đột (bao gồm cả gạt và thu gọn), trong trường hợp này
bộ phân tích sẽ phải dùng các thông tin dự đoán, dựa vào việc nhìn ký hiệu đầu vào
tiếp theo để quyết định nên sử dụng mục có nghĩa nào với tiền tố x
(tức là sẽ cho
tương ứng gạt hay thu gọn)
. Nếu quá trình này cho những quyết định không xung đột
(duy nhất) tại mọi trạng thái thì ta nói văn phạm đó phân tích được bởi thuật toán
LR.
- Tư tưởng của phương pháp phân tích LR là phải xây dựng được tập tất cả
các mục có nghĩa đối với tất cả các tiền tố khả tồn.
4) Tập chuẩn tắc LR(0)
LR(0) là tập các mục có nghĩa cho tất cả các tiền tố khả tồn.
LR(0) theo nghĩa: LR nói lên đây là phương pháp phân tích LR, còn số 0 có
nghĩa là số ký tự nhìn trước là 0.
5) Văn phạm gia tố(
Augmented Grammar)
(mở rộng)
Văn phạm G - ký hiệu bắt đầu S, thêm một ký hiệu bắt đầu mới S' và luật sinh
S' S để được văn phạm mới G' gọi là văn phạm gia tố.
Ví dụ: cho văn phạm G gồm các sản xuất S -> aSb | a thì văn phạm gia tố của G, ký hiệu là
G’ gồm các sản xuất S’-S, S->aSb | a với S’ là ký hiệu bắt đầu.

Ta xây dựng văn phạm gia tố của một văn phạm theo nghĩa, đối với văn phạm ban
đầu, quá trình phân tích sẽ bắt đầu bởi các sản xuất có vế trái là S. Khi đó, chúng ta xây
dựng văn phạm gia tố G’ thì mọi quá trình phân tích sẽ bắt đầu từ sản xuất S’->S
Sử dụng hai phép toán: phép tính bao đóng closure(I) của một tập mục I và phép sinh ra
tập mục cho các tiền tố khả tồn mới goto(I,X) như sau:
6) Phép toán closure
Nếu I là một tập các mục của một văn phạm G thì closure(I) là tập các mục
được xây dựng từ I bằng hai qui tắc sau:
1. khởi đầu mỗi mục trong I đều được đưa vào closure(I)
2. nếu [A ->
α
.B
β
]
∈
closure(I) và B->
γ
là một sản xuất thì thêm [B
-> .
γ
] vào closure(I) nếu nó chưa có ở đó. Áp dụng qui tắc này đến khi không
thêm được một mục nào vào closure(I) nữa.
Trực quan:
nếu [A ->
α
.B
β
] là một mục có nghĩa đối với một tiền tố khả tồn x
α
thì với
B->
γ
là một sản xuất ta cũng có [B->.
γ
] là một mục có nghĩa đối với tiền tố khả
tồn x
α
.
Phép toán tính bao đóng của một mục là để tìm tất cả các mục có nghĩa tương
đương của các mục trong tập đó.
Theo định nghĩa của một mục là có nghĩa đối với một tiền tố khả tồn, chúng ta có suy dẫn S
=>*rm xAy =>rm x
α
B
β
y
sử dụng sản xuất B ->
γ
ta có suy dẫn S =>*rm x
α γ β
y. Vậy thì [B->.
γ
] là một mục
có nghĩa của tiền tố khả tồn x
α
Ví dụ:
Xét văn phạm mở rộng của biểu thức:
E'
→
E E
→
E + T | T T
→
T * F | F F
→
(E) | id
Nếu I là tập hợp chỉ gồm văn phạm {E'
→
•
E} thì closure(I) bao gồm:
E'
→
•
E (Luật 1) E
→
•
E + T (Luật 2)
E
→
•
T (Luật 2) T
→
•
T * F (Luật 2)
T
→
•
F (Luật 2) F
→
•
(E) (Luật 2)
F
→
•
id (Luật 2)
E'
→
•
E được đặt vào closure(I) theo luật 1. Khi có một E đi ngay sau một
• ,
bằng
luật 2 ta thêm các sản xuất E với các chấm nằm ở đầu trái ( E
→
•
E + T và E
→
•
T).
Bây giờ lại có T đi theo sau một
•,
ta lại thêm
T
→
•
T * F và T
→
•
F vào. Cuối cùng
ta có Closure(I) như trên.
Chú ý rằng : Nếu một B - luật sinh được đưa vào closure(I) với dấu chấm mục nằm ở
đầu vế phải thì tất cả các B - luật sinh đều được đưa vào.
* Phép toán goto
goto(I,X) với I là một tập các mục và X là một ký hiệu văn phạm.

goto(I,X) được định nghĩa là bao đóng của tập tất cả các mục [A->
α
X.
β
]
sao cho [A->
α
.X
β
]
∈
I.
Trực quan:
Nếu I là tập các mục có nghĩa đối với một tiền tố khả tồn
γ
nào đó thì
goto(I,X) là tập các mục có nghĩa đối với tiền tố khả tồn
γ
X.
gọi tập J=goto(I,X) thì cách tính tập J như sau:
1.
nếu [A->
α
.X
β
]
∈
I thì thêm [A->
α
X.
β
] vào J
2.
J=closure(J)
Phép toán goto là phép phát triển để xây dựng tất cả các tập mục cho tất cả các
tiền tố khả tồn có thể.
Ví dụ : Giả sử I = {E'
→
E
•
, E
→
E
•
+ T}. Tính goto (I, +) ?
Ta có J = { E
→
E +
•
T}
⇒
goto (I, +) = closure(I') bao gồm các mục :
E E +
•
T (Luật 1)
T
•
T * F (Luật 2)
T
•
F (Luật 2)
F
•
(E) (Luật 2)
F
•
id (Luật 2)
Tính Goto(I,+) bằng cách kiểm tra I cho các mục với dấu + ở ngay bên phải chấm.
E’
→
E
•
không phải mục như vậy nhưng E
→
E
•
+ T thì đúng. Ta chuyển dấu chấm qua
bên kia dấu + để nhận được E
→
E +
•
T và sau đó tính closure cho tập này.
Như vậy, cho trước một văn phạm, ta có thể sử dụng hai phép toán trên để sinh ra tất cả
các tiền tố khả tồn có thể và tập mục có nghĩa của từng tiền tố khả tồn. Với việc sử dụng phép
tính closure và goto như trên, chúng ta xây dựng được tập các mục gọi là tập mục LR(0).
Thuật toán xây dựng LR(0) như sau:
Cho văn phạm G, văn phạm gia tố của nó là G’
Tập C là tập các tập mục LR(0) được tính theo thuật toán như sau:
1). C = {closure({[S’->.S]})}
2). Đối với mỗi mục I trong C và mỗi ký hiệu văn phạm X, tính
goto(I,X). Thêm goto(I,X) vào C nếu không rỗng và không trùng với bất kỳ tập nào
có trong C
Thực hiện bước 2 đến khi nào không thêm được tập nào nữa vào C
C là tập xác định tất cả các mục có nghĩa đối với tất cả các tiền tố khả tồn vì chúng ta xuất
phát từ mục [S’ -> .S] và xây dựng các mục có nghĩa cho tất cả các tiền tố khả tồn.

Xây dựng tập C dựa trên hàm goto có thể được xem như một sơ đồ chuyển trạng thái của
một DFA. Trong đó, I
0
là trạng thái xuất phát, bằng cách xây dựng các trạng thái tiếp bằng
chuyển trạng thái theo đầu vào là các ký hiệu văn phạm. Đường đi của các ký hiệu đầu vào
chính là các tiền tố khả tồn. Các trạng thái chính là tập các mục có nghĩa của các tiền tố khả tồn
đó.
Ví dụ: Cho văn phạm G
:
E -> E + T | T; T -> T * F | F; F -> ( E ) | id
Hãy tính LR(0)
- Xét văn phạm G’ là văn phạm gia tố của G. Văn phạm G’ gồm các sản xuất sau:
E’ -> E; E -> E + T | T; T -> T * F | F; F -> ( E ) | a
Tính theo thuật toán trên ta có kết quả như sau:
Closure({E'
→
E}):
I
0
: E’ -> .E
E -> .T
T -> .F
F -> .(E)
F -> .a
Goto (I
0
, id)
I
5
:
F -> a.
Goto (I
0
, E)
I
1
:
E’ -> E.
E -> E.+T
Goto (I
1
, +)
I
6
: E -> .E+T
E -> E+.T
T -> .T*F
T -> .F
F -> .(E)
F -> .a
Goto (I
0
, T)
I
2
:
E -> T.
T -> T.*F
Goto (I
2
, *)
I
7
:
T -> T*.F
F -> .(E)
F -> .a
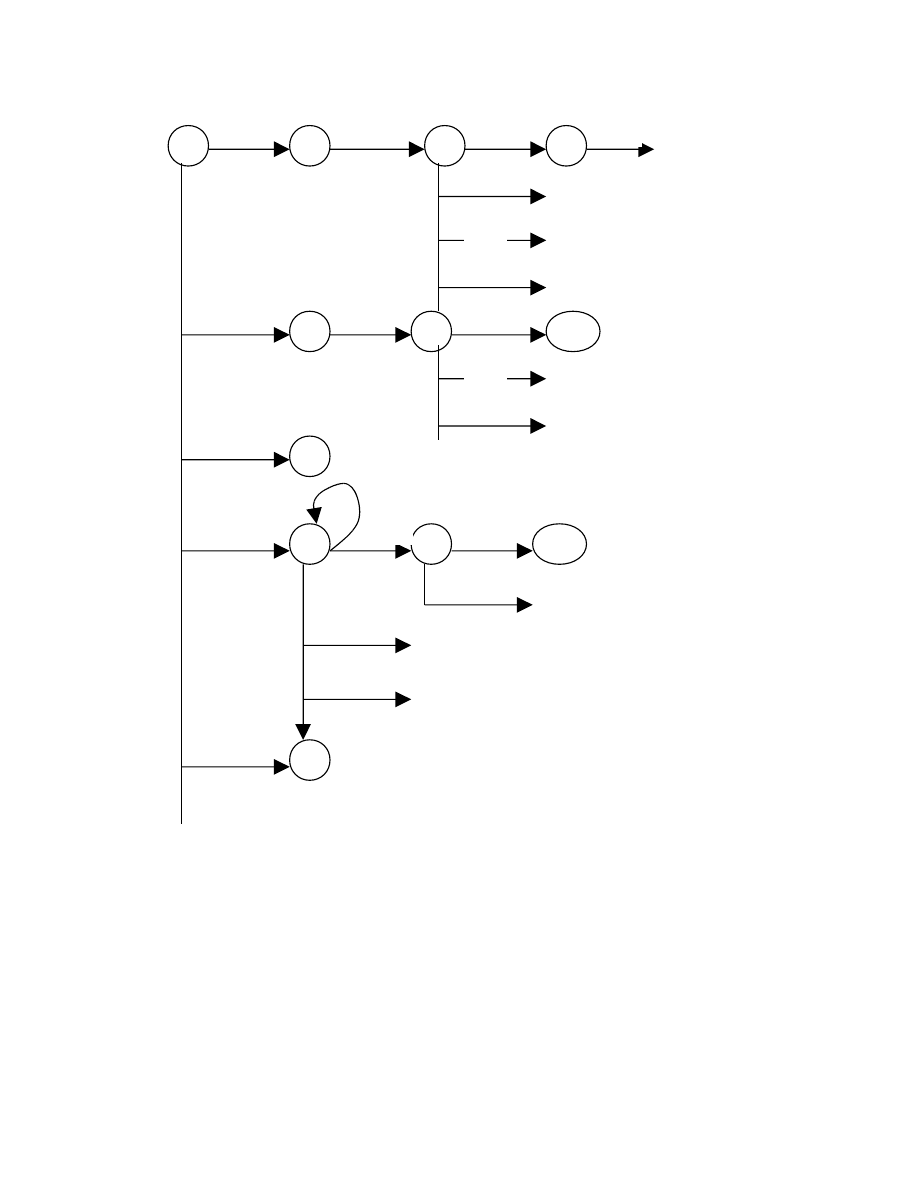
Sơ đồ chuyển trạng thái của DFA cho các tiền tố khả tồn:
I
0
I
1
I
6
I
9
I
7
I
4
I
3
I
5
I
2
I
7
I
10
I
4
I
5
I
3
I
4
I
8
I
11
I
6
I
2
I
3
I
5
E
+
T
*
F
(
a
T
*
F
(
a
F
(
E
)
+
(
T
F
a
a

2.3.4.2. Văn phạm LR.
Làm thế nào để xây dựng được một bảng phân tích cú pháp LR cho một văn phạm đã cho ?
Một văn phạm có thể xây dựng được một bảng phân tích cú pháp cho nó được gọi
là văn phạm LR.
Có những văn phạm phi ngữ cảnh không thuộc lọai LR, nhưng nói chung là
ta có thể tránh được những văn phạm này trong hầu hết các kết cấu ngôn ngữ lập trình điển
hình.
Sự khác biệt rất lớn giữa các văn phạm LL và LR:
Ðối với văn phạm LR(k), ta phải có khả năng nhận diện được sự xuất hiện của
vế phải của một sản xuất nào đó bằng cách xem tất cả những gì suy dẫn được từ vế
phải qua k kí hiệu vào được nhìn vượt quá. Ðòi hỏi này ít khắt khe hơn so với các
văn phạm LL(k).
Đối với văn phạm LL(k): ta phải nhận biết được sản xuất nào được dùng chỉ với
k kí hiệu đầu tiên mà vế phải của nó suy dẫn ra.
Vì vậy, các văn phạm LR có thể mô tả được nhiều ngôn ngữ hơn so với các văn
phạm LL
.
2.3.4.3. Xây dựng bảng phân tích SLR.
Phần này trình bày cách xây dựng một bảng phân tích cú pháp LR từ văn phạm. Chúng ta sẽ
đưa ra 3 phương pháp khác nhau về tính hiệu quả cũng như tính dễ cài đặt. Phương pháp thứ
nhất được gọi là "LR đơn giản" (Simple LR - SLR), là phương pháp "yếu" nhất nếu tính theo số
lượng văn phạm có thể xây dựng thành công bằng phương pháp này, nhưng đây lại là phương
pháp dễ cài đặt nhất. Ta gọi bảng phân tích cú pháp tạo ra bởi phương pháp này là bảng SLR và
bộ phân tích cú pháp tương ứng là bộ phân tích cú pháp SLR, với văn phạm tương đương là văn
phạm SLR.
Phương pháp thứ 2 là phương pháp LR chuẩn ( canonical LR): phương pháp mạnh nhất
nhưng tốn kém nhất.
Phương pháp thứ 3: LR nhìn vượt (LALR – LookaheadLR) là phương pháp trung gian về sức
mạnh và chi phí giữ 2 phương pháp trên. Phương pháp này làm việc với hầu hết các văn phạm.
Trong phần này ta sẽ xem xét cách xây dựng các hàm action và goto của phân tích SLR từ
ôtômát hữu hạn đơn định dùng để nhận dạng các tiền tố có thể có.

Cho văn phạm G, ta tìm văn phạm gia tố của G là G’, từ G’ xây dựng C là tập
chuẩn các tập mục cho G’, xây dựng hàm phân tích Action và hàm nhẩy goto từ C
bằng thuật toán sau.
Input: Một văn phạm tăng cường G'
Output: Bảng phân tích SLR với hàm action và goto
Phương pháp:
1.
Xây dựng C = { I
0
, I
1
, ..., I
n
}, họ tập hợp các mục LR(0) của G'.
2. Trạng thái i được xây dựng từ Ii .Các action tương ứng trạng thái i được xác
định như sau:
2.1
. Nếu A
→
α
•
a
β
∈
I
i
và goto (I
i
, a) = I
j
thì action[i, a] = "shift j". Ở
đây a là ký hiệu kết thúc.
2.2. Nếu A
→
α
•
∈
I
i
thì action[i, a] = "reduce (A
→
α
)",
∀
a
∈
FOLLOW(A). Ở đây A không phải là S'
2.3. Nếu S'
→
S
•
∈
I
i
thì action[i, $] = "accept".
Nếu một action đụng độ được sinh ra bởi các luật trên, ta nói văn phạm
không phải là SLR(1). Giải thuật sinh ra bộ phân tích cú pháp sẽ thất bại trong
trường hợp này.
3. Với mọi ký hiệu chưa kết thúc A, nếu goto (I
i
,A) = I
j
thì goto [i, A] = j
4. Tất cả các ô không xác định được bởi 2 và 3 đều là “error”
5. Trạng thái khởi đầu của bộ phân tích cú pháp được xây dựng từ tập các mục
chứa S’
→
•
S
Ví dụ Ta xây dựng bảng phân tích cú pháp SLR cho văn phạm tăng cường G' trong ví dụ
trên.
E'
→
E E
→
E + T | T T
→
T * F | F F
→
(E) | id
(0)
E'
→
E
(1)
E
→
E + T
(2)
E
→
T
(3)
T
→
T * F
(4)
T
→
F
(5)
F
→
(E)
(6) F
→
id
1. C = { I
0
, I
1
, ... I
11
}
2. FOLLOW(E) = {+, ), $}
FOLLOW(T) = {*, +, ), $}
FOLLOW(F) = {*, +, ), $}
Dựa vào họ tập hợp mục C đã được xây dựng trong ví dụ 4.22, ta thấy:
Trước tiên xét tập mục I
0
: Mục F
→
•
(E) cho ra action[0, (] = "shift 4", và mục F
→
•
id cho action[0, id] = "shift 5". Các mục khác trong I
0
không sinh được hành động nào.
Bây giờ xét I
1
: Mục E'
→
E
•
cho action[1, $] = "accept", mục E
→
E
•
+ T cho
action[1, +] = "shift 6".
Kế đến xét I
2
: E
→
T
•
T
→
T
•
* F
Vì FOLLOW(E) = {+, ), $}, mục đầu tiên làm cho action[2, $] = action[2,+] = "reduce
(E
→
T)". Mục thứ hai làm cho action[2,*] = "shift 7".
Tiếp tục theo cách này, ta thu được bảng phân tích cú pháp SLR:
trạng
thái
Action
goto
a
+
*
(
)
$
E
T
F
0
s5
S4
1
2
3
1
s6
acc
2
r2
s7
r2
r2
3
r4
r4
r4
r4
4
s5
S4
8
2
3
5
r6
r6
r6
r6
6
s5
S4
9
3
7
s5
S4
10
8
s6
s11
9
r1
s7
r1
r1
10
r3
r3
r3
r3
11
r5
r5
r5
r5
Bảng phân tích xác định bởi giải thuật 4.7 gọi là bảng SLR(1) của văn phạm G, bộ
phân tích LR sử dụng bảng SLR(1) gọi là bộ phân tích SLR(1) và văn phạm có một bảng
SLR(1) gọi là văn phạm SLR(1).
Mọi văn phạm SLR(1) đều không mơ hồ, Tuy nhiên
có
những văn phạm không mơ hồ nhưng không phải là
SLR(1).
Ví dụ: Xét văn phạm G với tập luật sinh như sau:
S
→
L = R S
→
R L
→
* R
L
→
id R
→
L
Ðây là một văn phạm không mơ hồ nhưng không
phải là văn phạm SLR(1).
Họ tập hợp các mục C bao gồm:
I
0
: S'
→
•
S
S
→
•
L = R
S
→
•
R
L
→
•
* R
L
→
•
id
R
→
•
L
I
1
: S'
→
S
•
I
2
: S
→
L
•
= R
R
→
L
•
I
3
: S
→
R
•
I
4
: L
→
*
•
R
R
→
•
L
L
→
•
* R
L
→
•
id
I
5
: L
→
id
•
I
6
: S
→
L =
•
R
R
→
•
L
L
→
•
* R
L
→
•
id
I
7
: L
→
* R
•
I
8
: R
→
L
•
I
9
: S
→
L = R
•

Khi xây dựng bảng phân tích SLR cho văn phạm, khi xét tập mục I2 ta thấy mục
đầu tiên trong tập này làm cho action[2, =] = "shift 6". Bởi vì =
∈
FOLLOW(R),
nên mục thứ hai sẽ đặt action[2, =] = "reduce (R
→
L)"
⇒
Có sự đụng độ tại
action[2, =]. Vậy văn phạm trên không là văn phạm SLR(1).
2.3.4.4. Xây dựng bảng phân tích LR chuẩn.
* Mục LR(1) của văn phạm G là một cặp dạng [A
→
α• β
, a], trong đó A
→
α β
là luật sinh, a là một ký hiệu kết thúc hoặc $.
* Thuật toán xây dựng họ tập hợp mục LR(1)
Giải thuật: Xây dựng họ tập hợp các mục LR(1)
Input : Văn phạm tăng cường G’
Output: Họ tập hợp các mục LR(1).
Phương pháp: Các thủ tục closure, goto và thủ tục chính Items như sau:
Function Closure (I);
begin
Repeat
For Mỗi mục [A
→
α
•
B
β
,a] trong I, mỗi luật sinh B
→
γ
trong G' và mỗi
ký hiệu kết thúc b
∈
FIRST (
β
a) sao cho [B
→
•
γ
, b]
∉
I do
Thêm [ B
→
•
γ
, b] vào I;
Until Không còn mục nào có thể thêm cho I được nữa;
return I;
end;
Function goto (I, X);
begin
Gọi J là tập hợp các mục [A
→
α
X
•β
, a] sao cho [A
→
α•
X
β
, a]
∈
I;
return Closure(J);
end;
Procedure Items (G');
begin

C := Closure ({[S'
→
•
S, $]})
Repeat
For Mỗi tập các mục I trong C và mỗi ký hiệu văn phạm X
sao cho goto(I, X)
≠
∅
và goto(I, X)
∉
C do
Thêm goto(I, X) vào C;
Until Không còn tập các mục nào có thể thêm cho C;
end;
Ví dụ: Xây dựng bảng LR chính tắc cho văn phạm gia tố G' có các luật sinh sau :
S' S
(1)
S L = R3
(2)
S R
(3)
L * R
(4)
L id
(5) R L
Trong đó: tập ký hiệu chưa kết thúc ={S, L, R} và tập ký hiệu kết thúc {=, *, id, $}
I
0
: S'
→
•
S, $
Closure (S'
•
S, $) S
→
•
L = R, $
S
→
•
R, $
L
→
•
* R, = | $
L
→
•
id, = | $
R
→
•
L, $
Goto (I
0
,S) I
1
: S'
→
S
•
, $
Goto (I
0
, L) I
2
: S
→
L
•
= R, $
R
→
L
•
, $
Goto (I
0
,R) I
3
: S
→
R
•
, $
Goto (I
0
,*) I
4
: L
→
*
•
R, = | $
R
•
L, = | $
L
→
•
* R, = | $
R
→
•
id, = | $
Goto (I
0
,id) I
5
: L
→
id
•
, = | $
Goto (I
2
,=)
I
6
: S
→
L =
•
R, $
R
→
•
L, $
L
→
•
* R, $
L
→
•
id, $
Goto (I
4
,R) I
7
: L
→
* R
•
, = | $
Goto (I
4
, L) I
8
: R
→
L
•
, = | $
Goto (I
6
,R) I
9
: S
→
L = R
•
, $
Goto (I
6
,L) I
10
:R
→
L
•
, $
Goto (I
6
,*) I
11
:L
→
*
•
R, $
R
→
•
L, $
L
→
•
* R, $
R
→
•
id, $
Goto (I
6
, id) I
12
:L
→
id
•
, $
Goto (I
11
,R) I
13
:R
→
* R
•
, $
Goto (I
11
,L)
≡
I
10
Goto (I
11
,*)
≡
I
11
Goto (I
11
,id)
≡
I
12
* Thuật toán xây dựng bảng phân tích cú pháp LR chính tắc

Giải thuật: Xây dựng bảng phân tích LR chính tắc
Input:
Văn phạm tăng cường G'
Output
: Bảng LR với các hàm action và goto
Phương pháp:
1
. Xây dựng C = { I0, I1, .... In } là họ tập hợp mục LR(1)
2. Trạng thái thứ i được xây dựng từ Ii. Các action tương ứng trạng thái i
được xác định như sau:
2.1. Nếu [A
→ α •
a
β
,b]
∈
Ii và goto(Ii,a) = Ij thì action[i, a]= "shift
j". Ở đây a phải là ký hiệu kết thúc.
2.2. Nếu [A
→ α •,
a
] ∈
Ii , A
≠
S' thì action[i, a] = "reduce (A
→ α)
2.3. Nếu [S'
→
S
•
,$]
∈
Ii thì action[i, $] = "accept".
Nếu có một sự đụng độ giữa các luật nói trên thì ta nói
văn phạm không
phải là LR(1) và giải thuật sẽ thất bại.
3. Nếu goto(Ii, A) = Ij thì goto[i,A] = j
4. Tất cả các ô không xác định được bởi 2 và 3 đều là "error"
5. Trạng thái khởi đầu của bộ phân tích cú pháp được xây dựng từ tập các
mục chứa [S'
→ •
S,$]
Bảng phân tích xác định bởi giải thuật 4.9 gọi là bảng phân tích LR(1) chính tắc của văn
phạm G, bộ phân tích LR sử dụng bảng LR(1) gọi là bộ phân tích LR(1) chính tắc và văn phạm
có một bảng LR(1) không có các action đa trị thì được gọi là văn phạm LR(1).
Ví dụ : Xây dựng bảng phân tích LR chính tắc cho văn phạm ở ví dụ trên
Trạng
thái
Action
Goto
=
*
id
$
S
L
R
0
s
4
s
5
1
2
3
1
acc
2
s
6
r
5
3
r
2
4
s
4
s
5
8
7
5
r
4
6
s
11
s
12
10
9
7
r
3
8
r
5
9
r
1
10
r
5
11
s
11
s
12
10
13

12
r
4
13
r
3
Hình 4.14 - Bảng phân tích cú pháp LR chính tắc
Mỗi văn phạm SLR(1) là một văn phạm LR(1), nhưng với một văn phạm SLR(1), bộ
phân tích cú pháp LR chính tắc có thể có nhiều trạng thái hơn so với bộ phân tích cú
pháp SLR cho văn phạm đó.
2.3.4.5. Xây dựng bảng phân tích LALR.
Phần này giới thiệu phương pháp cuối cùng để xây dựng bộ phân tích cú pháp LR - kỹ
thuật LALR (Lookahead-LR), phương pháp này thường được sử dụng trong thực tế bởi vì những
bảng LALR thu được nói chung là nhỏ hơn nhiều so với các bảng LR chính tắc và phần lớn các
kết cấu cú pháp của ngôn ngữ lập trình đều có thể được diễn tả thuận lợi bằng văn phạm LALR.
a. Hạt nhân (core) của một tập hợp mục LR(1)
1. Một tập hợp mục LR(1) có dạng {[A
→
α• β
, a]}, trong đó A
→
α β
là một
luật sinh và a là ký hiệu kết thúc có hạt nhân (core) là tập hợp {A
→
α
•β
}.
2. Trong họ tập hợp các mục LR(1) C = {I
0
, I
1
, ..., I
n
} có thể có các tập hợp các
mục có chung một hạt nhân.
Ví dụ : Trong ví dụ 4.25, ta thấy trong họ tập hợp mục có một số các mục có chung hạt
nhân là :
I4 và I11
I5 và I12
I7 và I13
I8 và I10
b. Thuật toán xây dựng bảng phân tích cú pháp LALR
Giải thuậ: Xây dựng bảng phân tích LALR
Input:
Văn phạm tăng cường G'
Output:
Bảng phân tích LALR
Phương pháp:
1
. Xây dựng họ tập hợp các mục LR(1) C = {I0, I1, ..., In }
2. Với mỗi hạt nhân tồn tại trong tập các mục LR(1) tìm trên tất cả các tập hợp
có cùng hạt nhân này và thay thế các tập hợp này bởi hợp của chúng.
3. Ðặt C' = {I0, I1, ..., Im } là kết quả thu được từ C bằng cách hợp các tập
hợp có cùng hạt nhân. Action tương ứng với trạng thái i được xây dựng từ Ji
theo cách thức như giải thuật 4.9.
Nếu có một sự đụng độ giữa các action thì giải thuật xem như thất bại và ta
nói văn phạm không phải là văn phạm LALR(1).
4. Bảng goto được xây dựng như sau
Giả sử J = I1
∪
I2
∪
...
∪
Ik . Vì I1, I2, ... Ik có chung một hạt nhân nên goto
(I1,X), goto (I2,X), ..., goto (Ik,X) cũng có chung hạt nhân. Ðặt K bằng hợp tất
cả các tập hợp có chung hạt nhân với goto (I1,X) ( goto(J, X) = K.
Ví dụ : Với ví dụ trên, ta có họ tập hợp mục C' như sau
C' = {I
0
, I
1
, I
2
, I
3
, I
411
, I
512
, I
6
, I
713
, I
810
, I
9
}
I
0
: S'
→
•
S, $
closure (S'
•
S, $) : S
→
•
L = R, $
S
→
•
R, $
L
→
•
* R, =
L
→
•
id, =
R
→
•
L, $
I
1
= Goto (I
0
,S) : S'
→
S
•
, $
I
2
= Goto (I
0
, L) : S
→
L
•
= R,
$
R
→
L
•
, $
I
3
= Goto (I
0
,R) : S
→
R
•
I
411
= Goto (I
0
,*), Goto (I
6
,*) :
L
→
*
•
R, = | $
R
→
•
L, = | $
L
→
•
* R, = | $
R
→
•
id, = | $
I
512
= Goto (I
0
,id), Goto (I
6
,id) :
L
→
id
•
, = | $
I
6
= Goto(I
2
,=) :
S
→
L =
•
R,$
R
→
•
L, $
L
→
•
* R, $
L
→
•
id, $
I
713
= Goto(I
411
, R) :
L
→
* R
•
, = | $
I
810
= Goto(I
411
, L), Goto(I
6
, L):
R
→
L
•
, = | $
I
9
= Goto(I
6
, R) :
S
→
L = R
•
, $
Ta có thể xây dựng bảng phân tích cú pháp LALR cho văn phạm như sau :
State
Action
Goto
=
*
id
$
S
L
R
0
s
411
s
512
1
2
3
1
acc
2
s
6
3
r
2
411
810
713
512
r
4
r
4
6
s
411
s
512
810
9
713
r
3
r
3
810
r
5
r
5
9
r
1
Hình - Bảng phân tích cú pháp LALR
Bảng phân tích được tạo ra bởi giải thuật 4.10 gọi là bảng phân tích LALR cho văn phạm G.
Nếu trong bảng không có các action đụng độ thì văn phạm đã cho gọi là văn phạm LALR(1). Họ
tập hợp mục C' được gọi là họ tập hợp mục LALR(1).
2.4. Bắt lỗi.
* Giai đoạn phân tích cú pháp phát hiện và khắc phục được khá nhiều
lỗi. Ví dụ lỗi do các từ tố từ bộ phân tích từ vựng không theo thứ tự của luật
văn phạm của ngôn ngữ.
* Bộ bắt lỗi trong phần phân tích cú pháp có mục đích:
+ Phát hiện, chỉ ra vị trí và mô tả chính xác rõ rang các lỗi.
+ Phục hồi quá trìh phân tích sau khi gặp lỗi đủ nhanh để có thể phát
hiện ra các lỗi tiếp theo.
+ Không làm giảm đáng kể thời gian xử lý các chương trình viết đúng.
* Các chiến lược phục hồi lỗi.
- Có nhiều chiến lược mà bộ phân tích có thể dùng để phục hồi quá
trình phân tích sau khi gặp một lỗi cú pháp. Không có chiến lược nào tổng
quát và hoàn hảo, có một số phương pháp dùng rộng rãi.
+ Phục hồi kiểu trừng phạt: Phương pháp đơn giản nhất và được áp
dụng trong đa số các bộ phân tích. Mỗi khi phát hiện lỗi bộ phân tích sẽ bỏ
qua một hoặc một số kí hiệu vào mà không kiểm tra cho đến khi nó gặp một kí
hiệu trong tập từ tố đồng bộ. Các từ tố đồng bộ thường được xác định trước
( VD: end, ; )
Người thiết kế chương trình dịch phải tự chọn các từ tố đồng bộ.
Ưu điểm: Đơn giản, không sợ bj vòng lặp vô hạn, hiệu quả khi gặp câu
lệnh có nhiều lỗi.
+ Khôi phục cụm từ: Mỗi khi phát hienj lỗi, bộ phân tích cố gắng phân
tích phần còn lại của câu lệnh. Nó có thể thay thế phần đầu của phần còn lại
xâu này bằng một xâu nào đó cho phép bộ phân tích làm việc tiếp. Những việc
này do người thiết kế chương trình dịch nghĩ ra.
+ Sản xuất lỗi: Người thiết kế phải có hiểu biết về các lỗi hường gặp và
gia cố văn phạm của ngôn ngữ này tại các luật sinh ra cấu trúc lỗi. Dùng văn
phạm này để khôi phục bộ phân tích. Nếu bọ phân tích dùng một luật lỗi có
thể chỉ ra các cấu trúc lỗi phát hiện ở đầu vào.
Ngoài ra ngừơi ta có cách bắt lỗi cụ thể hơn trong từng phương pháp phân
tích khác nhau.
2.4.1. Khôi phục lỗi trong phân tích tất định LL.
* Một lỗi được phát hiện trong phân tích LL khi:
- Ký hiệu kết thúc nằm trên đỉnh ngăn xếp không đối sánh được với ký hiệu
đầu vào hiện tại.
- Mục M(A,a) trong bảng phân tích là lỗi (rỗng).
* Khắc phục lỗi theo kiểu trừng phạt là bỏ qua các ký hiệu trên xâu vào cho
đến khi xuất hiện một ký hiệu thuộc tập ký hiệu đã xác định trước gọi là tập ký hiệu
đồng bộ. Xét một số cách chọn tập đồng bộ như sau:
a)
Đưa tất cả các ký hiệu trong Follow(A) vào tập đồng bộ hoá của ký
hiệu không kết thúc A. Nếu gặp lỗi, bỏ qua các từ tố của xâu vào cho đến khi gặp
một phần tử của Follow(A) thì lấy A ra khỏi ngăn xếp và tiếp tục quá trình phân tích.
b)
Đưa tất cả các ký hiệu trong First(A) vào tập đồng bộ hoá của ký hiệu
không kết thúc A. Nếu gặp lỗi, bỏ qua các từ tố của xâu vào cho đến khi gặp một
phần tử thuộc First(A) thì quá trình phân tích được tiếp tục.
Ví dụ: với ví dụ trên, ta thử phân tích xâu vào có lỗi là “)id*+id” với tập đồng bộ
hoá của các ký hiệu không kết thúc được xây dựng từ tập First và tập Follow của
ký hiệu đó.
Ngăn xếp
Xâu vào
Hành động
$E
)id*+id$
M(E,)) = lỗi, bỏ qua ‘)’ để găp id
∈
First(E)
$E
id*+id$
E->TE’
$E’T
id*+id$
T->FT’
$E’T’F
id*+id$
F->id
$E’T’id
id*+id$
rút gọn id
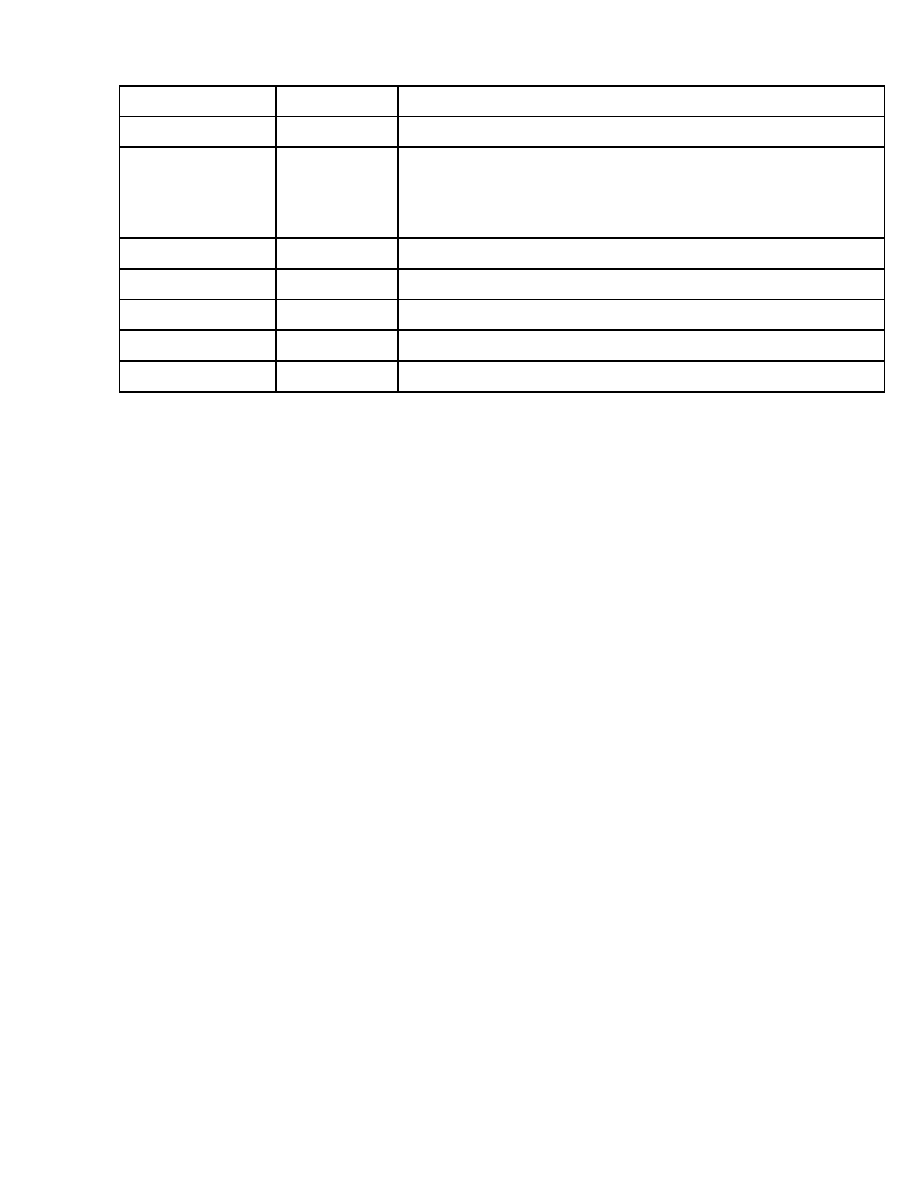
$E’T’
*+id$
T’->*FT’
$E’T’F*
*+id$
rút gọn *
$E’T’F
+id$
M(F,+) = lỗi, bỏ qua. Tại đây xảy ra hai trường hợp(ta
chọn a): a).bỏ qua + vì id
∈
First(F)
b).bỏ qua F vì +
∈
Follow(F)
$E’T’F
id$
F->id
$E’T’id
id$
rút gọn id
$E’T’
$
T’->
ε
$E’
$
E’->
ε
$
$
2.4.2. Khôi phục lỗi trong phân tích LR.
Một bộ phân tích LR sẽ phát hiện ra lỗi khi nó gặp một mục báo lỗi trong
bảng action (chú ý sẽ không bao giờ bộ phân tích gặp thông báo lỗi trong bảng
goto). Chúng ta có thể thực hiện chiến lược khắc phục lỗi cố gắng cô lập đoạn câu
chứa lỗi cú pháp: quét dọc xuống ngăn xếp cho đến khi tìm được một trạng thái s
có một hành động goto trên một ký hiệu không kết thúc A ngay sau nó. Sau đó bỏ
đi không hoặc nhiều ký hiệu đầu vào cho đến khi gặp một ký hiệu kết thúc a thuộc
Follow(A), lúc này bộ phân tích sẽ đưa trạng thái goto(s,A) vào ngăn xếp và tiếp
tục quá trình phân tích.
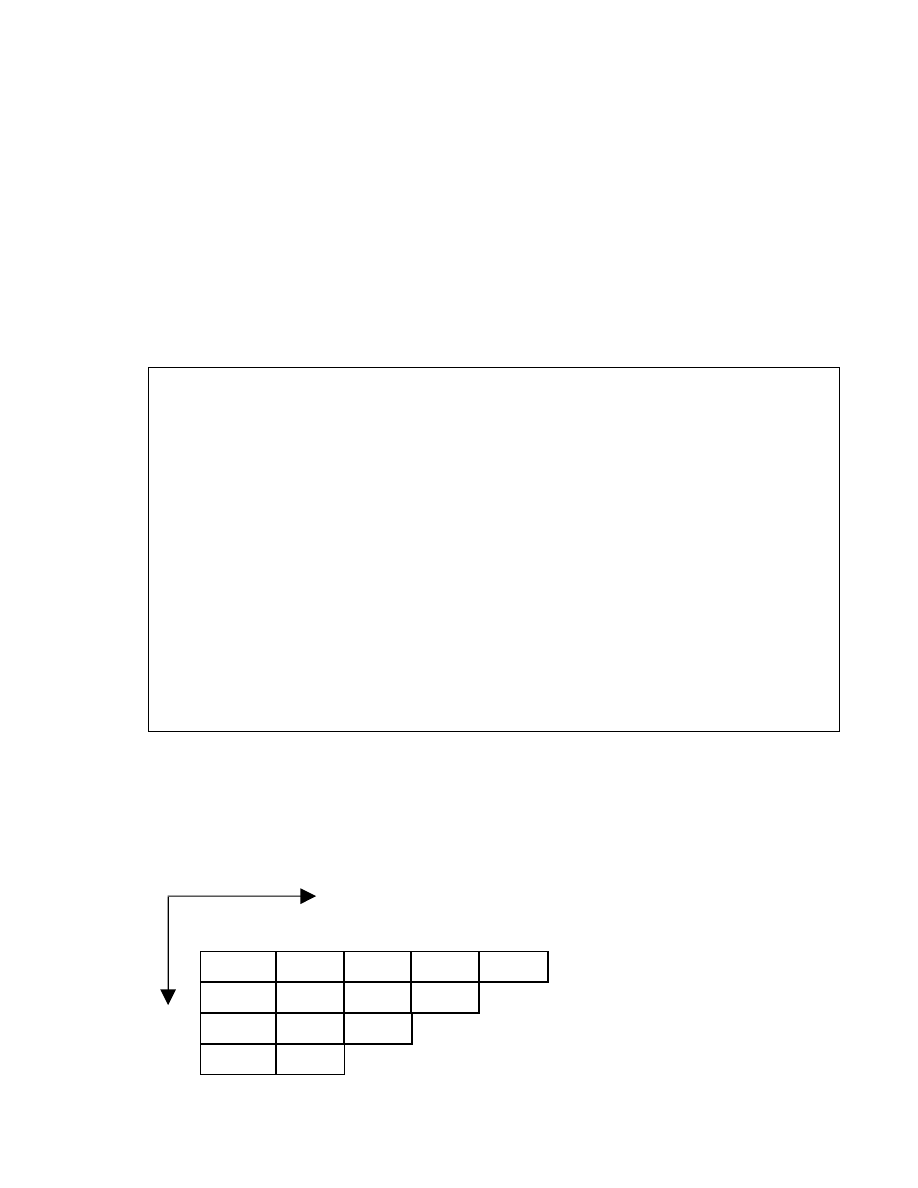
Phương pháp phân tích bảng CYK (Cocke – Younger – Kasami)
- Giải thuật làm việc với tất cả các VP PNC. Thời gian phân tích là: n
3
(n là
độ dài xâu vào cần phân tích), nếu văn phạm không nhập nhằng thì thờI gian phân
tích là: n
2
.
- Điều kiện của thuật toán là văn phạm PNC ở dạng chuẩn chômsky (CNF)
và không có
ε
sản xuất (sản xuất A
→
ε
) và các kí hiệu vô ích.
Giải thuật CYK:
- Tạo một hình tam giác (mỗi chiều có độ dài là n , n là độ dài của xâu).
Thực hiện giải thuật:
Begin
1) For i:=1 to n do
∆
ij
= { A | A
→
a là một sản xuất và a là kí hiệu thứ i trong w};
2) For j:=2 to n do
For i:=1 to (n – j +1) do
Begin
∆
ij
=
∅
;
For k:=1 to (j -1) do
∆
ij
=
∆
ij
∪
{ A | A
→
BC là một sản xuất; B
∈
∆
ik
C
∈
∆
i+k, j -k
};
end;
end;
Ví dụ: Xét văn phạm chuẩn chômsky
S
→
AB|BC; A
→
BA|a; B
→
CC|b; C
→
AB|a;
(1) (2) (3) (4) (5) (6) (7) (8)
Xâu vào w= baaba;
i
j
b a a b a
B
A,C
A,C
B
A,C
S,A
B
S,C
S,A
∅
B
B
∅
S,A,C
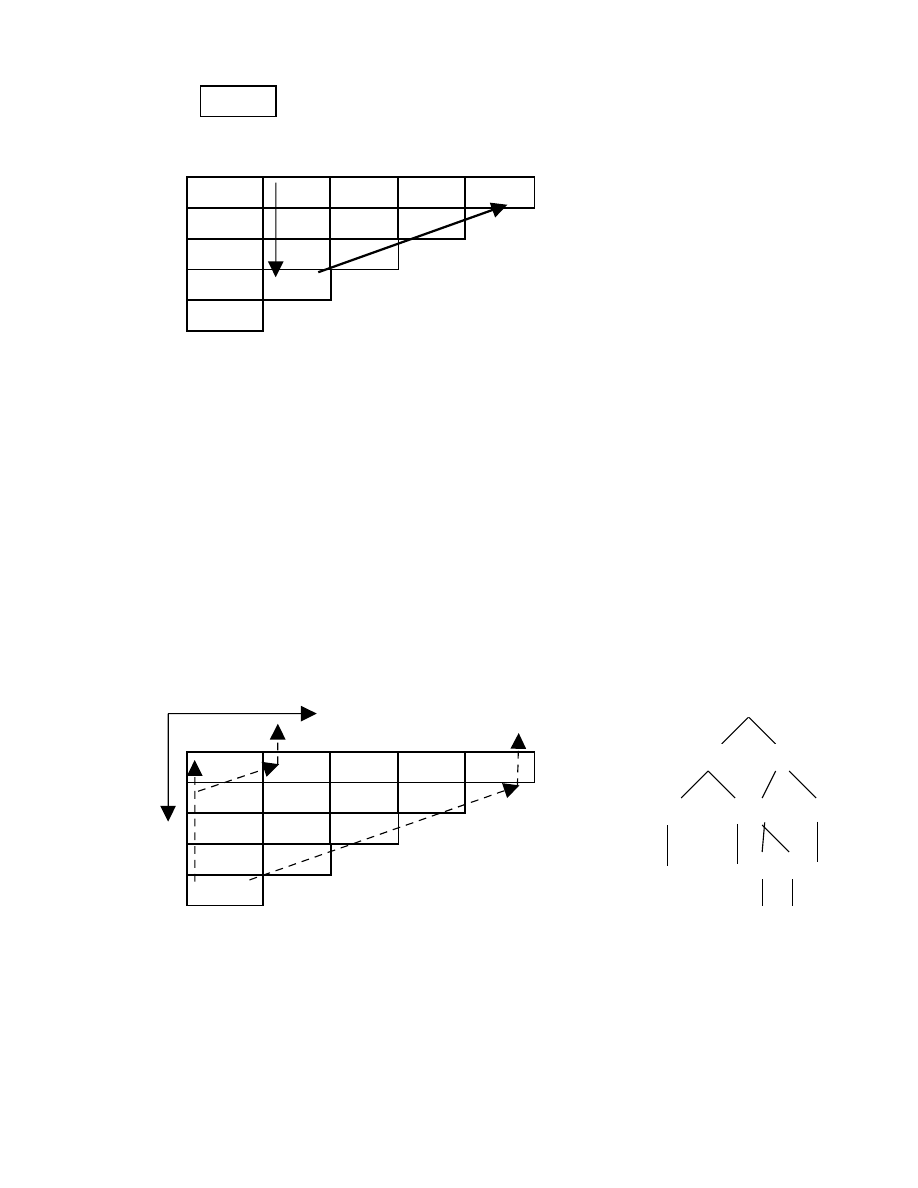
S,A,C
b a a b a
B
A,C
A,C
B
A,C
S,A
B
S,C
S,A
∅
B
B
∅
S,A,C
S,A,C
- Quá trình tính
∆
ij
. VD: tính
∆
24
, Tính:
∆
21 =
{A,C},
∆
33
= {B},
∆
21
∆
33
= {AB,CB} Do (1), (7) nên đưa S,C vào
∆
24
.
∆
22 =
{B},
∆
42
= {S,A},
∆
22
∆
42
= {BS,BA} Do (3) nên đưa A vào
∆
24
.
∆
23 =
{B},
∆
51
= {A,C},
∆
23
∆
51
= {BA,BC} (2),(3) nên đưa S,C vào
∆
24
.
Kết quả:
∆
24
= {S,A,C}.
- Nếu S ở ô cuối cùng thì ta kết luận: Xâu vào phân tích thành công và có
thể dựng được cây phân tích cho nó. Số lượng cây phân tích = số lượng S có
trong ô này.
b a a b a
B
A,C
A,C
B
A,C
S,A
B
S,C
S,A
∅
B
B
∅
S,A,C
S,A,C
A
B
S
B
B
A C
C
b
a
C
A B a
a
b

Bài tập
Luyện tập:
cho văn phạm
E -> T + E | T
T -> a
Hãy xây dựng bảng SLR(1) cho văn phạm trên
Thực hành: Thử nghiệm trên văn phạm biểu thức nêu trên
1) xây dựng tập LR(0) tự động
2) xây dựng bảng phân tích SLR(1) tự động
3) phân tích xâu vào

CHƯƠNG 5 BIÊN DỊCH DỰA CÚ PHÁP.
1. MỤC ĐÍCH, NHIỆM VỤ.
- Các hành động dịch phụ thuộc rất nhiều vào cú pháp của chương trình nguồn
cần dịch.Quá trình dịch được điều khiển theo cấu trúc cú pháp của chương
trình nguồn, cú pháp này được xác định thông qua bộ phân tích cú pháp.
- Nhằm điều khiển các phần hoạt động theo cú pháp, cách thường dùng là gia
cố các luật sản xuất ( mà ta biết cụ thể những luật nào và thứ tự thực hiện ra
sao thông qua cây phân tích) bằng cách thêm các thuộc tính cho văn phạm
đấy, và các qui tắc sinh thuộc tính gắn với từng luật cú pháp. Các qui tắc đó,
ta gọi là qui tắc ngữ nghĩa (semantic rules).
- thực hiện các qui tắc ngữ nghĩa đó sẽ cho thông tin về ngữ nghĩa, dùng để
kiểm tra kiểu, lưu thông tin vào bảng ký hiệu và sinh mã trung gian.
- Có hai tiếp cận để liên kết (đặc tả) các qui tắc ngữ nghĩa vào các luật cú pháp
(sản xuất) là cú pháp điều khiển (syntax-directed definition) và lược đồ dịch
(translation scheme).
- Các luật ngữ nghĩa còn có các hành động phụ (ngoài việc sinh thuộc tính cho
các ký hiệu văn phạm trong sản xuất) như in ra một giá trị hoặc cập nhật một
biến toàn cục.
Các kiến thức trong phần này không nằm trong khối chức năng riêng rẽ nào của chương
trình dịch mà được dùng làm cơ sở cho toàn bộ các khối nằm sau khối phân tích cú pháp.
Một xâu vào
→
Cây phân tích
→
Đồ thị phụ thuộc
→
thứ tựđánh giá cho các luật ngữ
nghĩa.
2. ĐỊNH NGHĨA CÚ PHÁP ĐIỀU KHIỂN.
Cú pháp điều khiển (syntax-directed definition) là một dạng tổng quát hoá của
văn phạm phi ngữ cảnh, trong đó mỗi ký hiệu văn phạm có một tập thuộc tính đi
kèm, được chia thành 2 tập con là thuộc tính tổng hợp (synthesized attribute) và
thuộc tính kế thừa (inherited attribute) của ký hiệu văn phạm đó.
Một cây phân tích cú pháp có trình bày các giá trị của các thuộc tính tại mỗi
nút được gọi là cây phân tích cú pháp có chú giải (hay gọi là cây phân tích đánh
dấu) (annotated parse tree).
2.1. Cú pháp điều khiển.
2.1.1. Dạng của định nghĩa cú pháp điều khiển.
Trong mỗi cú pháp điều khiển, mỗi sản xuất A->
α
có thể được liên kết với
một tập các qui tắc ngữ nghĩa có dạng b = f(c
1
, . . .,c
k
) với f là một hàm và
a)
b là một thuộc tính tổng hợp của A, còn c
1
, . . .,c
k
là các thuộc tính của các ký
hiệu trong sản xuất đó. Hoặc
b)
b là một thuộc tính kế thừa của một trong những ký hiệu ở vế phải của sản
xuất, còn c
1
, . . . ,c
k
là thuộc tính của các ký hiệu văn phạm.
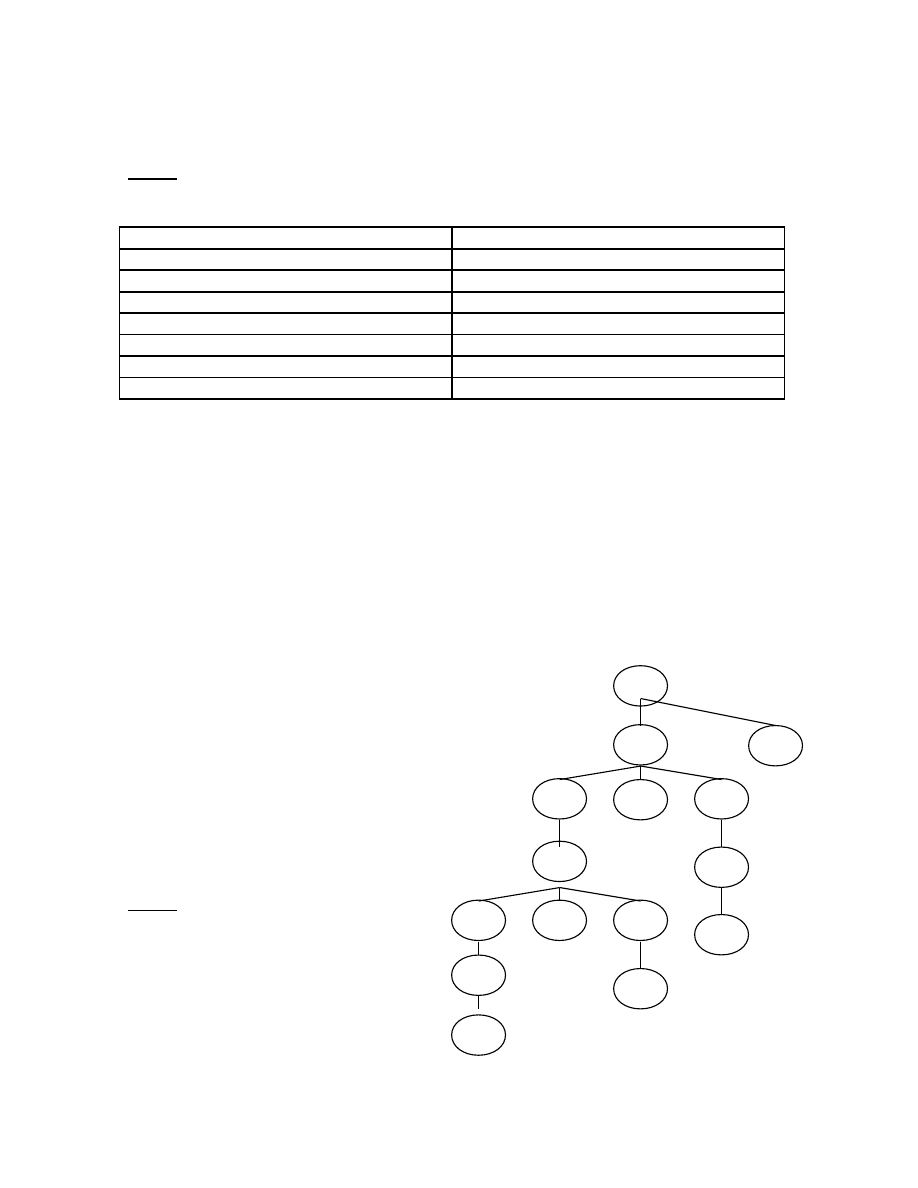
Ta nói là thuộc tính b phụ thuộc vào các thuộc tính c
1
, . . .,c
k.
- Một văn phạm thuộc tính (Attribute Grammar) là một cú pháp điều khiển
mà các luật ngữ nghĩa không có hành động phụ.
Ví dụ: Sau đây là văn phạm cho một chương trình máy tính bỏ túi với val là một
thuộc tính biểu diễn giá trị của ký hiệu văn phạm.
Sản xuất
Luật ngữ nghĩa
L -> E n
Print(E.val)
E -> E
1
+ T
E.val = E
1
.val + T.val
E -> T
E.val = T.val
T -> T
1
* F
T.val = T
1
.val * F.val
T -> F
T.val = F.val
F -> ( E )
F.val = E.val
F -> digit
F.val = digit.lexval
Từ tố digit có thuộc tính Lexval: là giá trị của digit đó được tính nhờ bộ phân tích từ vựng. Kí
hiệu n : xuống dòng, Print : in kết quả ra màn hình.
2.1.2. Thuộc tính tổng hợp.
Trên một cây phân tích, thuộc tính tổng hợp được tính dựa vào các thuộc ở
các nút con của nút đó, hay nói cách khác thuộc tính tổng hợp được tính cho các ký
hiệu ở vế trái của sản xuất và tính dựa vào thuộc tính của các ký hiệu ở vế phải.
Một cú pháp điều khiển chỉ sử dụng các thuộc tính tổng hợp được gọi là cú
pháp điều khiển thuần tính S (S-attribute definition).
Một cây phân tích cho văn phạm cú pháp điều khiển thuần tính S có thể thực
hiện các luật ngữ nghĩa theo hướng từ lá đến gốc và có thể sử dụng trong phương
pháp phân tích LR.
Ví dụ: vẽ cây cho đầu vào: 3*4+4n
ví dụ 1
Chúng ta duyệt và thực hiện các hành
động ngữ nghĩa của ví dụ trên theo đệ
qui
trên xuống: khi gặp một nút ta sẽ thực
hiện tính thuộc tính tổng hợp của các
con của nó rồi thực hiện hành động ngữ
nghĩa trên nút đó. Nói cách khác, khi phân tích cú pháp theo kiểu bottom-up, thì khi nào
L
E
1
E
2
T
3
T
1
T
2
*
F
2
F
1
3
+
F
3
n
4
4
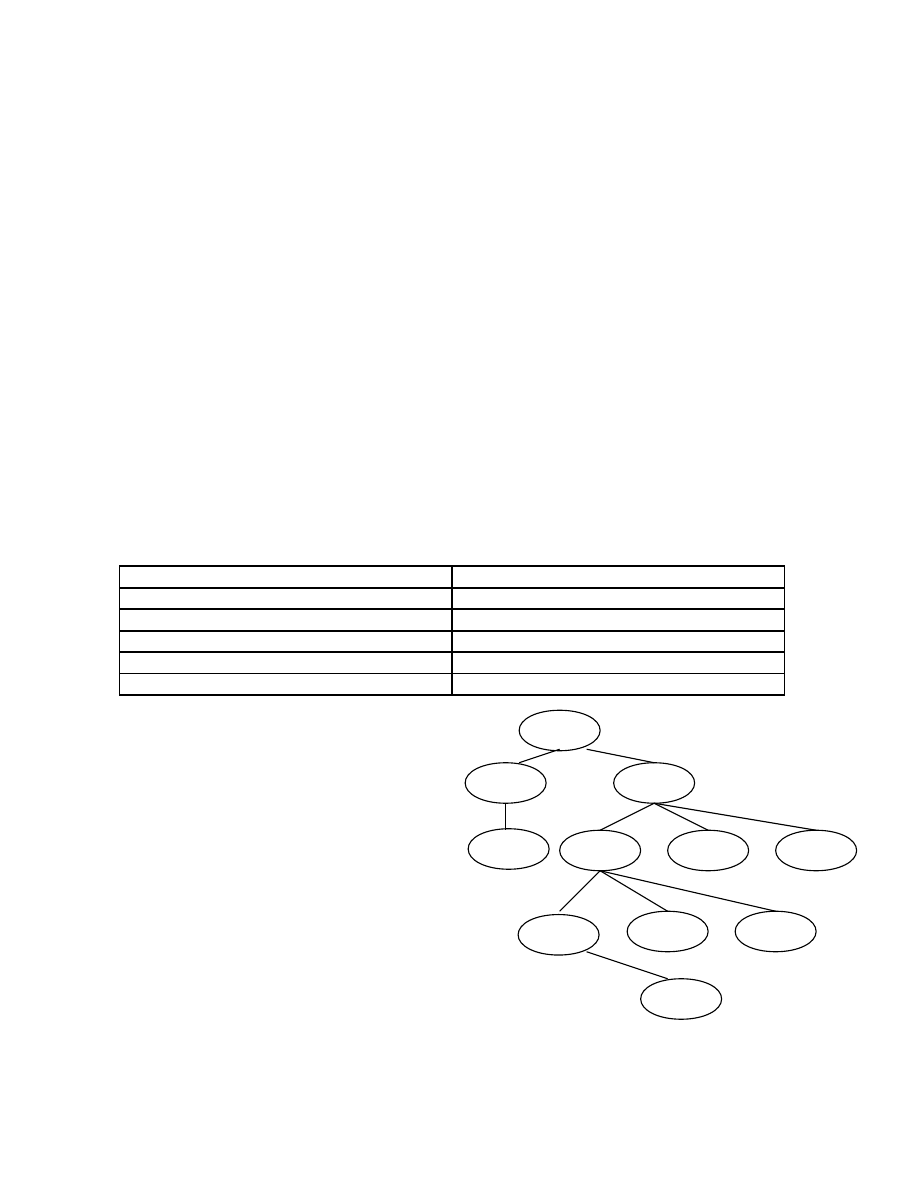
gặp hành động thu gọn, chúng ta sẽ thực hiện hành động ngữ nghĩa để đánh giá thuộc
tính tổng hợp.
F
1
.val=3 (syntax: F
1
->3 semantic: F
1
.val=3.lexical)
F
2
.val=4 (syntax: F
2
->3 semantic: F
2
.val=4.lexical)
T
2
.val=3 (syntax: T
2
->F
1
semantic: T
2
.val=F
1
.val )
T
1
.val=3*4=12 (syntax: T
1
->T
2
*F
2
semantic: T
1
.val=T
2
.val*F
2
.val)
F
3
.val=4 (syntax: F
3
->4 semantic: F
3
.val=4.lexical)
T
3
.val=4 (syntax: T
3
->F
3
semantic: T
3
.val=F
3
.val )
E
1
.val=12+4=16 (syntax: E
1
->E
2
+T
3
semantic: E
1
.val=E
2
.val+T
3
.val)
“16” (syntax: L->E
1
n semantic: print(E
1
.val))
2.1.3. Thuộc tính kế thừa.
Thuộc tính kế thừa (inherited attribute) là thuộc tính tại một nút có giá trị
được xác định theo giá trị thuộc tính của cha hoặc anh em của nó.
Thuộc tính kế thừa rất có ích trong diễn tả sự phụ thuộc ngữ cảnh. Ví dụ
chúng ta có thể xem một định danh xuất hiện bên trái hay bên phải của toán tử gán
để quyết định dùng địa chỉ hay giá trị của định danh.
Ví dụ về khai báo:
sản xuất
luật ngữ nghĩa
D -> T L
L.in := T.type
T -> int
T.type := interger
T -> real
T.type := real
L -> L
1
, id
L
1
.in := L.in ; addtype(id.entry, L.in)
L -> id
addtype(id.entry,L.in)
Ví dụ: int a,b,c Ta có cây cú pháp:
Chúng ta duyệt và thực hiện các hành
động ngữ nghĩa sẽ được kết quả như
sau:
T.type = interger (syntax:T->int semantic: T.type=interger)
L
1
.in = interger (syntax: D -> T L
1
semantic: L
1
.in=T.type)
D
T
L
1
int
L
2
a
,
L
3
b
,
c

L
2
.in = interger (syntax: L
1
-> L
2
, a semantic: L
2
.in = L
1
.in )
a.entry = interger (syntax: L
1
-> L
2
, a semantic: addtype(a.entry,L
1
.in) )
L
3
.in = interger (syntax: L
2
-> L
3
, b semantic: L
3
.in = L
2
.in )
b.entry = interger (syntax: L
2
-> L
3
, b semantic: addtype(b.entry,L
2
.in) )
c.entry = interger (syntax: L
3
-> c semantic: addtype(c.entry,L
3
.in) )
Bài luyện tập:
1) Cho văn phạm sau định nghĩa một số ở hệ cơ số 2
B -> 0 | 1 | B 0 | B 1
Hãy định nghĩa một cú pháp điều khiển để dịch một số ở hệ cơ số 2 thành một số ở hệ cơ số
10 (hay nói cách khác là tính giá trị của một số ở hệ cơ số 2). Xây dựng cây đánh dấu(xây
dựng cây cú pháp cùng với giá trị thuộc tính trên mỗi nút) với đầu vào là “1001”.
Mở rộng: sinh viên tự làm bài toán này với các sản xuất định nghĩa một số thực ở hệ cơ số 2:
S->L.L | L
L->LB | B
B->0 | 1
Lời giải: Định nghĩa thuộc tính tổng hợp val của ký hiệu B để chứa giá trị tính được của số
biểu diễn bởi B.
xuất phát từ cách tính:
(a
n
a
n-1
. . . a
1
a
0
)
2
:= a
n
*2
n
+a
n-1
*2
n-1
+. . . +a
1
*2+a
0
:= 2*(a
n
*2
n-1
+. . .+a
1
)+a
0
:= 2*(a
n
. . .a
1
)+a
0
Do đó nếu có
B -> B
1
1 thì B.val := 2*B
1
.val+1
B -> B
1
0 thì B.val := 2*B
1
.val
Vì vậy, chúng ta xây dựng các luật dịch như sau:
Luật phi ngữ cảnh
Luật dịch
B->0
B.val=0;
B->1
B.val:=1;
B->B
1
0
B.val:=2*B
1
.val +0
B->B 1
B.val:=2*B
1
.val+1
Cây đánh dấu:
1
0
0
B
: val:=2*1+0=2
B
: val:=2*2+0=4
B
: val:=2*4+1=9

Xét một cây đánh dấu khác cho xâu vào “1011”
2.2. Đồ thị phụ thuộc.
Nếu một thuộc tính b tại một nút trong cây phân tích cú pháp phụ thuộc vào một
thuộc tính c, thế thì hành động ngữ nghĩa cho b tại nút đó phải được thực hiện sau khi
thực hiện hành động ngữ nghĩa cho c. Sự phụ thuộc qua lại của các thuộc tính tổng hợp
và kế thừa tại các nút trong một cây phân tích cú pháp có thể được mô tả bằng một đồ thị
có hướng gọi là đồ thị phụ thuộc (dependency graph).
- Đồ thị phụ thuộc là một đồ thị có hướng mô tả sự phụ thuộc giữa các thuộc
tính tại mỗi nút của cây phân tích cú pháp.
Trước khi xây dựng một đồ thị phụ thuộc cho một cây phân tích cú pháp,
chúng ta chuyển mỗi hành động ngữ nghĩa thành dạng b := f(c
1
,c
2
,. . .,c
k
) bằng cách
dùng một thuộc tính tổng hợp giả b cho mỗi hành động ngữ nghĩa có chứa một lời
gọi thủ tục. Đồ thị này có một nút cho mỗi thuộc tính, một cạnh đi vào một nút cho
b từ một nút cho c nếu thuộc tính b phụ thuộc vào thuộc tính c. Chúng ta có thuật
toán xây dựng đồ thị phụ thuộc cho một văn phạm cú pháp điều khiển như sau:
for mỗi nút n trong cây phân tích cú pháp do
for mỗi thuộc tính a của ký hiệu văn phạm tại n do
B
: val:=1
1
1
1
0
B
: val:=1
1
B
: val:=2*1+0=2
B
: val:=2*2+1=5
B
:
val:=5*2+1=11
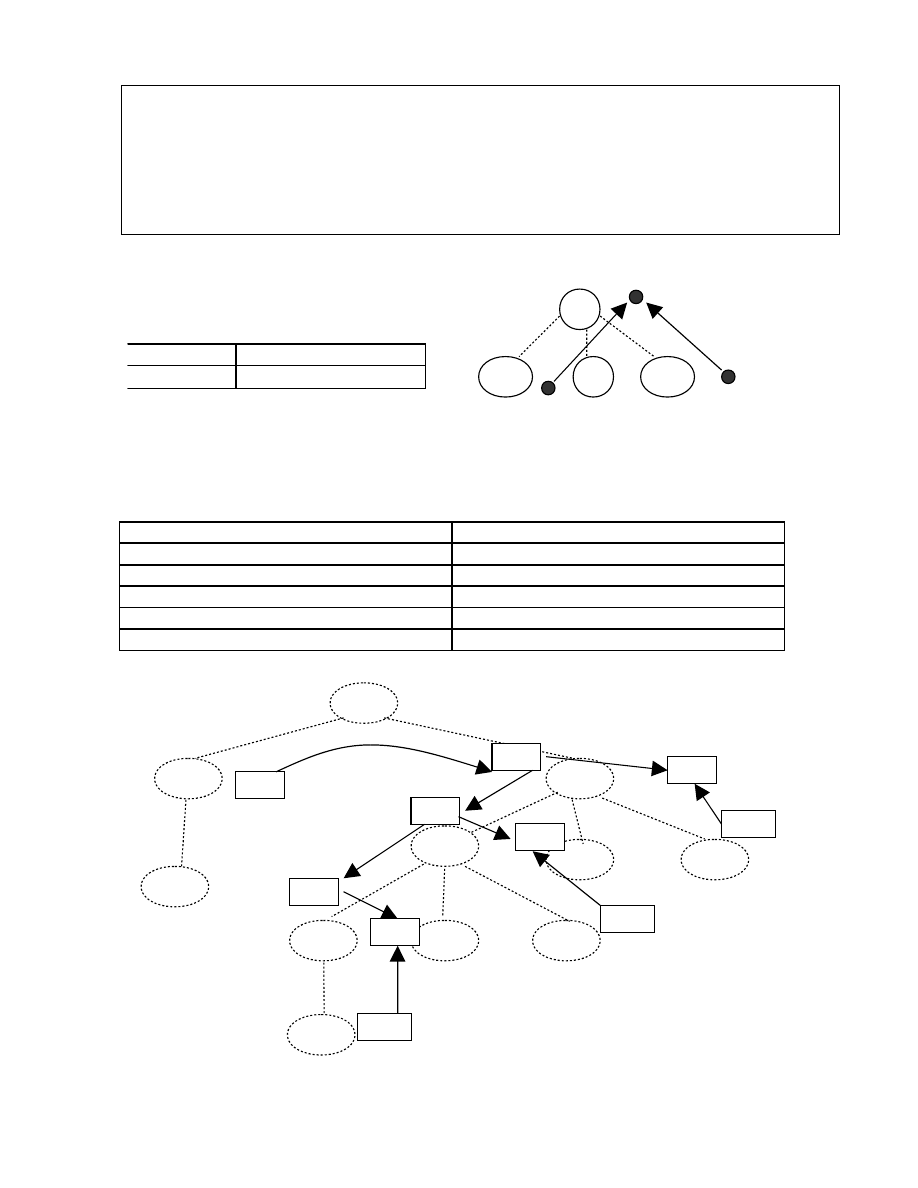
xây dựng một nút trong đồ thị phụ thuộc cho a;
for mỗi nút n trong cây phân tích cú pháp do
for mỗi hành động ngữ nghĩa b:=f(c
1
,c
2
, . . .,c
k
)
đi kèm với sản xuất được dùng tại n do
for i:=1 to k do
xây dựng một cạnh từ nút c
i
đến nút b
VD 1: Dựa vào cây phân tích ( nét đứt đoạn) và luật ngữ nghĩa ứng với sản xuất ở bảng, ta thêm
các nút và cạnh thành đồ thị phụ thuộc:
Ví dụ 2:
Với ví dụ 2, ta có một đồ thị phụ thuộc như sau:
chú ý:
+ chuyển hành động ngữ nghĩa addentry(id.entry,L.in) của sản xuất L->L , id thành thuộc tính giả
f phụ thuộc vào entry và in
sản xuất
luật ngữ nghĩa
D -> T L
L.in := T.type
T -> int
T.type := interger
T -> real
T.type := real
L -> L
1
, id
L
1
.in := L.in ; addtype(id.entry, L.in)
L -> id
addtype(id.entry,L.in)
D
T
L
rea
l
c
L
,
b
L
,
a
type
in
in
in
entry
entry
entry
f
f
f
Sản xuất
Luật ngữ nghĩa
E
→
E
1
| E
2
E.val = E
1
.val + E
2
.val
E
E
1
+
E
2
Val
Val

2.3. Thứ tự đánh giá thuộc tính.
Trên đồ thị DAG được xây dựng như ví dụ trên, chúng ta phải xác định thứ
tự của các nút để làm sao cho khi duyệt các nút theo thứ tự này thì một nút sẽ có
thứ tự sau nút mà nó phụ thuộc ta gọi là một sắp xếp topo. Tức là nếu các nút được
đánh thứ tự m
1
, m
2
, . . .,m
k
thì nếu có m
i
->m
j
là một cạnh từ m
i
đến m
j
thì m
i
xuất
hiện trước m
j
trong thứ tự đó hay i<j. Nếu chúng ta duyệt theo thứ tự đã được sắp
xếp này thì sẽ được một cách duyệt hợp lý cho các hành động ngữ nghĩa. Nghĩa là
trong một sắp xếp topo, giá trị các thuộc tính phụ thuộc c
1
,c
2
,
. . .
,c
k
trong một hành
động ngữ nghĩa b:=f(c
1
,c
2
,
. . .
,c
k
) đã được tính trước khi ta ước lượng f.
Đối với một đồ thị tổng quát, chúng ta phải để ý đến các đặc điểm sau:
+ xây dựng đồ thị phụ thuộc cho các thuộc tính của ký hiệu văn phạm phải
được xây dựng trên cây cú pháp. Tức là xây dựng cây cú pháp với mỗi nút (đỉnh)
đại diện cho một ký hiệu văn phạm sau đó mới xây dựng đồ thị phụ thuộc theo
thuật toán 5.1
+ trong đồ thị phụ thuộc, mỗi nút đại diện cho một thuộc tính của một ký
hiệu văn phạm.
+ có thể một loại thuộc tính này lại phụ thuộc vào một loại thuộc tính khác,
chứ không nhất thiết là chỉ các thuộc tính cùng loại mới phụ thuộc vào nhau. Trong
ví dụ trên, thuộc tính entry phụ thuộc vào thuộc tính in.
+ có thể có “vòng” trong đồ thị phụ thuộc, khi đó chúng ta sẽ không tính
được giá trị ngữ nghĩa cho các nút vì gặp một hiện tượng khi tính a cần tính b, mà
khi tính b lại cần tính a.
Chính vì vậy, trong thực tế chúng ta chỉ xét đến văn phạm cú pháp ngữ nghĩa
mà đồ thị phụ thuộc của nó là một DAG không có vòng.
Đối với ví dụ trên, chúng ta xây dựng được một thứ tự phụ thuộc trên các
thuộc tính đối với cây cú pháp cho câu vào “real a,b,c” như sau:
D
T
L
rea
l
c
L
,
b
,
type: 4
in: 5
in: 7
in: 8
entry: 3
entry: 2
f: 8
f: 6
f: 9

Sau khi chúng ta đã có đồ thị phụ thuộc này, chúng ta thực hiện các hành động ngữ
nghĩa theo thứ tự như sau (ký hiệu a
i
là giá trị thuộc tính ở nút thứ i):
- đối với nút 1,2 ,3 chúng ta duyệt qua nhưng chưa thực hiện hành động ngữ
nghĩa nào cả
-
nút 4: ta có a
4
:= real
-
nút 5: a
5
:= a
4
:= real
-
nút 6: addtype(c.entry,a
5
) = addtype(c.entry,real)
-
nút 7: a
7
:= a
5
:= real
-
nút 8: addtype(b.entry,a
7
) = addtype(b.entry,real)
-
nút 9: addtype(a.entry,a
8
) = addtype(a.entry,real)
Các phương pháp duyệt hành động ngữ nghĩa
1.
Phương pháp dùng cây phân tích cú pháp. Kết quả trả về của phân tích cú
pháp phải là cây phân tích cú pháp, sau đó xây dựng một thứ tự duyệt hay
một sắp xếp topo của đồ thị từ cây phân tích cú pháp đó. Phương pháp này
không thực hiện được nếu đồ thị phụ thuộc có “vòng”.
2.
Phương pháp dựa trên luật. Vào lúc xây dựng trình biên dịch, các luật ngữ
nghĩa được phân tích (thủ công hay bằng công cụ) để thứ tự thực hiện các
hành động ngữ nghĩa đi kèm với các sản xuất được xác định trước vào lúc
xây dựng.
3.
Phương pháp quên lãng (oblivious method). Một thứ tự duyệt được lựa chọn
mà không cần xét đến các luật ngữ nghĩa. Thí dụ nếu quá trình dịch xảy ra
trong khi phân tích cú pháp thì thứ tự duyệt phải phù hợp với phương pháp
phân tích cú pháp, độc lập với luật ngữ nghĩa. Tuy nhiên phương pháp này
chỉ thực hiện trên một lớp các cú pháp điều khiển nhất định.
Phương pháp dựa trên qui tắc và phương pháp quên lãng không nhất thiết phải xây dựng một đồ
thị phụ thuộc, vì vậy nó rất là hiệu quả về mặt thời gian cũng như không gian tính toán.
Trong thực tế, các ngôn ngữ lập trình thông thường có yêu cầu quá trình phân tích là tuyến tính,
quá trình phân tích ngữ nghĩa phải kết hợp được với các phương pháp phân tích cú pháp tuyến
tính như LL, LR. Để thực hiện được điều này, các thuộc tính ngữ nghĩa cũng cần thoả mãn điều
kiện: một thuộc tính ngữ nghĩa sẽ được sinh ra chỉ phụ thuộc vào các thông tin trước nó. Chính
vì vậy chúng ta sẽ xét một lớp cú pháp điều khiển rất thông dụng và được sử dụng hiệu quả gọi
là cú pháp điều khiển thuần tính L.
Cú pháp điều khiển thuần tính L
Một thứ tự duyệt tự nhiên đặc trưng cho nhiều phương pháp dịch Top-down và Bottom-up
là thủ tục duyệt theo chiều sâu (depth-first order). Thủ tục duyệt theo chiều sâu được trình bày
như dưới đây:
procedure dfvisit(n:node);
L
a
entry: 1

begin
for mỗi con m của n tính từ trái sang phải do
begin
tính các thuộc tính kế thừa của m
dfvisit(m)
end
tính các thuộc tính tổng hợp của n
end
Một lớp các cú pháp điều khiển được gọi là cú pháp điều khiển thuần tính L hay gọi là
điều khiển thuần tính L (L-attributed definition) có các thuộc tính luôn có thể tính toán theo chiều
sâu.
Cú pháp điều khiển thuần tính L:
Một cú pháp điều khiển gọi là thuần tính L nếu mỗi thuộc tính kế thừa của X
i
ở vế phải của luật sinh A -> X
1
X
2
. . . X
n
với 1<=j<=n chỉ phụ thuộc vào:
1.
các thuộc tính của các ký hiệu X
1
, X
2
, . . .,X
j-1
ở bên trái của X
j
trong
sản xuất và
2.
các thuộc tính kế thừa của A
Chú ý rằng mỗi cú pháp điều khiển thuần tính S đều thuần tính L vì các điều
kiện trên chỉ áp dụng cho các thuộc tính kế thừa.
Ta thấy nếu ngôn ngữ mà ngữ nghĩa của một từ tố được xác định chỉ phụ
thuộc vào ngữ cảnh bên trái (các từ tố bên trái) thì một phương pháp duyệt cú pháp
từ trái sang phải cho đầu vào có thể kết hợp với điều khiển ngữ nghĩa để duyệt cả
cú pháp và ngữ nghĩa đồng thời. Từ đó, ta thấy cú pháp điều khiển thuần tính L
thoả mãn điều kiện này. Hay với cú pháp điều khiển thuần tính L, ta có thể duyệt
đầu vào từ trái sang phải để sinh các thông tin cú pháp và ngữ nghĩa một cách đồng
thời. Với phương pháp phân tích cú pháp tuyến tính LL và LR, ta có thể kết hợp để
thực hiện cả các hành động ngữ nghĩa thuần tính L.
Nhưng nếu mô tả các hành động ngữ nghĩa theo cú pháp điều khiển thì
không xác định thứ tự của các hành động trong một sản xuất. Vì vậy ở đây ta xét
một tiếp cận khác là dùng lược đồ dịch để mô tả luật ngữ nghĩa đồng thời với
thứ
tự
thực hiện chúng trong một sản xuất
.
Thực hiện hành động ngữ nghĩa trong phân tích LL
Thiết kế dịch là dịch một lượt: khi ta đọc đầu vào đến đâu thì chúng ta sẽ
phân tích cú pháp đến đó và thực hiện các hành động ngữ nghĩa luôn.
Một phương pháp xây dựng chương trình phân tích cú pháp kết hợp với thực
hiện các hành động ngữ nghĩa như sau:
- với mỗi một ký hiệu không kết thúc được gắn với một hàm thực hiện. Giả sử
với ký hiệu không kết thúc A, ta có hàm thực hiện
void ParseA(Symbol A);

- mỗi ký hiệu kết thúc được gắn với một hàm đối sánh xâu vào
-
giả sử ký hiệu không kết thúc A là vế trái của luật A->
α
1
|
α
2
| . . . |
α
n
Như vậy hàm phân tích ký hiệu A sẽ được định nghĩa như sau:
void ParseA(Symbol A, Rule r, ...)
{
if(r==A->
α
1
)
gọi hàm xử lý ngữ nghĩa tương ứng luật A->
α
1
else if(r==A->
α
2
)
gọi hàm xử lý ngữ nghĩa tương ứng luật A->
α
2
. . .
else if(r==A->
α
n
)
gọi hàm xử lý ngữ nghĩa tương ứng luật A->
α
n
}
Đối chiếu ký hiệu đầu vào và A, tìm trong bảng phân tích LL xem sẽ khai
triển A theo luật nào. Chẳng hạn ký hiệu xâu vào hiện thời a
∈
first(
α
i
),
chúng ta sẽ khai triển A theo luật A -> X
1
. . . X
k
với
α
i
= X
1
. . . X
k
Ở đây, ta sẽ sử dụng lược đồ dịch để kết hợp phân tích cú pháp và ngữ nghĩa.
Do đó đó khi khai triển A theo vế phải, ta sẽ gặp 3 trường hợp sau:
1. nếu phần tử đang xét là một ký hiệu kết thúc, ta gọi hàm đối sánh với xâu
vào, nếu thoả mãn thì nhẩy con trỏ đầu vào lên một bước, nếu trái lại là
lỗi.
2. nếu phần tử đang xét là một ký hiệu không kết thúc, chúng ta gọi hàm
duyệt ký hiệu không kết thúc này với tham số bao gồm các thuộc tính của
các ký hiệu anh em bên trái, và thuộc tính kế thừa của A.
3. nếu phần tử đang xét là một hành động ngữ nghĩa, chúng ta thực hiện
hành động ngữ nghĩa này.
Ví dụ:
E -> T {R.i:=T.val}
R {E.val:=R.s}
R -> +
T {R
1
.i:=R.i+T.val}
R
1
{R.s:=R
1
.s}
R ->
ε
{R.s:=R.i}
T -> ( E ) {T.val:=E.val}
T -> num {T.val:=num.val}
void ParseE(...)
{
// chỉ có một lược đồ dịch:
// E -> T {R.i:=T.val}
// R {E.val:=R.s}
ParseT(...);
R.i := T.val
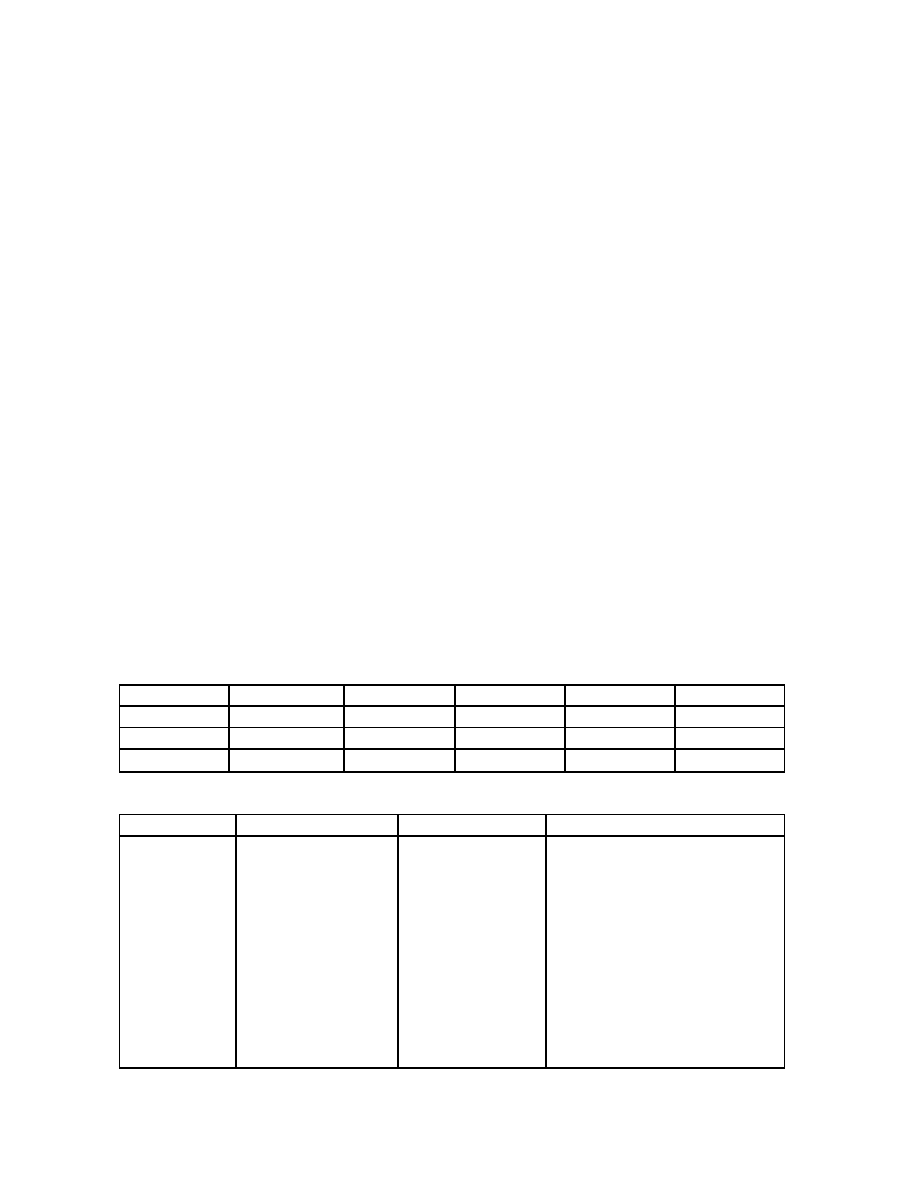
ParseR(...);
E.val := R.s
}
void ParseR(...)
{
// trường hợp 1
//R -> +
//T {R1.i:=R.i+T.val}
//R1 {R.s:=T.val+R1.i}
if(luật=R->TR
1
)
{
match(‘+’);// đối sánh
ParseT(...); R
1
.i:=R.i+T.val;
ParseR(...); R.s:=R
1
.s
}
else if(luật=R->
ε
)
{ // R ->
ε
{R.s:=R.i}
R.s:=R.i
}
}
Tương tự đối với hàm ParseT()
Bây giờ ta xét xâu vào: “6+4”
First(E)=First(T) = {(,num}
First(R) = {
ε
,+}
Follow(R) = {$,)}
Xây dựng bảng LL(1)
num
+
(
)
$
E
E->TR
E->TR
T
T->num
T->(E)
R
R->+TR
R->
ε
R->
ε
Đầu vào “6+4”, sau khi phân tích từ vựng ta được “num1 + num2”
Ngăn xếp
Đầu vào
Luật sản xuất
Luật ngữ nghĩa
$E
$RT
$Rnum1
$R
$R
1
T+
$R
1
T
$R
1
num2
$R
1
$
num1 + num2 $
num1 + num2 $
num1 + num2 $
+ num2 $
+ num2 $
num2 $
num2 $
$
$
E->TR
T->num1
R->+TR
1
T->num2
R
1
->
ε
T.val=6
R.i=T.val=6
T.val=4
R
1
.i=T.val=4
R
1
.s=T.val+R
1
.i=10
R.s=R
1
.s=10
E.val=R.s=10
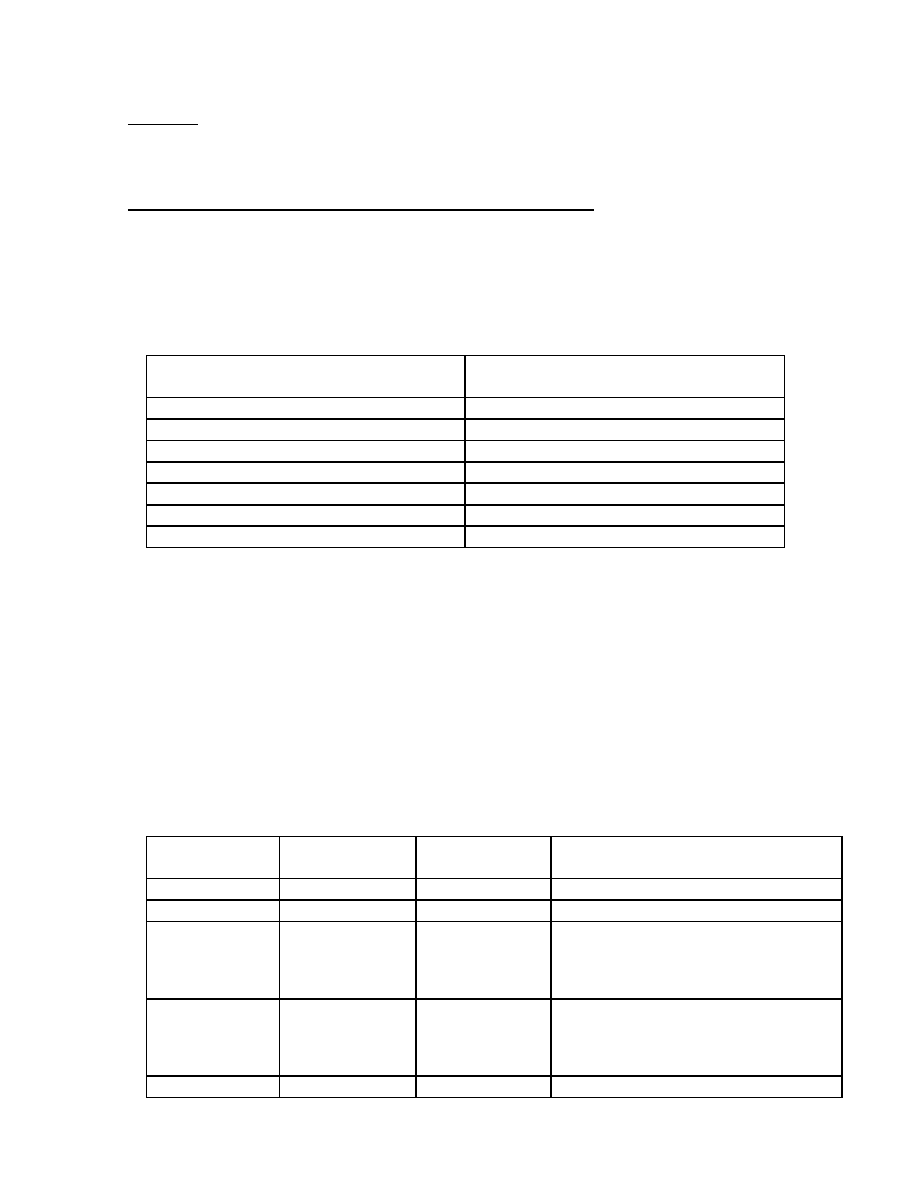
Nhận xét:
Mọi cú pháp điều khiển thuần tính L dựa trên văn phạm LL(1) đều có thể kết hợp quá
trình phân tích cú pháp tuyến tính với việc thực hiện các hành động ngữ nghĩa.
Thực hiện hành động ngữ nghĩa trong phân tích LR
Đối với cú pháp điều khiển thuần tính S (chỉ có các thuộc tính tổng hợp), tại mỗi
bước thu gọn bởi một luật, chúng ta thực hiện các hành động ngữ nghĩa tính thuộc tính
tổng hợp của vế trái dựa vào các thuộc tính tổng hợp của các ký hiệu vế phải đã được
tính.
Ví dụ, đối với cú pháp điều khiển tính giá trị biểu thức cho máy tính bỏ túi:
Luật cú pháp
Luật ngữ nghĩa (luật dịch)
L->E n
print(E.val)
E->E
1
+T
E.val:=E
1
.val+T.val
E->T
E.val:=T.val
T->T
1
*F
T.val:=T
1
.val*F.val
T->F
T.val:=F.val
F->(E)
F.val:=E.val
F->digit
F.val:=digit.lexval
Chẳng hạn chúng ta sẽ thực hiện các luật ngữ nghĩa này bằng cách sinh ra thêm một
ngăn xếp để lưu giá trị thuộc tính val cho các ký hiệu (gọi là ngăn xếp giá trị). Mỗi khi
trong ngăn xếp trạng thái có ký hiệu mới, chúng ta lại đặt vào trong ngăn xếp giá trị
giá trị thuộc tính val cho ký hiệu mới này. Còn nếu khi ký hiệu bị loại bỏ ra khỏi ngăn
xếp trạng thái thì chúng ta cũng loại bỏ giá trị tương ứng với nó ra khỏi ngăn xếp giá
trị. Chúng ta có thể xem qua quá trình phân tích gạt, thu gọn với ví dụ cho xâu vào
“3*5+4”:
chú ý:
+ phân tích từ tố cho ta kết quả xâu vào là (ký hiệu d là digit):
d1(3)*d2(5)+d3(4)n
+ với ký hiệu không có giá trị val, chúng ta ký hiệu ‘-‘ cho val của nó
xâu vào
ngăn xếp trạng
thái
ngăn xếp giá
trị
luật cú pháp, ngữ nghĩa
d1 * d2 + d3 n
gạt
* d2 + d3 n
d1
3
F->digit
* d2 + d3 n
F
3
F.val:=digit.lexval
(loại bỏ digit)
T->F
* d2 + d3 n
T
3
T.val:=F.val
(loại bỏ F)
gạt
d2 + d3 n
* T
- 3
gạt
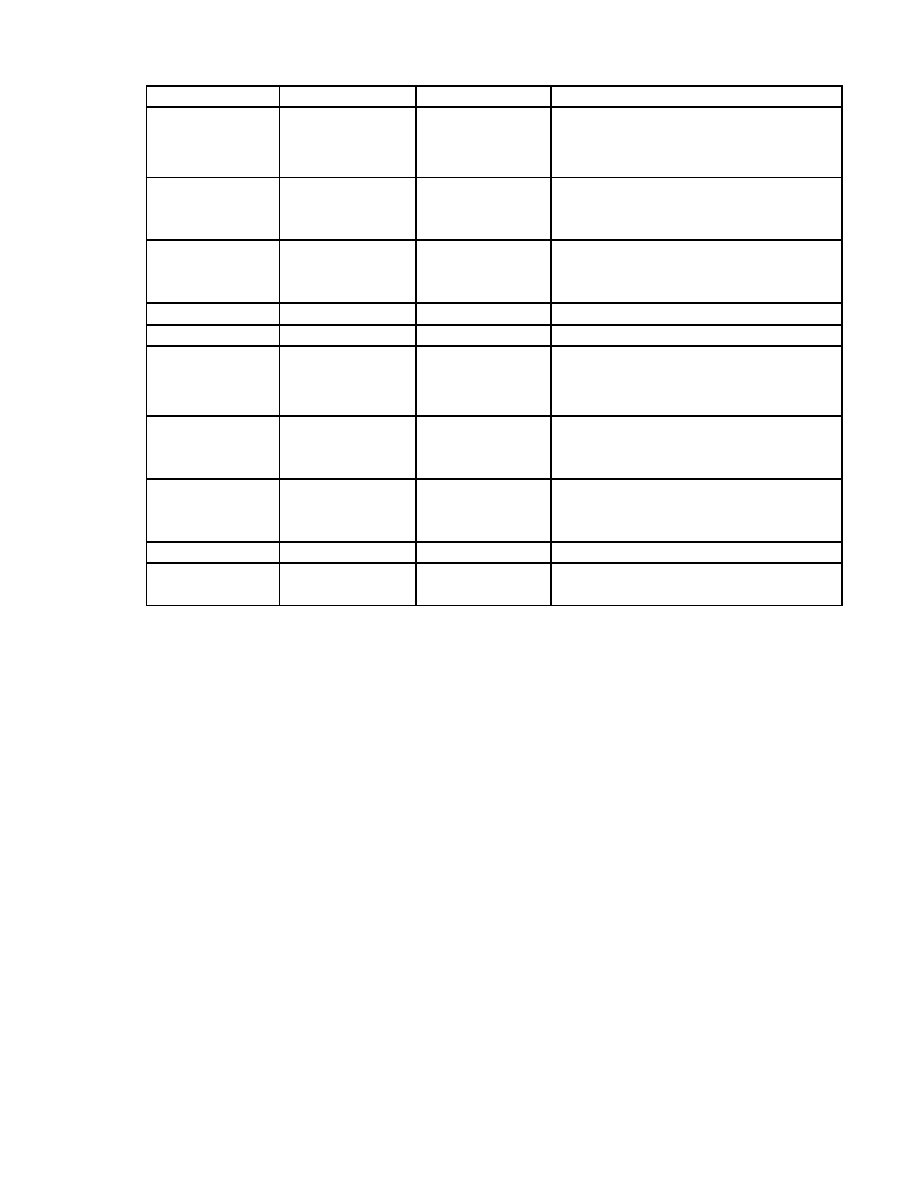
+ d3 n
d2 * T
5 - 3
F->digit
+ d3 n
F * T
5 – 3
F.val:=digit.lexval
(loại bỏ digit)
T->T
1
*F
+ d3 n
T
15
T.val:=T
1
.val*F.val
(loại bỏ T
1
,*,F)
E->T
+ d3 n
E
15
E.val:=T.val
(loại bỏ T)
gạt
d3 n
+ E
- 15
gạt
n
d3 + E
4 - 15
F->digit
n
F + E
4 – 15
F.val:=digit.lexval
(loại bỏ digit)
T->F
n
T + E
4 - 15
T.val:=F.val
(loại bỏ F)
E->E
1
+T
n
E
19
E.val:=E
1
.val+T.val
(loại bỏ E
1
,+,T )
gạt
E n
- 19
L->E n
L
19
L.val:=E.val
(loại bỏ E,n)
Chú ý là không phải mọi cú pháp điều khiển thuần tính L đều có thể kết hợp thực hiện các
hành động ngữ nghĩa khi phân tích cú pháp mà không cần xây dựng cây cú pháp. Chỉ có một
lớp hạn chế các cú pháp điều khiển có thể thực hiện như vậy, trong đó rõ nhất là cú pháp điều
khiển thuần tuý S.
Sau đây, chúng ta giới thiệu một số cú pháp điều khiển khác mà cũng có thể thực hiện khi
phân tích LR bằng một số kỹ thuật:
1) loại bỏ việc gắn kết các hành động ngữ nghĩa ra khỏi lược đồ dịch
2) kế thừa các thuộc tính trên ngăn xếp
3) Mô phỏng thao tác đánh giá các thuộc tính kế thừa
4) Thay thuộc tính kế thừa bằng thuộc tính tổng hợp
Sinh viên tự tham khảo trong tài liệu các phần này.
3. LƯỢC ĐỒ CHUYỂN ĐỔI(Lược đồ dịch) - Translation Scheme
Lược đồ chuyển đổi là một văn phạm phi ngữ cảnh trong đó các thuộc tính
được liên kết với các ký hiệu văn phạm và các hành động ngữ nghĩa nằm giữa hai
dấu ngoặc móc {} được chèn vào một vị trí nào đó bên vế phải của sản xuất.
+ Lược đồ dịch vẫn có cả thuộc tính tổng hợp và thuộc tính kế thừa
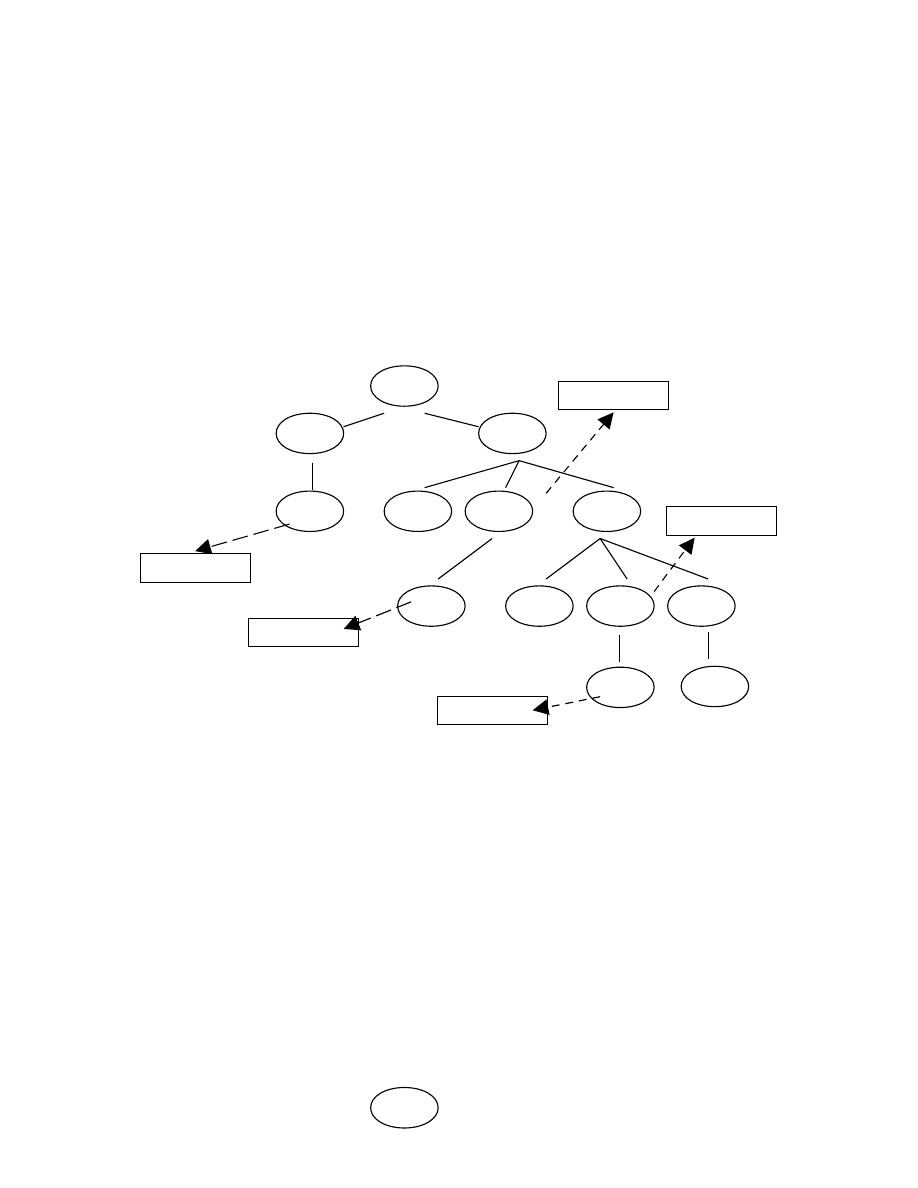
+ Lược đồ dịch xác định thứ tự thực hiện hành động ngữ nghĩa trong mỗi sản
xuất
Ví dụ: một lược đồ dịch để sinh biểu thức hậu vị cho một biểu thức như sau:
E -> T R
R -> + T {print(‘+’)} R
R ->
ε
T -> num {print(num.val)}
Xét biểu thức “3+1+5”
Chúng ta duyệt theo thủ tục duyệt theo chiều sâu. Các hành động ngữ nghĩa được
đánh thứ tự lần lượt 1,2,3, . . .
Kết quả dịch là “3 1 + 5 +”
Chú ý là nếu trong lược đồ dịch ta đặt hành động ngữ nghĩa ở vị trí khác đi, chúng ta sẽ
có kết quả dịch khác ngay. Ví dụ, đối với lược đồ dịch, ta thay đổi một chút thành lược đồ
dịch như sau:
E -> T R
R -> + T R {print(‘+’)}
R ->
ε
T -> num {print(num.val)}
Xét biểu thức “3+1+5”
Chúng ta duyệt theo thủ tục duyệt theo chiều sâu. Các hành động ngữ nghĩa được
đánh thứ tự lần lượt 1,2,3, . . .
E
T
R
3
+
T
R
+
T
R
1
5
1: print(‘3’)
2: print(‘1’)
3: print(‘+’)
4: print(‘5’)
ε
5: print(‘+’)
E
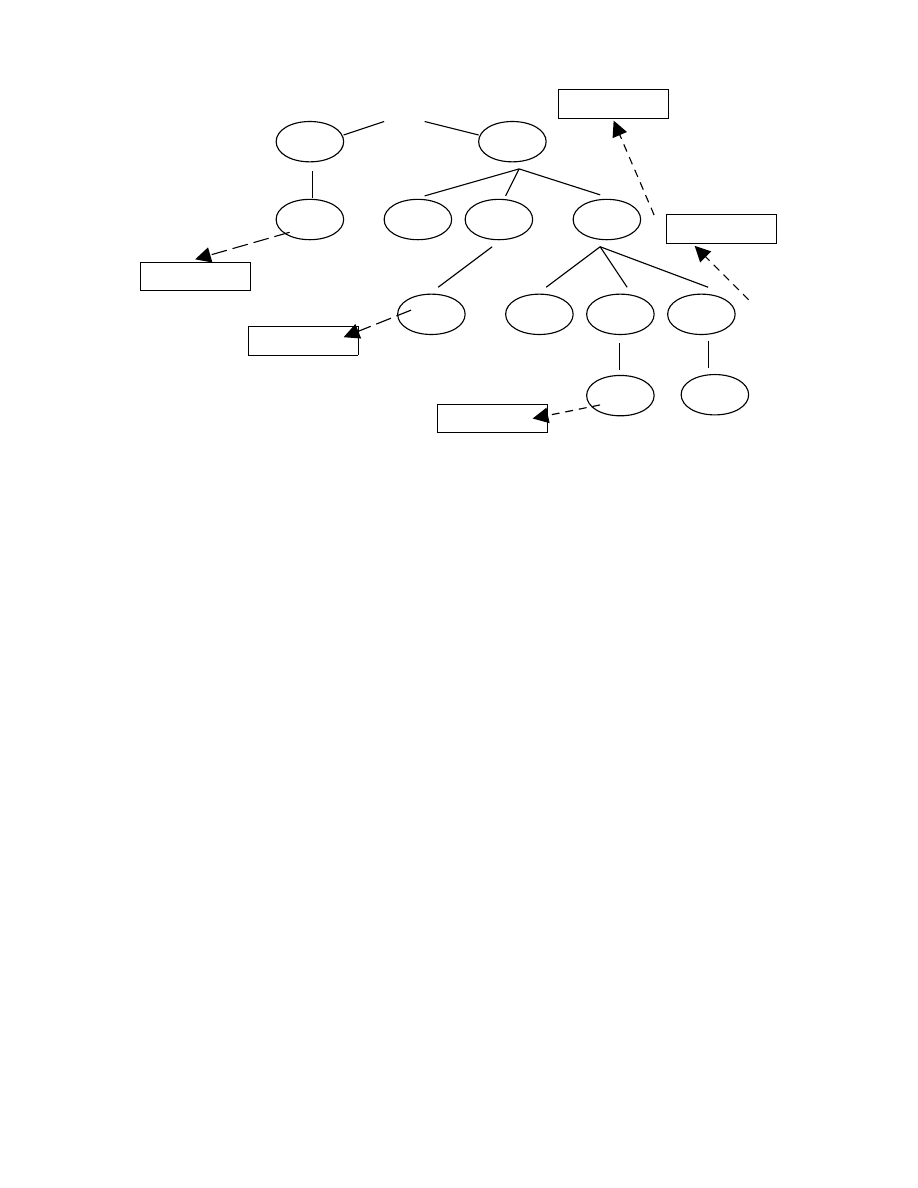
Kết quả dịch là “3 1 5 + +”
Khi thiết kế lược đồ dịch, chúng ta cần một số điều kiện để đảm bảo rằng
một giá trị thuộc tính phải có sẵn khi chúng ta tham chiếu đến nó:
1. Một thuộc tính kế thừa cho một ký hiệu ở vế phải của một sản xuất phải
được tính ở một hành động nằm trước ký hiệu đó.
2. Một hành động không được tham chiếu đến thuộc tính của một ký hiệu ở
bên phải của hành động đó.
3. Một thuộc tính tổng hợp cho một ký hiệu không kết thúc ở vế trái chỉ có
thể được tính sau khi tất cả thuộc tính nó cần tham chiếu đến đã được tính
xong. Hành động như thế thường được đặt ở cuối vế phải của luật sinh.
Ví dụ lược đồ dịch sau đây không thoả mãn các yêu cầu này:
S -> A
1
A
2
{A
1
.in:=1; A
2
.in:=2}
A -> a {print(A.in)}
Ta thấy thuộc tính kế thừa A.in trong luật thứ 2 chưa được định nghĩa vào lúc muốn in ra
giá trị của nó khi duyệt theo hướng sâu trên cây phân tích cho đầu vào aa. Để thoả mãn
thuộc tính L, chúng ta có thể sửa lại lược đồ trên thành như sau:
S -> {A
1
.in:=1 } A
1
{A
2
.in:=2} A
2
A -> a {print(A.in)}
Như vậy, thuộc tính A.in được tính trước khi chúng ta duyệt A.
Những điều kiện này được thoả nếu văn phạm có điều khiển thuần tính L.
Khi đó chúng ta sẽ đặt các hành động theo nguyên tắc như sau:
1. Hành động tính thuộc tính kế thừa của một ký hiệu văn phạm A bên vế
phải được đặt trước A.
T
R
3
+
T
R
+
T
R
1
5
1: print(‘3’)
2: print(‘1’)
5: print(‘+’)
3: print(‘5’)
ε
4: print(‘+’)
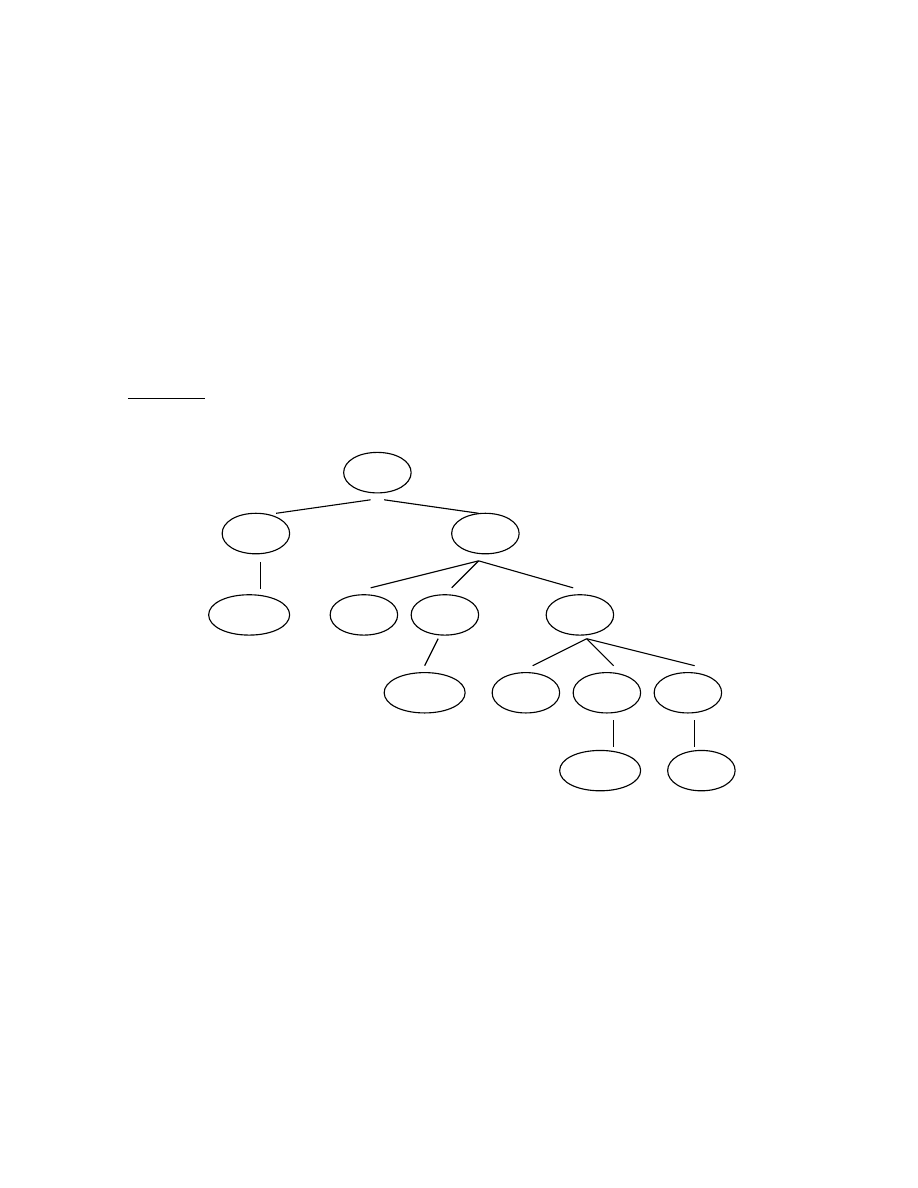
2. Hành động tính thuộc tính tổng hợp của ký hiệu vế trái được đặt ở cuối
luật sản xuất.
Ví dụ:
Cho văn phạm biểu diễn biểu thức gồm các toán tử + và - với toán hạng là các số:
E -> T R
R -> + T R
R -> - T R
R ->
ε
T -> ( E )
T -> num
Xây dựng lược đồ dịch trên văn phạm này để tính giá trị của biểu thức.
Giải đáp:
Trước hết, chúng ta thử xem cây phân tích cú pháp cho đầu vào “6+4-1”
Gọi val là thuộc tính chứa giá trị tính được của các ký hiệu văn phạm E và T.
Thuộc tính s là thuộc tính tổng hợp và i là thuộc tính kế thừa để chứa giá trị tính
được của ký hiệu R. Chúng ta đặt R.i chứa giá trị của phần biểu thức đứng trước R
và R.s chứa kết quả. Chúng ta xây dựng lược đồ dịch như sau:
E -> T {R.i:=T.val}
R {E.val:=R.s}
R -> +
T {R
1
.i:=R.i+T.val}
R
1
{R.s:=R
1
.s }
R -> -
T { R
1
.i:=R.i-T.val }
E
T
R
num(6
)
+
T
R
-
T
R
ε
num(4
)
num(1
)
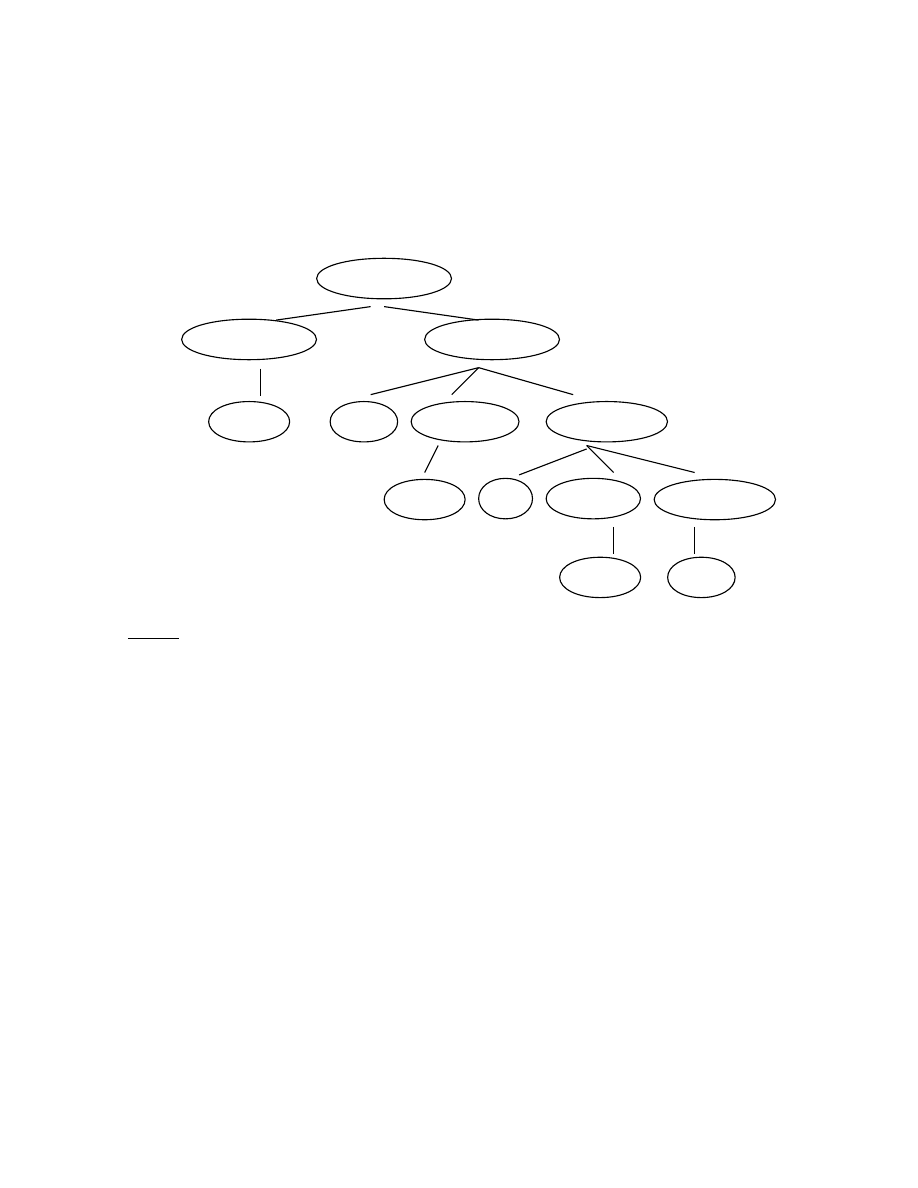
R
1
{R.s:=R
1
.s}
R ->
ε
{R.s:=R.i}
T -> ( E ) {T.val:=E.val}
T -> num {T.val:=num.val}
Lưu ý:
nếu chúng ta xác định một cách duyệt khác cách duyệt theo hướng sâu thì cách đặt
hành động dịch vào vị trí nào sẽ được làm khác đi. Tuy nhiên cách duyệt theo hướng
sâu là cách duyệt phổ biến nhất và tự nhiên nhất (vì ngữ nghĩa sẽ được xác định dần
theo chiều duyệt đầu vào từ trái sang phải) nên chúng ta coi khi duyệt một cây phân
tích, chúng ta sẽ duyệt theo hướng sâu
.
4. DỰNG CÂY CÚ PHÁP.
4.1. Cây cú pháp.
Cây cú pháp (syntax - tree) là dạng rút gọn của cây phân tích cú pháp dùng
để biểu diễn cấu trúc ngôn ngữ. Trong cây cú pháp các toán tử và từ khóa không
phải là nút lá mà là các nút trong.
Ví dụ với luật sinh S
→
if B then S1 else S2 được biểu diễn bởi cây cú pháp:
E val=9
T val=6
R i=6 s=9
num(6
)
+
T
val=4
R i=10 s=9
-
T val=1
R i=9 s=9
ε
num(4
)
num(1
)

Xây dựng cây cú pháp cho biểu thức.
Tương tự như việc dịch một biểu thức thành dạng hậu tố. Xây dựng cây con cho
biểu thức con bằng cách tạo ra một nút cho toán hạng và toán tử. Con của nút toán
tử là gốc của cây con biểu diễn cho biểu thức con toán hạng của toán tử đó. Mỗi
một nút có thể cài đặt bằng một mẩu tin có nhiều trường.
Trong nút toán tử, có một trường chỉ toán tử như là nhãn của nút, các trường còn lại
chứa con trỏ, trỏ tới các nút toán hạng.
Để xây dựng cây cú pháp cho biểu thức chúng ta sử dụng các hàm sau đây:
1/ mknode(op, left, right) : Tạo một nút toán tử ó nhãn là op và hai trờng chứa con
trỏ, trỏ tới left và right.
2/ mkleaf(id, entry): Tạo một nút lá với nhãn là id và một trờng chứa con trỏ entry,
trỏ tới ô trong bảng ký hiệu danh biểu.
3/ mkleaf(num,val): Tạo một nút lá với nhãn là num và trờng val, giá trị của số.
Ví dụ: Để xây dựng cây cú pháp cho biểu thức: a - 4 + c ta dùng một dãy các lời
gọi các hàm nói trên.
(1): p1 := mkleaf(id, entrya) (4): p4 := mkleaf(id, entryc)
(2): p2 := mkleaf(num,4) (5): p5 := mknode(" +", p3, p4)
(3): p3 := mknode(" -", p1, p2)
Cây được xây dựng từ dưới lên
entrya là con trỏ, trỏ tới ô của a trong bảng ký hiệu
entryc là con trỏ, trỏ tới ô của c trong bảng ký hiệu
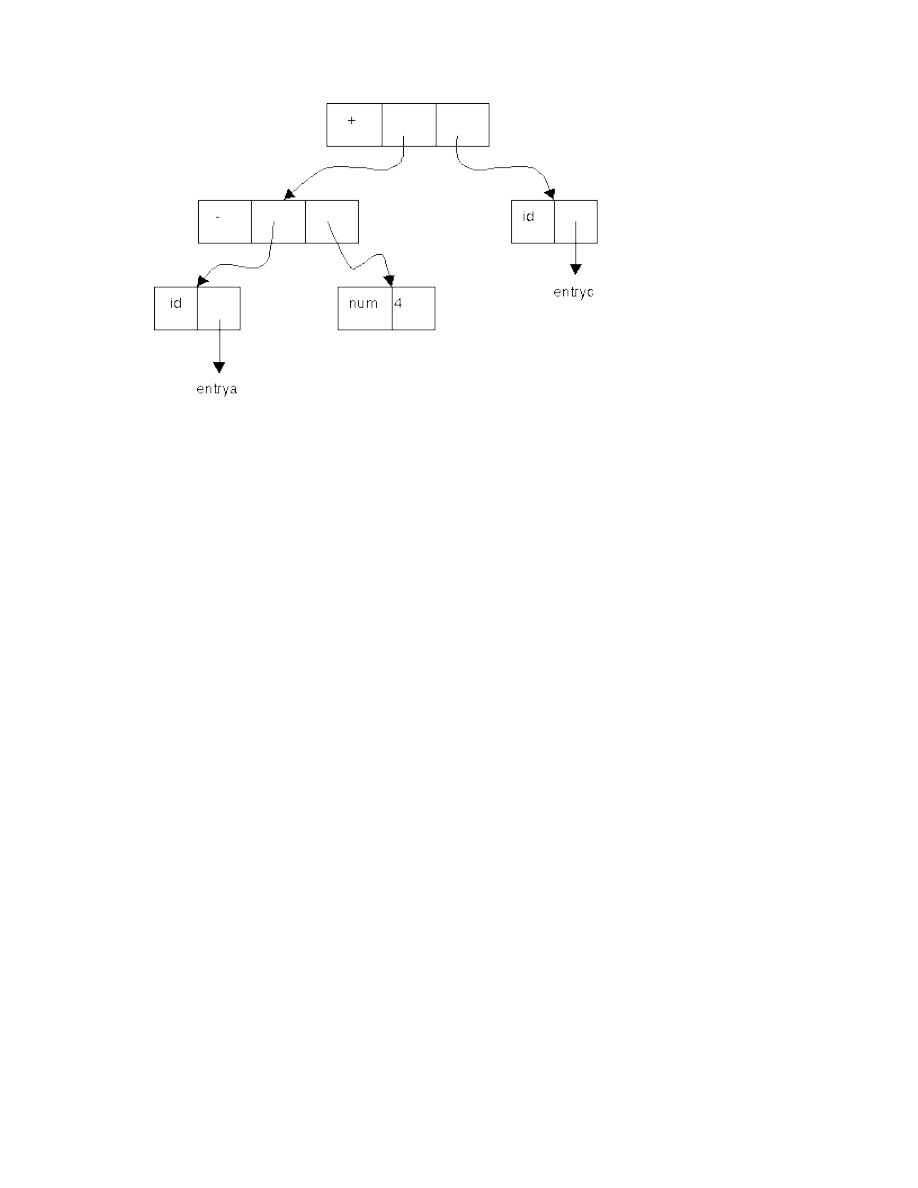
* xây dựng cây cú pháp từ định nghĩa trực tiếp cú pháp.
Căn cứ vào các luật sinh văn phạm và luật ngữ nghĩa kết hợp mà ta phân bổ việc
gọi các hàm mknode và mkleaf để tạo ra cây cú pháp.
Ví dụ: Định nghĩa trực tiếp cú pháp giúp việc xây dựng cây cú pháp cho biểu thức
là:
Luật sinh Luật ngữ nghĩa
E
→
E1 + T E.nptr := mknode('+', E1.nptr, T.nptr)
E
→
E1 - T E.nptr := mknode('-', E1.nptr, T.nptr)
E
→
T E.nptr := T.nptr
T
→
(E) T.nptr := E.nptr
T
→
id T. nptr := mkleaf(id, id.entry)
T
→
num T.nptr := mkleaf(num, num.val)
Với biểu thức a - 4 + c ta có cây phân tích cú pháp (biểu diễn bởi đường chấm)
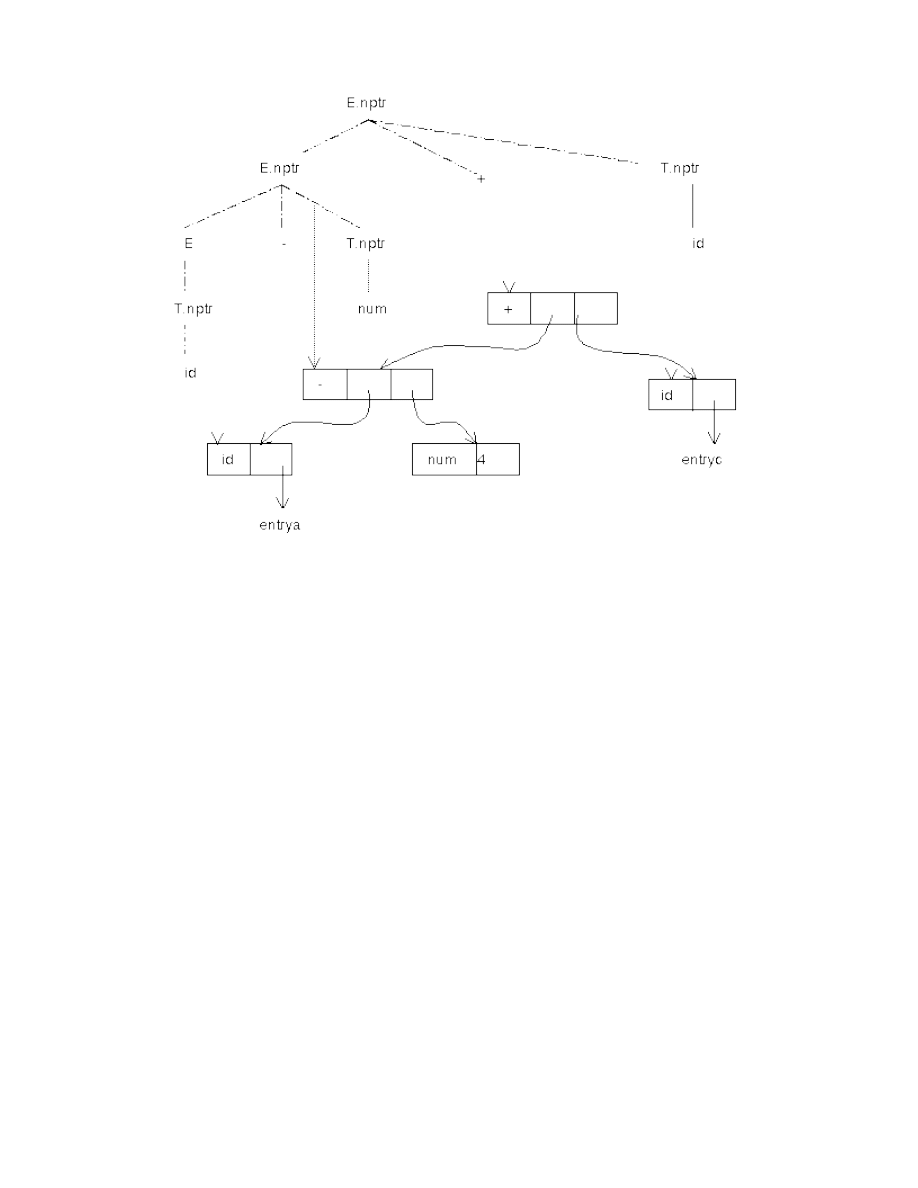
Luật ngữ nghĩa cho phép tạo ra cây cú pháp. Cây cú pháp có ý nghĩa về mặt cài đặt
còn cây phân tích cú pháp chỉ có ý nghĩa về mặt logic.
4.3. Đồ thị DRAG.
DAG ( Directed Acyclic Graph): Đồ thị bao gồm các đỉnh chứa các thuộc tính và
cỏc cạnh cú hướng để biểu thị sự phụ thuộc giữa các đỉnh. Cũng giống như cây cú
pháp, tuy nhiên trong cây cú pháp các biểu thức con giống nhau biểu diễn lặp lại
còn trong DAG thì không. Trong DAG, một nút con có thể có nhiều "cha"
.
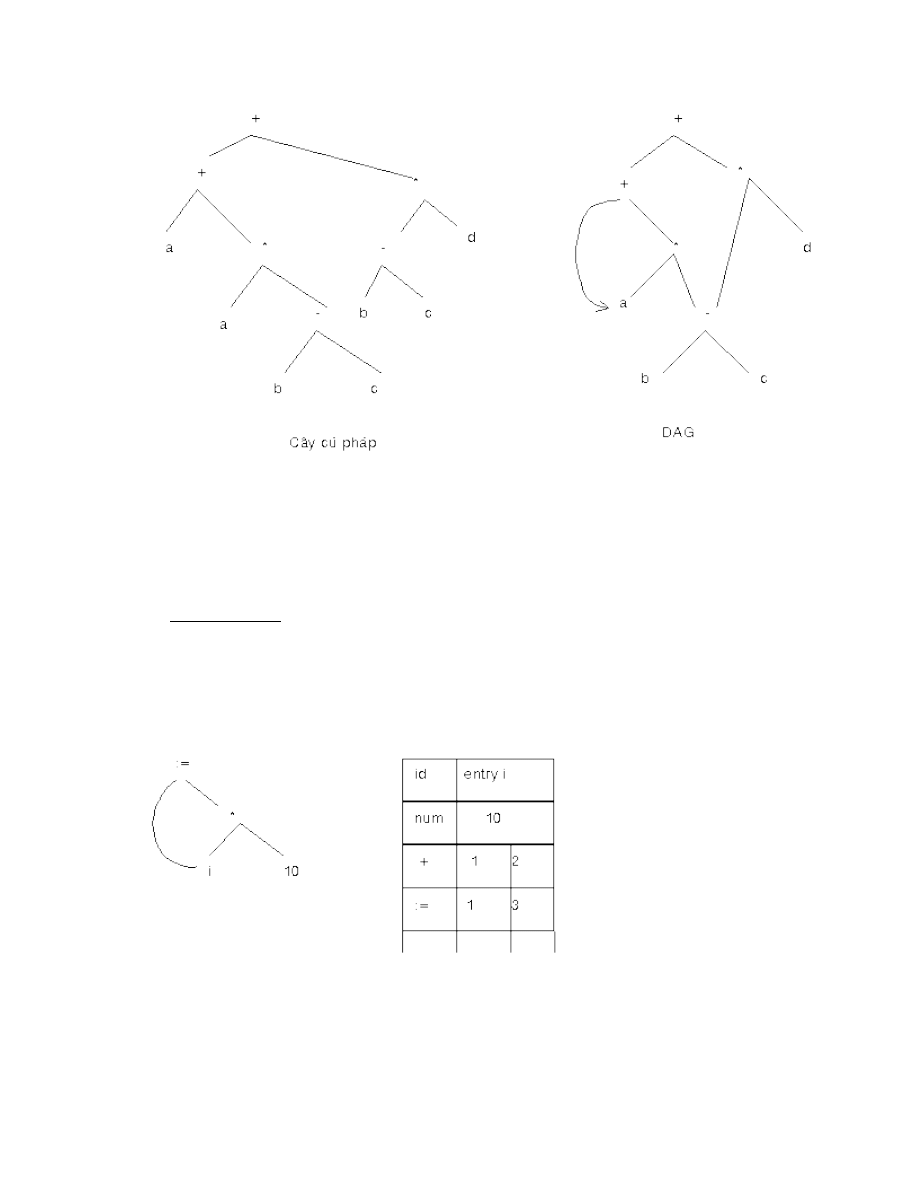
Ví dụ: cho biểu thức a + a * (b - c) + (b - c) * d
Để xây dựng một DAG, trước khi tạo một nút phải kiểm tra xem nút đó đã tồn
tại chưa, nếu đã tồn tại thì hàm tạo nút (mknode, mkleaf) trả về con trỏ của nút đã
tồn tại, nếu chưa thì tạo nút mới.
Cài đặt DAG
Người ta thường sử dụng một mảng mẩu tin , mỗi mẩu tin là một nút. Ta có
thể tham khảo tới nút bằng chỉ số của mảng.
Ví dụ:
Lệnh gán DAG Biểu diễn i := i + 10
Nút 1: có nhãn là id, con trỏ trỏ tới entry i.
Nút 2: có nhãn là num, giá trị là 10.
Nút 3: có nhãn là +, con trái là nút 1, con phải là nút 2.
Nút 4: có nhãn là :=, con trái là nút 1, con phải là nút 3.

Giải thuật 5.1: Phương pháp value_number để xây dựng một nút trong
DAG.
Giả sử rằng các nút được lưu trong một mảng và mỗi nút đợc tham khảo bởi số giá
trị của nó. Mỗi một nút toán tử là một bộ ba <op, l, r >
Input: Nhãn op, nút l và nút r.
Output: Một nút với <op, l, r>
Phương pháp: Tìm trong mảng một nút m có nhãn là op con trái là l, con phải là r.
Nếu tìm thấy thì trả về m, ngợc lại tạo ra một nút mới n, có nhãn là op, con trái là l,
con phải là r và trả về m.

CHƯƠNG 6
PHÂN TÍCH NGỮ NGHĨA
.
1. MỤC ĐÍCH NHIỆM VỤ.
Nhiệm vụ: kiểm tra tính đúng đắn về mặt ngữ nghĩa của chương trình nguồn.
Việc kiểm tra được chia làm hai loại là kiểm tra tĩnh và kiểm tra động
(Việc kiểm tra
của chương trình dịch được gọi là tĩnh, việc kiểm tra thực hiện trong khi chương trình đích chạy
gọi là động. Một kiểu hệ thống đúng đắn sẽ xoá bỏ sự cần thiết kiểm tra động.).
Xét một số dạng của kiểm tra tĩnh:
- Kiểm tra kiểu: kiểm tra về tính đúng đắn của các kiểu toán hạng trong biểu
thức.
- Kiểm tra dòng điều khiển: một số điều khiển phải có cấu trúc hợp lý,
ví dụ
như lệnh break trong ngôn ngữ pascal phải nằm trong một vòng lặp.
- Kiểm tra tính nhất quán: có những ngữ cảnh mà trong đó một đối tượng
được định nghĩa chỉ đúng một lần.
Ví dụ, trong Pascal, một tên phải được khai báo duy
nhất, các nhãn trong lệnh case phải khác nhau, và các phần tử trong kiểu vô hướng không được
lặp lại.
- Kiểm tra quan hệ tên: Đôi khi một tên phải xuất hiện từ hai lần trở lên.
Ví
dụ, trong Assembly, một chương trình con có một tên mà chúng phải xuất hiện ở đầu và cuối của
chương trình con này.
Trong phạm vi tài liệu này, ta chỉ xét một số dạng trong kiểm tra kiểu của chương trình
nguồn.
2. BIỂU THỨC KIỂU
(type expressions)
Kiểu của một cấu trúc ngôn ngữ được biểu thị bởi “biểu thức kiểu”. Một biểu
thức kiểu có thể là một kiểu cơ bản hoặc được xây dựng từ các kiểu cơ bản theo
một số toán tử nào đó.
Ta xét một lớp các biểu thức kiểu như sau:
1). Kiểu cơ bản:
Gồm boolean, char, interger, real. Có các kiểu cơ bản đặc biệt là type_error
(để trả về một cấu trúc bị lỗi kiểu), void (biểu thị các cấu trúc không cần xác định
kiểu như câu lệnh).
2). Kiểu hợp thành:

+ Mảng: Nếu T là một biểu thức kiểu thì array(I,T) là một biểu thức kiểu đối
với một mảng các phần tử kiểu T và I là tập các chỉ số.
Ví dụ, trong ngôn ngữ Pascal khai báo: var A: array[1..10] of interger;
sẽ xác định kiểu của A là array(1..10,interger)
+ Tích của biểu thức kiểu: là một biểu thức kiểu. Nếu T
1
và T
2
là các kiểu biểu
thức kiểu thì tích Đề các của T
1
xT
2
là một biểu thức kiểu.
+ Bản ghi: Kiểu của một bản ghi chính là biểu thức kiểu được xây dựng từ các
kiểu của các trường của nó.
Ví dụ trong ngôn ngữ Pascal:
type row=record
address: interger;
lexeme: array[1..15] of char;
end;
var table: array[1..101] of row;
như vậy một biến của row thì tương ứng với một biểu thức kiểu là:
record((address x interger) x (lexeme x array(1..15,char)))
+ Con trỏ: Giả sử T là một biểu thức kiểu thì pointer(T) là một biểu thị một
biểu thức kiểu xác định kiểu cho con trỏ của một đối tượng kiểu T.
Ví dụ, trong ngôn ngữ Pascal: var p: ^row thì p có kiểu là pointer(row)
+ Hàm: Một hàm là một ánh xạ từ các phần tử của một tập vào một tập khác.
Kiểu một hàm là ánh xạ từ một kiểu miền D vào một kiểu phạm vi R. Biểu thức
kiểu cho một hàm như vậy sẽ được ký hiệu là D->R.
Ví dụ trong ngôn ngữ Pascal, một hàm khai báo như sau: function f(a,b:interger):
^interger;
có kiểu miền là interger x interger và kiểu phạm vi là pointer(interger). Và như vậy biểu thức
kiểu xác định kiểu cho hàm đó là: 0 interger x interger -> pointer(interger)
3. CÁC HỆ THỐNG KIỂU.
Một hệ thống kiểu là một tập các luật để xác định kiểu cho các phần trong
chương trình nguồn. Một bộ kiểm tra kiểu làm nhiệm vụ thực thi các luật trong hệ
thống kiểu này. Ở đây, hệ thống kiểu được xác định bởi các luật ngữ nghĩa dựa trên
luật cú pháp. Các vấn đề được nghiên cứu trong phần cú pháp điều khiển và lược
đồ dịch.
Một hệ thống kiểu đúng đắn sẽ xoá bỏ sự cần thiết phải kiểm tra động (vì nó cho phép xác
định tĩnh, các lỗi không xảy ra trong lúc chương trình đích chạy). Một ngôn ngữ gọi là định kiểu
mạnh nếu chương trình dịch của nó có thể bảo đảm rằng các chương trình mà nó dịch tốt sẽ hoạt
động không có lỗi về kiểu. Điều quan trọng là khi bộ kiểm tra phát hiện lỗi, nó phải khắc phục
lỗi dể tiếp tục kiểm tra. trước hết nó thông báo về lỗi mô tả và vị trí lỗi. Lỗi xấut hiện gây ảnh
hưởng đếncác luật kiểm tra lỗi, do vậy phải thiết kế kiểu hệ thống như thế nào để các luật có thể
đương đầu với các lỗi này.
3.1. Một số luật ngữ nghĩa kiểm tra kiểu
Đối với câu lệnh không có giá trị, ta có thể gán cho nó kiểu cơ sở đặc biệt void. Nếu có lỗi
về kiểu được phát hiện trong câu lệnh thì ta gán cho nó giá trị kiểu là type_error
Xét cách xây dựng luật ngữ nghĩa kiểm tra kiểu qua một số ví dụ sau:
VD1: Văn phạm cho khai báo:
D -> D ; D
D -> id : T
T -> interger
T -> char
T -> ^ T
T -> array [num] of T
Luật cú pháp
Luật ngữ nghĩa
D -> id : T
AddType(id.entry,T.type)
T -> char
T.type := char
T -> interger
T.type := interger
T -> ^T
1
T.type := pointer(T
1
.type)
T -> array [num] of T
1
T.type := array(num.val,T
1
.type)
VD2: Văn phạm sau cho biểu thức
S -> id := E
E -> E + E
E -> E mod E
E -> E
1
[ E
2
]
E -> num
E -> id
Luật cú pháp
Luật ngữ nghĩa
S -> id := E
S.type := if id.type=E.type then void
else type_error
E -> E
1
+ E
2
E.type:=
if E
1
.type=interger and E
2
.type=interger then interger
else if E
1
.type=interger and E
2
.type=real then real
else if E
1
.type=real and E
2
.type=interger then real
else if E
1
.type=real and E
2
.type=real then real
else type_error
E -> num
E.type := interger
E -> id
E.type := GetType(id. entry)
E -> E
1
mod E
2
E.type := if E
1
.type=interger and E
2
.type=interger then interger
else type_error
E -> E
1
[ E
2
]
E.type := if E
2
.type=interger and E
1
.type=array(s,t) then t else
type_error
VD3: Kiểm tra kiểu cho các câu lệnh:
S -> if E then S
S -> while E do S
S -> S
1
; S
2
Luật cú pháp
Luật ngữ nghĩa
S -> if E then S
1
S.type := if E.type=boolean then S
1
.type
else type_error

S -> while E do S
1
S.type := if E.type=boolean then S
1.
type
else type_error
S -> S
1
; S
2
S.type := if S
1
.type=void and S
2
.type=void then
void
else type_error
VD4: Kiểu hàm: luật cú pháp sau đây thể hiện lời gọi hàm: E -> E
1
( E
2
)
Ví dụ:
function f(a,b:char):^interger;
begin
. . .
end;
var
p:^interger; q:^char;
x,y:interger;
begin
. . .
p:=f(x,y);// đúng
q:=f(x,y);// sai
end;
Luật cú pháp
Luật ngữ nghĩa
E -> E
1
( E
2
)
E.type := if E
2
.type=s and E
1
.type=s->t then t
else type_error
3.2. Ví dụ về một bộ kiểm tra kiểu đơn giản.
Ví dụ về một ngôn ngữ đơn giản mà kiểu của các biến phải được khai báo trước khi dùng.
Bộ kiểm tra kiểu này là một cú pháp dạng lược đồ chuyển đổi nhằm tập hợp kiểu của từng biểu
thức từ các kiểu của các biểu thức con. Bộ kiểm tra kiểu có thể làm việc với các mảng, các con
trỏ, lệnh, hàm.
*
Một văn phạm dưới đây sinh ra các chương trình, biểu diẽn bởi biến P, bao
gồm một chuỗi các khai báo D theo sau một biểu thức đơn E, các kiểu T.
P
→
D;E

D
→
D;D|tên:T
T
→
char| integer| array| số| of T| ^T
E
→
chữ cái| Số | Tên| E mod E | E; E |E^
- Một chương trình có thể sinh ra từ văn phạm trên như sau:
Key: Integer;
Key mod 1999
* Lược đồ chuyển đổi như sau:
P
→
D; E
D
→
D;D
D
→
Tên:T
{addtype (tên.entry, T.type)}
T
→
Char
{T.type:= char}
T
→
integer
{T.type:= integer}
T
→
^T
1
{T.type:= pointer(T
1
.type)}
T
→
array | số | of T
1
{T.type:= aray(số.val,T
1
.type)}
Hành động ứng với sản xuất
D
→
Tên:T lưu vào bảng kí hiệu một kiểu cho một tên.
Hàm
{addtype (tên.entry, T.type)} nghĩa là cất một thuộc tính T.type vào bản kí hiệu ở vị trí
entry.
* Kiểm tra kiểu của các biểu thức.
Trong các luật sau:
E
→
chữ cái {E.type : = char}
E
→
Số { E.type := integer}
Kiểu của thuộc tính tổng hợp của E cho biểu thưc được gán bằng kiểu hệ
thống để sinh biểu thức bởi E. Các luật ngữ nghĩa cho thấy các hằng số biểu diễn
bằng từ tố chữ cái và số có kiểu char và integer.
Ta dùng hàm lookup(e) để lấy kiểu caats trong bảng ký hiệu trỏ bởi e. Khi một
tên xuất hiện trong biểu thức kiểu khao báo của nó được lấy và gán cho thuộc tính
kiểu
E
→
tên {E.type:= lookup (tên.entry)}
- Một biểu thức được tạo bởi lệnh mod cho 2 biểu thức con có kiểu integer thì
nó cũng có kiểu là integer nếu không là kiểu type_error.
E
→
E
1
mod E
2
{E.type : = if E
1
.type = integer and E
2
.type = integer then
integer else type_error}

- Đối với mảng E
1
[E
2
]bieeur thức chỉ số E
2
phải có kiểu là integer các phần tử
của mảng có kiểu t chính là kiểu array(s,t) của E
t
E
→
E
1
[E
2
] {E.type :=if E
2
.type = integer and E
t
.type = array(s,t) then t else
type_error}
- Đối với thuật toán lấy giá trị con trỏ.
E
→
E
t
^ {E.type := if E
1
.type = pointer (t) then else type_error}
* Kiểm tra kiểu của câu lệnh:
Đối với câu lệnh không có giá trị: gán kiểu đặc biệt void . nếu có lỗi được
phát hiện trong câu lệnh : kiểu câu lệnh là : type_error.
Các câu lệnh gồm: lệnh gán, điều kiện, vòng lặp while. Chuooix các câu lệnh
phân cách nhau bằng dấu chấm phẩy. một chương trình hoàn chỉnh có luật dạng P
→
D ; S cho biết một chương trình bao gồm các khai báo và theo sau là các câu
lệnh .
S
→
tên: = E { S.type:= if tên.type= E.type then void else type _error }
S
→
if E else S
1
{S.type := if E.type = boolean then S
1
.type else type_error }
S
→
While E do S
1
{S.type:= if E.type = boolean then S
1
.type = void then void
else type_error }
* kiểm tra biểu thức của hàm.
Các hàm với tham số có sản xuất dạng: E
→
E (E)
Các luật ứng với kiểu biểu thức của kí hiệu không kết thúc T có thể làm thừa
số theo các sản xuất sau:
T
→
T
1
’
→
’ T
2
{T.type := T
1
.type
→
T
2
.type}
Luật kiểm tra kiểu của một hàm là: E
→
E
1
(E
2
) {E.type : =if E
2
.type =s
→
t
then t else type_error}
luật này cho biết trong một biểu thức được tạo bằng cách áp dụng E
1
vào E
2
kiểu của s
→
t phải là một hàm từ kiểu của s vào kiểu nào đó t. kiểu E
1
(E
2
) là t.
3. MỘT SỐ VẤN ĐỀ KHÁC CỦA KIỂM TRA KIỂU.
3.1. Sự tương đương của kiểu biểu thức.
Nhiều luật có dạng “if kiểu của 2 biểu thức giống nhau thì trả về kiểu đó else
trả về type _error” Vậy làn sao để xác định chính xác khi nào thì 2 kiểu biểu thức
là tương đương?
Hàm dùng để kiểm tra sự tương đương về cấu trúc của kiểu biểu thức.

Function sequiv(s,t): boolean;
begin
if s và t cùng kiểu cơ sở then return true;
else if s = array (s
1,
s
2
) and t = array (t
1
,t
2
) then
return sequiv(s
1,
t
1
) and sequiv(s
2
,t
2
)
else if s=pointer(s
1
) and t=pointer(t
1
) then return sequiv(s
1,
t
1
)
else if s=s
1
→
s
2
and t = t
1
→
t
2
then return sequiv(s
1,
t
1
) and sequiv(s
2
,t
2
)
else return false;
end;
3.2. Đổi kiểu.
Xét biểu thức dạng : x+i, (x: kiểu real, i kiểu integer)
Biểu diễn real và integer trong máy tính là khác nhau đồng thời cách thực hiện phép cộng
đối với số real và số integer khác nhau
. Để thực hiện phép cộng, trớc tiên chương trình
dịch đổi cả 2 toán tử về một kiểu (kiểu real) sau đó thực hiện cộng.
Bộ kiểm tra kiểu trong chương trình dịch được dùng để chèn thêm phép toán
vào các biểu diễn trung gian của chương trình nguồn.
Ví dụ: chèn thêm phép toán inttoreal (dùng chuyển một số integer thành số
real) rồi mới thực hiện phép cộng số thực real + như sau: xi inttoreal real +
* Ép kiểu:
Một phép đổi kiểu được gọi là không rõ (ẩn) nếu nó thực hiện một cách tự
động bởi chương trình dịch, phép đổi kiểu này còn gọi là ép kiểu.
(ép kiểu thường gây
mất thông tin)
Một phép đổi kiểu được gọi là rõ nếu người lập trình phải viết số thứ để thực
hiện phép đổi này. Ví dụ:
Sản xuất
Luật ngữ nghĩa
E
→
Số
E.type:= integer
E
→
Số.số
E.type:= real
E
→
tên
E.type:= lookup (tên.entry)

E
→
E
1
op E
2
E,type:= if E
1
.type = integer and E
2
.type = integer Then integer
Else if E
1
.type = integer and E
2
.type = real Then real
Else if E
1
.type = real and E
2
.type = integer Then real
Else if E
1
.type = real and E
2
.type = real Then real
Else type_error
3.3. Định nghĩa chồng của hàm và các phép toán.
Kí hiệu chồng là kí hiệu có nhiều nghĩa khác nhau phụ thộc vào ngữ cảnh của
nó.
VD: + là toán tử chồng, A+B ý nghĩa khác nhau đối với từng trường hợp A,B là số
nguyên, số thực, số phức, ma trận…
Định nghĩa chồng cho phép tạo ra nhiều hàm khác nhau nhưng có cùng một
tên. Để xác định thực sự dùng định nghĩa chồng nào ta phải căn cứ vào ngữ cảnh
lúc áp dụng.
Điều kiện để thực hiện toán tử chồng là phải có sự khác nhau về kiểu hoặc số
tham số. Do đó ta có thể dựa vào luật ngữ nghĩa để kiểm tra kiểu và gọi các hàm xử
lý.

CHƯƠNG 7 BẢNG KÍ HIỆU.
1. MỤC ĐÍCH, NHIỆM VỤ.
Một chương trình dịch cần phải thu thập và sử dụng các thông tin về các tên
trong chương trình nguồn. Các thông tin này được lưu trong một cấu trúc dữ liệu
gọi là một bảng kí hiệu. Các thông tin bao gồm tên, kiểu, dạng của nó ( một biến
hay là một cấu trúc), vị trí cảu nó trong bộ nhớ, các thuộc tính khác phụ thuộc vào
ngôn gnữ lập trình.
Mỗi lần tên cần xem xét, chương trình dịch sẽ tìm trong bảng kí hiệu xem đã
có tên đó chưa. Nếu tên đó là mớithì thêm vào bảng. Các thông tin về tên được tìm
và đưa vào bảng trong giai đoạn phân tích từ vựng và cú pháp.
Các thông tin trong bảng kí hiệu được dùng trong phân tích ngữ nghĩa,
( kiểm traviệc dùng các tên có khớp với khai báo không) trong giai đoạn sinh mã
( kích thước của tên, loại bộ nhớ phải cấp phát cho một tên).
Dùng bảng kí hiệu trong quá trình phát hiện và khôi phục lỗi.
2. CÁC YÊU CẦU ĐỐI VỚI BẢNG KÍ HIỆU.
Ta cần có một số khả năng làm viếc với bảng như sau:
1) phát hiện một tên cho trước có trong bảng hay không?
2) thêm tên mới.
3) lấy thông tin tương ứng với tên cho trước.
4) thêm thông tin mới vào tên cho trước.
5) xoá một tên hoặc nhóm tên.
Các thông tin trong bảng kí hiệu có thể gồm:
1) Xâu kí tự tạo nên tên.
2) Thuộc tính của tên.
3) các tham số như số chiều của mảng.
4) Có thể có con trỏ đên tên cấp phát.
Các thông tin đưa vào bảgn trong những thời điểm khác nhau.
3. CẤU TRÚC DỮ LIỆU CỦA BẢNG KÍ KIỆU
Có nhiều cách tổ chức bảng kí hiệu khác nhau như có thể tách bảng riêng rẽ ứng với tên biến,
nhãn, hằng số, tên hàm và các kiểu tên khác… tuỳ thuộc vào từng ngôn ngữ.
Về cách tổ chức dữ liệu có thể tỏ chức bởi danh sách tuyến tính, cây tìm kiếm, bảng băm…
Mỗi ô trong bảng ký hiệu tương ứng với một tên. Ðịnh dạng của các ô này
thường không giống nhau vì thông tin lưu trữ về một tên phụ thuộc vào việc sử
dụng tên đó. Thông thường một ô được cài đặt bởi một mẩu tin có dạng ( tên, thuộc
tính).
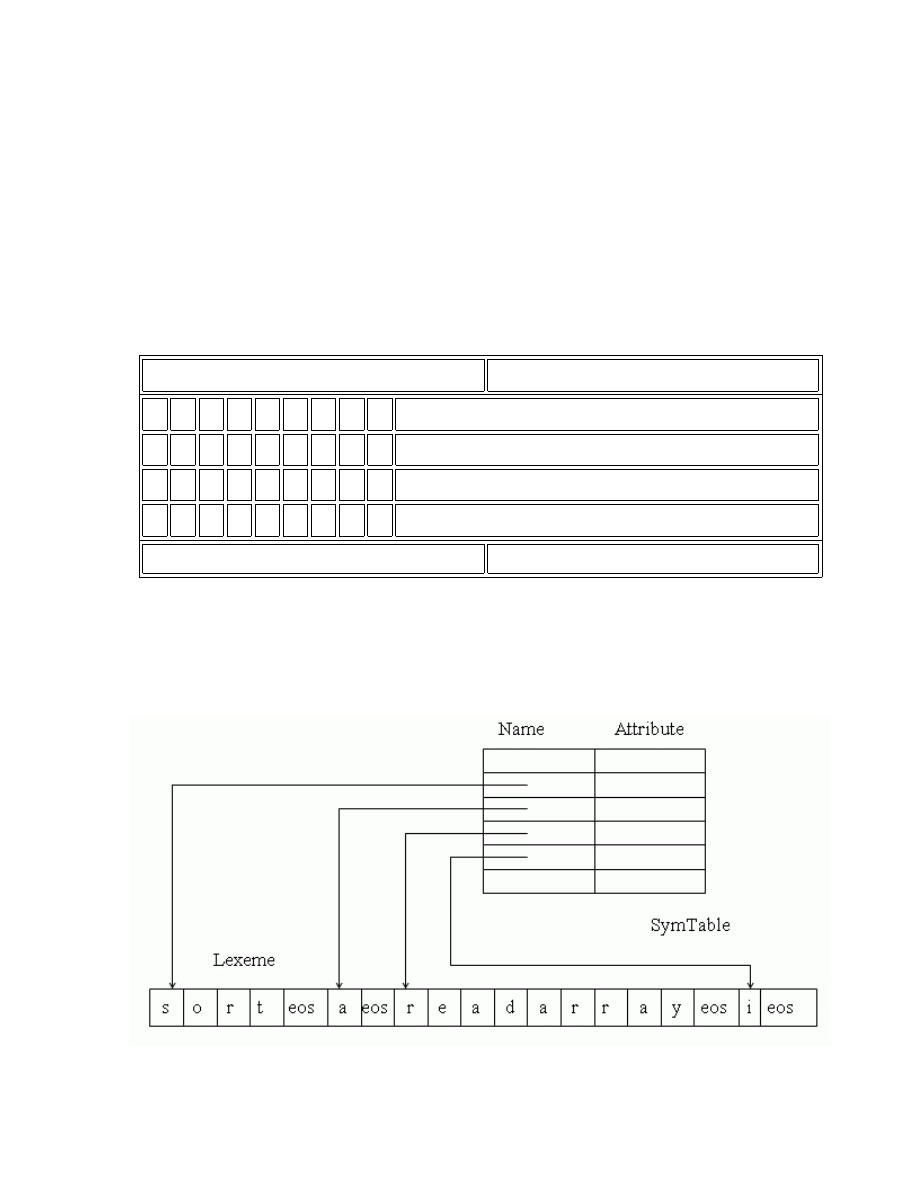
Nếu muốn có được sự đồng nhất của các mẩu tin ta có thể lưu thông tin bên
ngoài bảng ký hiệu, trong mỗi ô của bảng chỉ chứa các con trỏ trỏ tới thông tin đó,
Trong bảng ký hiệu cũng có thể có lưu các từ khóa của ngôn ngữ. Nếu vậy thì
chúng phải được đưa vào bảng ký hiệu trước khi bộ phân tích từ vựng bắt đầu.
*
Nếu ghi trực tiếp tên trong trường tên của bảng thì: ưu điểm: đơn giản, nhanh.
Nhược điểm: Độ dài tên bị giới hạn bởi kích thước của trường , hiệu quả sử dụng
bộ nhớ không cao.
Trường hợp danh biểu bị giới hạn về độ dài thì chuỗi các ký tự tạo nên
danh biểu được lưu trữ trong bảng ký hiệu.
Name
Attribute
s o r
t
a
r e a d a r
r a y
i
Hình 7.19 - Bảng ký hiệu lưu giữ các tên bị giới hạn độ dài
Trường hợp độ dài tên không bị giới hạn thì các Lexeme được lưu trong một
mảng riêng và bảng ký hiệu chỉ giữ các con trỏ trỏ tới đầu mỗi Lexeme
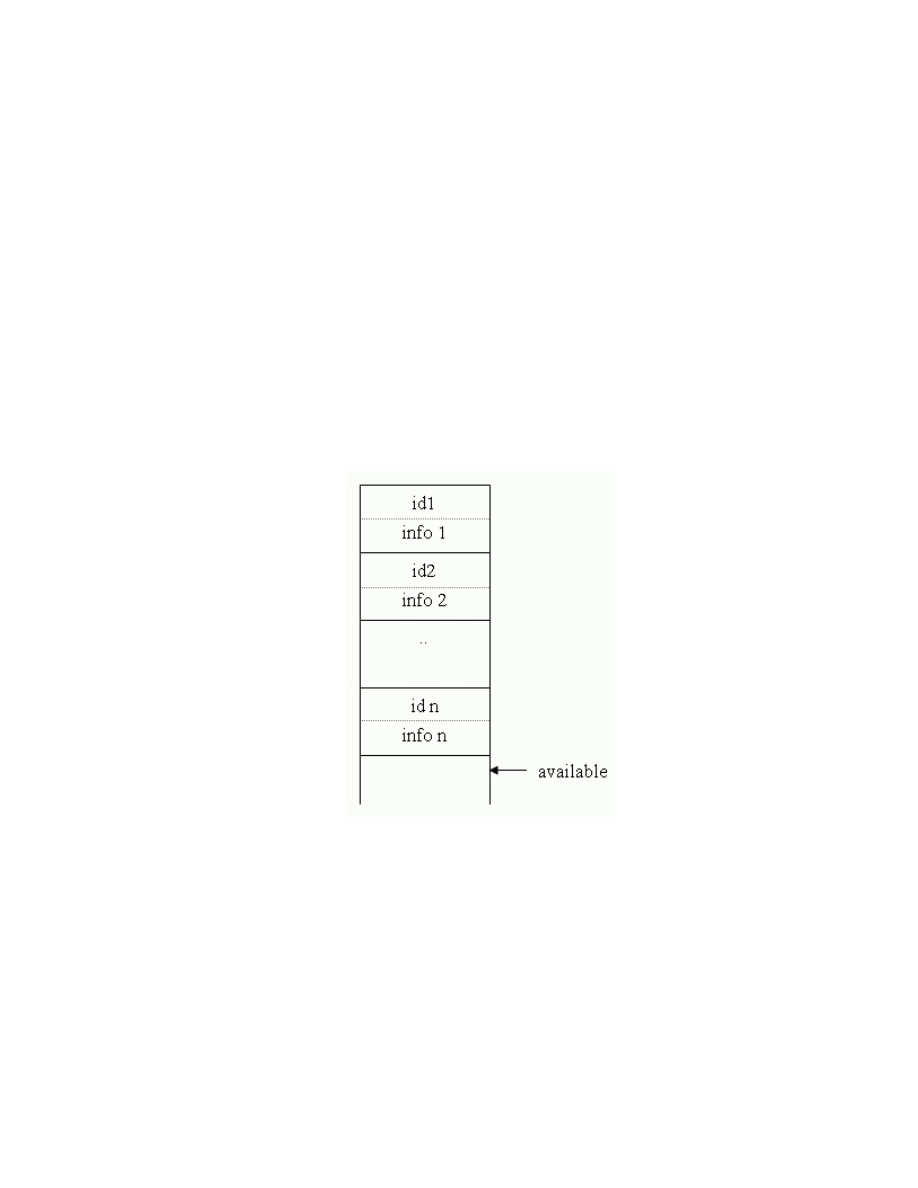
Hình 7.20 - Bảng ký hiệu lưu giữ các tên không bị giới hạn độ dài
3.1 Danh sách.
Cấu trúc đơn giản, dễ cài đặt nhất cho bảng ký hiệu là danh sách tuyến tính của các
mẩu tin.
Ta dùng một mảng hoặc nhiều mảng tương đương để lưu trữ tên và các thông tin
kết hợp với chúng. Các tên mới được đưa vào trong danh sách theo thứ tự mà
chúng được phát hiện. Vị trí của mảng được đánh dấu bởi con trỏ available chỉ ra
một ô mới của bảng sẽ được tạo ra.
Việc tìm kiếm một tên trong bảng ký hiệu được bắt đầu từ available đến đầu
bảng. Trong các ngôn ngữ cấu trúc khối sử dụng quy tắc tầm tĩnh. Thông tin kết
hợp với tên có thể bao gồm cả thông tin về độ sâu của tên. Bằng cách tìm kiếm từ
available trở về đầu mảng chúng ta đảm bảo rằng sẽ tìm thấy tên trong tầng gần
nhất.
Hình 7.21 - Danh sách tuyến tính các mẩu tin
3.2. Cây tìm kiếm.
Một trong các dạng cây tìm kiếm hiệu quả là: cây tìm kiếm nhị phân tìm
kiếm. Các nút của cây có khoá là tên của bản ghi, hai con tro Left, right.
Đối với mọi nút trên cây phải thoả mãn:
- Mọi khoá thuộc cây con trái nhỏ hơn khoá của gốc.
- Mọi nút của cây con phải lớn hơn khoá của gốc.
Giải thuật tìm kiếm trên cây nhị phân:
- So sánh giá trị tìm kiếm x với khoá của gốc:
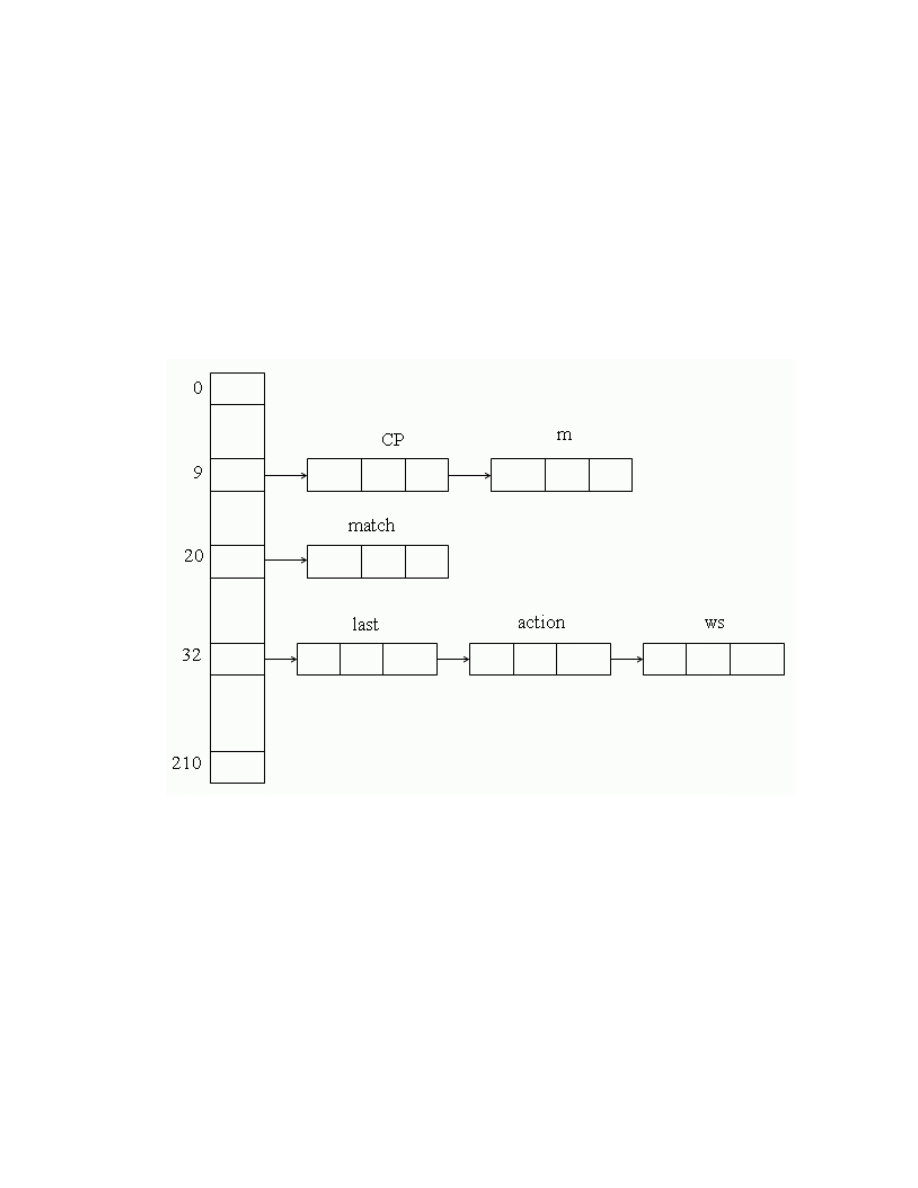
+ Nếu trùng: tìm kiếm thoả mãn.
+ Nếu < hơn: Thực hiện lại cách tìm kiểm với cây con bên trái.
+ Nếu > gốc: thực hiện lại cách tìm kiếm với cây con bên phải.
Để đảm bảo thời gian tìm kiếm người ta thay thé cây nhị phân tìm kiếm bằng cây nhị
phân cân bằng.
3.3. Bảng Băm.
Kỹ thuật sử dụng bảng băm để cài đặt bảng ký hiệu thường được sử dụng vì tính hiệu quả của
nó.
Cấu tạo bao gồm hai phần; bảng băm và các danh sách liên kết.
Hình 7.22 - Bảng băm có kích thước 211
1. Bảng băm là một mảng bao gồm m con trỏ.
2. Bảng danh biểu được chia thành m danh sách liên kết, mỗi danh sách liên kết
được trỏ bởi một phần tử trong bảng băm.
Việc phân bổ các danh biểu vào danh sách liên kết nào do hàm băm (hash
function) quy định. Giả sử s là chuỗi ký tự xác định danh biểu, hàm băm h tác động
lên s trả về một giá trị nằm giữa 0 và m- 1 h(s) = t => Danh biểu s được đưa vào
trong danh sách liên kết được trỏ bởi phần tử t của bảng băm.
Có nhiều phương pháp để xác định hàm băm.
Phương pháp đơn giản nhất như sau:

1. Giả sử s bao gồm các ký tự c1, c2, c3, ..., ck. Mỗi ký tự cho ứng với một số
nguyên dương n1, n2, n3,...,nk; lấy h = n1 + n2 +...+ nk.
2. Xác định h(s) = h mod m
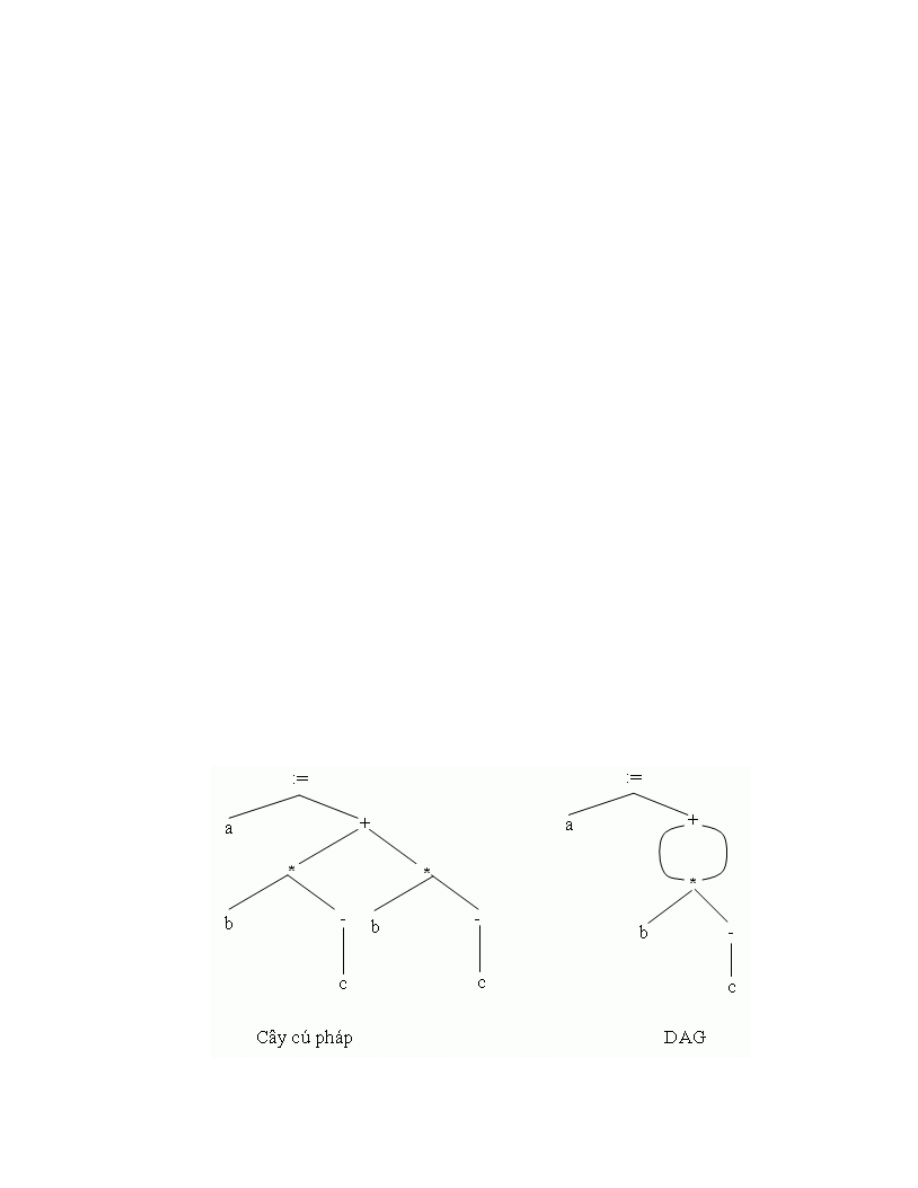
CHƯƠNG 8
SINH MÃ TRUNG GIAN
.
1. MỤC ĐÍCH NHIỆM VỤ.
* Sinh mã trung gian có những ưu điểm như sau:
- Dễ thiết kế từng phần
- Sinh được mã độc lập với từng máy tính cụ thể. Từ đó làm giảm độ phức tạp
của sinh mã thực sự.
- Dễ tối ưu mã.
* Các vấn đề của bộ sinh mã trung gian là:
- Dùng mã trung gian nào.
- Thuật toán sinh mã trung gian.
Hành động sinh mã trung gian thực hiện qua cú pháp điều khiển.
Ngôn ngữ trung gian là ngôn ngữ nằm giữa ngôn ngữ nguồn và ngôn ngữ đích. Chương
trình viết bằng ngôn ngữ trung gian vẫn tương đương với chương trình viét bàng ngôn ngữ
nguồn về chức năng nhiệm vụ. Sau đây ta xét loại mã trung gian thông dụng nhất.
2. CÁC NGÔN NGỮ TRUNG GIAN
Cây cú pháp, ký pháp hậu tố và mã 3 địa chỉ là các loại biểu diễn trung gian.
2.1. Đồ thị.
Cây cú pháp mô tả cấu trúc phân cấp tự nhiên của chương trình nguồn. DAG cho ta
cùng lượng thông tin nhưng bằng cách biểu diễn ngắn gọn hơn trong đó các biểu
thức con không được biểu diễn lặp lại.
Ví dụ 8.1: Với lệnh gán a := b * - c + b * - c, ta có cây cú pháp và DAG:
Hình 8.1 - Biểu diễn đồ thị của a :=b * - c + b * - c
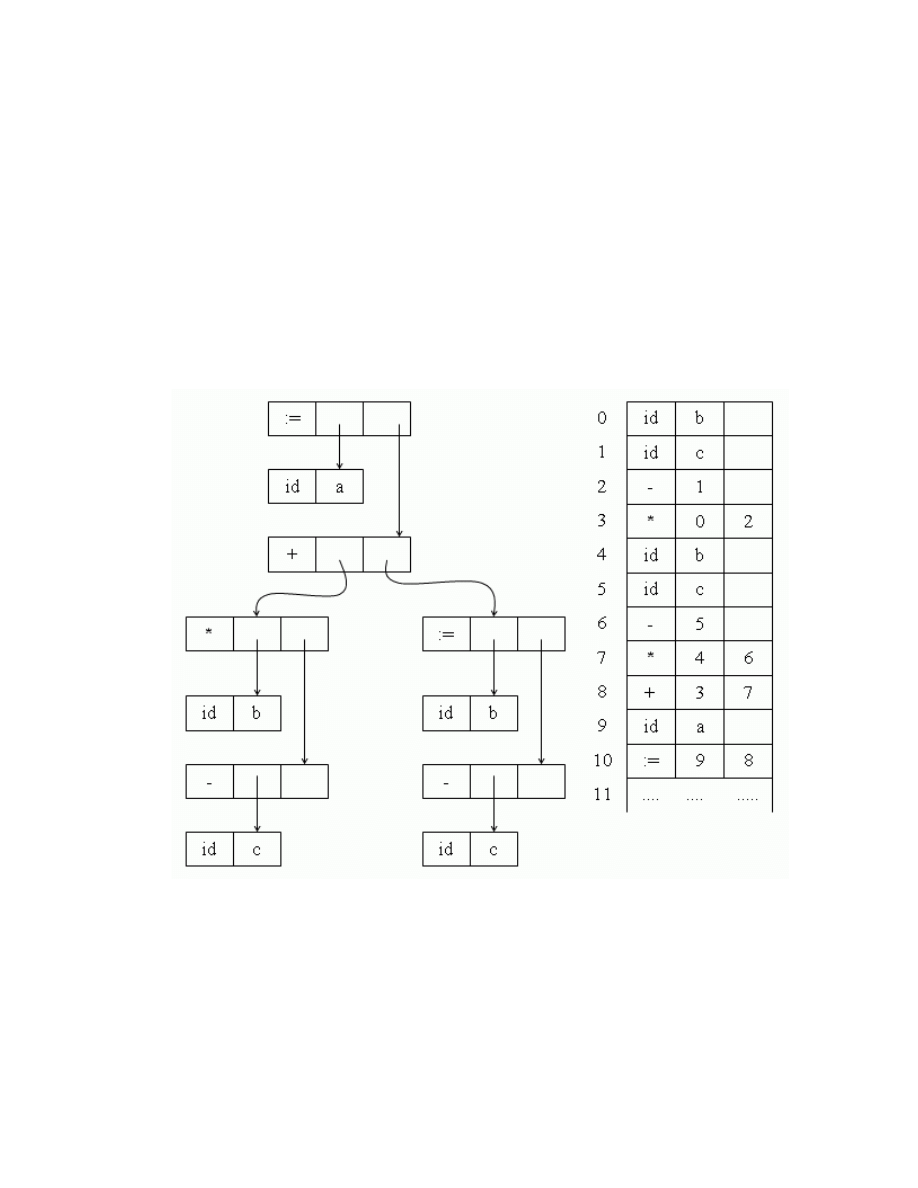
Ký pháp hậu tố là một biểu diễn tuyến tính của cây cú pháp. Nó là một danh
sách các nút của cây, trong đó một nút xuất hiện ngay sau con của nó .
a b c - * b c - * + := là biểu diễn hậu tố của cây cú pháp hình trên.
Cây cú pháp có thể được cài đặt bằng một trong 2 phương pháp:
- Mỗi nút được biểu diễn bởi một mẫu tin, với một trường cho toán tử và các
trường khác trỏ đến con của nó.
- Một mảng các mẩu tin, trong đó chỉ số của phần tử mảng đóng vai trò như là
con trỏ của một nút.
Tất cả các nút trên cây cú pháp có thể tuân theo con trỏ, bắt đầu từ nút gốc tại 10
Hình 8.2 - Hai biểu diễn của cây cú pháp trong hình 8.1
2.2. Kí pháp hậu tố.
Định nghĩa kí pháp hậu tố của một biểu thức:
1) E là một biến hoặc hằng số, kí pháp hậu tố của E là E.
2) E là biểu thức dạng: E
1
op E
2
với op là toán tử 2 ngôi thì kí pháp hậu tố của E là:
E’
1
E’
2
op với E’
1
, E’
2
là kí pháp hậu tố của E
1
, E
2
tương ứng.

3) Nếu E là biểu thức dạng (E
1
), thì kí pháp hậu tố của E
1
cũng là kí pháp hậu tố
của E.
Ví dụ:
Ví dụ: Kí pháp hậu tố của (9-5)+2 là 95-2+;
Kí pháp hậu tố của 9-(5+2) là 952+-;
Kí pháp hậu tố của câu lệnh
if a then if c-d then a+c else a*c else a+b
là a?(c-d?a+c:a*c):a+b tức là: acd-ac+ac*?ac+?
* Định nghĩa cú pháp điều khiển tạo mã hậu tố.
MÃ 3 ĐỊA CHỈ.
Mã ba địa là một chuỗi các câu lệnh, thông thường có dạng: x:= y op z
X,y,z là tên, hằng do người lập trình tự đặt, op là một phép toán nào đó phép toán
toán học, logic
…
Dưới đây là một số câu lệnh ba địa chỉ thông dụng:
1.
Các câu lệnh gán có dạng x := y op z, trong đó op là một phép toán số
học hai ngôi hoặc phép toán logic.
2.
Các phép gán có dạng x := op y, trong đó op là phép toán một ngôi.
Các phép toán một ngôi chủ yếu là phép trừ, phép phủ định logic, phép chuyển
đổi kiểu, phép dịch bít.
3.
Các câu lệnh sao chép dạng x := y, gán y vào x.
4.
Lệnh nhảy không điều kiện goto L. Câu lệnh ba địa chỉ có nhãn L là
câu lệnh được thực hiện tiếp theo.
5.
Các lệnh nhảy có điều kiện như if x relop y goto L. Câu lệnh này thực
hiện một phép toán quan hệ cho x và y, thực hiện câu lệnh có nhãn L nếu quan
hệ này là đúng, nếu trái lại sẽ thực hiện câu lệnh tiếp theo.
6.
Câu lệnh param x và call p,n dùng để gọi thủ tục. Còn lệnh return y để
trả về một giá trị lưu trong y. Ví dụ để gọi thủ tục p(x
1
,x
2
,...,x
n
) thì sẽ sinh các
câu lệnh ba địa chỉ tương ứng như sau:
param x
1
param x
2
. . .
param x
n
call p, n
7. Các phép gán chỉ số có dạng x := y[i] có ý nghĩa là gán cho x giá trị
tại vị trí i sau y
tương tự đối với x[i] := y
8. Phép gán địa chỉ và con trỏ có dạng x := &y, x := *y, *x := y
2.1. Cài đặt các câu lệnh ba địa chỉ
Trong chương trình dịch, những câu lệnh mã 3 địa chỉ có thể được cài đặt như các
cấu trúc với các trường chứa các toán tử và toán hạng. Những biểu diễn đó là bộ tứ
(quadruple) và bộ ba (triple
).
2.1.1. Bộ tứ
Bộ tứ là một cấu trúc bản ghi với bốn trường, được gọi là op, arg1, arg2 và
result.
Ví dụ: câu lệnh x := y + z
op là +, arg1 là y, arg2 là z và result chứa x. Đối với toán tử một ngôi thì không dùng
arg2.
Ví dụ: Câu lệnh a := -b * (c+d)
sẽ được chuyển thành đoạn mã ba địa chỉ như sau:
t1 := - b
t2 := c+d
t3 := t1 * t2
a := t3
và được biểu diễn bằng bộ tứ như sau:
Op
arg1
arg2
result
0
Uminus
b
t1
1
+
c
d
t2
2
*
t1
t2
t3
3
Assign
t3
a
2.1.2. Bộ ba
Để tránh phải đưa các tên tạm thời vào bảng ký hiệu, chúng ta có thể tham
chiếu đến một giá trị tạm bằng vị trí của câu lệnh dùng để tính nó (tham chiếu đến
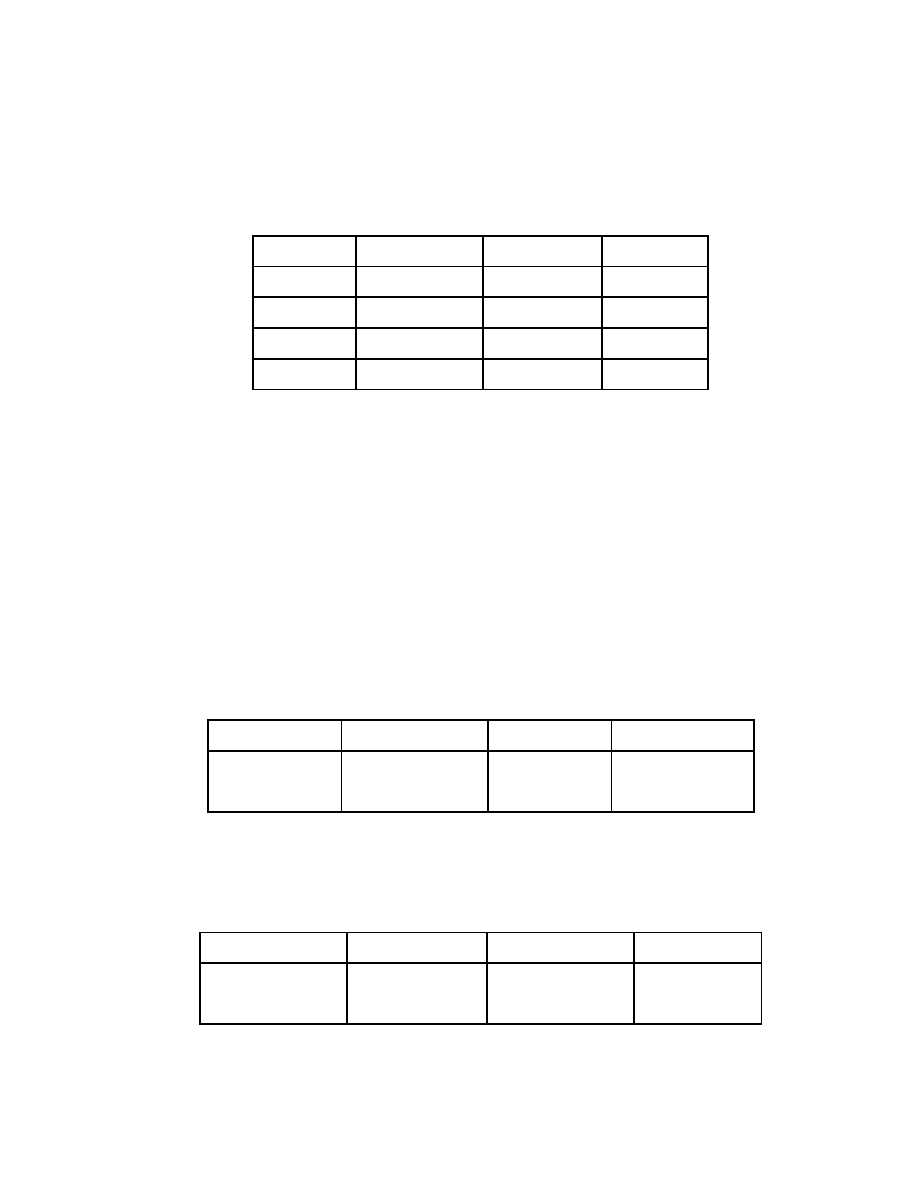
câu lệnh đó chính là tham chiếu đến con trỏ chứa bộ ba của câu lệnh đó). Nếu
chúng ta làm như vậy, câu lệnh mã ba địa chỉ sẽ được biểu diễn bằng một cấu trúc
chỉ gồm có ba trường op, arg1 và arg2.
Ví dụ trên sẽ được chuyển thành bộ ba như sau:
op
arg1
arg2
0
uminus
b
1
+
c
d
2
*
(0)
(1)
3
assign
a
(2)
Chú ý, câu lệnh sao chép đặt kết quả trong arg1 và tham số trong arg2 và toán tử là
assign.
Các số trong ngoặc tròn biểu diễn các con trỏ chỉ đến một cấu trúc bộ ba, còn
con trỏ chỉ đến bảng ký hiệu được biểu diễn bằng chính các tên. Trong thực hành,
thông tin cần để diễn giải các loại mục ghi khác nhau trong arg1 và arg2 có thể
được mã hoá vào trường op hoặc đưa thêm một số trường khác.
Chú ý, phép toán ba ngôi như x[i] := y cần đến hai mục trong cấu trúc bộ ba
như được chỉ ra như sau:
op
arg1
arg2
(0)
(1)
[]=
assign
x
(0)
i
y
tương tự đối với phép toán ba ngôi x := y[i]
op
arg1
arg2
(0)
(1)
[]=
assign
y
x
i
(0)
2.2. Cú pháp điều khiển sinh mã ba địa chỉ
Đối với mỗi ký hiệu X, ký hiệu:

-
X.place là nơi để chứa mã ba địa chỉ sinh ra bởi X (dùng để chứa các kết quả
trung gian).
Vì thế sẽ có một hàm định nghĩa là newtemp dùng để sinh ra một biến trung gian
(biến tạm) để gán cho X.place.
-
X.code chứa đoạn mã ba địa chỉ của X
-
Thủ tục gen để sinh ra câu lệnh ba địa chỉ.
Sau đây, chúng ta xét ví dụ sinh mã ba địa chỉ cho một số dạng câu lệnh.
2.2.1. Sinh mã ba địa chỉ cho biểu thức số học:
Sản xuất
Luật ngữ nghĩa
S -> id := E
S.code := E.code || gen(id.place ‘:=’ E.place)
E -> E
1
+ E
2
E.place := newtemp;
E.code := E
1
.code || E
2
.code || gen(E.place ‘:=’ E
1
.place
‘+’ E
2
.place)
E -> E
1
* E
2
E.place := newtemp;
E.code := E
1
.code || E
2
.code || gen(E.place ‘:=’ E
1
.place
‘+’ E
2
.place)
E -> - E
1
E.place := newtemp;
E.code := E
1
.code || gen(E.place ‘:=’ ‘uminus’ E
1
.place)
E -> ( E
1
)
E.place := E
1
.place
E.code := E
1
.code
E -> id
E.place := id.place
E.code := ‘’
Ví dụ:
Hãy sinh mã ba địa chỉ cho câu lệnh sau “x := a + ( b * c )”
S
=> x := E
=> x := E
1
+ E
2
=> x := a + E
2
=> x := a + ( E
3
)

=> x := a + ( E
4
* E
5
)
=> x := a+ ( b * E
5
)
=> x := a + ( b * c )
E
5
.place := c E
5
.code := ‘’
E
4
.place := b E
4
.code := ‘’
E
3
.place := t
1
E
3
.code := t
1
:= b * c
E
2
.place := t
1
E
2
.code := t
1
:= b * c
E
1
.place := a E
1
.code := ‘’
E
1
.place := a E
1
.code := ‘’
E.place := t
2
E.code := t
1
:= b * c || t
2
:= a + t
1
S.code := t
1
:= b * c || t
2
:= a + t
1
|| x := t
2
2.2.2. Sinh mã ba địa chỉ cho biểu thức Boole:
Đối với một biểu thức Boole E, ta dịch E thành một dãy các câu lệnh ba địa
chỉ, trong đó đối với các phép toán logic sẽ sinh ra các lệnh nhảy có điều kiện và
không có điều kiện đến một trong hai vị trí: E.true, nơi quyền điều khiển sẽ chuyển
tới nếu E đúng, và E.false, nơi quyền điều khiển sẽ chuyển tới nếu E sai.
Ví dụ: E có dạng a<b. Thế thì mã sinh ra sẽ có dạng
if a<b goto E.true
goto E.false
Ví dụ đoạn lệnh sau:
if a>b then
a:=a-b;
else
b:=b-a;
được chuyển thành mã ba địa chỉ như sau
E.true = L1 và E.false = L2
if a>b goto L1
goto L2
L1:
t1 := a –b
a := t1
goto Lnext
L2:
t2 := b-a
b := t2
Lnext:
Một số cú pháp điều khiển sinh mã ba địa chỉ cho các biểu thức Boole.
Để sinh ra các nhãn, chúng ta sử dụng thủ tục newlable để sinh ra một nhãn mới.
Sản xuất
Luật ngữ nghĩa
E -> E
1
or E
2
E
1
.true := E.true;
E
1
.false := newlable;
E
2
.true := E.true;
E
2
.false := E.false;
E.code := E
1
.code || gen(E
1
.false ‘:’) || E
2
.code
E -> E
1
and E
2
E
1
.true := newlable;
E
1
.false := E.false;
E
2
.true := E.true;
E
2
.false := E.false;
E.code := E
1
.code || gen(E
1
.true ‘:’) || E
2
.code
E -> not E
1
E
1
.true := E.false;
E
1
.false := E.true;
E.code := E
1
.code;
E -> ( E
1
)
E
1
.true := E.true;
E
1
.false := E.false;
E.code := E
1
.code;
E -> id
1
relop id
2
E.code := gen(‘if’ id
1
.place relop.op id
2
.place ‘goto’ E.true) ||
gen(‘goto’ E.false)
E -> true
E.code := gen(‘goto’ E.true)
E -> false
E.code := gen(‘goto’ E.false)
Ví dụ: Sinh mã ba địa chỉ cho đoạn chương trình sau:
if a>b and c>d then
x:=y+z
else
x:=y-z
Lời giải:
Nếu coi E là biểu thức logic a>b and c>d thì đoạn chương trình trên trở thành

if E then x:=y+z , khi đó mã ba địa chỉ cho đoạn chương trình có dạng:
E.code {
if E=true goto E.true
goto E.false }
E.true: t1:= y+z
x := t1;
E.false :
t2 := y-z
x :=t2
Như vậy chúng ta phải phân tích bên trong của biểu thức E, và dễ thấy các lệnh nhảy bên
trong E chính là E.true và E.false, điều đó giải thích tại sao chúng ta lại có các luật ngữ nghĩa
như bảng trên.
Áp dụng các luật sinh mã ba địa chỉ trong bảng trên chúng ta có đoạn mã ba
địa chỉ cho đoạn chương trình nguồn ở trên là:
if a>b goto L1
goto L3
L1:
if c>d goto L2
goto L3
L2:
t1 := y+z
x := t1
goto L4
L3:
t2 := y-z
x := t2
L4:
2.2.3. Sinh mã ba địa chỉ cho một số lệnh điều khiển:
Trong các câu lệnh điều khiển có điều kiện, ta dựa vào biểu thức logic E để
chuyển việc thực hiện các câu lệnh tới vị trí thích hợp. Do đó ta cần hai nhãn:
E.true (
để xác định vị trí câu lệnh chuyển tới khi biểu thức logic E là đúng
), nhãn
E.false (
để xác định vị trí câu lệnh chuyển tới khi biểu thức logic E là sai
).
Để sinh ra một nhãn mới, ta dùng thủ tục newlable.
Nhãn S.next đối với khối lệnh sinh ra bởi ký hiệu S là nhãn xác định vị trí tiếp
theo của các lệnh sau S.
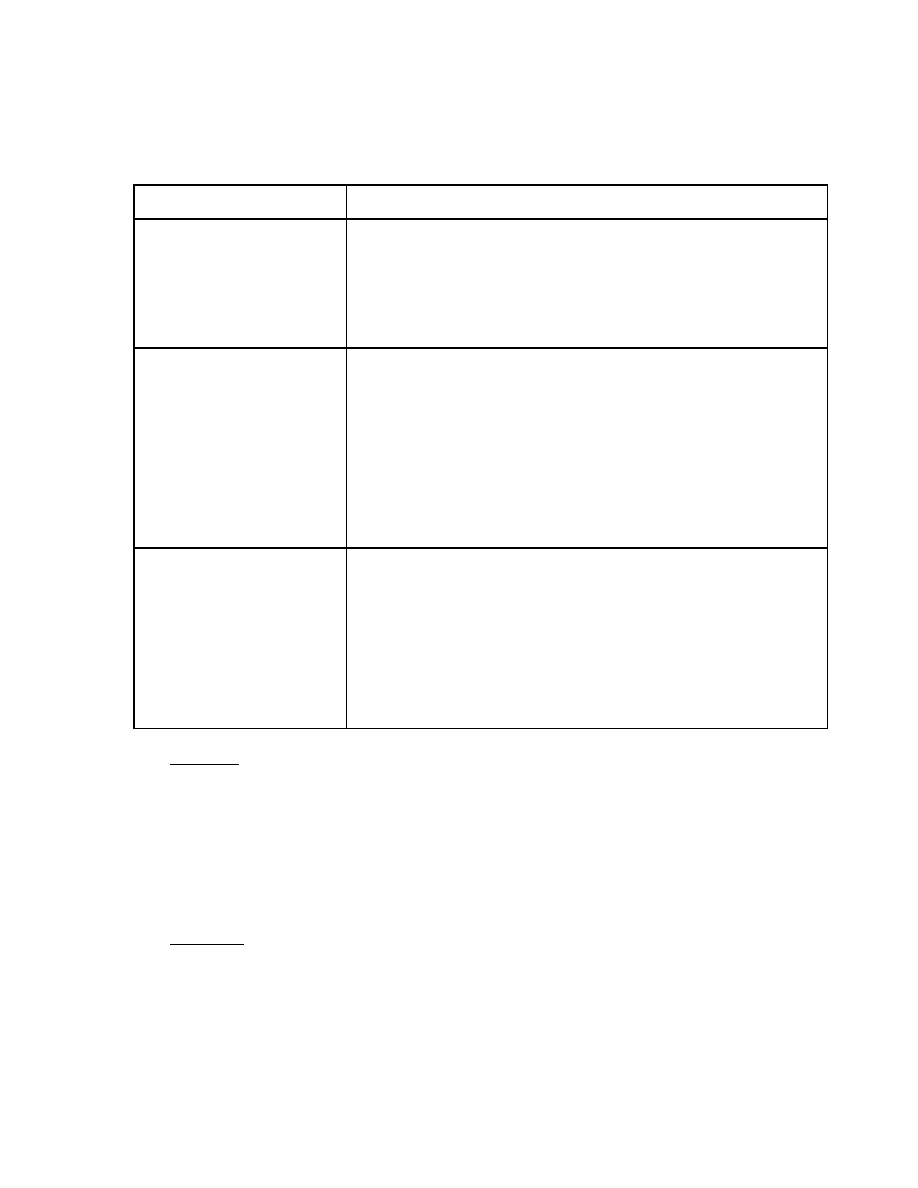
Đối với câu lệnh S -> while E do S
1
ta cần có một nhãn bắt đầu của khối lệnh này để nhảy đến mỗi khi E đúng, vì
vậy cần nhãn S.begin để xác định vị trí bắt đầu khối lệnh này.
Sản xuất
Luật ngữ nghĩa
S -> if E then S
1
E.true := newlable;
E.false := S.next;
S
1
.next := S.next;
S.code := E.code || gen(E.true ‘:’) || S
1
.code
S -> if E then S
1
else
S
2
E.true := newlable;
E.false := newlable;
S
1
.next := S.next;
S
2
.next := S.next;
S.code := E.code || gen(E.true ‘:’) || S
1
.code ||
gen(‘goto’ S.next) || gen(E.false ‘:’) || S
2
.code
S -> while E do S
1
S.begin := newlable;
E.true := newlable;
E.false := S.next
S
1
.next := S.begin;
S.code := gen(S.begin ‘:’) || E.code || gen(E.true ‘:’) ||
S
1
.code || gen(‘goto’ S.begin)
Ví dụ 1: sinh đoạn mã ba địa chỉ cho đoạn mã nguồn sau:
while a<>b do
if a>b then
a:=a-b
else
b:=b-a
Lời giải
:
L1:
if a<>b goto L2
goto Lnext
L2:
if a>b goto L3
goto L4
L3:
t1 := a-b

a := t1
goto L1
L4:
t2 := b-a
b := t2
goto L1
Lnext:
2.2.3.Các khai báo.
Đối với các khai báo định danh, ta không sinh ra mã lệnh tương ứng trong mã
ba địa chỉ mà dùng bảng ký hiệu để lưu trữ.
Như vậy có thể hiểu là kết quả của sinh mã
ba địa chỉ từ chương trình nguồn là tập lệnh ba địa chỉ và bảng ký hiệu quản lý các định danh.
Với mỗi định danh, ta lưu các thông tin về kiểu và địa chỉ tương đối để lưu giá
trị cho định danh đó.
Ví dụ:
Giả sử ký hiệu offset để chứa địa chỉ tương đối của các định danh; mỗi số
interger chiếm 4 byte, số real chứa 8 byte và mỗi con trỏ chứa 4 byte; giả sử hàm
enter dùng để nhập thông tin về kiểu và địa chỉ tương đối cho một định danh, chúng
ta có ví dụ dưới đây mô ta việc sinh thông tin vào bảng ký hiệu cho các khai báo.
Sản xuất
Luật ngữ nghĩa
P -> D
offset := 0
D -> D ; D
D -> id : T
enter(id.name,T.type, offset) ;
offset := offset + T. width
T -> interger
T.type := interger;
T. width := 4
T -> real
T.type := real; T. width := 8
T -> array [ num ] of T
1
T.type := array(num.val,T
1
.type);
T.width := num.val * T
1
. width
T -> ^T
1
T.type := pointer(T
1
.type)
T. width := 4
Trong các đoạn mã ba địa chỉ, khi đề cập đến một tên, ta sẽ tham chiếu đến bảng ký
hiệu để lấy thông tin về kiểu, địa chỉ tương ứng để sử dụng trong các câu lệnh.
Hay
nói cách khác chúng ta có thể thay một định danh bởi chỉ mục của định danh đó trong bảng ký
hiệu.
Chú ý: Địa chỉ tương đối của một phần tử trong mảng, ví dụ x[i], được tính bằng
địa chỉ của x cộng với i lần độ dài của mỗi phần tử.
Bài tập
Bài tập 1: Hãy chuyển các câu lệnh hoặc đoạn chương trình sau thành đoạn mã ba
địa chỉ:
1)
a * - (b+c)
2)
đoạn chương trình C
main ()
{ int i; int a[100];
i=1;
while(i<=10)
{ a[i]=0;
i=i+1;
}
}
.1. Dịch biểu thức : a * - ( b + c) thành các dạng :
a) Cây cú pháp.
b) Ký pháp hậu tố.
c) Mã lệnh máy 3 - địa chỉ.
8.2. Trình bày cấu trúc lưu trữ biểu thức - ( a + b) * ( c + d ) + ( a + b + c) ở các dạng :
a) Bộ tứ .
b) Bộ tam.
c) Bộ tam gián tiếp.
8.3. Sinh mã trung gian ( dạng mã máy 3 - địa chỉ) cho các biểu thức C đơn giản sau :
a) x = 1
b) x = y
c) x = x + 1
d) x = a + b * c
e) x = a / ( b + c) - d * ( e + f )
8.4. Sinh mã trung gian ( dạng mã máy 3 - địa chỉ) cho các biểu thức C sau :

a) x = a [i] + 11
b) a [i] = b [ c[j] ]
c) a [i][j] = b [i][k] * c [k][j]
d) a[i] = a[i] + b[j]
e) a[i] + = b[j]
8.5. Dịch lệnh gán sau thành mã máy 3 - địa chỉ :
A [ i,j ] := B [ i,j ] + C [A[ k,l]] + D [ i + j ]
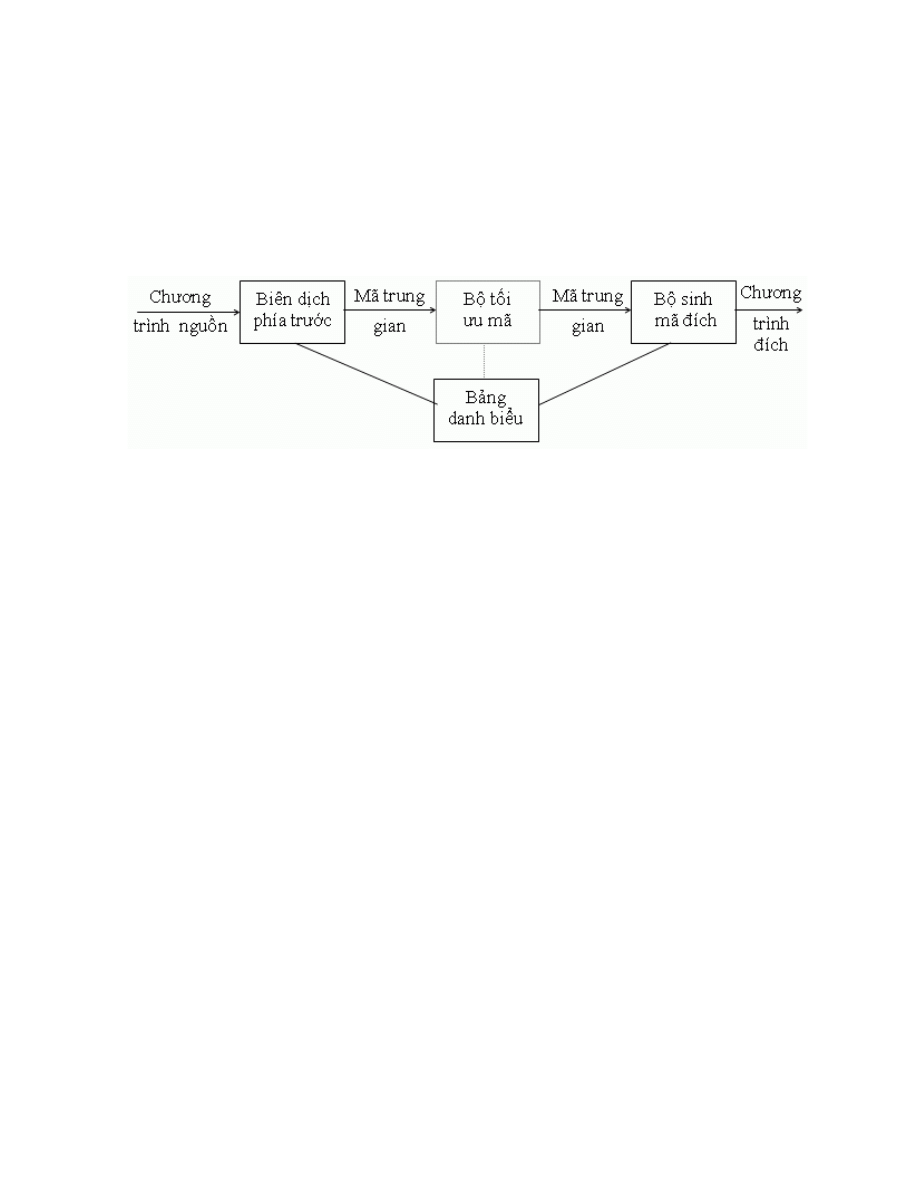
CHƯƠNG 9
SINH MÃ
1. MỤC ĐÍCH NHIỆM VỤ
Giai đoạn cuối của quá trình biên dịch là sinh mã đích.
Kỹ thuật sinh mã đích được
trình bày trong chương này không phụ thuộc vào việc dùng hay không dùng giai đoạn tối ưu mã
trung gian
.
Sinh mã tốt rất khó, mã sinh ra thường gắn với một loại máy tính cụ thể nào
đó.
Đầu vào của bộ sinh mã là mã trung gian, đầu ra là một chương trình viết
dạng mã đối tượng nào đó và gọi là chương trình đích.
Ðầu vào của bộ sinh mã gồm biểu diễn trung gian của chương trình nguồn, cùng
thông tin trong bảng danh biểu được dùng để xác định địa chỉ của các đối tượng dữ liệu
trong thời gian thực thi. Các đối tượng dữ liệu này được tượng trưng bằng tên trong biểu
diễn trung gian. Biểu diễn trung gian của chương trình nguồn có thể ở một trong các
dạng: ký pháp hậu tố, mã ba địa chỉ, cây cú pháp, DAG
Tiêu chuẩn quan trọng nhất đối với bộ sinh mã là sinh mã đúng.
Tính đúng của mã
có một ý nghĩa rất quan trọng. Với những quy định về tính đúng của mã, việc thiết kế bộ
sinh mã sao cho nó được thực hiện, kiểm tra, bảo trì đơn giản là mục tiêu thiết kế quan
trọng .
2. CÁC DẠNG MÃ ĐỐI TƯỢNG.
2.1. Mã máy định vị tuyệt đối.
Một chương trình mã máy tuyệt đối có các lệnh mã máy được định vị tuyệt
đối. Chương trình dịch xác định hoàn toàn chương trình đối tượng này.
Mã được một chương trình dịch thực sự tạo ra và đặt vào các vị trí này nên
chương trình có thể hoạt động ngay.

Ưu điểm: giảm số
2.2. Mã đối tượng có thể định vị lại được.
2.3. Mã đối tượng thông dịch.
Việc tạo ra chương đích ở dạng hợp ngữ cho phép ta dùng bộ biên dịch hợp ngữ để
tạo ra mã máy.
3. CÁC VẤN ĐỀ THIẾT KẾ CỦA BỘ SINH MÃ.
Sự lựa chọn chỉ thị
Tập các chỉ thị của máy đích sẽ xác định tính phức tạp của việc lựa chọn chỉ thị. Tính
chuẩn và hoàn chỉnh của tập chỉ thị là những yếu tố quan trọng. Nếu máy đích không
cung cấp một mẫu chung cho mỗi kiểu dữ liệu thì mỗi trường hợp ngoại lệ phải xử lý
riêng. Tốc độ chỉ thị và sự biểu diễn của máy cũng là những yếu tố quan trọng. Nếu ta
không quan tâm đến tính hiệu quả của chương trình đích thì việc lựa chọn chỉ thị sẽ đơn
giản hơn. Với mỗi lệnh ba địa chỉ ta có thể phác họa một bộ khung cho mã đích. Giả sử
lệnh ba địa chỉ dạng x := y + z, với x, y, z được cấp phát tĩnh, có thể được dịch sang
chuỗi mã đích:
MOV y, R0 /* Lưu y vào thanh ghi Ro */
ADD z, R0 /* cộng z vào nội dung Ro, kết quả chứa trong Ro */
MOV R0, x /* lưu nội dung Ro vào x */
Tuy nhiên việc sinh mã cho chuỗi các lệnh ba địa chỉ sẽ dẫn đến sự dư thừa mã. Chẳng
hạn với:
a:= b + c
d:= a + e
ta chuyển sang mã đích:
MOV b, R
o
ADD c, R
o
MOV R
o
, a
MOV a, R
0
ADD e,R
o
MOV R
o
, d
và ta nhận thấy rằng chỉ thị thứ tư là thừa.
Chất lượng mã được tạo ra, được xác định bằng tốc độ và kích thước của mã. Một máy
đích có tập chỉ thị phong phú có thể sẽ cung cấp nhiều cách để hiện thực một tác vụ cho
trước. Ðiều này có thể dẫn đến tốc độ thực hiện chỉ thị rất khác nhau. Chẳng hạn, nếu máy

đích có chỉ thị INC thì câu lệnh ba địa chỉ a := a + 1 có thể được cài đặt chỉ bằng câu
lệnh INC a. Cách nầy hiệu quả hơn là dùng chuỗi các chỉ thị sau:
MOV a, R
o
ADD # 1, R
o
MOV R
o ,
a
Như ta đã nói, tốc độ của chỉ thị là một trong những yếu tố quan trọng để thiết kế chuỗi
mã tốt. Nhưng, thông tin thời gian thường khó xác định.
Việc quyết định chuỗi mã máy nào là tốt nhất cho câu lệnh ba điạ chỉ còn phụ thuộc
vào ngữ cảnh của nơi chưá câu lệnh đó.
Cấp phát thanh ghi
Các chỉ thị dùng toán hạng thanh ghi thường ngắn hơn và nhanh hơn các chỉ thị dùng
toán hạng trong bộ nhớ. Vì thế, hiệu quả của thanh ghi đặc biệt quan trọng trong việc
sinh mã tốt. Ta thường dùng thanh ghi trong hai trường hợp:
1. Trong khi cấp phát thanh ghi, ta lựa chọn tập các biến lưu trú trong các thanh ghi tại
một thời điểm trong chương trình.
2. Trong khi gán thanh ghi, ta lấy ra thanh ghi đặc biệt mà biến sẽ thường trú trong đó.
Việc tìm kiếm một lệnh gán tối ưu của thanh ghi, ngay với cả các giá trị thanh ghi đơn,
cho các biến là một công việc khó khăn. Vấn đề càng trở nên phức tạp hơn vì phần cứng
và / hoặc hệ điều hành của máy đích yêu cầu qui ước sử dụng thanh ghi.
3.3. Quản lý bộ nhớ.
Trong phần này ta sẽ nói về việc sinh mã để quản lý các mẩu tin hoạt động trong thời
gian thực hiện. Hai chiến lược cấp phát bộ nhớ chuẩn được trình bầy trong chương VII là
cấp phát tĩnh và cấp phát Stack. Với cấp phát tĩnh, vị trí của mẩu tin hoạt động trong bộ
nhớ được xác định trong thời gian biên dịch. Với cấp phát Stack, một mẩu tin hoạt động
được đưa vào Stack khi có sự thực hiện một thủ tục và được lấy ra khỏi Stack khi hoạt
động kết thúc. Ở đây, ta sẽ xem xét cách thức mã đích của một thủ tục tham chiếu tới các
đối tượng dữ liệu trong các mẩu tin hoạt động. Như ta đã nói ở chương VII, một mẩu tin
hoạt động cho một thủ tục có các trường: tham số, kết quả, thông tin về trạng thái máy, dữ
liệu cục bộ, lưu trữ tạm thời và cục bộ, và các liên kết. Trong phần nầy, ta minh họa các
chiến lược cấp phát sử dụng trường trạng thái để giữ giá trị trả về và dữ liệu cục bộ, các
trường còn lại được dùng như đã đề cập ở chương VII.
Việc cấp phát và giải phóng các mẩu tin hoạt động là một phần trong chuỗi hành vi gọi
và trả về của chương trình con. Ta quan tâm đến việc sinh mã cho các lệnh sau:
1. call
2. return
3. halt
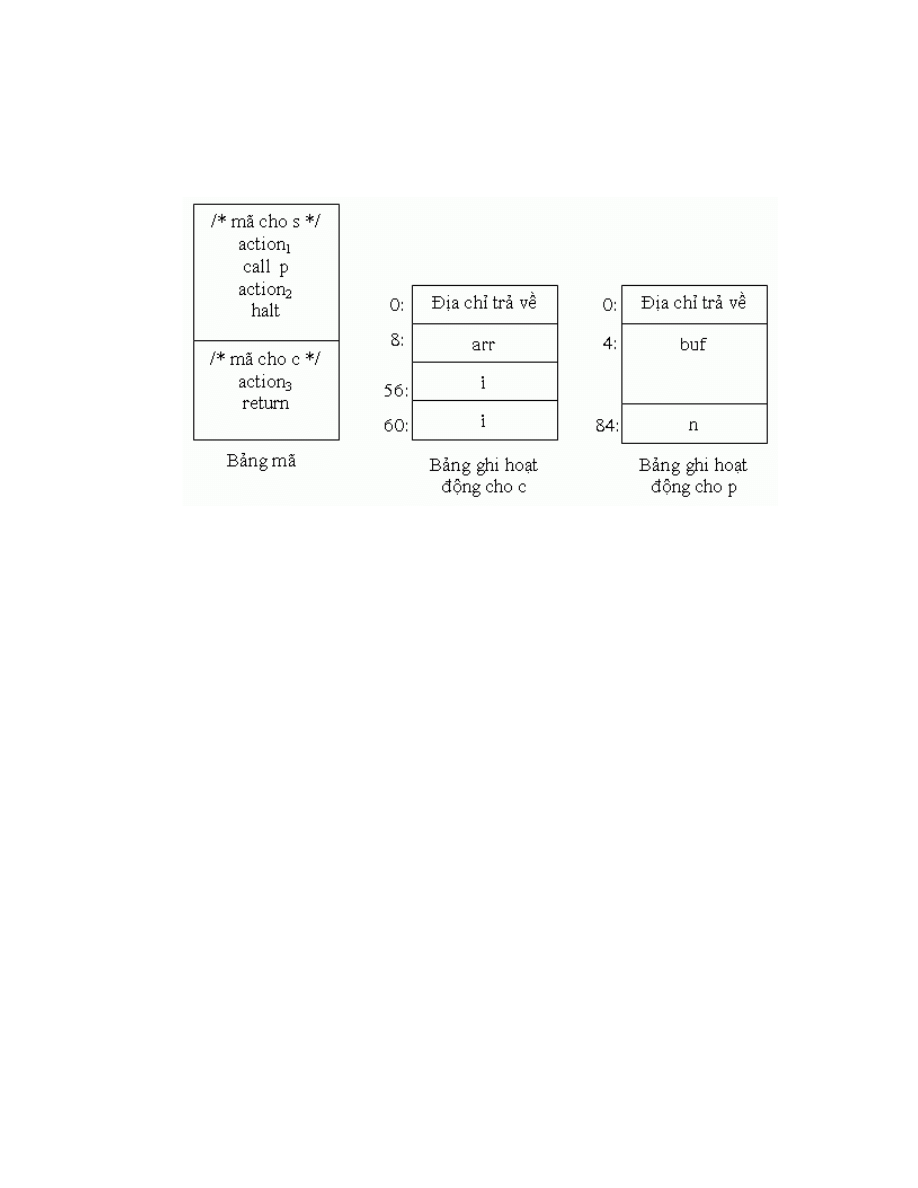
4. action /* tượng trưng cho các lệnh khác */
Chẳng hạn, mã ba địa chỉ, chỉ chứa các loại câu lệnh trên, cho các chương trình c và p
cũng như các mẩu tin hoạt động của chúng:
Hình 9.2 - Ðầu vào của bộ sinh mã
Kích thước và việc xếp đặt các mẩu tin được kết hợp với bộ sinh mã nhờ thông tin về
tên trong bảng danh biểu.
Ta giả sử bộ nhớ thời gian thực hiện được phân chia thành các vùng cho mã, dữ liệu
tĩnh và Stack.
1. Cấp phát tĩnh
Chúng ta sẽ xét các chỉ thị cần thiết để thực hiện việc cấp phát tĩnh. Lệnh call trong mã
trung gian được thực hiện bằng dãy hai chỉ thị đích. Chỉ thị MOV lưu địa chỉ trả về. Chỉ
thị GOTO chuyển quyền điều khiển cho chương trình được gọi.
MOV # here + 20, callee.static_area
GOTO callee.code_area
Các thuộc tính callee.static_area và callee.code_area là các hằng tham chiếu tới các địa
chỉ của mẩu tin hoạt động và chỉ thị đầu tiên trong đoạn mã của chương trình con được
gọi. # here + 20 trong chỉ thị MOV là địa chỉ trả về. Nó cũng chính là địa chỉ của chỉ thị
đứng sau lệnh GOTO. Mã của chương trình con kết thúc bằng lệnh trả về chương trình
gọi, trừ chương trình chính, đó là lệnh halt. Lệnh này trả quyền điều khiển cho hệ điều
hành. Lệnh trả về được dịch sang mã máy là GOTO *callee_static_area thực hiện việc
chuyển quyền điều khiển về địa chỉ được lưu giữ ở ô nhớ đầu tiên của mẩu tin hoạt động
.

Ví dụ 9.1: Mã đích trong chương trình sau được tạo ra từ các chương trình con c và p ở
hình 9.2. Giả sử rằng: các mã đó được lưu tại địa chỉ bắt đầu là 100 và 200, mỗi chỉ thị
action chiếm 20 byte, và các mẩu tin hoạt động cho c và p được cấp phát tĩnh bắt đầu tại
các địa chỉ 300 và 364 . Ta dùng chỉ thị action để thực hiện câu lệnh action. Như vậy, mã
đích cho các chương trình con:
/* mã cho c*/
100: ACTION
1
120: MOV #140, 364 /* lưu địa chỉ trả về 140 */
132: GOTO 200 /* gọi p */
140: ACTION
2
160: HALT
/* mã cho p */
200: ACTION
3
220: GOTO *364 /* trả về địa chỉ được lưu tại vị trí 364 */
/* 300-364 lưu mẩu tin hoạt động của c */
300: /* chứa địa chỉ trả về */
304: /* dữ liệu cục bộ của c */
/* 364 - 451 chứa mẩu tin hoạt động của p */
364: /* chứa địa chỉ trả về */
368: /* dữ liệu cục bộ của p */
Hình 9.3 - Mã đích cho đầu vào của hình 9.2
Sự thực hiện bắt đầu bằng chỉ thị action tại địa chỉ 100. Chỉ thị MOV ở địa chỉ 120 sẽ
lưu địa chỉ trả về 140 vào trường trạng thái máy, là từ đầu tiên trong mẩu tin hoạt động
của p. Chỉ thị GOTO 200 sẽ chuyển quyền điều khiển về chỉ thị đầu tiên trong đoạn mã
của chương trình con p. Chỉ thị GOTO *364 tại địa chỉ 132 chuyển quyền điều khiển sang
chỉ thị đầu tiên trong mã đích của chương trình con được gọi.
Giá trị 140 được lưu vào địa chỉ 364, *364 biểu diễn giá trị 140 khi lệnh GOTO tại địa
chỉ 220 được thực hiện. Vì thế quyền điều khiển trả về địa chỉ 140 và tiếp tục thực hiện
chương trình con c.
2. Cấp phát theo cơ chế Stack
Cấp phát tĩnh sẽ trở thành cấp phát Stack nếu ta sử dụng địa chỉ tương đối để lưu giữ
các mẩu tin hoạt động. Vị trí mẩu tin hoạt động chỉ được xác định trong thời gian thực thi.
Trong cấp phát Stack, vị trí nầy thường được lưu vào thanh ghi. Vì thế các ô nhớ của mẩu
tin hoạt động được truy xuất như là độ dời (offset) so với giá trị trong thanh ghi đó.
Thanh ghi SP chứa địa chỉ bắt đầu của mẩu tin hoạt động của chương trình con nằm
trên đỉnh Stack. Khi lời gọi của chương trình con xuất hiện, chương trình bị gọi được cấp

phát, SP được tăng lên một giá trị bằng kích thước mẩu tin hoạt động của chương trình
gọi và chuyển quyền điều khiển cho chương trình con được gọi. Khi quyền điều khiển trả
về cho chương trình gọi, SP giảm đi một khoảng bằng kích thước mẩu tin hoạt động của
chương trình gọi. Vì thế, mẩu tin của chương trình con được gọi đã được giải phóng.
Mã cho chương trình con đầu tiên có dạng:
MOV # Stackstart, SP /* khởi động Stack */
Ðoạn mã cho chương trình con
HALT /* kết thúc sự thực thi */
Trong đó chỉ thị đầu tiên MOV #Stackstart, SP khởi động Stack theo cách đặt SP bằng
với địa chỉ bắt đầu của Stack trong vùng nhớ.
Chuỗi gọi sẽ tăng giá trị của SP, lưu giữ địa chỉ trả về và chuyển quyền điều khiển về
chương trình được gọi.
ADD # caller.recordsize, SP
MOV # here + 16, *SP /* lưu địa chỉ trả về */
GOTO callee.code_area
Thuộc tính caller.recordsize biểu diễn kích thước của mẩu tin hoạt động. Vì thế, chỉ thị
ADD đưa SP trỏ tới phần bắt đầu của mẩu tin hoạt động kế tiếp. #here +16 trong chỉ thị
MOV là địa chỉ của chỉ thị theo sau GOTO, nó được lưu tại địa chỉ được trỏ bởi SP.
Chuỗi trả về gồm hai chỉ thị:
1. Chương trình con chuyển quyền điều khiển tới địa chỉ trả về
GOTO *0(SP) /* trả về chương trình gọi */
SUB #caller.recordsize, SP
Trong đó O(SP) là địa chỉ của ô nhớ đầu tiên trong mẩu tin hoạt động. *O(SP) trả về
địa chỉ được lưu tại đây.
2. Chỉ thị SUB #caller.recordsize, SP: Giảm giá trị của SP xuống một khoảng bằng
kích thước mẩu tin hoạt động của chương trình gọi. Như vậy mẩu tin hoạt động chương
trình bị gọi đã xóa khỏi Stack .
Ví dụ 9.2: Giả sử rằng kích thước của các mẩu tin hoạt động của các chương trình con s,
p, và q được xác định tại thời gian biên dịch là ssize, psize, và qsize tương ứng. Ô nhớ
đầu tiên trong mỗi mẩu tin hoạt động lưu địa chỉ trả về. Ta cũng giả sử rằng, đoạn mã cho
các chương trình con nầy bắt đầu tại các địa chỉ 100, 200, 300 tương ứng, và địa chỉ bắt
đầu của Stack là 600. Mã đích cho chương trình trong hình 9.4 được mô tả trong hình
9.5:

/* mã cho s */
action1
call q
action2
halt
/* mã cho p */
action3
return
/* mã cho q */
action
4
call p
action
5
call q
action
6
call q
return
Hình 9.4 - Mã ba địa chỉ minh hoạ cấp phát sử dụng Stack
/* mã cho s*/
100: MOV # 600, SP /* khởi động Stack */
108: ACTION
1
128: ADD #ssize, SP /* chuỗi gọi bắt đầu */
136: MOV #152, *SP /* lưu địa chỉ trả về */
144: GOTO 300 /* gọi q */
152: SUB #ssize, SP /* Lưu giữ SP */
160: ACTION
2
180: HALT
/* mã cho p */
200: ACTION
3
220: GOTO *0(SP) /* trả về chương trình gọi */
/* mã cho q */
300: ACTION4 /* nhảy có điều kiện về 456 */
320: ADD #qsize, SP
328: MOV #344, *SP /* lưu địa chỉ trả về */
336: GOTO 200 /* gọi p */
344: SUB #qsize, SP
352: ACTION
5
372: ADD #qsize, SP
380: MOV #396, *SP /* lưu địa chỉ trả về */
388: GOTO 300 /* gọi q */

396: SUB #qsize, SP
404: ACTION
6
424: ADD #qsize, SP
432: MOV #448, *SP /* lưu địa chỉ trả về */
440: GOTO 300 /* gọi q */
448: SUB #qsize, SP
456: GOTO *0(SP) /* trả về chương trình gọi */
600: /* địa chỉ bắt đầu của Stack trung tâm */
Hình 9.5 - Mã đích cho chuỗi ba địa chỉ trong hình 9.4
Ta giả sử rằng action4 gồm lệnh nhảy có điều kiện tới địa chỉ 456 có lệnh trả về từ q.
Ngược lại chương trình đệ quy q có thể gọi chính nó mãi. Trong ví dụ này chúng ta giả sử
lần gọi đầu tiên trên q sẽ không trả về chương tình gọi ngay, nhưng những lần sau thì có
thể. SP có giá trị lúc đầu là 600, địa chỉ bắt đầu của Stack. SP lưu giữ giá trị 620 chỉ trước
khi chuyển quyền điều khiển từ s sang q vì kích thước của mẩu tin hoạt động s là 20. Khi
q gọi p, SP sẽ tăng lên 680 khi chỉ thị tại địa chỉ 320 được thực hiện, Sp chuyển sang 620
sau khi chuyển quyền điều khiển cho chương trình con p. Nếu lời gọi đệ quy của q trả về
ngay thì giá trị lain nhất của SP trong suốt quá trình thực hiện là 680. Vị trí được cấp phát
theo cơ chế Stack có thể lên đến địa chỉ 739 vì mẩu tin hoạt động của q bắt đầu tại 680 và
chiếm 60 byte.
3. Ðịa chỉ của các tên trong thời gian thực hiện
Chiến lược cấp phát lưu trữ và xếp đặt dữ liệu cục bộ trong mẩu tin hoạt động của
chương trình con xác định cách thức truy xuất vùng nhớ của tên.
Nếu chúng ta dùng cơ chế cấp phát tĩnh với vùng dữ liệu được cấp phát tại địa chỉ
static. Với lệnh gán x := 0, địa chỉ tương đối của x trong bảng danh biểu là 12. Vậy địa chỉ
của x trong bộ nhớ là static + 12. Lệnh gán x:=0 được chuyển sang mã ba địa chỉ
static[12] := 0. Nếu vùng dữ liệu bắt đầu tại địa chỉ 100, mã đích cho chỉ thị là:
MOV #0,112
Nếu ngôn ngữ dùng cơ chế display để truy xuất tên không cục bộ, giả sử x là tên cục
bộ của chương trình con hiện hành và thanh ghi R3 lưu giữ địa chỉ bắt đầu của mẩu tin
hoạt động đó thì chúng ta sẽ dịch lệnh x := 0 sang chuỗi mã ba địa chỉ:
t
1
:= 12 + R
3
* t
1
:= 0
Từ đó ta chuyển sang mã đích:
MOV #0, 12(R
3
)

Chú ý rằng, giá trị thanh ghi R3 không được xác định trong thời gian biên dịch
3.4. Chọn chỉ thị lệnh.
Tập các chỉ thị của máy đích sẽ xác định tính phức tạp của việc lựa chọn chỉ thị. Tính
chuẩn và hoàn chỉnh của tập chỉ thị là những yếu tố quan trọng. Nếu máy đích không
cung cấp một mẫu chung cho mỗi kiểu dữ liệu thì mỗi trường hợp ngoại lệ phải xử lý
riêng. Tốc độ chỉ thị và sự biểu diễn của máy cũng là những yếu tố quan trọng. Nếu ta
không quan tâm đến tính hiệu quả của chương trình đích thì việc lựa chọn chỉ thị sẽ đơn
giản hơn. Với mỗi lệnh ba địa chỉ ta có thể phác họa một bộ khung cho mã đích. Giả sử
lệnh ba địa chỉ dạng x := y + z, với x, y, z được cấp phát tĩnh, có thể được dịch sang
chuỗi mã đích:
MOV y, R0 /* Lưu y vào thanh ghi Ro */
ADD z, R0 /* cộng z vào nội dung Ro, kết quả chứa trong Ro */
MOV R0, x /* lưu nội dung Ro vào x */
Tuy nhiên việc sinh mã cho chuỗi các lệnh ba địa chỉ sẽ dẫn đến sự dư thừa mã. Chẳng
hạn với:
a:= b + c
d:= a + e
ta chuyển sang mã đích:
MOV b, R
o
ADD c, R
o
MOV R
o
, a
MOV a, R
0
ADD e,R
o
MOV R
o
, d
và ta nhận thấy rằng chỉ thị thứ tư là thừa.
Chất lượng mã được tạo ra, được xác định bằng tốc độ và kích thước của mã. Một máy
đích có tập chỉ thị phong phú có thể sẽ cung cấp nhiều cách để hiện thực một tác vụ cho
trước. Ðiều này có thể dẫn đến tốc độ thực hiện chỉ thị rất khác nhau. Chẳng hạn, nếu máy
đích có chỉ thị INC thì câu lệnh ba địa chỉ a := a + 1 có thể được cài đặt chỉ bằng câu
lệnh INC a. Cách nầy hiệu quả hơn là dùng chuỗi các chỉ thị sau:
MOV a, R
o
ADD # 1, R
o
MOV R
o ,
a
Như ta đã nói, tốc độ của chỉ thị là một trong những yếu tố quan trọng để thiết kế chuỗi
mã tốt. Nhưng, thông tin thời gian thường khó xác định.

Việc quyết định chuỗi mã máy nào là tốt nhất cho câu lệnh ba điạ chỉ còn phụ thuộc
vào ngữ cảnh của nơi chưá câu lệnh đó.
3.5. Sử dụng thanh ghi.
Các chỉ thị dùng toán hạng thanh ghi thường ngắn hơn và nhanh hơn các chỉ thị dùng
toán hạng trong bộ nhớ. Vì thế, hiệu quả của thanh ghi đặc biệt quan trọng trong việc
sinh mã tốt. Ta thường dùng thanh ghi trong hai trường hợp:
1. Trong khi cấp phát thanh ghi, ta lựa chọn tập các biến lưu trú trong các thanh ghi tại
một thời điểm trong chương trình.
2. Trong khi gán thanh ghi, ta lấy ra thanh ghi đặc biệt mà biến sẽ thường trú trong đó.
Việc tìm kiếm một lệnh gán tối ưu của thanh ghi, ngay với cả các giá trị thanh ghi đơn,
cho các biến là một công việc khó khăn. Vấn đề càng trở nên phức tạp hơn vì phần cứng
và / hoặc hệ điều hành của máy đích yêu cầu qui ước sử dụng thanh ghi.
3.6. Thứ tự làm việc.
Thứ tự thực hiện tính toán có thể ảnh hưởng đến tính hiệu quả của mã đích . Một số
thứ tự tính toán có thể cần ít thanh ghi để lưu giữ các kết quả trung gian hơn các thứ tự
tính toán khác. Việc lựa chọn được thứ tự tốt nhất là một vấn đề khó. Ta nên tránh vấn đề
này bằng cách sinh mã cho các lệnh ba địa chỉ theo thứ tự mà chúng đã được sinh ra bởi
bộ mã trung gian.
Sinh mã
Tiêu chuẩn quan trọng nhất của bộ sinh mã là phải tạo ra mã đúng. Tính đúng của mã
có một ý nghĩa rất quan trọng. Với những quy định về tính đúng của mã, việc thiết kế bộ
sinh mã sao cho nó được thực hiện, kiểm tra, bảo trì đơn giản là mục tiêu thiết kế quan
trọng .
4. MÁY ĐÍCH.
Trong chương trình này, chúng ta sẽ dùng máy đích như là máy thanh ghi (register
machine). Máy này tượng trưng cho máy tính loại trung bình. Tuy nhiên, các kỹ thuật
sinh mã được trình bầy trong chương này có thể dùng cho nhiều loại máy tính khác nhau.
Máy đích của chúng ta là máy tính địa chỉ byte với mỗi từ gồm bốn byte và có n thanh
ghi : R
0
, R
1
... R
n-1
. Máy đích gồm các chỉ thị hai địa chỉ có dạng chung:
op source, destination
Trong đó op là mã tác vụ. Source (nguồn) và destination (đích) là các trường dữ liệu.
Ví dụ một số mã tác vụ:
MOV chuyển source đến destination
ADD cộng source và destination
SUB trừ source cho destination
Source và destination của một chỉ thị được xác định bằng cách kết hợp các thanh ghi
và các vị trí nhớ với các mode địa chỉ. Mô tả content (a) biểu diễn cho nội dung của thanh
ghi hoặc điạ chỉ của bộ nhớ được biểu diễn bởi a.
mode địa chỉ cùng với dạng hợp ngữ và giá kết hợp:
Mode
Dạng
Ðịa chỉ
Giá
Absolute
Register
Indexed
Indirect register
Indirect indexed
M
R
c(R)
*R
*c(R)
M
R
c + contents ( R)
contents ( R)
contents (c+ contents ( R))
1
0
1
0
1
Vị trí nhớ M hoặc thanh ghi R biểu diễn chính nó khi đưọc sử dụng như một nguồn
hay đích. Ðộ dời địa chỉ c từ giá trị trong thanh ghi R được viết là c( R).
Chẳng hạn:
1. MOV R
0
, M : Lưu nội dung của thanh ghi R
0
vào vị trí nhớ M .
2. MOV 4(R
0
), M : Xác định một địa chỉ mới bằng cách lấy độ dời tương đối
(offset) 4 cộng với nội dung của R
0
, sau đó lấy nội dung tại địa chỉ này, contains(4 +
contains(R
0
)), lưu vào vị trí nhớ M.
3. MOV * 4(R
0
) , M : Lưu giá trị contents (contents (4 + contents (R
0
))) vào vị trí
nhớ M.
4. MOV #1, R
0
: Lấy hằng 1 lưu vào thanh ghi R
0
.
Giá của chỉ thị
Giá của chỉ thị (instrustion cost) được tính bằng một cộng với giá kết hợp mode địa chỉ
nguồn và đích trong bảng trên. Giá này tượng trưng cho chiều dài của chỉ thị. Mode địa
chỉ dùng thanh ghi sẽ có giá bằng không và có giá bằng một khi nó dùng vị trí nhớ hoặc
hằng. Nếu vấn đề vị trí nhớ là quan trọng thì chúng ta nên tối thiểu hóa chiều dài chỉ thị.
Ðối với phần lớn các máy và phần lớn các chỉ thị, thời gian cần để lấy một chỉ thị từ bộ
nhớ bao giờ cũng xảy ra trước thời gian thực hiện chỉ thị. Vì vậy, bằng việc tối thiểu hóa
độ dài chỉ thị, ta còn tối thiểu hoá được thời gian cần để thực hiện chỉ thị.
Một số minh họa việc tính giá của chỉ thị:

1. Chỉ thị MOV R
0
, R
1
: Sao chép nội dung thanh ghi R
0
vào thanh ghi R
1
. Chỉ thị này
có giá là một vì nó chỉ chiếm một từ trong bộ nhớ .
2. MOV R
5
, M: Sao chép nội dung thanh ghi R
5
vào vị trí nhớ M. Chỉ thị này có giá
trị là hai vì địa chỉ của vị trí nhớ M là một từ sau chỉ thị.
3. Chỉ thị ADD #1, R
3
: cộng hằng 1 vào nội dung thanh ghi R
3
. Chỉ thị có giá là hai vì
hằng 1 phải xuất hiện trong từ kế tiếp sau chỉ thị.
4. Chỉ thị SUB 4(R
0
), *12 (R
1
) : Lưu giá trị của contents (contents (12 + contents
(R1))) - contents (4 + contents (R
0
)) vào đích *12( R
1
). Giá của chỉ thị nầy là ba vì hằng 4
và 12 được lưu trữ trong hai từ kế tiếp theo sau chỉ thị.
Với mỗi câu lệnh ba địa chỉ, ta có thể có nhiều cách cài đặt khác nhau. Ví dụ câu lệnh
a := b + c - trong đó b và c là biến đơn, được lưu chứa trong các vị trí nhớ phân biệt có tên
b, c - có những cách cài đặt sau:
1. MOV b, R
o
ADD c, R0 giá = 6
MOV R
o
, a
2. MOV b, a giá = 6
ADD c, a
3. Giả sử thanh ghi R0, R1, R2 giữ địa chỉ của a, b, c. Chúng ta có thể dùng hai địa
chỉ sau cho việc sinh mã lệnh:
a := b + c =>
MOV *R1, *Ro giá = 2
ADD * R
2
, *R
o
4. Giả sử thanh ghi R1 và R2 chứa giá trị của b và c và trị của b không cần lưu lại
sau lệnh gán. Chúng ta có thể dùng hai chỉ thị sau:
ADD R2, R1 giá = 3
MOV R
1
, a
Như vậy, với mỗi cách cài đặt khác nhau ta có những giá khác nhau. Ta cũng thấy rằng
muốn sinh mã tốt thì phải hạ giá của các chỉ thị . Tuy nhiên việc làm khó mà thực hiện
được. Nếu có những quy ước trước cho thanh ghi, lưu giữ địa chỉ của vị trí nhớ chứa giá
trị tính toán hay địa chỉ để đưa trị vào, thì việc lựa chọn chỉ thị sẽ dễ dàng hơn.
5. MỘT BỘ SINH MÃ ĐƠN GIẢN.
Ta giả sử rằng, bộ sinh mã này sinh mã đích từ chuỗi các lệnh ba địa chỉ. Mỗi toán tử
trong lệnh ba địa chỉ tương ứng với một toán tử của máy đích. Các kết quả tính toán có
thể nằm lại trong thanh ghi cho tới bao lâu có thể được và chỉ được lưu trữ khi:
(a) Thanh ghi đó được sử dụng cho sự tính toán khác
(b) Trước khi có lệnh gọi chương trình con, lệnh nhảy hoặc lệnh có nhãn.
Ðiều kiện (b) chỉ ra rằng bất cứ giá trị nào cũng phải được lưu vào bộ nhớ trước khi
kết thúc một khối cơ bản. Vì sau khi ra khỏi khối cơ bản, ta có thể đi tới các khối khác
hoặc ta có thể đi tới một khối xác định từ một khối khác. Trong trường hợp (a), ta không

thể làm được điều nầy mà không giả sử rằng số lượng được dùng bởi khối xuất hiện
trong cùng thanh ghi không có cách nào để đạt tới khối đó. Ðể tránh lỗi có thể xảy ra, giải
thuật sinh mã đơn giản sẽ lưu giữ tất cả các giá trị khi đi qua ranh giới của khối cơ bản
cũng như khi gọi chương trình con.
Ta có thể tạo ra mã phù họp với câu lệnh ba địa chỉ a := b + c nếu ta tạo ra chỉ thị đơn
ADD Rj, Ri với giá là 1. Kết quả a được đưa vào thanh ghi Ri chỉ nếu thanh ghi Ri chứa
b, thanh ghi Rj chứa c, và b không được sử dụng nữa.
Nếu b ở trong Ri , c ở trong bộ nhớ , ta có thể tạo chỉ thị:
ADD c, Ri giá = 2
Hoặc nếu b ở trong thanh ghi Ri và giá trị của c được đưa từ bộ nhớ vào Rj sau đó
thực hiện phép cộng hai thanh ghi Ri, Rj, ta có thể tạo các chỉ thị:
MOV c, R
j
ADD Rj , Ri giá = 3
Qua các trường hợp trên chúng ta thấy rằng có nhiều khả năng để tạo ra mã đích cho
một lệnh ba địa chỉ. Tuy nhiên, việc lựa chọn khả năng nào lại tuỳ thuộc vào ngữ cảnh
của mỗi thời điểm cần tạo mã.
1. Mô tả thanh ghi và địa chỉ
Giải thuật sinh mã đích dùng bộ mô tả (descriptor) để lưu giữ nội dung thanh ghi và
địa chỉ của tên.
1. Bộ mô tả thanh ghi sẽ lưu giữ những gì tồn tại trong từng thanh ghi cũng như cho ta
biết khi nào cần một thanh ghi mới. Ta giả sử rằng lúc đầu, bộ mô tả sẽ khởi động sao cho
tất cả các thanh ghi đều rỗng. Khi sinh mã cho các khối cơ bản, mỗi thanh ghi sẽ giữ giá
trị 0 hoặc các tên tại thời điểm thực hiện.
2. Bộ mô tả địa chỉ sẽ lưu giữ các vị trí nhớ nơi giá trị của tên có thể được tìm thấy tại
thời điểm thực thi. Các vị trí đó có thể là thanh ghi, vị trí trên Stack, địa chỉ bộ nhớ. Tất cả
các thông tin này được lưu chứa trong bảng danh biểu và sẽ được dùng để xác định
phương pháp truy xuất tên.
2. Giải thuật sinh mã đích
Giải thuật sinh mã sẽ nhận vào chuỗi các lệnh ba địa chỉ của một khối cơ bản. Với mỗi
lệnh ba địa chỉ dạng x := y op z ta thực hiện các bước sau:
1. Gọi hàm getreg để xác định vị trí L nơi lưu giữ kết quả của phép tính y op z. L
thường là thanh ghi nhưng nó cũng có thể là một vị trí nhớ.

2. Xác định địa chỉ mô tả cho y để từ đó xác định y’ một trong những vị trí hiện hành
của y. Chúng ta ưu tiên chọn thanh ghi cho y’ nếu cả thanh ghi và vị trí nhớ đang giữ giá
trị của y. Nếu giá trị của y chưa có trong L, ta tạo ra chỉ thị:
MOV y', L để lưu bản sao của y vào L.
3. Tạo chỉ thị op z', L với z' là vị trí hiện hành của z. Ta ưu tiên chọn thanh ghi cho z'
nếu giá trị của z được lưu giữ ở cả thanh ghi và bộ nhớ. Việc xác lập mô tả địa chỉ của x
chỉ ra rằng x đang ở trong vị trí L. Nếu L là thanh ghi thì L là đang giữ trị của x và loại bỏ
x ra khỏi tất cả các bộ mô tả thanh ghi khác.
4. Nếu giá trị hiện tại của y và/ hoặc z không còn được dùng nữa khi ra khỏi khối, và
chúng đang ở trong thanh ghi thì sau khi ra khỏi khối ta phải xác lập mô tả thanh ghi để
chỉ ra rằng các thanh ghi trên sẽ không giữ trị y và/hoặc z.
Nếu mã ba địa chỉ có phép toán một ngôi thì các bước thực hiện sinh mã đích cũng
tương tự như trên.
Một trường hợp cần đặc biệt lưu ý là lệnh x := y. Nếu y ở trong thanh ghi, ta phải thay
đổi thanh ghi và bộ mô tả địa chỉ, là giá trị của x được tìm thấy ở thanh ghi chứagiá trị của
y. Nếu y không được dùng tiếp thì thanh ghi đó sẽ không còn lưu trị của y nữa. Nếu y ở
trong bộ nhớ, ta dùng hàm getreg để tìm một thanh ghi tải giá trị của y và xác lập rằng
thanh ghi đó là vị trí của x. Nếu ta thông báo rằng vị trí nhớ chứa giá trị của x là vị trí nhớ
của y thì vấn đề trở nên phức tạp hơn vì ta không thể thay đổi giá trị của y nếu không tìm
một chỗ khác để lưu giá trị của x trước đó.
3. Hàm getreg
Hàm getreg sẽ trả về vị trí nhớ L lưu giữ giá trị của x trong lệnh x := y op z. Sau đây là
cách đơn giản dùng để cài đặt hàm:
1. Nếu y đang ở trong thanh ghi và y sẽ không được dùng nữa sau khi thực hiện x := y
op z thì trả thanh ghi chứa y cho L và xác lập thông tin cho bộ mô tả địa chỉ của y rằng y
không còn trong L.
2. Ngược lại, trả về một thanh ghi rỗng (nếu có).
3. Nếu không có thanh ghi rỗng và nếu x còn được dùng tiếp trong khối hoặc toán tử
op cần thanh ghi, ta chọn một thanh ghi không rỗng R. Lưu giá trị của R vào vị trí nhớ M
bằng chỉ thị MOV R,M. Nếu M chưa chứa giá trị nào, xác lập thông tin bộ mô tả địa chỉ
cho M và trả về R. Nếu R giữ trị của một số biến, ta phải dùng chỉ thị MOV để lần lượt
lưu giá trị cho từng biến.
4. Nếu x không được dùng nữa hoặc không có một thanh ghi phù hợp nào được tìm
thấy, ta chọn vị trí nhớ của x như L.
Ví dụ 9.5 : Lệnh gán d := (a - b) + (a - c) + (a - c)
Có thể được chuyển sang chuỗi mã ba địa chỉ:
t := a - b
u := a - c
v := t + u
d := v + u
và d sẽ “sống” đến hết chương trình. Từ chuỗi lệnh ba địa chỉ nầy, giải thuật sinh mã
vừa được trình bày sẽ tạo chuỗi mã đích với giả sử rằng: a, b, c luôn ở trong bộ nhớ và t,
u, v là các biến tạm không có trong bộ nhớ .
Câu lệnh 3
địa chỉ
Mã đích
Giá
Bộ mô tả thanh ghi
Bộ mô tả địa chỉ
t := a - b
u := a - c
v := t + u
d := v + u
MOV a, R
0
SUB b, R
0
MOV a, R
1
SUB c, R
1
ADD R
1
, R
0
ADD R
1
, R
0
MOV R
0
, d
2
2
2
2
1
1
2
Thanh ghi rỗng, R
0
chứa t
R
0
chứa t
R
1
chứa u
R
0
chứa v
R
1
chúa u
R
0
chứa d
t ở trong R
0
t ở trong R
0
u ở rong R
1
u ở trong R
1
v ở trong R
0
d ở rong R
0
d ở trong bộ nhớ
Hình 9.9 - Chuỗi mã đích
Lần gọi đầu tiên của hàm getreg trả về R
0
như một vị trí để xác định t. Vì a không ở
trong R
0
, ta tạo ra chỉ thỉ MOV a, R
0
và SUB b, R
0
. Ta cập nhật lại bộ mô tả để chỉ ra
rằng R
0
chứa t.
Việc sinh mã đích tiếp tục tiến hành theo cách nầy cho đến khi lệnh ba địa chỉ cuối
cùng d := v + u được xử lý. Chú ý rằng R
0
là rỗng vì u không còn được dùng nữa. Sau đó
ta tạo ra chỉ thị, cuối cùng của khối, MOV R
0
, d để lưu biến “sống” d. Giá của chuỗi mã
đích được sinh ra như ở trên là 12. Tuy nhiên, ta có thể giảm giá xuống còn 11 bằng cách
thay chỉ thị MOV a, R
1
bằng MOV R
0
, R
1
và xếp chỉ thị nầy sau chỉ thị thứ nhất.
4. Sinh mã cho loại lệnh khác
Các phép toán xác định chỉ số và con trỏ trong câu lệnh ba địa chỉ được thực hiện
giống như các phép toán hai ngôi. Hình sau minh họa việc sinh mã đích cho các câu lệnh
gán: a := b[i], a[i] := b và giả sử b được cấp phát tĩnh .
Câu lệnh
3 địa chỉ
(1)
i trong thanh ghi R
i
(2)
i trong bộ nhớ Mi
(3)
i trên Stack
Mã
Giá
Mã
Giá
Mã
Giá
a:= b[ i ]
a[i]:=b
MOV b(R
i
), R
MOV b, a(R
i
)
2
3
MOV M
i
, R
MOV b(R), R
MOV M
i
, R
MOV b, a (R)
4
5
MOV S
i
(A), R
MOV b(R), R
MOV S
i
(A), R
MOV b, a (R)
4
5

Hình 9.10 - Chuỗi mã đích cho phép gán chỉ mục
Với mỗi câu lệnh ba địa chỉ trên ta có thể có nhiều đoạn mã đích khác nhau tuỳ thuộc
vào i đang ở trong thanh ghi, hoặc trong vị trí nhớ M
i
hoặc trên Stack tại vị trí S
i
và con
trỏ trong thanh ghi A chỉ tới mẩu tin hoạt động của i. Thanh ghi R là kết quả trả về khi
hàm getreg được gọi. Ðối với lệnh gán đầu tiên, ta đưa a vào trong R nếu a tiếp tục được
dùng trong khối và có sẵn thanh ghi R. Trong câu lệnh thứ hai ta giả sử rằng a được cấp
phát tĩnh.
Sau đây là chuỗi mã đích được sinh ra cho các lệnh gán con trỏ dạng a := *p và *p :=
a. Vị trí nhớ p sẽ xác định chuỗi mã đích tương ứng.
Câu lệnh
3 địa chỉ
p trong thanh ghi
R
p
p trong bộ nhớ Mi
p trong Stack
Mã
Giá
Mã
Giá
Mã
Giá
a:= *p
*p:= a
MOV *R
p
, a
MOV a, *R
p
2
2
MOV M
p
, R
MOV *R, R
MOV M
p
, R
MOV a, *R
3
4
MOV S
p
(A), R
MOV *R, R
MOV a, R
MOV R, *S
p
(A)
3
4
Hình 9.11 - Mã đích cho phép gán con trỏ
Ba chuỗi mã đích tuỳ thuộc vào p ở trong thanh ghi R
p
, hoặc p trong vị trí nhớ M
p
,
hoặc p ở trong Stack tại offset là S
p
và con trỏ, trong thanh ghi A, trỏ tới mẩu tin hoạt
động của p. Thanh ghi R là kết quả trả về khi hàm getreg được gọi. Trong câu lệnh gán
thứ hai ta giả sử rằng a được cấp phát tĩnh.
5. Sinh mã cho lệnh điều kiện
Máy tính sẽ thực thi lệnh nhảy có điều kiện theo một trong hai cách sau:
1. Rẽ nhánh khi giá trị của thanh ghi được xác định trùng với một trong sáu điều kiện
sau: âm, không, dương, không âm, khác không, không dương. Chẳng hạn, câu lệnh ba địa
chỉ if x < y goto z có thể được thực hiện bằng cách lấy x trong thanh ghi R trừ y. Sau đó
sẽ nhảy về z nếu giá trị trong thanh ghi R là âm.
2. Dùng tập các mã điều kiện để xác định giá trị trong thanh ghi R là âm, bằng không
hay dương. Chỉ thị so sánh CMP sẽ kiểm tra mã điều kiện mà không cần biết trị tính toán
cụ thể. Chẳng hạn, CMP x, y xác lập điều kiện dương nếu x > y,... Chỉ thị nhảy có điều
kiện được thực hiện nếu điều kiện < , =, >, >=,<>, <= được xác lập. Ta dùng chỉ thị nhảy
có điều kiện CJ <= z để nhảy đến z nếu mã điều kiện là âm hoặc bằng không.
Chẳng hạn, lệnh điều kiện if x < y goto z được dịch sang mã máy như sau.
CMP x,y
CJ < z
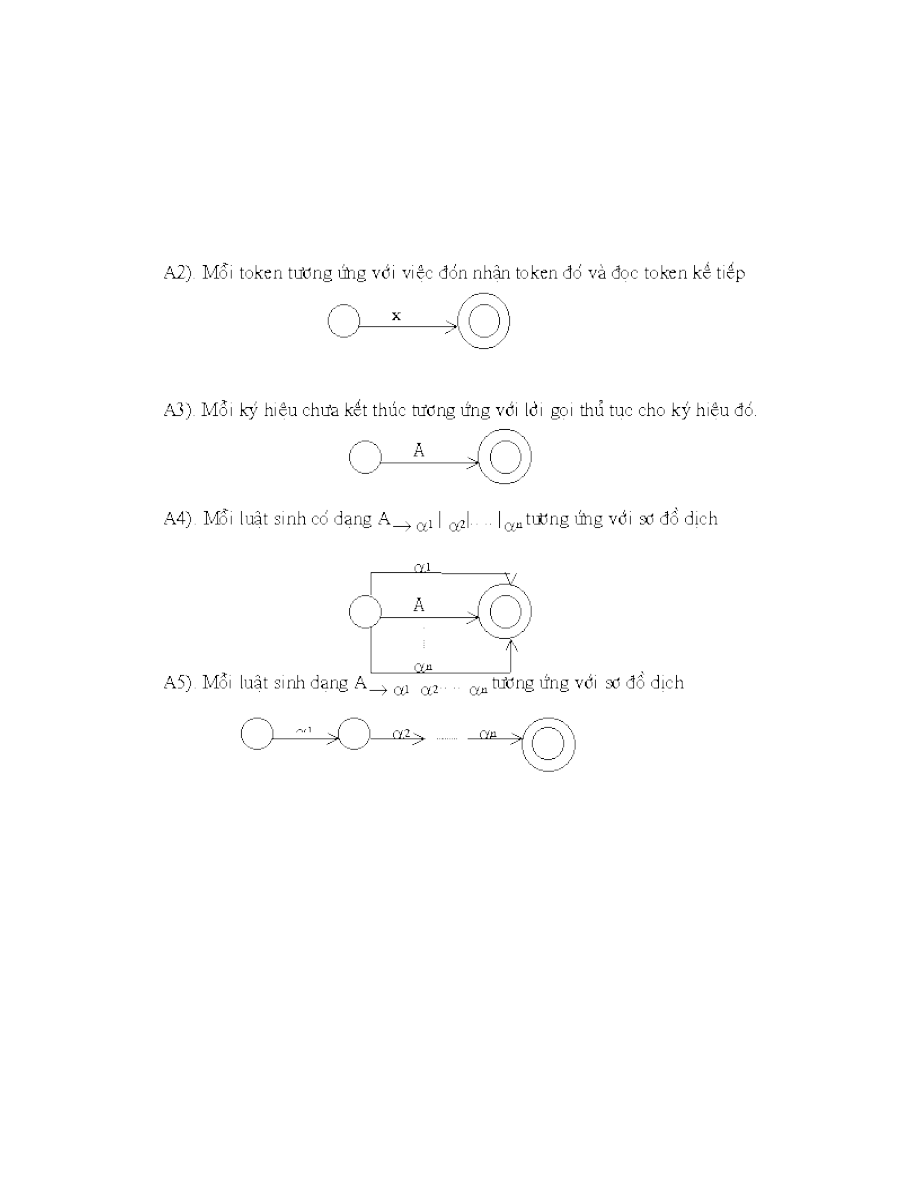
§Ó x©y dùng s¬ ®å dÞch cho ph¬ng ph¸p ph©n tÝch duyÖt
lïi, tríc hÕt lo¹i bá ®Ö qui tr¸i, t¹o nh©n tè tr¸i cña v¨n ph¹m s¬
®å dÞch theo nguyªn t¾c sau:
A1). Mçi ký hiÖu cha kÕt thóc t¬ng øng víi mét s¬ ®åtrong ®ã
nh·n cho c¸c c¹nh lµ token hoÆc ký hiÖu cha kÕt thóc.
VÝ dô :XÐt v¨n ph¹m sinh biÓu thøc to¸n häc
E
→
E + T |T
E
→
T * E | F
F
→
E0 | id
Khö ®Ö qui tr¸i ta ®îc
E
→
TE'
E'
→
+ TE' |
ε
T
→
FT'
T'
→
* FT' |
ε
F
→
(E) | id S¬ ®å dÞch t¬ng øng

Rót gän s¬ ®å b»ng c¸c thay thÕ t¬ng øng

CS 3240 Homework I
Scanning and Parsing
Let us consider the language of arithmetic expressions
The alphabet of this language is the set
{+, -, *, /, (, ), x, y, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Note commas are not a part of the alphabet in the above set – they are only shown to separate
elements of the set. That is, strings in this language can be composed only by using one or more
of the following
+ - * / ( ) x y 0 1 2 3 4 5 6 7 8 9
The tokens in this language are of the following classes
MOPER
: * /
AOPER
: + -
CONS
: Strings made of 0 through 9
VAR
: x y
OPARAN
: (
CPARAN
: )
Consider a compiler that scans and parses the language of arithmetic expressions
Question 1: As you scan the following expression from left to right, list the tokens and the token
class identified by the scanner for each of the arithmetic expressions below. Identify, explain
and clearly mark the errors if any (30 points)
a.
( x * ( y + 100 ) + y – ( x + y – 320 ) )
b.
( y + 100 * x + ( 2 + x^3 ) / y )
c.
x * ) 4 + / 100 - y
d.
y * ( ( x + 100
e.
(20 + x * 4 / 30y3 )
The grammar for the language of arithmetic expressions is as follows
<EXPR>
→
<TERM> AOPER <TERM>
<EXPR>
→
<TERM>
<TERM>
→
<FAC> MOPER <FAC>
<TERM>
→
<FAC>
<FAC>
→
OPARAN <EXPR> CPARAN
<FAC>
→
VAR
<FAC>
→
CONS
Question 2: What are the terminals and non-terminals in this grammar? (10 points)
Question 3: For each of the expressions below, scan it from left to right; list the tokens returned
by the scanner and the rules used by the parser (showing appropriate expansions of the non-
terminals) for matching. Identify, explain and clearly mark the errors if any
(40 points)
a.
a.
( x + y )
b.
b.
( y * - x ) + 10
c.
c.
( x * ( y + 10 ) )
d.
d.
( x + y ) * ( y + z )
e.
e.
( x + ( y – ( 2 ) )
Question 4: You are asked the count the number of constants (CONS), variables (VAR) and
MOPER in an expression. Insert action symbols in the grammar described before Question 2,
explain what semantic actions they trigger and what each semantic action does.
(20 points)
Regular Expressions
Question 1: Consider the concept of “closure”. A set S is said to be closed under a (binary)
operation
⊕
if and only if applying the operation to two elements in the set results in another
element in the set. For example, consider the set of natural numbers N and the “+” (addition)
operation. If we add any two natural numbers, we get a natural number. Formally x, y are
elements of N implies x + y is an element of N. State true or false and explain why
a. Only infinite sets (sets with infinite number of elements, like the set of natural numbers)
can be closed
b. Infinite sets are closed under all operations
c. The set [a-z]* is closed under concatenation operation
Question 2:
For each of the regular expressions below, state if they describe the same set of strings (state if
they are equivalent). If they are equivalent, what is the string they describe?
1.
[a-z][a-z]*
and
[a-z]+
2.
[a-z0-9]+
and
[a-z]+[0-9]+
3.
[ab]?[12]?
and
a1|b1|a2|b2
4.
[ab12]+
and
a|b|1|2|[ab12]*
5.
[-az]*
and
[a-z]*
6.
[abc]+
and
[cba]+

7.
[a-j][k-z]
and
[a-z]
Question 3:
For each of the strings described below, write a regular expression that describes them and draw a
finite automaton that accepts them.
1.
1.
The string of zero or more a followed by three b followed zero or more c
2.
2.
The string of zero or more a, b and c but every a is followed by two or
more b
3.
3.
All strings of digits that represent even numbers
4.
4.
All strings of a’s and b’s that contain no three consecutive b’s.
5.
5.
All strings that can be made from {0, 1} except the strings 11 and 111

Question 1: Pumping Lemma and Regular Languages
You can use the pumping lemma and the closure of the class of regular
languages under
union, intersection and complement to answer the following question. Proofs
should be
rigorous. Note that for each of the questions below, you may or may not have
to use the
pumping lemma.
Note that the notation 0
m
means “0 repeated m times”. So the language of
strings of the
form 0
m
such that m ¡Ý 0 would contain strings like the null string 0, 00, 000,
… (this is
[0]*. Whereas the language of strings of the form 0
m
such that m ¡Ý 1 would
be [0]+)
a. Is the language of strings of the form 0
m
1
n
0
m
such that m, n
¡Ý 0 regular? If
it is regular,
prove that it is regular. If it is not regular, prove that is not regular. Note
that, a rigorous
proof is needed. General reasoning or explanations that are not rigorous will
not get full
credit. (15 points)
b. Consider a language whose alphabet is from the set {a, b}. Is the
language of
palindromes over this alphabet regular? If it is regular, prove that it is
regular. If it is not
regular, prove that is not regular. Note that, a rigorous proof is needed.
General reasoning
or explanations that are not rigorous will not get full credit. (15 points)
Hint: A palindrome is a word such that when read backwards, is the same
word. For
example the word “mom” when read left to right is the same as it is when it
is read right
to left. In general, the first half, when reversed, yields the second half. If the
length of the
string is odd, the middle character is left as it is. For example, consider the
word
“redivider”. Reversing “redi” yields “ider” and “v” is left as it is. For strings
with
alphabet {a, b}, “aaabaaa” is a palindrome but “abaaa” is not.
c. A language, whose alphabet is {a, b}, such that the strings of the
language contain
equal number of “ab” and “ba”. Note that “aba” is part of the language,
because the first
letter and the second letter form “ab” and the second and third form “ba”. Is
this language
regular? If it is regular, prove that it is regular. If it is not regular, prove that
is not

regular. Note that, a rigorous proof is needed. General reasoning or
explanations that are
not rigorous will not get full credit. (15 points)
d. The class of regular languages is closed under union. That is of A is a
regular language
and B is a regular language, then C is a regular language, where C = A . B.
Note that B
. C. (B is a subset of C). Let D be some subset of C (that is, D . C). In general,
is D
regular? If it is regular, prove that it is regular. If it is not regular, prove that
is not
regular. Note that, a rigorous proof is needed. General reasoning or
explanations that are
not rigorous will not get full credit. (15 points)
Question 2:
Consider the language described by the regular expression a+b*a, the set of
all strings
that has one or more a’s followed by zero or more b’s and ending in a single
a.
a. Construct a NFA which recognizes this language. Note that you need to
construct a
primitive NFA using the constructions describe in class. (10 points)
b. Convert the above NFA to a DFA using . closure. Clearly indicate the steps
of .
closure. (20 points)
c. Convert the above DFA to an optimized DFA (10 points)

HomeWork
1. Work on the homework individually. Do not collaborate or copy from others
2. The homework is due on Tuesday, April 24 In Class. No late submissions
will be entertained
3. Do not email your answers to either the Professor or the TA. Emailed
answers will not be
considered for evaluation
Question 1. (50 Points)
Consider the following grammar. Construct LR(0) items, DFA for this grammar
showing LR(0) shiftreduce
table. Is this grammar LR(0)? Indicate all possible shift-reduce as well as
reduce-reduce
conflicts. Using the concept of look-ahead, generate SLR(1) table – which
LR(0) conflicts get
eliminated? Using the input (ID + ID) * ID show the SLR(1) parse - show the
stack states and shifts
and reductions as shown in the examples in the Louden book.
Grammar:
E' -> E
E -> E + T
E -> T
T -> T * ID
T -> ID
T -> (E)
Question 2. (50 Points)
Construct a pushdown automaton for the following language:
L = { a
i
b
j
c
k
| i, j, k >= 0, either i = j or j = k}

Practice
Q #1. Design a Turing machine for recognizing the language (please give a
formal
description including tape alphabet, full state transition diagram identifying
the
acceptance and rejection states if any)
L = {a
n
b
n
c
n
| n >= 0}
L = { w | w contains twice as many 0's as 1's, w is made from {0,1}* }
Q #2. Design a Turing machine to perform multiplication of two natural
numbers
represented as the number of zeroes. For example, number five is
represented as 00000
Hint: Use repeated addition
Q #3 Design LR(0) items, their DFA and SLR(1) parse table for the following
grammar
showing the parse for the following input : ((a), a, (a, a)) Also show the parse
tree
obtained. Is this a LR(0) grammar? If not show the conflicts and show how
you can
resolve them through SLR(1) construction
Grammar :
E -> (L)| a
L -> L, E| E
Q #4 Design Context free grammars for the following languages (alphabet is
{0,1})
a. {w | w starts and ends with the same symbol (either 0 or 1, which is the
alphabet)}
b. {w | w = w
r
ie, w is a palindrome}
c. {a
i
b
j
c
k
| i = j or j = k, i, j, k >= 0}
Q #5 Design pushdown automata (PDA) for the following language:
{w | w has odd length and the middle character is 0}
Q #6 Show first, follow and predict sets for the following grammar after
removing left
recursion and left factoring:
E -> E + T
E -> T
T -> T * P
T -> P
P -> (E)
P -> ID
Q # 7 Using the pumping lemma show that the following languages are not
regular:
{0
m
1
n
| m not equal to n}
{0
2n
| n >= 0}
Q #8 Design NFA, DFA and minimize the DFA for the regular expression:
0
*
1
*
0
*
0

Test 1
Question 1: DFAs (Choose any three questions out of five: 30 points)
Devise DFAs for:
1. All strings that start with 1 must end with a 0 and those which start with
0 must end with 1 (alphabet of this language is {0,1}), no null string
2. All strings from the alphabet {a, b} which contain an odd number of a’s
and even (but non-zero) number of b’s
3. All strings that must have 0110 as the substring (alphabet {0,1})
4. All strings which have a length greater than or equal to 3 and ending on
b or two consecutive a’s
5. Strings that do not contain 3 consecutive a’s
Question 2: Regular expressions (Choose any three questions out of
five: 30 points)
Write regular expressions for:
1. Expressions that enumerate all positive integers (including 0) upto 100000
but without any leading zeroes
2. Strings made from {a, b} that start and end on the same letter (ie, strings
starting with a end on a and those starting with b end on b)
3. Floats using decimal point representation with integer and fractional parts
– no leading or trailing zeros and precision upto 4 places after decimal
4. Identifiers that start with a digit or lowercase letter following which one
can optionally have one or more of digits or letters or underscores.
Identifiers can not end on an underscore (consecutive underscores ok
though)
5. Positive integers no leading zeros in which all 2’s should occur only after
3’s and all 1’s should occur only after 2’s (ie, no 2 should occur before a 3
or no 1 should occur before a 2).
Question 3: Regular Expression . NFA . DFA (30 points)
Convert the following regular expression into a NFA and convert the NFA to
DFA
showing the key steps (such as computing å-closures of sets of states etc.) :
b[ab]
*
Show
all possible NFA transitions (using parallel tree) for the string babba and
verify the state
transitions in corresponding DFA
Question 4: State True or False (10 points)
a. Consider a language S=(a|b)*. Consider a Regular Language L, whose
alphabet is
from the set .= {a, b}. Let M be a DFA that Recognizes L. Let M' be a DFA
obtained from M by changing all accepting states of the M into non-accepting
states, and by changing all non-accepting states of M to accepting states. M'
recognizes the complement of language L given by S – L
b. For every NFA and its equivalent DFA, the number of states in equivalent
DFA
must be at least equal to the number of states in the NFA.
c. Consider languages L and L’ such that L . L’. Let M be a DFA that
recognizes L

and M’ be DFA that recognizes L’ then the number of states in M’ must be
equal
to or greater than those in M.
d. Consider languages L and L’ such that L . L’. Let M be a DFA that
recognizes L
and M’ be DFA that recognizes L’ then the number of states in M’ must be
lesser
than or equal to those in M.
e. For every regular expression there can exist more than one DFA that
recognizes
the language described by the regular expression.
.

Tesst 2

Project
Notes:
1. This project has two phases. Phase 1 is due by April 14
th
by 5pm. Phase 2
is due by April 28
th
by 5pm.
2. There will be no extensions for either phases
3. You will work in groups of three
4. Each group should submit a report and source code for each phase. If
multiple source files, they
must be tarred along with the makefile
5. You can program in C, C++ or Java. Do not use tools (like lex and yacc) or
the standard
template library
6. Code should be properly documented with meaningful variable and
function names. Short
elegant code will get bonus points.
7. You will find the course slides on DFA/NFA/scanner/recursive descent
parser useful.
8. Each phase of the project is worth 100 points. The bonus section is worth
50 points.
Phase 1:
Objective: To write a scanner and parser which can construct and execute an
NFA for any regular
expression.
Consider the language of regular expressions. The alphabet of this language
is the set
{a, b, *,
+, (, ), ., |}
(commas and spaces are not part of the language). Using
this alphabet one can
write any regular expression. Our goal in this project is to be able to read any
regular expression
described by the following grammar and construct primitive NFAs and join
them together to form a
NFA that will recognize strings described by the regular expression. We will
do this step by step by
developing answers to the following questions. The production rules for this
language are given by
R . R*
R . R+
R . (R)
R . (R | R)
R . R
.
R
R . a
R . b
Question 1: Rewrite the grammar to remove left recursion.
Question 2: Identify the tokens of this language and write a scanner program
which can scan this
language and return tokens .

Question 3: Write a recursive descent parser which can parse this language
(based on the modified
grammar which removed left recursion) and yield a parse tree. Note that this
grammar has implicit
precedence. That is for a regular expression, a.b* the “*” operates on “b” and
not a.b as a whole. This
is true unless it is bracketed. In, (a.b)* on the other hand, the “*” operates on
(a.b) When you build a
parse tree you must take care of such precedences
Question 4: Now you need to write a program which can construct a NFAs
based on the parse tree
based on primitive NFAs. As discussed in class, primitive NFAs should be
joined together to form
NFA for the complete regular expression. This final NFA will be represented
as an adjacency matrix
described below. Thus the output of this program should be an adjacency
matrix.
Adjacency matrix: Any NFA is a directed graph. A directed graph G consists of
a set of nodes (in our
case states) and directed edges (in our case, transitions). For example, in the
graph below, A,B,C are
nodes and 1,2,3 are edges
A
B
C
1 2
3
Any directed graph can be represented by an adjacency matrix. For example,
the matrix below
represents the graph. Since edge “1” connects A to B, there is a “1” in the
row corresponding to “A”
and the column corresponding to “B”.
A B C
A 1 3
B 2
C
Similarly an NFA can be represented by an adjacency matrix. Note that more
than one element can be
present in a cell. For example, in the NFA if the edge from A to B is labeled
a,b then you would have
both “a” and “b” in the corresponding cell.
Question 5: Given such an adjacency matrix of an NFA and given an input
string consisting of a’s and
b’s write a program to simulate the NFA and output if the string is accepted
or rejected. Note : NFAs
can progress on multiple paths and you should simulate this effect – if one of
the paths results in accept
state then the input string is accepted by NFA.

Phase 2:
To write a program which will construct a DFA from any NFA. You
will use adjacency
matrix as the representation and use epsilon closures to generate DFA.
Finally write a program to
simulate the DFA.
Bonus:
Given an adjacency matrix for a DFA, write a program to produce
minimal DFA by state
merging.

Document Outline
- MOVF id3, R2
- * Có 2 loại dệ quy trái :
- * Phép thừa số hoá trái
- * Handle của một chuỗi
- Ký hiệu đầu vào
- Đầu ra
- Action
- Bảng phân tích cú pháp
- Quá trình phân tích LR
- 5) Văn phạm gia tố(Augmented Grammar)(mở rộng)
- 6) Phép toán closure
- * Phép toán goto
- Các phương pháp duyệt hành động ngữ nghĩa
- Cú pháp điều khiển thuần tính L
- Thực hiện hành động ngữ nghĩa trong phân tích LL
- Thực hiện hành động ngữ nghĩa trong phân tích LR
- Scanning and Parsing
Wyszukiwarka
Podobne podstrony:
Slide Lập Thẩm Định Dự Án Đầu Tư xây Dựng Pgs Ts Nguyễn Văn Hiệp
Choroba MĂŠniereÂ
Giám Sát Thi Công Và Nghiệm Thu Lắp Đặt Thiết Bị Trong Công Trình Dân Dụng (NXB Hà Nội 2002) Lê Kiề
Slide Quy Chuẩn Và Tiêu Chuẩn Xây Dựng Pgs Ts Nguyễn Văn Hiệp
BCVT Giám Sát Thi Công Kết Cấu Bê Tông Cốt Thép (NXB Giao Thông Vận Tải 2004) Nguyễn Viết Trung, 54
Tóm Tắt Thuyết Minh Kỹ Thuật Biện Pháp Tổ Chức Thi Công Dự Án Chống Xói Lở Sông Tiền
Bài Tập Ổn Định Có Hướng Dẫn Giải Nhiều Tác Giả, 25 Trang
Giáo Trình Khai Thác, Kiểm Định, Sửa Chữa, Tăng Cường Cầu Gs Ts Nguyễn Viết Trung, 72 Trang
Hướng Dẫn Cấu Hình Các Chức Năng Cơ Bản Của Cisco Router Nhiều Tác Giả, 94 Trang
KLIMAT14, Zasady dzia˙ania urz˙dze˙ ch˙odniczych
ĐHCT Giáo Trình Thực Hành Lập Trình Hệ Thống (NXB Cần Thơ 2008) Nguyễn Hứa Duy Khang, 39 Trang
Biên Dịch Nhân Linux Hoàng Ngọc Diêu, 42 Trang
Giám Sát Công Tác Trắc Địa Xây Dựng Công Trình Đường Ks Nguyễn Tấn Lộc, 32 Trang
pan wołodyjowski, 25, Ksi˙dz Kami˙ski, za m˙odych lat ˙o˙nierz i kawaler wielkiej fantazji, siedzia˙
Hướng Dẫn Sử Dụng Phần Mềm Kiểm Tra Ổn Định Mái Dốc Geo Slope, 53 Trang
NOCUŃ-~1, Dow˙dca jako nauczyciel i wychowawca-w procesie wychowania dow˙dca spe˙nia rol˙ kierownicz
7 6, Pan Wo˙odyjowski, s˙awny i stary ˙o˙nierz, cho˙ cz˙owiek m˙ody, siedzia˙, jako si˙ rzek˙o, w Pa
Badanie urzadzenia do ciecia plazma, Badanie urz˙dzenia do ci˙cia metali plazm˙ argonow˙ z plazmotro
więcej podobnych podstron