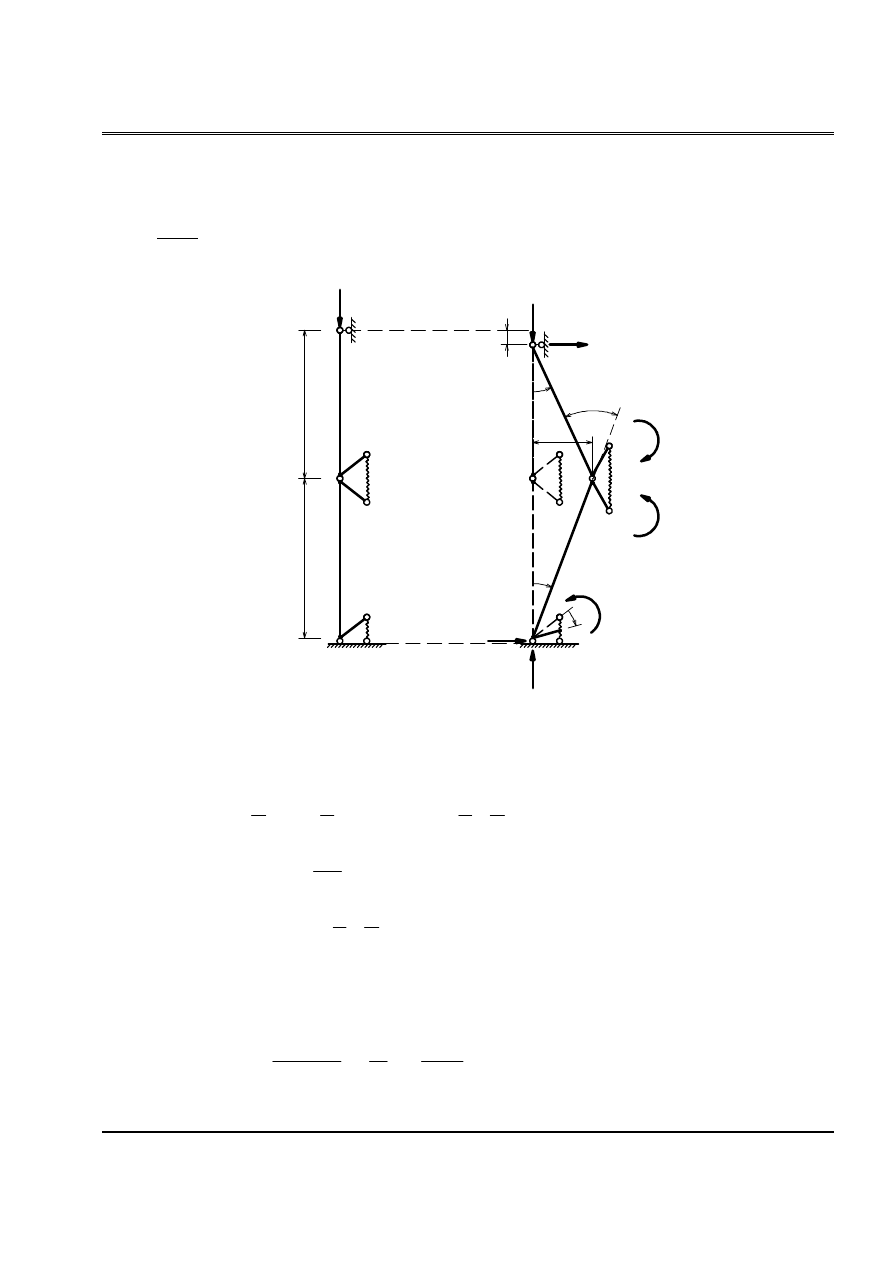
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 1
Baìi 1: Cho hãû nhæ hçnh (H.1). k
1
, k
2
laì âäü cæïng cuía caïc liãn kãút âaìn häöi C vaì B (mämen
phaït sinh khi liãn kãút xoay bàòng âån vë). Tçm læûc tåïi haûn theo:
a. Phæång phaïp thiãút láûp vaì giaíi phæång trçnh âaûi säú
Giaíi:
a. Phæång phaïp thiãút láûp vaì giaíi phæång trçnh âaûi säú
Taûo hãû åí traûng thaïi lãûch nhæ hçnh
Ta coï:
2
1
1
2
2
2
1
1
1
1
2
;
;
;
(
);
A
B
C
A
B
B
B
C
C
y
y
y
y
l
l
l
l
k y
M
k
l
y
y
M
k
k
l
l
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
=
=
=
+
= +
=
=
=
=
+
'
0
tr
C
M
=
∑
2
0
A
C
Py V l
M
⇒
−
−
=
1
2
1
2
2
2
1 2
C
A
Py
M
P
l
l
V
k
y
l
l
l l
−
+
⇒
=
=
−
(1)
A
B
P
E
J=
∞
E
J=
∞
A
B
l
2
l
1
P
E
J=
∞
E
J=
∞
C
k
1
k
2
C
C'
ϕ
Α
ϕ
Β
P
V
A
V
B
ϕ
Β
Mc
Mc
M
B
y
ϕ
c
δ
(H.1)
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 2
1
2
0
(
)
0
B
A
B
M
V l
l
M
=
⇒
+ −
=
∑
2
1
2
1
1
2
(
)
B
A
M
k
V
y
l
l
l l
l
⇒
=
=
+
+
(2)
Tæì (1), (2)...
Âiãöu kiãûn täön taûi traûng thaïi lãûch laì
0
y
≠
, vç váûy:
2
1
2 2
1 2
1
2
...
(
)
th
k
k l
P
l l l
l
+
=
+
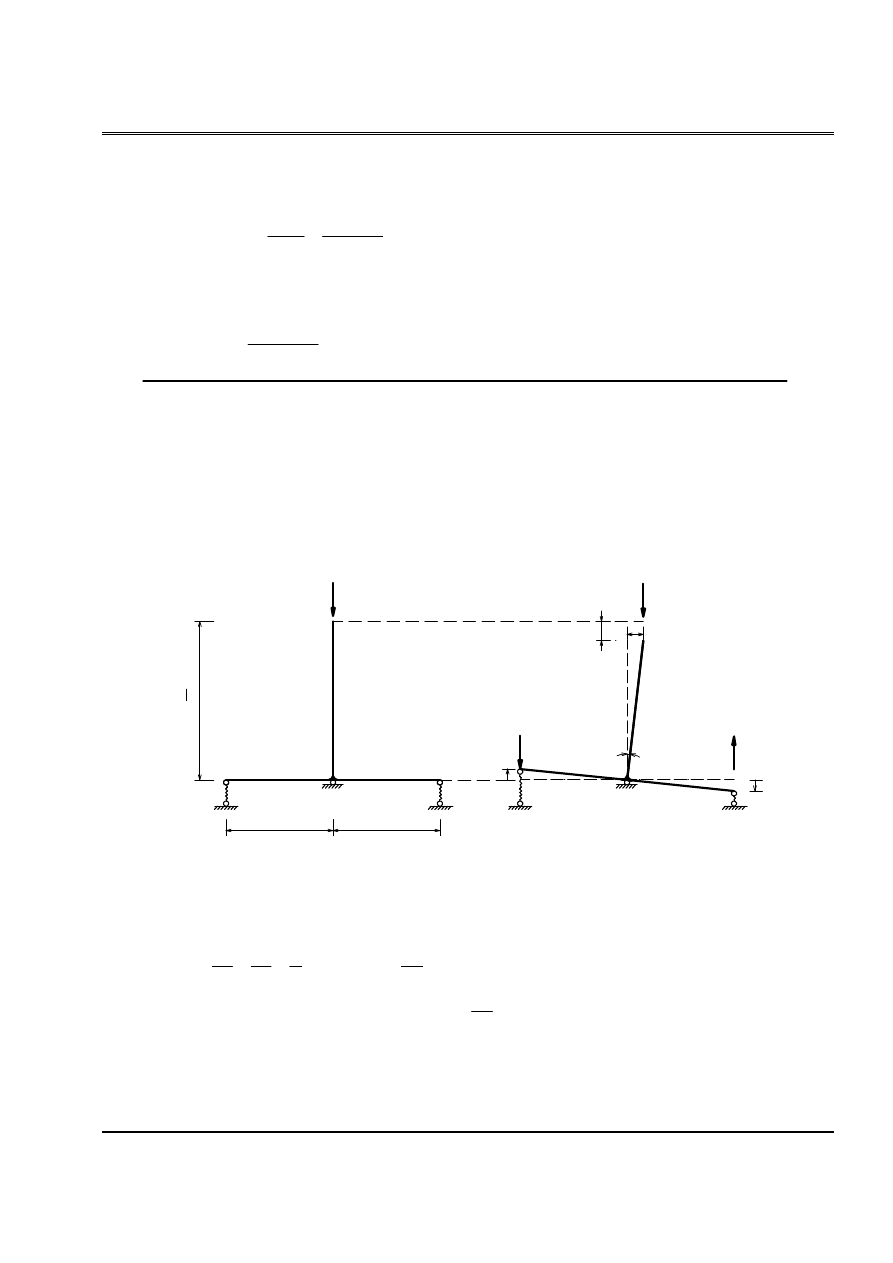
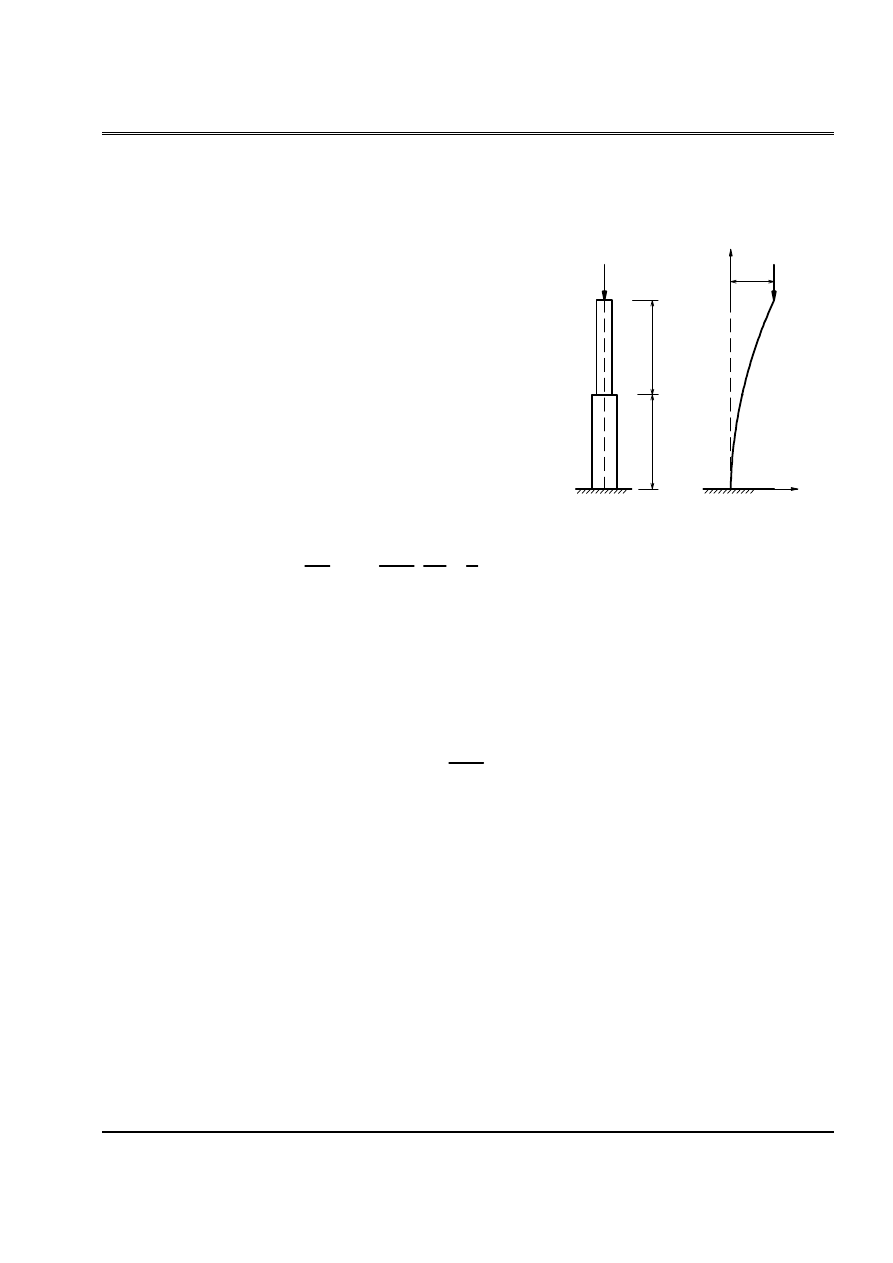
Baìi 2: Cho hçnh chëu læûc neïn P nhæ hçnh (H.2). k laì âäü cæïng cuía liãn kãút âaìn häöi B, C
(phaín læûc phaït sinh khi liãn kãút chuyãøn vë bàòng âån vë). Tênh læûc tåïi haûn theo:
a. Phæång phaïp thiãút láûp vaì giaíi phæång trçnh âaûi säú
Giaíi:
a. Phæång phaïp thiãút láûp vaì giaíi phæång trçnh âaûi säú
A
E
J=
∞
P
V
B
V
C
B
C
δ
S
A
S
C
∆
ϕ
Α
A
l=
3a 2
E
J=
∞
a
a
P
B
C
(H.2)
Taûo hãû åí traûng thaïi lãûch. Âáöu thanh âæïng lãûch
δ
Khi âoï chuyãøn vë åí caïc gäúi B, C láön læåüc laì S
B
, S
C
xaïc âënh theo cäng thæïc sau:
C
B
S
S
a
a
l
δ
=
=
B
C
a
S
S
l
δ
⇒
=
=
Phaín læûc taûi caïc gäúi B, C láön læåüc laì
B
C
a
V
k
V
l
δ
=
=
(chiãöu nhæ hçnh veî)
Ta coï:
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 3
2
0
0
..............
2
(
)
0
A
A
B
M
P
V a V a
ka
P
l
δ
δ
=
⇒
−
−
=
⇒
−
=
∑
Âãø täön taûi biãún daûng lãûch thç
0
δ
≠
, tæïc laì
2
2
0
ka
P
l
−
=
Do âoï:
2
2
th
ka
P
l
=
. Khi
3
2
a
l
=
thç
4
3
th
ak
P
=
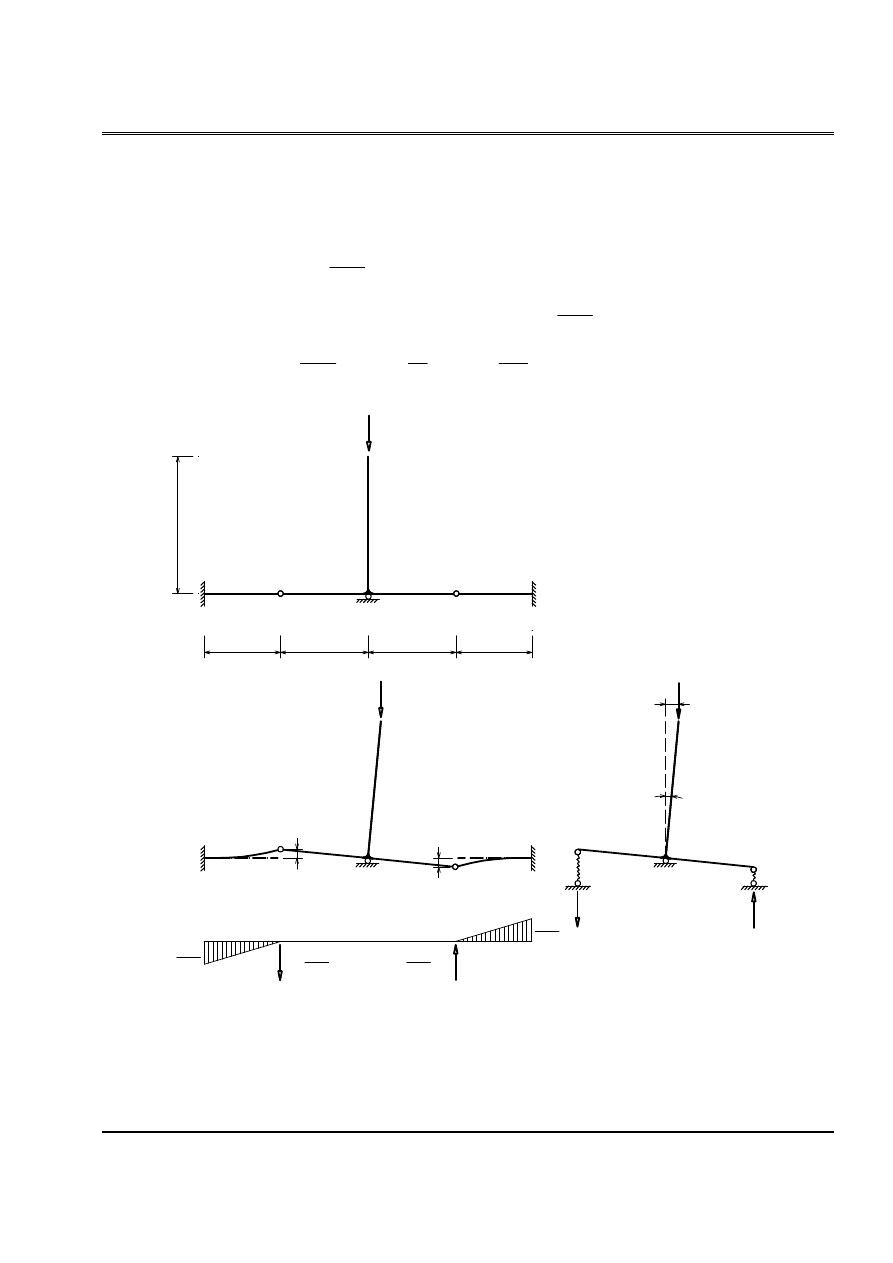
Baìi 3:
Cho hãû chëu læûc neïn P nhæ trãn hçnh (H.3). Tçm læûc tåïi haûn.
A
l
E
J=
∞
a
a
P
c
A
P
c
EJ
0
EJ
0
k
k
P
C
D
C
D
B
∆
C
∆
D
ϕ
Α
δ
B
R
D
R
C
=r
D1
r
C1
=
3EJ
0
c
2
3EJ
0
c
2
3EJ
0
c
3
3EJ
0
c
3
Phaín læûc taûi C vaì D do chuyãøn vë thàóng
1
C
D
∆ = ∆ =
gáy ra:
Trong âoï
1
1
C
D
k
r
r
=
=
laì phaín læûc phaït sinh khi liãn kãút chuyãøn vë 1 âån vë.
Xaïc âënh k : Cho chuyãøn vë âáöu console 1âv, xaïc âënh k
(H.3)
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 4
3
0
3
0
3
1
2
1
2 3
EJ
c k
k
EJ
c
= ⇒ =
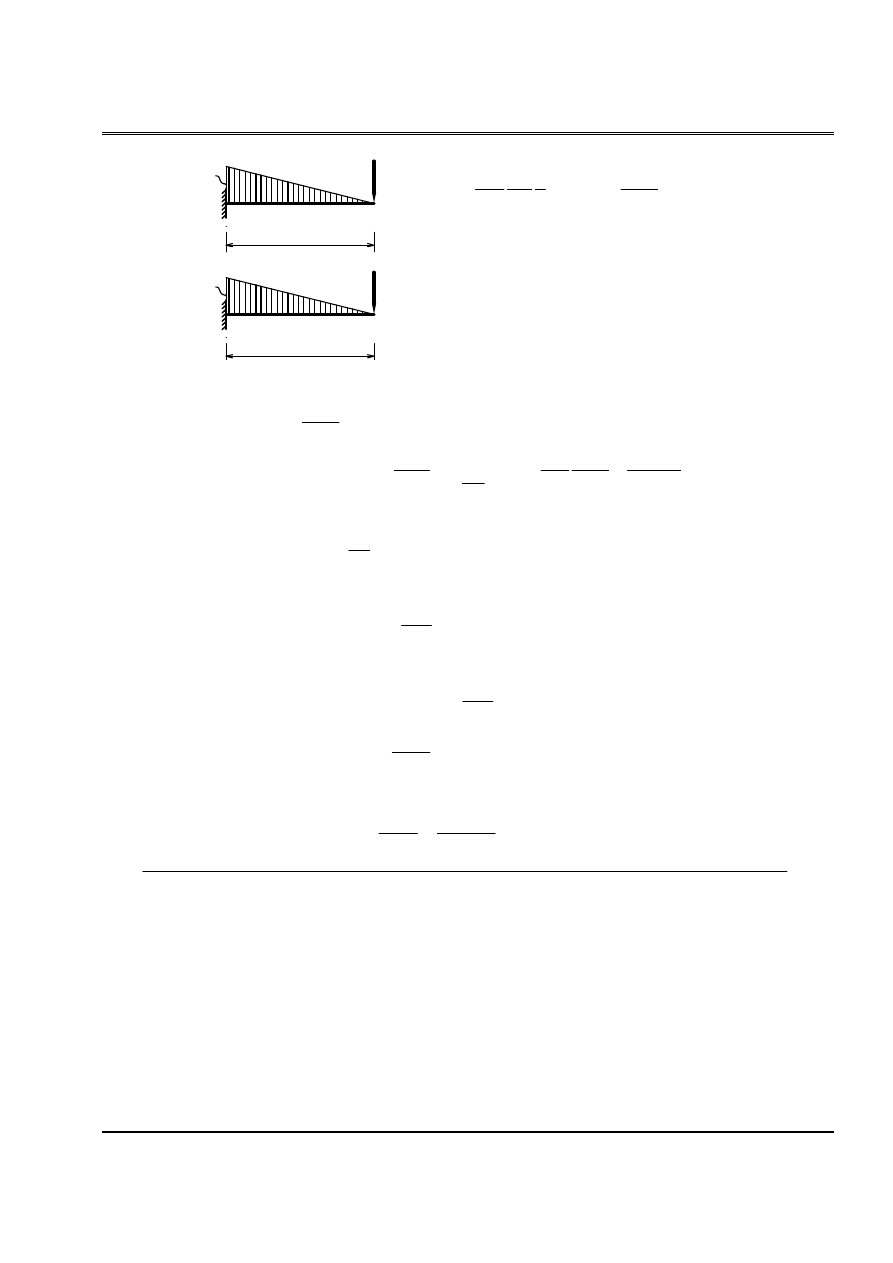
Så âäö ban âáöu coï thãø thay bàòng så âäö våïi gäúi âaìn häöi taûi C vaì D, trong âoï âäü
cæïng cuía loì xo
0
3
3EJ
k
c
=
.
Theo kãút quaí baìi 2
0
3
2
2
2
0
0
3
3
3
3
6
2
2
th
th
EJ
k
c
EJ
a EJ
ka
a
P
P
l
l
c
c l
=
=
→
=
=
Hoàûc coï thãø giaíi nhæ sau:
Hoàûc
B
A
l
δ
ϕ
=
Âäü daîn cuía liãn kãút C vaì D laì:
B
C
D
a
l
δ
∆ = ∆ =
Phaín læûc taûi C vaì D:
B
C
D
C
a
R
R
k
k
l
δ
=
= ∆ =
2
0
2
0
B
A
B
a
M
k
P
l
δ
δ
= ⇒
−
=
∑
Âãø hãû coï cán bàòng lãûch:
0
B
δ
≠
2
2
0
3
6
2
th
a EJ
ka
P
l
c l
⇒
=
=
c
P=1
c
c
P=k
ck
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 5
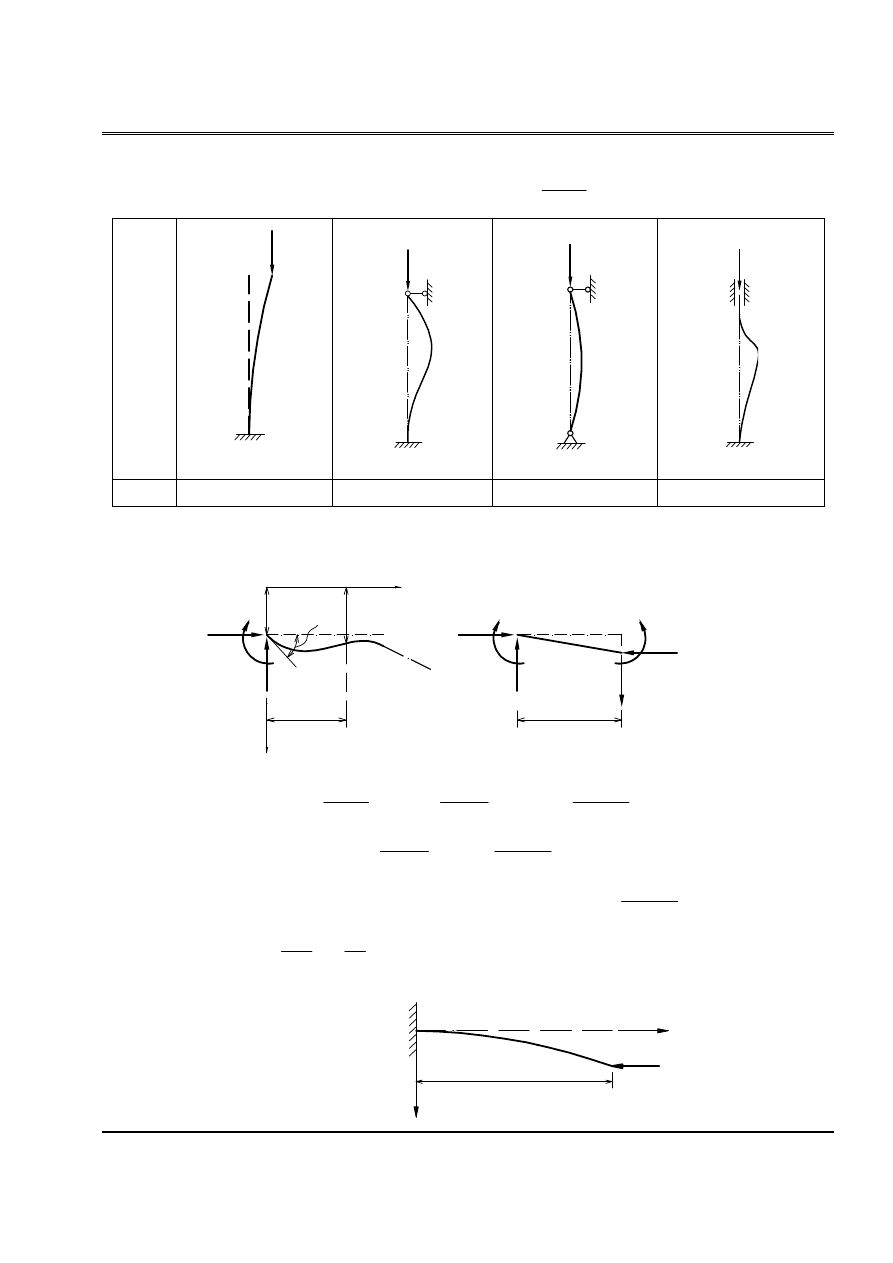
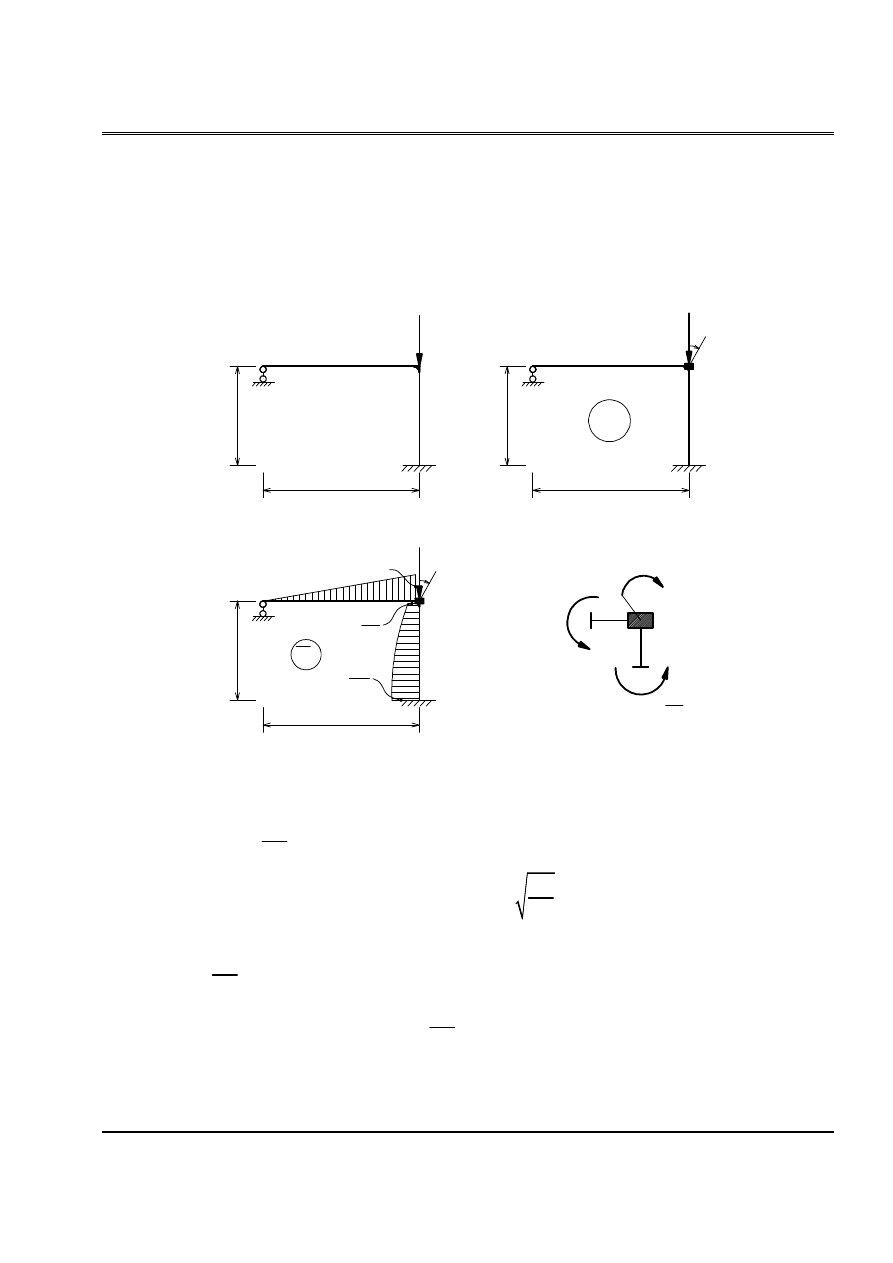
Baìi 4:
Cho hãû chëu læûc neïn P nhæ trãn hçnh (H.4). Tçm læûc tåïi haûn.
a. Phæång phaïp chênh xaïc
b. Phæång phaïp sai phán hæîu haûn (4 âoaûn)
Giaíi:
a. Phæång phaïp chênh xaïc:
Ta viãút phæång trçnh vi phán cho hai âoaûn:
Âoaûn 1:
2
l
z
l
≤ ≤
"
1
1
EJy
Py
P
δ
+
=
Âoaûn 2: 0 z l
≤ ≤
"
2
2
2EJy
Py
P
δ
+
=
Nghiãûm cuía phæång trçnh trãn coï daûng:
1
1
1
1
1
2
2
2
2
2
sin
sin
y
A
z
B cos z
y
A
z
B cos
z
α
α
δ
α
α
δ
=
+
+
=
+
+
Trong âoï:
2
2
2
2
1
2
2
1
1
;
;
2
2
P
P
EJ
EJ
α
α
α
α
=
=
=
Âiãöu kiãûn biãn:
'
2
0;
0
z
y
=
=
(1)
1
2 ;
z
l y
δ
=
=
(2)
Âiãöu kiãûn gheïp näúi giæîa hai âoaûn
'
'
1
2
;
z
l y
y
=
=
(3)
"
"
"
1
2
1
2
2
2
2
EJ
M
M
y
y
y
EJ
=
⇒
=
=
(4)
Ta coï:
'
1
1
1
1
1
1
1
"
1
'
2
2
2
2
2
2
2
"
2
sin
............
sin
............
y
A cos z
B
z
y
y
A cos
z
B
z
y
α
α
α
α
α
α
α
α
=
−
=
=
−
=
Thay vaìo (1), (2), (3), (4), ta coï:
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
1
1
1
1
1
1
2
2
2
sin
2
2
0
sin
sin
0
sin
2
0
A
l
B cos
l
A cos l
B
l
B
l
A
l
B cos l
B cos
l
α
α
α
α
α
α
α
α
α
α
α
α
α
α
+
=
−
+
=
+
−
=
Hay
2EJ
EJ
δ
P
2EJ
EJ
l
l
y
z
P
(H.4)
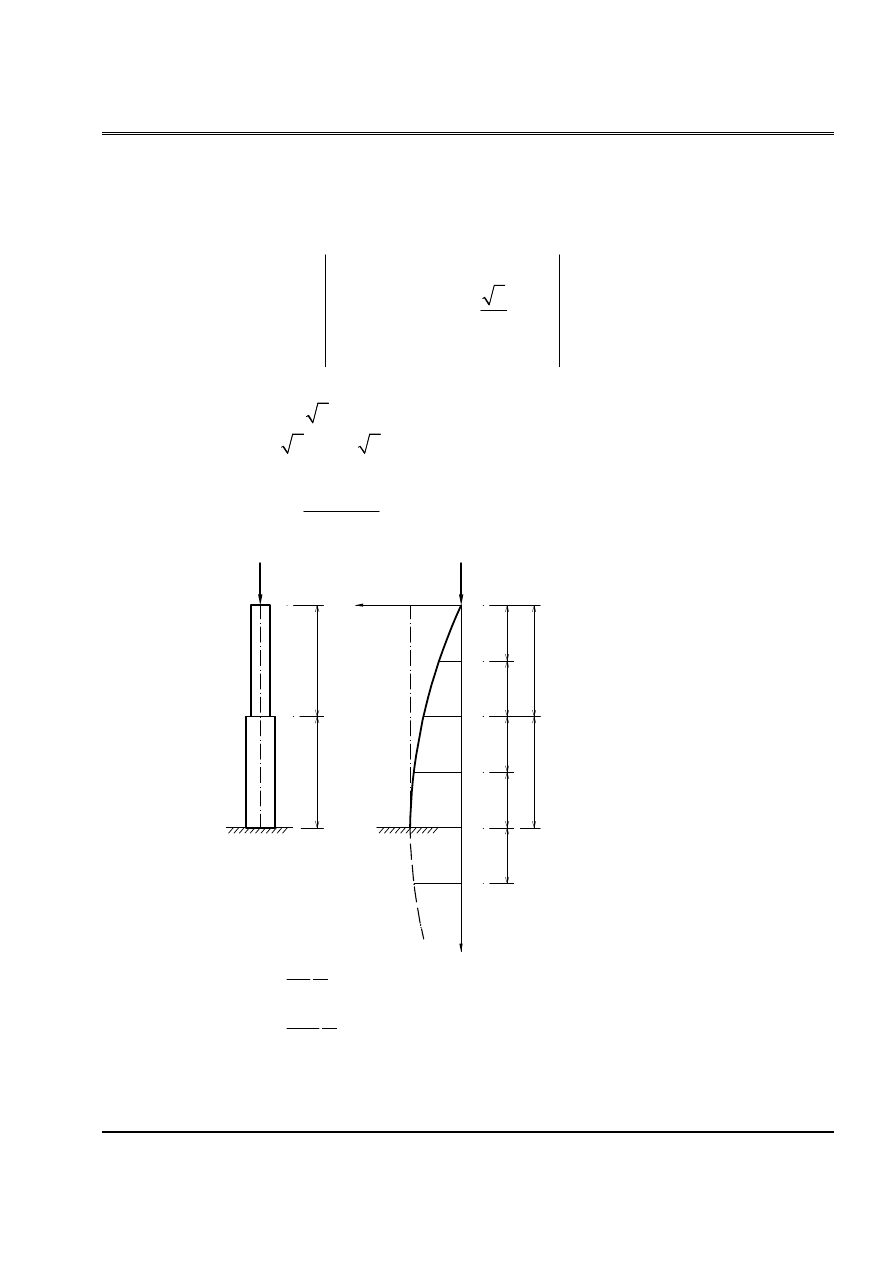
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 6
1
1
1
1
1
1
1
1
2
2
sin
2
2
0
...............
sin
0
A
l
B cos
l
A
l
B cos l
B cos
l
α
α
α
α
α
+
=
+
−
=
Âiãöu kiãûn täön taûi traûng thaïi cán bàòng lãûch:
1
1
1
1
2
1
1
2
sin
2
2
0
2
( )
sin
sin
0
2
sin
l
cos
l
D
cos l
l
l
l
cos l
cos
l
α
α
α
α
α
α
α
α
α
=
−
=
−
Âàût
2
l
α
ν
=
1
2
l
α
ν
=
2
2
tg
tg
ν ν
=
Giaíi phæång trçnh, ta coï:
2
1,0342
th
EJ
P
l
=
b. Phæång phaïp sai phán hæîu haûn (4 âoaûn)
P
2EJ
EJ
l
l
P
y
z
y
1
y
2
y
3
y
4
y
3
l/2
l/2
l/2
l/2
l/2
l
l
2
2
2
1
2
0
2
2
2
3
4
0
2
4
(*)
2
4
P l
EJ
P l
EJ
β
β
β
β
β
β
=
=
=
=
=
=
Ta coï caïc phæång trçnh sai phán:
H.4

CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 7
2
0
1
2
0
1
1
2
2
1
0
2
3
1
2
2
3
2
2
0
3
4
2
3
3
4
2
3
0
4
3
4
4
3
(2
2)
0
0
0
(
2)
0
(2
2)
0
0
(
2)
0
0
(
2)
0
(
2)
0
0
0
2
(
2)
0
(
2)
0
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
β
β
β
β
β
β
β
β
−
+
+
+
=
+
−
+
=
+
−
+
+
=
+
−
+
=
⇒
+
+
−
+
=
+
−
+
=
+
+
+
−
=
+
−
+
=
Phæång trçnh äøn âënh:
0
0
0
0
(2
2)
1
0
0
1
(2
2)
1
0
0
0
1
(
2)
1
0
0
2
(
2)
β
β
β
β
−
−
=
−
−
0
0
0
0
0
0
0
0
4
3
2
0
0
0
0
0
0
0
(2
2)
1
0
0
(2
2)
1
0
1
(2
2)
1
0
(2
2)
1
(
2)
1
0
1
(
2)
1
0
2
(
2)
0
0
2
(
2)
1
0
0
1 1
(
2)
1
4
24
41
22
2
0
0,1132
0
2
(
2)
β
β
β
β
β
β
β
β
β
β
β
β
β
β
β
−
−
−
=
−
−
−
−
−
−
−
=
−
+
−
+ = ⇒
=
−
Thay vaìo (*), ta coï:
2
2
0,1132
0,906
2
4
th
P l
EJ
P
EJ
l
=
⇒
=
:
Baìi 5: Cho hãû chëu læûc neïn P nhæ trãn hçnh (H.5).
Mämen quaïn tênh thay âäøi theo quy luáût
0
2
4 (
)
z l
z
J
J
l
−
=
Tçm læûc tåïi haûn theo:
c. Phæång phaïp sai phán hæîu haûn (4 âoaûn)

CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 8
Giaíi:
c. Phæång phaïp sai phán hæîu haûn (4 âoaûn)
Ta coï:
0
4
0
y
y
=
=
1
3
y
y
=
1
0
0
2
4. (
)
3
4
4.
4
l
l l
J
J
J
l
−
=
=
2
2
1
1
2
2
2
0
..........
16
16
P l
EJ
P l
A
EJ
β
β
=
=
=
=
Caïc phæång trçnh sai phán hæîu haûn:
2
0
1
1
2
2
1
2
2
3
2
1
1
2
2
1
2
2
1
2
1
2
(
2)
0
(
2)
0
(
2)
0
2
(
2)
0
4
(
2)
0
3
2
(
2)
0
y
y
y
y
y
y
y
y
y
y
A
y
y
y
A
y
β
β
β
β
+
−
+
=
+
−
+
=
−
+
=
⇒
+
−
=
−
+
=
⇒
+
−
=
Phæång trçnh äøn âënh:
1
2
2
4
0,5
(
2)
1
0
2
7
3
0
3
3
2
(
2)
A
A
A
A
A
A
=
−
= ⇒
−
+ = ⇒
=
−
Våïi
0
1
2
8
0, 5
th
EJ
A
P
l
=
⇒
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 9
CHÆÅNG III: ÄØN ÂËNH CAÏC THANH THÀÓNG
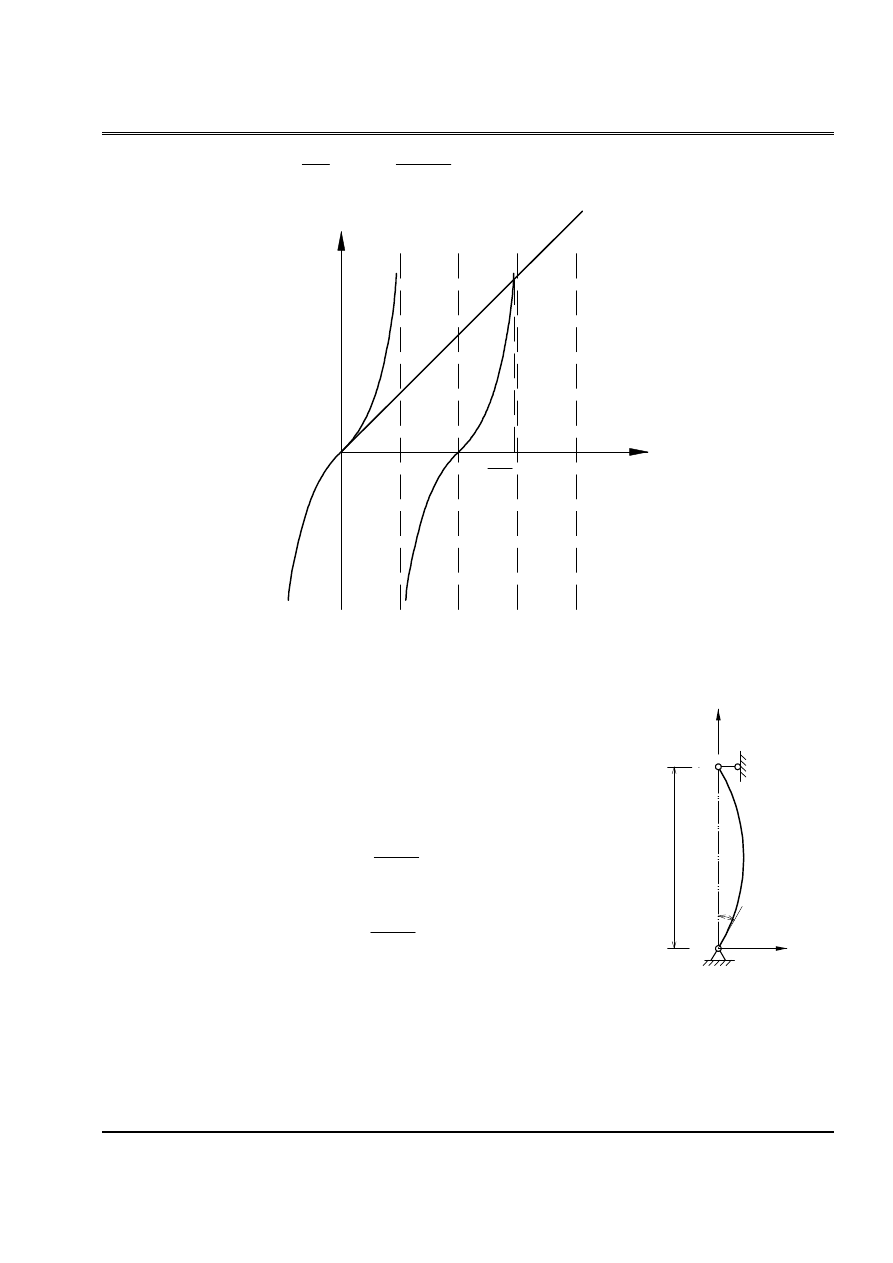
Baìi 7:
Chæïng minh caïc cäng thæïc sau
2
2
(
)
th
EJ
P
l
π
µ
=
Så
âä
ö tha
nh
P
P
P
P
µ
2
0,7
1
0,5
Âãø chæïng minh caïc cäng thæïc naìy thç ta cáön aïp duûng caïc cäng thæïc thäng säú ban
âáöu sau:
0
z
y
y
y
(
0
)
P
Q*
(0)
M
(0)
y'
(
0
)
z
P
Q*(z)
M
dz
0
Q*(z)+dQ*(z)
P
M+dM
a)
b)
2
3
0
0
0
0
y'( )
M ( )
Q* ( )
y( z )
y( )
sin z
(1-cos z)-
( z
sin z)
EJ
EJ
α
α
α
α
α
α
α
=
+
−
−
(1)
2
0
0
0
1
M ( )
Q* ( )
y'( z )
y'( )cos z
sin z
(
cos z )
EJ
EJ
α
α
α
α
α
=
−
−
−
(2)
0
0
0
Q* ( )
M ( z )
EJy"( z )
EJy'( ) sin z
M ( )cos z
sin z
α
α
α
α
α
= −
=
+
+
(3)
* ( )
dM
dy
Q
z
P
dz
dz
=
−
(4)
a. Så âäö 1:
y
Z
l
P

CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 10
Âäúi våïi træåìng håüp naìy, caïc thäng säú ban âáöu coï giaï trë nhæ sau:
(0)
?
'(0)
?
(0)
0
* (0)
0
y
y
M
Q
=
=
=
=
Âiãöu kiãûn åí âáöu b:
( )
0
'( )
0
y l
y l
=
=
Ta coï:
2
2
'(0)
( )
0
(0)
sin
0
0
'( )
0
2
'(0)
0
(2 )
th
th
y
y l
y
l
cos l
l
y l
y
cos l
EJ
P
l
α
π
α
α
α
α
π
=
+
=
⇒
⇒
= ⇒
=
=
=
⇒
=
b. Så âäö 2:
P
Z
y
Âäúi våïi træåìng håüp naìy, caïc thäng säú ban âáöu coï giaï trë nhæ sau:
(0)
0
'(0)
0
y
y
=
=
Âiãöu kiãûn biãn åí âáöu b
( )
0
( )
0
y l
M l
=
=
Ta coï:
2
3
(0)
* (0)
(1 cos
)+
(
sin
)=0
( )
0
( )
0
* (0)
(0)
0
(0)(1- cos
)+ *(0)(
sin l)=0
(0)
*(0)
0
M
Q
l
l
l
y l
EJ
EJ
M l
Q
M
cos l
sin l
M
l
Q
l
M
cos l
Q
Sin l
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
−
−
=
⇒
=
+
=
−
⇒
+
=
Hãû coï cán bàòng lãûch tæïc phaíi täön taûi ...
Phæång trçnh äøn âënh:
...
Giaíi phæång trçnh naìy ..., ta coï:
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 11
2
2
0, 7
(0,7 )
th
EJ
l
P
l
π
π
α
=
⇒
=
y
ν
0
π/2
π
3π/2
2π
y
=
tg
ν
y
=ν
10π
7
y
=
tg
ν
c. Så âäö 3:
Âäúi våïi træåìng håüp naìy, caïc thäng säú ban âáöu coï giaï trë nhæ sau:
(0)
0
'(0)
?
(0)
0
* (0)
0
y
y
M
Q
=
=
=
=
Do âoï, tæì phæång trçnh täøng quaït (3-5):
0
y'( )
y( z )
sin z
α
α
=
Theo âiãöu kiãûn biãn, khi z = l thç y(l) = 0, ta coï :
0
0
y'( )
y( l )
sin l
α
α
=
=
Âiãöu kiãûn naìy thoía maîn våïi hai khaí nàng:
0
0
0
y'( )
sin l
α
=
=
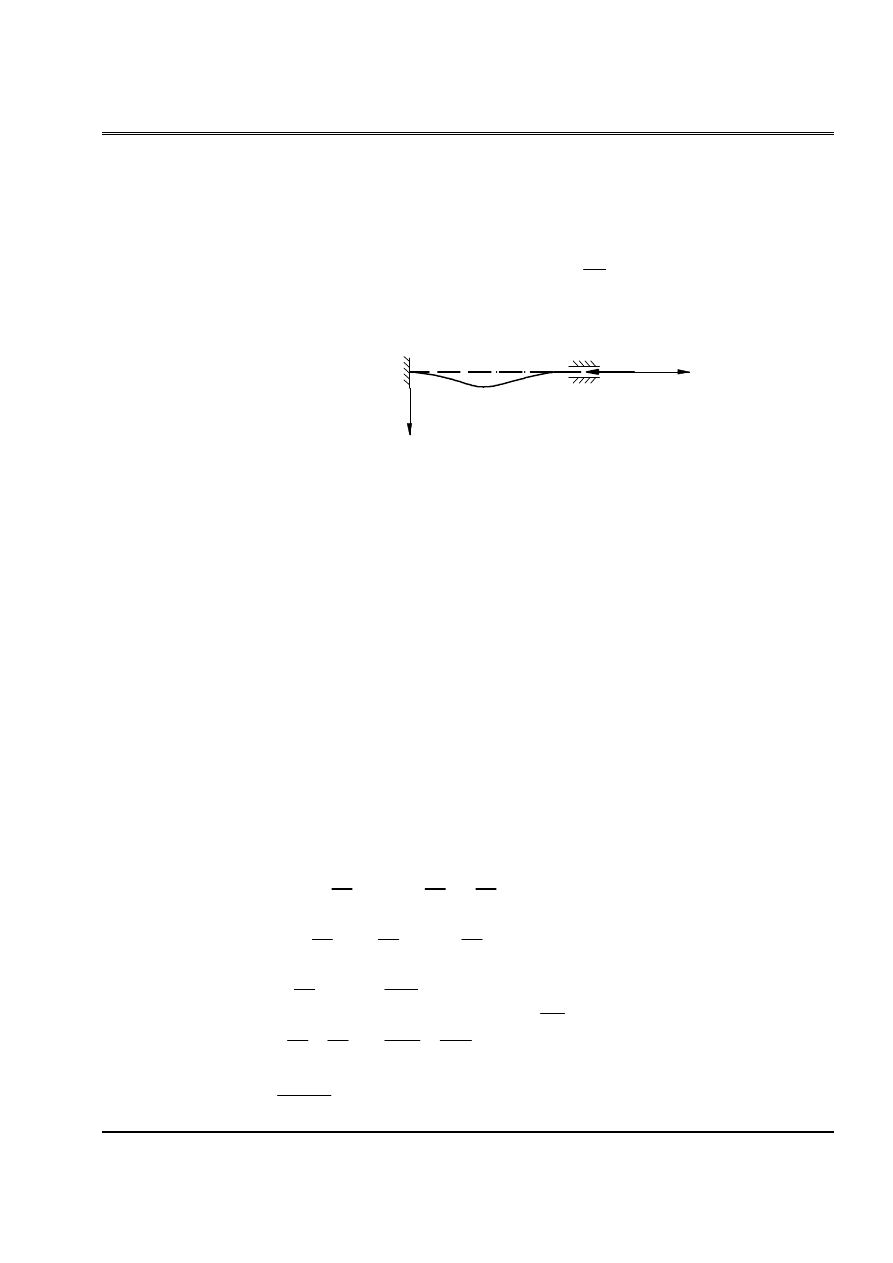
a) Nãúu y’(0) = 0 thç y(z) ≡ 0, tæïc thanh váùn thàóng chæa máút äøn âënh.
z
l
0
y
y'(
0
)
Hçnh 3-2
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 12
b) Muäún P âaût tåïi giaï trë tåïi haûn æïng våïi traûng thaïi máút äøn âënh, thç trong
hãû phaíi täön taûi mäüt traûng thaïi cán bàòng khaïc våïi traûng thaïi cán bàòng ban âáöu, tæïc
y’(0) ≠ 0. Vç váûy, âiãöu kiãûn âãø âaût âæåüc traûng thaïi cán bàòng lãûch laì:
sinαl = 0
⇒
αl = kπ (k =1, 2, ...)
Taíi troüng tåïi haûn nhoí nháút æïng våïi k =1
⇒
2
1
2
th
P
EJ
l
π
=
d. Så âäö 4:
P
Z
y
Âäúi våïi træåìng håüp naìy, caïc thäng säú ban âáöu coï giaï trë nhæ sau:
(0)
0
'(0)
0
(0)
?
* (0)
?
y
y
M
Q
=
=
=
=
Âiãöu kiãûn åí âáöu b:
( )
0
....
'( )
0
(0)(1-cos l)+ * (0)(
sin l)
0
(0) sin
* (0)(1
)
0
y l
y l
M
Q
l
M
l
Q
cos l
α
α
α
α
α
α
α
=
⇒
=
−
=
⇒
+
−
=
Hãû coï cán bàòng lãûch tæïc phaíi täön taûi (0), *(0)
M
Q
Phæång trçnh äøn âënh:
2
2
2
(1-cos
)(1-cos
)-sin
(
sin
)
0
1 2
sin
sin
0
2(1
)
sin
0
4sin
2
sin
0
2
2
2
sin
(2sin
)
0
2
2
2
l
l
l
l
l
cos l
cos
l
l
l
l
cos l
l
l
l
l
l
l
cos
l
l
l
lcos
α
α
α α
α
α
α
α α
α
α
α
α
α
α
α
α
α
α
α
α
−
=
⇒ −
+
+
−
=
⇒
−
−
=
⇒
−
=
⇒
−
=
1
2
2
2
sin
0
2
2
2
10
2
7
2
2
(0,5 )
th
th
th
th
l
l
l
l
l
l
tg
EJ
P
l
α
α
π
π
α
α
π
α
α
π
=
=
⇒
⇒
⇒
=
=
=
=
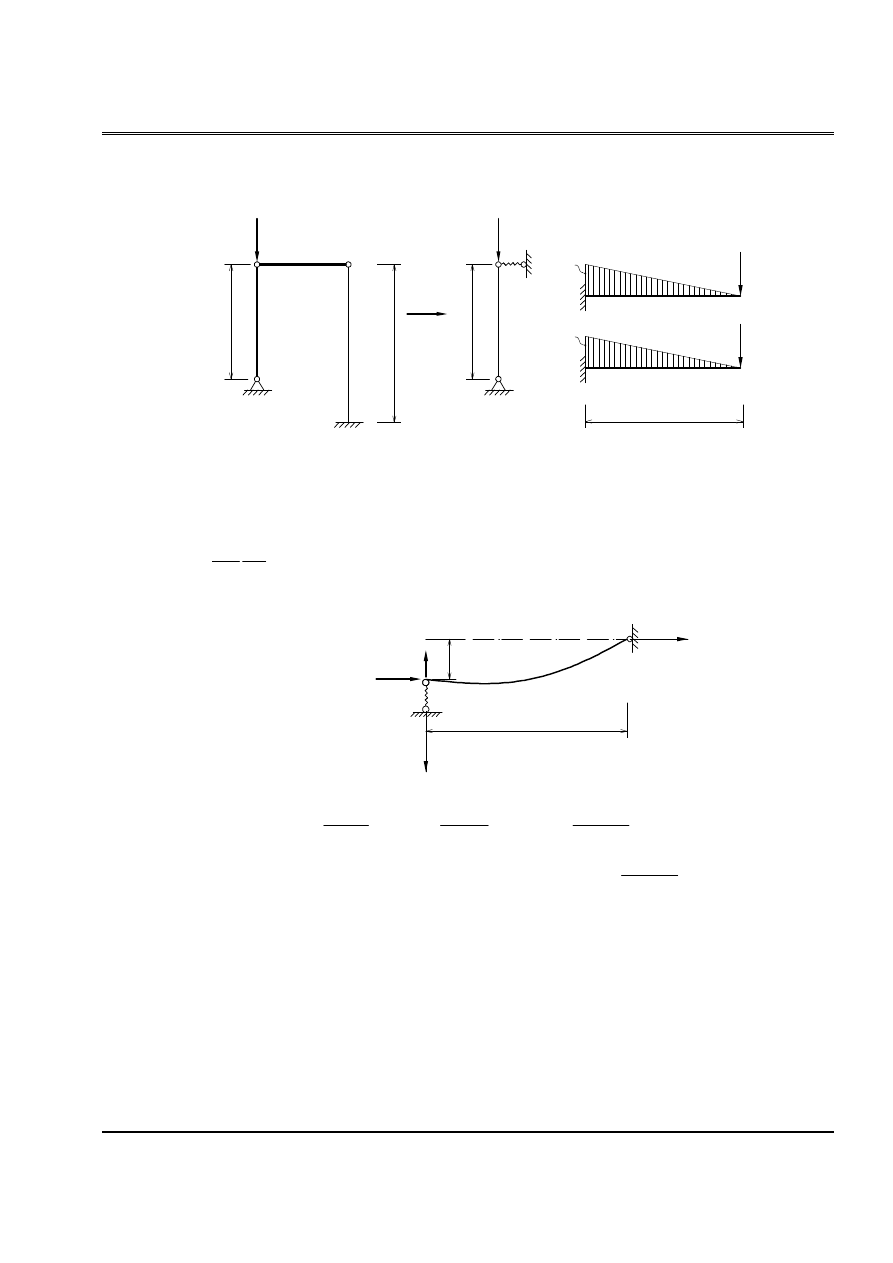
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 13
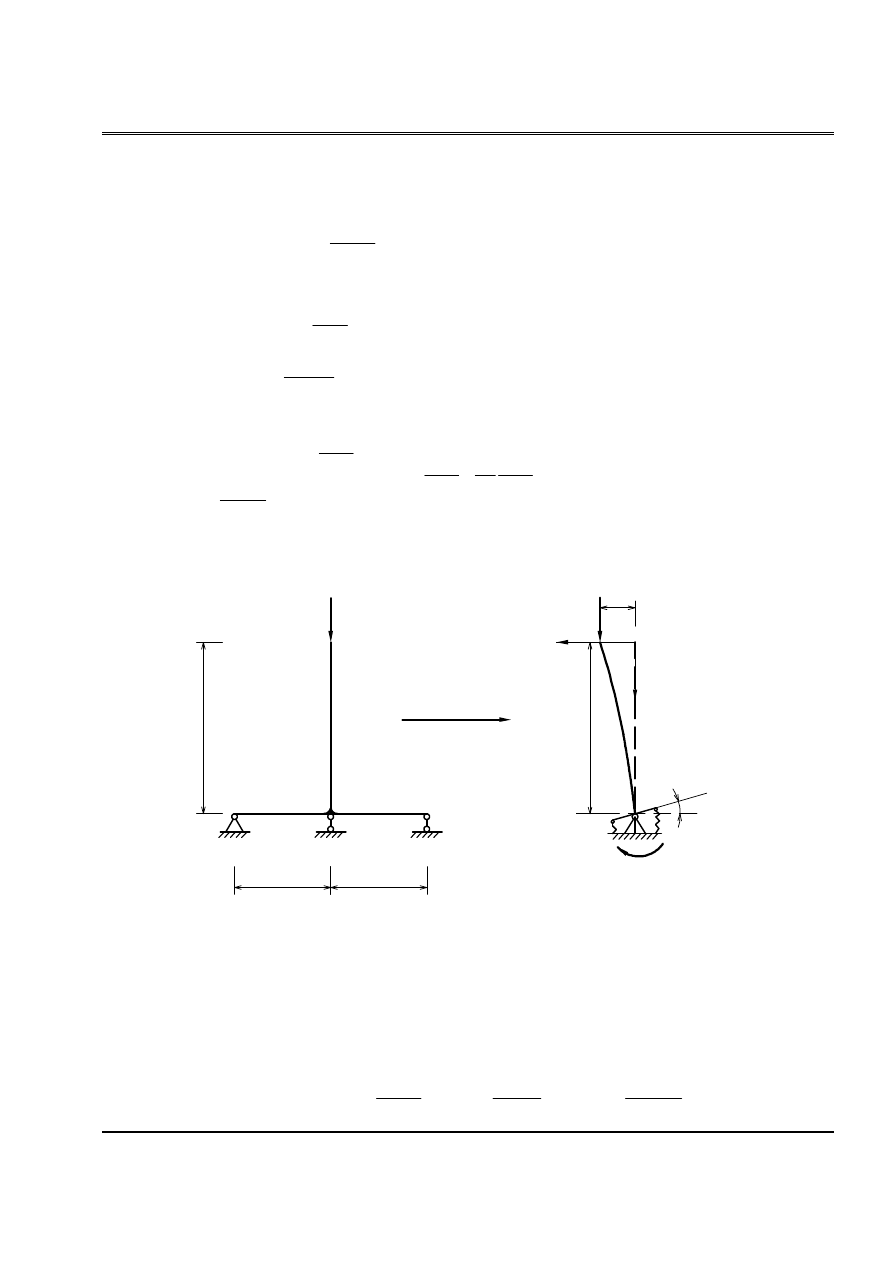
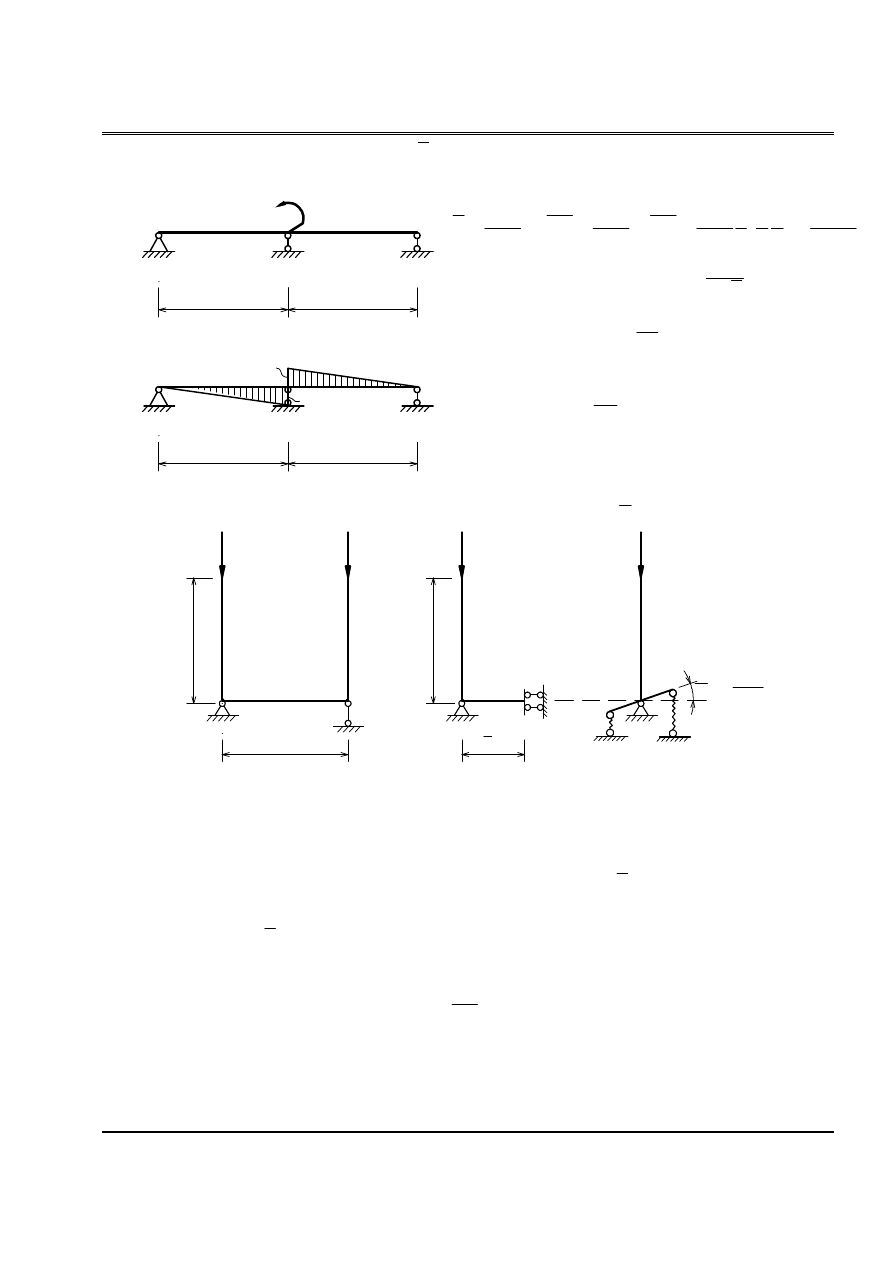
Baìi 8: Cho hãû nhæ hçnh veî (H.7). Tçm så âäö tênh vaì láûp phæång trçnh äøn âënh.
P
l
EA=
∞
EJ
EJ
1
l
1
P
l
EJ
k
k
EJ
1
l
1
P=1
l
1
EJ
1
P=k
kl
1
(H.7)
Thay taïc dung thanh âæïng bãn phaíi vaì thanh ngang thaình gäúi âaìn häöi. Hãû säú âaìn
häöi laì k (læûc phaït sinh khi chuyãøn vë bàòng 1 âån vë).
Xaïc âënh k bàòng phæång phaïp nhán biãøu âäö, cho chuyãøn vë âáöu console =1âvë.
2
1
1
1
... 1
...
2
kl
k
EJ
= ⇒ =
* Láûp phæång trçnh äøn âënh:
P
y
Z
l
Q(0)=ky
0
k
y
0
Ta coï:
2
3
0
0
0
0
y'( )
M ( )
Q* ( )
y( z )
y( )
sin z
(1-cos z)-
( z
sin z)
EJ
EJ
α
α
α
α
α
α
α
=
+
−
−
0
0
0
Q* ( )
M ( z )
EJy"( z )
EJy'( ) sin z
M ( )cos z
Sin z
α
α
α
α
α
= −
=
+
+
Caïc âiãöu kiãûn ban âáöu baìi toaïn:
Âáöu traïi:
'
(0)
?
(0)
?
(0)
0
(0)
(0)
y
y
M
Q
ky
=
=
=
=
Âáöu phaíi:
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 14
( )
0
( )
0
y l
M l
=
=
Thay âiãöu kiãûn biãn vaìo:
0
0
0
0
0
0
0
0
0
0
y'( )
y( l )
y( )
sin l
...( l
sin l)=0
M ( l )
EJy'( )sin l
...Sin l
sin
y( )...
y'( )
k sin
y( )
EJSin y'( )
α
α
α
α
α
α
α
ν
α
ν α
ν
α
=
+
−
−
=
+
=
−
=
⇒
+
=
(
l
ν α
=
)
Phæång trçnh äøn âënh:
3
sin
...
sin
sin
0
0
sin
...
k
EJ
k
ν
ν α
ν
α
ν
ν
α
−
= ⇒ −
+
=
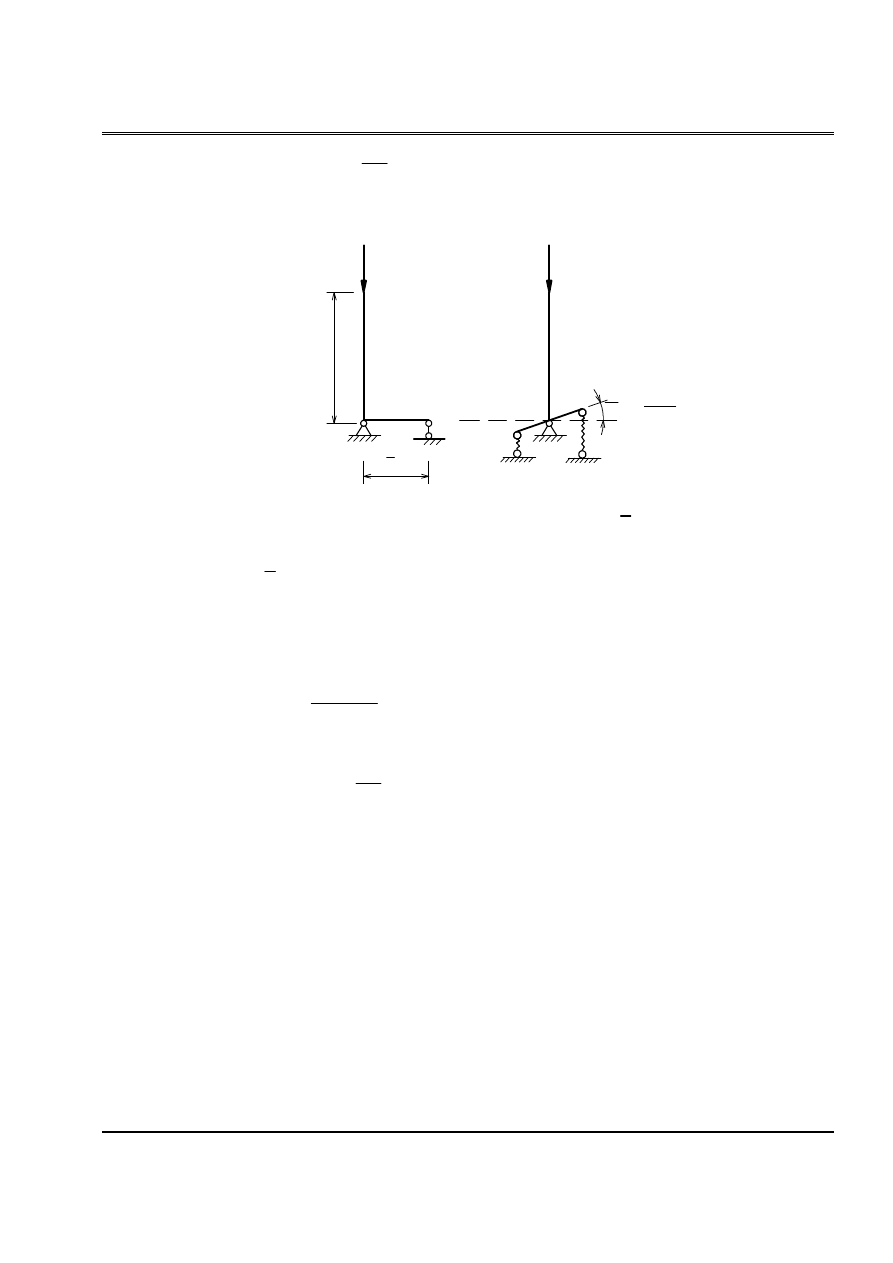
Baìi 9: Cho hãû nhæ hçnh veî (H.8). Tçm så âäö tênh vaì láûp phæång trçnh äøn âënh.
a. Caïc thäng säú ban âáöu:
(0)
?
'(0)
?
(0)
0
* (0)
0
y
y
M
Q
=
=
=
=
Ta coï:
2
3
0
0
0
0
y'( )
M ( )
Q* ( )
y( z )
y( )
sin z
(1-cos z)-
( z
sin z)
EJ
EJ
α
α
α
α
α
α
α
=
+
−
−
(3-5)
l
EJ
l/2
l/2
P
2EJ
2EJ
P
Z
l
y(
0
)
y
0
Py
(0)
ϕ
Thay gäúi
âaìn häöi
H.8
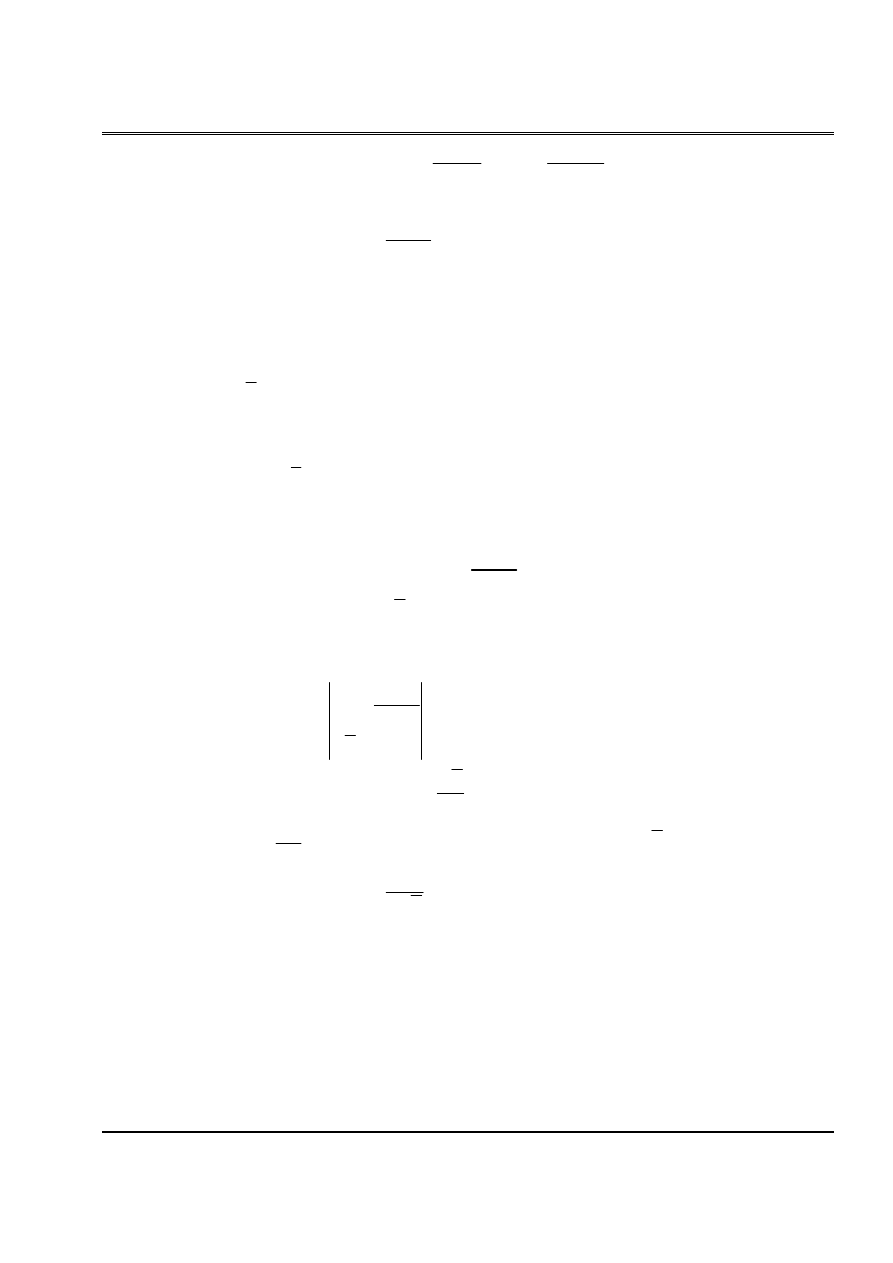
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 15
2
0
0
0
1
M ( )
Q* ( )
y'( z )
y'( )cos z
sin z
(
cos z )
EJ
EJ
α
α
α
α
α
=
−
−
−
Thay caïc thäng säú ban âáöu vaìo:
0
0
0
y'( )
y( z )
y( )
sin z
y'( z )
y'( )cos z
α
α
α
=
+
=
b. Caïc âiãöu kiãûn biãn:
( )
0
'( )
y l
y l
ϕ
=
=
Goüi ϕ - hãû säú âaìn häöi cuía liãn kãút (tæïc laì goïc xoay cuía ngaìm âaìn häöi do mämen
bàòng âån vë gáy ra), thç trong træåìng håüp naìy, vç mämen taûi ngaìm âaìn häöi bàòng
(0)
Py
−
,
cho nãn:
(0)
Py
ϕ
ϕ
= −
(chiãöu mämen ngæåüc chiãöu chuyãøn vë)
Dæûa vaìo âiãöu kiãûn biãn, ta láûp âæåüc hãû phæång trçnh âaûi säú tuyãún tênh thuáön nháút
âãø xaïc âënh y(0) vaì y’(0):
Ta coï:
0
0
0
0
0
0
0
sin l
y( )
y'( )
y( l )
y'( l )
P .y( ) (cos l )y'( )
α
α
ϕ
ϕ
α
+
=
=
⇒
=
+
=
c. Tæì âiãöu kiãûn täön taûi traûng thaïi cán bàòng lãûch so våïi traûng thaïi cán bàòng ban âáöu,
tæïc y(0)
≠
0, y’(0)
≠
0, ta âæåüc phæång trçnh äøn âënh:
1
0
0
sin l
D(
)
P
cos l
P
D(
)
cos l
sin l
α
α
α
ϕ
α
ϕ
α
α
α
α
=
=
=
−
=
Vç
2
2
0
P
P
EJ
D(
)
cos l (sin l ). EJ
EJ
α
α
α
α
α α ϕ
=
⇒ =
⇒
=
−
=
l
hay l.tg l
EJ
α
α
ϕ
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 16
Trong baìi toaïn naìy, ϕ âæåüc xaïc âënh nhæ sau:
Baìi 10:
Tçm læûc tåïi haûn cho khung hçnh (H.9), våïi
2
1
2
3
l
l
=
P
A
B
A
A
ϕ
Α
=
3EJ
l
1
l
1
EJ
1
l
2
EJ
1
EJ
2
P
P
l
1
EJ
1
1
2l
2
P
(H.9)
(Træåìng håüp biãún daûng âäúi xæïng)
1. Træåìng håüp hãû biãún daûng âäúi xæïng: âæa hãû vãö tênh næía hãû nhæ hçnh veî.
Taûi A, thay bàòng liãn kãút âaìn häöi.
AC mäüt âáöu khåïp, mäüt âáöu ngaìm træåüt nãn goïc xoay
ϕ
do mämen bàòng âån vë
gáy ra laì:
...
ϕ
=
Baìi toaïn âaî giaíi våïi phæång trçnh âàûc træng:
1
1
. (
)
...
l tg
l
α
α
=
våïi
2
P
EJ
α
=
Hay:
1
1
. (
)
3
( )
3
l tg
l
tg
α
α
ν ν
= ⇒
=
våïi
1
l
ν α
=
Giaíi phæång trçnh ta coï:
1,1922
ν
=
l/2
l/2
2EJ
2EJ
M=1
l/2
l/2
1/2
1/2
1
1
2
2 1
.
.
(
)
2
2
2
8 3 2
24
k
k
l
l
M M
M
EJ
EJ
EJ
EJ
ϕ
=
=
Ω
=
=
Thay vaìo phæång trçnh
l
l.tg l
EJ
α
α
ϕ
=
ta coï:
24
24
l.tg l
cotg
ν
α
α
ν
=
⇒
=
Giaíi phæång trçnh naìy bàòng âäö thë hoàûc giaíi têch:
2
1, 5
2,3
th
th
EJ
P
l
ν
=
⇒
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 17
2
1
1, 4213
dx
th
EJ
P
l
=
2. Træåìng håüp hãû biãún daûng phaín xæïng: âæa hãû vãö tênh næía hãû nhæ hçnh veî.
P
A
A
ϕ
Α
=
9EJ
l
1
l
1
EJ
1
1
2
l
2
P
Taûi A, thay bàòng liãn kãút âaìn häöi.
AC mäüt âáöu khåïp, mäüt âáöu gäúi di âäüng nãn goïc xoay ϕ do mämen bàòng âån vë
gáy ra laì:
...
ϕ
=
Phæång trçnh âàûc træng
1
1
. (
)
...
l tg
l
α
α
=
Hay: .
9
tg
ν ν
=
, giaíi phæång trçnh, ta coï:
1, 414
ν
=
2
1
1,999
px
th
EJ
P
l
=
So saïnh hai læûc tåïi haûn, ta coï:
2
1
1, 4213
th
EJ
P
l
=
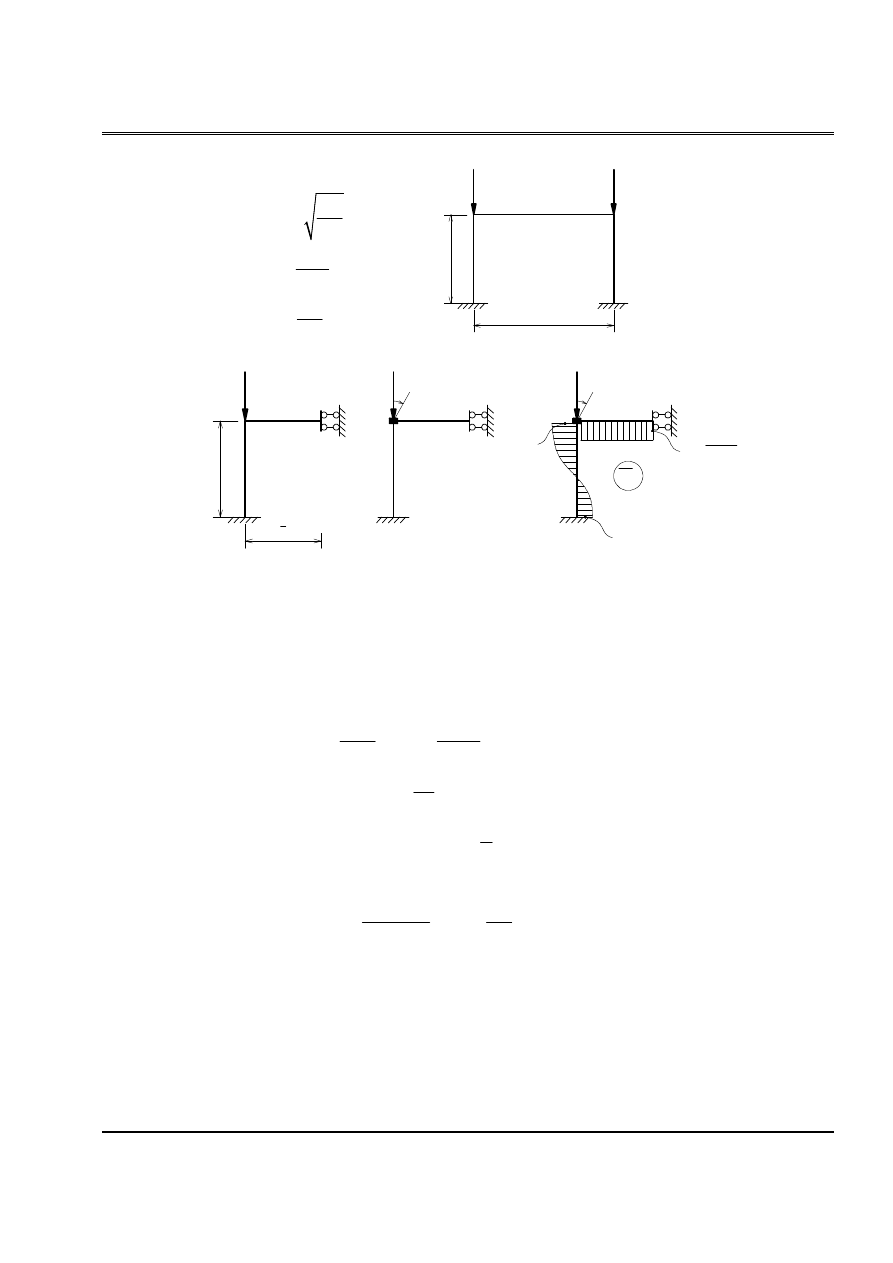
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 18
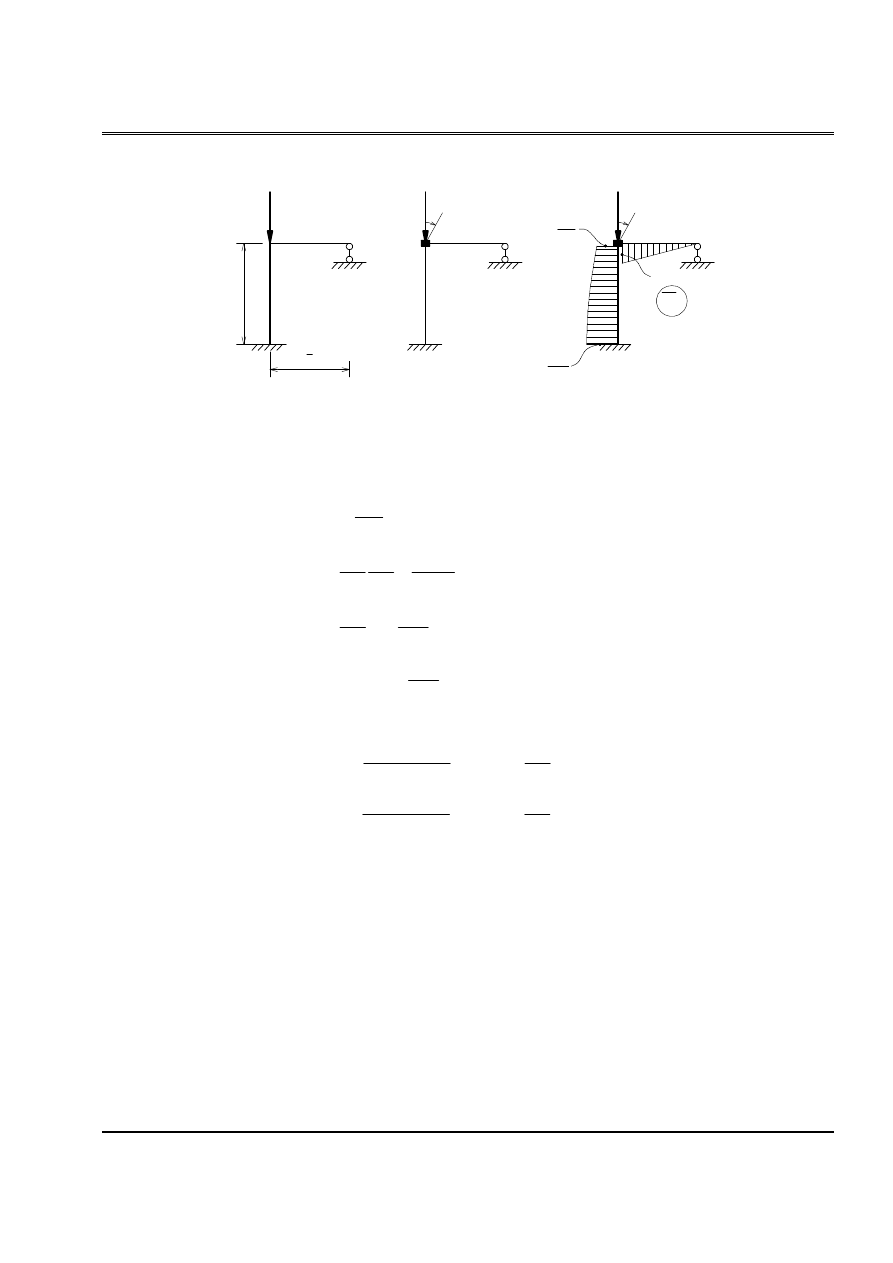
Baìi 11:
Thiãút láûp phæång trçnh äøn âënh cho khung vaì tçm læûc tåïi haûn træåìng håüp.
2,
2
k
l
h
=
=
P
h
EJ
ν
=
n
kEJ
i
l
=
d
EJ
i
l
=
1. Træåìng håüp biãún daûng âäúi xæïng ta âæa vãö tênh næía hãû:
P
1
h
l
2
J
P
1
Z
1
HCB
P
1
Z
1
=1
M
1
4i
d
ϕ
2
(
ν
)
i'
n
=
2i
d
ϕ
3
(
ν
)
2kEJ
l
Phæång trçnh chênh tàõc:
11
1
0
r Z
=
Phæång trçnh äøn âënh:
11
'
2
2
2
0
4
( )
0
4
2
( )
0
( )
2
d
n
r
i
i
EJ
kEJ
h
l
kh
l
ϕ ν
ϕ ν
ϕ ν
=
⇒
+ =
⇒
+
=
⇒
= −
Våïi
2
1
2,
2 ;
( )
2
k
l
h
ϕ ν
=
=
= −
Tra baíng
5,02
ν
=
2
2
2
5,02
25, 2
dx
th
EJ
EJ
P
h
h
=
=
P
1
P
2
h
l
kJ
J
J
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 19
2. Træåìng håüp biãún daûng phaín xæïng, ta âæa vãö tênh næía hãû;
P
1
h
l
2
J
P
1
Z
1
HCB
P
1
Z
1
=1
M
1
i
d
ν
3i'
n
tg
ν
i
d
ν
sin
ν
Phæång trçnh chênh tàõc:
11
1
0
r Z
=
Phæång trçnh äøn âënh:
11
'
0
3
0
6
0
6
d
n
r
i
i
tg
EJ v
kEJ
h tgv
l
v
kh
tgv
l
ν
ν
=
⇒
+
=
⇒
+
=
⇒
= −
Våïi
2,
2 ;
6
tg
k
l
h
ν
ν
=
=
= −
Tra baíng:
2,7163
ν
=
2
2
2
2,7163
7,3783
px
th
EJ
EJ
P
h
h
=
=
So saïnh choün:
2
2
2
2,7163
7,3783
th
EJ
EJ
P
h
h
=
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 20
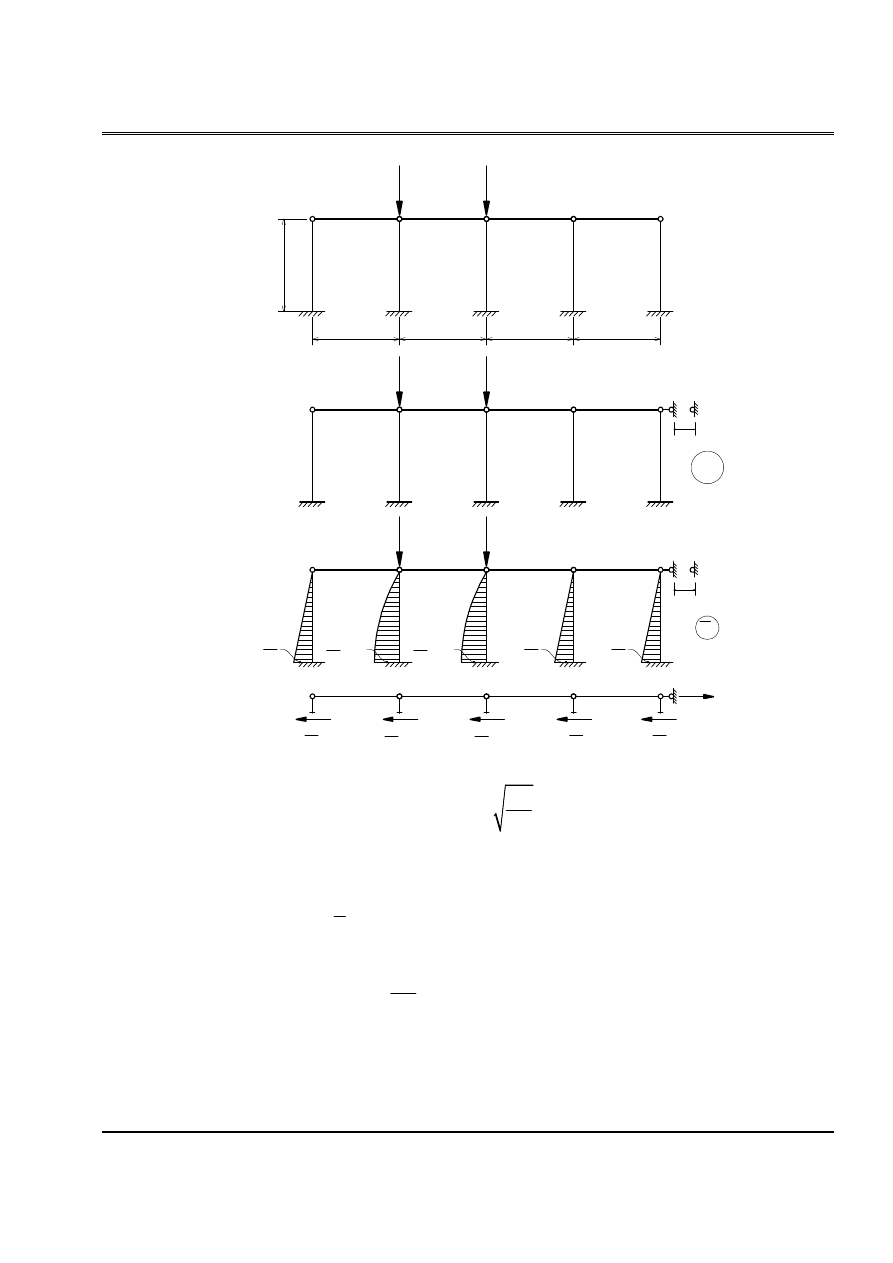
Baìi 12:
Tçm læûc tåïi haûn cho hãû:
P
h
l
l
l
l
P
r
11
3
EJ
h
3
EJ
h
3
3
EJ
h
3
ϕ
1
(
ν
)
3
EJ
3
ϕ
1
(
ν
)
h
3
3
EJ
h
2
ϕ
1
(
ν
)
3
EJ
h
3
P
P
Z
1
EF=
∞
J
J
J
J
J
EF=
∞
EF=
∞
EF=
∞
HCB
P
P
Z
1
=1
M
1
3
EJ
h
2
3
EJ
h
2
3
EJ
h
2
3
EJ
h
2
ϕ
1
(
ν
)
P
v
h
EJ
=
Phæång trçnh äøn âënh
11
1
...
3
( )
1,5
2
r
v
η
=
= − = −
Tra baíng ta coï:
2, 4521
ν
=
2
...
6,0128
th
EJ
P
h
= =
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 21
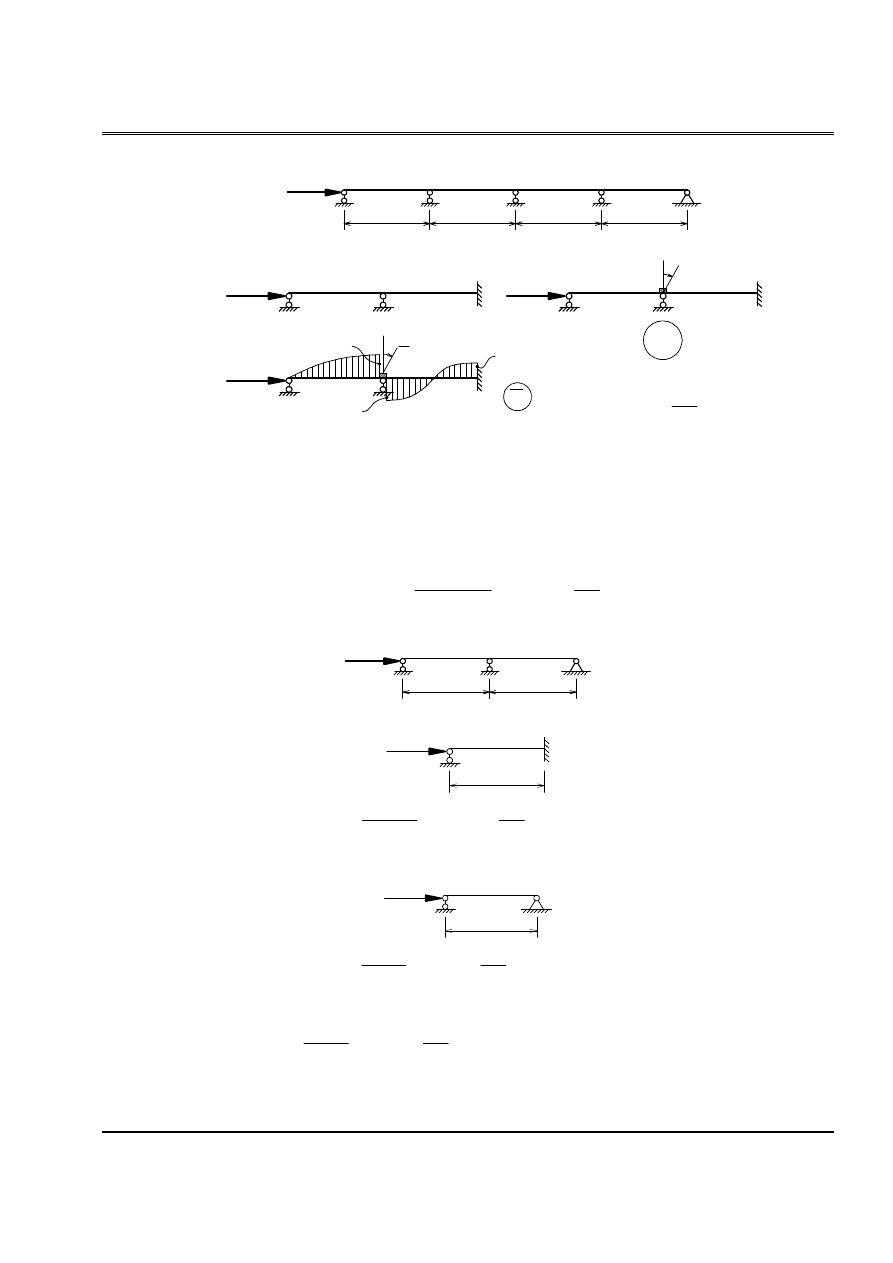
Baìi 13:
Tçm læûc tåïi haûn træåìng håüp.
l
P
EJ=const
l
l
l
1. Træåìng håüp biãún daûng âäúi xæïng ta âæa vãö tênh næía hãû:
P
P
Z
1
HCB
P
3i
ϕ
1
(
ν
)
4i
ϕ
2
(
ν
)
2i
ϕ
3
(
ν
)
Z
1
=1
M
1
Phæång trçnh äøn âënh:
11
1
2
1
2
0
3
( )
4
( )
0
3 ( )
4
( )
0
r
i
v
i
v
v
v
ϕ
ϕ
ϕ
ϕ
=
⇒
+
=
⇒
+
=
Thæí dáön ta âæåüc
3,575
ν
=
2
2
2
3,575
12,7806
dx
th
EJ
EJ
P
l
l
=
=
2. Træåìng håüp biãún daûng phaín xæïng, ta âæa vãö tênh næía hãû;
P
l
l
a, Hãû biãún daûng âäúi xæïng:
P
l
EJ
2
2
2
2
20,1421
(0,7 )
th
EJ
EJ
P
l
l
π
=
=
b, Hãû biãún daûng phaín xæïng:
P
l
EJ
2
3
2
2
9,8696
th
EJ
EJ
P
l
l
π
=
=
So saïnhæûc tåïi haûn, ta choün:
2
2
2
9,8696
th
EJ
EJ
P
l
l
π
=
=
Våïi
EJ
i
l
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 22
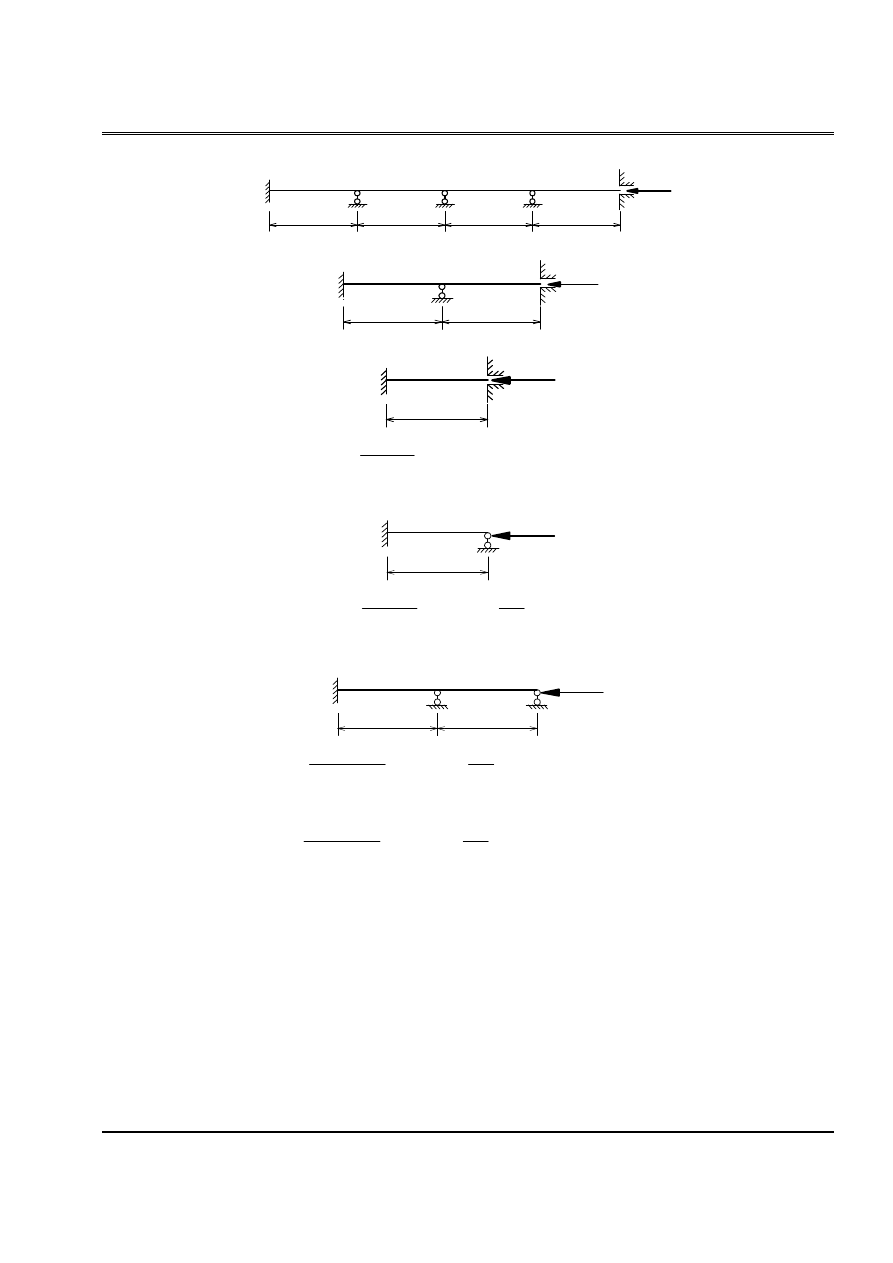
Baìi 14:
Tçm læûc tåïi haûn cho hãû.
P
l
l
l
l
EJ=const
1. Træåìng håüp biãún daûng âäúi xæïng ta âæa vãö tênh næía hãû:
P
l
l
a, Hãû biãún daûng âäúi xæïng:
P
l
EJ
2
1
2
39, 4784
(0,5 )
th
EJ
P
l
π
=
=
b, Hãû biãún daûng phaín xæïng:
P
l
EJ
2
2
2
2
20,1421
(0, 7 )
th
EJ
EJ
P
l
l
π
=
=
2. Træåìng håüp biãún daûng phaín xæïng, ta âæa vãö tênh næía hãû;
P
l
l
EJ=const
2
3
2
2
3,575
12,7806
th
EJ
EJ
P
l
l
=
=
So saïnh 3 læûc tåïi haûn ta choün:
2
2
2
3,575
12,7806
th
EJ
EJ
P
l
l
=
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 23
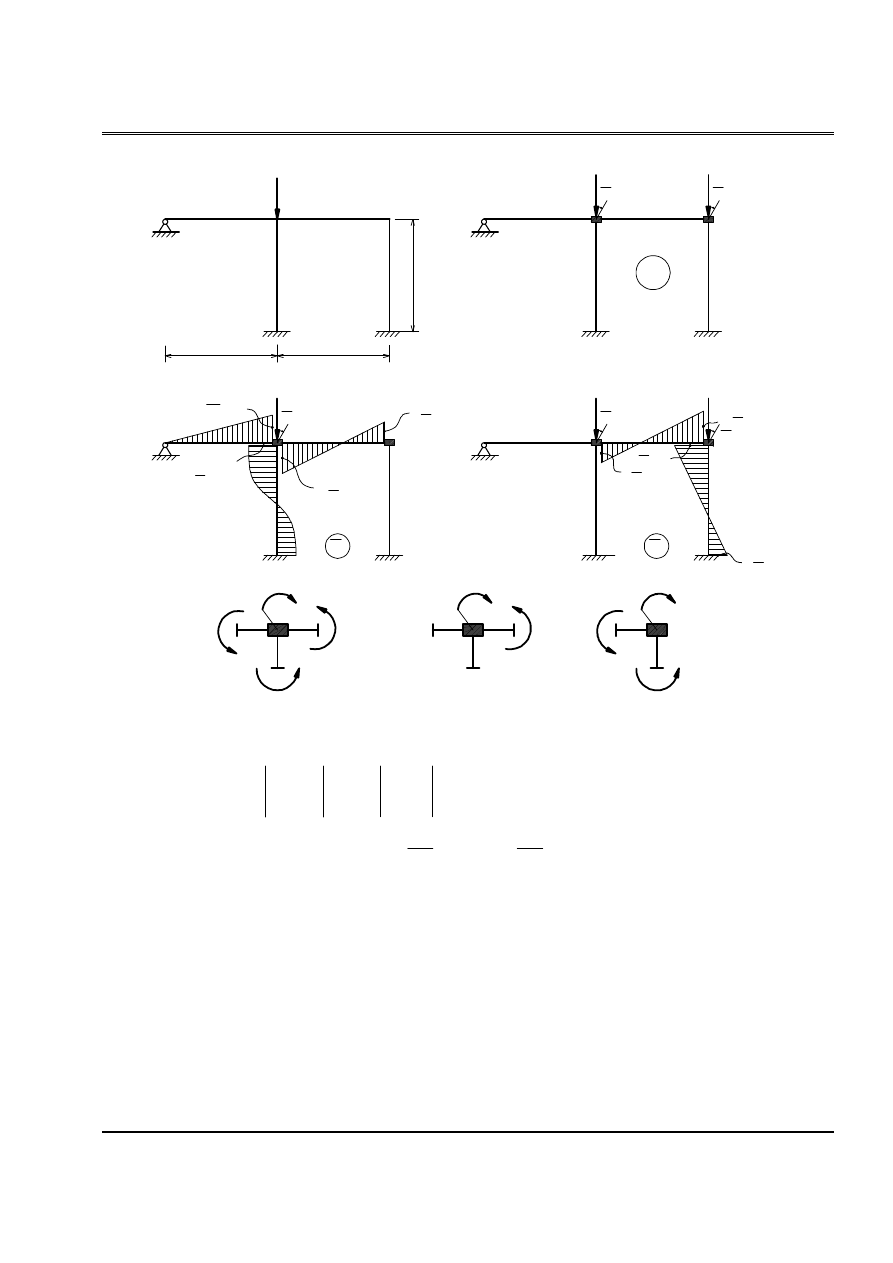
Baìi 15:
Tçm læûc tåïi haûn cho hãû.
P
Z
1
=1
M
2
4(
EJ
l
)=4i
2(
EJ
l
)=2i
P
Z
1
=1
P
Z
2
=1
HCB
4(
EJ
l
)=4i
2(
EJ
l
)=2i
P
Z
2
=1
r
12
2i
P
EJ=const
l
l
l
P
Z
1
=1
M
1
r
11
4i
3i
r
22
4i
3( EJ
l
)=3i
4(
EJ
l
)=4i
4(
EJ
l
)
= 4i
ϕ
2
(
ν
)
ϕ
2
(
ν
)
2(
EJ
l
)=2i
4i
ϕ
2
(
ν
)
4i
11
2
12
21
22
7
4
( );
2 ;
8
r
i
i
v
r
r
i r
i
ϕ
= +
=
=
=
Phæång trçnh äøn âënh:
11
12
2
21
22
2
2
...
2
0
0
( )
...
1, 625
2
...
...
...
30,9804
th
r
r
i
v
r
r
i
EJ
EJ
v
P
l
l
ϕ
= ⇒
= ⇒
= = −
⇒ = ⇒
=
=
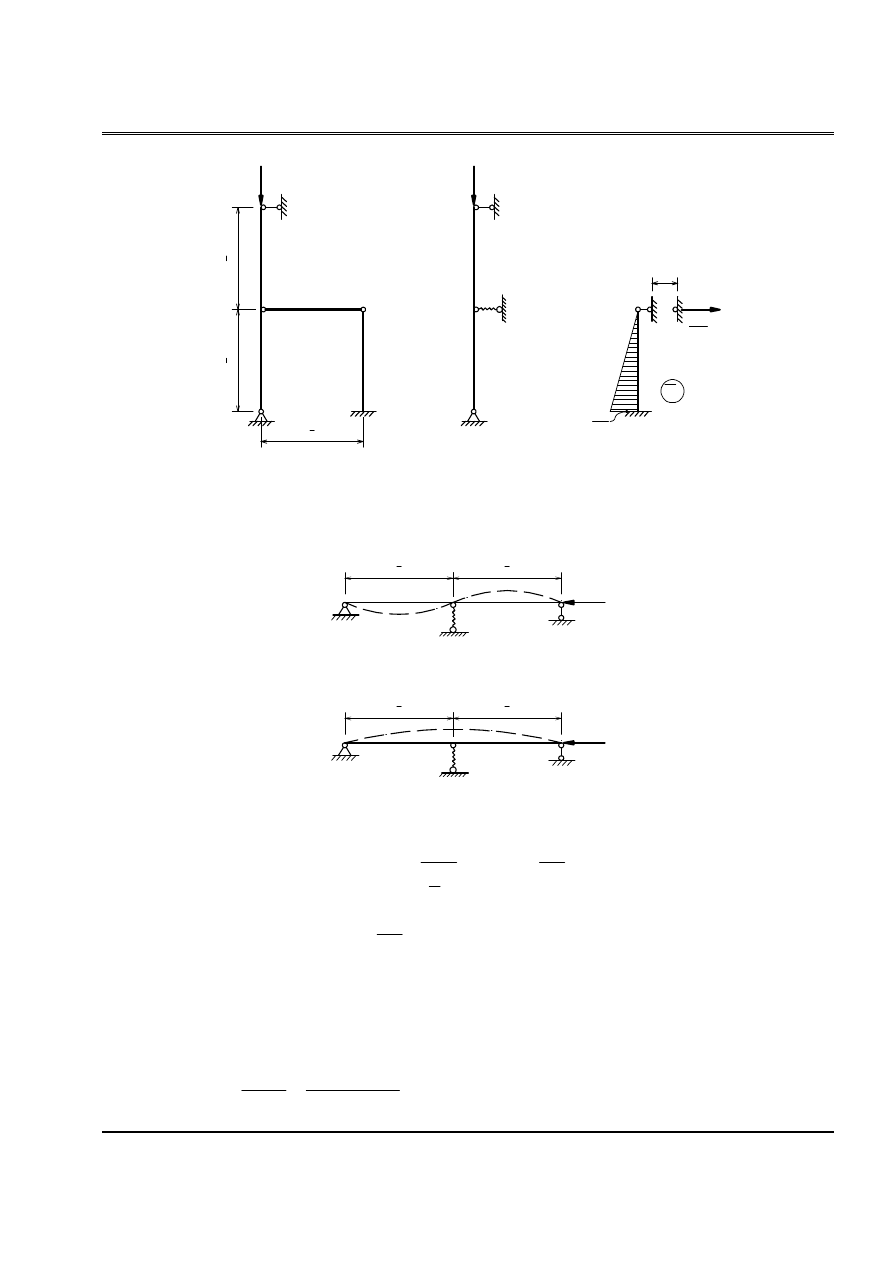
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 24
Baìi 16: Tçm læûc tåïi haûn cho hãû
12i
l
2
6
i
l
M
∆
P
l 2
EA=
∞
EJ
EJ
EJ
l 2
l
2
P
EJ
EJ
k
∆
=1
Ta âæa vãö tênh dáöm liãn tuûc våïi gäúi trung gian âaìn häöi.
...
k
=
(giaíi bàòng caïch nhán biãøu âäö)
a. Træåìng håüp máút äøn âënh daûng phaín xæïng:
P
l
2
EJ
EJ
l
2
k
...
px
th
P
=
b. Træåìng håüp máút äøn âënh daûng âäúi xæïng:
P
l
2
EJ
EJ
l
2
k
1
2
2
2
( )
...
0,5
1,9161
1,9161
14,6858
( )
2
dx
th
v
v
EJ
EJ
P
l
l
η
= = −
=
=
=
So saïnh choün:
2
...
th
EJ
P
l
=
4
4
4
4
6
1,344.200
31,5371
.0,7.10 .1
l
EJ
β
γ
π
π
=
=
=
CAÏC BAÌI TÁÛP COÏ HÆÅÏNG DÁÙN
Âaì Nàông 2007
Trang 25
Baìi 19: Tçm læûc tåïi haûn cho caïc hãû sau:
a. Khi
1
2
;
EJ
EJ
EJ
h
l
=
=
=
b. Khi
1
EJ
= ∞
c. Khi
1
0
EJ
=
Giaíi:
a. Khi
1
2
;
EJ
EJ
EJ
h
l
=
=
=
EJ
2
P
h
l
EJ
1
EJ
2
Z
1
P
h
l
Z
1
=1
i
2
ν
tg
ν
i
2
ν
sin
ν
3i
1
HCB
M
1
r
11
3i
1
i
2
ν
tg
ν
P
h
l
EJ
1
(Thanh âæïng, âáöu trãn nhæ laì liãn kãút ngaìm træåüt)
Ta coï: Phæång trçnh äøn âënh:
11
1
2
0
3
0
r
v
i
i
tgv
=
+
=
Våïi âiãöu kiãûn baìi toaïn thç:
1
2
;
;
P
i
i
v
h
EJ
α
α
=
=
=
Do âoï phæång trçnh äøn âënh tråí thaình:
3
v
tgv
= −
Giaíi ta âæåüc:
2
2, 46
6,05
th
EJ
v
P
h
=
⇒
=
b. Khi
1
EJ
= ∞
: thanh âæïng khäng thãø xoay nhæng coï thãø chuyãøn vë thàóng, nãn
så âäö tênh nhæ hçnh H.19b
Wyszukiwarka
Podobne podstrony:
ĐHBK Tài Liệu Hướng Dẫn Thiết Kế Thiết Bị Điện Tử Công Suất Trần Văn Thịnh, 122 Trang
BCVT Bài Tập Tiếng Anh Chuyên Ngành Điện Từ Viễn Thông Ths Nguyễn Quỳnh Giao, 86 Trang
ĐHĐL Giáo Trình Điện Tử Căn Bản Phan Văn Nghĩa, 177 Trang
Hướng Dẫn Lập Và Quản Lý Chi Phí Đầu Tư Xây Dựng Công Trình Bộ Xây Dựng, 46 Trang
Hướng Dẫn Cấu Hình Các Chức Năng Cơ Bản Của Cisco Router Nhiều Tác Giả, 94 Trang
Quy Phạm Trang Bị Điện 4 Bảo Vệ Và Tự Động
Bài Tập Lớn Sức Bền Vật Liệu Triệu Tuấn Anh, 11 Trang
Bài Tập Lớn Cơ Học Kết Cấu F1 Đại Học Gtvt
Giáo Trình Bảo Trì Máy Tính Và Cài Đặt Phần Mềm Nhiều Tác Giả, 68 Trang
Nghiên cứu sự làm việc đồng thời móng băng, bè cọc và nền đất Ks Phan Huy Đông
Bài Giảng Quang Điện Tử Và Quang Điện Ts Nguyễn Văn Cường, 56 Trang
ĐHĐN Giáo Trình Quy Hoạch Đô Thị 2 Ths Tô Văn Hùng & Phan Hữu Bách, 28 Trang
Bài Tập Lập Trình C Lương Trần Hy Hiền, 18 Trang
Cơ Học Lý Thuyết (Tóm Tắt Lý Thuyết & Bài Tập Mẫu) Trịnh Anh Ngọc, 71 Trang
Bài Tập Lớn Thủy Văn Công Trình Phạm Văn Hôi, 26 Trang
ĐHCN Giáo Trình Lý Thuyết Trường Điện Từ Võ Xuân Ân, 108 Trang
ĐHĐN Giáo Trình Quy Hoạch Đô Thị 1 Ths Tô Văn Hùng & Phan Hữu Bách, 71 Trang
ĐHMO Thực Hành Điện Tử Tương Tự Ks Nguyễn Phúc Ân, 38 Trang
więcej podobnych podstron